An Analytical Model for the Effect of Vertical Wind Veer on Wind Turbine Wakes
Abstract
1. Introduction
2. Large-Eddy Simulation Framework
2.1. LES Governing Equations
2.2. Numerical Setup
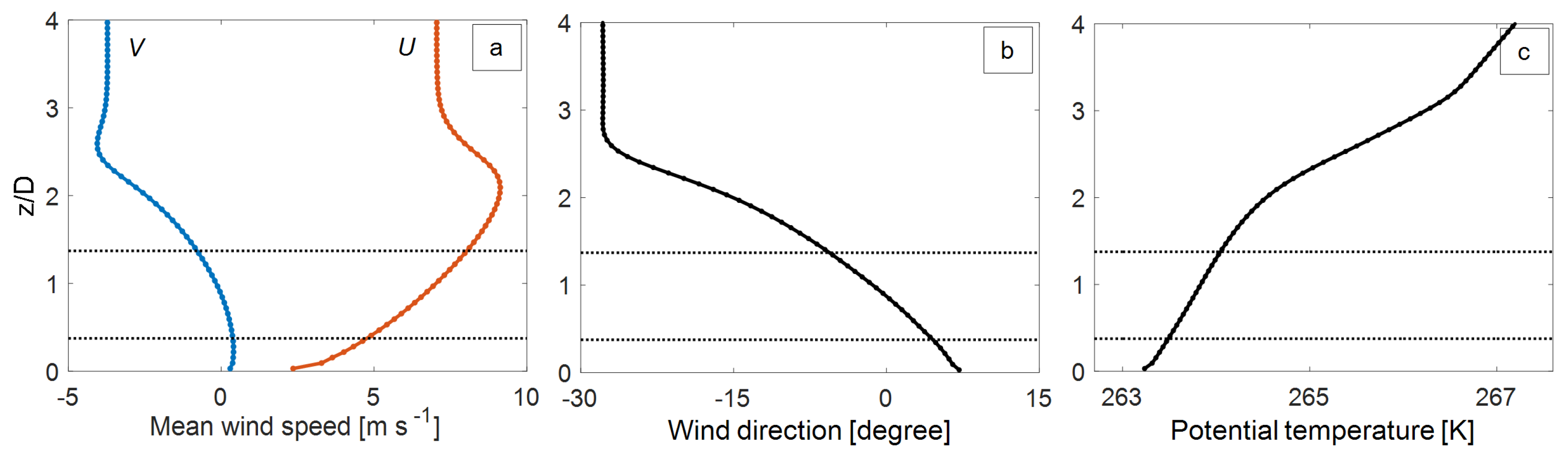
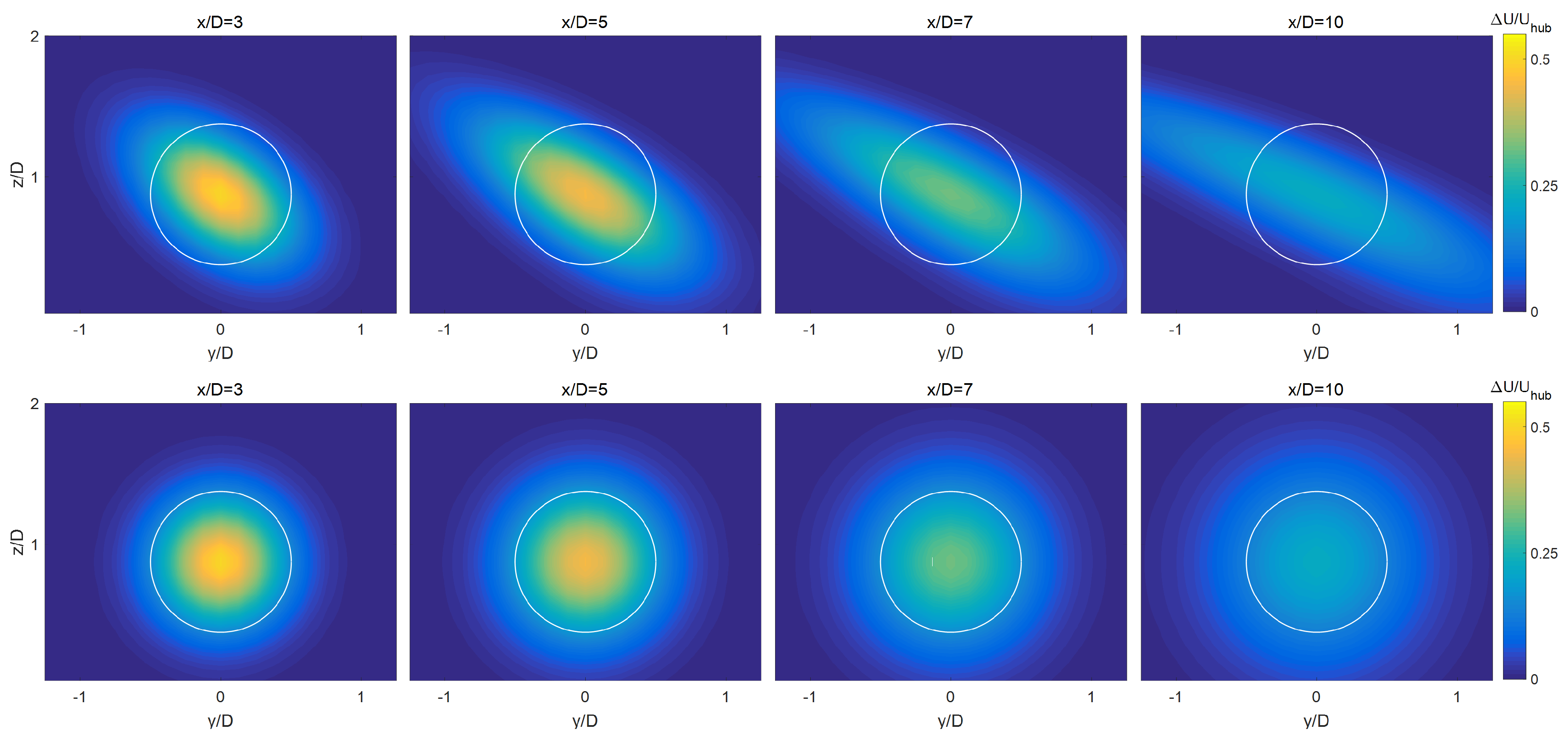
2.3. LES Results
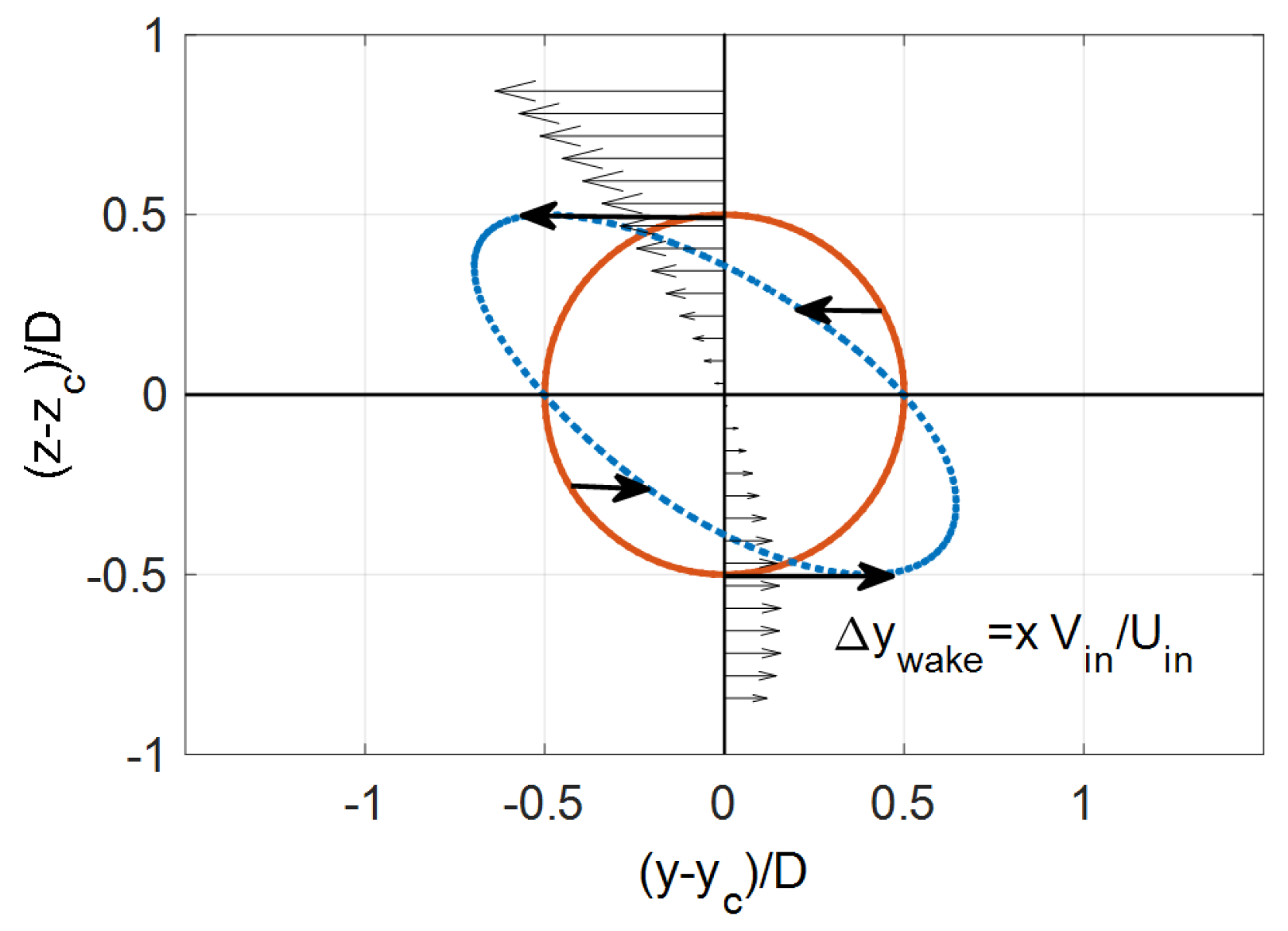
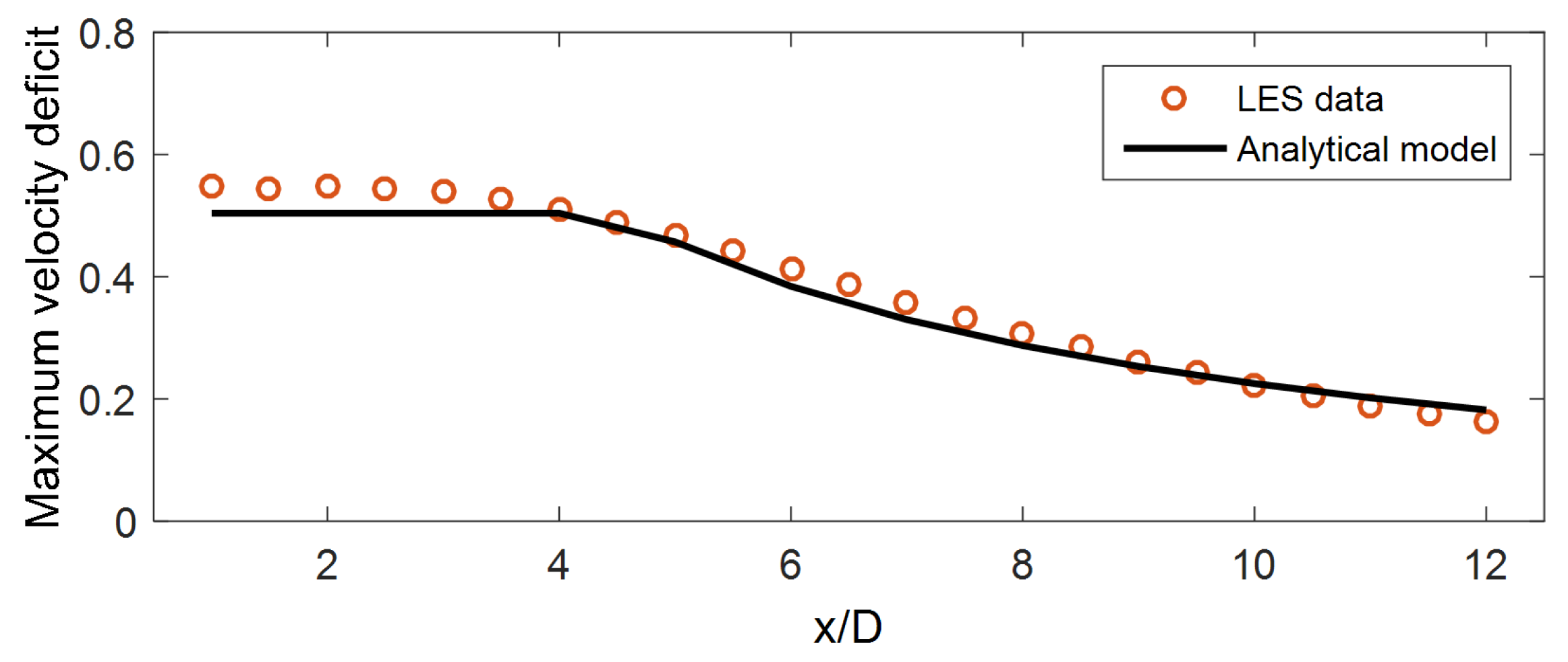
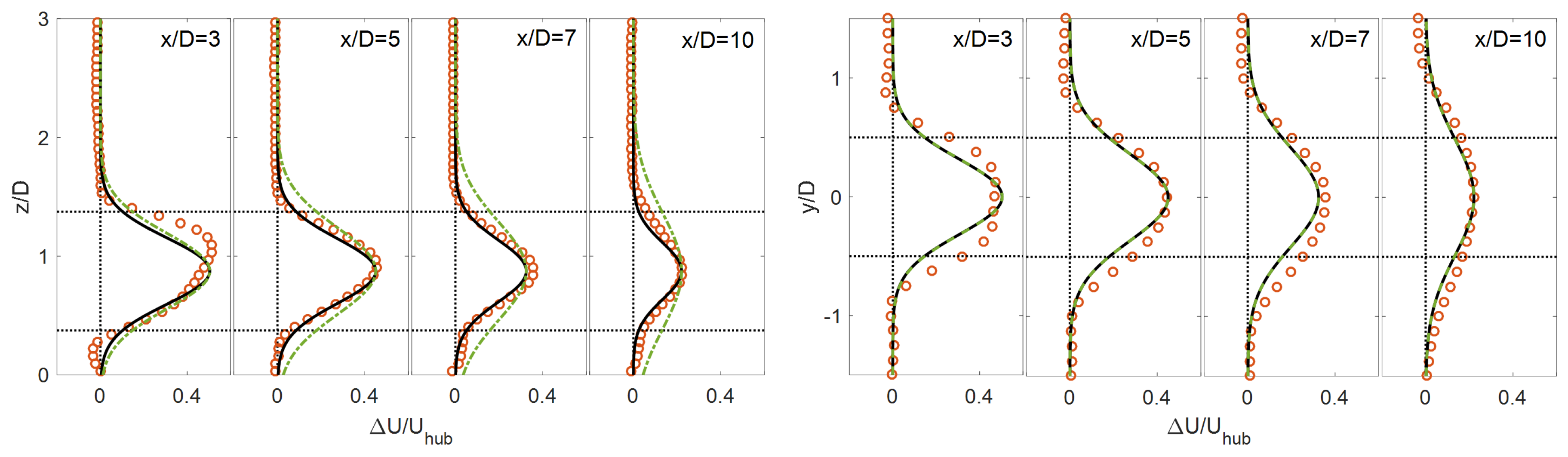
3. Analytical Wake Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Magnusson, M.; Smedman, A.S. Influence of atmospheric stability on wind turbine wakes. Wind Eng. 1994, 18, 139–152. [Google Scholar]
- Lu, H.; Porté-Agel, F. Large-eddy simulation of a very large wind farm in a stable atmospheric boundary layer. Phys. Fluids 2011, 23, 065101. [Google Scholar] [CrossRef]
- Mirocha, J.D.; Rajewski, D.A.; Marjanovic, N.; Lundquist, J.K.; Kosović, B.; Draxl, C.; Churchfield, M.J. Investigating wind turbine impacts on near-wake flow using profiling lidar data and large-eddy simulations with an actuator disk model. J. Renew. Sustain. Energy 2015, 7, 043143. [Google Scholar] [CrossRef]
- Bhaganagar, K.; Debnath, M. The effects of mean atmospheric forcings of the stable atmospheric boundary layer on wind turbine wake. J. Renew. Sustain. Energy 2015, 7, 013124. [Google Scholar] [CrossRef]
- Vollmer, L.; van Dooren, M.; Trabucchi, D.; Schneemann, J.; Steinfeld, G.; Witha, B.; Trujillo, J.; Kühn, M. First comparison of LES of an offshore wind turbine wake with dual-Doppler lidar measurements in a German offshore wind farm. J. Phys. Conf. Ser. 2015, 625, 012001. [Google Scholar] [CrossRef]
- Lundquist, J.; Churchfield, M.; Lee, S.; Clifton, A. Quantifying error of lidar and sodar Doppler beam swinging measurements of wind turbine wakes using computational fluid dynamics. Atmos. Meas. Tech. 2015, 8, 907–920. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Influence of the Coriolis force on the structure and evolution of wind turbine wakes. Phys. Rev. Fluids 2016, 1, 063701. [Google Scholar] [CrossRef]
- Bromm, M.; Vollmer, L.; Kühn, M. Numerical investigation of wind turbine wake development in directionally sheared inflow. Wind Energy 2017, 20, 381–395. [Google Scholar] [CrossRef]
- Howland, M.F.; Ghate, A.S.; Lele, S.K. Influence of the horizontal component of Earth’s rotation on wind turbine wakes. J. Phys. Conf. Ser. 2018, 1037, 072003. [Google Scholar] [CrossRef]
- Abkar, M.; Sharifi, A.; Porté-Agel, F. Wake flow in a wind farm during a diurnal cycle. J. Turbul. 2016, 17, 420–441. [Google Scholar] [CrossRef]
- Allaerts, D.; Meyers, J. Effect of inversion-layer height and Coriolis forces on developing wind-farm boundary layers. In Proceedings of the 34th Wind Energy Symposium, San Diego, CA, USA, 4–8 January 2016; p. 1989. [Google Scholar]
- van der Laan, M.P.; Sørensen, N.N. Why the Coriolis force turns a wind farm wake clockwise in the Northern Hemisphere. Wind Energy Sci. 2017, 2, 285. [Google Scholar] [CrossRef]
- Xie, S.; Archer, C.L. A Numerical Study of Wind-Turbine Wakes for Three Atmospheric Stability Conditions. Bound. Lay. Meteorol. 2017, 165, 87–112. [Google Scholar] [CrossRef]
- Jensen, N. A Note on Wind Turbine Interaction; Technical Report Ris–M–2411; Roskilde National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renew. Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
- Niayifar, A.; Porté-Agel, F. Analytical modeling of wind farms: A new approach for power prediction. Energies 2016, 9, 741. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Simulation of Turbulent Flow Inside and Above Wind Farms: Model Validation and Layout Effects. Bound. Lay. Meteorol. 2013, 146, 181–205. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. The Effect of Free-Atmosphere Stratification on Boundary-Layer Flow and Power Output from Very Large Wind Farms. Energies 2013, 6, 2338–2361. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Mean and turbulent kinetic energy budgets inside and above very large wind farms under conventionally-neutral condition. Renew. Energy 2014, 70, 142–152. [Google Scholar] [CrossRef]
- Wu, Y.T.; Porté-Agel, F. Modeling turbine wakes and power losses within a wind farm using LES: An application to the Horns Rev offshore wind farm. Renew. Energy 2015, 75, 945–955. [Google Scholar] [CrossRef]
- Deardorff, J.W. Three-dimensional numerical study of the height and mean structure of a heated planetary boundary layer. Bound. Lay. Meteorol. 1974, 7, 81–106. [Google Scholar] [CrossRef]
- Meyers, J.; Meneveau, C. Large Eddy Simulations of Large Wind-Turbine Arrays in the Atmospheric Boundary Layer. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Wu, Y.T.; Porté-Agel, F. Large-Eddy Simulation of Wind-Turbine Wakes: Evaluation of Turbine Parametrisations. Bound. Lay. Meteorol. 2011, 138, 345–366. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. A new wind-farm parameterization for large-scale atmospheric models. J. Renew. Sustain. Energy 2015, 7, 013121. [Google Scholar] [CrossRef]
- Stoll, R.; Porté-Agel, F. Dynamic subgrid-scale models for momentum and scalar fluxes in large-eddy simulations of neutrally stratified atmospheric boundary layers over heterogeneous terrain. Water Resour. Res. 2006, 42, W01409. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Meneveau, C.; Parlange, M.B. A Scale-Dependent Dynamic Model for Large-Eddy Simulation: Application to a Neutral Atmospheric Boundary Layer. J. Fluid Mech. 2000, 415, 261–284. [Google Scholar] [CrossRef]
- Porté-Agel, F. A scale-dependent dynamic model for scalar transport in large-eddy simulations of the atmospheric boundary layer. Bound. Lay. Meteorol. 2004, 112, 81–105. [Google Scholar] [CrossRef]
- Stoll, R.; Porté-Agel, F. Large-eddy simulation of the stable atmospheric boundary layer using dynamic models with different averaging schemes. Bound. Lay. Meteorol. 2008, 126, 1–28. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. A new boundary condition for large-eddy simulation of boundary-layer flow over surface roughness transitions. J. Turbul. 2012, 13, 1–18. [Google Scholar] [CrossRef]
- Abkar, M.; Bae, H.; Moin, P. Minimum-dissipation scalar transport model for large-eddy simulation of turbulent flows. Phys. Rev. Fluids 2016, 1, 041701. [Google Scholar] [CrossRef]
- Abkar, M.; Moin, P. Large-Eddy Simulation of Thermally Stratified Atmospheric Boundary-Layer Flow Using a Minimum Dissipation Model. Bound. Lay. Meteorol. 2017, 165, 405–419. [Google Scholar] [CrossRef]
- Yang, X.I.; Abkar, M. A hierarchical random additive model for passive scalars in wall-bounded flows at high Reynolds numbers. J. Fluid Mech. 2018, 842, 354–380. [Google Scholar] [CrossRef]
- Esau, I.N.; Zilitinkevich, S.S. Universal dependences between turbulent and mean flow parameters instably and neutrally stratified Planetary Boundary Layers. Nonlin. Process. Geophys. 2006, 13, 135–144. [Google Scholar] [CrossRef]
- Beare, R.J.; MacVean, M.K.; Holtslag, A.A.M.; Cuxart, J.; Esau, I.; Golaz, J.C.; Jimenez, M.A.; Khairoutdinov, M.; Kosovic, B.; Lewellen, D.; et al. An intercomparison of large-eddy simulations of the stable boundary layer. Bound. Lay. Meteorol. 2006, 118, 247–272. [Google Scholar] [CrossRef]
- Moeng, C. A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 46, 2311–2330. [Google Scholar] [CrossRef]
- Basu, S.; Porté-Agel, F. Large-eddy simulation of stably stratified atmospheric boundary layer turbulence: A scale-dependent dynamic modeling approach. J. Atmos. Sci. 2006, 63, 2074–2091. [Google Scholar] [CrossRef]
- Sescu, A.; Meneveau, C. A control algorithm for statistically stationary large-eddy simulations of thermally stratified boundary layers. Q. J. R. Meteorol. Soc. 2014, 140, 2017–2022. [Google Scholar] [CrossRef]
- Jimenez, A.; Crespo, A.; Migoya, E.; Garcia, J. Advances in large-eddy simulation of a wind turbine wake. J. Phys. Conf. Ser. 2007, 75, 012041. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind turbine array boundary layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef]
- Chamorro, L.; Porté-Agel, F. A wind-tunnel investigation of wind-turbine wakes: Boundary-layer turbulence effects. Bound. Lay. Meteorol. 2009, 132, 129–149. [Google Scholar] [CrossRef]
- Abkar, M.; Porté-Agel, F. Influence of atmospheric stability on wind turbine wakes: A large-eddy simulation study. Phys. Fluids 2015, 27, 035104. [Google Scholar] [CrossRef]
- Xie, S.; Archer, C. Self-similarity and turbulence characteristics of wind turbine wakes via large-eddy simulation. Wind Energy 2015, 18, 1815–1838. [Google Scholar] [CrossRef]
- Bastankhah, M.; Porté-Agel, F. Experimental and theoretical study of wind turbine wakes in yawed conditions. J. Fluid Mech 2016, 806, 506–541. [Google Scholar] [CrossRef]
- Ishihara, T.; Qian, G.W. A new Gaussian-based analytical wake model for wind turbines considering ambient turbulence intensities and thrust coefficient effects. J. Wind Eng. Ind. Aerodyn. 2018, 177, 275–292. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Abkar, M.; Dabiri, J.O. Self-similarity and flow characteristics of vertical-axis wind turbine wakes: An LES study. J. Turbul. 2017, 18, 373–389. [Google Scholar] [CrossRef]
- Carbajo Fuertes, F.; Markfort, C.D.; Porté-Agel, F. Wind Turbine Wake Characterization with Nacelle-Mounted Wind Lidars for Analytical Wake Model Validation. Remote Sens. 2018, 10, 668. [Google Scholar] [CrossRef]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; Wiley: New York, NY, USA, 2001. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abkar, M.; Sørensen, J.N.; Porté-Agel, F. An Analytical Model for the Effect of Vertical Wind Veer on Wind Turbine Wakes. Energies 2018, 11, 1838. https://doi.org/10.3390/en11071838
Abkar M, Sørensen JN, Porté-Agel F. An Analytical Model for the Effect of Vertical Wind Veer on Wind Turbine Wakes. Energies. 2018; 11(7):1838. https://doi.org/10.3390/en11071838
Chicago/Turabian StyleAbkar, Mahdi, Jens Nørkær Sørensen, and Fernando Porté-Agel. 2018. "An Analytical Model for the Effect of Vertical Wind Veer on Wind Turbine Wakes" Energies 11, no. 7: 1838. https://doi.org/10.3390/en11071838
APA StyleAbkar, M., Sørensen, J. N., & Porté-Agel, F. (2018). An Analytical Model for the Effect of Vertical Wind Veer on Wind Turbine Wakes. Energies, 11(7), 1838. https://doi.org/10.3390/en11071838






