Critical Resolution and Sample Size of Digital Rock Analysis for Unconventional Reservoirs
Abstract
1. Introduction
2. Materials and Methods
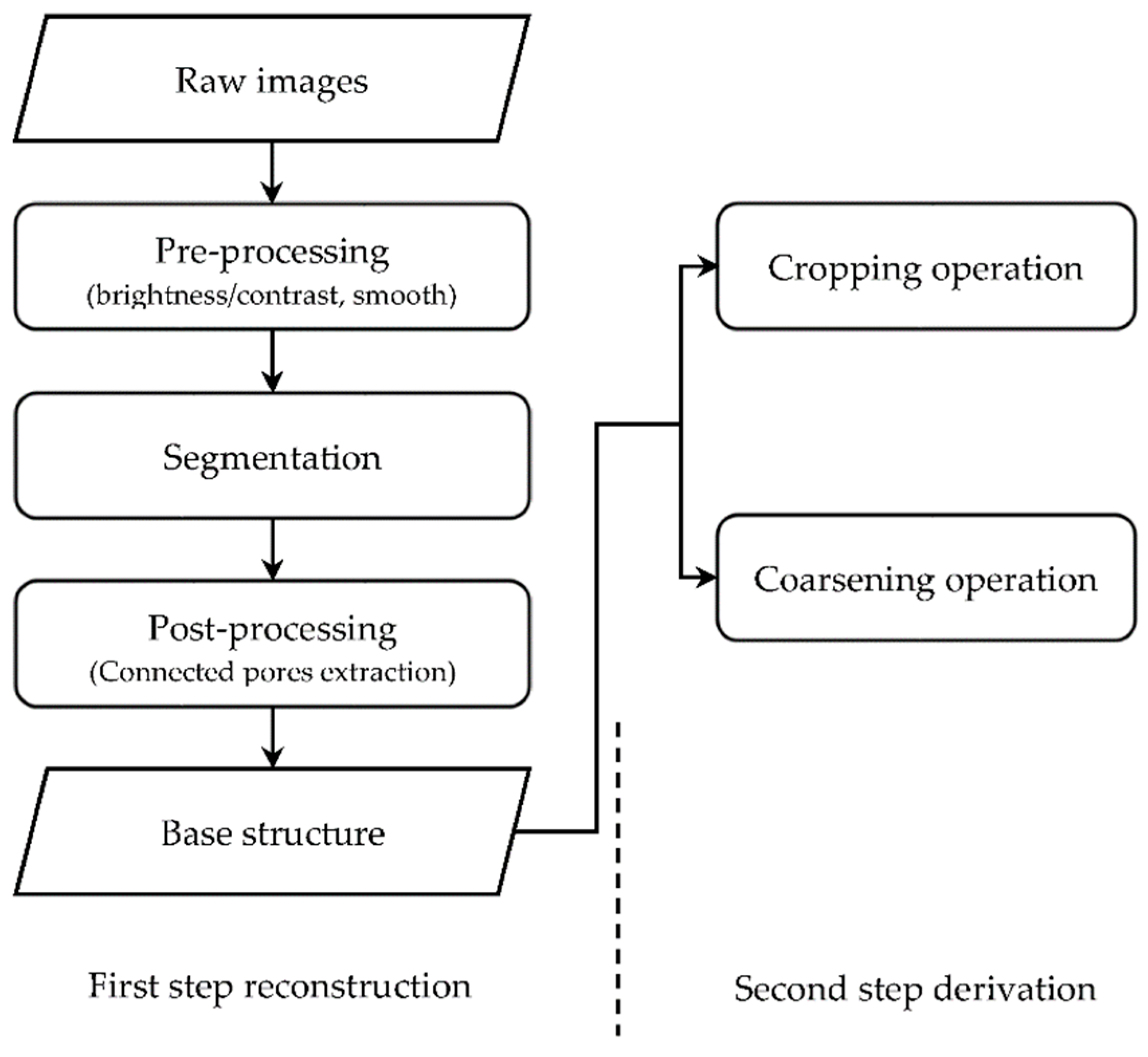
2.1. Structure Reconstruction Procedure
2.2. Permeability Calculation
2.2.1. Case Set-Up
2.2.2. Extrapolation Permeability Calculation
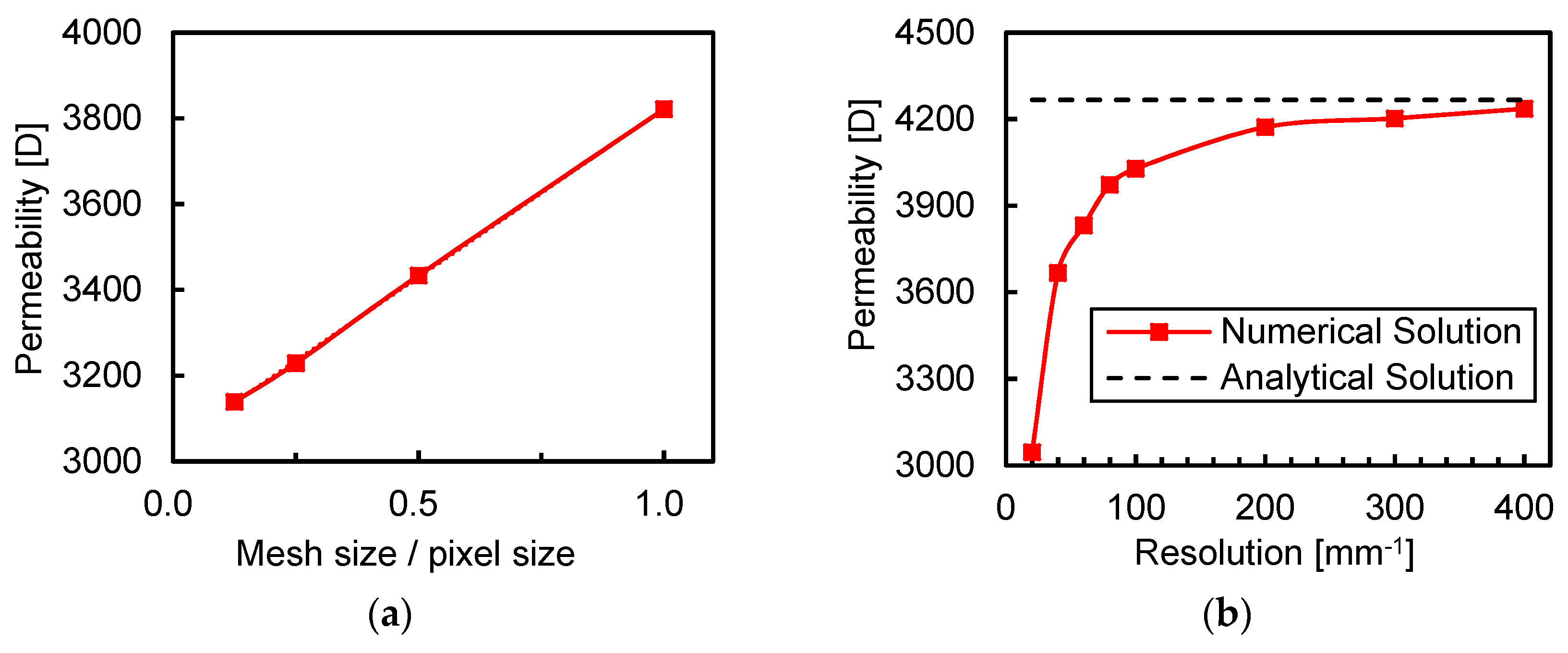
2.2.3. Validation
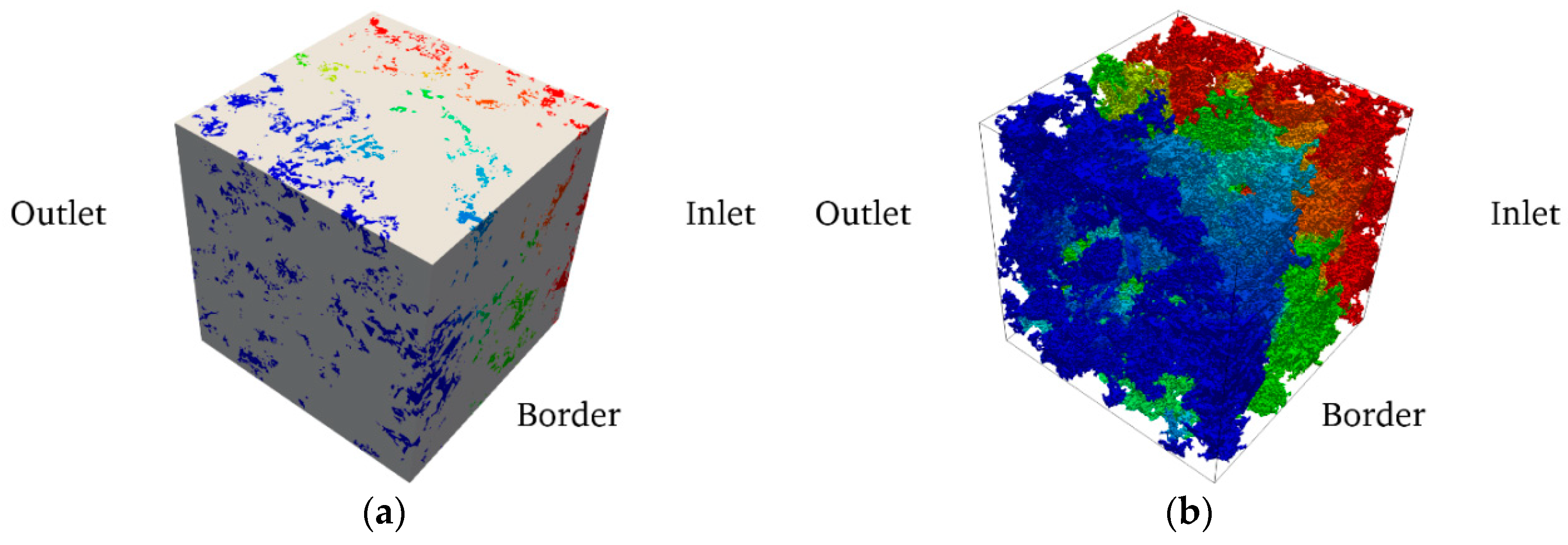
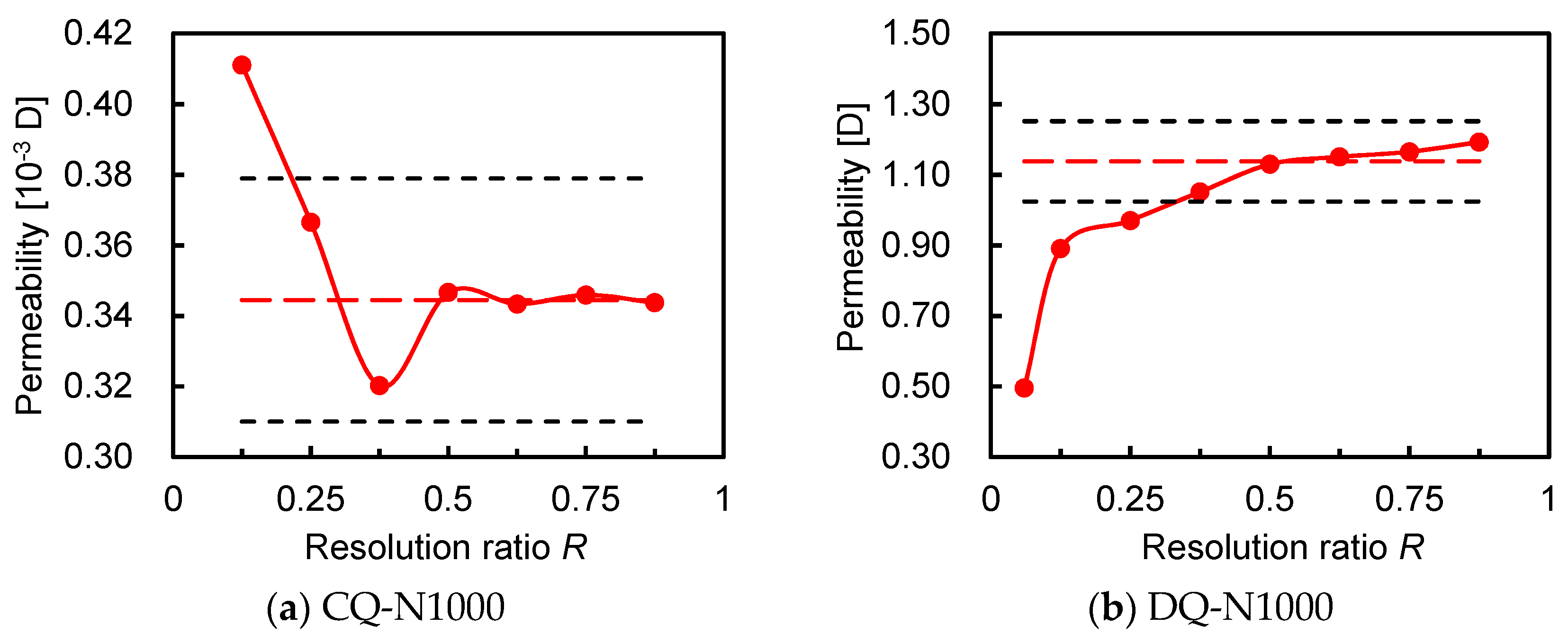
2.2.4. REV and COR Determination Approach
3. Results and Discussions
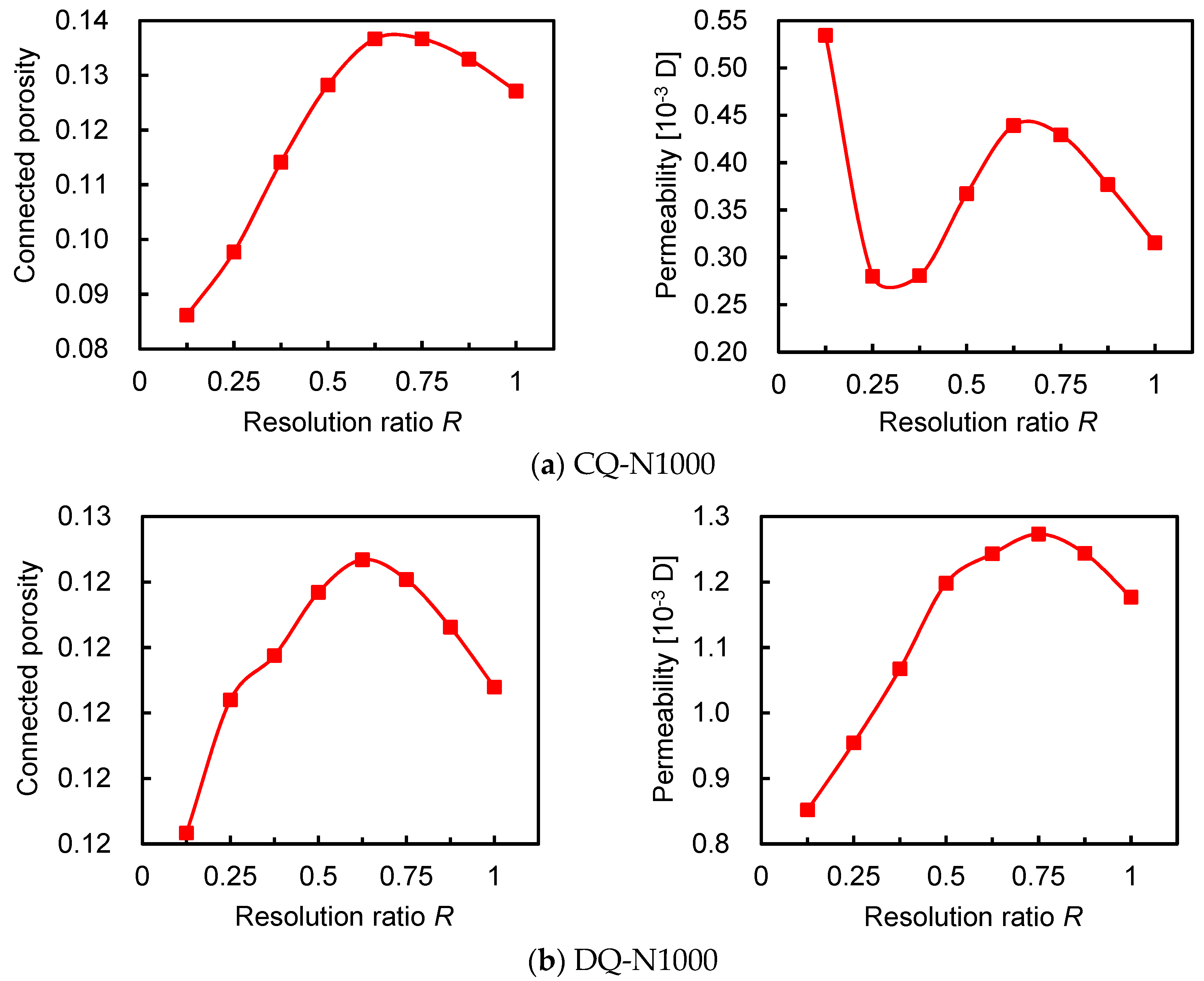
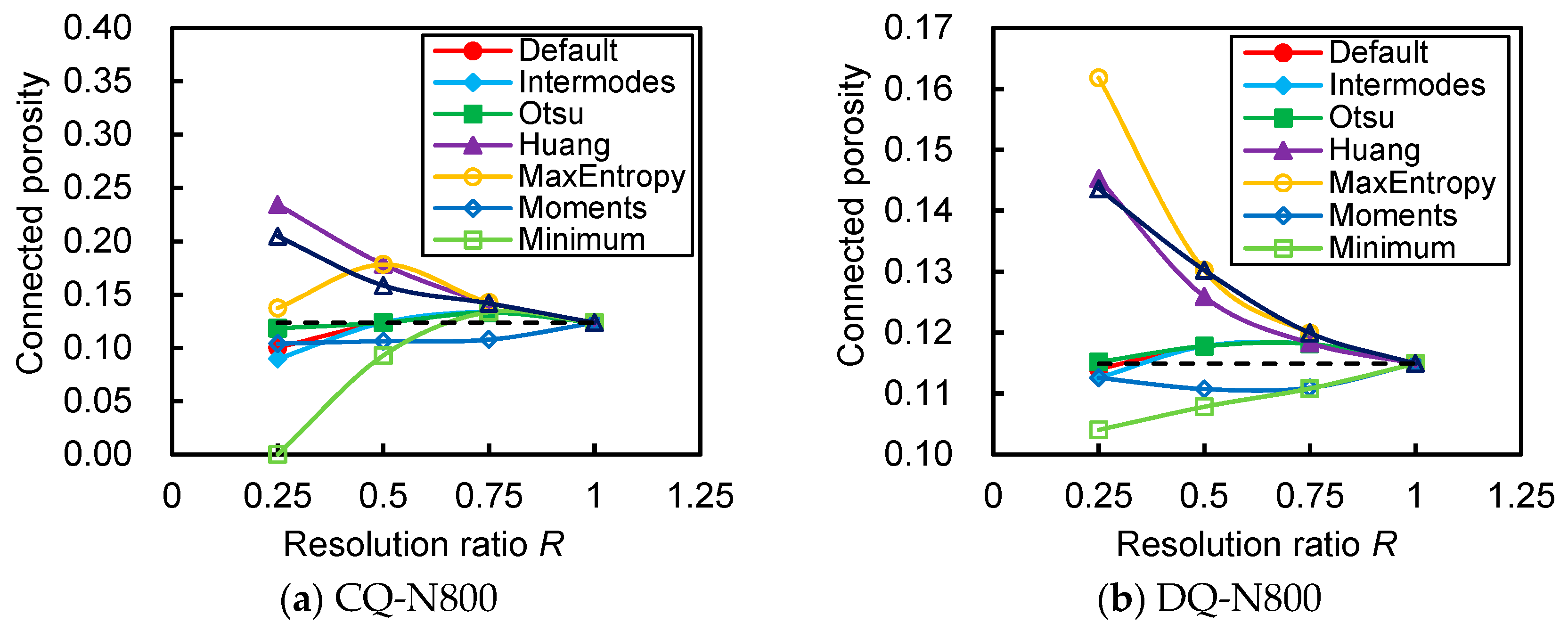
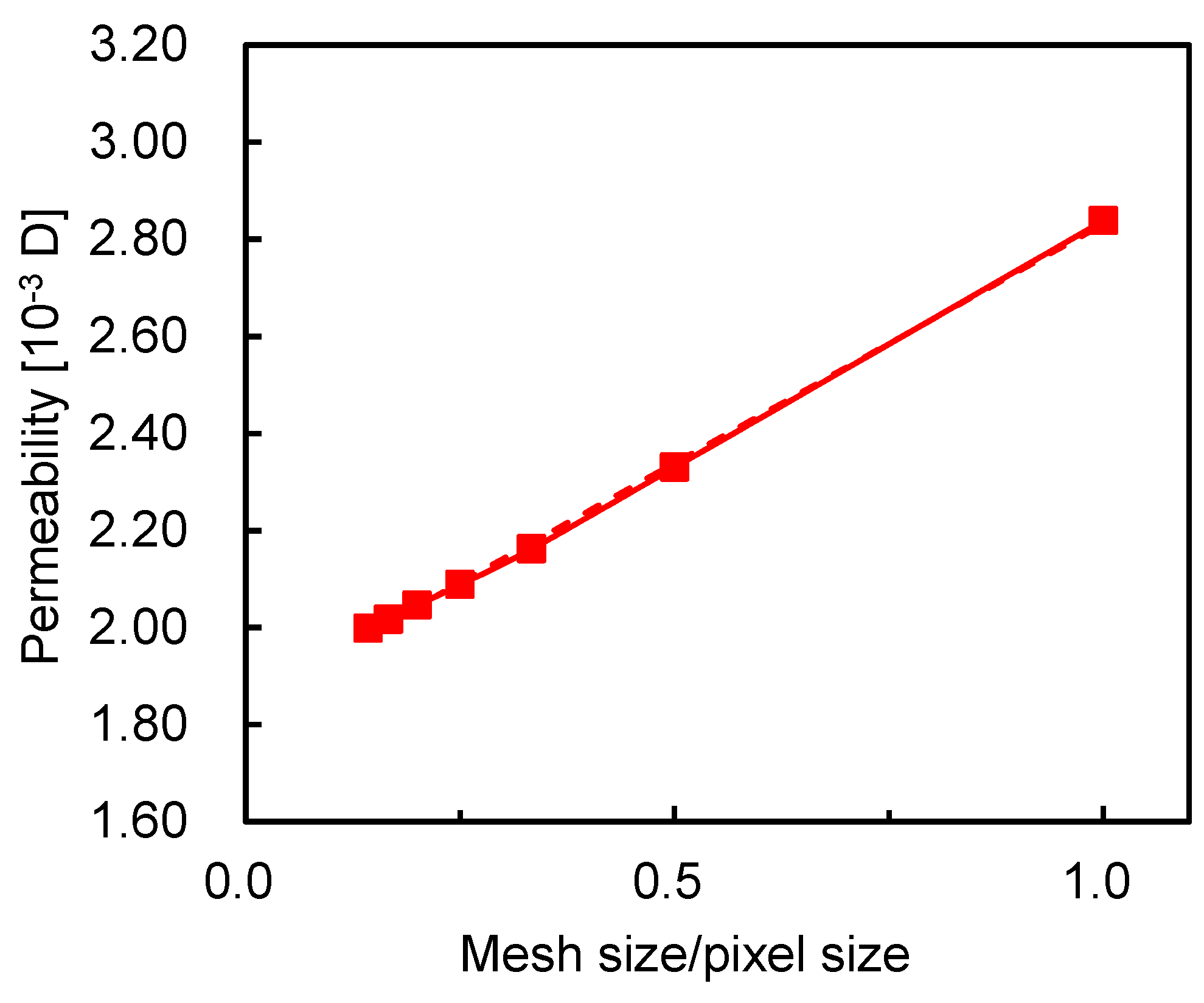
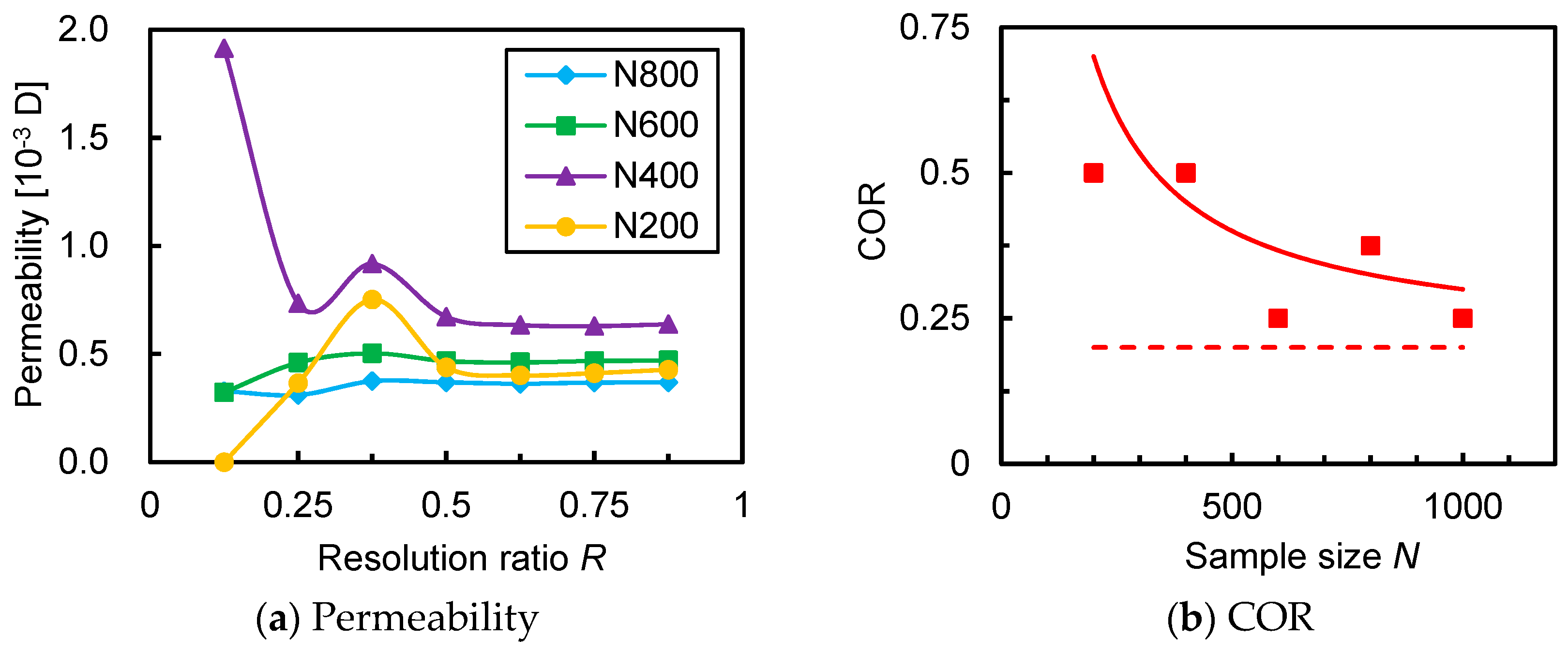
3.1. Resolution Effect
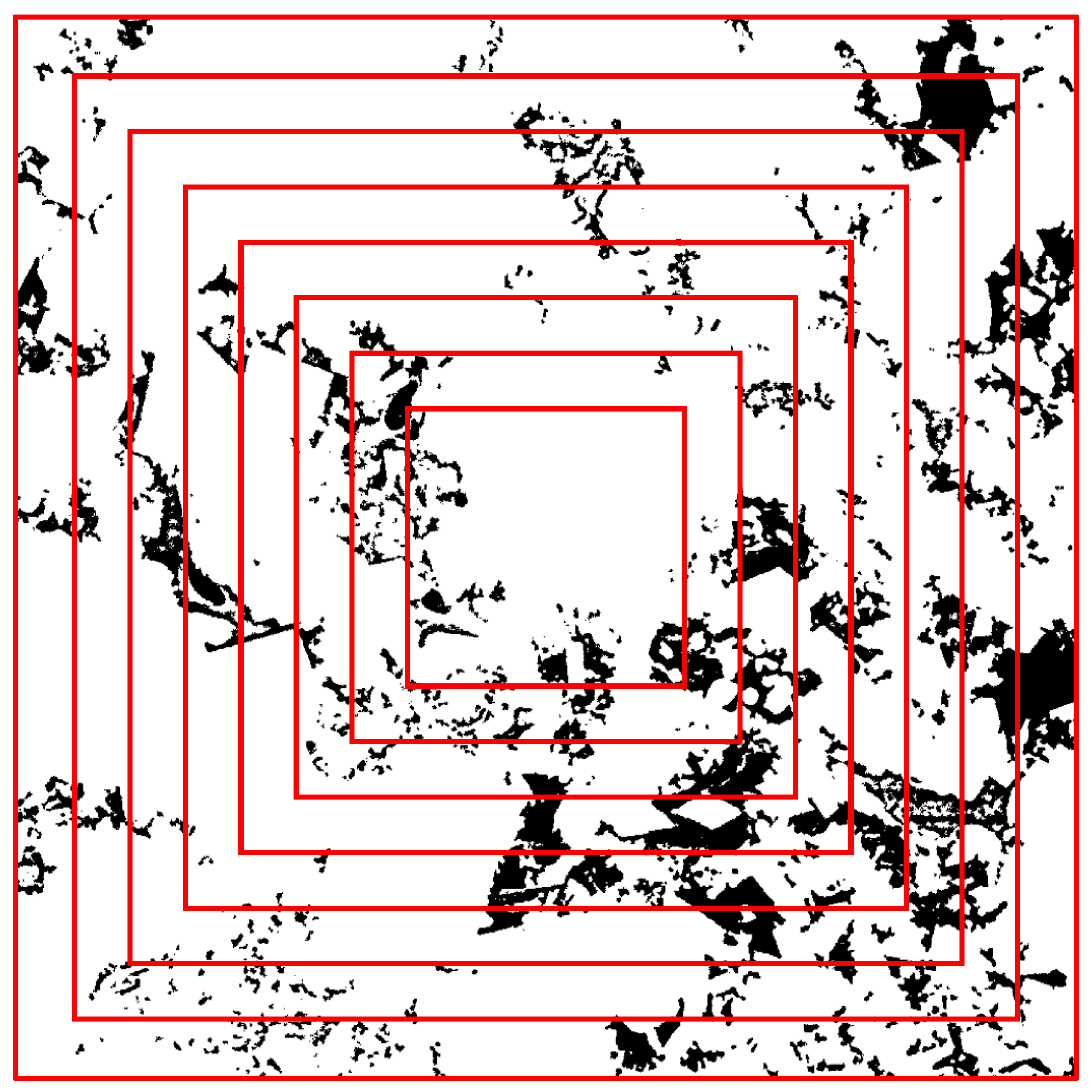
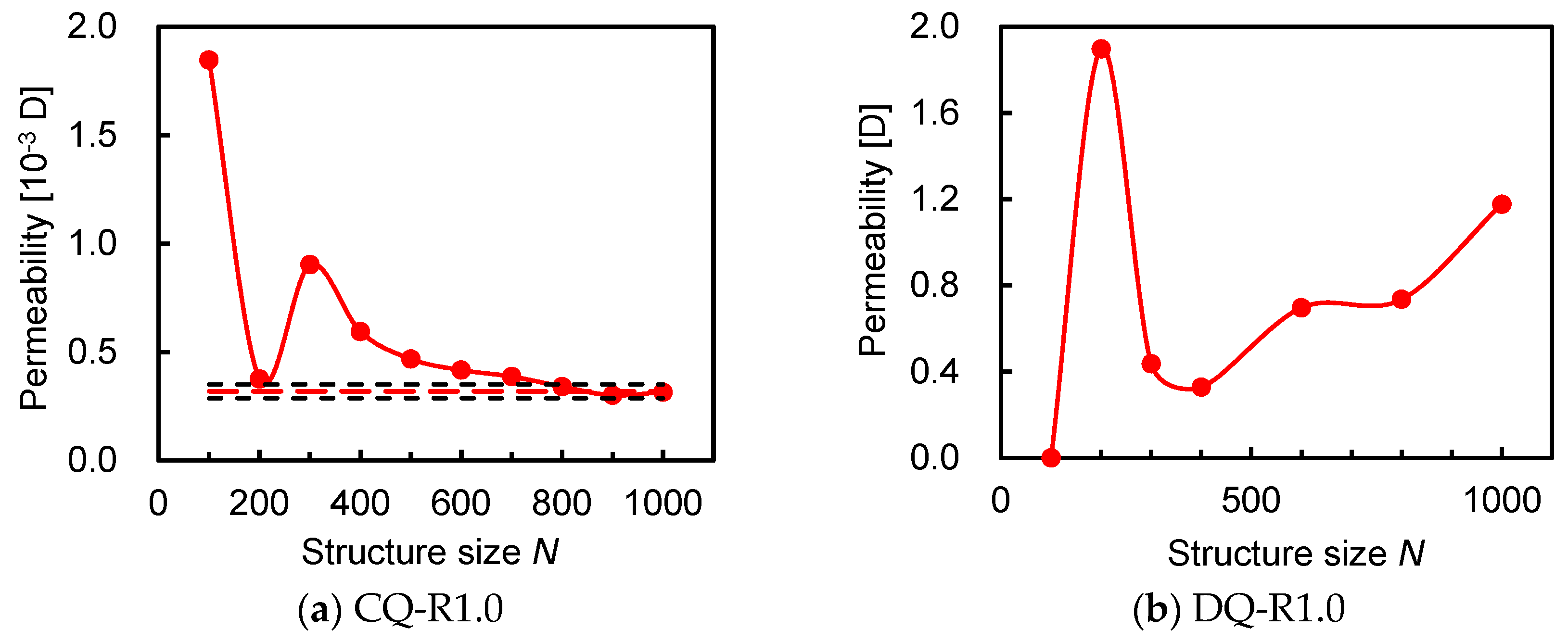
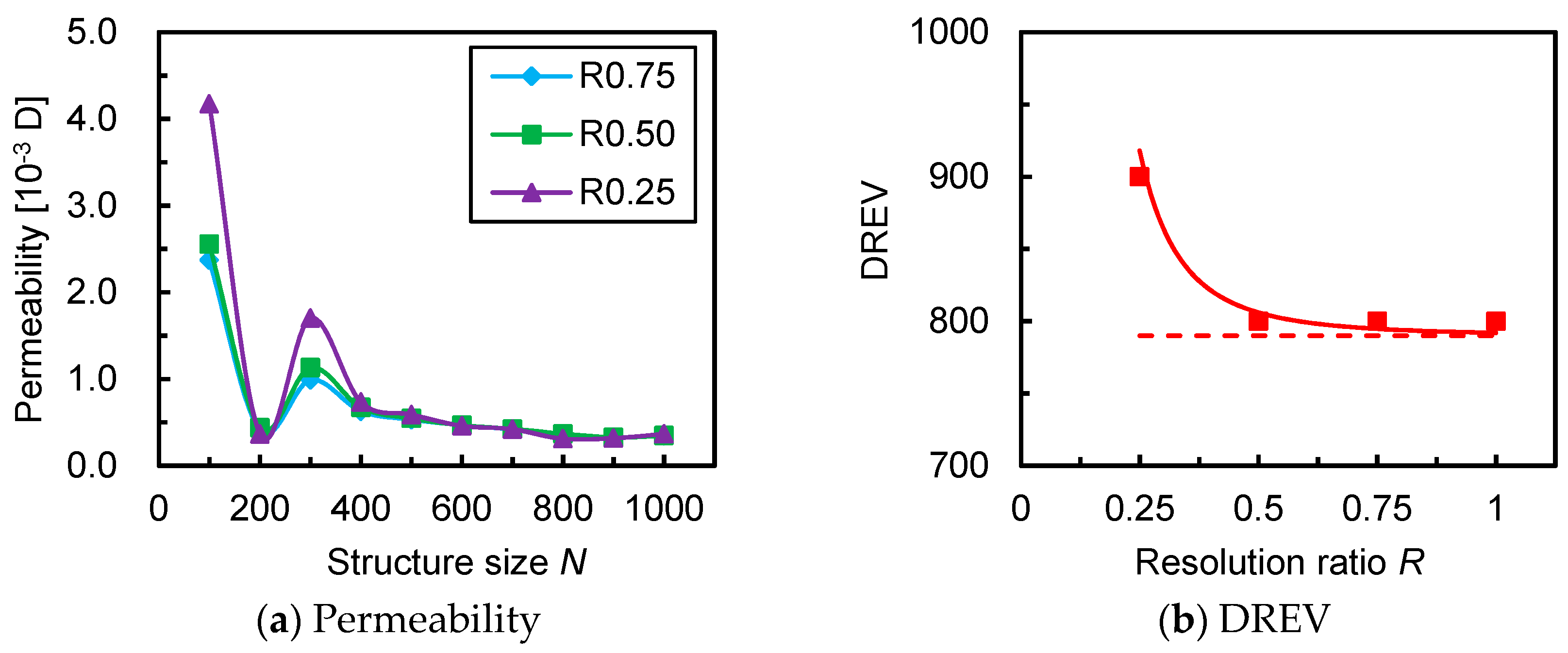
3.2. Sample Size Effect
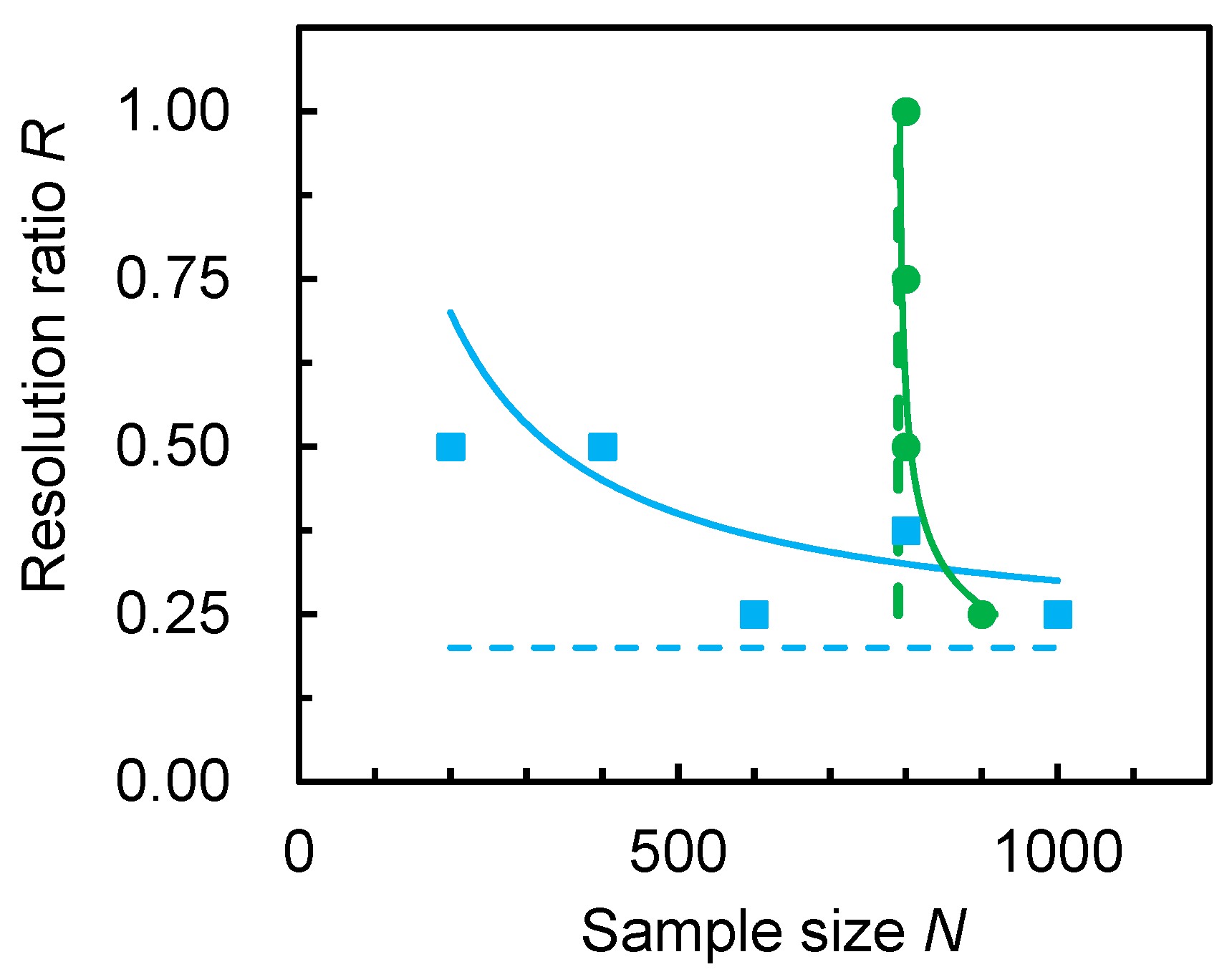
3.3. Critical Resolution and Sample Size
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Al-Marzouqi, H. Digital rock physics using CT scans to compute rock properties. IEEE Signal Process. Mag. 2018, 35, 121–131. [Google Scholar] [CrossRef]
- Rassenfoss, S. Need a faster measure of relative permeability? Take a CT scan and follow with digital rock analysis. J. Pet. Technol. 2017, 69, 28–31. [Google Scholar] [CrossRef]
- Jerauld, G.R.; Fredrich, J.; Lane, N.; Sheng, Q.; Crouse, B.; Freed, D.M.; Fager, A.; Xu, R. Validation of a workflow for digitally measuring relative permeability. In Proceedings of the SPE Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, UAE, 13–16 November 2017. [Google Scholar]
- Koronfol, S.; Grader, A.; Suhrer, M.; Toelke, J.; Mu, Y.; Dernaika, M.; Pratap, M.; Al Hammadi, M.; Al Ratrout, A.; Kalam, M.Z. Capillary pressure and relative permeability assessment on whole core samples from a giant middle easteren carbonate reservoir utilizing digital rock physics. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 10–13 November 2017. [Google Scholar]
- Arns, C.H.; Knackstedt, M.A.; Pinczewski, M.V.; Lindquist, W. Accurate estimation of transport properties from microtomographic images. Geophys. Res. Lett. 2001, 28, 3361–3364. [Google Scholar] [CrossRef]
- Keehm, Y.; Mukerji, T.; Nur, A. Permeability prediction from thin sections: 3D reconstruction and lattice-boltzmann flow simulation. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Madadi, M.; Jones, A.C.; Arns, C.H.; Knackstedt, M.A. 3D imaging and simulation of elastic properties of porous materials. Comput. Sci. Eng. 2009, 11, 65–73. [Google Scholar] [CrossRef]
- Saenger, E.H.; Enzmann, F.; Keehm, Y.; Steeb, H. Digital rock physics: Effect of fluid viscosity on effective elastic properties. J. Appl. Geophy. 2011, 74, 236–241. [Google Scholar] [CrossRef]
- Grader, A.; Kalam, M.; Toelke, J.; Mu, Y.; Derzhi, N.; Baldwin, C.; Stenger, B. A comparative study of digital rock physics and laboratory scal evaluations of carbonate cores. In Proceedings of the International Symposium of the Society-of-Core-Analysts, Halifax, Novia Scotia, Canada, 4–7 October 2010. [Google Scholar]
- Kalam, M.Z. Digital rock physics for fast and accurate special core analysis in carbonates. In New Technologies in the Oil and Gas Industry; InTech: London, UK, 2012. [Google Scholar]
- Miller, K.; Vanorio, T.; Keehm, Y. Evolution of permeability and microstructure of tight carbonates due to numerical simulation of calcite dissolution. J. Geophys. Res. 2017, 122, 4460–4474. [Google Scholar] [CrossRef]
- Lopez, O.; Mock, A.; Øren, P.E.; Long, H.; Kalam, Z.; Vahrenkamp, V.; Gibrata, M.; Seraj, S.; Chacko, S.; Al Hammadi, M. Validation of fundamental carbonate reservoir core properties using digital rock physics. In Proceedings of the International Symposium of the Society of Core Analysts, Aberdeen, Scotland, UK, 27–30 August 2012. [Google Scholar]
- Andrä, H.; Combaret, N.; Dvorkin, J.; Glatt, E.; Han, J.; Kabel, M.; Keehm, Y.; Krzikalla, F.; Lee, M.; Madonna, C. Digital rock physics benchmarks—part ii: Computing effective properties. Comput. Geosci. 2013, 50, 33–43. [Google Scholar] [CrossRef]
- Nunes, J.P.P.; Blunt, M.J.; Bijeljic, B. Pore-scale simulation of carbonate dissolution in micro-CT images. J. Geophys. Res. 2016, 121, 558–576. [Google Scholar] [CrossRef]
- Almarzooq, A.; AlGhamdi, T.; Koronfol, S.; Dernaika, M.; Walls, J. Shale gas characterization and property determination by digital rock physics. In Proceedings of the SPE Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 21–24 April 2014. [Google Scholar]
- Sun, H.; Yao, J.; Cao, Y.C.; Fan, D.Y.; Zhang, L. Characterization of gas transport behaviors in shale gas and tight gas reservoirs by digital rock analysis. Int. J. Heat Mass Transf. 2017, 104, 227–239. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Jin, X.; Wang, X.Q.; Sun, L.; Wang, M.R. Pore-scale geometry effects on gas permeability in shale. J. Nat. Gas Sci. Eng. 2016, 34, 948–957. [Google Scholar] [CrossRef]
- Sakellariou, A.; Arns, C.H.; Sheppard, A.P.; Sok, R.M.; Averdunk, H.; Limaye, A.; Jones, A.C.; Senden, T.J.; Knackstedt, M.A. Developing a virtual materials laboratory. Mater. Today 2007, 10, 44–51. [Google Scholar] [CrossRef]
- Dvorkin, J.; Armbruster, M.; Baldwin, C.; Fang, Q.; Derzhi, N.; Gomez, C.; Nur, B.; Nur, A. The future of rock physics: Computational methods vs. Lab testing. First Break 2008, 26, 63–68. [Google Scholar]
- Bultreys, T.; De Boever, W.; Cnudde, V. Imaging and image-based fluid transport modeling at the pore scale in geological materials: A practical introduction to the current state-of-the-art. Earth Sci. Rev. 2016, 155, 93–128. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, P.; Wu, J.; Mezzatesta, A.; Jin, G.; Satti, R.; Koliha, N.; Bautista, J.; Crouse, B.; Freed, D. Using digital rock modeling to estimate permeability and capillary pressure from NMR and geochemical logs. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Manama, Bahrain, 6–9 March 2017. [Google Scholar]
- Houben, M.E.; Desbois, G.; Urai, J.L. A comparative study of representative 2D microstructures in shaly and sandy facies of opalinus clay (mont terri, switzerland) inferred form BIB-SEM and MIP methods. Mar. Pet. Geol. 2014, 49, 143–161. [Google Scholar] [CrossRef]
- Vlahinić, I.; Andò, E.; Viggiani, G.; Andrade, J.E. Towards a more accurate characterization of granular media: Extracting quantitative descriptors from tomographic images. Granul. Matter 2014, 16, 9–21. [Google Scholar] [CrossRef]
- Kelly, S.; El-Sobky, H.; Torres-Verdín, C.; Balhoff, M.T. Assessing the utility of fib-sem images for shale digital rock physics. Adv. Water Resour. 2016, 95, 302–316. [Google Scholar] [CrossRef]
- Li, G.G.; Diaz, E.; Nur, A.M. Rock physical properties computed from digital core and cuttings with applications to deep gas exploration and development. In Proceedings of the SPE Deep Gas Conference and Exhibition, Manama, Bahrain, 24–26 January 2010. [Google Scholar]
- Gualda, G.A.; Rivers, M. Quantitative 3D petrography using x-ray tomography: Application to bishop tuff pumice clasts. J. Volcanol. Geotherm. Res. 2006, 154, 48–62. [Google Scholar] [CrossRef]
- Caubit, C.; Hamon, G.; Sheppard, A.; Øren, P. Evaluation of the reliability of prediction of petrophysical data through imagery and pore network modelling. Petrophysics 2009, 50, 322–334. [Google Scholar]
- Cnudde, V.; Boone, M.; Dewanckele, J.; Dierick, M.; Van Hoorebeke, L.; Jacobs, P. 3D characterization of sandstone by means of x-ray computed tomography. Geosphere 2011, 7, 54–61. [Google Scholar] [CrossRef]
- Khalili, A.D.; Arns, C.H.; Arns, J.-Y.; Hussain, F.; Cinar, Y.; Pinczewski, W.V.; Latham, S.; Funk, J. Permeability upscaling for carbonates from the pore-scale using multi-scale Xray-CT images. In Proceedings of the SPE/EAGE European Unconventional Resources Conference & Exhibition-From Potential to Production, Vienna, Austria, 20–22 March 2012. [Google Scholar]
- Smith, M.M.; Sholokhova, Y.; Hao, Y.; Carroll, S.A. Co 2-induced dissolution of low permeability carbonates. Part i: Characterization and experiments. Adv. Water Resour. 2013, 62, 370–387. [Google Scholar] [CrossRef]
- Nordahl, K.; Ringrose, P.S. Identifying the representative elementary volume for permeability in heterolithic deposits using numerical rock models. Math. Geosci. 2008, 40, 753–771. [Google Scholar] [CrossRef]
- Borujeni, A.T.; Lane, N.; Thompson, K.; Tyagi, M. Effects of image resolution and numerical resolution on computed permeability of consolidated packing using LB and FEM pore-scale simulations. Comput. Fluids 2013, 88, 753–763. [Google Scholar] [CrossRef]
- Mostaghimi, P.; Blunt, M.J.; Bijeljic, B. Computations of absolute permeability on micro-CT images. Math. Geosci. 2013, 45, 103–125. [Google Scholar] [CrossRef]
- Alyafei, N.; Raeini, A.Q.; Paluszny, A.; Blunt, M.J. A sensitivity study of the effect of image resolution on predicted petrophysical properties. Transp. Porous Media 2015, 110, 157–169. [Google Scholar] [CrossRef]
- Shah, S.; Gray, F.; Crawshaw, J.; Boek, E. Micro-computed tomography pore-scale study of flow in porous media: Effect of voxel resolution. Adv. Water Resour. 2016, 95, 276–287. [Google Scholar] [CrossRef]
- Cui, D.; Sun, W.; Wang, Q.N.; Gu, C.P. Use of tomography to estimate the representative elementary volume in mortars stained with potassium iodide. Mater. Des. 2018, 147, 80–91. [Google Scholar] [CrossRef]
- Ledesma-Alonso, R.; Barbosa, R.; Ortegon, J. Effect of the image resolution on the statistical descriptors of heterogeneous media. Phys. Rev. E 2018, 97, 023304. [Google Scholar] [CrossRef] [PubMed]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Kameda, A.; Dvorkin, J.; Keehm, Y.; Nur, A.; Bosl, W. Permeability-porosity transforms from small sandstone fragments. Geophysics 2006, 71, N11–N19. [Google Scholar] [CrossRef]
- Okabe, H.; Oseto, K. Pore-scale heterogeneity assessed by the lattice-boltzmann method. In Proceedings of the International Symposium of the Society of Core Analysts, Trondheim, Norway, 12–16 September 2006. [Google Scholar]
- Al-Raoush, R.; Papadopoulos, A. Representative elementary volume analysis of porous media using X-ray computed tomography. Powder Technol. 2010, 200, 69–77. [Google Scholar] [CrossRef]
- Mu, Y.; Sungkorn, R.; Toelke, J. Identifying the representative flow unit for capillary dominated two-phase flow in porous media using morphology-based pore-scale modeling. Adv. Water Resour. 2016, 95, 16–28. [Google Scholar] [CrossRef]
- Madonna, C.; Almqvist, B.S.; Saenger, E.H. Digital rock physics: Numerical prediction of pressure-dependent ultrasonic velocities using micro-ct imaging. Geophys. J. Int. 2012, 189, 1475–1482. [Google Scholar] [CrossRef]
- Beckingham, L.E.; Peters, C.A.; Um, W.; Jones, K.W.; Lindquist, W.B. 2D and 3D imaging resolution trade-offs in quantifying pore throats for prediction of permeability. Adv. Water Resour. 2013, 62, 1–12. [Google Scholar] [CrossRef]
- Sheppard, A.P.; Sok, R.M.; Averdunk, H. Techniques for image enhancement and segmentation of tomographic images of porous materials. Physica A 2004, 339, 145–151. [Google Scholar] [CrossRef]
- Schlüter, S.; Sheppard, A.; Brown, K.; Wildenschild, D. Image processing of multiphase images obtained via x-ray microtomography: A review. Water Resour. Res. 2014, 50, 3615–3639. [Google Scholar] [CrossRef]
- Huang, L.-K.; Wang, M.-J.J. Image thresholding by minimizing the measures of fuzziness. Pattern Recognit. 1995, 28, 41–51. [Google Scholar] [CrossRef]
- Sezgin, M.; Sankur, B. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 2004, 13, 146–168. [Google Scholar] [CrossRef]
- Jasak, H.; Jemcov, A.; Tukovic, Z. OpenFOAM: A C++ library for complex physics simulations. In Proceedings of the International Workshop on Coupled Methods in Numerical Dynamics, Dubrovnik, Croatia, 19–21 September 2007. [Google Scholar]
- Sangani, A.S.; Acrivos, A. Slow flow through a periodic array of spheres. Int. J. Multiph. Flow 1982, 8, 343–360. [Google Scholar] [CrossRef]
- Larson, R.E.; Higdon, J.J.L. A periodic grain consolidation model of porous media. Phys. Fluids A 1989, 1, 38–46. [Google Scholar] [CrossRef]
- Holmes, D.W.; Williams, J.R.; Tilke, P. Smooth particle hydrodynamics simulations of low Reynolds number flows through porous media. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 419–437. [Google Scholar] [CrossRef]
- Pletcher, R.H.; Tannehill, J.C.; Anderson, D. Computational Fluid Mechanics and Heat Transfer, 3rd ed.; Taylor & Francis: Abingdon-on-Thames, UK, 2012. [Google Scholar]
- Abràmoff, M.D.; Magalhães, P.J.; Ram, S.J. Image processing with ImageJ. Biophotonics Int. 2004, 11, 36–42. [Google Scholar]


| Image Parameter | Changqing | Daqing |
|---|---|---|
| Image size |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Jin, X.; Wang, M. Critical Resolution and Sample Size of Digital Rock Analysis for Unconventional Reservoirs. Energies 2018, 11, 1798. https://doi.org/10.3390/en11071798
Liu T, Jin X, Wang M. Critical Resolution and Sample Size of Digital Rock Analysis for Unconventional Reservoirs. Energies. 2018; 11(7):1798. https://doi.org/10.3390/en11071798
Chicago/Turabian StyleLiu, Tong, Xu Jin, and Moran Wang. 2018. "Critical Resolution and Sample Size of Digital Rock Analysis for Unconventional Reservoirs" Energies 11, no. 7: 1798. https://doi.org/10.3390/en11071798
APA StyleLiu, T., Jin, X., & Wang, M. (2018). Critical Resolution and Sample Size of Digital Rock Analysis for Unconventional Reservoirs. Energies, 11(7), 1798. https://doi.org/10.3390/en11071798






