Numerical Simulation of Water Transport in a Proton Exchange Membrane Fuel Cell Flow Channel
Abstract
1. Introduction
2. Numerical Methodology
2.1. Mathematical Models
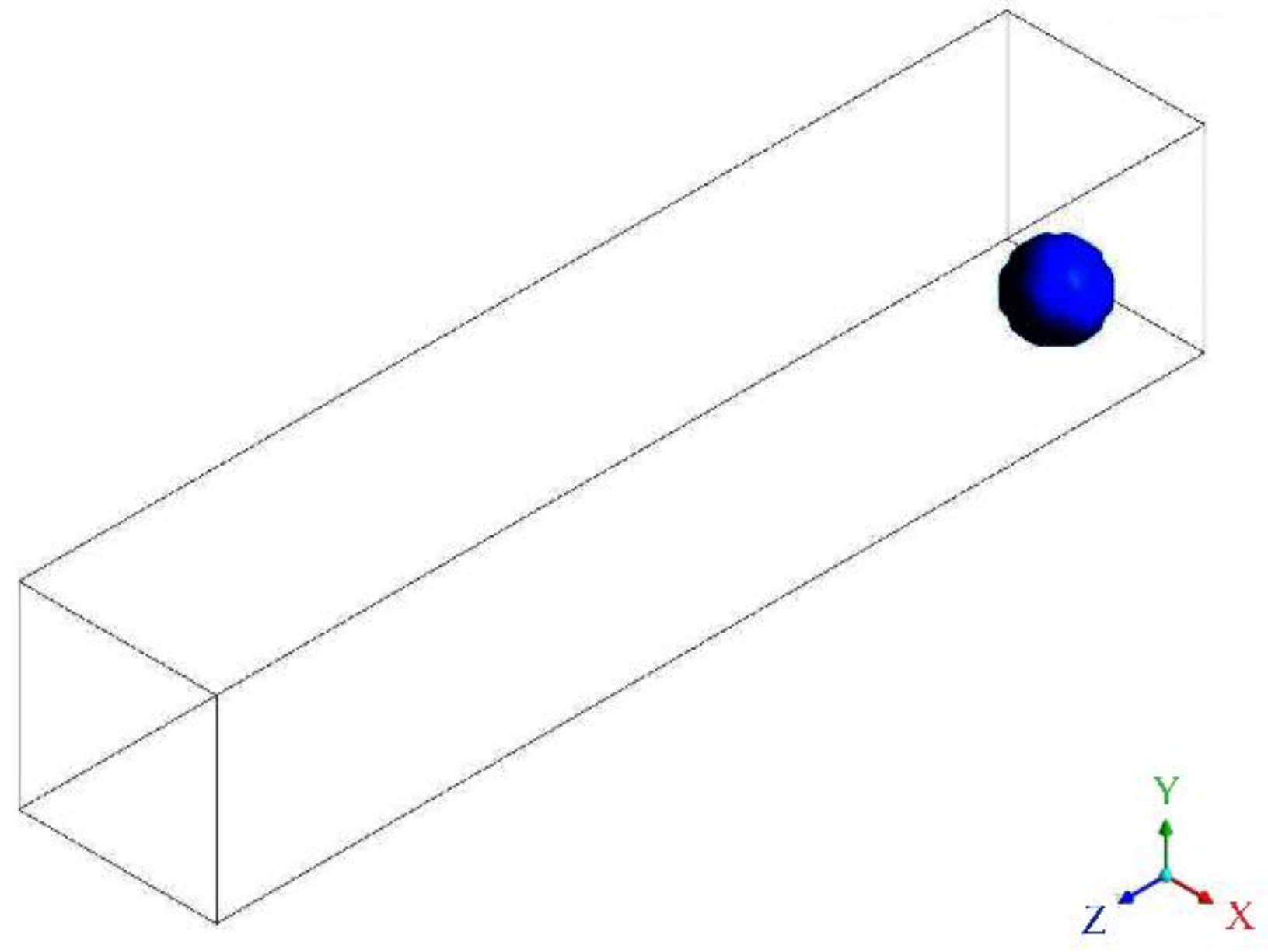
2.1.1. Configuration 1: Conventional Straight Channel
- (a)
- The operating pressure is set to 1 atm.
- (b)
- The gas-liquid surface tension coefficient is set to 0.072 N·m−1.
- (c)
- The time step size is set to 10−6 s.
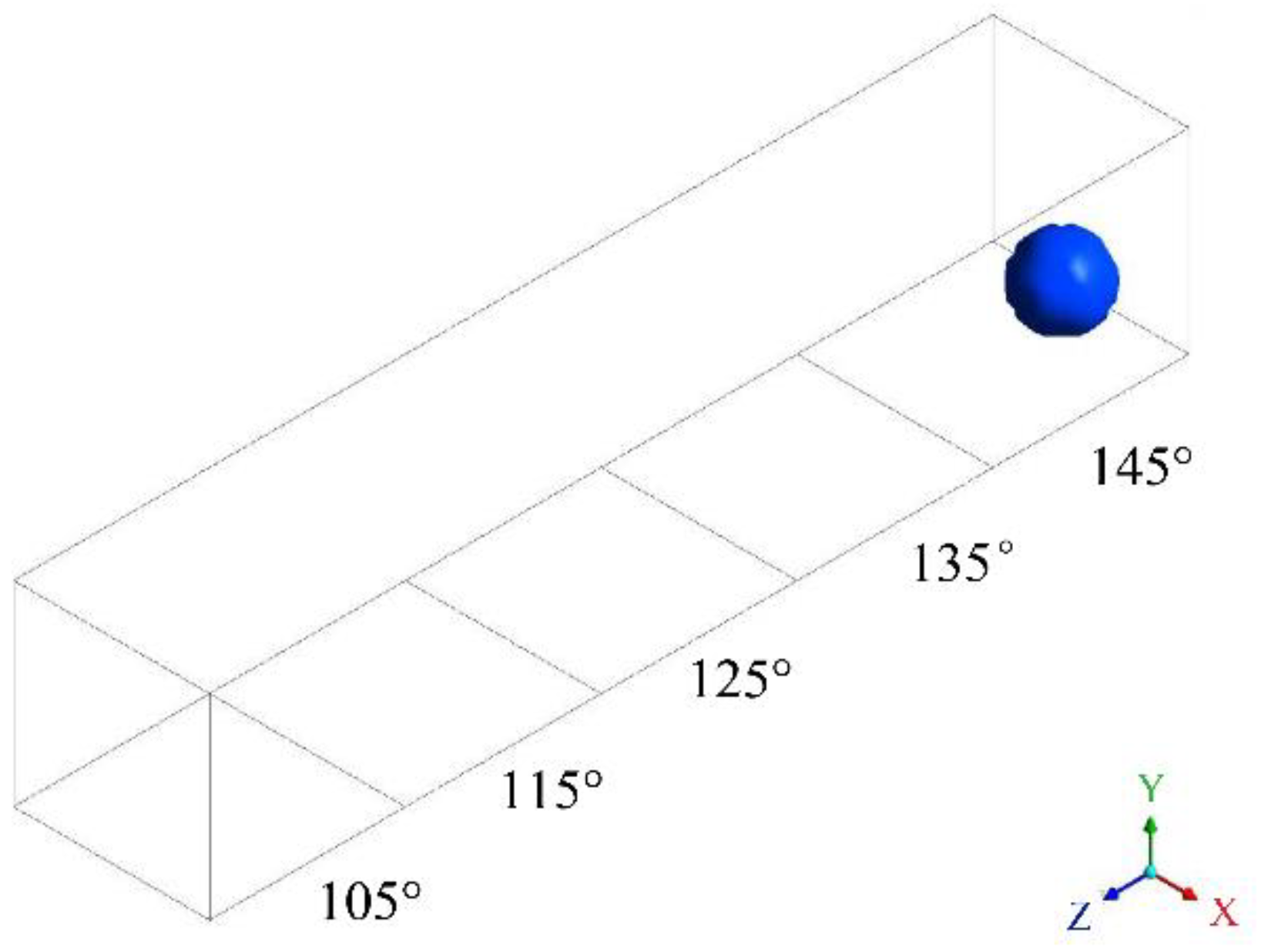
2.1.2. Configuration 2: Modified GDL Surface
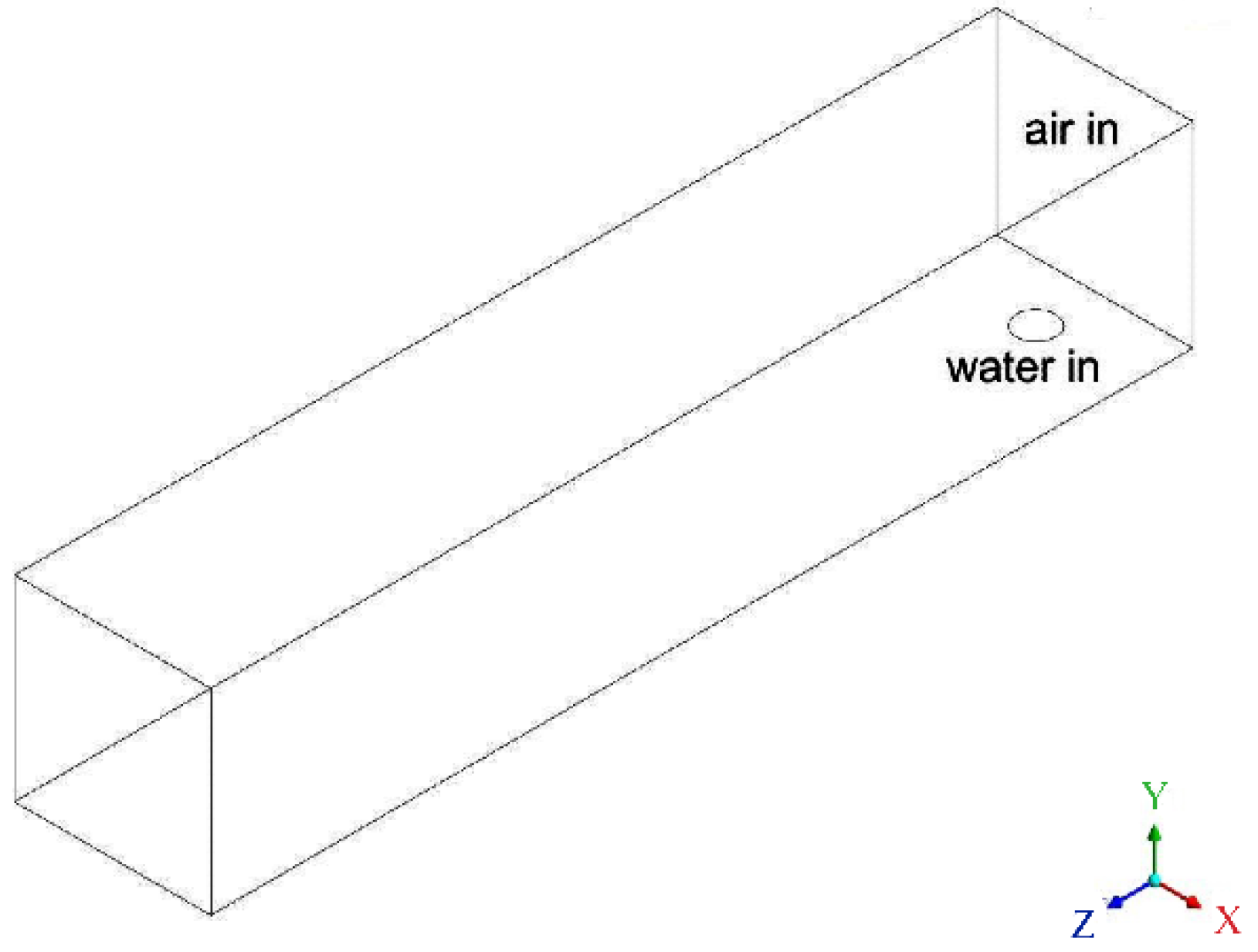
2.1.3. Configuration 3: Straight Channel with a Water Inlet Hole
2.2. Governing Equation
2.2.1. Without Considering Phase Transition
- Phase volume:
- Volume averaged density:
- Volume averaged dynamic viscosity:
2.2.2. Considering Phase Transition
3. Results and Discussion
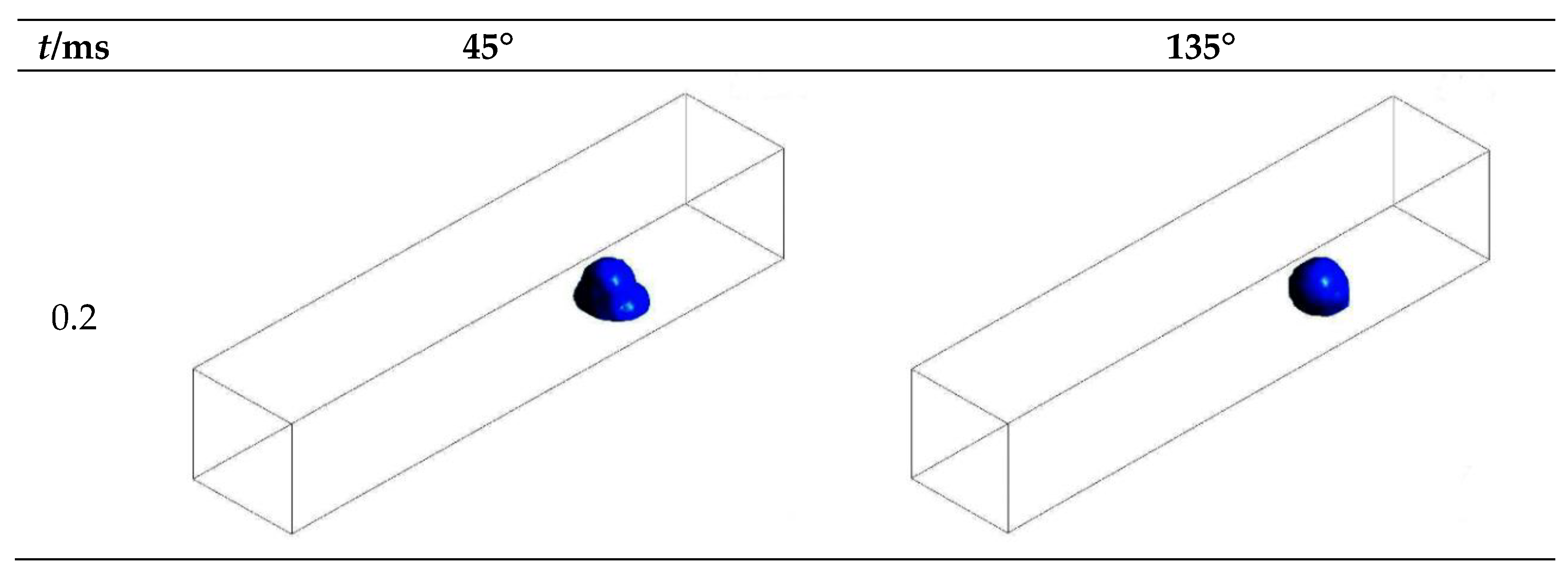
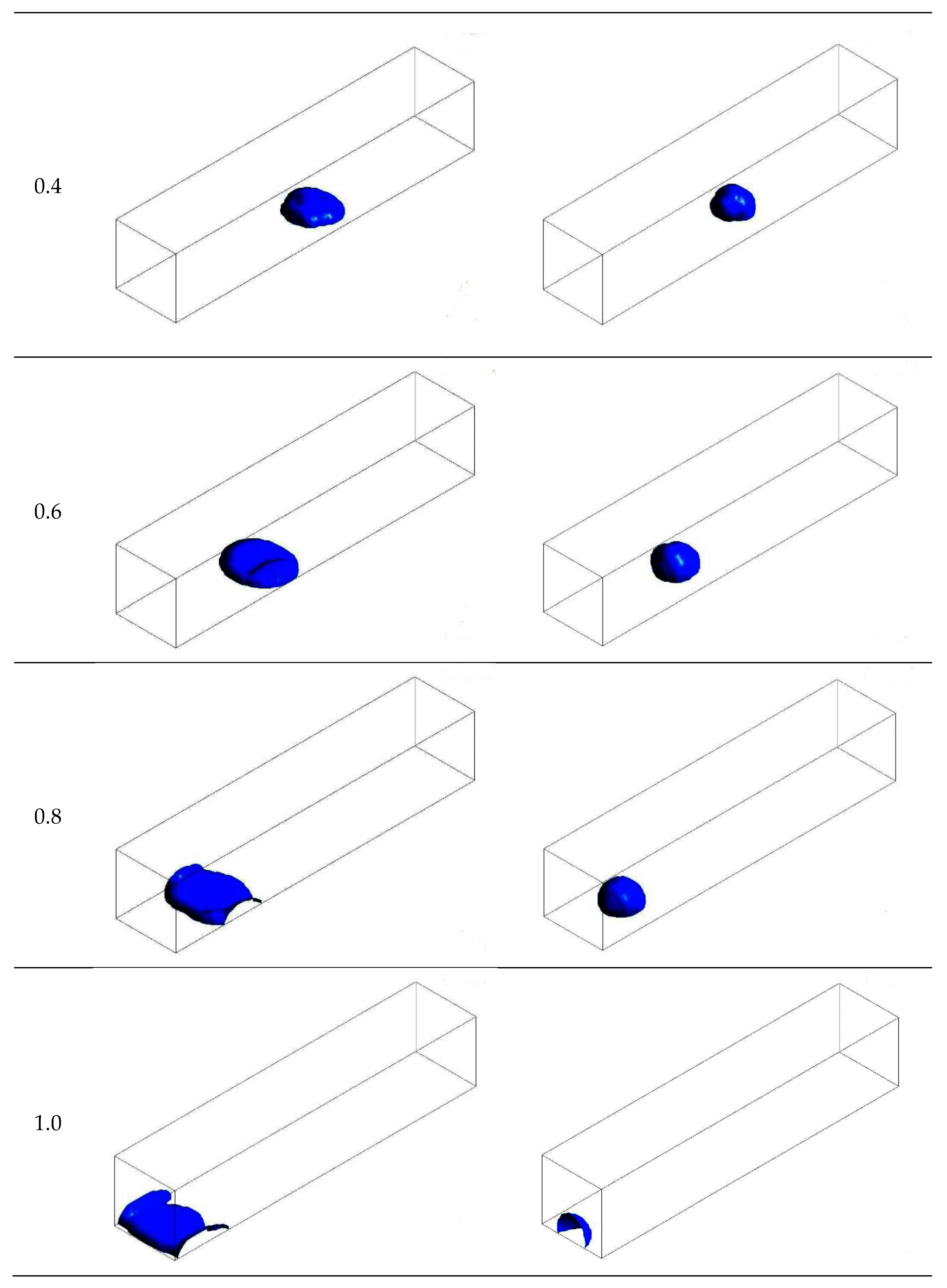
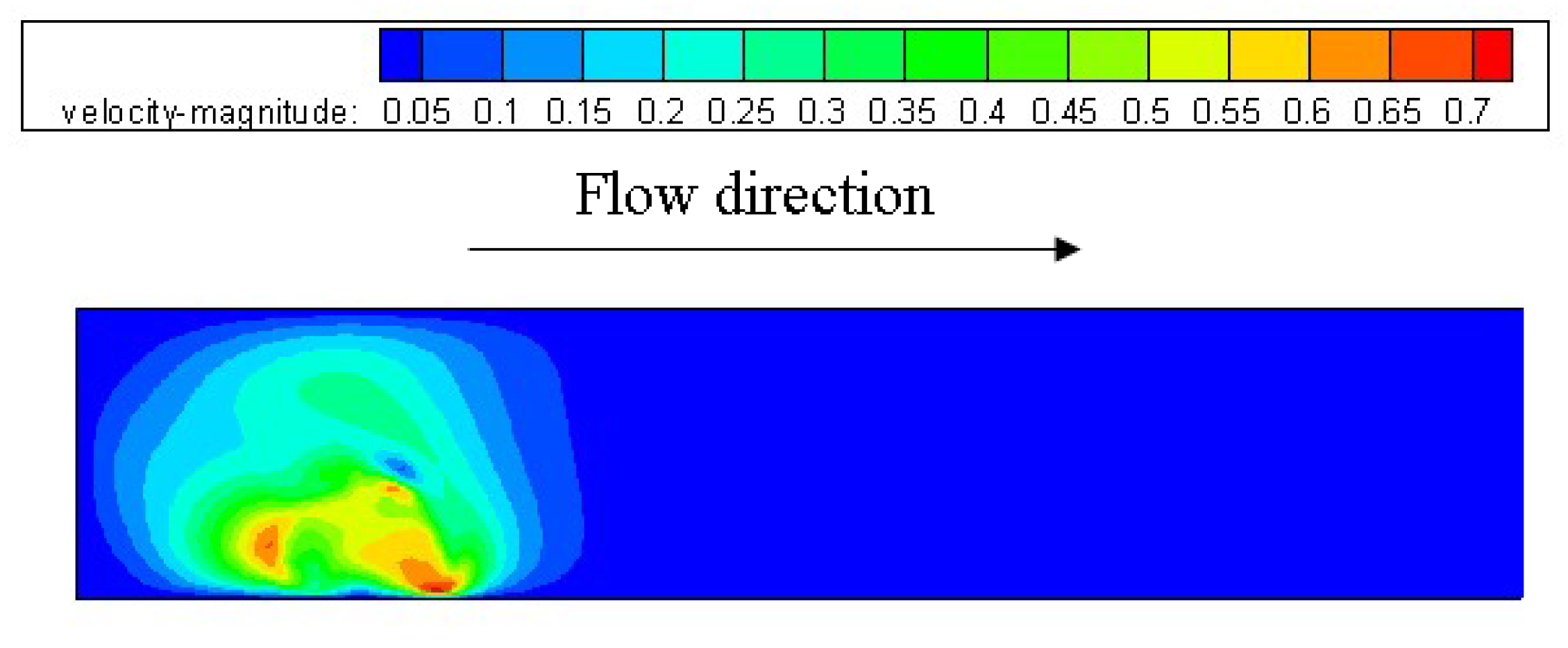
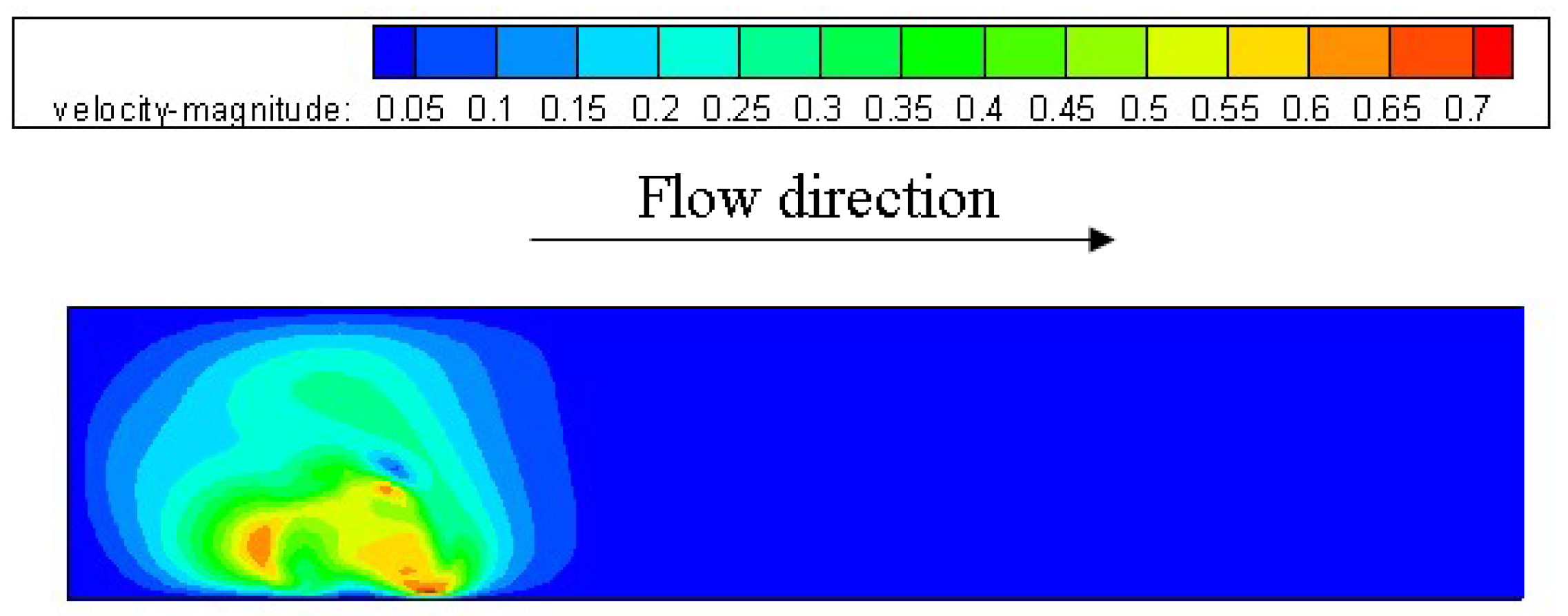
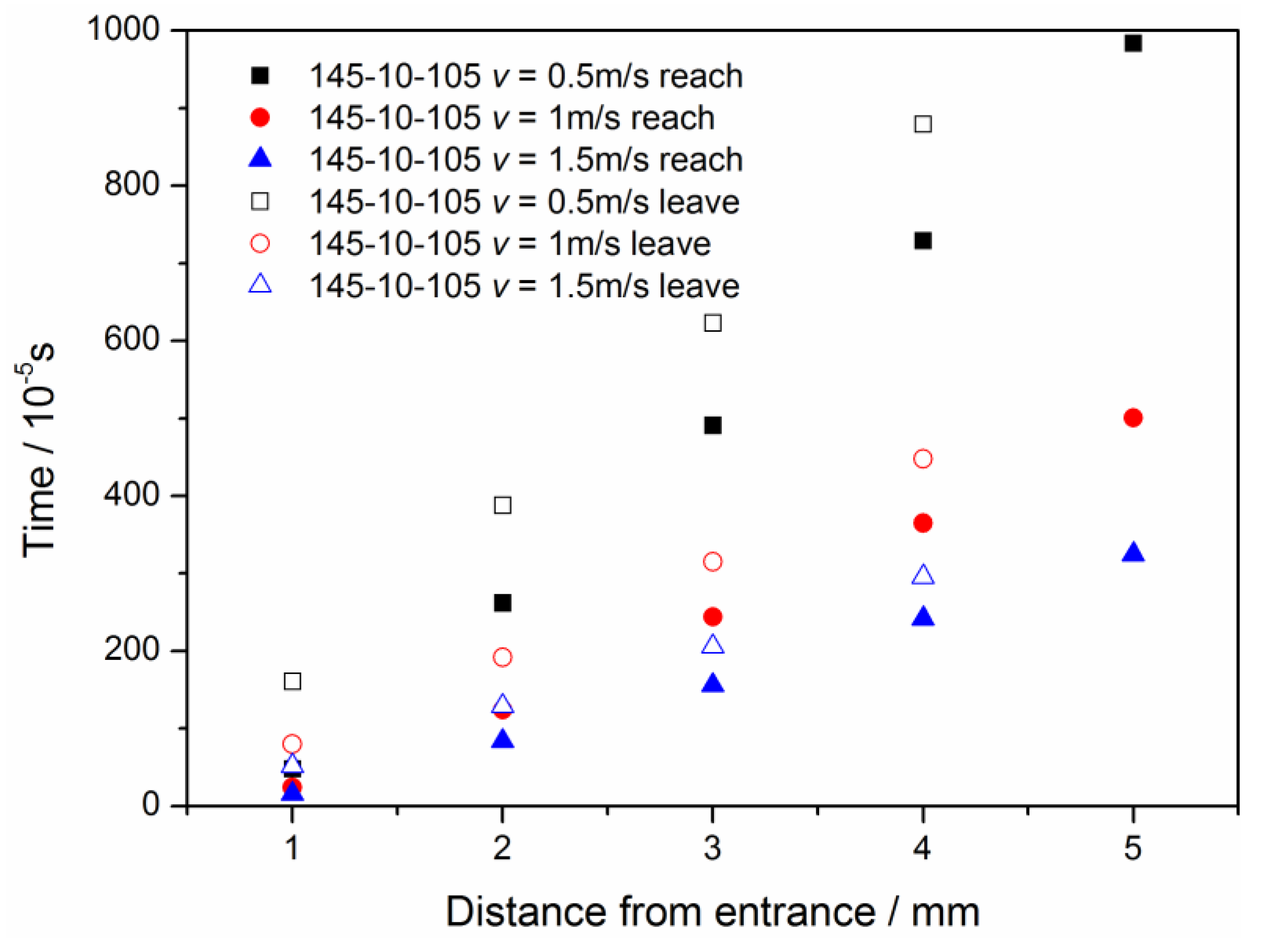
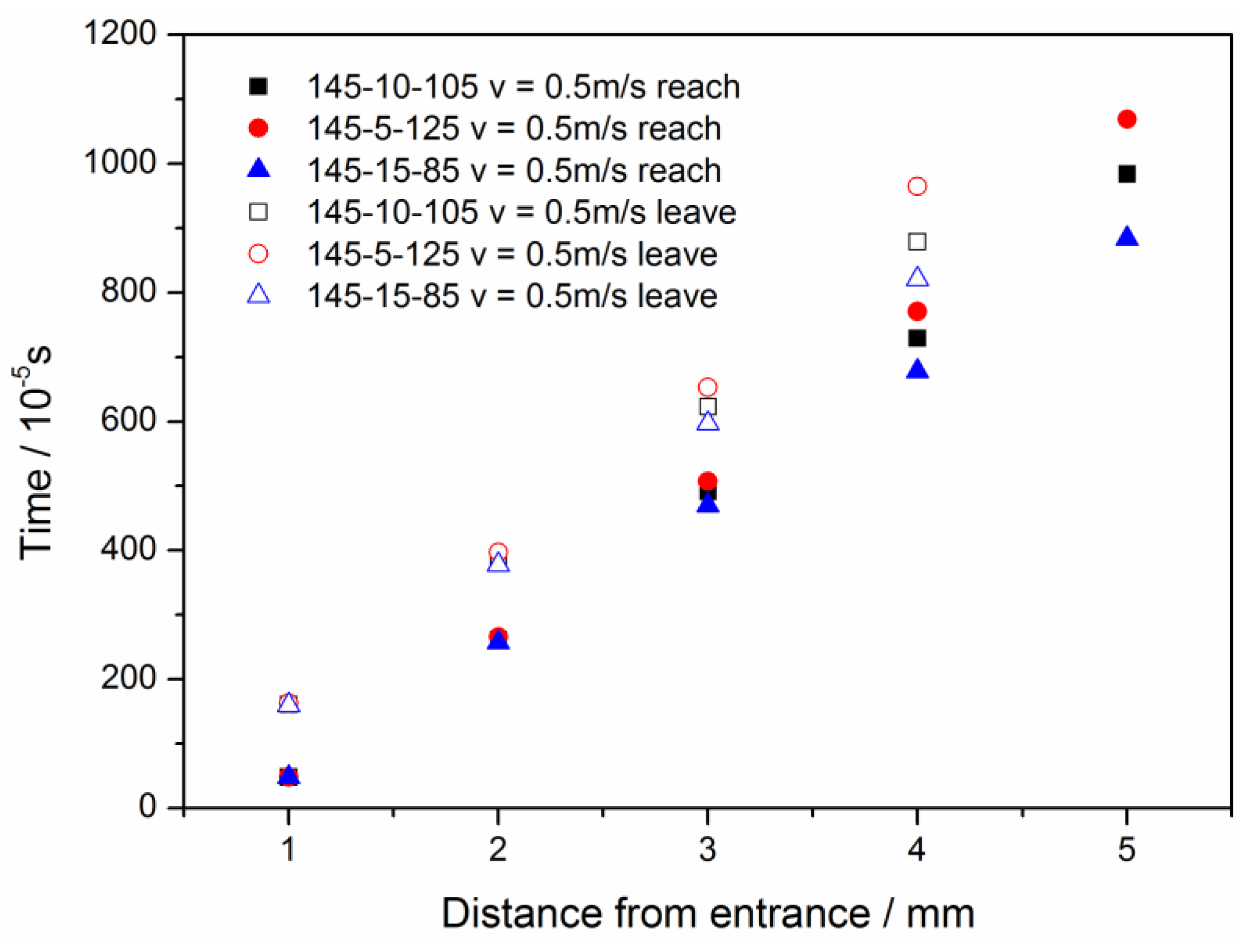
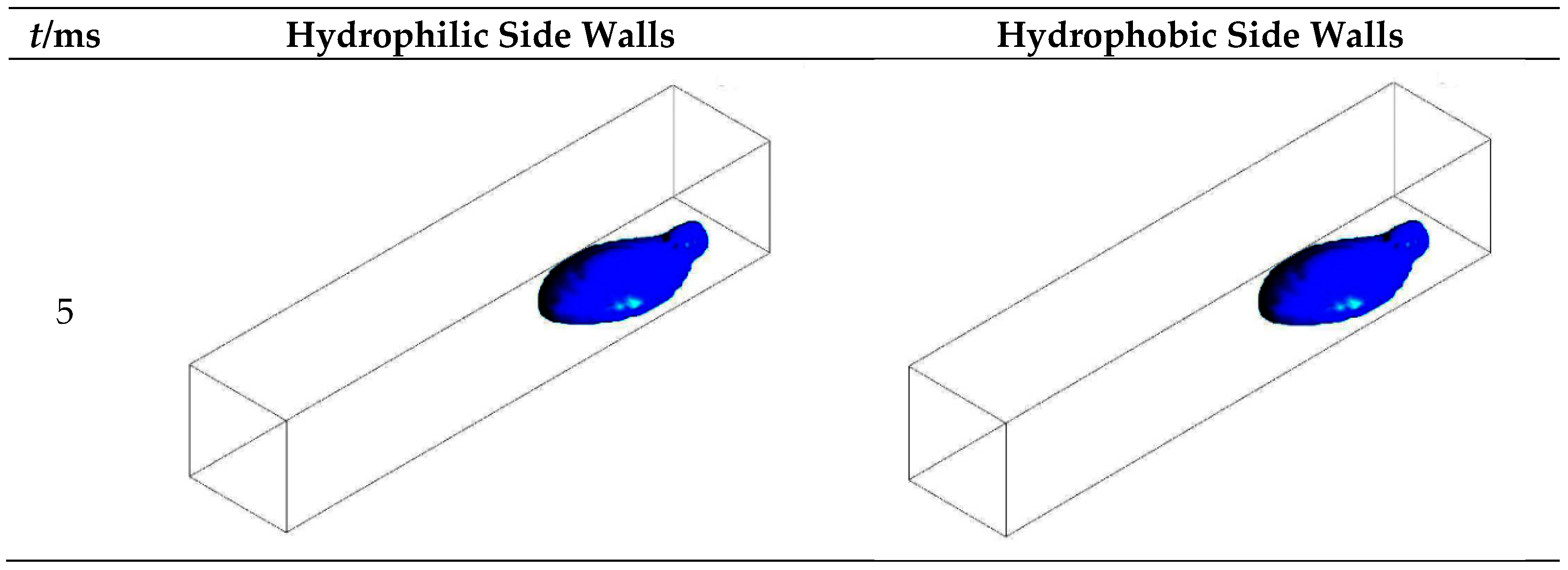
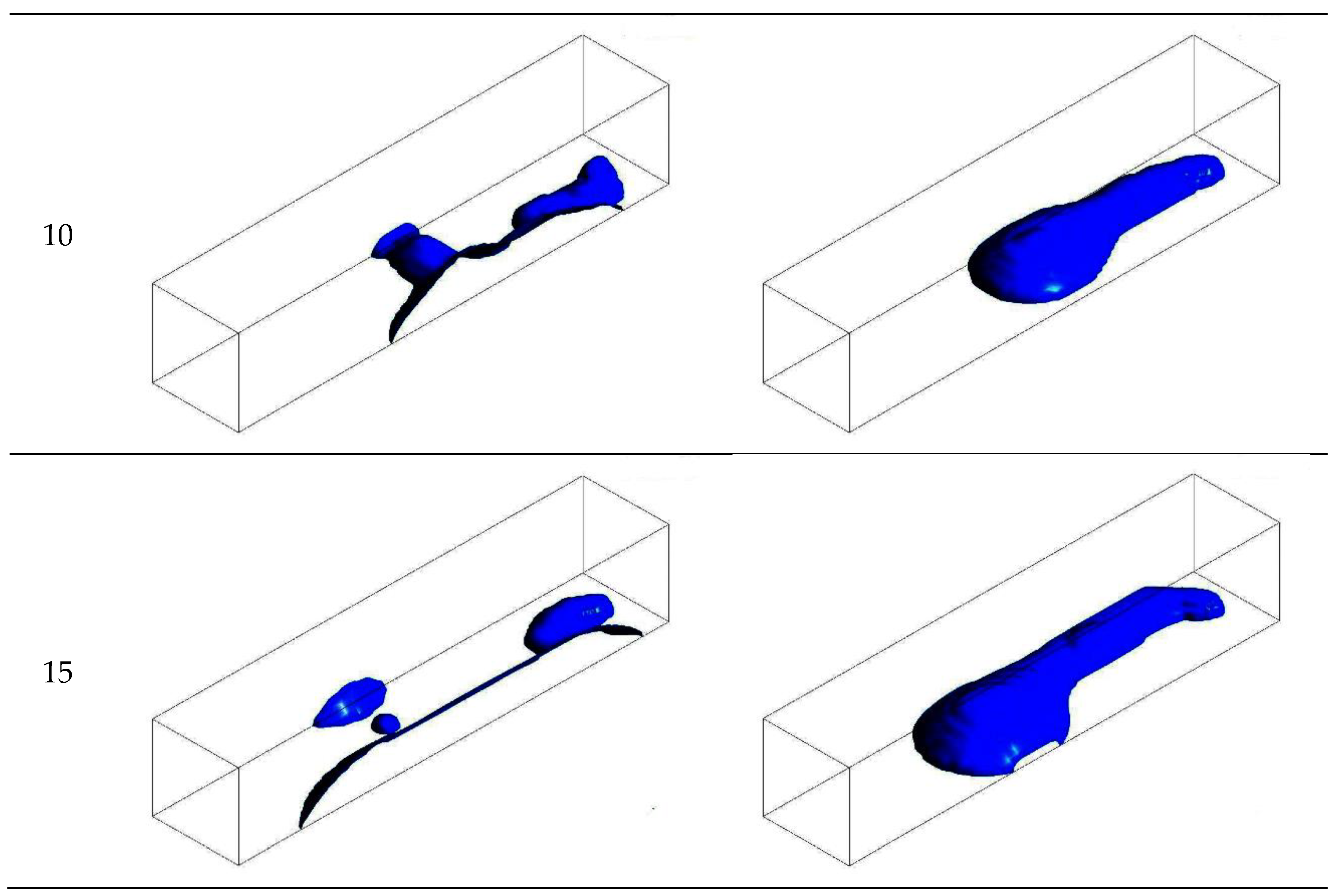
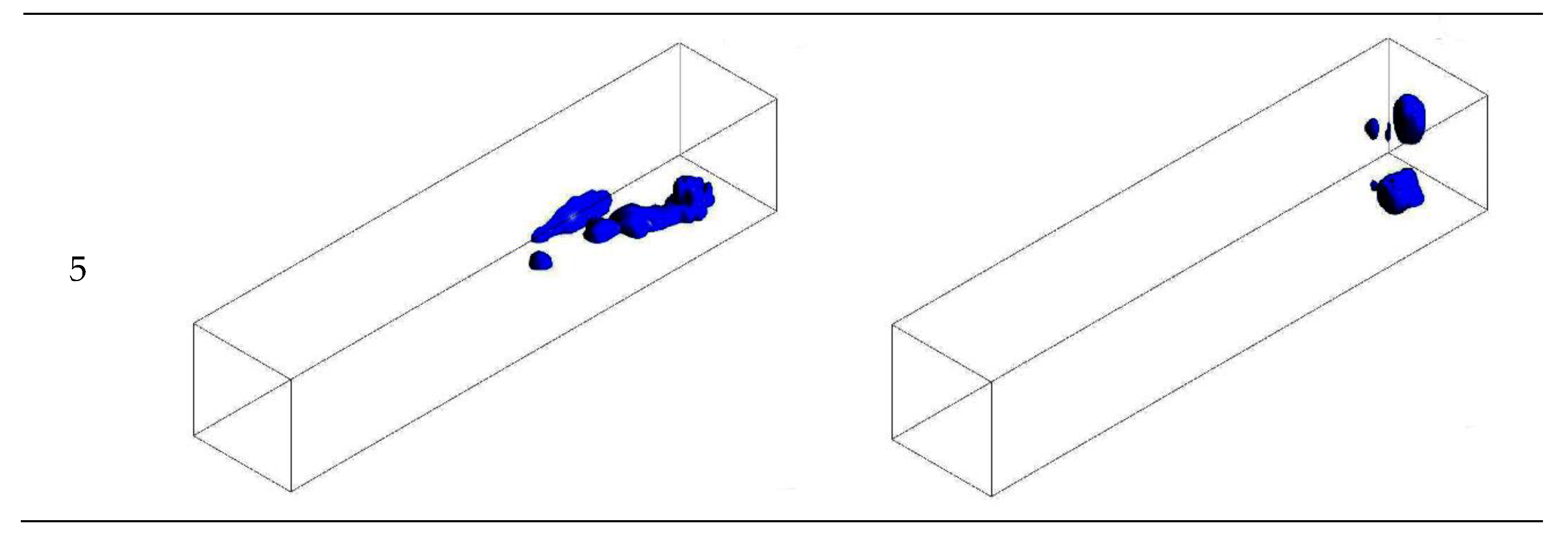
3.1. Configuration of the Straight Channel
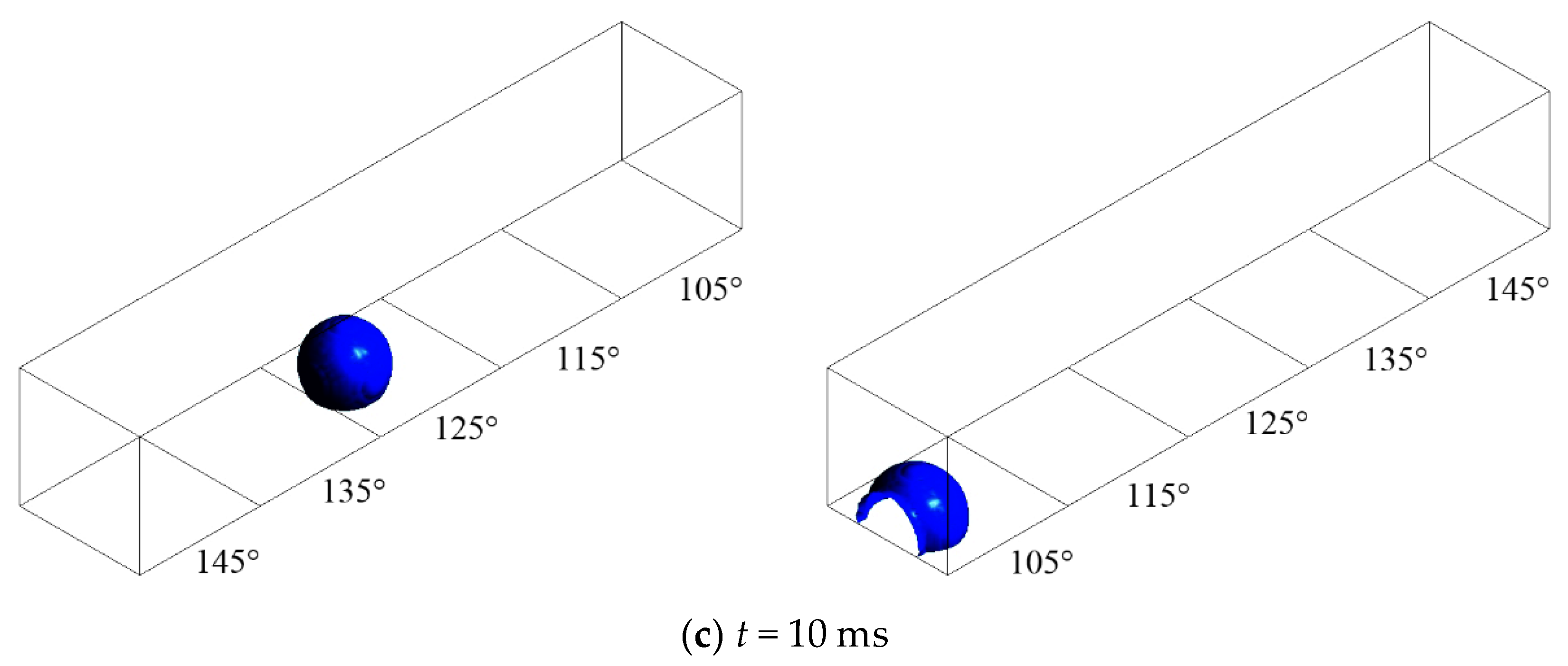
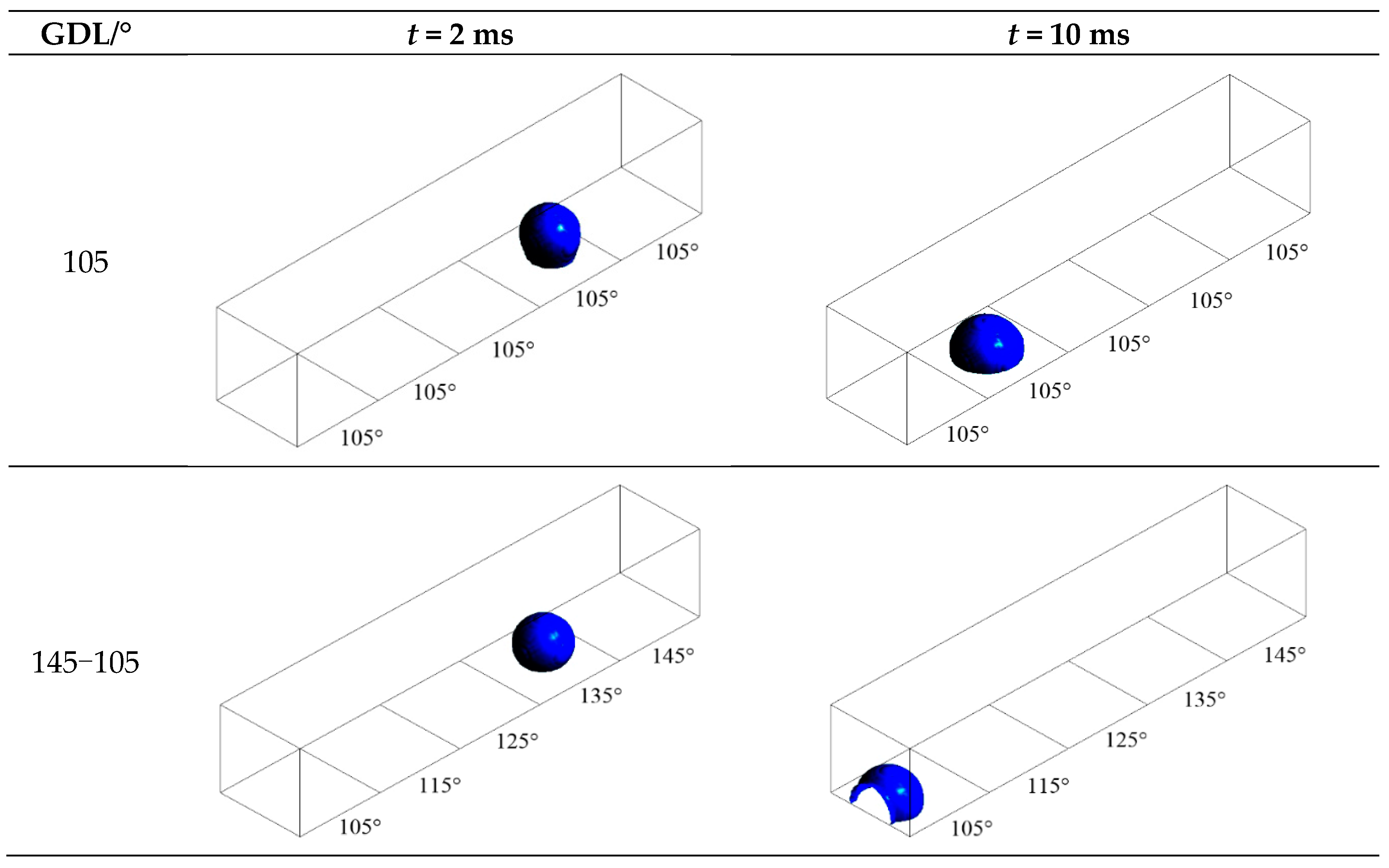
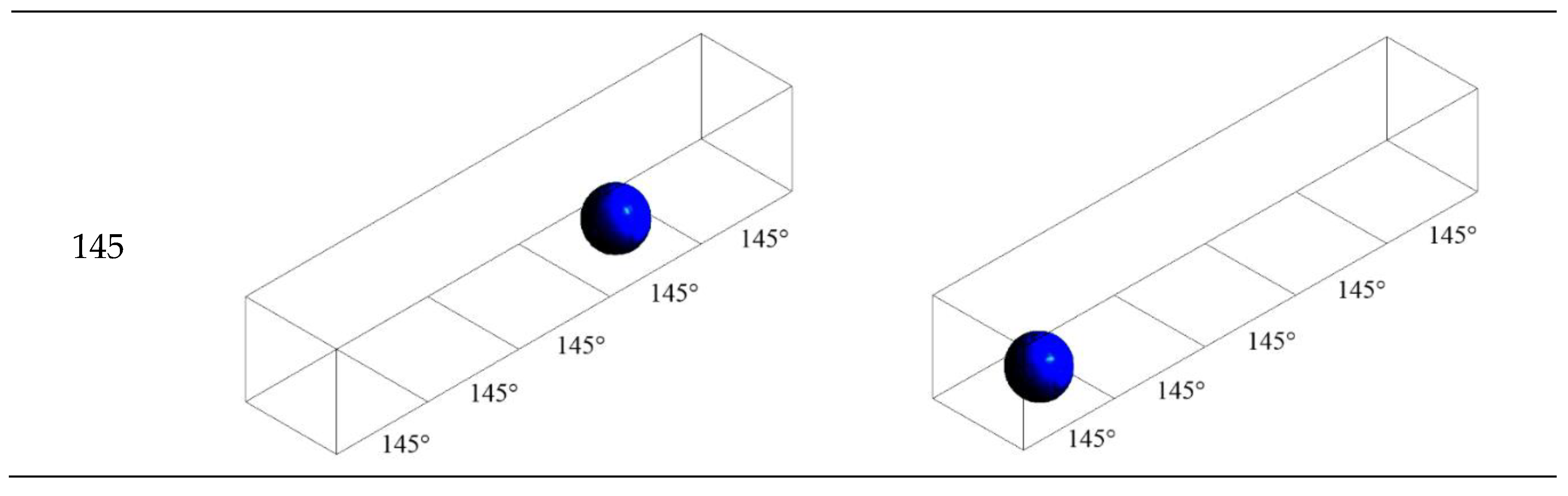
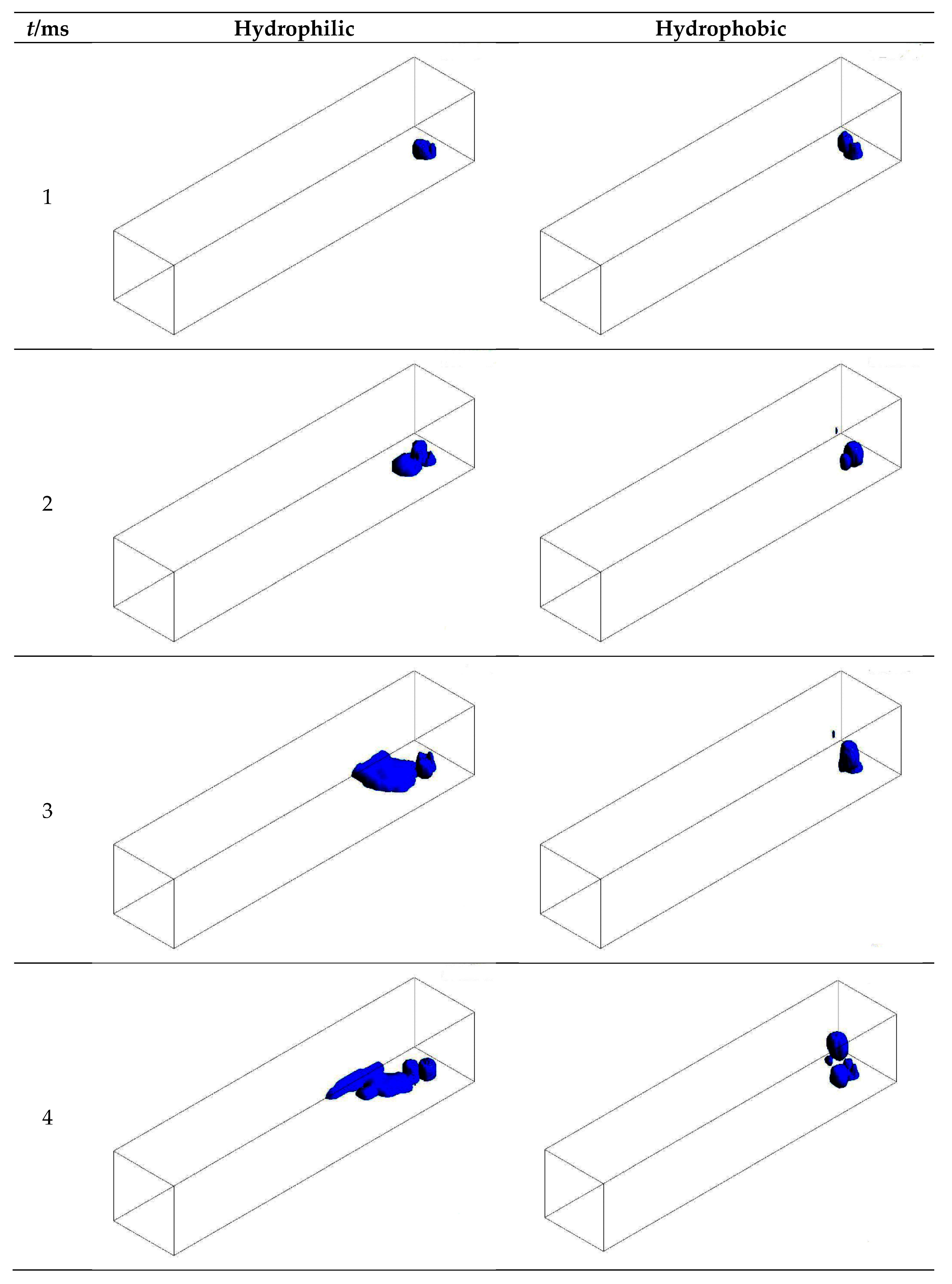
3.2. Configuration of Modified GDL Surface
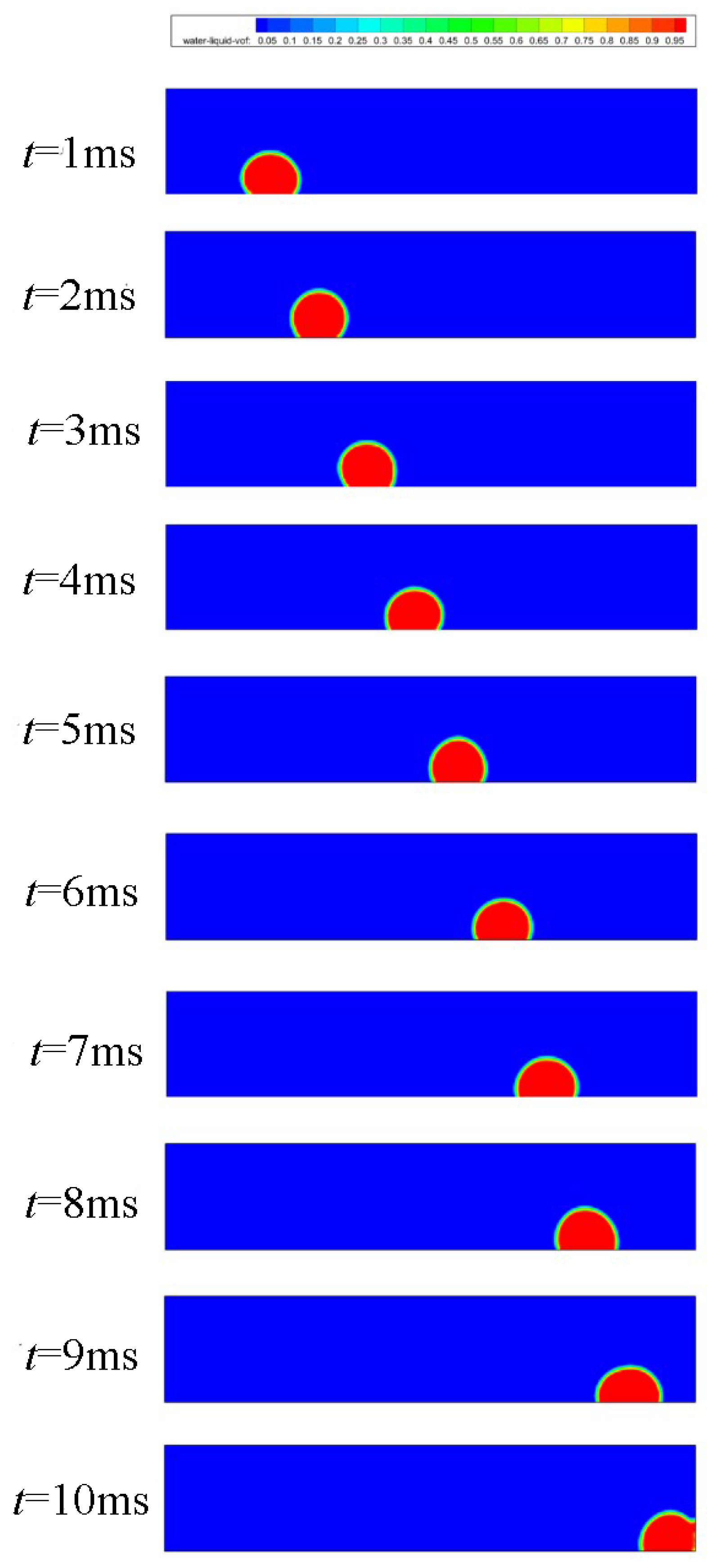
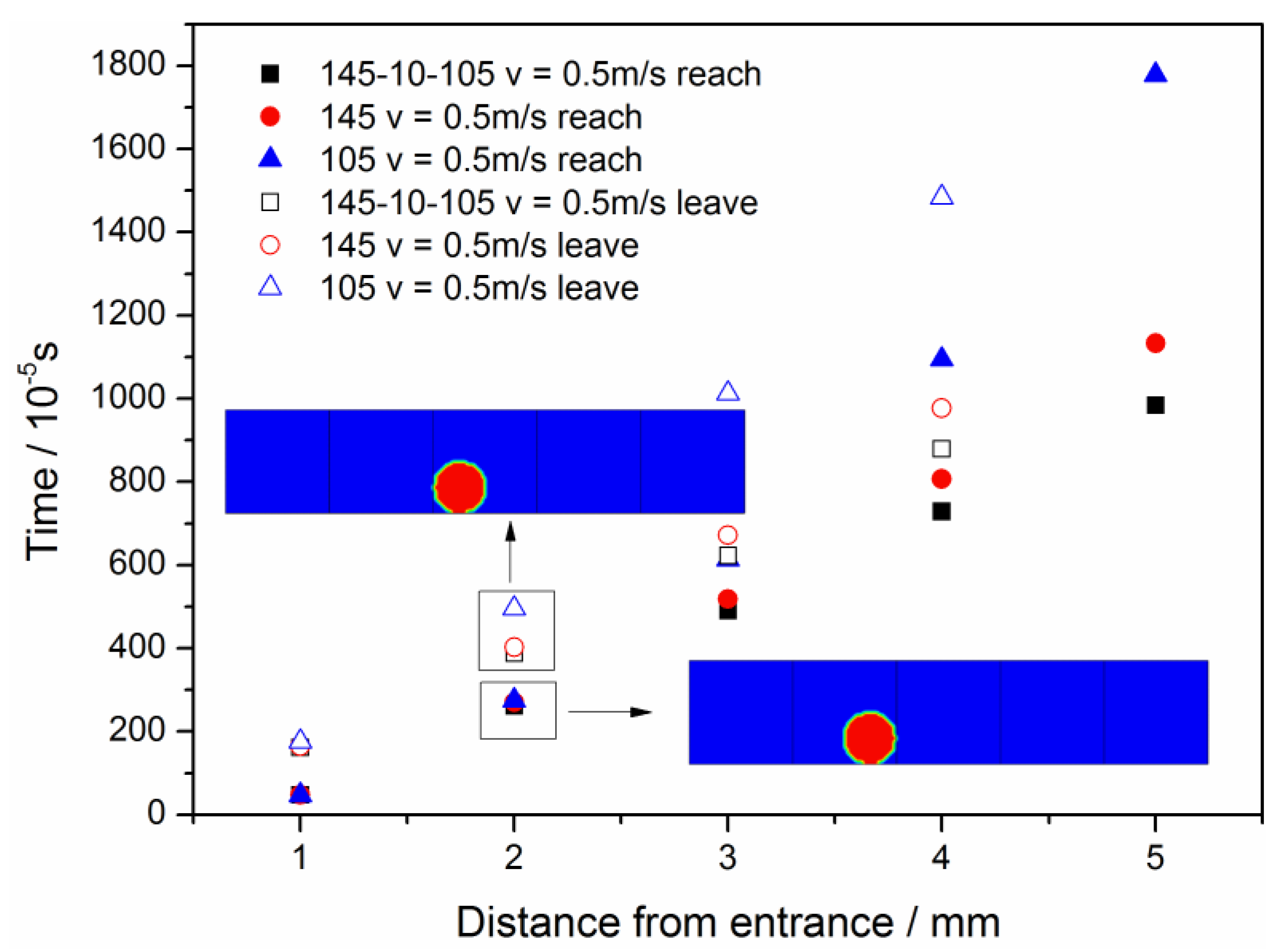
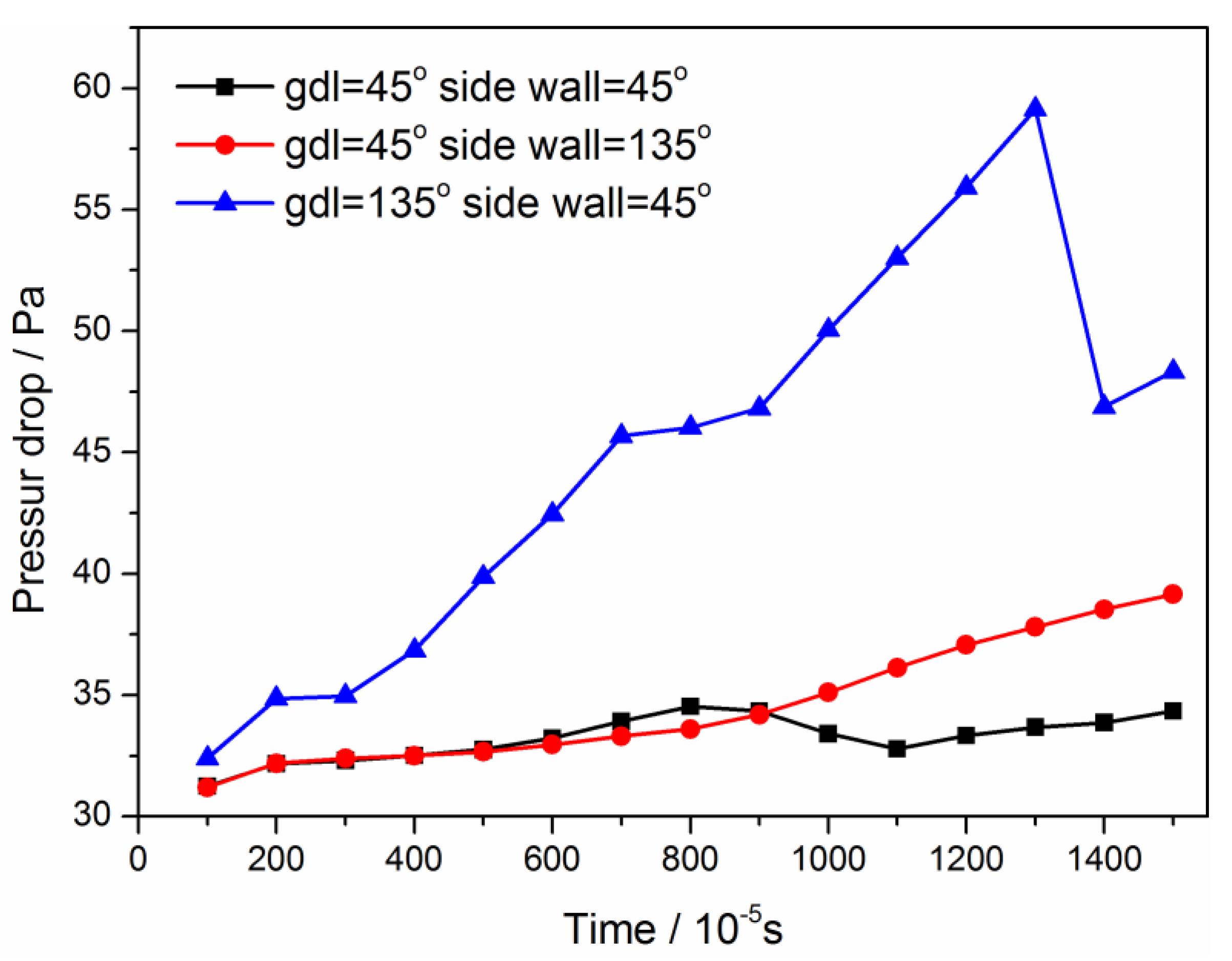
3.3. Straight Channel Configuration with a Water Inlet Hole
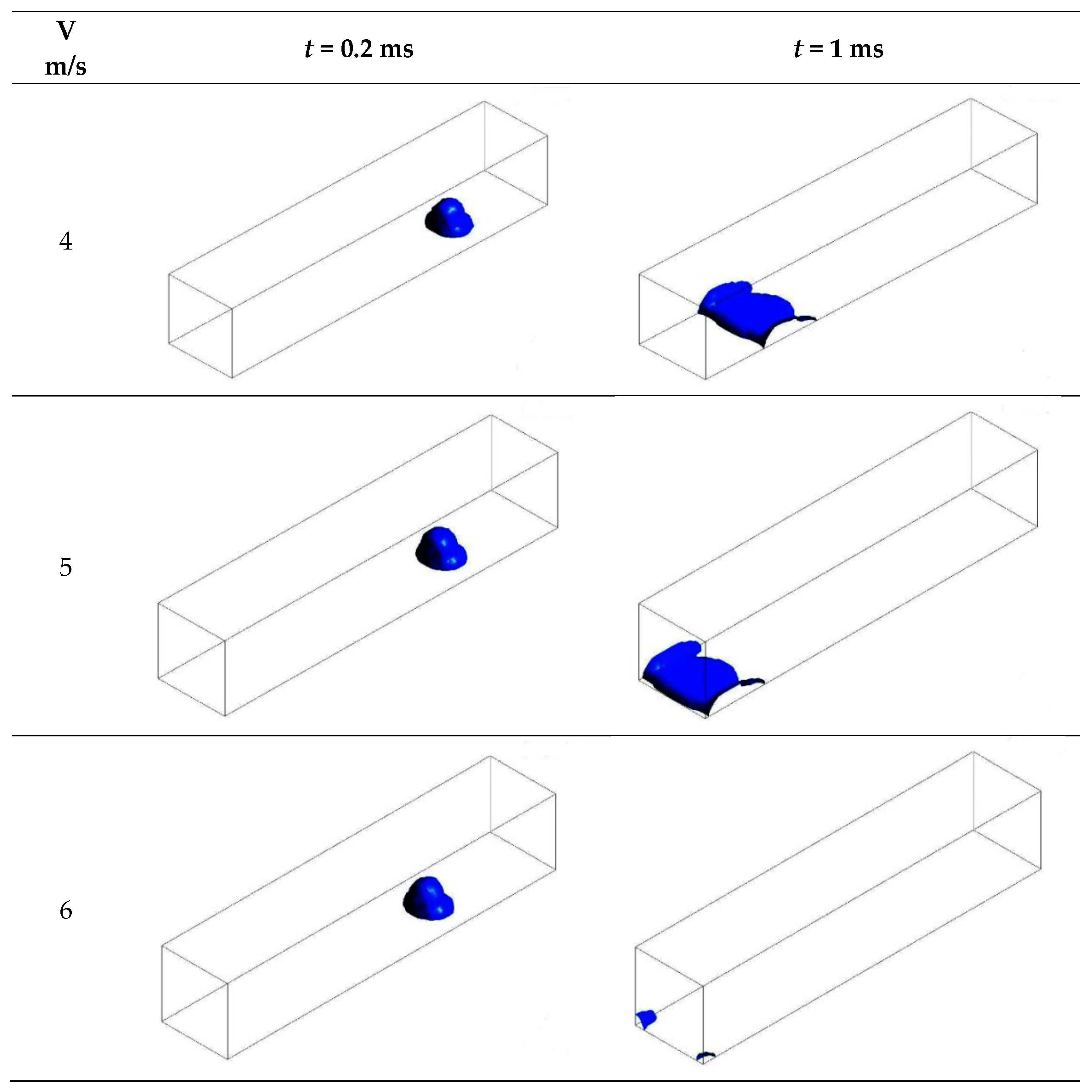
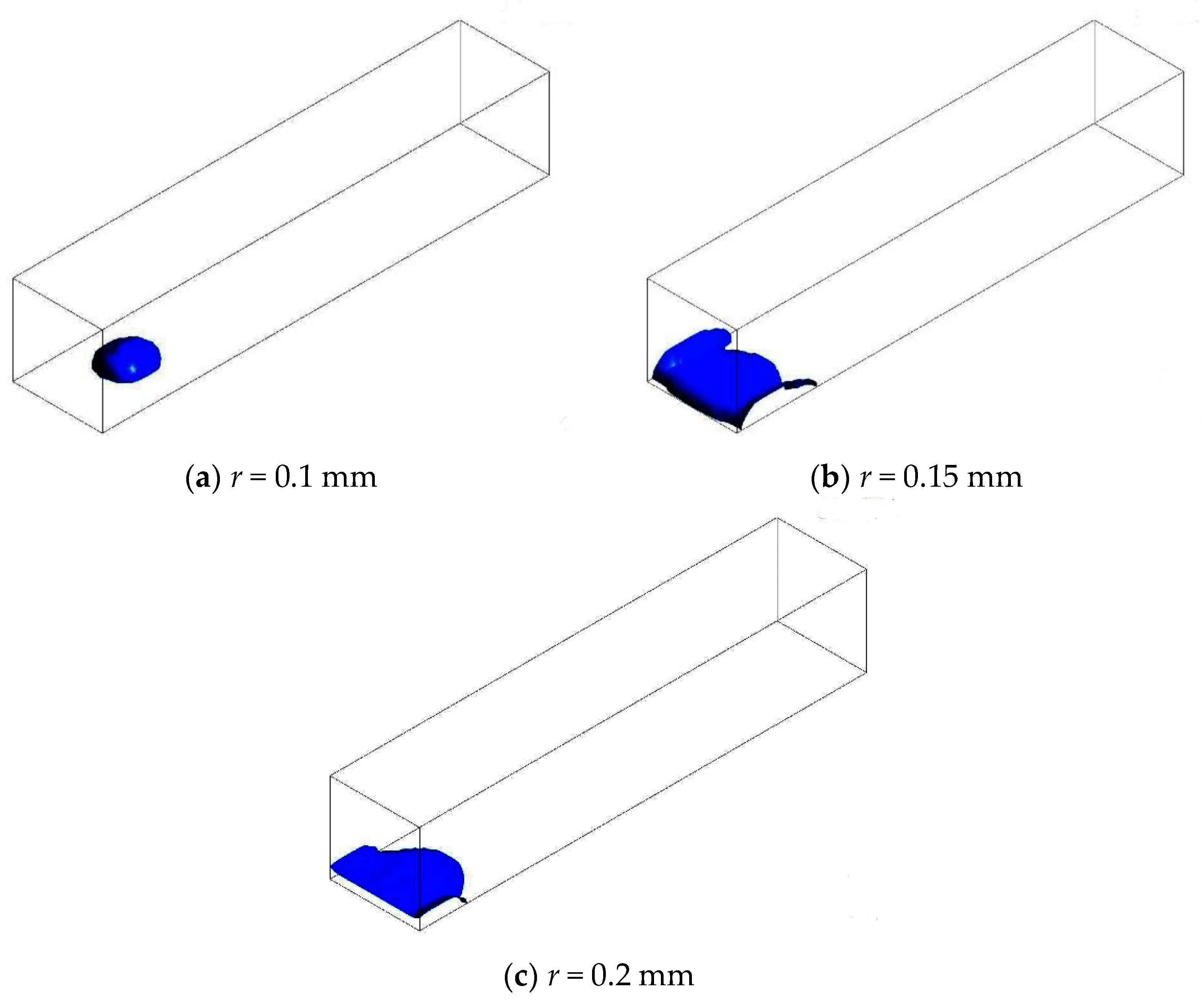
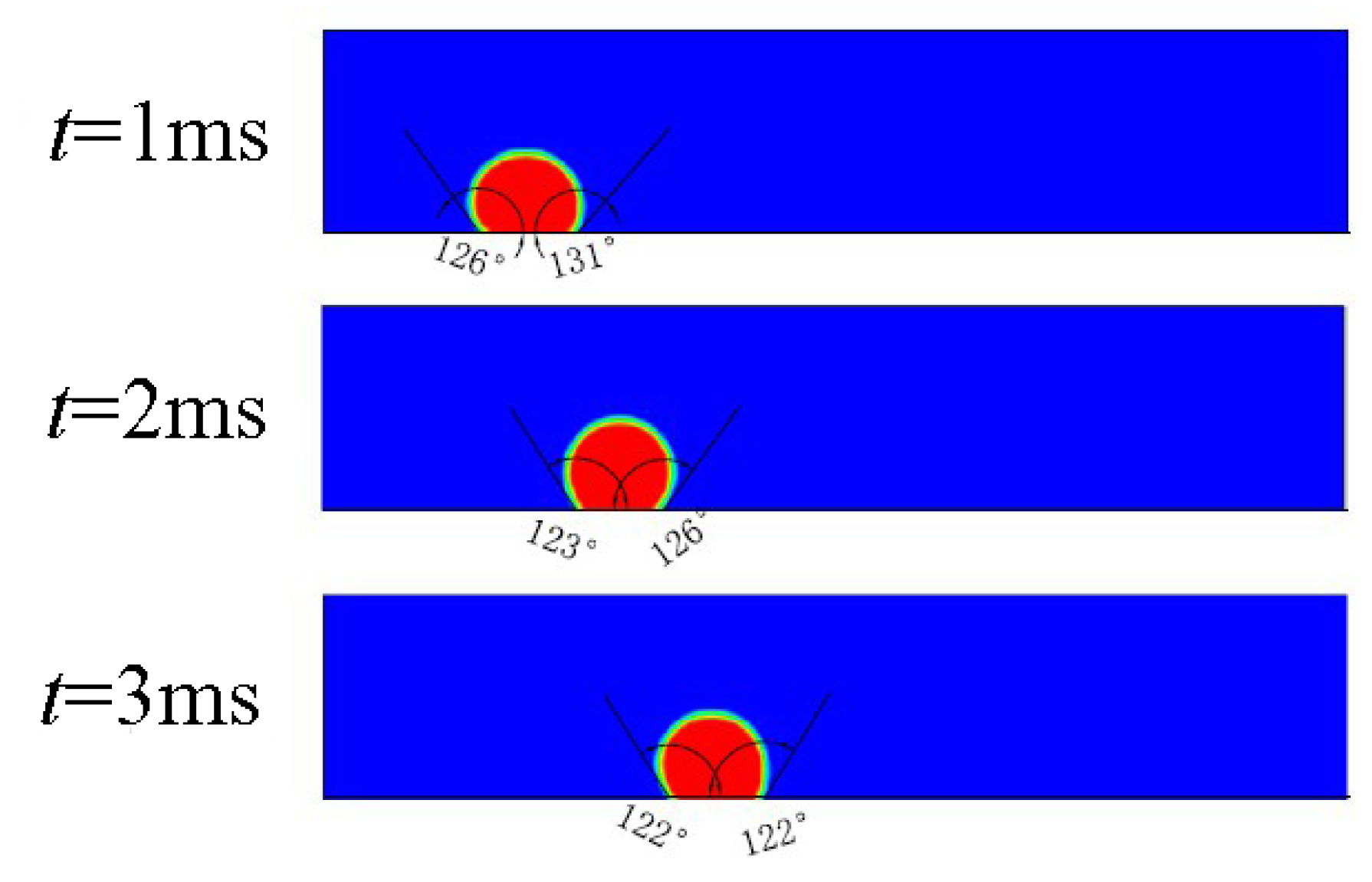
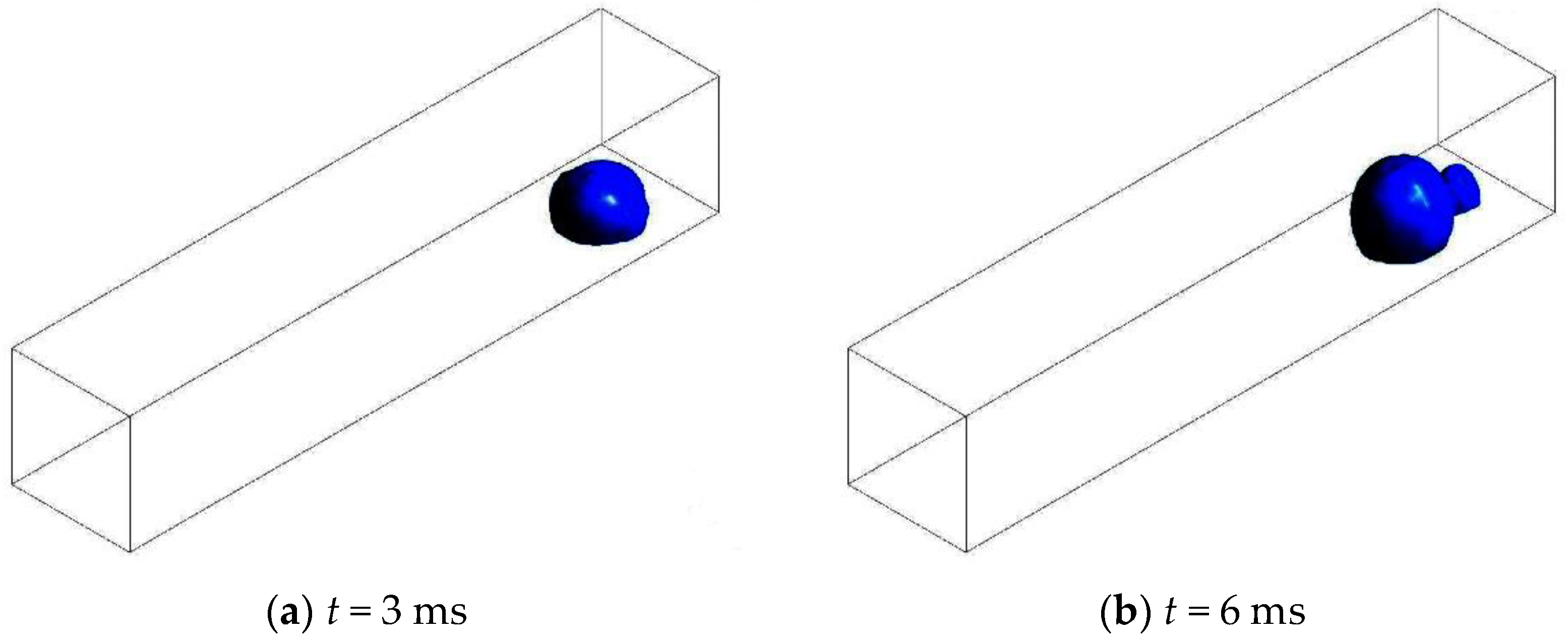
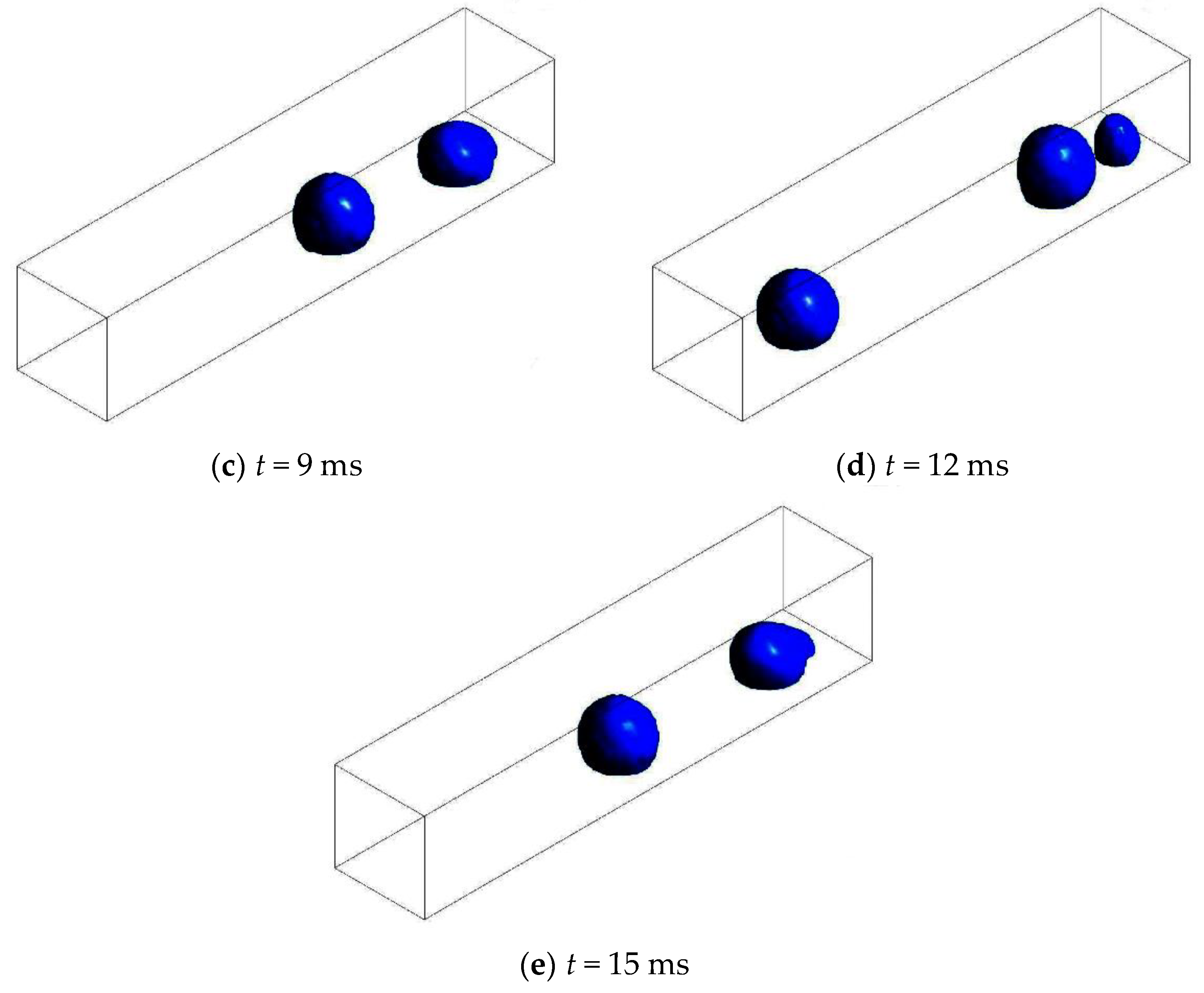
3.3.1. Without Considering Phase Transition
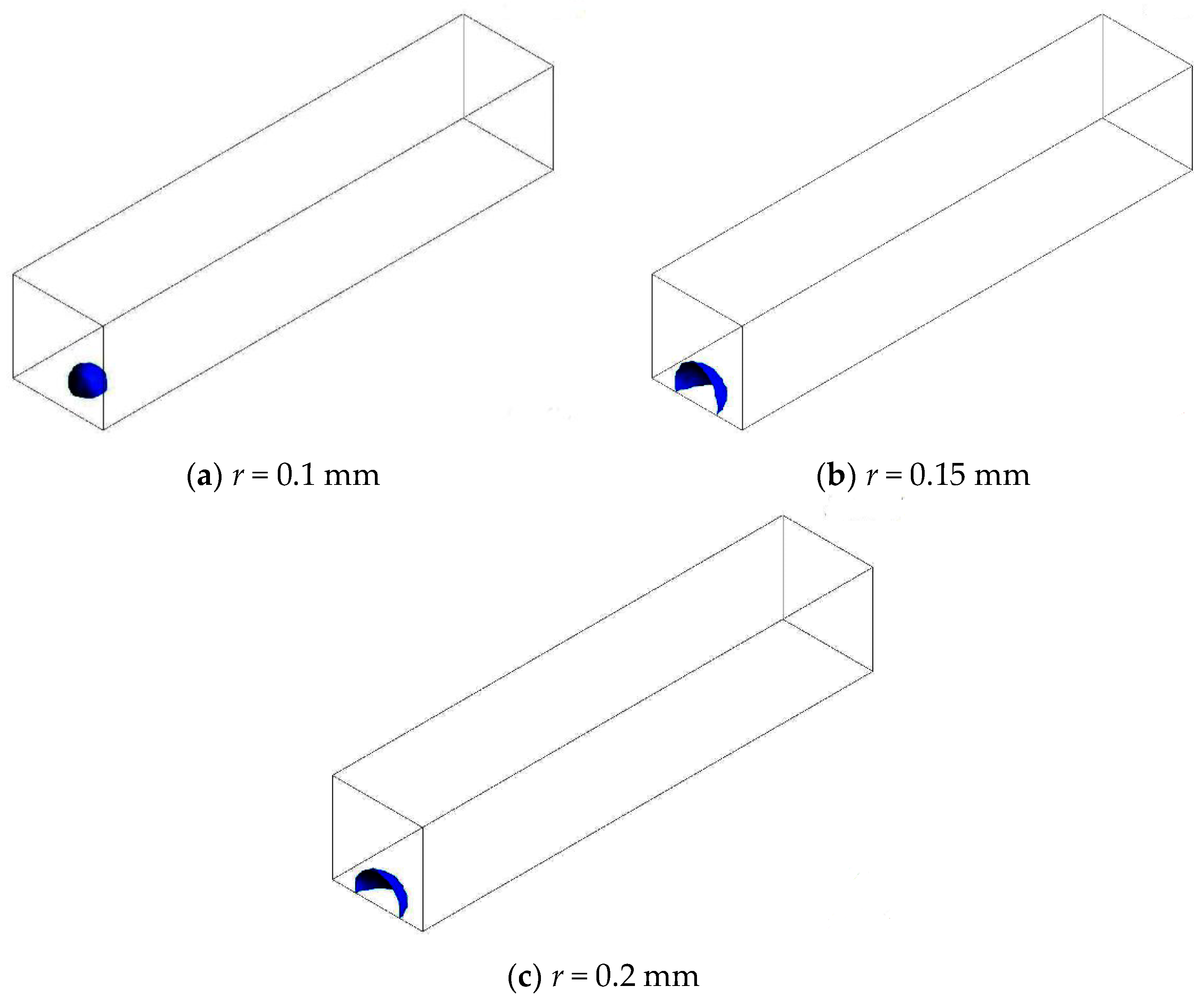
3.3.2. Considering Phase Transition
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviation
| Specific heat capacity kJ·kg−1·K−1 | |
| Condensation rate constant s−1 | |
| Latent heat of vaporization kJ·kg−1 | |
| Species | |
| Curvature | |
| keff | Effective thermal conductivity W·m−1·K−1 |
| Condensation rate kg·m−3·s−1 | |
| Time s | |
| Velocity m·s−1 | |
| Volume fraction | |
| Dynamic viscosity N·s·m−2 | |
| Volume average density kg·m−3 | |
| Surface tension N·m−1 |
References
- Wang, Y.; Chen, K.S.; Mishler, J.; Cho, S.C.; Adroher, X.C. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef]
- Chen, Y.H.; Chen, C.Y.; Lee, S.C. Technology forecasting of new clean energy: The example of hydrogen energy and fuel cell. Afr. J. Bus. Manag. 2010, 4, 1372–1380. [Google Scholar]
- Stambouli, A.B. Fuel cells: The expectations for an environmental-friendly and sustainable source of energy. Renew. Sustain. Energy Rev. 2011, 15, 4507–4520. [Google Scholar] [CrossRef]
- Castelain, C.; Lasbet, Y.; Auvity, B.; Peerhossaini, H. Experimental study of the thermal performance of chaotic geometries for their use in PEM fuel cells. Int. J. Therm. Sci. 2016, 101, 181–192. [Google Scholar] [CrossRef]
- Jung, S.H.; Kim, S.L.; Min, S.K.; Park, Y.; Lim, T.W. Experimental study of gas humidification with injectors for automotive PEM fuel cell systems. J. Power Sources 2007, 170, 324–333. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Yang, T.; Cai, Y.; Pan, M.; Tu, Z.; Zhang, C.; Chan, S.H.; Yu, Y. Mitigation studies of carbon corrosion by optimizing the opening size of the cathode outlet in a proton exchange membrane fuel cell with dead-ended anode. Energy Convers. Manag. 2016, 119, 60–66. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Yang, T.; Cai, Y.; Zhang, C.; Chan, S.H.; Yu, Y.; Tu, Z. Carbon corrosion and performance degradation mechanism in a proton exchange membrane fuel cell with dead-ended anode and cathode. Energy 2016, 106, 54–62. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; See, E.J.; Gopalan, P.; Koz, M.; Banerjee, R. Two-phase Flow in GDL and Reactant Channels of a Proton Exchange Membrane Fuel Cell. Int. J. Hydrog. Energy 2014, 39, 6620–6636. [Google Scholar] [CrossRef]
- Li, H.; Tang, Y.; Wang, Z.; Shi, Z.; Wu, S.; Song, D.; Zhang, J.; Fatih, K.; Zhang, J.; Wang, H.; et al. A review of water flooding issues in the proton exchange membrane fuel cell. J. Power Sources 2008, 178, 103–117. [Google Scholar] [CrossRef]
- Misran, E.; Hassan, N.S.M.; Wan, R.W.D.; Majlan, E.H.; Rosli, M.I. Water transport characteristics of a PEM fuel cell at various operating pressures and temperatures. Int. J. Hydrog. Energy 2013, 38, 9401–9408. [Google Scholar] [CrossRef]
- Lottin, O.; Antoine, B.; Colinart, T.; Didierjean, S.; Maranzana, G.; Moyne, C.; Ramousse, J. Modelling of the operation of Polymer Exchange Membrane Fuel Cells in the presence of electrodes flooding. Int. J. Therm. Sci. 2009, 48, 133–145. [Google Scholar] [CrossRef]
- Wan, Z.; Liu, J.; Luo, Z.; Tu, Z.; Liu, Z.; Liu, W. Evaluation of self-water-removal in a dead-ended proton exchange membrane fuel cell. Appl. Energy 2013, 104, 751–757. [Google Scholar] [CrossRef]
- Wan, Z.; Wan, J.; Liu, J.; Tu, Z.; Pan, M.; Liu, Z.; Liu, W. Water recovery and air humidification by condensing the moisture in the outlet gas of a proton exchange membrane fuel cell stack. Appl. Therm. Eng. 2012, 42, 173–178. [Google Scholar] [CrossRef]
- Liu, Z.; Shen, J.; Pei, H.; Tu, Z.; Wang, J.; Wan, Z.; Liu, W. Effect of humidified water vapor on heat balance management in a proton exchange membrane fuel cell stack. Int. J. Energy Res. 2015, 39, 504–515. [Google Scholar] [CrossRef]
- Djilali, N.; Lu, D. Influence of heat transfer on gas and water transport in fuel cells. Int. J. Therm. Sci. 2002, 41, 29–40. [Google Scholar] [CrossRef]
- Anderson, R.; Zhang, L.; Ding, Y.; Blanco, M.; Bi, X.; Wilkinson, D.P. A critical review of two-phase flow in gas flow channels of proton exchange membrane fuel cells. J. Power Sources 2010, 195, 4531–4553. [Google Scholar] [CrossRef]
- Zhu, X.; Sui, P.; Djilali, N. Three-dimensional numerical simulations of water droplet dynamics in a PEMFC gas channel. J. Power Sources 2008, 181, 101–115. [Google Scholar] [CrossRef]
- Jiao, K.; Zhou, B. Innovative gas diffusion layers and their water removal characteristics in PEM fuel cell cathode. J. Power Sources 2007, 169, 296–314. [Google Scholar] [CrossRef]
- Amara, M.E.A.B.; Nasrallah, S.B. Numerical simulation of droplet dynamics in a proton exchange membrane (PEMFC) fuel cell micro-channel. Int. J. Hydrog. Energy 2015, 40, 1333–1342. [Google Scholar] [CrossRef]
- Banerjee, R.; Kandlikar, S.G. Liquid water quantification in the cathode side gas channels of a proton exchange membrane fuel cell through two-phase flow visualization. J. Power Sources 2014, 247, 9–19. [Google Scholar] [CrossRef]
- Gao, S.; Liao, Q.; Liu, W.; Liu, Z. Coalescence-Induced Jumping of Nanodroplets on Textured Surfaces. J. Phys. Chem. Lett. 2017, 9, 13–18. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Liao, Q.; Liu, W.; Liu, Z. Nanodroplets Impact on Rough Surfaces: A Simulation and Theoretical Study. Langmuir 2018, 34, 5910–5917. [Google Scholar] [CrossRef] [PubMed]
- Ous, T.; Arcoumanis, C. Visualisation of water droplets during the operation of PEM fuel cells. J. Power Sources 2007, 173, 137–148. [Google Scholar] [CrossRef]
- Lee, D.; Bae, J. Visualization of flooding in a single cell and stacks by using a newly-designed transparent PEMFC. Int. J. Hydrog. Energy. 2012, 37, 422–435. [Google Scholar] [CrossRef]
- Zhan, Z.; Wang, C.; Fu, W.; Pan, M. Visualization of water transport in a transparent PEMFC. Int. J. Hydrog. Energy 2012, 37, 1094–1105. [Google Scholar] [CrossRef]
- Kumbur, E.C.; Sharp, K.V.; Mench, M.M. Liquid droplet behavior and instability in a polymer electrolyte fuel cell flow channel. J. Power Sources 2006, 161, 333–345. [Google Scholar] [CrossRef]
- Bazylak, A.; Sinton, D.; Liu, Z.S.; Djilali, N. Effect of compression on liquid water transport and microstructure of PEMFC gas diffusion layers. J. Power Sources 2007, 163, 784–792. [Google Scholar] [CrossRef]
- Sinha, P.K.; Wang, C.Y. Pore-network modeling of liquid water transport in gas diffusion layer of a polymer electrolyte fuel cell. Electrochim. Acta 2007, 52, 7936–7945. [Google Scholar] [CrossRef]
- Pasaogullari, U.; Wang, C.Y. Two-phase transport and the role of micro-porous layer in polymer electrolyte fuel cells. Electrochim. Acta 2004, 49, 4359–4369. [Google Scholar] [CrossRef]
- Nam, J.H.; Kaviany, M. Effective diffusivity and water-saturation distribution in single-and two-layer PEMFC diffusion medium. Int. J. Heat Mass Transf. 2003, 46, 4595–4611. [Google Scholar] [CrossRef]
- ANSYS 14.0 Help Connecting Modeling Multiphase Flows; ANSYS, Inc.: Canonsburg, PA, USA, 2011.
- Han, B.; Meng, H. Lattice Boltzmann simulation of liquid water transport in turning regions of serpentine gas channels in proton exchange membrane fuel cells. J. Power Sources 2012, 217, 268–279. [Google Scholar] [CrossRef]
- Han, B.; Yu, J.; Meng, H. Lattice Boltzmann simulations of liquid droplets development and interaction in a gas channel of a proton exchange membrane fuel cell. J. Power Sources 2012, 202, 175–183. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, X.; Ge, Y.; Shen, J.; Liu, W. Multi-objective optimization of operating conditions and channel structure for a proton exchange membrane fuel cell. Int. J. Heat Mass Transf. 2017, 111, 289–298. [Google Scholar] [CrossRef]
- Zeng, X.; Ge, Y.; Shen, J.; Zeng, L.; Liu, Z.; Liu, W. The optimization of channels for a proton exchange membrane fuel cell applying genetic algorithm. Int. J. Heat Mass Transf. 2017, 105, 81–89. [Google Scholar] [CrossRef]
- Ge, Y.; Liu, Z.C.; Sun, H.N.; Liu, W. Optimal design of a segmented thermoelectric generator based on three-dimensional numerical simulation and multi-objective genetic algorithm. Energy 2018, 147, 1060–1069. [Google Scholar] [CrossRef]
- Ge, Y.; Shan, F.; Liu, Z.C.; Liu, W. Optimal Structural Design of a Heat Sink with Laminar Single-Phase Flow Using Computational Fluid Dynamics-Based Multi-Objective Genetic Algorithm. J. Heat Transf. 2017, 140, 022803. [Google Scholar] [CrossRef]
- Ge, Y.; Liu, Z.C.; Liu, W. Multi-objective genetic optimization of the heat transfer for tube inserted with porous media. Int. J. Heat Mass Transf. 2016, 101, 981–987. [Google Scholar] [CrossRef]
- Ge, Y.; Liu, Z.; Liu, W.; Chen, G. Active optimization design theory and method for heat transfer unit and its application on shape design of cylinder in convective heat transfer. Int. J. Heat Mass Transf. 2015, 90, 702–709. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Liu, Z.; Liu, F.; Liu, W. Numerical Simulation of Water Transport in a Proton Exchange Membrane Fuel Cell Flow Channel. Energies 2018, 11, 1770. https://doi.org/10.3390/en11071770
Shen J, Liu Z, Liu F, Liu W. Numerical Simulation of Water Transport in a Proton Exchange Membrane Fuel Cell Flow Channel. Energies. 2018; 11(7):1770. https://doi.org/10.3390/en11071770
Chicago/Turabian StyleShen, Jun, Zhichun Liu, Fan Liu, and Wei Liu. 2018. "Numerical Simulation of Water Transport in a Proton Exchange Membrane Fuel Cell Flow Channel" Energies 11, no. 7: 1770. https://doi.org/10.3390/en11071770
APA StyleShen, J., Liu, Z., Liu, F., & Liu, W. (2018). Numerical Simulation of Water Transport in a Proton Exchange Membrane Fuel Cell Flow Channel. Energies, 11(7), 1770. https://doi.org/10.3390/en11071770





