Improvement in Harmonic Compensation of a Smart Charger with a Constant DC-Capacitor Voltage-Control-Based Strategy for Electric Vehicles in Single-Phase Three-Wire Distribution Feeders
Abstract
:1. Introduction
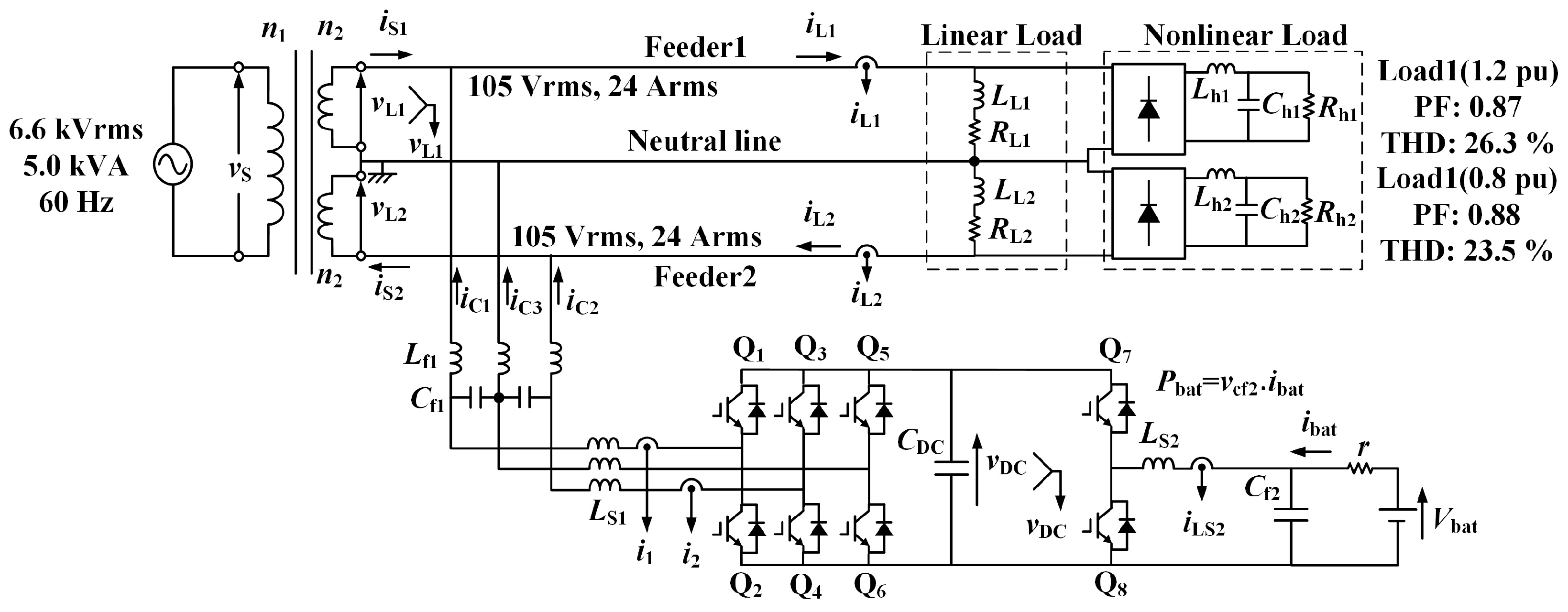
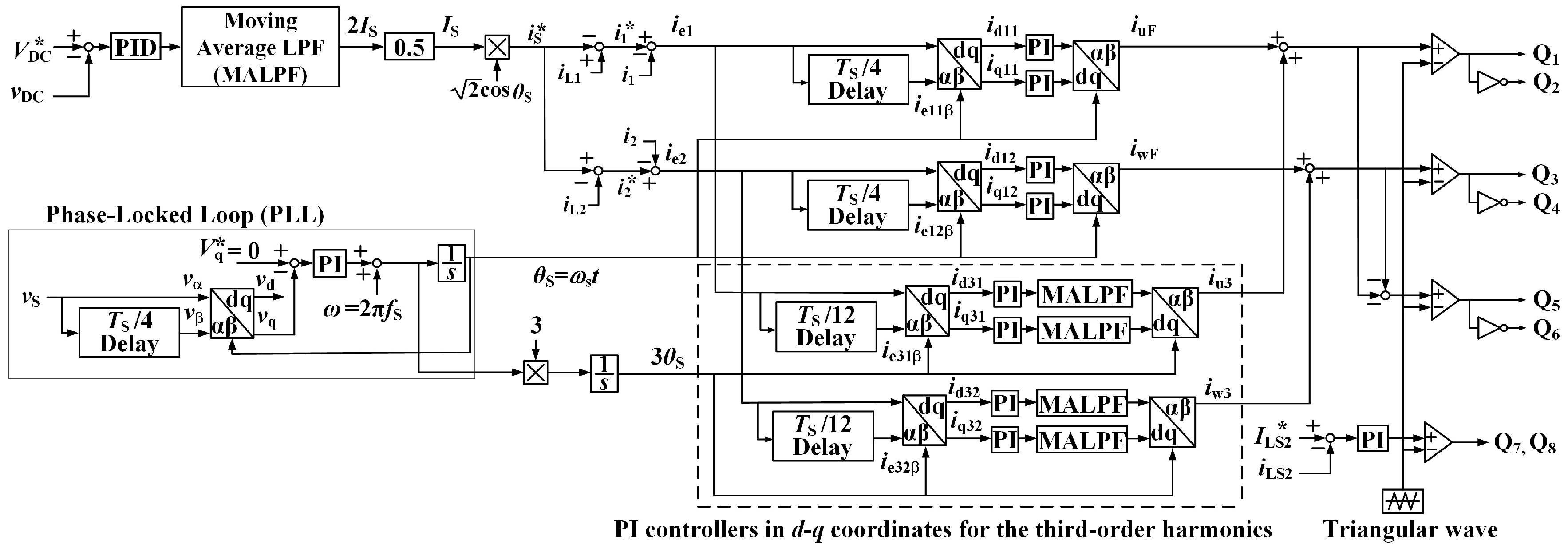
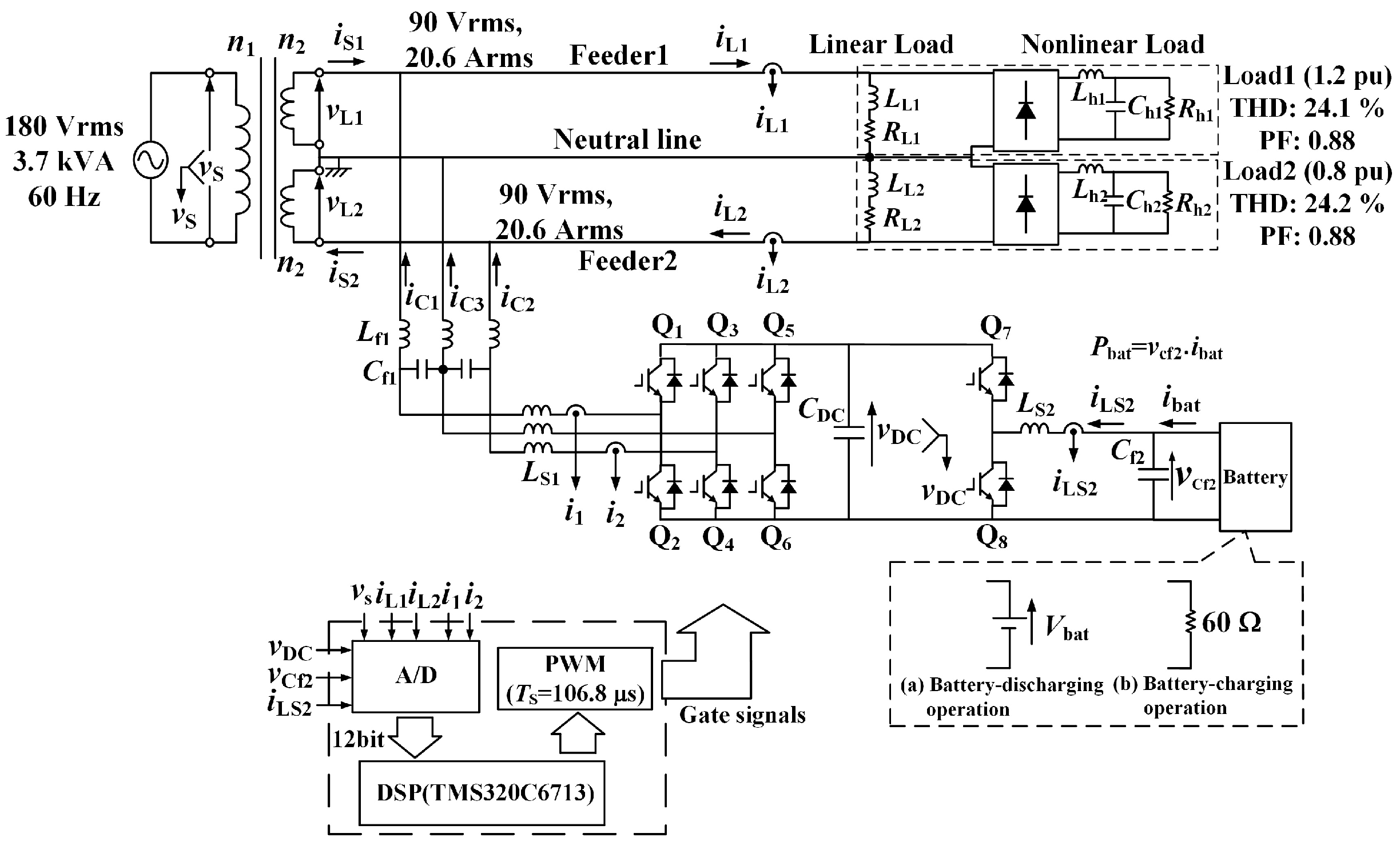
2. Smart Charger for EVs
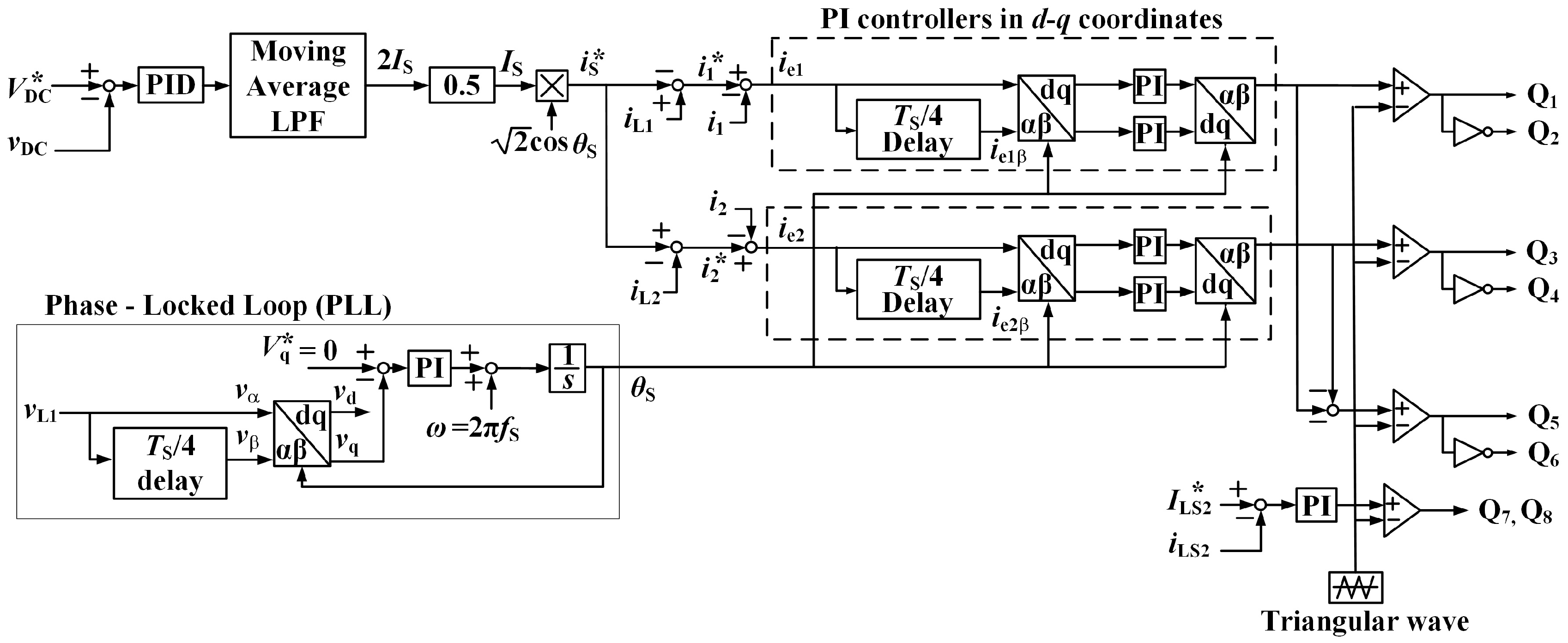
2.1. Constant DC-Capacitor Voltage-Control Strategy for Harmonic Compensation
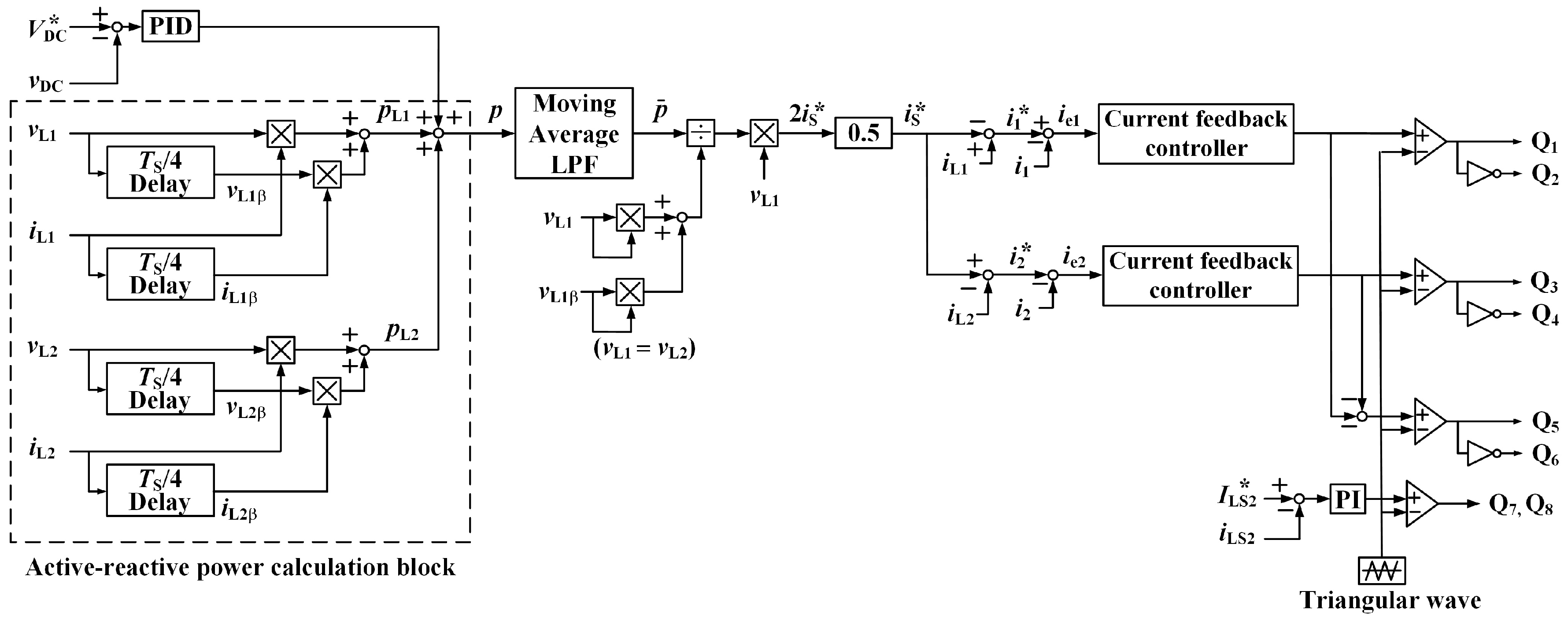
2.2. Improvement in Harmonic Compensation for a Smart Charger
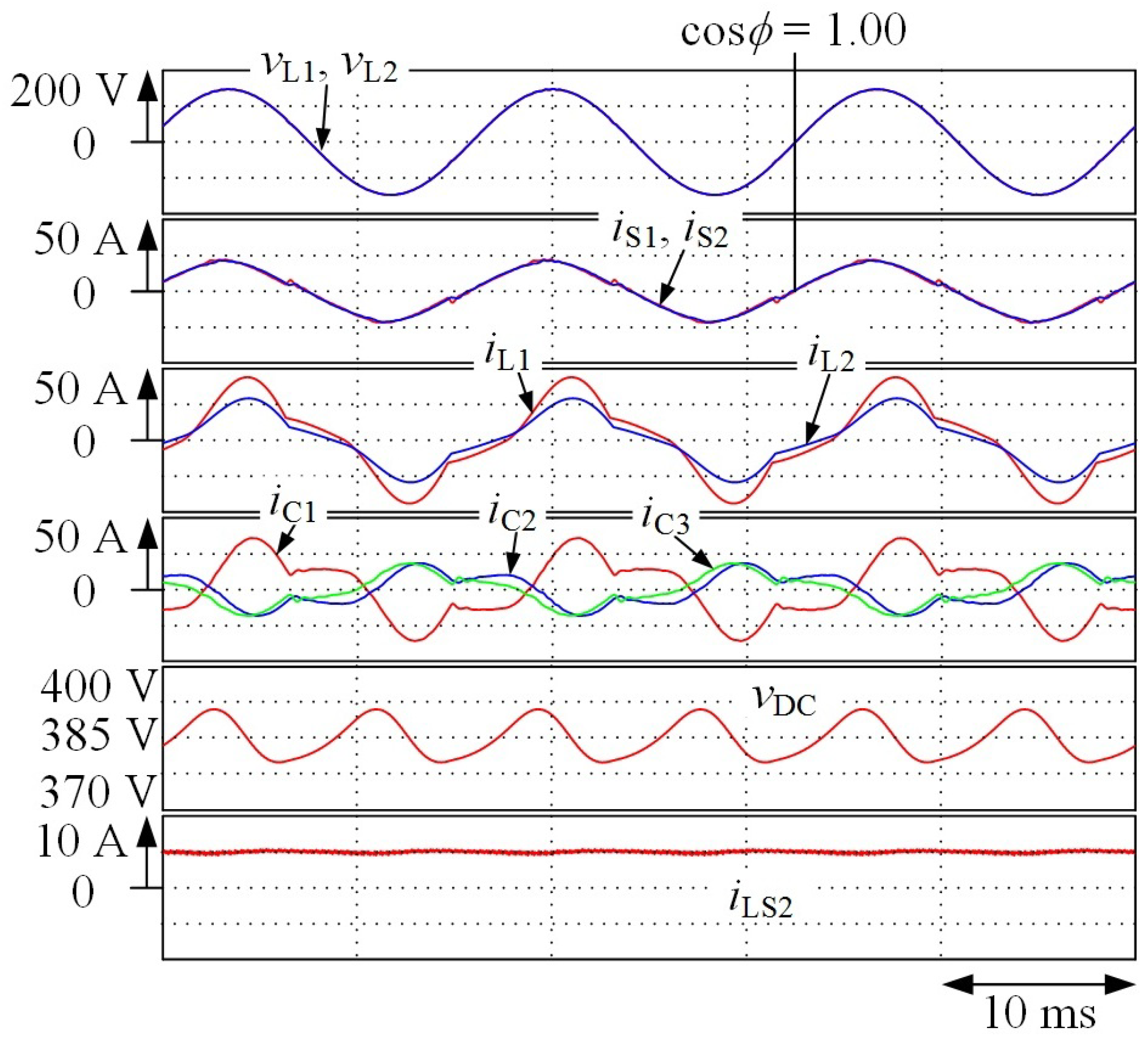
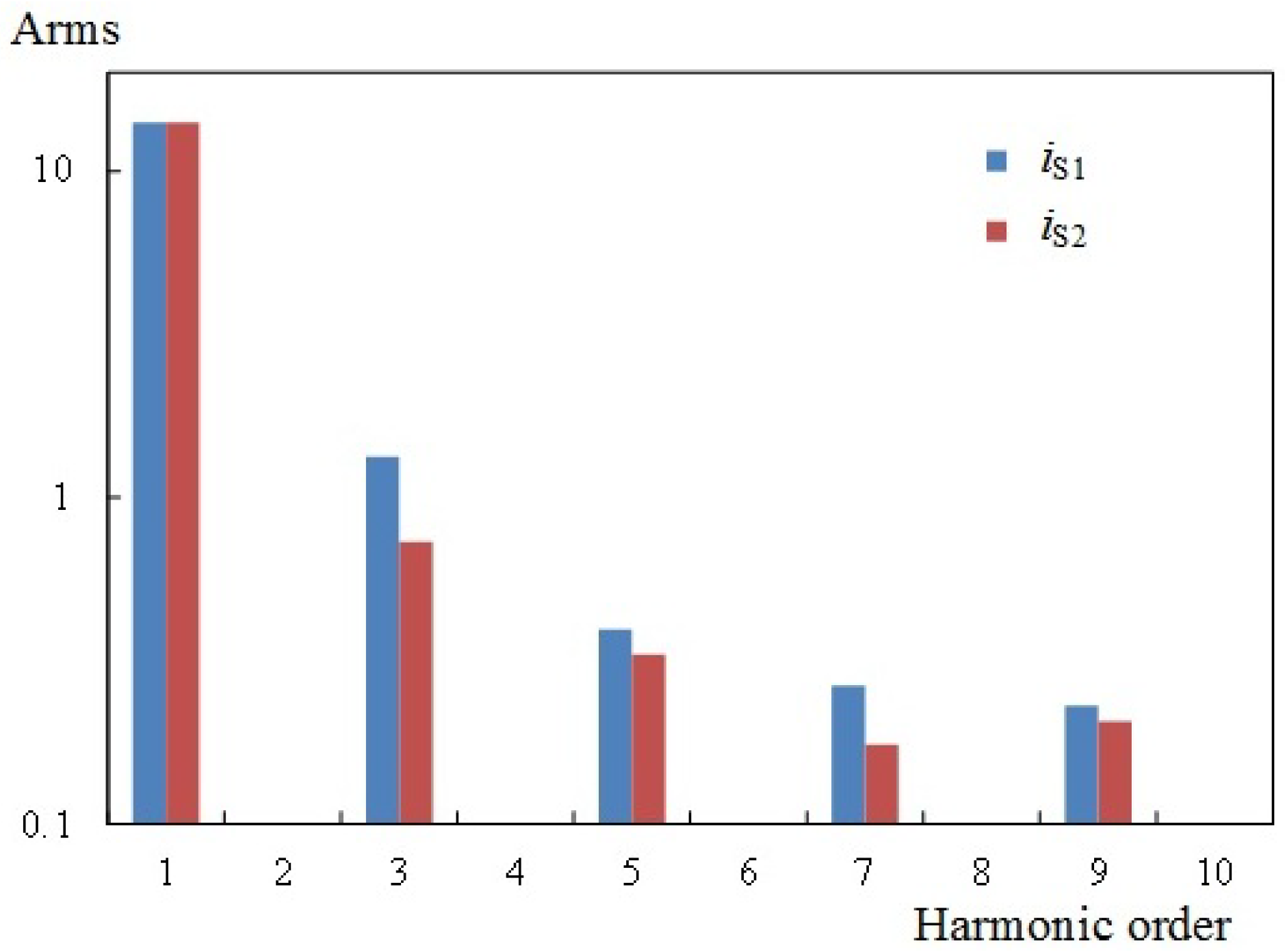
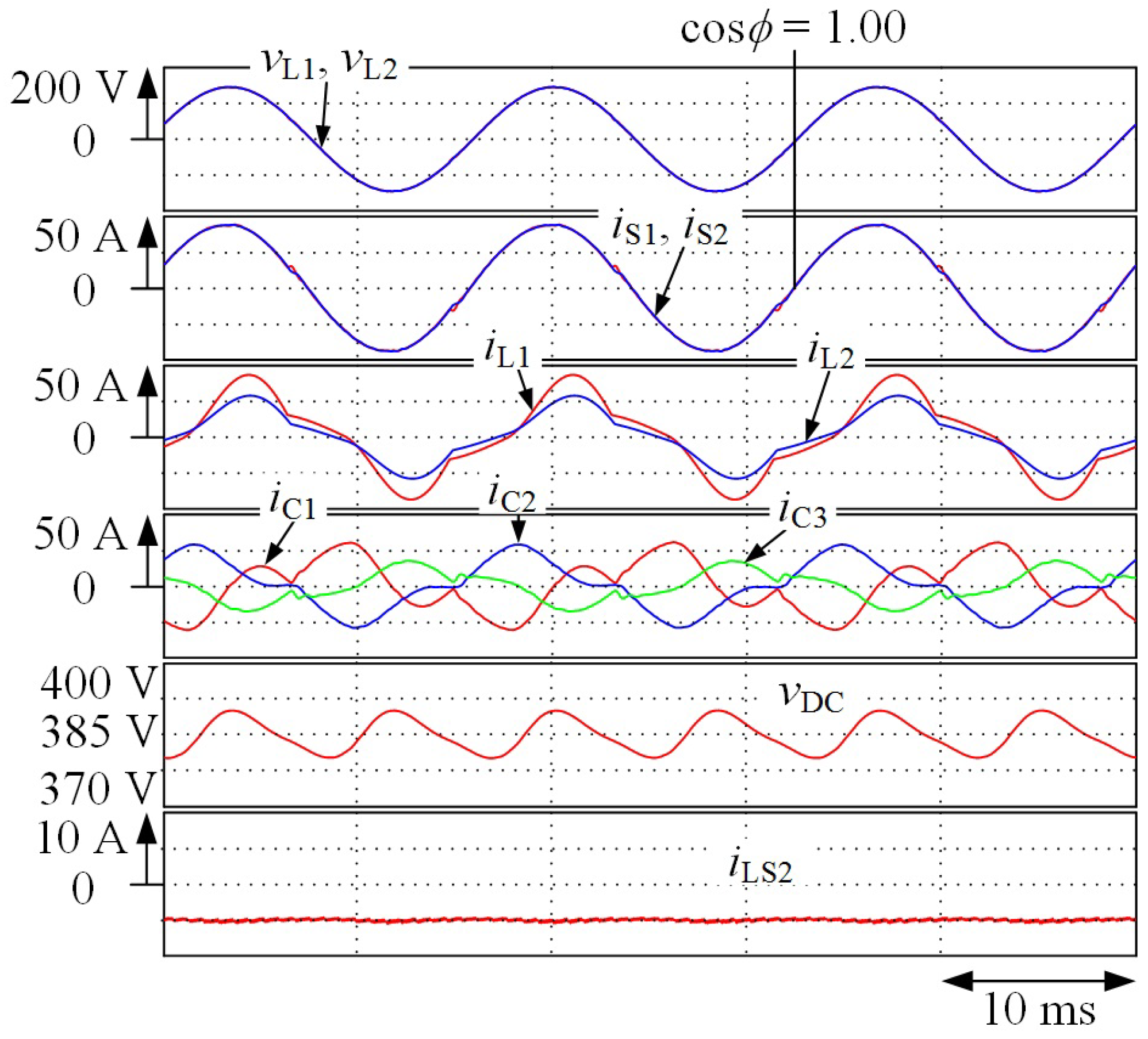
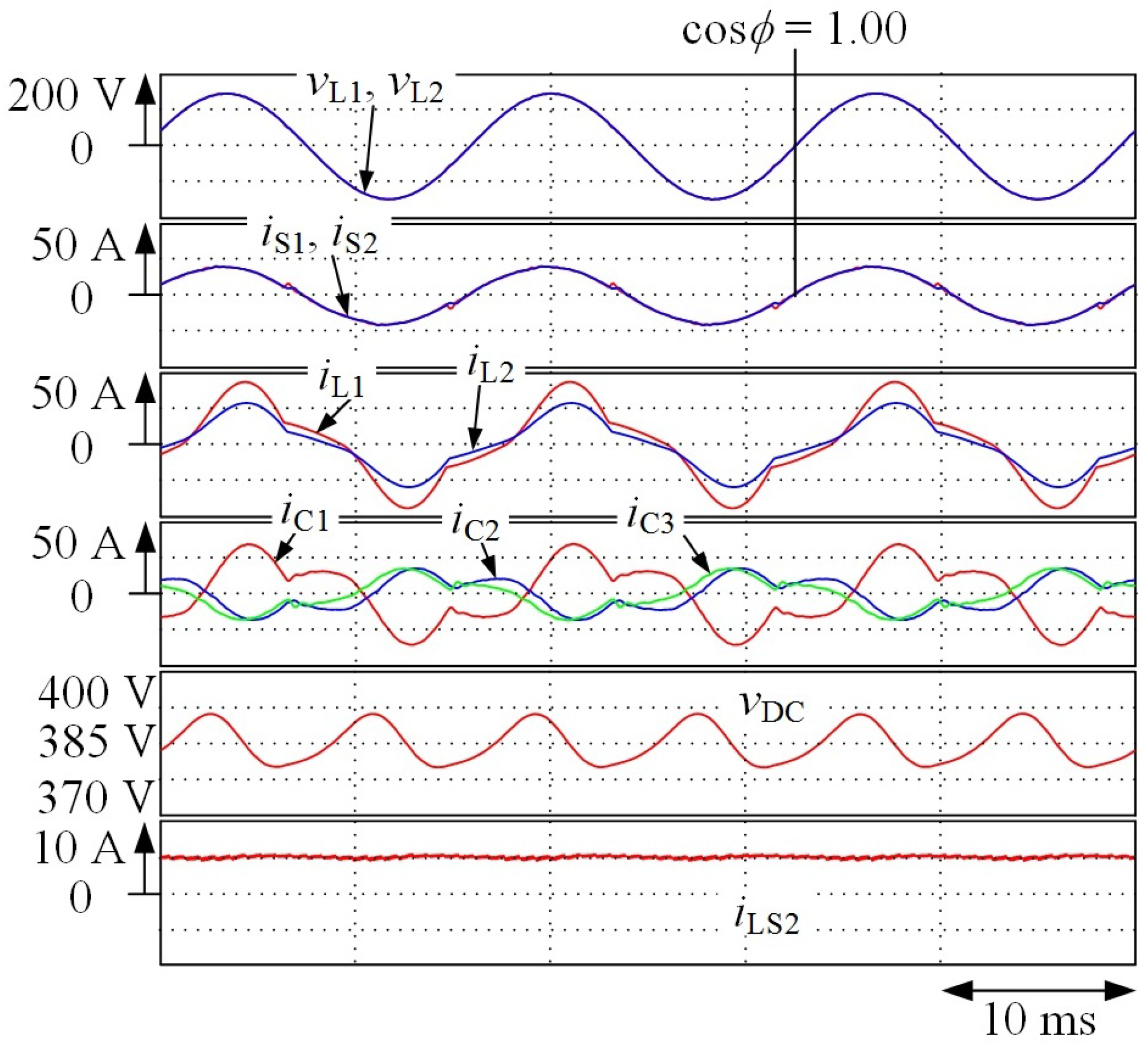
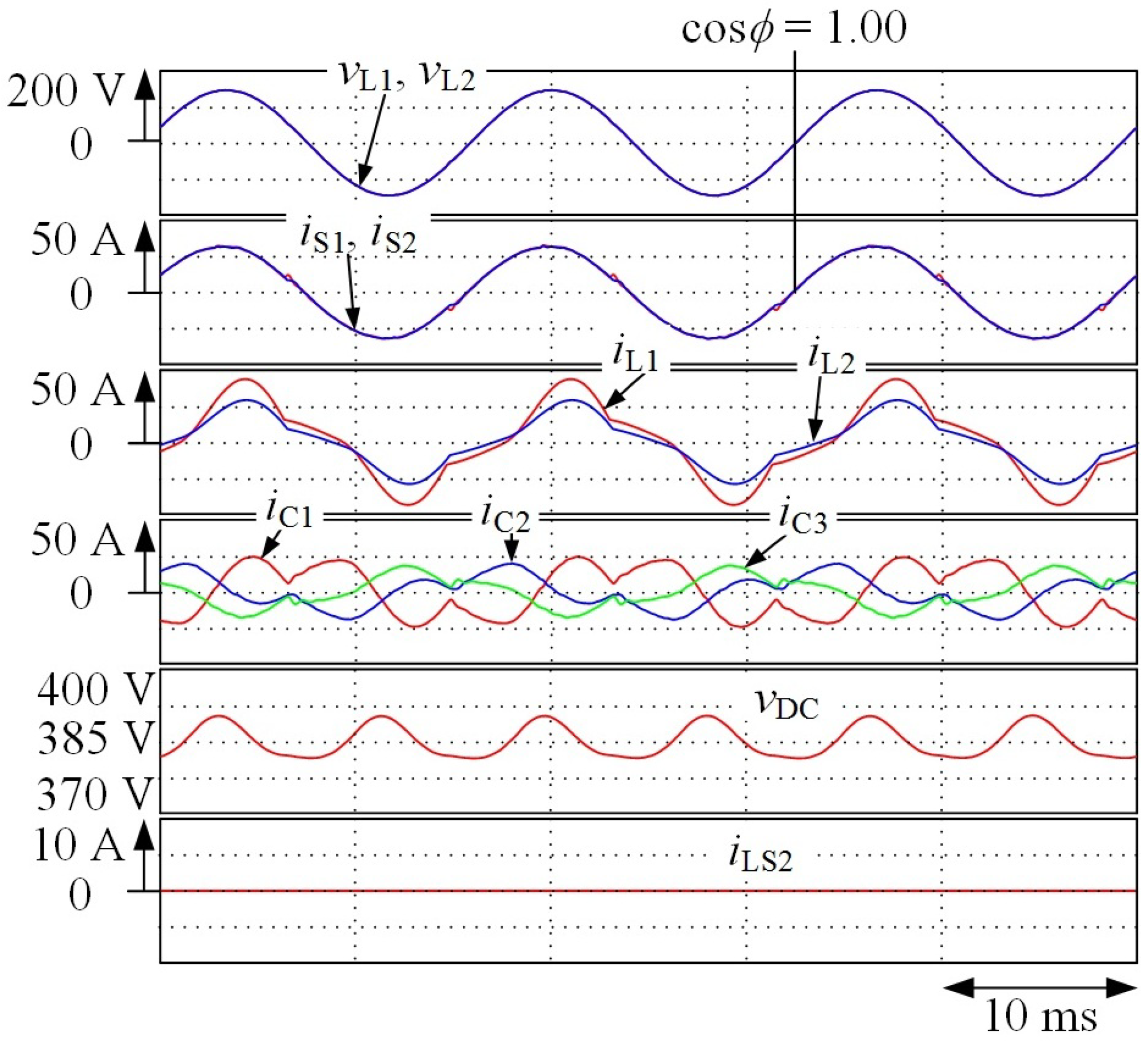
3. Simulation Results
- = 0.6, = 0.03 s, and = 0.01 ms are used in the PID controller of the CDCVC;
- = 0.06 and = 8 ms are used in the PI controllers in d-q coordinates for both fundamental and the 3rd harmonic components of the currents; and
- = 0.15 and = 3 ms are used in the PI controller for the current feedback of the bidirectional dc-dc converter.
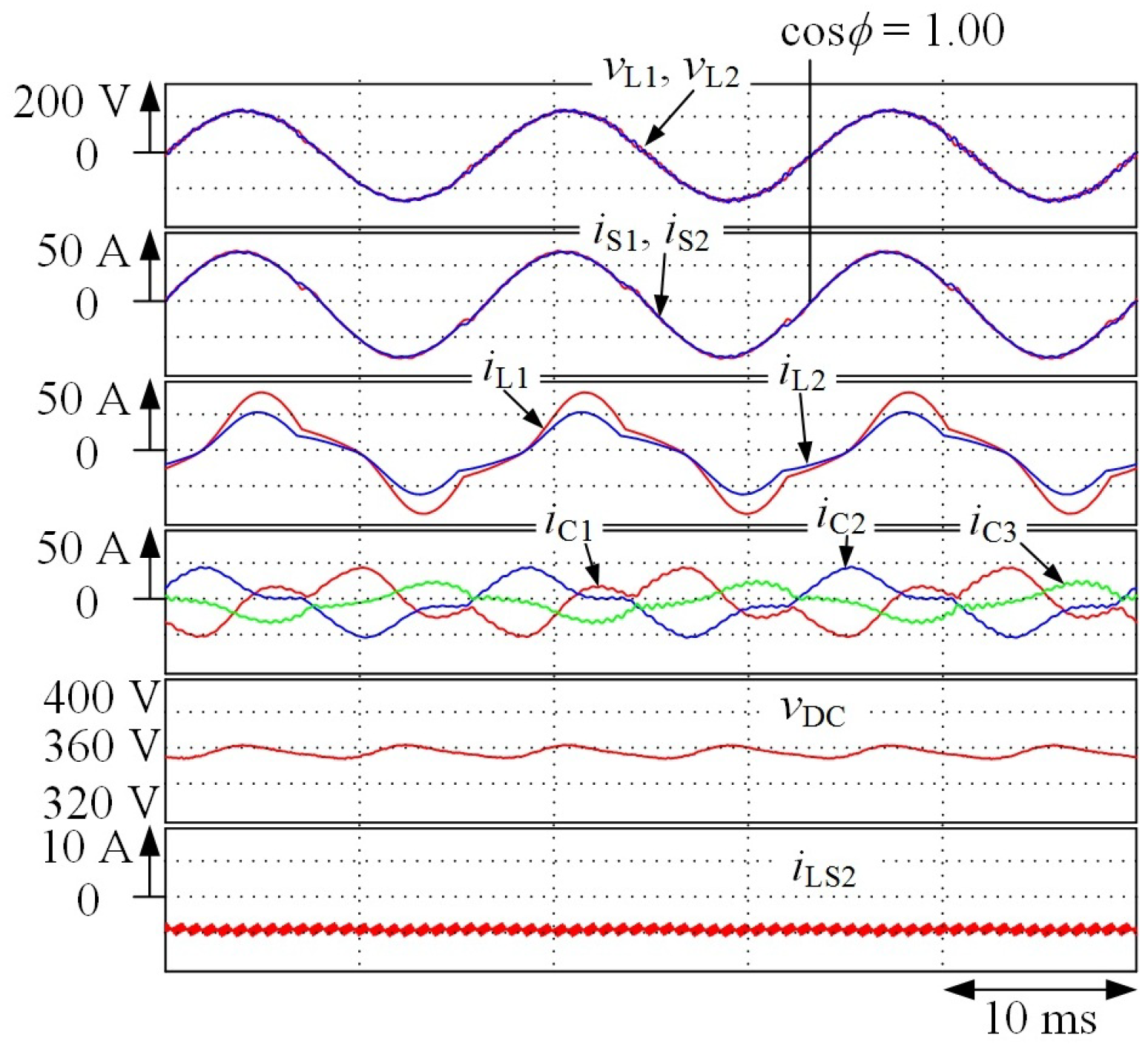
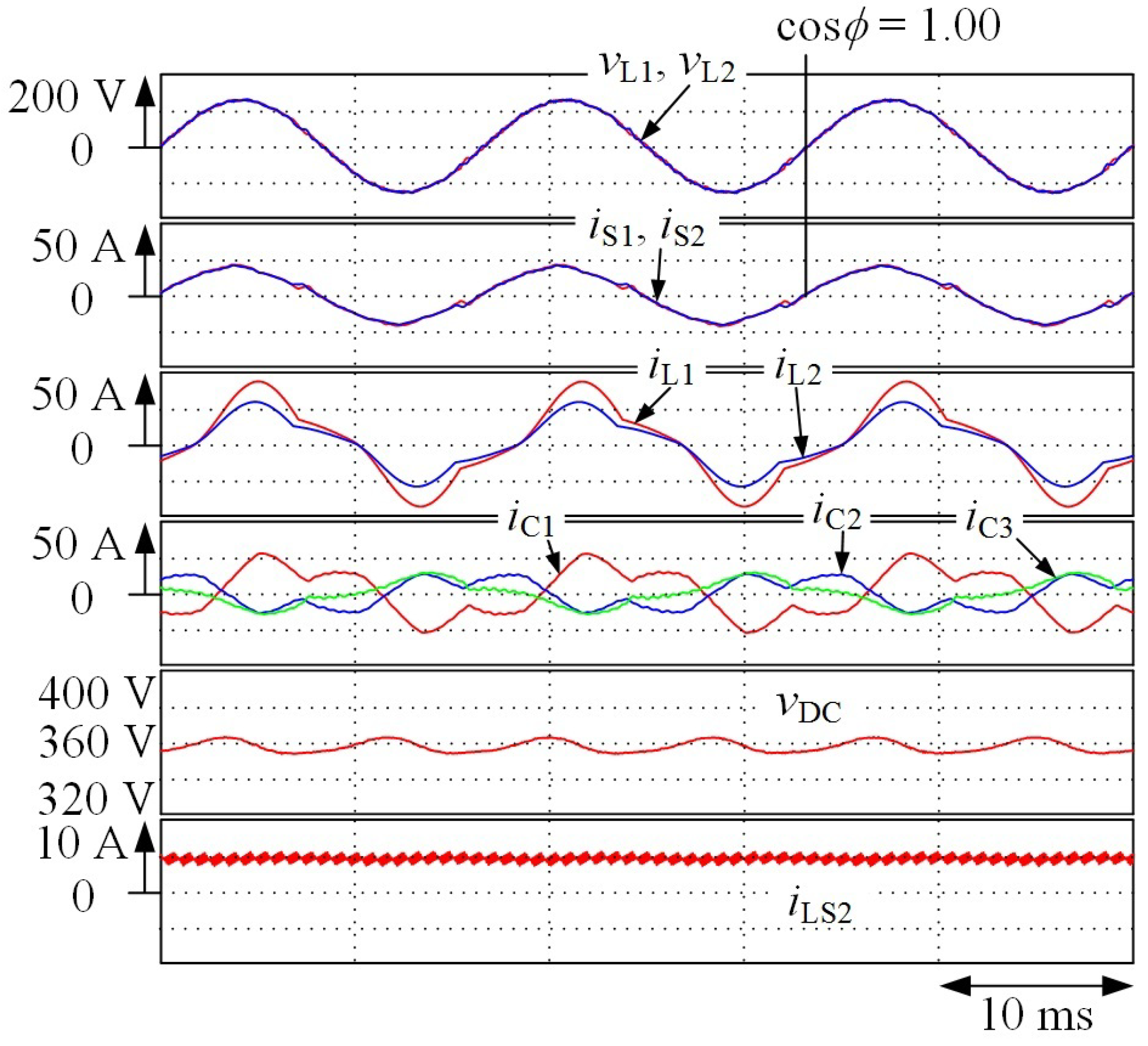
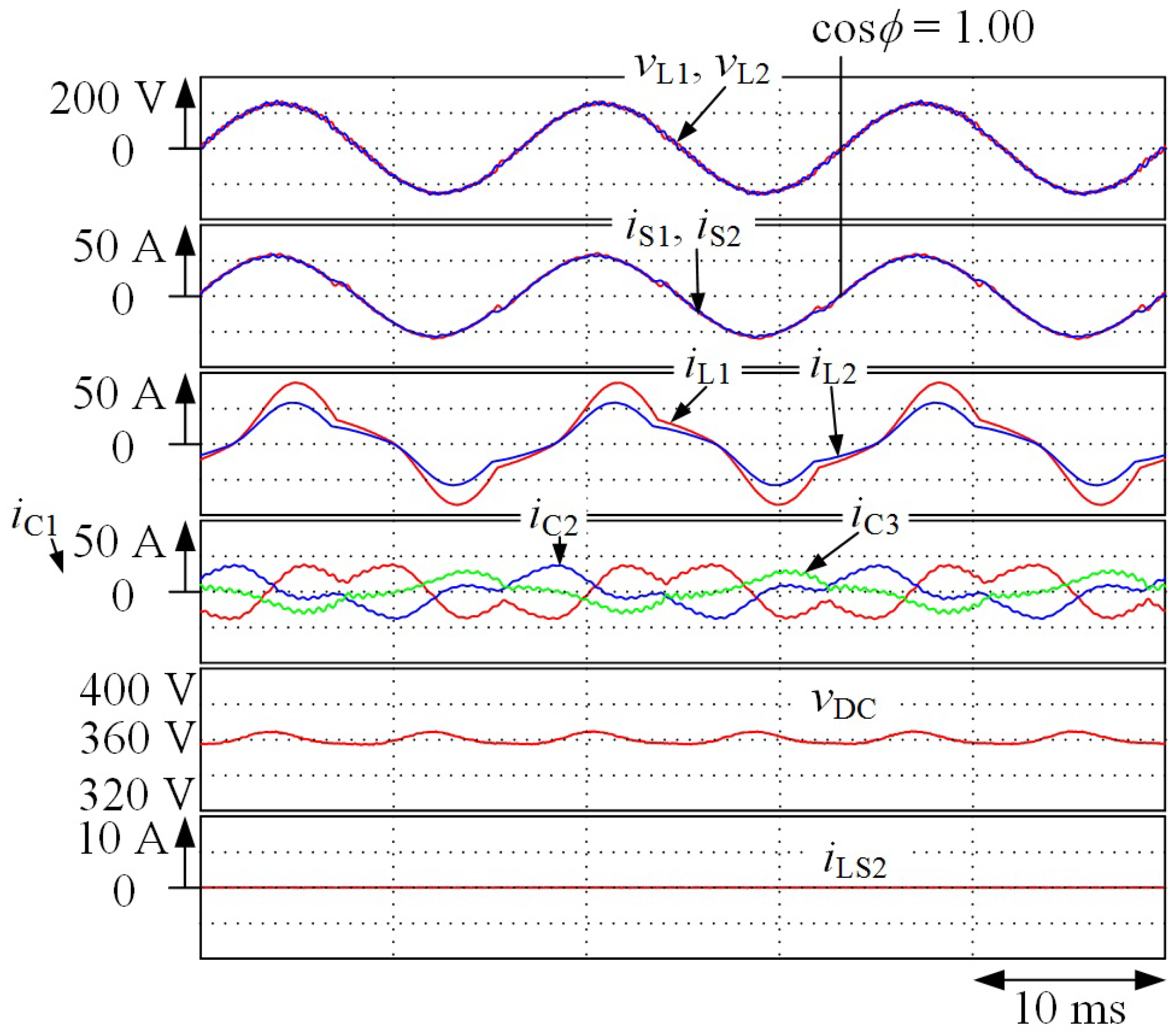
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tanaka, T.; Sekiya, T.; Tanaka, H.; Okamoto, M.; Hiraki, E. Smart charger for electric vehicles with power quality compensator on single-phase three-wire distribution feeders. IEEE Trans. Ind. Appl. 2013, 49, 2628–2635. [Google Scholar] [CrossRef]
- Ikeda, F.; Yamada, H.; Tanaka, T.; Okamoto, M. Constant dc-capacitor voltage-control-based harmonics compensation strategy of smart charger for electric vehicles in single-phase three-wire distribution feeders. Energies 2017, 10, 13. [Google Scholar] [CrossRef]
- Akagi, H.; Kanazawa, Y.; Nabae, A. Instantaneous reactive power compensators comprising switching devices without energy storage components. IEEE Trans. Ind. Appl. 1984, 3, 625–630. [Google Scholar] [CrossRef]
- Peng, F.Z.; Ott, G.W.; Adams, D.J. Harmonic and reactive power compensation based on the generalized instantaneous reactive power theory for the three-phase four-wire systems. IEEE Trans. Power Electron. 1998, 13, 1174–1181. [Google Scholar] [CrossRef]
- Geddada, N.; Karanki, S.B.; Mishra, M.K.; Kumar, B.K. Modified four leg DSTATCOM topology for compensation of unbalanced and nonlinear loads in three phase four wire system. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–10. [Google Scholar]
- Dixon, J.W.; Garcia, J.J.; Moran, L. Control system for three-phase active power filter which simultaneously compensates power factor and unbalanced loads. IEEE Trans. Ind. Electron. 1995, 42, 636–641. [Google Scholar] [CrossRef]
- Abellan, A.; Garcera, G.; Pascual, M.; Figueres, E. A new current controller applied to four-branch inverter shunt active filters with UPF control method. In Proceedings of the 2001 IEEE 32nd Annual Power Electronics Specialists Conference, Vancouver, BC, Canada, 17–21 June 2001; Volume 3, pp. 1402–1407. [Google Scholar]
- Haque, M.T. Single-phase pq theory for active filters. In Proceedings of the 2002 IEEE Region 10 Conference on Computers, Communications, Control and Power Engineering (TENCOM’02), Beijing, China, 28–31 October 2002; Volume 3, pp. 1941–1944. [Google Scholar]
- Arruda, L.N.; Silva, S.M. PLL structures for utility connected systems. In Proceedings of the 36th IAS Annual Meeting, Conference Record of the 2001 IEEE Industry Applications Conference, Chicago, IL, USA, 30 September–4 October 2001; pp. 2655–2660. [Google Scholar]
- Silva, S.M.; Lopes, B.M.; Campana, R.P.; Bosventura, W.C. Performance evaluation of PLL algorithms for single-phase grid-connected systems. In Proceedings of the 39th IAS Annual Meeting, Conference Record of the 2004 IEEE Industry Applications Conference, Seattle, WA, USA, 3–7 October 2004; pp. 2259–2263. [Google Scholar]
- Zhang, R.S. Control of Single Phase Power Converter in d-q Rotating Coordinates. U.S. Patent 6,621,252 B2, 16 September 2003. [Google Scholar]
- Japan Electric Association. Indoor Wiring Guidelines; JESC E0005; Japan Electric Association: Tokyo, Japan, 2005; p. 32. (In Japanese) [Google Scholar]
- IEC 61000-3-4. Raprort Technique Technical Report; International Electrotechnical Commission: Geneva, Switzerland, 1998. [Google Scholar]
| Item | Symbol | Value | |
|---|---|---|---|
| Simulation | Experiment | ||
| Filter inductor for three-leg PWM rectifier | 0.46 mH | ||
| Filter capacitor for three-leg PWM rectifier | 10.4 F | ||
| Switching inductor for three-leg PWM rectifier | 1.0 mH | ||
| dc capacitor | 2700 F | ||
| dc-capacitor voltage | 385 Vdc | 360 Vdc | |
| Switching inductor for dc-dc converter | 4.4 mH | ||
| Filter capacitor for dc-dc converter | 1000 F | ||
| Battery voltage | 360 Vdc | 257 Vdc | |
| Inductor current for dc-dc converter | 5 Adc | 4.29 Adc | |
| Internal resistance of battery | r | 72 m | |
| Switching frequency | 9.36 kHz | ||
| Dead time | 3.5 s | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nishikawa, K.; Ikeda, F.; Okamoto, Y.; Yamada, H.; Tanaka, T.; Okamoto, M. Improvement in Harmonic Compensation of a Smart Charger with a Constant DC-Capacitor Voltage-Control-Based Strategy for Electric Vehicles in Single-Phase Three-Wire Distribution Feeders. Energies 2018, 11, 1604. https://doi.org/10.3390/en11061604
Nishikawa K, Ikeda F, Okamoto Y, Yamada H, Tanaka T, Okamoto M. Improvement in Harmonic Compensation of a Smart Charger with a Constant DC-Capacitor Voltage-Control-Based Strategy for Electric Vehicles in Single-Phase Three-Wire Distribution Feeders. Energies. 2018; 11(6):1604. https://doi.org/10.3390/en11061604
Chicago/Turabian StyleNishikawa, Kei, Fuka Ikeda, Yuki Okamoto, Hiroaki Yamada, Toshihiko Tanaka, and Masayuki Okamoto. 2018. "Improvement in Harmonic Compensation of a Smart Charger with a Constant DC-Capacitor Voltage-Control-Based Strategy for Electric Vehicles in Single-Phase Three-Wire Distribution Feeders" Energies 11, no. 6: 1604. https://doi.org/10.3390/en11061604
APA StyleNishikawa, K., Ikeda, F., Okamoto, Y., Yamada, H., Tanaka, T., & Okamoto, M. (2018). Improvement in Harmonic Compensation of a Smart Charger with a Constant DC-Capacitor Voltage-Control-Based Strategy for Electric Vehicles in Single-Phase Three-Wire Distribution Feeders. Energies, 11(6), 1604. https://doi.org/10.3390/en11061604




