Evaluation of the Reactive Power Support Capability and Associated Technical Costs of Photovoltaic Farms’ Operation
Abstract
:1. Introduction
2. PV Farm Models
2.1. Single-Stage PV Farm Model
2.2. Two-Stage PV Farm Model
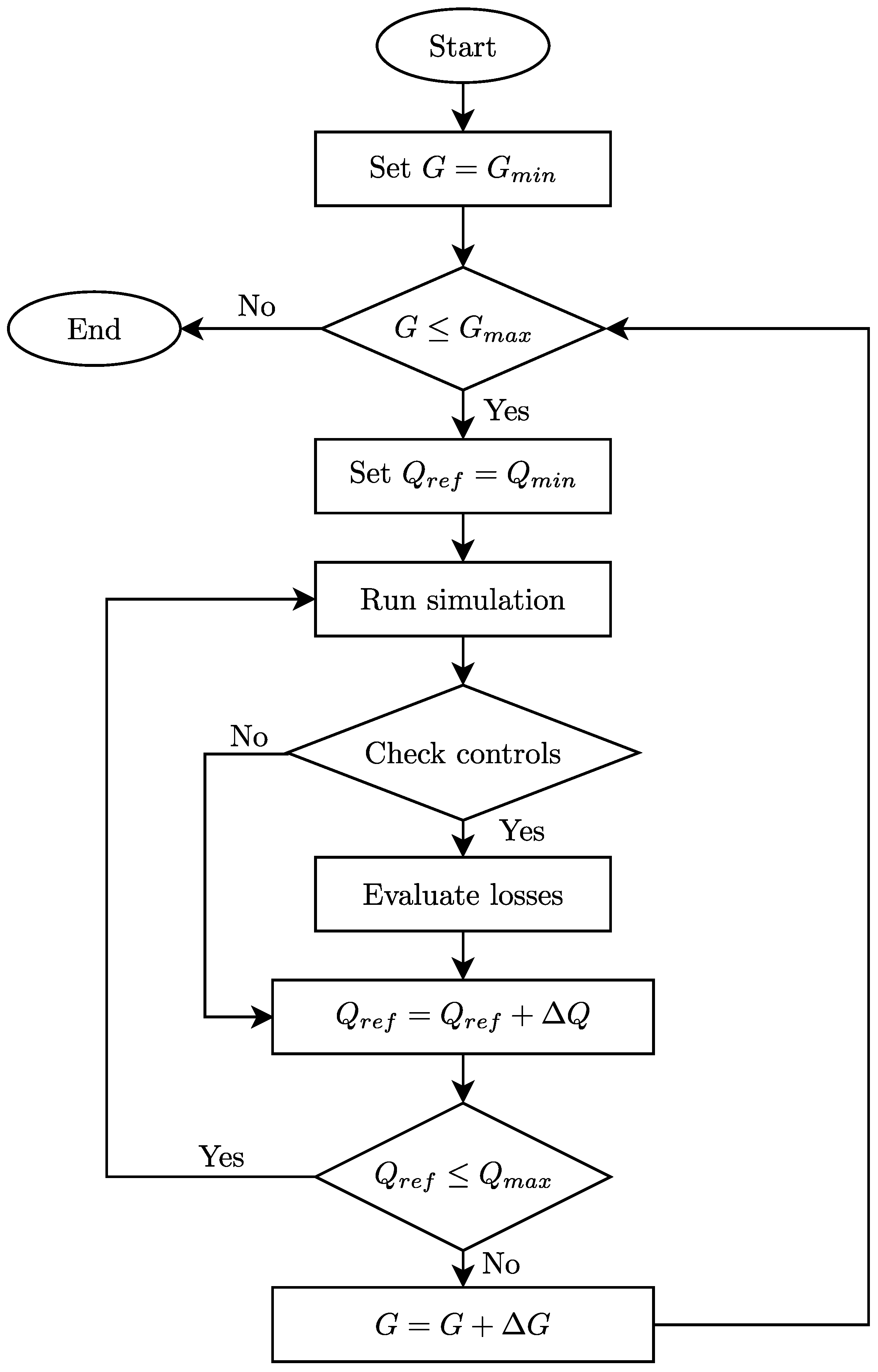
3. Methodology
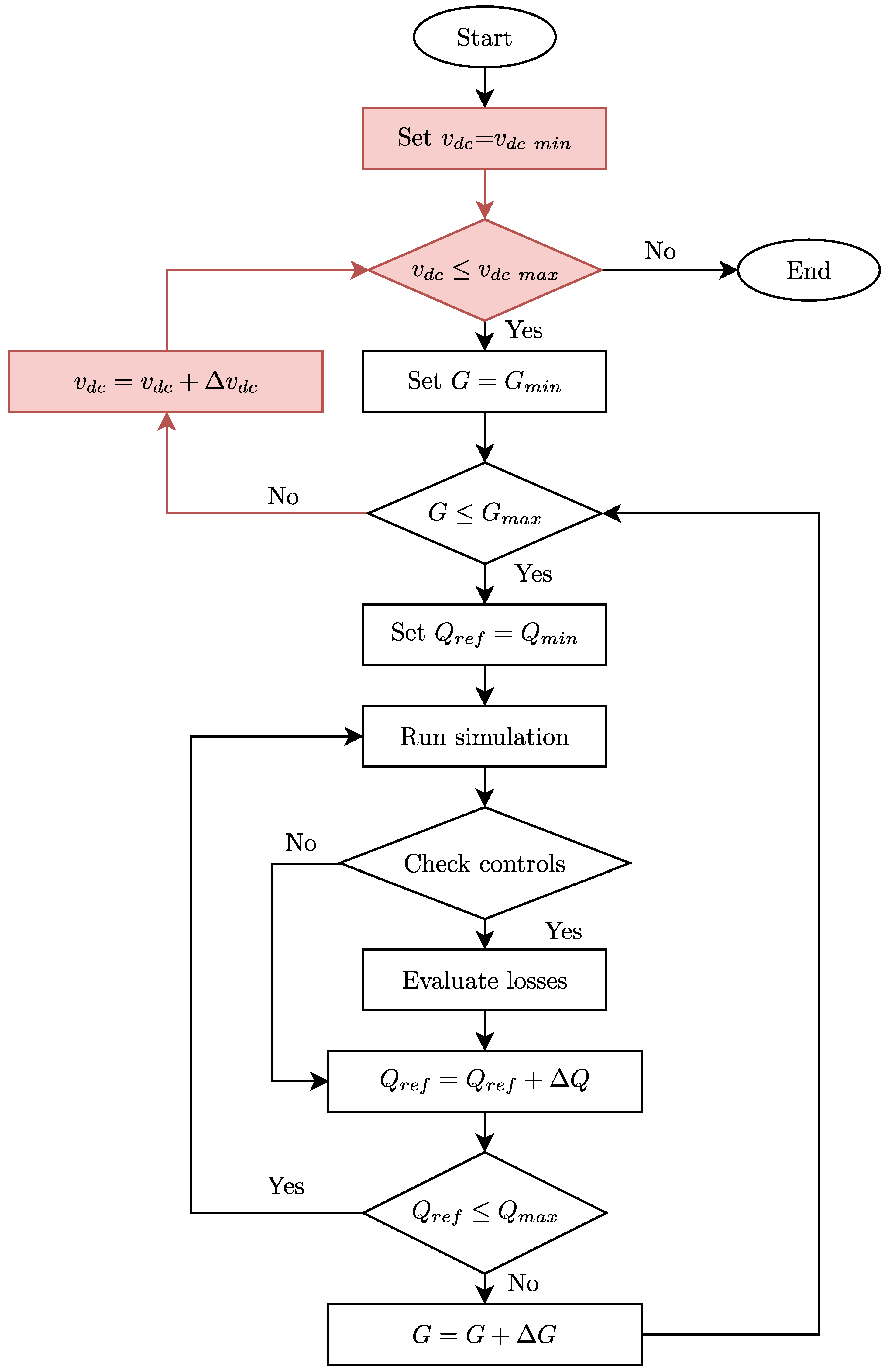
3.1. Flowcharts
3.2. PV System Losses
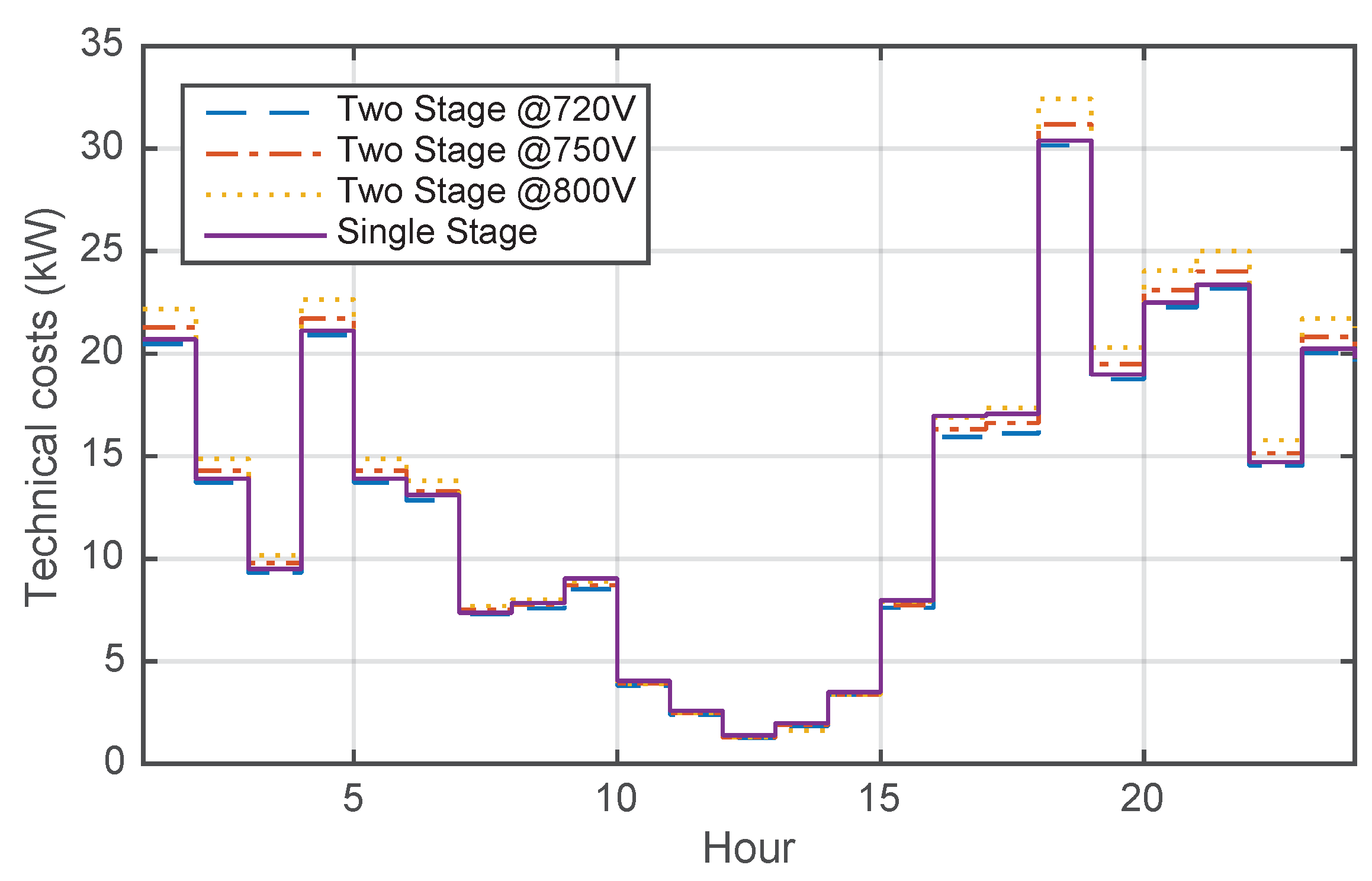
3.3. Technical Costs
4. Operation without Reactive Power Support
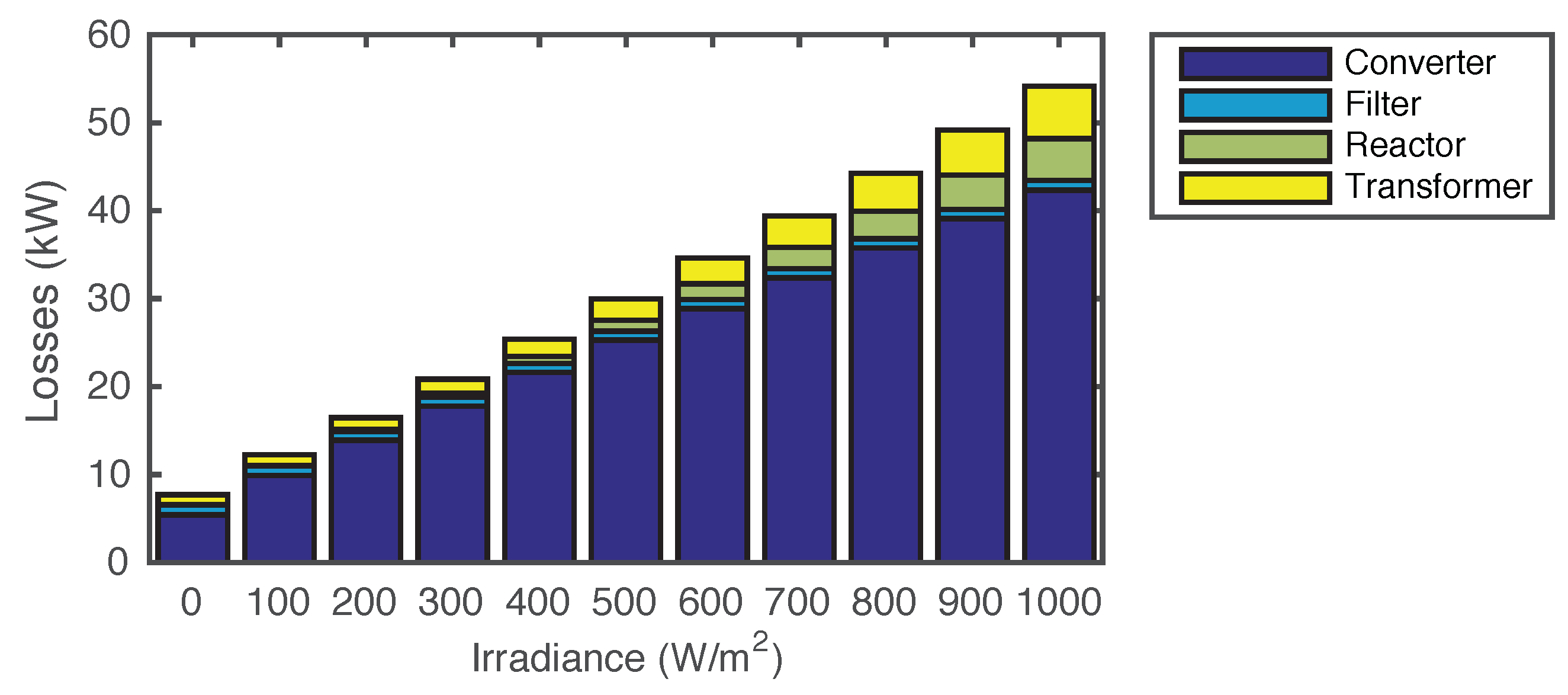
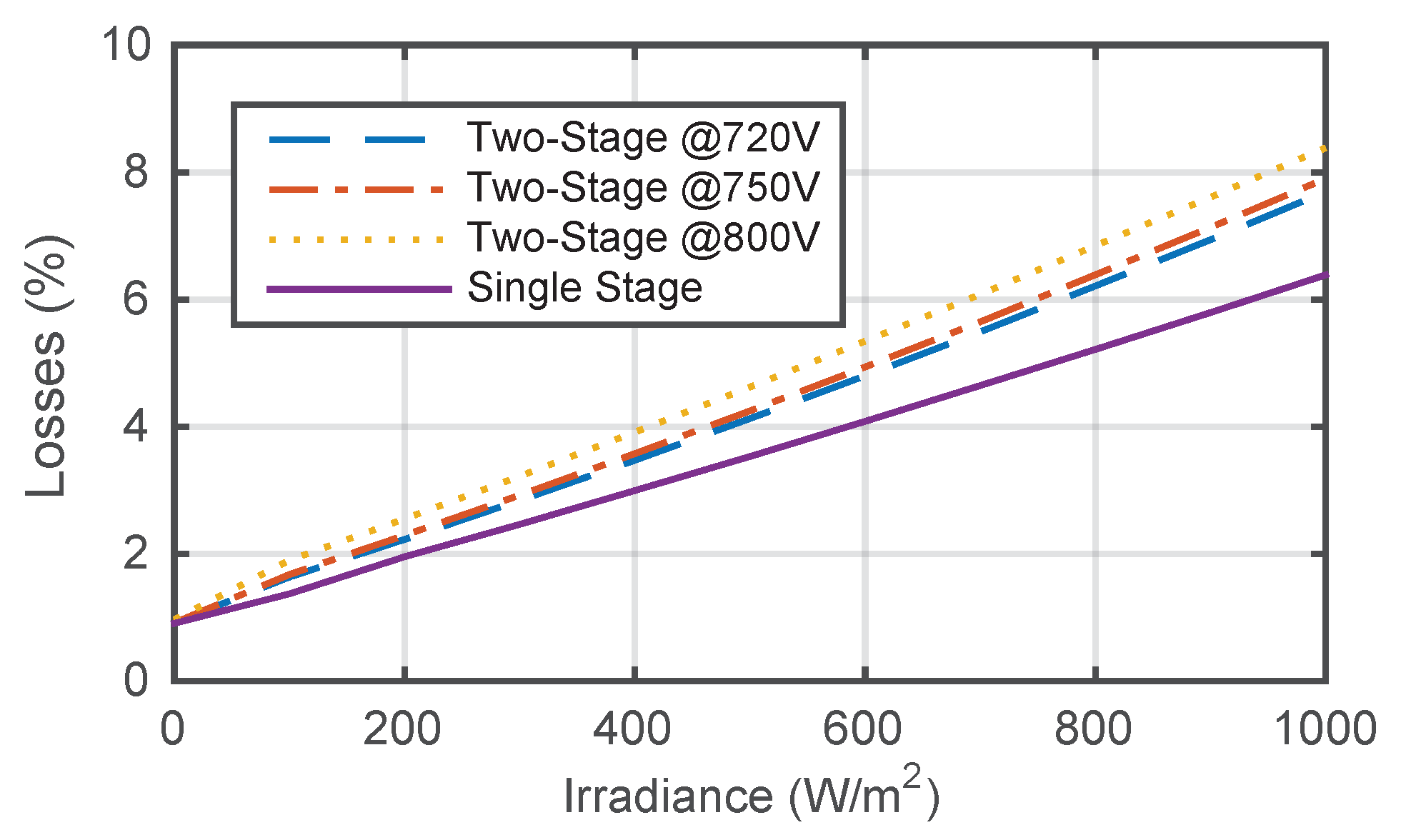
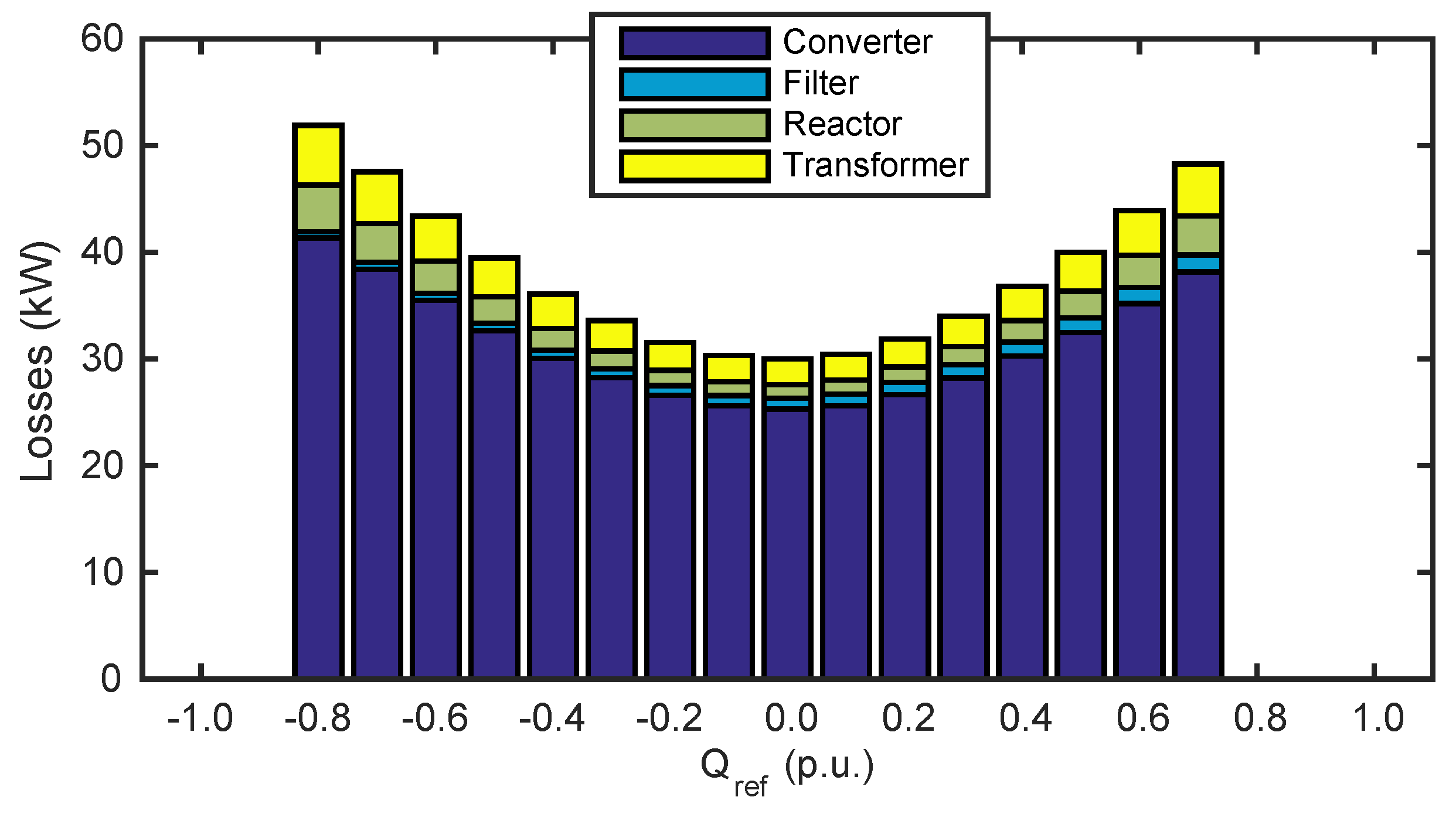
4.1. Single-Stage PV Farm Losses without Reactive Power Support
4.2. Two-Stage PV Farm Losses without Reactive Power Support
5. Operation with Reactive Power Support
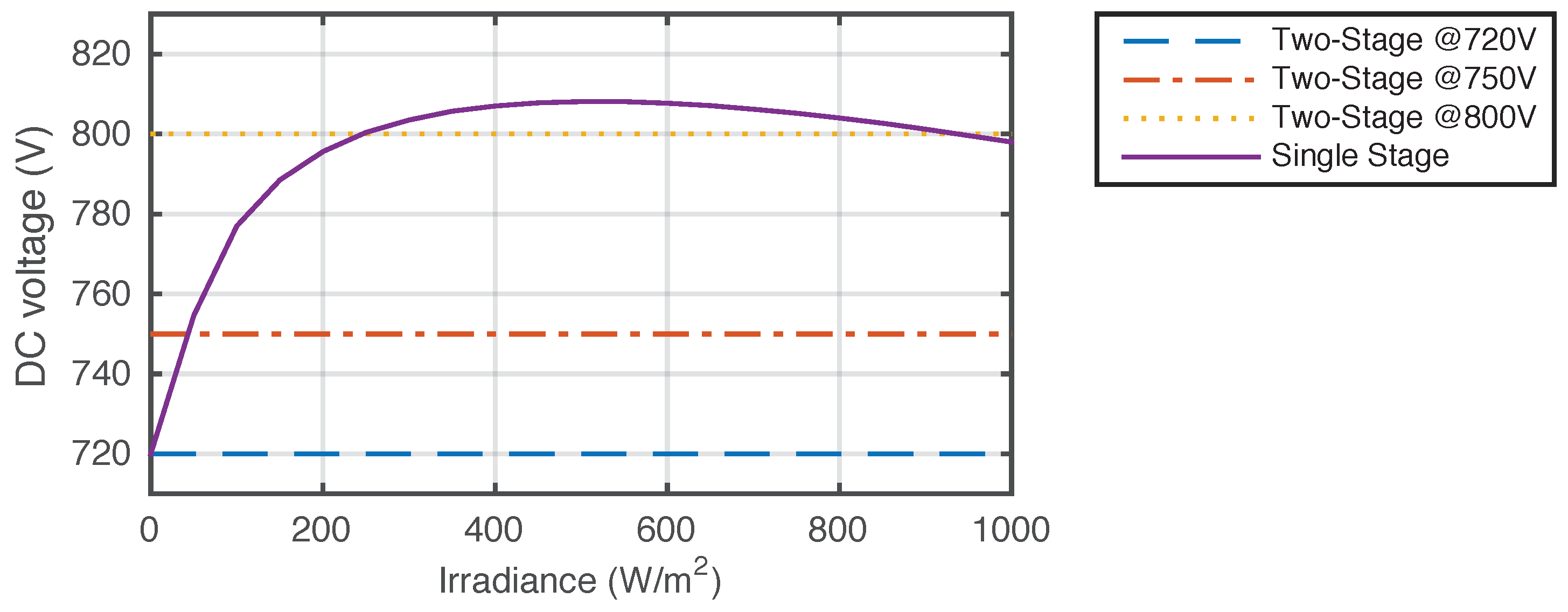
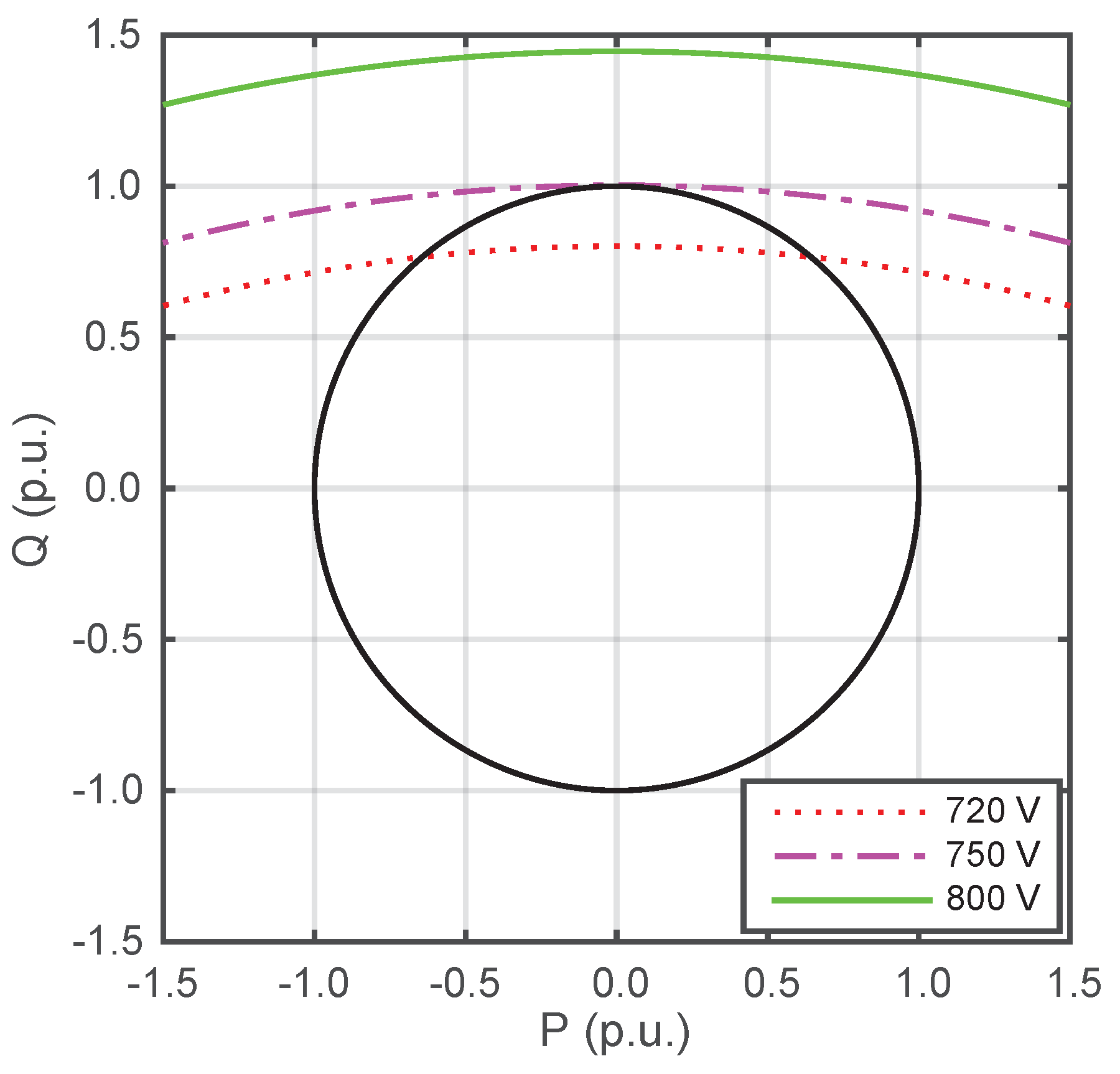
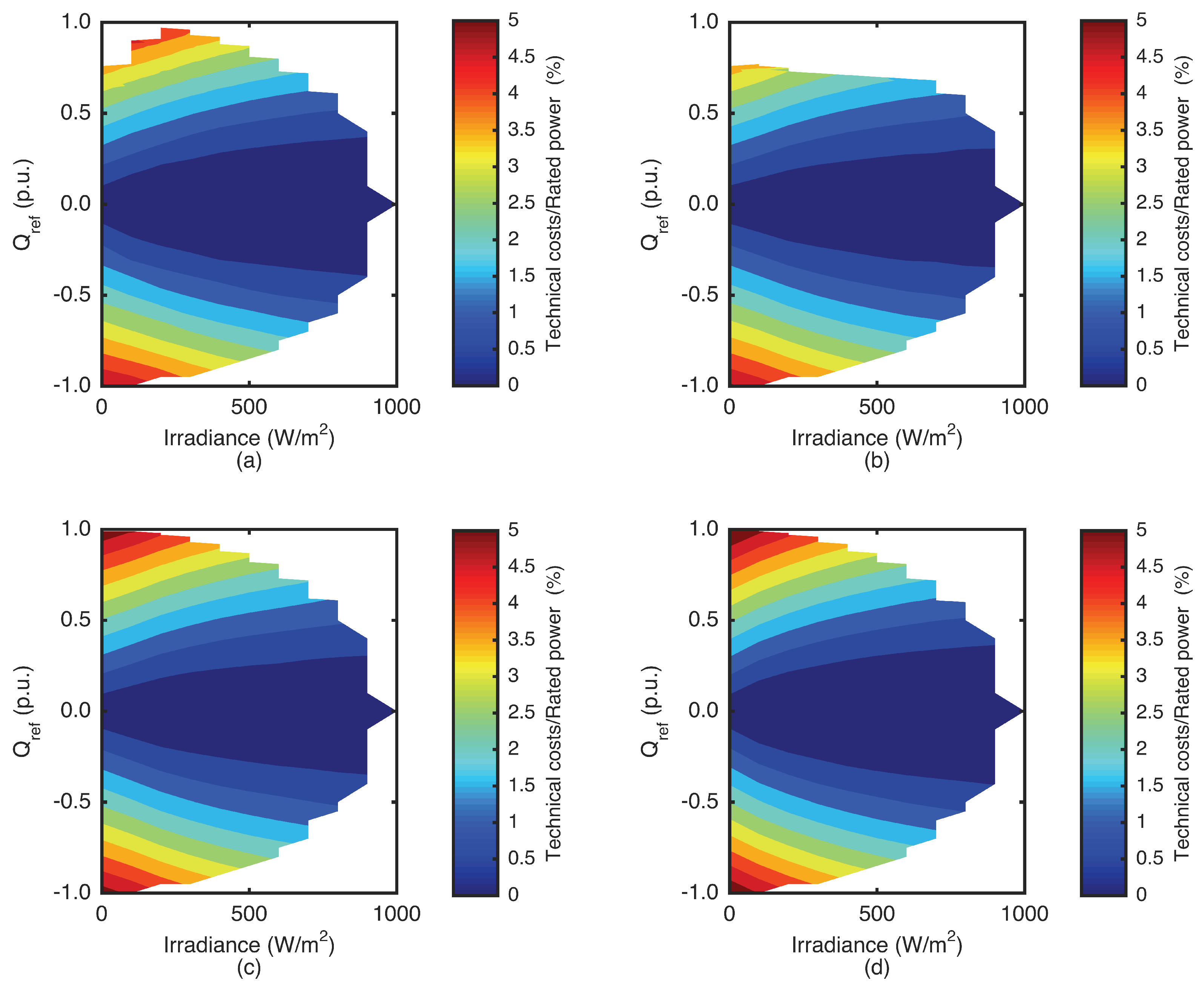
5.1. Reactive Power Support Capability Area
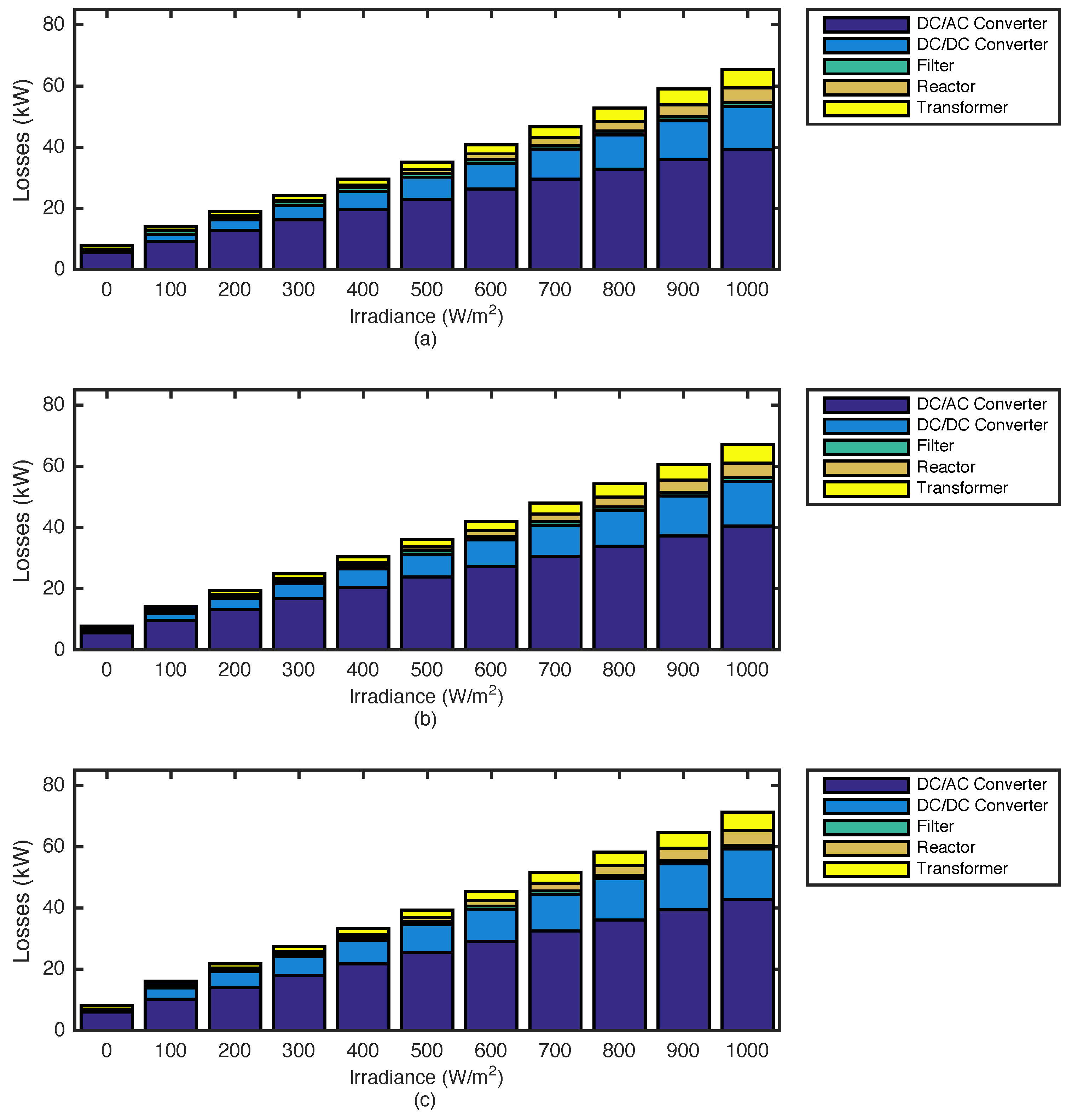
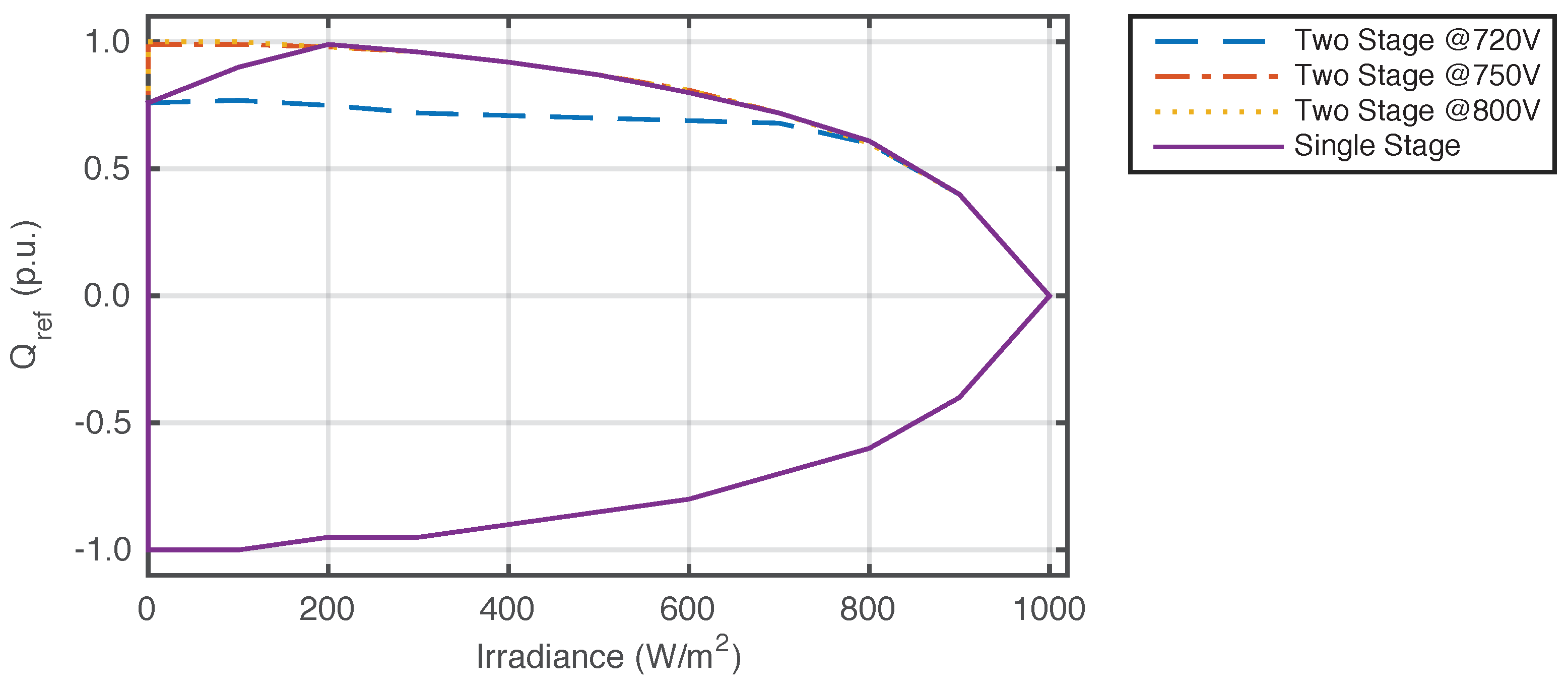
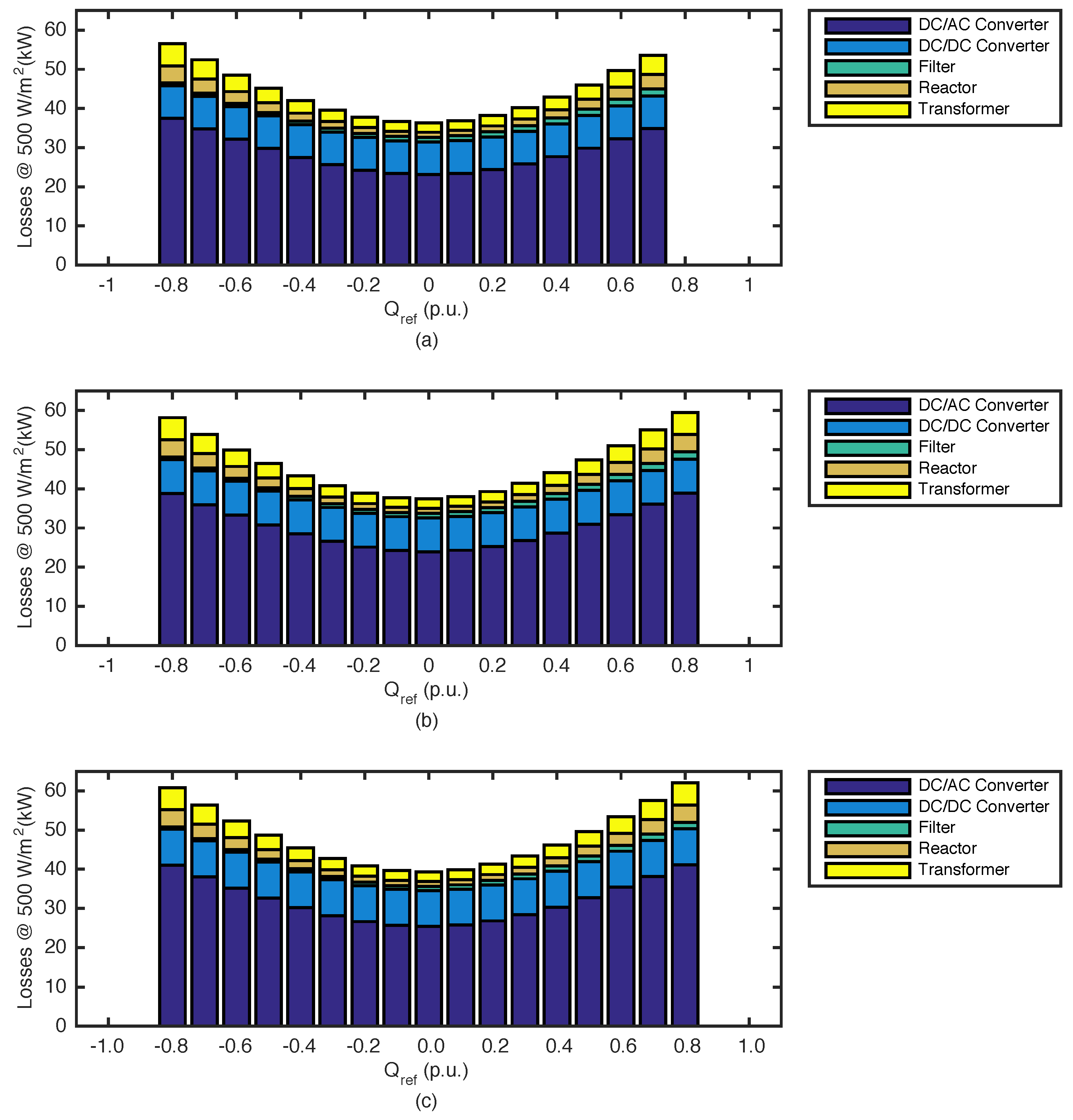
5.2. PV Farm Losses with Reactive Power Support
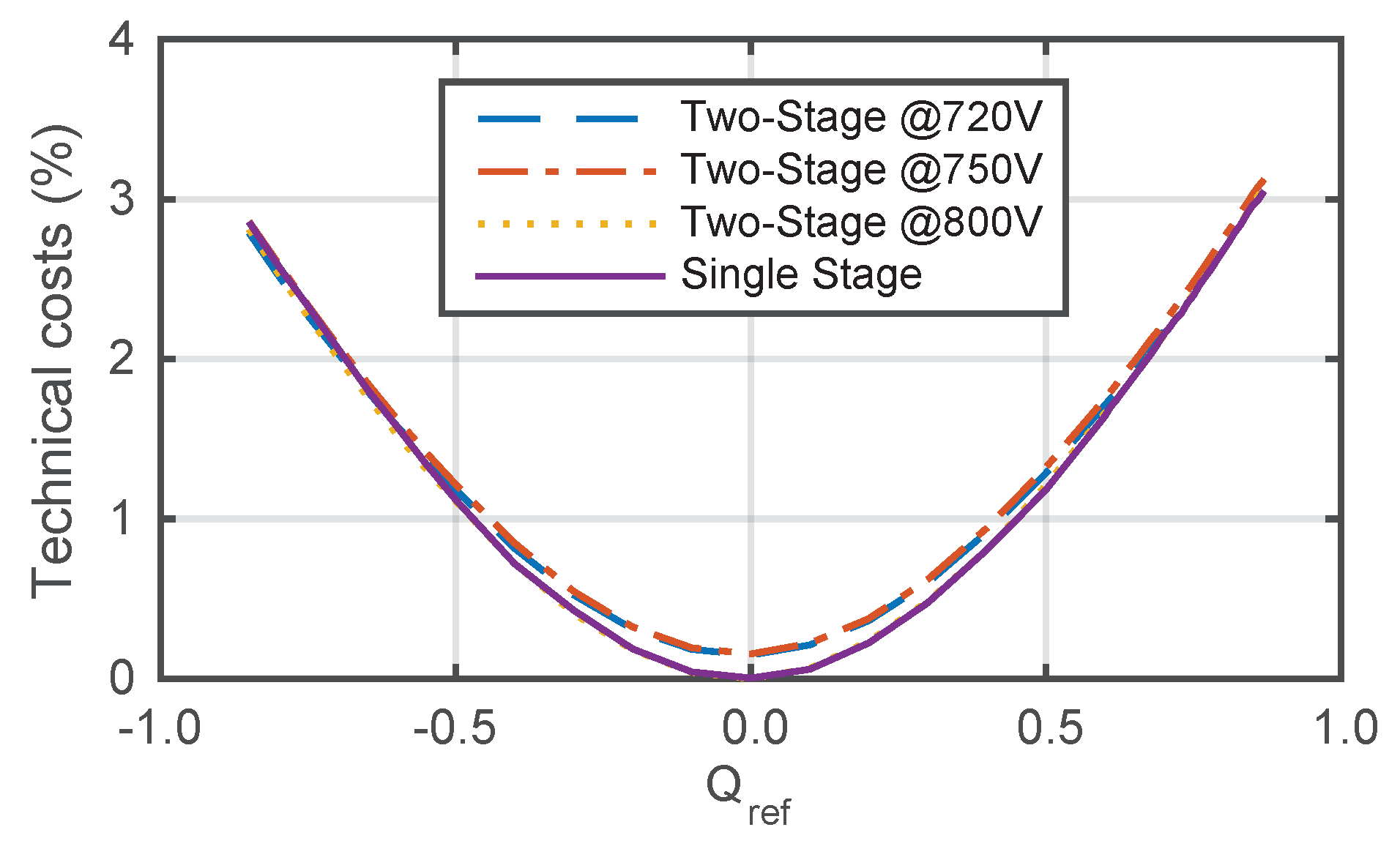
5.3. Technical Cost for Reactive Power Support
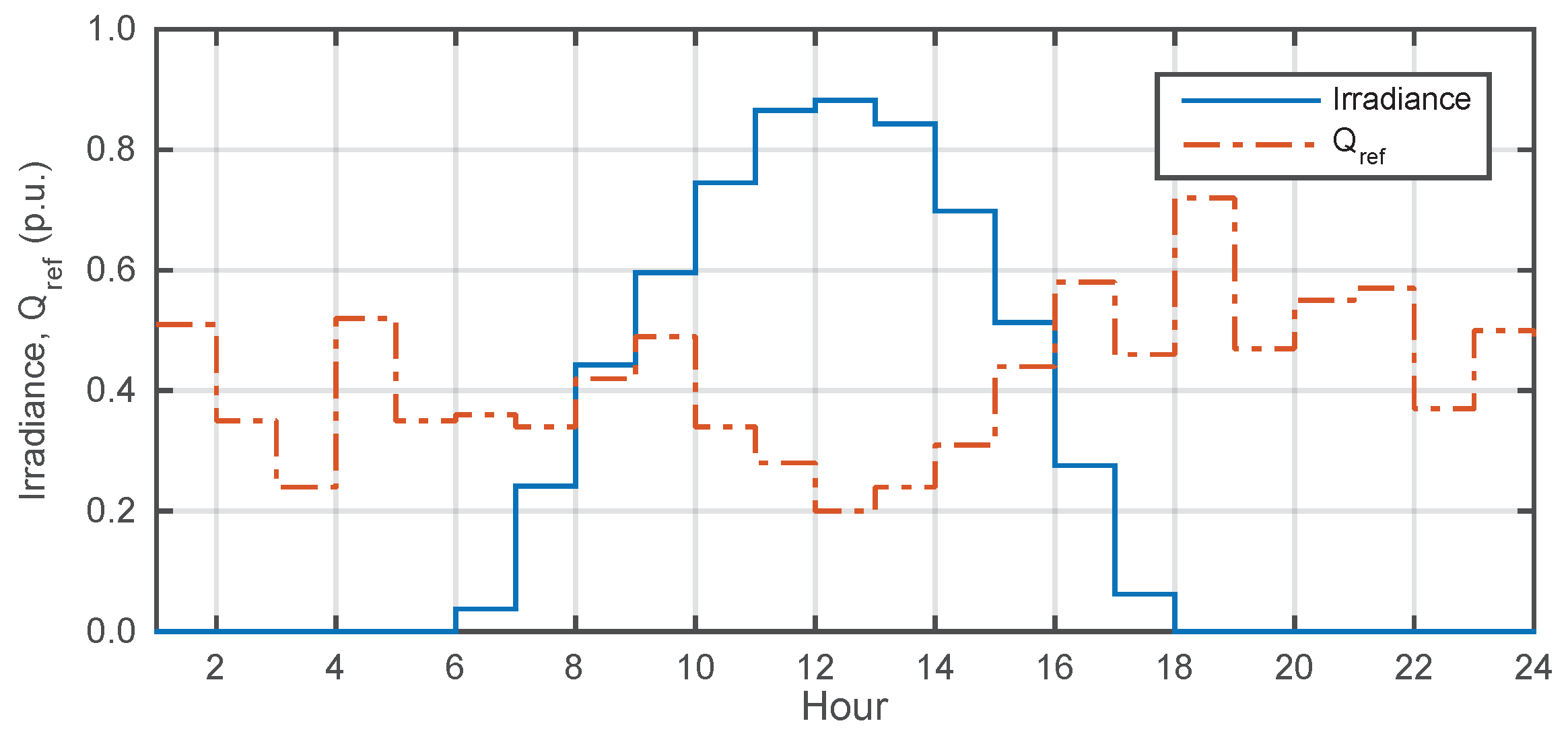
5.4. Reactive Power Support Economics
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- SolarPower Europe. Global Market Outlook for Solar Power 2015–2019; Technical Report; Euoropean Photovoltaic Industry Association: Bruxelles, Belgium, 2015. [Google Scholar]
- Quitmann, E.; Erdmann, E. Power system needs—How grid codes should look ahead. IET Renew. Power Gener. 2014, 9, 3–9. [Google Scholar] [CrossRef]
- Industrial Standards Committee. IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems; IEEE Standard 1547; Institute of Electrical and Electronics Engineers: New York, NY, USA, 2003. [Google Scholar]
- European Standard. Voltage Characteristics of Public Distribution Systems; EN Standard 50160; EN: Bruxelles, Belgium, 2004. [Google Scholar]
- Technischen Richtlinie Erzeugungsanlagen am Mittelspannungsnetz. Richtlinie für Anschluss und Parallelbetrieb von Erzeugungsanlagen am Mittelspannungsnetz. Available online: http://www.megamonheim.de/assets/bdew_rl_ea-am-ms-netz_juni_2008_end.pdf (accessed on 12 June 2018).
- Gil, J.B.; San Román, T.G.; Rios, J.A.; Martin, P.S. Reactive power pricing: A conceptual framework for remuneration and charging procedures. IEEE Trans. Power Syst. 2000, 15, 483–489. [Google Scholar]
- Thomas, R.J.; Mount, T.D.; Schuler, R.; Schulze, W.; Zimmerman, R.; Alvarado, F.; Lesieutre, B.C.; Overholt, P.N.; Eto, J.H. Efficient and reliable reactive-power supply and consumption: Insights from an integrated program of engineering and economic research. Electr. J. 2008, 21, 70–81. [Google Scholar] [CrossRef]
- Chattopadhyay, D.; Chakrabarti, B.B.; Read, E.G. A spot pricing mechanism for voltage stability. Int. J. Electr. Power Energy Syst. 2003, 25, 725–734. [Google Scholar] [CrossRef]
- Amjady, N.; Rabiee, A.; Shayanfar, H. Pay-as-bid based reactive power market. Energy Convers. Manag. 2010, 51, 376–381. [Google Scholar] [CrossRef]
- Hinz, F.; Moest, D. Techno-economic Evaluation of 110 kV Grid Reactive Power Support for the Transmission Grid. IEEE Trans. Power Syst. 2018. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. Active-reactive optimal power flow in distribution networks with embedded generation and battery storage. IEEE Trans. Power Syst. 2012, 27, 2026–2035. [Google Scholar] [CrossRef]
- Varma, R.K.; Khadkikar, V.; Seethapathy, R. Nighttime application of PV solar farm as STATCOM to regulate grid voltage. IEEE Trans. Energy Convers. 2009, 24, 983–985. [Google Scholar] [CrossRef]
- Varma, R.K.; Rahman, S.A.; Mahendra, A.; Seethapathy, R.; Vanderheide, T. Novel nighttime application of PV solar farms as STATCOM (PV-STATCOM). In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Varma, R.K.; Das, B.; Axente, I.; Vanderheide, T. Optimal 24-hr utilization of a PV solar system as STATCOM (PV-STATCOM) in a distribution network. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 24–29 July 2011; pp. 1–8. [Google Scholar]
- Varma, R.K.; Rahman, S.A.; Vanderheide, T. New control of PV solar farm as STATCOM (PV-STATCOM) for increasing grid power transmission limits during night and day. IEEE Trans. Power Deliv. 2015, 30, 755–763. [Google Scholar] [CrossRef]
- Mulolani, F.; Armstrong, M.; Zahawi, B. Modeling and simulation of a grid-connected photovoltaic converter with reactive power compensation. In Proceedings of the 9th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP), Manchester, UK, 23–25 July 2014; pp. 888–893. [Google Scholar]
- Romero-Cadaval, E.; Francois, B.; Malinowski, M.; Zhong, Q.C. Grid-connected photovoltaic plants: An alternative energy source, replacing conventional sources. IEEE Ind. Electron. Mag. 2015, 9, 18–32. [Google Scholar] [CrossRef]
- Albuquerque, F.L.; Moraes, A.J.; Guimarães, G.C.; Sanhueza, S.M.; Vaz, A.R. Photovoltaic solar system connected to the electric power grid operating as active power generator and reactive power compensator. Sol. Energy 2010, 84, 1310–1317. [Google Scholar] [CrossRef]
- Samadi, A.; Ghandhari, M.; Söder, L. Reactive power dynamic assessment of a PV system in a distribution grid. Energy Procedia 2012, 20, 98–107. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. Active-reactive optimal power flow for low-voltage networks with photovoltaic distributed generation. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 381–386. [Google Scholar]
- Ullah, N.R.; Bhattacharya, K.; Thiringer, T. Wind farms as reactive power ancillary service providers—Technical and economic issues. IEEE Trans. Energy Convers. 2009, 24, 661–672. [Google Scholar] [CrossRef]
- Jung, S.; Jang, G. A Loss Minimization Method on a reactive power supply process for Wind Farm. IEEE Trans. Power Syst. 2017, 32, 3060–3068. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, W.; Hou, P.; Tan, J.; Soltani, M.; Chen, Z. Review of Reactive Power Dispatch Strategies for Loss Minimization in a DFIG-based Wind Farm. Energies 2017, 10, 856. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. Evaluation of reactive power capability by optimal control of wind-vanadium redox battery stations in electricity market. Renew. Energy Power Qual. J. 2011, 1–6. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. On variable reverse power flow—Part I: Active-Reactive optimal power flow with reactive power of wind stations. Energies 2016, 9, 121. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. On variable reverse power flow—Part II: An electricity market model considering wind station size and location. Energies 2016, 9, 235. [Google Scholar] [CrossRef]
- Lourenço, L.F.N. Technical Cost of Operating a PV Installation as a STATCOM during Nightime. Master’s Thesis, Universidade de São Paulo, São Paulo, Brazil, 2017. [Google Scholar]
- Lourenço, L.F.N.; Salles, M.B.C.; Monaro, R.M.; Quéval, L. Technical Cost of Operating a Photovoltaic Installation as a STATCOM at Nighttime. IEEE Trans. Sustain Energy 2018. [Google Scholar] [CrossRef]
- Lourenço, L.F.N.; Salles, M.B.C.; Monaro, R.M.; Quéval, L. Technical cost of PV-STATCOM applications. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; pp. 534–538. [Google Scholar]
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-connected photovoltaic systems: An overview of recent research and emerging PV converter technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Yazdani, A.; Di Fazio, A.R.; Ghoddami, H.; Russo, M.; Kazerani, M.; Jatskevich, J.; Strunz, K.; Leva, S.; Martinez, J.A. Modeling guidelines and a benchmark for power system simulation studies of three-phase single-stage photovoltaic systems. IEEE Trans. Power Deliv. 2011, 26, 1247–1264. [Google Scholar] [CrossRef]
- De Brito, M.A.; Sampaio, L.P.; Luigi, G.; e Melo, G.A.; Canesin, C.A. Comparative analysis of MPPT techniques for PV applications. In Proceedings of the 2011 International Conference on Clean Electrical Power (ICCEP), Ischia, Italy, 14–16 June 2011; pp. 99–104. [Google Scholar]
- Huang, L.; Qiu, D.; Xie, F.; Chen, Y.; Zhang, B. Modeling and Stability Analysis of a Single-Phase Two-Stage Grid-Connected Photovoltaic System. Energies 2017, 10, 2176. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Jaeger, U.; Munk-Nielsen, S. Power losses in PWM-VSI inverter using NPT or PT IGBT devices. IEEE Trans. Power Electron. 1995, 10, 358–367. [Google Scholar] [CrossRef]
- Hansen, A.D.; Michalke, G. Modelling and control of variable-speed multi-pole permanent magnet synchronous generator wind turbine. Wind Energy 2008, 11, 537–554. [Google Scholar] [CrossRef]
- Liserre, M.; Blaabjerg, F.; Dell’Aquila, A. Step-by-step design procedure for a grid-connected three-phase PWM voltage source converter. Int. J. Electron. 2004, 91, 445–460. [Google Scholar] [CrossRef]
- Fronius International GmbH Solar Energy Division. Sizing the Maximum DC Voltage of PV Systems; Fronius International GmbH Solar Energy Division: Wels, Austria, 2015. [Google Scholar]
- Martinez, J.A.; Mork, B.A. Transformer modeling for low-and mid-frequency transients—A review. IEEE Trans. Power Deliv. 2005, 20, 1625–1632. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Pedersen, J.K.; Sigurjonsson, S.; Elkjaer, A. An extended model of power losses in hard-switched IGBT-inverters. In Proceedings of the Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting (IAS’96), San Diego, CA, USA, 6–10 October 1996; Volume 3, pp. 1454–1463. [Google Scholar]
- Rajapakse, A.; Gole, A.; Wilson, P. Electromagnetic transients simulation models for accurate representation of switching losses and thermal performance in power electronic systems. IEEE Trans. Power Deliv. 2005, 20, 319–327. [Google Scholar]
- Wong, C. EMTP modeling of IGBT dynamic performance for power dissipation estimation. IEEE Trans. Ind. Appl. 1997, 33, 64–71. [Google Scholar] [CrossRef]
- Drofenik, U.; Kolar, J.W. A general scheme for calculating switching-and conduction-losses of power semiconductors in numerical circuit simulations of power electronic systems. In Proceedings of the 2005 International Power Electronics Conference (IPEC 9205), Niigata, Japan, 4–8 April 2005; pp. 4–8. [Google Scholar]
- Munk-Nielsen, S.; Tutelea, L.N.; Jaeger, U. Simulation with ideal switch models combined with measured loss data provides a good estimate of power loss. In Proceedings of the Conference Record of the IEEE Industry Applications Conference, Rome, Italy, 8–12 October 2000; Volume 5, pp. 2915–2922. [Google Scholar]
- Cole, S. Steady-State and Dynamic Modelling of VSC HVDC Systems for Power System Simulation. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2010. [Google Scholar]
- Haghighat, H.; Kennedy, S. A model for reactive power pricing and dispatch of distributed generation. In Proceedings of the IEEE Power and Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010; pp. 1–10. [Google Scholar]
- Tarifas de Energia de Otimização e de Serviços Ancilares para 2018 (Optimization and Ancillary Services Tariffs for 2018). Available online: http://www.aneel.gov.br/sala-de-imprensa-exibicao-2/-/asset_publisher/zXQREz8EVlZ6/content/fixadas-as-tarifas-de-energia-de-otimizacao-e-de-servicos-ancilares-para-2018/656877?inheritRedirect=false (accessed on 7 June 2018).
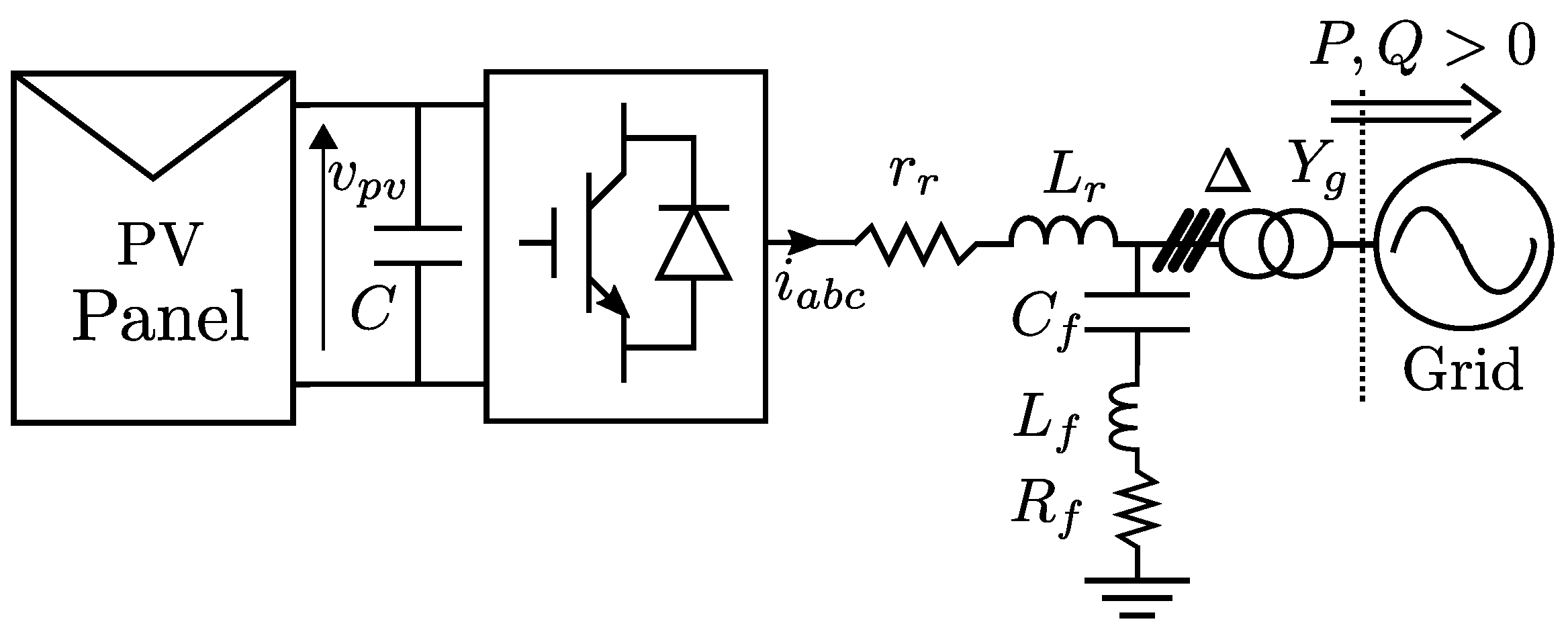
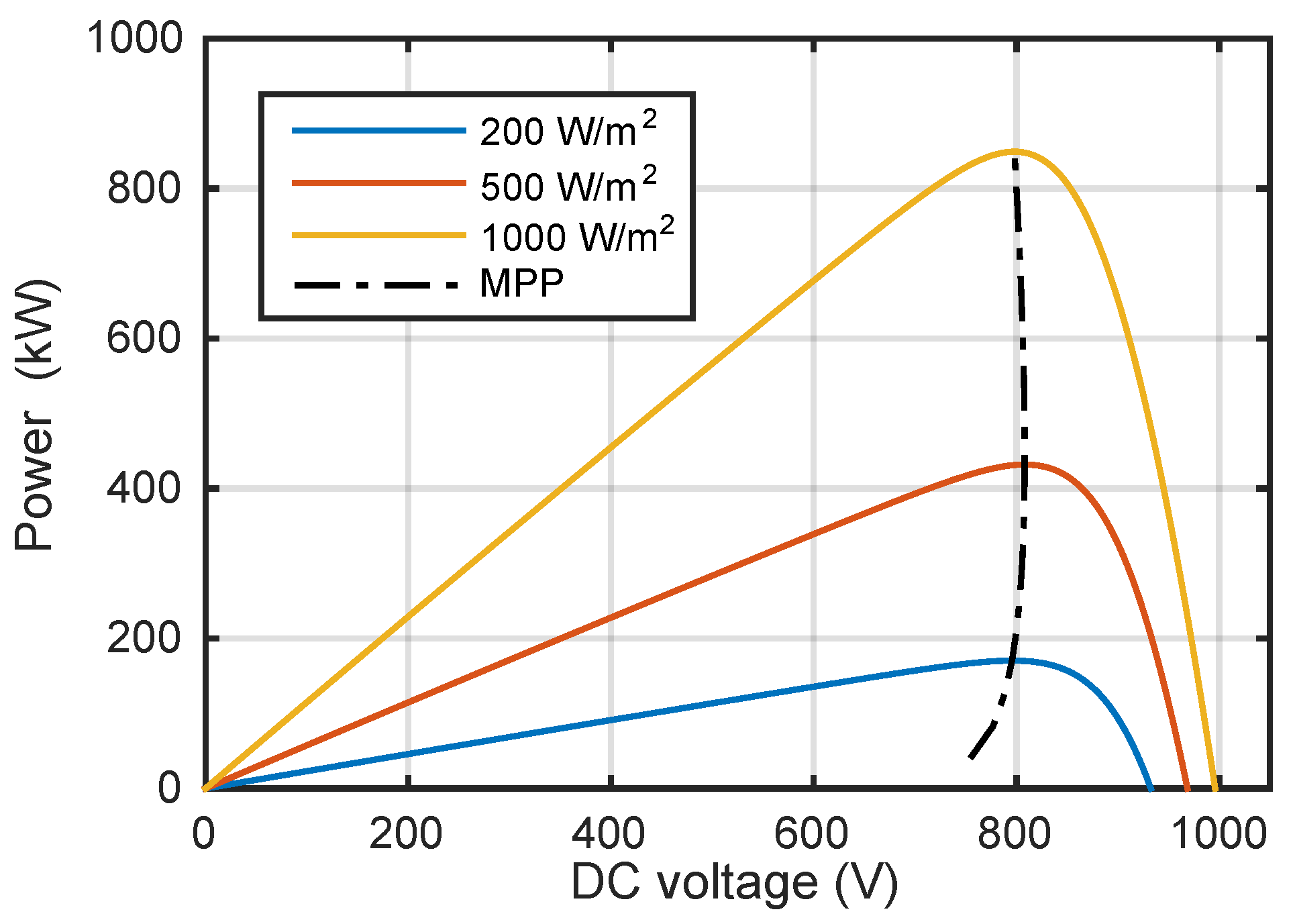

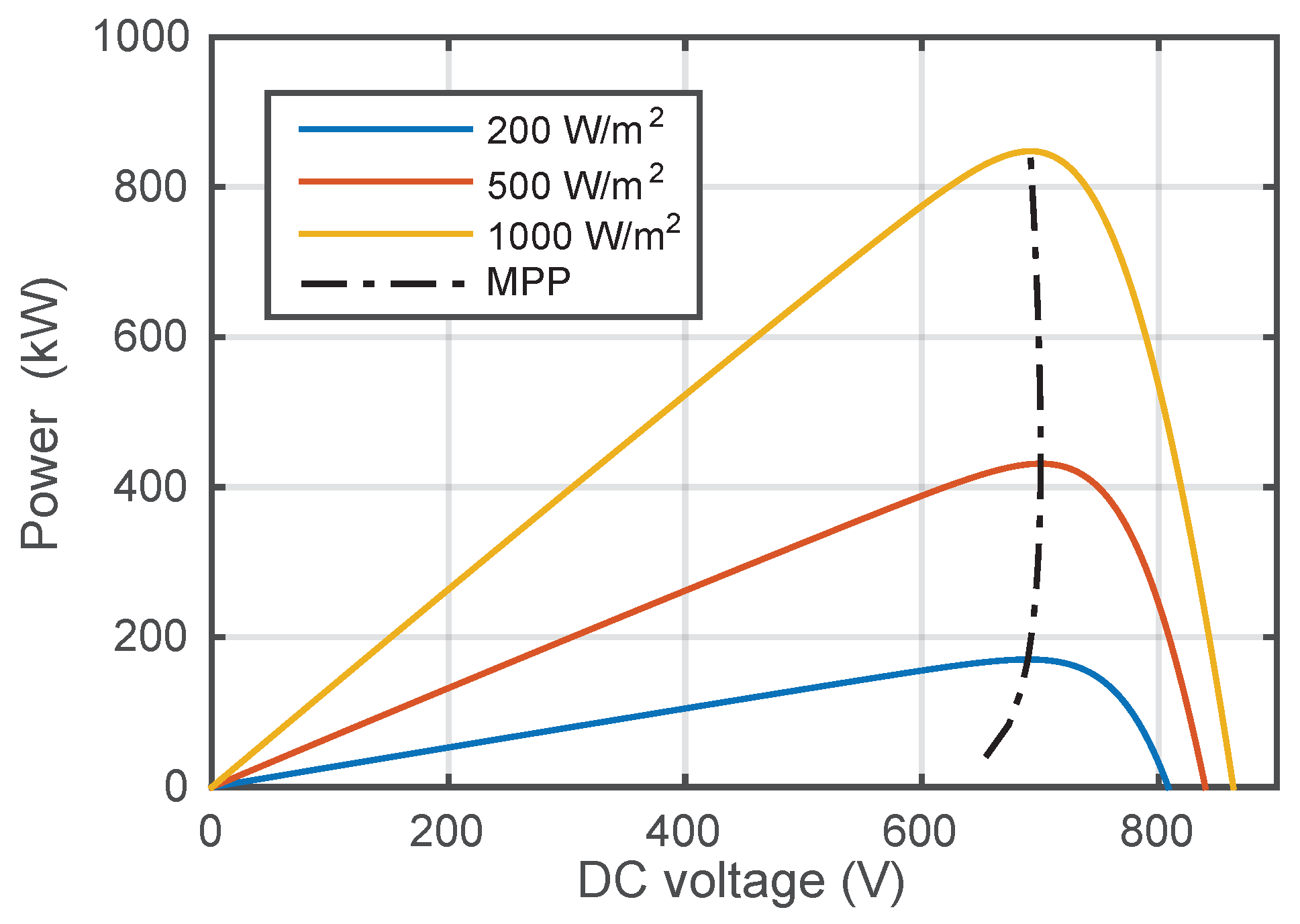
| Parameter | Value | Unit | Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|---|---|---|
| Rated power | 850 | kW | 380 | V | 0.5 | |||
| @1000 W/m | 798 | V | f | 50 | Hz | 397.8 | H | |
| C | 87.8 | mF | 1 | m | 0.64 | F | ||
| 54.1 | H | |||||||
| Component | Reference | Series modules | Parallel modules | Total | ||||
| PV module | Kyocera Solar KD205GX-LP | 30 | 138 | 4.140 | ||||
| DC/AC converter | ABB 5SNA1600N170100 IGBT | 1 | 2 | 12 | ||||
| Parameter | Value | Unit | Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|---|---|---|
| Rated power | 850 | kW | 380 | V | f | 50 | Hz | |
| @ 1000 W/m | 691 | V | 1 | m | 0.5 | |||
| C, | 87.8 | mF | 5.0 | mH | 397.8 | H | ||
| 1 | m | 54.1 | H | 0.64 | F | |||
| Component | Reference | Series modules | Parallel modules | Total | ||||
| PV module | Kyocera Solar KD205GX-LP | 26 | 159 | 4.134 | ||||
| DC/DC converter | ABB 5SNA1600N170100IGBT | 1 | 1 | 1 | ||||
| DC/AC converter | ABB 5SNA1600N170100IGBT | 1 | 2 | 12 | ||||
| Test System | Reactive Power (MVArh) | Technical Costs (MWh) | Revenue | Expenses | Profit |
|---|---|---|---|---|---|
| Single-stage | 8.59 | 0.046 | 59.06 | 46.53 | 12.16 |
| Two-stage @720V | 8.59 | 0.045 | 59.06 | 45.57 | 13.12 |
| Two-stage @750V | 8.59 | 0.047 | 59.06 | 47.18 | 11.51 |
| Two-stage @800V | 8.59 | 0.049 | 59.06 | 48.93 | 9.75 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lourenço, L.F.N.; Monaro, R.M.; Salles, M.B.C.; Cardoso, J.R.; Quéval, L. Evaluation of the Reactive Power Support Capability and Associated Technical Costs of Photovoltaic Farms’ Operation. Energies 2018, 11, 1567. https://doi.org/10.3390/en11061567
Lourenço LFN, Monaro RM, Salles MBC, Cardoso JR, Quéval L. Evaluation of the Reactive Power Support Capability and Associated Technical Costs of Photovoltaic Farms’ Operation. Energies. 2018; 11(6):1567. https://doi.org/10.3390/en11061567
Chicago/Turabian StyleLourenço, Luís F. N., Renato M. Monaro, Maurício B. C. Salles, José R. Cardoso, and Loïc Quéval. 2018. "Evaluation of the Reactive Power Support Capability and Associated Technical Costs of Photovoltaic Farms’ Operation" Energies 11, no. 6: 1567. https://doi.org/10.3390/en11061567
APA StyleLourenço, L. F. N., Monaro, R. M., Salles, M. B. C., Cardoso, J. R., & Quéval, L. (2018). Evaluation of the Reactive Power Support Capability and Associated Technical Costs of Photovoltaic Farms’ Operation. Energies, 11(6), 1567. https://doi.org/10.3390/en11061567






