Preventive Security-Constrained DCOPF Formulation Using Power Transmission Distribution Factors and Line Outage Distribution Factors

Abstract

This study proposes a very effective formulation to carry out the security-constrained direct current (DC)-based optimal power flow (OPF) problem using two linear factors: (i) the power transmission distribution factors (PTDF) and (ii) the line outage distribution factors (LODF). The security-constrained (SC) DCOPF problem has been reformulated using these linear distribution factors, and mainly the pre- and post-contingency constraints have been added into the optimization problem based on the active power unit generation (decision variables). The main advantage of this formulation is the reduction of decision variables as well as equality and inequality constraints. To validate the introduced formulation, several experiments have been conducted using MatPower, DIgSILENT Power Factory and Gurobi. Simulation results demonstrate both the feasibility to carry out the SCOPF problem and the potential applicability of the proposed formulation to medium and large-scale power systems.

1. Introduction

Carpentier introduced the OPF concept in 1960, and this problem couples the economic dispatch problem with a power flow solution [1].

In the technical literature, there is a wide range of mathematical models to carry out diverse optimization problems using several objective functions, constraints and decision variables [2,3]. The OPF problem determines an optimal operating point using an objective function and is subject to technical constraints and control limits. If it is computationally expensive and complex to formulate the alternating current (AC) OPF problem due to time constraints, computing power, or lack of a robust solution algorithm, researchers in the power systems field have used DCOPF. A DCOPF problem is an approximation using several conditions related to voltage magnitudes, voltage angles, admittances, and reactive power.

In the technical literature review, the most common transmission network modelling used to figure out operation and planning problems is the so-called DC model. For example, a congestion analysis accomplished by the independent system operator (ISO)-New England was solved using the DC model and linear methods to estimate a security analysis [4].

Note that in real-time power system operation, ISOs and regional transmission organizations (RTOs) carry out an analysis considering the outage of a generation or a transmission component; this analysis is known as the N−1 condition, and it must be executed very quickly. The contingency analysis must guarantee that operational constraints will be not violated during the post-contingency condition. DC models are also applied to solve contingency analysis considering the outage of a transmission element and verifying that there are not overload conditions [5].

There are two very important concerns that power system engineers should consider in the power system analysis: (i) to model and simulate the electrical power system using fast algorithms/solvers, and (ii) to choose the most important disturbances (contingency selection or contingency screening) that could impact the operation of the power system. The OPF problem including a contingency analysis is known in the technical literature as security-constrained OPF (SCOPF) problem.

1.1. DCOPF Literature Review

The main goal of the SCOPF is to achieve an operational point where the system is kept in a secure condition after the outage of a transmission line and power unit generator [6,7]. In the state-of-the-art, the SCOPF problem is classified using two approaches: (i) the preventive formulation, and (ii) the corrective formulation.

(i)

In the first OPF problem, the mathematical formulation includes only the control variables that are feasible simultaneously for both the pre- and the post-contingency constraints. For this analysis, the optimization problem (variables and constraints) is larger than the traditional OPF because the post-contingency constraints are included in the problem. Furthermore, modelling several outages for large-scale power systems is a demanding and time-consuming issue in the SCOPF problem [7,8].

(ii)

On the other hand, the corrective OPF problem is because some overload conditions caused by the contingency can occur in the power system without affecting the safety in the power components. Notice that the ISO has a short time to take actions in the post-contingency control variables to accomplish a safe operational state; for instance, re-dispatching the power unit generation and moving the transformer taps. For this mathematical formulation, it is necessary to include more decision variables and constraints. Therefore, it would need a large number of actions for modelling a selected number of contingencies [4,9,10,11].

For a recent literature review in these issues, we recommend the following references: References [12,13,14].

1.2. Transmission Network Modelling

The classical DC-based formulation has been used to model the transmission network using the active power unit generation and the voltage phase angles as decision variables [6].

In the technical literature, there is another formulation which uses the nodal admittance matrix to transform the linear (DC) network balance constraints. This transformation obtains one power balance equation which is also used in the economic dispatch to meet the demand of the customers. Replacing the nodal matrix into the transmission power flow definition, the inequality constraints accomplished are a function of the PTDF and the net power injected in the electrical buses. For solving the OPF problem, the decision variables are only the active power generation of each unit [15,16]. With this formulation, there is a very important reduction in decision variables as well as equality and inequality constraints in comparison with the classical DC-based formulation. In [15], the authors apply an interior-point algorithm to figure out the PTDF-based formulation. The algorithm was developed using DIgSILENT Programming Language (DPL); however, the optimization problem does not include the security-constrained analysis.

In the technical literature, the classical DC-based formulation is extensively used to carry out operation and planning problems: unit commitment [17], optimal power flow [15,18,19], security constrained unit commitment [20], generation capacity expansion planning [16,21], and transmission capacity expansion planning [22].

The post-contingency analysis could be carried out using the LODF [6]. Although two balance equations are obtained (pre- and post-contingency), only one equation is needed since active power generation for each condition is the same. Wood and Wollenberg [6] propose to obtain the post-contingency power flows using this linear distribution factors and the pre-contingency power flows. Based on previous studies [15,16], we will model these pre-contingency power flows using the PTDF-based transformation.

In this study, the authors cope with the preventive SCOPF problem. The authors in [4], figured out the same security problem, but the branch outages (lines or transformers) are handled using two fictitious injections at both ends of the transmission line. These power injections are computed using the PTDF matrix. Nevertheless, the goal to be validated is that the power balance for each electrical bus must be equal for both the pre- and the post-contingency conditions. On the other hand, the pre- and post-contingency constraints have been included by Hinojosa et al. [16] to carry out the generation expansion planning problem; however, the SCOPF problem has not been introduced in the OPF field using PTDF, LODF and active power generation as decision variables.

1.3. Contributions

First, in the state-of-the-art, there is no evidence about the performance of both classical and PTDF-based formulations to figure out the DCOPF problem using an interior-point algorithm.

The main contribution of this study is the simultaneous application for the pre- and post-contingency conditions using linear distribution factors and active power generation as decision variables. Notice that these transformations are not sacrificing the OPF and SCOPF optimality. It has conducted several analyses using an interior-point algorithm and a commercial solver (Gurobi) to determine the performance of the proposed formulation applied to different test power systems. Results show that very promising performance and simulation times are obtained in the OPF problem bringing great practical advantages for modelling stochastic programming problems, real-time operation of large-scale power systems, and mainly improving the complexity of the optimization problem given in [4,6,19].

This study has been organized as follows. In Section 2, we have reviewed the OPF problem formulation. Section 3 presents the mathematical formulations applied to OPF and SCOPF using linear distribution factors, and it contains numerical experiments and comparisons. Section 4 concludes the paper.

2. Classical DC-Based Optimal Power Flow

A DC-based OPF problem approximates the nonlinear (AC) OPF under several simplifying conditions:

(i)

High voltage transmission lines can be considered lossless; that is, the line resistance can be disregarded;

(ii)

The voltage angle differences in a transmission element are very small, and

(iii)

The voltage magnitudes for each electrical bus are close to the nominal voltage. Based on this consideration, it is possible to eliminate the Q vs. V relationship. Therefore, the reactive power is eliminated as a variable in the transmission network modelling.

Applying these conditions to the active nonlinear transmission equations, the power flow equations obtained are linear functions of the voltage bus angles. Additionally, angles and active power generation variables are in per unit system (p.u.).

The classical DC-based OPF problem is mathematically expressed as follows:

Objective function (OF): The most common OF used in the OPF problem is the total fuel cost (C_total).

$$\min (C_{total})=\min {\displaystyle \sum _{i=1}^{n_g}{C}_i(P_i)}$$

(1)

where n_g is the total number of power units and the quadratic generation fuel cost of each unit is defined using C(P_i) = a_i + b_i P_i + c_i P_i²; a_i, b_i and c_i are constants of the i-th thermal unit.

The optimization problem contains the following technical constraints:

Nodal power balance constraints: For each electrical bus, the net power injected must equal to the power flows in the transmission lines (B*δ).

$$P-P^d-B*\delta =0$$

(2)

where P is the power unit generation, P^d is the customer demand for each electrical bus, B is the nodal admittance matrix, and δ is the bus voltage angles. In this study, the DC power losses are not modelled in the mathematical formulation.

Power generation limits: The active power supplied by each thermal unit is constrained using their P_min and P_max limits:

$$P^{\min }\le P\le P^{\max }$$

(3)

Transmission network modelling: The active transmission power flow is constrained using its thermal limit (F^max):

$$-F^{\max }\le y*A*\delta \le F^{\max }$$

(4)

where y is the primitive admittance matrix, and A is the incidence matrix.

In the proposed formulation, the voltage bus angles could be constrained. In addition, the voltage bus angle for the reference bus could be previously defined (${\delta }_{ref}=0$).

In this optimization problem, the decision variables (n) are the active power generation and the voltage angles.

$$n=n_b+n_g$$

(5)

The equality constraints (n_e) are:

$$n_e=n_b+1$$

(6)

The inequality constraints (n_i) are:

$$n_i=2\left(n_b+n_g+n_l\right)$$

(7)

where n_b is the number of electrical buses, and n_l is the number of transmission elements (lines or transformers).

2.1. DCOPF Formulation Using PTDF

Nodal power balance constraints: Let us use the inverse of the admittance matrix to transform the balance constraints (Equation (2) into only one equality balance constraint using Equation (8)):

$${\displaystyle \sum _{i=1}^{n_g}{P}_i-{\displaystyle \sum _{j=1}^{n_b}{P}_j^d={\displaystyle \sum _{i=1}^{n_g}{P}_i}-D=0}}$$

(8)

where D is the total load of the power system.

It must be noted that this approach avoids the bus voltage angles as a variable in the OPF problem. The main advantage of this transformation is the lower number of decision variables.

Transmission network modelling: When the voltage angles are also replaced in Equation (4) using the inverse of the admittance matrix, the PTDF are obtained—Equation (9):

$$PTDF=y*A_r*{[A^T{}_r*y*A_r]}^{-1}$$

(9)

where A_r is the reduced incidence matrix. Notice that the PTDF matrix is computed using a slack bus [6]. Additionally, the transmission network constraints are formulated using Equation (10):

$$-F^{\max }\le PTDF*(P-P^d)\le F^{\max }$$

(10)

where F^max contains the thermal limit for each transmission line. The PDTF (n_l * n_b) represents the linear relationship between transmission power flows and power injections.

In the PTDF-based formulation, the variables are only the active power unit generation. Therefore, the decision variables are reduced to n_g variables. Notice that the power unit generation supplied by each unit can be in p.u. or in real units (MW)

In this mathematical problem, there are n_e = 1 (equality constraint) and n_i = 2(n_l + n_g) (inequality constraints). The main advantage of this linear transformation is the lower mathematical formulation because there are n_b lower variables, as well as n_b and 2n_b lower equality and inequality constraints, respectively.

The transmission network modelling using the PTDF-based formulation has been previously carried out in References [15,16,19].

2.2. SC-OPF Formulation Using PTDF and LODF

2.2.1. Post-Contingency Handling Constraints

The optimization problem presented in the previous Section can be improved considering the outage of a transmission element. These security constraints allow the DCOPF problem to handle simultaneously pre-contingency as well as post-contingency constraints.

In the power systems, not all contingencies will produce a post-overload condition. To limit the number of contingencies that will be included in the SCOPF problem, it is supposed that the worst potential case (N − 1 analysis) will be added to the security problem.

By definition [6], the LODF is computed as follows:

$$LOD{F}_{j,k}=\frac{\Delta f_j}{f_k^o}$$

(11)

where Δf_j is the power flow change on the line j, f_k⁰ is the pre-contingency power flow on the line k and LODF_j,k is the linear distribution factor of line j when line k is out. When transmission power flows on the line j and line k are previously determined, the active power flow on the line j can be calculated using Equation (12):

$${\widehat{f}}_j=f_j^0+LOD{F}_{j,k}*f_k^0$$

(12)

where f_j⁰ and f_k⁰ are the pre-contingency power flows on lines j and k, respectively, and ${\widehat{f}}_j$ is the post-contingency power flows.

When the PTDF definition (Equation (10)) is used to model f_j⁰ and f_k⁰, the post-contingency transmission constraints for the j-th branch can be obtained using the following equation:

$$-F^{\max }\le [PTDF+LOD{F}_{j,k}*PTD{F}_j]*(P-P^d)\le F^{\max }$$

(13)

It is worth emphasizing that pre- and post-contingency transmission power flows depend on the net power injected; that is, the decision variables are only P. Notice that it is not necessary to obtain the post-contingency bus voltage angles for modelling the transmission power flows.

In the SCOPF problem, the pre- and post-contingency constraints are mathematically formulated using Equation (14a) and Equation (14b), respectively:

$$-F_{pre}{}^{\max }+PTDF*P^d\le PTDF*P\le F_{pre}{}^{\max }+PTDF*P^d$$

(14a)

$$\begin{array}{l}-F_{post}{}^{\max }+[PTDF+LOD{F}_{j,k}*PTD{F}_j]*P^d\le [PTDF+LOD{F}_{j,k}*PTD{F}_j]*P\le \\ F_{post}{}^{\max }+[PTDF+LOD{F}_{j,k}*PTD{F}_j]*P^d\end{array}$$

(14b)

In this optimization problem, these constraints are incorporated assuming that the active power generation (P) is the same for the pre- and post-contingency condition. Therefore, the ramp-up and ramp-down constraints are not required in the optimization problem.

2.2.2. Mathematical Formulation

The DC-based SCOPF formulation is modelled as follows:

Objective function:

$$\min (C_{total})=\min {\displaystyle \sum _{i=1}^{n_g}{C}_i(P_i)}$$

(15)

s.t.

$${\displaystyle \sum _{i=1}^{n_g}{P}_i}-D=0$$

(16)

$$-F_{pre}{}^{\max }+PTDF*P^d\le PTDF*P\le F_{pre}{}^{\max }+PTDF*P^d$$

(17)

$$-F_{post}{}^{\max }+G*P^d\le G*P\le F_{post}{}^{\max }+G*P^d$$

(18)

$$P^{\min }\le P\le P^{\max }$$

(19)

where: G = PTDF + LODF_j,k * PTDF_j.

Notice that this is a very efficient SCOPF formulation for solving the pre- and post-contingency constraints simultaneously using only linear distribution factors (PTDF and LODF). Additionally, these factors are constant for the security-constrained analysis.

2.2.3. Interior-Point Algorithm

In the OPF field, the interior-point algorithm has become popular due to its excellent computational performance [23]. We have developed the primal-dual interior-point algorithm applied the OPF problem as well as the SCOPF problem using pure-MATLAB code (Version 2014b, Mathworks, Natick, MA, USA). Additionally, we have decided to use this algorithm to compare results obtained in the technical literature [15,24,25].

The optimization algorithm has no problems solving quadratic objective functions. More details about the algorithm could be reviewed in Chapter 5 [15].

Based on the OPF problem, the main difference between the proposed approach and MatPower is that the last one uses the power generation and the voltage phase angles (classical DC-based formulation) as decision variables. Using the classical model (two decision variables), a more complex optimization problem will be achieved for solving large-scale power systems.

3. Results

In this study, we have conducted several experiments to find out the performance of the proposed formulation. The optimization problem was solved using MATLAB [26] and Gurobi [27] on a computer with the following characteristics: Intel Core i7 3930 (3.20 GHz) with RAM 32 GB.

3.1. DCOPF Based on PTDF Factors

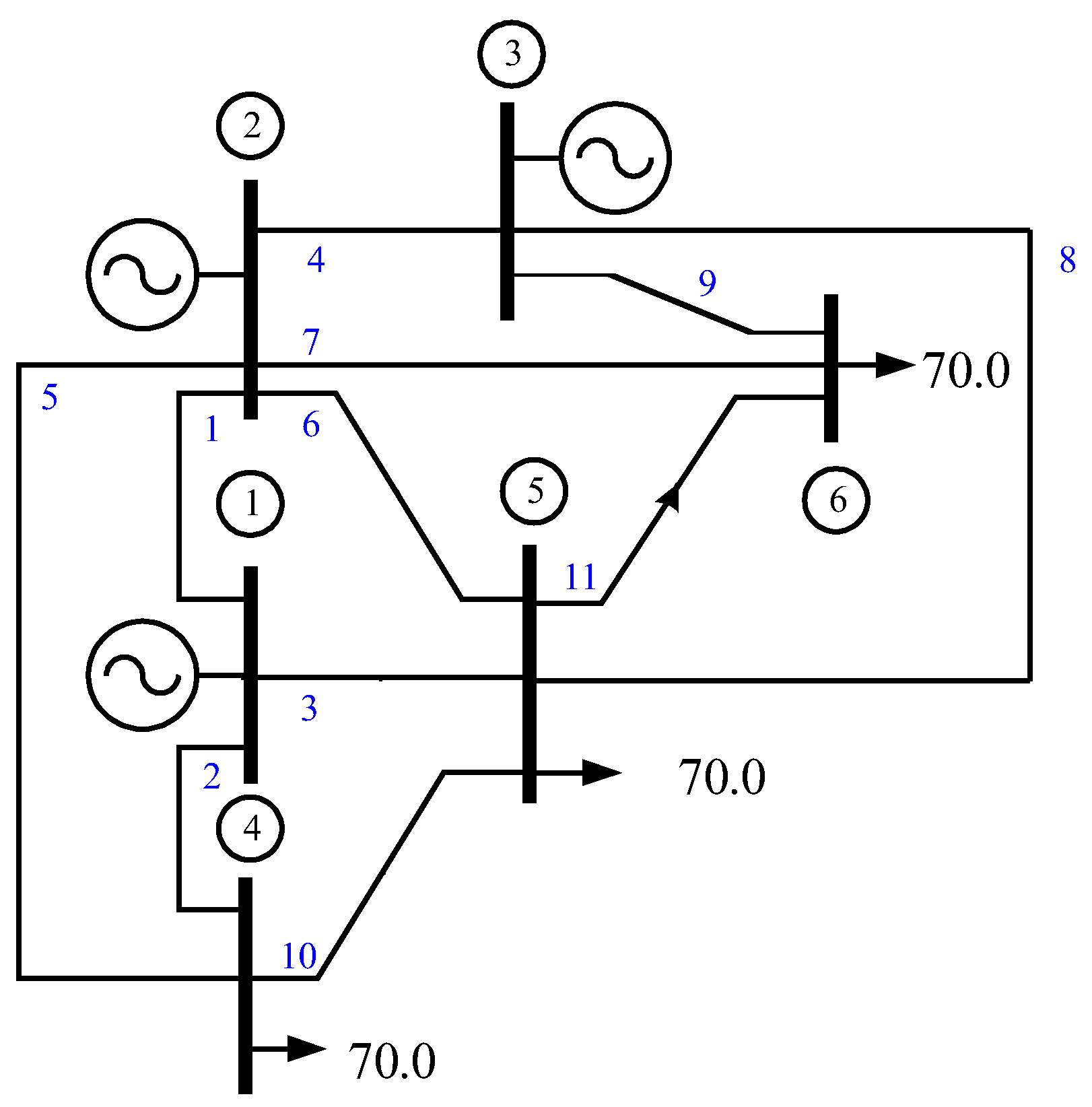
• The classic 6-bus power system introduced by Wood and Wollenberg [6] is used to illustrate the OPF using both the classical DC-based and the PTDF-based formulations. In Figure 1, shows the electrical transmission network. The electrical power system contains three generators and eleven transmission lines. The power generation and transmission data can be seen in Reference [6] or in MatPower [24].

The OPF mathematical formulation using quadratic cost functions and PTDF (bus 1 is the slack bus) is presented below:

$$\min \left({\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]}^T\left[\begin{array}{ccc}0.00533& 0& 0\\ 0& 0.00889& 0\\ 0& 0& 0.00741\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]+{\left[\begin{array}{c}11.669\\ 10.333\\ 10.833\end{array}\right]}^T\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\right)$$

s.t.

$${\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]}^T\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]=210$$

$$\left[\begin{array}{c}-133.0133\\ -135.0039\\ -101.9829\\ \begin{array}{l}-59.6245\\ -63.9812\\ -43.3072\\ -126.1005\\ -66.4848\\ -103.1397\\ -28.9851\\ -50.7598\end{array}\end{array}\right]\le \left[\begin{array}{l}\begin{array}{ccc}0& -0.4706& -0.4026\\ 0& -0.3149& -0.2949\\ \begin{array}{l}0\\ 0\\ 0\\ 0\end{array}& \begin{array}{l}-0.2145\\ 0.0544\\ 0.3115\\ 0.0993\end{array}& \begin{array}{l}-0.3026\\ -0.3416\\ 0.2154\\ -0.0342\end{array}\end{array}\\ \begin{array}{ccc}0& 0.0642& -0.2422\\ 0& 0.0622& 0.2890\\ \begin{array}{l}0\\ 0\\ 0\end{array}& \begin{array}{l}-0.0077\\ -0.0034\\ -0.0565\end{array}& \begin{array}{l}0.3695\\ -0.0795\\ -0.1273\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\le \left[\begin{array}{c}-33.0133\\ -15.0039\\ -21.9827\\ \begin{array}{l}20.3755\\ 56.0188\\ 16.6928\\ 53.8995\\ 73.5152\\ 56.8603\\ 11.0149\\ 29.2402\end{array}\end{array}\right]$$

$$\left[\begin{array}{c}50.0\\ 37.5\\ 45.0\end{array}\right]\le \left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\le \left[\begin{array}{c}200.0\\ 150.0\\ 180.0\end{array}\right]$$

When the DCOPF problem is solved using the classical DC-based formulation and the PTDF-based formulation, the optimal cost is C_total = 3046.41 $/h. The power generation solution is P₁ = 50.00 MW, P₂ = 88.0736 MW and P₃ = 71.9264 MW. Additionally, there is no congestion in the transmission network.

Table 1. Convergence criteria reached by the optimal solution: Test System I.

Description	Value
Feasibility condition	0.00
Gradient condition	1.37 × 10−16
Complementary condition	2.86 ×10−7
Cost condition	3.82 × 10−10

shows the interior-point convergence parameters for the optimal solution.

The optimal solution is compared with the interior-point algorithm developed in DIgSILENT Power Factory [15]. Both solutions are the same. Therefore, the PTDF-based formulation developed in MATLAB is corroborated.

• The next simulation considers that two transmission lines are limited: (1) line 2–4 to 40 MW and (2) line 2–6 to 50 MW. The OPF formulation is as follows:

$$\min \left({\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]}^T\left[\begin{array}{ccc}0.00533& 0& 0\\ 0& 0.00889& 0\\ 0& 0& 0.00741\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]+{\left[\begin{array}{c}11.669\\ 10.333\\ 10.833\end{array}\right]}^T\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\right)$$

s.t.

$${\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]}^T\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]=210$$

$$\left[\begin{array}{c}-133.0133\\ -135.0039\\ -101.9829\\ \begin{array}{l}-59.6245\\ -43.9812\\ -43.3072\\ -86.1005\\ -66.4848\\ -103.1397\\ -28.9851\\ -50.7598\end{array}\end{array}\right]\le \left[\begin{array}{l}\begin{array}{ccc}0& -0.4706& -0.4026\\ 0& -0.3149& -0.2949\\ \begin{array}{l}0\\ 0\\ 0\\ 0\end{array}& \begin{array}{l}-0.2145\\ 0.0544\\ 0.3115\\ 0.0993\end{array}& \begin{array}{l}-0.3026\\ -0.3416\\ 0.2154\\ -0.0342\end{array}\end{array}\\ \begin{array}{ccc}0& 0.0642& -0.2422\\ 0& 0.0622& 0.2890\\ \begin{array}{l}0\\ 0\\ 0\end{array}& \begin{array}{l}-0.0077\\ -0.0034\\ -0.0565\end{array}& \begin{array}{l}0.3695\\ -0.0795\\ -0.1273\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\le \left[\begin{array}{c}-33.0133\\ -15.0039\\ -21.9827\\ \begin{array}{l}20.3755\\ 36.0188\\ 16.6928\\ 13.8995\\ 73.5152\\ 56.8603\\ 11.0149\\ 29.2402\end{array}\end{array}\right]$$

$$\left[\begin{array}{c}50.0\\ 37.5\\ 45.0\end{array}\right]\le \left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\le \left[\begin{array}{c}200.0\\ 150.0\\ 180.0\end{array}\right]$$

In comparison with the previous formulation, the differences can be seen in the rhs of line 2–4 and 2–6.

The optimal solution is C_total = 3059.888 $/h, and the power generation solution is P₁ = 73.5154 MW, P₂ = 68.9212 MW, and P₃ = 67.5634 MW. For this case, there is congestion in the transmission line 2–4. Therefore, there is a higher cost caused by the congestion, and it is necessary to meet the demand of the customers using more expensive generation. This result will be used as the base case (pre-contingency solution) to compare with the post-contingency solution.

• Different test systems are used to check both formulations applied to the DCOPF problem: 9-bus system (three generators and nine transmission lines); 14-bus system (five generators and twenty transmission lines); 30-bus system (six generators and forty-one transmission lines); 57-bus system (seven generators and eighty transmission lines); and 118-bus system (fifty-four generators and one hundred eighty-six transmission lines). Technical data can be seen in MatPower.

Table 2. Application of the interior-point algorithm to different test power systems.

System	Number of Iterations	Cost, $/h
9-bus	14	20,393.15
14-bus	11	7642.59
30-bus	10	960.09
57-bus	10	41,006.74
118-bus	11	125,954.42

shows the optimal cost for each test power system. Additionally, the number of iterations for the convergence of the interior-point algorithm has been included. The same results were obtained for both the classical DC-based and the PTDF-based formulations.

Using the interior-point algorithm, it is possible to realize that there is not necessarily many iterations for solving medium-scale power systems.

The results are compared with the DCOPF problem computed by MatPower, and both solutions are the same (total cost, power generation level, and transmission power flow). As a result, it is validated that both OPF formulations are equivalent because both problems accomplish the global solution.

• To determine the performance for each formulation, the authors have decided to program the OPF quadratic formulation using Gurobi.

  Table 3. Simulation time using both formulations applied to different power systems.

  Power	Classical Formulation			PTDF Formulation			Improving
  System	Min, ms	Max, ms	Average, ms	Min, ms	Max, ms	Average, ms	%
  9-bus	0.9784	1.3668	1.0851	0.7898	1.1708	0.9211	3.74
  14-bus	0.9993	1.4488	1.1281	0.7687	1.1779	0.8968	5.22
  30-bus	2.1078	2.4357	2.2149	0.9460	1.4597	1.1152	19.94
  57-bus	2.2244	3.2354	2.3990	1.0157	1.4885	1.1586	21.77
  118-bus	6.2514	7.0087	6.7132	3.4785	3.8957	3.6131	46.18

  shows the performance of simulation times for both formulations considering 100 trials. Additionally, included are the minimum, the maximum and the average simulation time.

In the last column, the simulation time improvement obtained by the PTDF-based formulation using different test power systems is determined.

Based on the lower simulation time, it is concluded that the PTDF-formulation achieves the best simulation time to figure out the DCOPF problem. This is caused by a lower number of decision variables as well as a lower number of equality and inequality constraints. Consequently, we recommend the PTDF-based formulation to carry out medium and large-scale power systems.

The drawback of this approach is that the solution does not compute the voltage bus angles. Nevertheless, it is possible to obtain these angles using the inverse admittance matrix and the optimal solution.

3.2. DCOPF Based on PTDF and LODF Factors

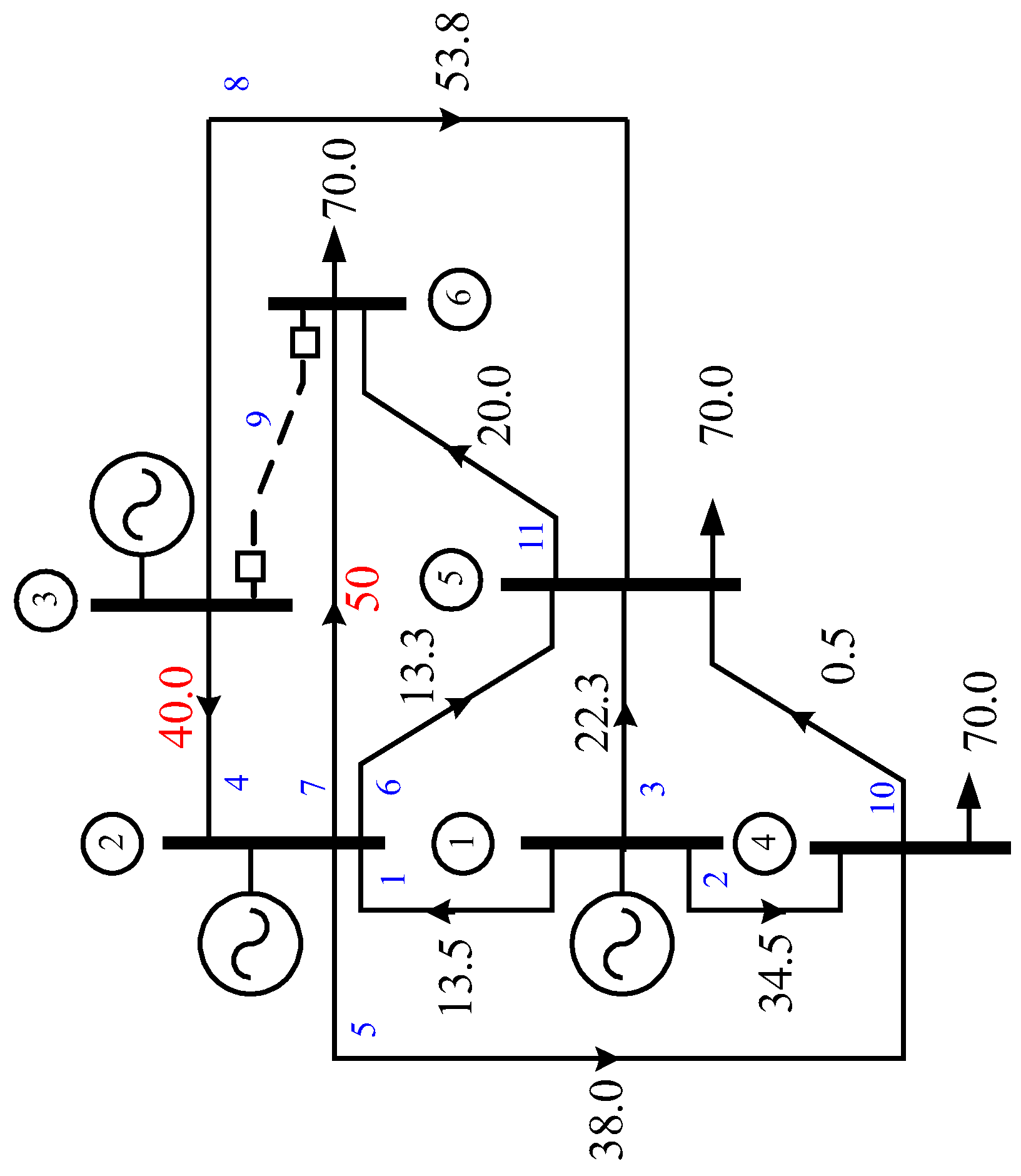
• For the 6-bus power system, the worst contingency considers the outage of transmission line 3–6. The SCOPF problem using the PTDF and LODF is introduced as follows:

$$\min \left({\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]}^T\left[\begin{array}{ccc}0.00533& 0& 0\\ 0& 0.00889& 0\\ 0& 0& 0.00741\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]+{\left[\begin{array}{c}11.669\\ 10.333\\ 10.833\end{array}\right]}^T\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\right)$$

s.t.

$${\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]}^T\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]=210$$

$$\left[\begin{array}{c}-133.0133\\ -135.0039\\ -101.9829\\ \begin{array}{l}-59.6245\\ -43.9812\\ -43.3072\\ -86.1005\\ -66.4848\\ -103.1397\\ -28.9851\\ -50.7598\end{array}\end{array}\right]\le \left[\begin{array}{l}\begin{array}{ccc}0& -0.4706& -0.4026\\ 0& -0.3149& -0.2949\\ \begin{array}{l}0\\ 0\\ 0\\ 0\end{array}& \begin{array}{l}-0.2145\\ 0.0544\\ 0.3115\\ 0.0993\end{array}& \begin{array}{l}-0.3026\\ -0.3416\\ 0.2154\\ -0.0342\end{array}\end{array}\\ \begin{array}{ccc}0& 0.0642& -0.2422\\ 0& 0.0622& 0.2890\\ \begin{array}{l}0\\ 0\\ 0\end{array}& \begin{array}{l}-0.0077\\ -0.0034\\ -0.0565\end{array}& \begin{array}{l}0.3695\\ -0.0795\\ -0.1273\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\le \left[\begin{array}{c}-33.0133\\ -15.0039\\ -21.9827\\ \begin{array}{l}20.3755\\ 36.0188\\ 16.6928\\ 13.8995\\ 73.5152\\ 56.8603\\ 11.0149\\ 29.2402\end{array}\end{array}\right]$$

$$\left[\begin{array}{c}-133.3247\\ -135.0955\\ -101.5798\\ \begin{array}{l}-47.4686\\ -43.5416\\ -42.6966\\ -99.6180\\ -77.4686\\ -28.6371\\ -60.3820\end{array}\end{array}\right]\le \left[\begin{array}{l}\begin{array}{ccc}0& -0.4706& -0.3976\\ 0& -0.3149& -0.2934\\ \begin{array}{l}0\\ 0\\ 0\\ 0\end{array}& \begin{array}{l}-0.2144\\ 0.0585\\ 0.3116\\ 0.0995\end{array}& \begin{array}{l}-0.3090\\ -0.5357\\ 0.2084\\ -0.0439\end{array}\end{array}\\ \begin{array}{ccc}0& 0.0597& -0.0264\\ 0& 0.0585& 0.4643\\ \begin{array}{l}0\\ 0\end{array}& \begin{array}{l}-0.0033\\ -0.0597\end{array}& \begin{array}{l}-0.0850\\ 0.0264\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\le \left[\begin{array}{c}-33.3247\\ -15.0955\\ -21.5798\\ \begin{array}{l}32.5314\\ 36.4584\\ 17.3034\\ 0.3820\\ 62.5314\\ 11.3629\\ 19.6180\end{array}\end{array}\right]$$

$$\left[\begin{array}{c}50.0\\ 37.5\\ 45.0\end{array}\right]\le \left[\begin{array}{c}{P}_1\\ P_2\\ P_3\end{array}\right]\le \left[\begin{array}{c}200.0\\ 150.0\\ 180.0\end{array}\right]$$

The optimization problem converged, and the optimal cost is C_total = 3071.679 $/h. The power generation is P₁ = 68.2956 MW, P₂ = 47.8582 MW, and P₃ = 93.8462 MW. It can be seen that there is no congestion for the pre- and the post-contingency conditions. For instance, the power flow solution for the pre-contingency case is f12 = 12.7 MW, f14 = 32.3 MW, f15 = 23.3 MW, f23 = −9.8 MW, f24 = 39.1 MW, f25 = 14.8 MW, f26 = 16.4 MW, f35 = 26.6 MW, f36 = 57.4 MW, f45 = 1.4 MW, and f56 = −3.9 MW.

Using the optimal power generation solution obtained by the PTDF and LODF-based formulation, authors carry out the outage of transmission line 3–6 using a DC power flow. The power flows through the transmission network are shown in Figure 2.

It is worth mentioning that the outage of transmission line 3–6 does not produce an overload condition in the transmission system; i.e., it is a preventive solution. However, there is congestion on transmission line 2–3 (maximal power flow is 40 MW) and line 2–6 (maximal power flow is 50 MW). The additional cost (11.791 $/h) is produced by the worst contingency modelling so that it is necessary to re-schedule more expensive generation to supply the load of the customers. Because MatPower does not carry out the security-constraint analysis, the authors have used Gurobi to figure out the quadratic programming problem. Both solutions are the same which validates the SCOPF formulation.

Table 4. Pre- and post-contingency solutions: 6-bus power system.

System	Base Case	Pre- and Post-Contingency Solution	Difference
P1,MW	75.52	68.29	‒7.23
P2,MW	68.92	47.85	−21.07
P3,MW	67.56	93.84	+26.28
Ctotal, $/h	3059.888	3071.679	+11.791

shows the OPF solution (base case) as well as the SCOPF solution. It is very clear that there is a re-scheduling (last column) in the power generation units to reach a secure preventive state after the outage of transmission line 3–6.

• Last, in MatPower, there is another power system case called “case13659pegase.m”. This model represents the Polish 400, 220 and 110 kV networks during the winter 1999–2000 peak conditions. In the system, there are 327 generators and 2896 transmission lines.

For solving the SCOPF with the outage of transmission line 11–4, the optimal cost is C_total = 1,800,888.062 $/h. In the PTDF and LODF formulation, the number of decision variables is n = 327, the number of equality and inequality constraints is n_e + n_i = 12,237, the number of non-zero elements is 2,899,573, and the number of Gurobi iterations to solve the problem is 100.

The results lead to the conclusion that the proposed formulation can be applied to simulate large-scale power systems without problems in convergence process and simulation time. These aspects are the most important goals for ISO to carry out OPF and SCOPF analyses.

4. Conclusions

This study introduced an effective formulation to carry out the security-constrained DC optimal power flow problem using linear distribution factors (PTDF and LODF). The main advantage of the proposed formulation is the feasibility to include simultaneously the pre- and post-contingency transmission network constraints using these linear factors and the power unit generation as decision variables. Notice that these transformations are not sacrificing the OPF and SCOPF optimality. Both problems have been illustrated and tested with different test systems using an interior-point algorithm and a commercial solver. The experiments conducted using a commercial solver have demonstrated the superior performance of the proposed formulation revealing a very important reduction in problem size and simulation time. Therefore, these formulations could be scaled up for medium and large-scale power systems. Finally, the inclusion of security criteria in the optimization problem strengthens the operational solution; i.e., the system is kept in a normal operation state after a major transmission outage.

It is expected that the generation expansion planning problem in DIgSILENT Power Factory program using a similar approach [16] will be modeled soon.