Multiple Fuel Machines Power Economic Dispatch Using Stud Differential Evolution

Abstract

This paper presents an optimization method for solving the Power Economic Dispatch (PED) problem of thermal generation units with multiple fuels and valve point loadings. The proposed optimizer is a variant of Differential Evolution (DE) characterized as a Stud Differential Evolution (SDE), which has been proposed earlier and implemented on a hydrothermal energy system. In SDE, an operator named Stud Crossover (SC) is introduced in the conventional DE during the trial vector updating process. In SC operator, a best vector gives its optimal information to all other population members through mating. The proposed algorithm’s effectiveness to solve Multiple Fuel PED problem, with and without Valve Point Loading Effects (VPLEs), has been validated by testing it on 10 machine multiple fuel standard test systems having 2400 MW, 2500 MW, 2600 MW, and 2700 MW load demands. The results depict the strength of SDE over various other methods in the literature.

1. Introduction

The Power Economic Dispatch (PED) is one of the essential steps in operation and planning of a power system. It is an online function and is carried out after every fifteen minutes or on request in control centers. It is a generation allocation problem that is defined as the determination of an optimal generation schedule of machines subjected to the satisfaction of equality and in-equality constraints. PED is non-convex in nature because of Valve Point Loading Effects (VPLEs), Multiple Fuel Options (MFOs), and Prohibited Operating Zones (POZs) [1]. However, most of the time it is addressed as a convex optimization problem solved by conventional techniques; e.g., equal incremental cost criterion, gradient search method [2], Newton’s Method (NM), Lambda Iteration Method (LIM), Lagrange Relaxation (LR) [3], Dynamic Programming (DP) [4], and Quadratic Programming (QP) [5], etc. In such techniques, a simple quadratic function represents the machine curve that ignores the practical constraints; e.g., MFOs, POZs, and VPEs. Therefore, these conventional techniques lack the ability of solving highly complex, non-linear, and non-convex optimization problems and thereby fail to find the optimal solution [6].

Thus, for solving such non-convex PED problems, Artificial Intelligence (AI) based approaches were developed, examples include Genetic Algorithm (GA) [7], Particle Swarm Optimization (PSO) [8], fuzzy logic [9], Artificial Neural Network (ANN), Simulated Annealing (SA) [10], and Tabu Search (TS) [11], etc. Many other nature inspired algorithms introduced in the literature of economic dispatch include Artificial Bee Colony (ABC) [12,13], Cuckoo Search Algorithm (CSA) [14], Flower Pollination Algorithm (FPA) [15], Bat Algorithm (BAT) [16], Lightning Flash Algorithm (LFA) [17], Ant Lion Optimizer (ALO) [18], Distributed Auction Optimization Algorithm (DAOA) based on the gossip communication mechanism [19], Stud Krill Herd (SKH) [20], Symbiotic Organisms Search (SOS) algorithm [21], and Water Cycle Algorithm (WCA) [22], etc. These techniques are sometimes used in a modified and hybridized manner, such as in Adaptive Cuckoo Search Algorithm (ACSA) [23], Enhanced Lagrangian Artificial Neural Network(ELANN) [24], Modified Symbiotic Organisms Search (MSOS) algorithm [25], Chaotic Bat Algorithm (CBA) [26], New particle swarm optimization with local random search (NPSO_LRS) [27], Improved Genetic Algorithm with Multiplier Updating (IGA_MU) [28], Conventional Genetic Algorithm with Multiplier Updating (CGA_MU) [28], and Particle Swarm Optimization with Gaussian Mutation (PSO_GM) [29] to further optimize search time and results. Evolutionary Algorithms (EAs) are also potential solution methodologies.

Differential Evolution (DE) [30] belongs to the class of EAs. It was first presented by Storn and Price in 1997 [31]. Since it was developed, it has earned the reputation of an efficient global optimization technique for solving non-linear and non-differentiable problems. Some of its advantages include its robustness, simplicity, easy usage, and speed. DE comprises both evolutionary and classic GA strategies. DE is an optimization technique that is most preferred by utility because of its immediate response to practical problems. During the past few years, many variants of DE have also been proposed to solve PED problem such as Self-adaptive DE (SaDE) [32], Improved DE (IDE) [33], Shuffled DE (SDE) [34], hybrid of Continuous Greedy Randomized Adaptive Search Procedure with DE (C-GRASP–DE) [35], hybrid of DE with Particle Swarm Optimization (DEPSO) [1], and many others. DE has a global search capability but it is not always able to search the global optimum solution due to pre-mature convergence. Additionally, its local search ability is also weak.

To cater to all these problems, a variant of DE named Stud Differential Evolution (SDE) has been proposed in this paper. Stud behavior has been proposed and implemented earlier with some evolutionary methods, such as GA [36] and KHA [37]. SDE was proposed by Haroon SS et al. in [38] and was successfully applied for the solution of the emissions constrained hydrothermal energy system problem. However, until now the effectiveness of stud incorporated DE (SDE) has not been examined as a competent solution to convex/non-convex power economic dispatch problems as well as a potential search approach, thereby rendering a research gap in the literature. Another major reason behind the development of SDE is the incompetency of conventional DE in solving complicated multi-modal problems efficiently as it does not always proceed to the global optimum solution. Therefore, a Stud Crossover (SC) operator unlike the conventional crossover operator is introduced that shares the information of an optimal vector with rest of the population vectors and restarts the search through cross-over. The introduced SC operator helps to avoid the entrapment in the local optimum and to find a global optimal solution. SC also empowers the local search ability of the proposed algorithm. Hence with the two said techniques combined, SDE balances the exploitation and exploration altogether, resulting in better performance towards complicated problems.

In this paper, a convex PED (with only MFOs) and a non-convex PED (with both MFOs and VPLEs) have been mapped in SDE. Hence the effectiveness of SDE has been determined by applying it on multiple fuel standard test systems comprising 10 generation-units with power demands of 2700 MW, 2600 MW, 2500 MW, and 2400 MW.

2. Problem Formulation

Mathematically, the PED problem is usually modeled by its objective function and constraints related to generating units. The objective function of PED is to minimize the total fuel cost of all power generation units while satisfying the power balance constraint and generation capacity constraint of the power system.

2.1. Objective Function

The objective of the PED problem is to minimize the overall power generation cost. Equation (1) is a mathematical representation of the objective function of PED.

$$min{F}_T={\displaystyle \sum }_{i=1}^N{F}_i (P_{G_i})$$

(1)

where, $F_T$ is the overall power generation cost to be minimized, $F_i(P_{G_i})$ is the fuel cost associated with ith unit, $P_{G_i}$ is the power generated from ith unit and $N$ is the number of units. The fuel cost equation of a simple PED problem, for an ideal power system, is a quadratic function and is given in Equation (2).

$$F_i(P_{G_i})= a_i+b_i{P}_{G_i}+c_i{P}_{G_i}^2$$

(2)

Here, $a_i$, $b_i\mathrm{and}{c}_i$ are the fuel cost coefficients of the ith generator. The fuel cost curve for above quadratic fuel cost equation has been shown in Figure 1. It depicts the fuel cost characteristics of a simple economic dispatch problem.

2.2. Constraints

The following are the constraints that are supposed to be satisfied while achieving the objective function of PED.

2.2.1. Equality Constraint

The sum of power generated from all units is required to be equal to the total power demand as represented through Equation (3).

$${\displaystyle \sum }_{i=1}^N{P}_{G_i}=P_d$$

(3)

2.2.2. In-Equality Constraint

The value of power generated by each unit should lie inside the maximum and minimum power generation limit of that unit. Equation (4) presents this constraint of generation capacity.

$$P_{G_i}^{min}\le P_{G_i}\le P_{G_i}^{max}$$

(4)

where, $P_D$ is the total power demand, $P_{G_i}$ is the power generated by ith unit and $P_{G_i}^{min}$ and $P_{G_i}^{max}$ are the minimum and maximum power limits from ith generation unit respectively.

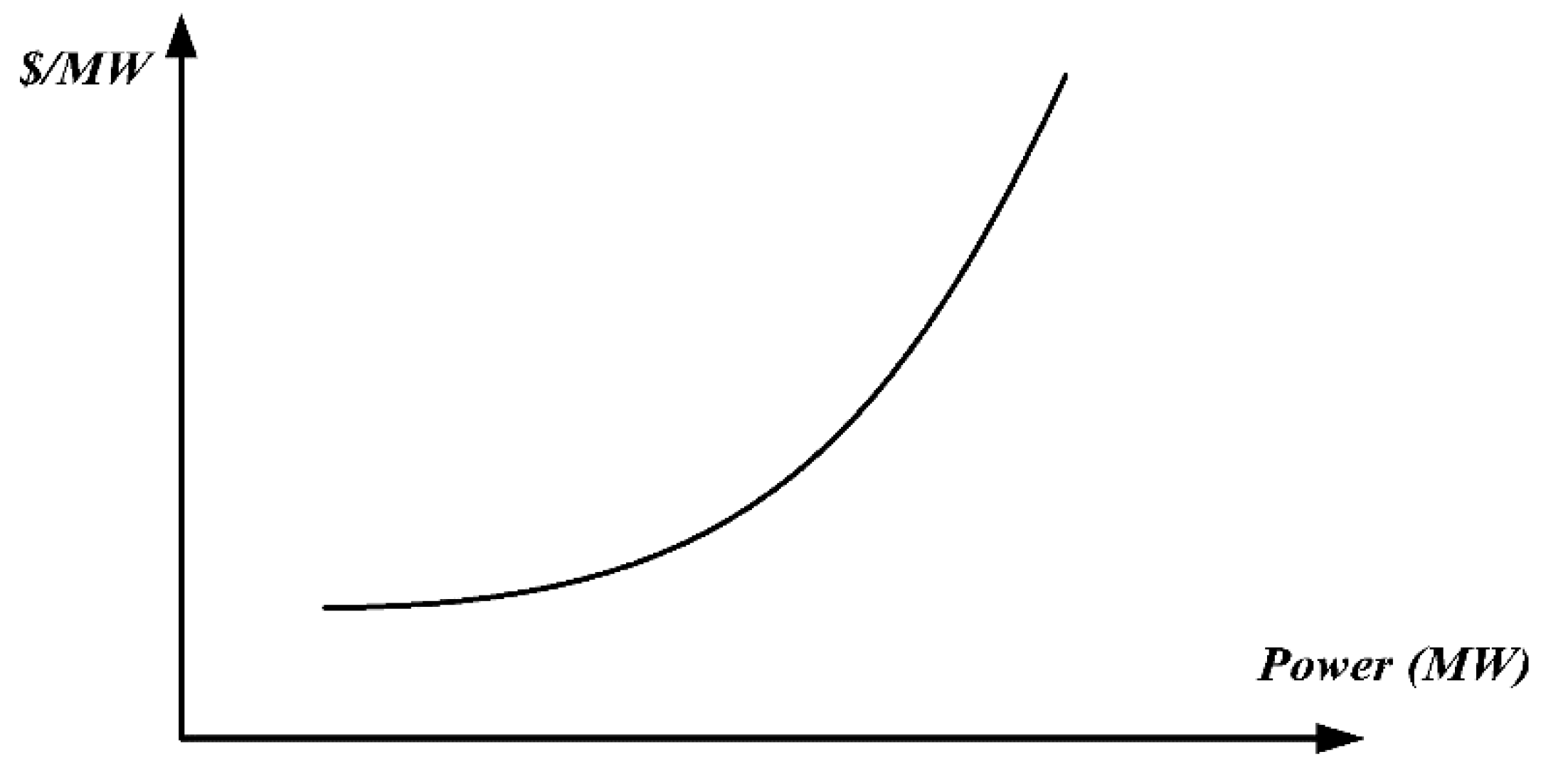
2.3. Fuel Cost Equations

Practically, the objective function of PED problem is non-differentiable and non-convex in nature because of VPLEs and MFOs. Therefore, the objective function of PED is modeled in terms of following fuel cost equations for practical power systems.

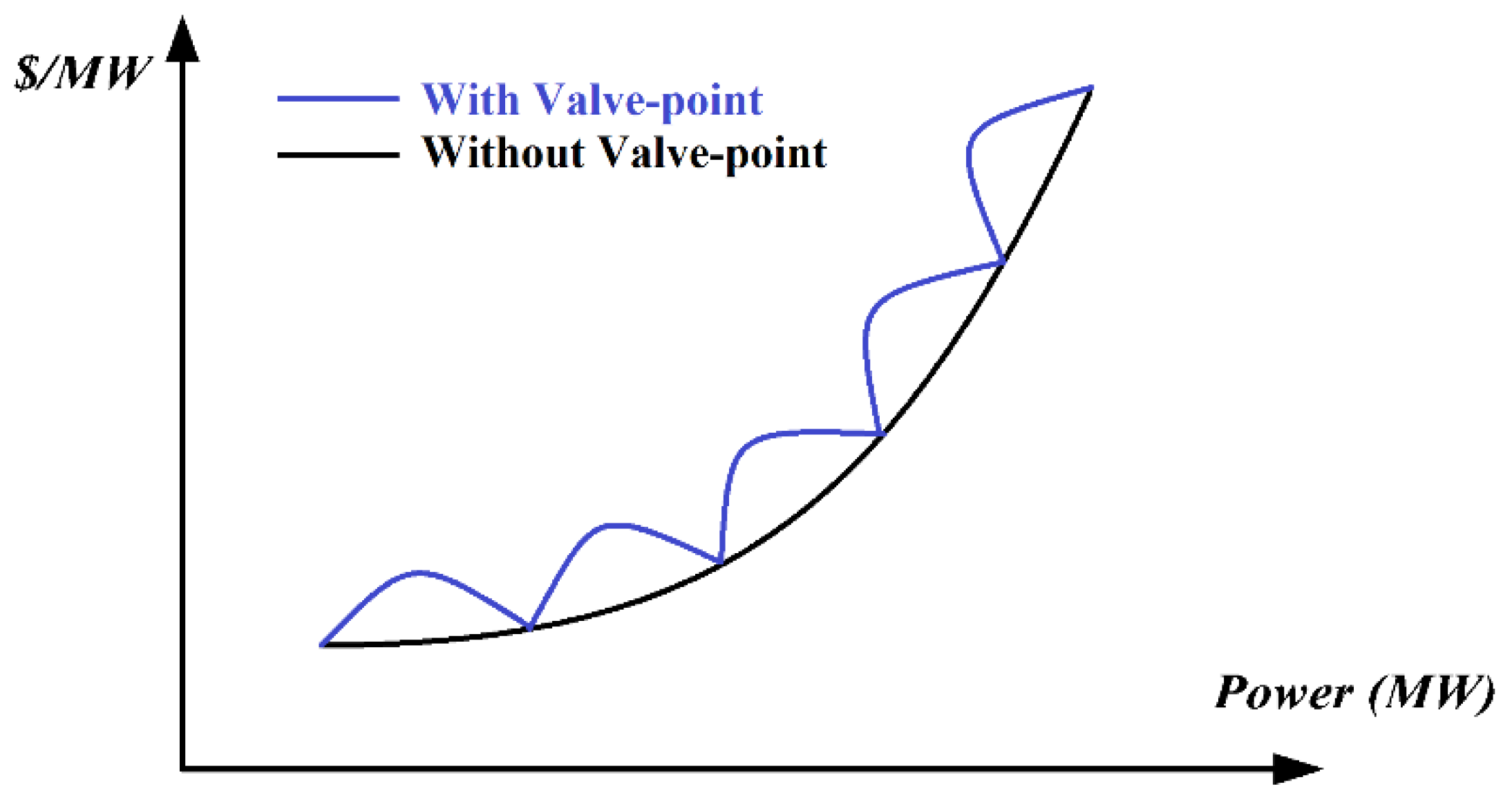
2.3.1. Power Economic Dispatch considering Valve Point Loading Effects Only

The fuel cost equation for a PED problem with only VPLEs is as under,

$$F_i(P_{G_i})= a_i+b_i{P}_{G_i}+c_i{P}_{G_i}^2+\left|e_{i}sin(f_i(P_{G_i}^{min}-P_{G_i}))\right|$$

(5)

The fuel cost curve for such type of PED has been presented in Figure 2.

2.3.2. Power Economic Dispatch Considering Multiple Fuel Options Only

The fuel cost equation for a PED problem with only MFOs, is as under in Equation (6).

$$F_i(P_{G_i})=\{\begin{array}{c}{a}_i{}_1+b_i{}_1{P}_{G_i}+c_i{}_1{P}_{G_i}^2,fuel1,P_{G_i}^{min}\le P_{G_i}\le P_i{}_1\\ a_i{}_2+b_i{}_2{P}_{G_i}+c_i{}_2{P}_{G_i}^2,fuel2,P_{i1}\le P_{G_i}\le P_i{}_2\\ ,\\ ,\\ ,\\ ,\\ ,\\ a_i{}_k+b_i{}_k{P}_{G_i}+c_i{}_k{P}_{G_i}^2,fuelk,P_{ik-1}\le P_{G_i}\le P_{G_i}^{max}\end{array}$$

(6)

where, $P_{ik}^{min}$ and $P_{ik}^{max}$ are the minimum and maximum power generations from ith unit consuming kth fuel respectively. $a_{ik}$, $b_{ik}\mathrm{and}{c}_{ik}$ are the cost coefficients of the ith generating unit consuming kth fuel. Figure 3 represents the fuel cost characteristics of a PED problem that considers only MFOs for generating units.

2.3.3. Power Economic Dispatch Considering Multiple Fuel Options and Valve Point Loading Effects Together

The fuel cost equation for a PED problem modeling both MFOs and VPLEs, is as under in Equation (7).

$$F_i(P_{G_i})=\{\begin{array}{c}{a}_i{}_1+b_i{}_1{P}_{G_i}+c_i{}_1{P}_{G_i}^2+|e_i{}_{1}sin(f_i{}_1(P_{G_i}^{min}-P_{G_i}))|\\ fuel 1,P_{G_i}^{min}\le P_{G_i}\le P_i{}_1\\ a_i{}_2+b_i{}_2{P}_{G_i}+c_i{}_2{P}_{G_i}^2+|e_i{}_{2}sin(f_i{}_2(P_{G_i}^{min}-P_{G_i}))|,\\ fuel 2,P_{i1}\le P_{G_i}\le P_i{}_2\\ ,\\ ,\\ ,\\ ,\\ ,\\ a_i{}_k+b_i{}_k{P}_{G_i}+c_i{}_k{P}_{G_i}^2+|e_i{}_{k}sin(f_i{}_k(P_{G_i}^{min}-P_{G_i}))|,\\ fuel k,P_{ik-1}\le P_{G_i}\le P_{G_i}^{max}\end{array}$$

(7)

3. Differential Evolution (DE)

DE is a population-based algorithm in which mutation, crossover, and selection are its essential components. It uses mutation as a main search strategy and employs the selection operator to direct the search towards the potential solution region. It builds two arrays: a primary array and a secondary array. Both arrays hold $NP$ number of potential solutions and each solution contains $\mathrm{D}$ number of parameters. These solutions are real valued vectors. In short, there is $NP$ number of $\mathrm{D}$-dimensional vectors. All vectors collectively are called a population. The first array comprises of the current vector population and the second array collects vectors that are selected for next generation.

Following is the stepwise description of DE.

Step 1: Randomly initialize the initial population $P_i^G$ (target vectors) of $NP$ size and of $D$ dimensions, in a feasible range.

$$P{S}^G=\left[P_1^G,P_2^G,\dots \dots \dots ..P_{Np}^G\right]$$

(8)

$$P_i^G=\left[P_{1,i}^G,P_{2,i}^G,\dots \dots \dots ..P_{D,i}^G\right] i=1,2,\dots \dots \dots ..,N_p$$

(9)

where, $P_i^G$ is the ith potential solution and $D$ is the Dth generating unit.

As the population is defined within permissible range,

$$P_{j,i}^0=P_{j,i}^{min}+{\delta }_j\ast (P_{j,i}^{max}-P_{j,i}^{min})$$

(10)

where, $i=1,2,\dots \dots \dots ..,N_{p}j=1,2,\dots \dots \dots ..,D$

In Equation (10), $D$ is the total number of decision parameters, $P_{j,i}^{min}$ and $P_{j,i}^{max}$ are the lower and upper limits of the jth parameter respectively and ${\delta }_j$ is a random number generated in a range 0–1 which is new for every new value of $j$.

Step 2: Calculate the fitness value for all generated target vectors.

Step 3: Generate the mutant vector $V_i^G$ by perturbing a randomly selected vector $P_k^G$ with the difference of two other randomly selected vectors $P_l^G$ and $P_m^G$ according to Rand/1/bin mutation strategy.

Step 4: Generate the trial vectors $(U_i^G)$ through crossover by randomly recombining the parameters of target vectors ($P_i^G$) and mutant vectors ($V_i^G$).

$$U_{j,i}^G=\{\begin{array}{c}{V}_{j,i}^G if ({\rho }_j<CR) or j=D \\ \\ P_{j,i}^G Otherwise \end{array}$$

(11)

Step 5: Calculate the fitness value for each trial vector generated in step 4.

Step 6: Perform 1-1 comparison between target vectors and trial vectors and select the vectors with improved fitness value for new offspring.

$$P_i^{G+1}=\{\begin{array}{c}{U}_i^G if f(U_i^G)>f(P_i^G)\\ \\ P_i^G Otherwise \end{array}$$

(12)

Step 7: Check whether desired fitness value is attained or maximum number of generations is achieved, if yes then stop this optimization process, otherwise go back to step 3.

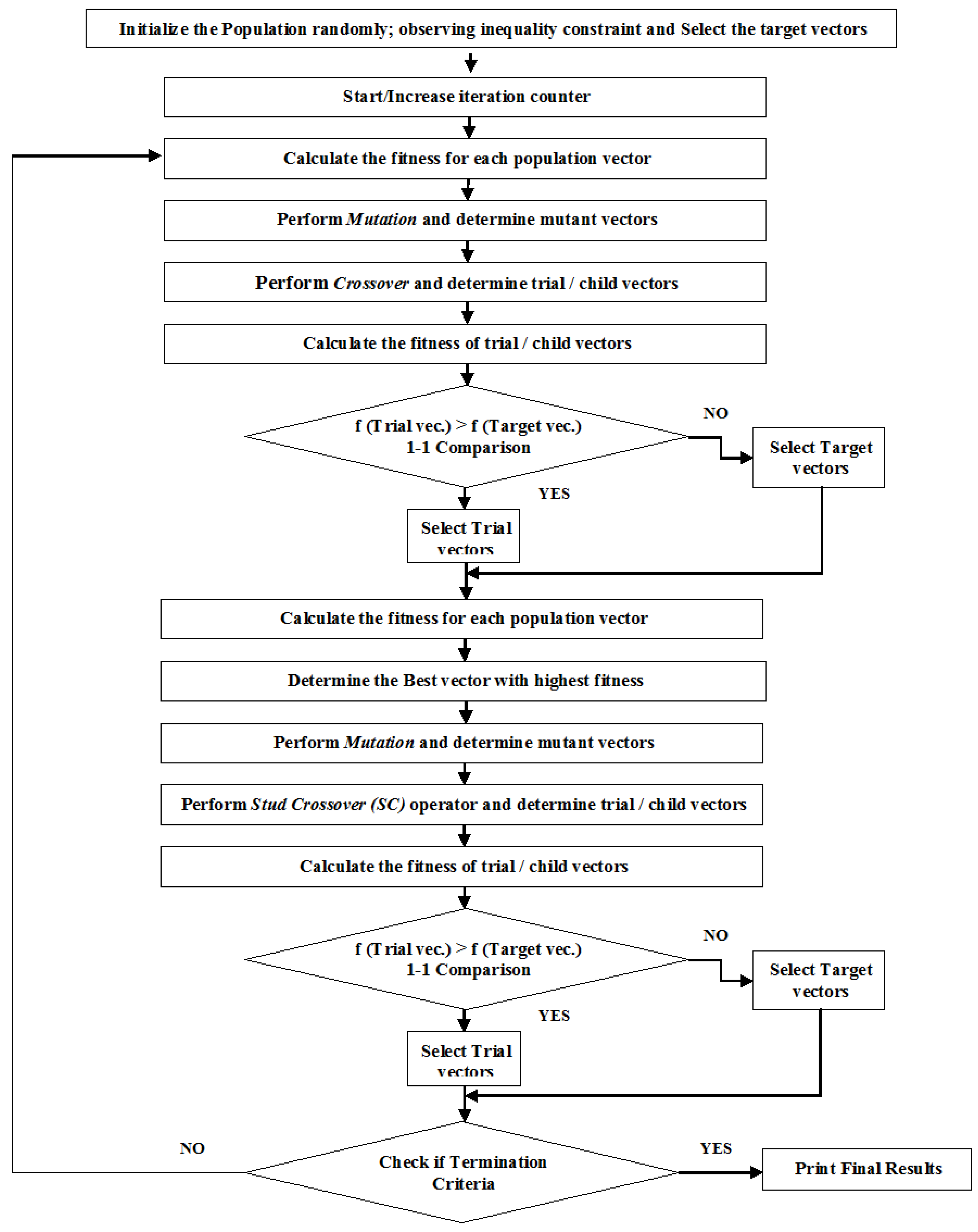
4. Stud Differential Evolution (SDE)

Because the conventional DE method suffers from premature convergence, it cannot always find the optimal solution, especially for the systems with turbulent search space. Therefore, in this research work, an improved strategy of crossover known as SC operator has been introduced in conventional DE in order to improve its performance in solving the PED problem of thermal units with MFOs and VPLEs. This improved version of DE called SDE is inspired by Stud GA. In SDE, to begin with, the conventional DE is implemented to reduce the research space to the strategic area and afterwards the SC operator is applied. SC operator is the heart of SDE and is utilized to mate all population vectors with only the best vector or the most optimal vector called stud. It results in the generation of better quality solutions instead of not so good solutions for upcoming offspring.

In SDE, the trial vectors $(U_i^G)$ are generated for all potential solutions (vectors) of population by recombining the parameters of best vector $P_{best}^G$ (instead of target vectors as in conventional DE) from the current generation $\mathrm{G}$ and mutant vectors ($V_i^G$). The SC operator is represented by the following mathematical expression.

$$U_{j,i}^G=\{\begin{array}{c}{V}_{j,i}^G if ({\rho }_j<CR) or j=D \\ \\ P_{best}^G Otherwise \end{array}$$

(13)

The mainframe of SDE operator and SC has been given in Algorithms 1 and 2 respectively. Figure 4 depicts the flowchart of the proposed optimization method.

As we can see in Algorithm 1, to begin with, the optimal vector (stud) is selected as first parent to mate with another parent vector to create a novel child/trial vector through crossover operator. It must be ensured that stud should not be selected as second parent. Then the quality of a generated child vector is determined by fitness function.

Algorithm 1: Stud Differential Evolution (SDE)

Begin   Randomly initialize the population P (target vectors) of NP size and of D dimensions, in a feasible range     Set the generation counter G = 1   Allot suitable values to all other control parameters i.e., crossover rate CR, mutation probability F etc.   Calculate the fitness for all generated population vectors.   While G < Maximum Generation do   Implement regular DE from conventional mutational and crossover all the way to selection.   for I = 1: NP do     Perform Mutation and generate mutant vector $V_i^G$     Perform the SC operator in Algorithm 2   end for i   Sort all the vectors and find the current best vector   G = G + 1;   end while   Display the best solution. End.

Algorithm 2: Stud Crossover (SC) Operator

Begin   Perform the Selection    Select the Stud/Best vector $P_{best}^G$ for mating   Perform the Crossover    Generate trial vector $U_i^G$, taking stud $P_{best}^G$ as first parent and mutant vector $V_i^G$as a second parent   Calculate fitness of trial vector ($f(U_i^G)$)    If ($f(U_i^G)>f(P_i^G)$) do       Accept the generated trial vector $U_i^G$ for next generationelse   else       Accept the generated target vector $P_i^G$ for next generation   end if End.

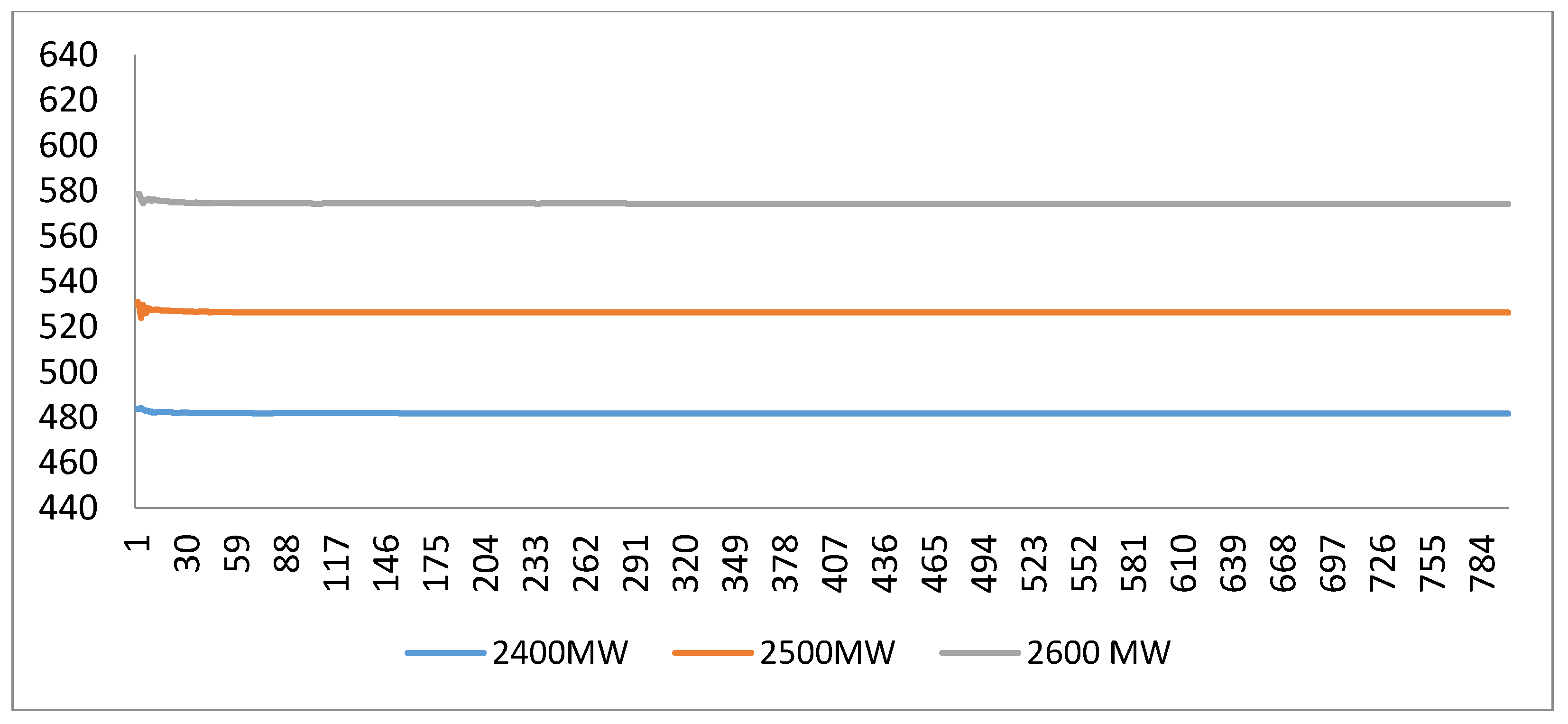
5. Simulation Results

The proposed SDE is implemented in a Visual C++ environment on various IEEE standard test systems. For computer implementation of SDE, a Pentium IV computer with 1 GB of RAM and 2.0 GHz processor speed is used. Software used is Microsoft Visual C++ version 8.0. In order to validate the effectiveness of the proposed SDE, it has been tested on two 10-machine multiple fuel test systems. In one system, VPLEs has been considered (a 10-machine system with non-convex cost function) while it has been neglected in the other one (a system with convex cost function). Further, four case studies for various load demands of 2400 MW, 2500 MW, 2600 MW, and 2700 MW have been conducted for each above mentioned system. The inputs to the proposed SDE are cost coefficients, power generation limits of each unit and demand power while the outputs of the proposed algorithm are power generation values from each unit, computation time, and type of fuel of each generating unit.

Parameter Selection: There are three main parameters in SDE that need to be predetermined; the population size (NP), mutation factor (F) and crossover rate (CR).

5.1. System 1: 10 Machine Multiple Fuel Convex PED (without Valve Point Loading Effects)

This system consists of 10 generating units, considering only MFOs while ignoring the VPLEs. The simulations for this system have been conducted for four different power demands of 2700 MW, 2600 MW, 2500 MW, and 2400 MW. The input data for the system has been taken from [39]. The selected parameters for this system are: Population size = 100, No. of iterations = 200, Crossover rate (CR) = 0.6, Mutation factor (MF) = 0.5 and the results are presented after 30 repeated trials.

Table 1. Cost comparison among various methodologies for System 1, P_d = 2700 MW.

Unit No.	Fuel Types	Methods
		MSFLA	MHNN	SaDE	IEP	SDE
P1	2	226.57	224.50	218.94	219.54	218.249988
P2	1	215.35	215.00	212.72	211.44	211.662614
P3	1	291.35	291.80	282.63	279.68	280.722785
P4	3	242.24	242.20	239.77	240.32	239.631553
P5	1	293.02	293.30	277.46	276.53	278.497228
P6	3	242.24	242.20	240.18	239.87	239.631562
P7	1	302.57	303.10	287.29	289.00	288.584580
P8	3	242.24	242.20	239.91	241.31	239.631491
P9	3	355.50	355.70	426.09	425.14	428.521600
P10	1	288.91	289.50	275.01	277.17	274.866600
Power Generated		2700.00	2699.70	2700.00	2700.00	2700.00
Total Cost		626.25	626.12	623.92	623.85	623.809154

,

Table 2. Cost comparison among various methodologies for System 1, P_d = 2600 MW.

Unit No.	Fuel Used	Methods
		HLN	LI	SaDE	SDE
P1	2	209.7882	209.788	218.23	216.544182
P2	1	207.9078	207.9078	211.71	210.905752
P3	1	269.9145	269.9146	276.77	278.544078
P4	3	236.9782	236.9782	239.37	239.096668
P5	1	263.7247	263.7247	275.65	275.519445
P6	3	236.9782	236.9782	240.18	239.096668
P7	1	274.359	274.3591	285.99	285.717009
P8	3	236.9782	236.9782	238.16	239.096669
P9	1	402.7945	402.7945	341.90	343.493387
P10	1	260.5768	260.5767	272.04	271.986142
Power Generated		2600.00	2600.00	2600.00	2600.00
Total Cost		574.74	574.74	574.54	574.380823

,

Table 3. Cost comparison among various methodologies for System 1, P_d = 2500 MW.

Unit No.	Fuel Used	Methods
		MPSO	EALHN	AIS	SDE
P1	2	206.5	206.5188	205.88	206.519016
P2	1	206.5	206.4573	206.33	206.457317
P3	1	265.7	265.7392	266.48	265.739085
P4	3	236.0	235.9531	235.79	235.953146
P5	1	258.0	258.0178	256.87	258.017644
P6	3	236.0	235.9531	236.65	235.953163
P7	1	268.9	268.8636	269.2	268.863542
P8	3	235.9	235.9531	235.51	235.953149
P9	1	331.5	331.4876	332.23	331.487723
P10	1	255.1	255.0564	255.02	255.056214
Power Generated		2500.00	2500.00	2500.00	2500.00
Total Cost		526.239	526.239	526.240	526.238760

and

Table 4. Cost comparison among various methodologies for System 1, P_d = 2400 MW.

Unit No.	Fuel Used	Methods
		MHNN	AIS	EALHN	MPSO	SDE
P1	1	192.7	189.683	189.7397	189.7	189.740527
P2	1	203.8	202.40	202.3427	202.3	202.342694
P3	1	259.1	253.814	253.8954	253.9	253.895318
P4	3	195.1	233.019	233.0456	233.0	233.045560
P5	1	248.7	241.94	241.8299	241.8	241.829619
P6	3	234.2	233.063	233.0456	233.0	233.045548
P7	1	260.3	253.374	253.2752	253.3	253.275055
P8	3	234.5	232.851	233.0456	233.0	233.045563
P9	1	324.7	320.452	320.3831	320.4	320.383139
P10	1	246.8	239.404	239.3973	339.4	239.396978
Power Generated		2399.8	2400.00	2399.80	2400	2400
Total Cost		487.87	481.723	481.72300	481.723	481.722624

indicate the power generation schedule and generation cost obtained by the proposed SDE for the load demands of 2700 MW, 2600 MW, 2500 MW, and 2400 MW respectively. In Table 1, the effectiveness of SDE in solving convex PED problem, for the power demand of 2700 MW, has been validated by comparing its results with other optimizers in the literature such as Modified Shuffled Frog Leaping Algorithm (MSFLA) [40], Modified Hopfield Neural Network (MHNN) [41], Self-adaptive Differential Evolution (SaDE) [32], and Improved Evolutionary Programming (IEP) [42]. Similarly, Table 2 shows the simulation result of SDE for the power demand of 2600 MW, compared with Hopfield Lagrange Network (HLN) [43], Lamda-Iteration (LI) [43], and SaDE [32]. Table 3 depicts the cost comparison of the proposed method to Modified Particle Swarm Optimization (MPSO) [44], Enhanced Augmented Lagrange Hopfield Network (EALHN) [45], and Artificial Immune System (AIS) [46] against the power demand of 2500 MW. Table 4 indicates the comparison of SDE simulation results among MHNN [41], AIS [46], EALHN [45], and MPSO [44] for the power demand of 2400 MW.

The best generation costs and computational times of the proposed method is compared to those from HNN [41], SaDE [32], IEP [42], ELANN [24], EALHN [45], MPSO [44], RCGA [47], DE [48], and LI [43] for all power demands of 2400 MW, 2500 MW, 2600 MW, and 2700 MW, as shown in

Table 5. Comprehensive comparison of total fuel cost and computation time for system 1 (without valve point loading effects), P_d = 2400 MW, 2500 MW, 2600 MW and 2700 MW.

(i)				(ii)
2400 MW				2500 MW
Methods	Total Power	Min. Cost	CT	Methods	Total Power	Min. Cost	CT
HNN [41]	2399.80	481.8700	~60	IEP [42]	2500.00	526.4000	NR
SaDE [32]	2400.00	481.8628	NR	SaDE [32]	2500.00	526.3232	NR
IEP [42]	2400.00	481.7790	NR	ELANN [24]	2500.00	526.2700	12.25
ELANN [24]	2400.00	481.7400	11.53	DE [48]	2500.00	526.2390	NR
EALHN [45]	2400.00	481.7230	0.008	EALHN [45]	2500.00	526.2390	0.006
MPSO [44]	2400.00	481.7230	NR	LI [43]	2500.00	526.2390	2.508
RCGA [47]	2400.00	481.7230	49.92	RCGA [47]	2500.00	526.2390	49.92
DE [48]	2400.00	481.7230	NR	MPSO [44]	2500.00	526.2390	NR
LI [43]	2399.99	481.7217	7.84	HNN [41]	2499.80	526.1300	~60
SDE	2400.00	481.7226	2.50	SDE	2500.00	526.2387	2.43
(iii)				(iv)
2600 MW				2700 MW
Methods	Total Power	Min. Cost	CT	Methods	Total Power	Min. Cost	CT
LI [43]	2600.00	574.7412	6.871	HNN [41]	2599.80	626.1200	~60
HLN [43]	2600.00	574.7413	0.152	SaDE [32]	2700.00	623.9225	NR
SaDE [32]	2600.00	574.5380	NR	ELANN [24]	2700.00	623.8800	21.36
IEP [42]	2600.00	574.4730	NR	IEP[42]	2700.00	623.8510	NR
ELANN [24]	2600.00	574.4100	~9.99	RCGA [47]	2700.00	623.8092	44.56
RCGA [47]	2600.00	574.3960	33.57	DE [48]	2700.00	623.8090	NR
DE [48]	2600.00	574.3810	NR	LI [43]	2699.99	623.8089	6.221
EALHN [45]	2600.00	574.3810	0.005	MPSO [44]	2700.00	623.8090	NR
MPSO [44]	2600.00	574.3810	NR	CGA-MU [28]	2700.00	623.8095	19.42
HNN [41]	2599.80	574.2600	~60	IGA-MU [28]	2700.00	623.8093	5.27
SDE	2600.00	574.3808	2.04	SDE	2700.00	623.8092	2.2

(i, ii, iii, iv) respectively. It is evident from the table that the total fuel cost obtained by the proposed SDE is less than all other algorithms except the LI for 2400 MW, HNN for 2500 MW and 2600 MW cases. However, computational time of the proposed SDE is shorter than LI and HNN for all cases. Additionally, HNN fails to meet the power balance constraint in all cases. As for the 2700 MW case, the simulation results of SDE are better than all mentioned algorithms. The convergence characteristics of the proposed method in solving the convex PED problem (with MFOs and without VPLEs), for 2600 MW, 2500 MW, and 2400 MW load demands, are shown in Figure 4 while those for 2700 MW load demand are presented in Figure 5.

5.2. System 2: 10 Machine Multiple Fuel Non-Convex PED (with Valve Point Loading Effects)

This system considers both MFOs and the VPLEs. The simulations for this system have also been conducted for 2700 MW, 2600 MW, 2500 MW and 2400 MW power demands. The selected parameters for this system are: Population size = 200, No. of iterations = 800, Crossover rate (CR) = 0.6, Mutation factor (MF) = 0.5 and the results are presented after 30 trials.

Table 6. Cost comparison among various methodologies for System 2, P_d = 2700 MW.

Unit No.	Fuel Used	Methods
		IGA_MU	MSFLA	PSO	DE	RGA	NPSO-LRS	BSA	CSA-Cauchy	BAT	SDE
P1	2	219.13	215.50	219.9962	218.2499	220.9376	223.33	218.58	218.1322	217.3232	218.593998
P2	1	211.16	210.72	212.7648	211.6626	212.6096	212.19	211.22	211.4116	209.9266	211.464175
P3	1	280.66	284.71	283.7391	280.7228	283.5811	276.21	279.56	281.6867	284.5552	280.657064
P4	3	238.48	239.77	240.5205	239.6315	240.0089	239.41	239.50	238.7456	237.2677	239.639428
P5	1	276.42	286.45	282.3127	278.4972	282.8920	274.64	279.97	279.8622	279.9804	279.934520
P6	3	240.47	240.18	240.5387	239.6315	240.4739	239.79	241.12	240.3328	240.1984	239.639428
P7	1	287.74	278.87	293.0846	288.5845	292.9792	285.53	289.80	287.7978	290.0943	287.727493
P8	3	240.76	242.06	240.2886	239.6315	240.1989	240.63	240.58	238.3435	238.3427	239.639428
P9	3	429.34	425.32	406.9797	428.5216	406.9988	429.26	426.89	427.8687	425.717	426.835856
P10	1	275.85	276.43	279.7752	274.8667	279.3199	278.65	272.80	275.8188	276.5845	275.868609
Power Generated		2700.00	2700.00	2700.00	2700.00	2700.00	2700.00	2700.00	2700.0	2700.00	2700.00
Total Cost		624.52	624.12	624.5074	624.5146	624.5081	624.13	623.90	623.8566	623.8425	623.826575

shows the results obtained from the proposed SDE in solving non-convex PED problem for the 2700 MW power demand and are compared to other optimizers in literature such as Improved Genetic Algorithm with Multiplier Updating (IGA_MU) [28], Modified Shuffled Frog Leaping Algorithm (MSFLA) [40], Particle Swarm Optimization (PSO) [49], conventional DE [49], Real-coded Genetic Algorithm (RGA) [49], New Particle Swarm Optimization with Local Random Search (NPSO-LRS) [50], Back-tracking Search Algorithm (BSA) [51], Cuckoo Search Algorithm with Cauchy distribution (CSA-Cauchy) [52] and BAT [16].

Table 7. Cost comparison among various methodologies for System 2, P_d = 2600 MW.

Unit No.	Fuel Used	Methods
		PSO	RGA	DE	MSFLA	GHS	BAT	SaDE	SDE
P1	2	-	-	-	218.59	209.35	218.1376	219.99	216.539998
P2	1	-	-	-	203.05	207.99	212.1547	212.76	210.721482
P3	1	-	-	-	271.58	269.63	279.6484	283.74	278.640638
P4	3	-	-	-	236.41	236.95	239.552	240.52	238.698832
P5	1	-	-	-	276.43	265.48	271.4263	282.31	276.157152
P6	3	-	-	-	241.92	235.88	237.2423	240.53	238.967574
P7	1	-	-	-	287.73	273.51	287.7358	293.08	285.356480
P8	3	-	-	-	240.85	237.76	236.4615	240.29	238.564461
P9	1	-	-	-	344.20	403.33	339.8086	406.98	343.645968
P10	1	-	-	-	279.23	260.11	277.8228	279.78	272.707417
Power Generated		2600.00	2600.00	2600.00	2600.00	2700.00	2600.00	2600.00	2600.00
Total Cost		575.161	575.161	575.175	574.89	574.79	574.5609	574.54	574.387064

shows the simulation results of SDE for the power demand of 2600 MW and are compared with conventional PSO [49], RGA [49], DE [49], MSFLA [40], Global-best Harmony Search (GHS) [40], BAT [16], SaDE [32]. In

Table 8. Cost comparison among various methodologies for System 2, P_d = 2500 MW.

Generation Schedule for Pd = 2500 MW and Non-Convex Cost
Unit No.				SDE
P1				206.269999
P2				206.512887
P3				266.542078
P4				236.414526
P5				258.350235
P6				236.280155
P7				268.759386
P8				235.608300
P9				331.467106
P10				253.795328
Power Generated				2500.00
Total Cost				526.245078
Comparison of Results for Pd = 2500 MW and Non-Convex Cost
Method Used	DE	RGA	PSO		ASA	SDE
Total Cost	527.03600	527.0189	527.01850		526.32310	526.245533

, SDE simulation results have been compared with DE [49], RGA [49], PSO [49] and Adaptive Simulated Annealing (ASA) [53] for 2500 MW load demand. For 2400 MW load demand, SDE outperforms all mentioned algorithms same as all other power demands (2700 MW, 2600 MW and 2500 MW), as illustrated by

Table 9. Cost comparison among various methodologies for System 2, P_d = 2400 MW.

Generation Schedule for Pd = 2400 MW and Non-Convex Cost
Unit No.			SDE
P1			188.517831
P2			202.551856
P3			253.435305
P4			232.786510
P5			240.439406
P6			233.189623
P7			254.533306
P8			233.055252
P9			320.395414
P10			241.095497
Power Generated			2400.00
Total Cost			481.734808
Comparison of Results for Pd = 2400 MW and Non-Convex Cost
Methods Used	ACO	DE	PSO	RGA	ASA	SDE
Total Cost	482.5267	482.5275	482.5088	482.5114	481.86290	481.734808

.

Table 10. Simulation results for various values of Crossover ratio.

Power Demand (MW)	Crossover Rate (CR)
	0.5	0.6	0.7
2400	481.747921	481.734808	481.764849
2500	526.253282	526.245533	526.277145
2600	574.402910	574.387064	574.464175
2700	623.832350	623.826575	623.843516

shows optimal solutions for different values of Crossover ratio (CR).

For the power demand of 2700 MW, the comparison of the proposed SDE with various optimization techniques in literature been performed in Table 10 comprising maximum, average and minimum generation costs, standard deviation and computational time of the reported algorithms. From all above result comparisons, it is clearly found that the proposed SDE provides high quality results compared to all other methodologies. The convergence characteristics of the proposed optimizer while solving the non-convex PED problem (with both MFOs and VPLEs) for 2600 MW, 2500 MW and 2400 MW load demands, are shown in Figure 6 while those for 2700 MW load demand are presented in Figure 7. It is also clear from the figures that SDE can converge to high quality solutions within reasonable time. It is robust and can converge to optimal solution at early iterations. The distribution of power-generation costs of the proposed SDE, for 2700 MW power demand during 30 repeated runs, has been illustrated in Figure 8. It is evident from the figure that the optimal generation cost has been achieved at 19th run by SDE. Figure 9 shows the cost distribution around 30 runs for system 2.

Table 11. Comprehensive comparison of simulation results, standard deviation and computation time for system 2 (with valve point loading effects), P_d = 2700 MW.

Methods	Min. Cost	Ave. Cost	Max. Cost	St. Deviation	CT (s)
CGA-MU [28]	624.7193	627.6087	633.8652	NR	25.65
IGA-MU [28]	624.5178	625.8692	630.8705	NR	7.14
DE (a) [49]	624.5146	624.5246	624.5458	0.0077	2.8236
RGA (a) [49]	624.5081	624.5079	624.5088	2.9476 × 10−5	4.1340
PSO (a) [49]	624.5074	624.5074	624.5074	1.9691 × 10−13	3.3852
GA [7]	624.5050	624.7419	624.8169	0.1005	18.3
PSO_GM [29]	624.3100	625.09	624.67	0.16	NR
TSA [7]	624.3078	635.0623	624.8285	1.1593	9.71
PSO_LRS [27]	624.2297	625.7887	628.3214	NR	0.93
CPSO [29]	624.1700	624.78	624.55	0.13	NR
NPSO [27]	624.1624	625.218	627.4237	NR	0.41
NPSO_LRS [27]	624.1273	624.9985	626.9981	NR	1.08
MSFLA [40]	624.11569	624.8958	628.3428	NR	NR
APSO [54]	624.0145	624.8185	624.8185	NR	0.52
PSO (b) [30]	624.0120	624.2055	624.4376	0.0889	0.308
CBPSO_RVM [29]	623.9600	624.29	624.08	0.06	NR
DE (b) [30]	623.9280	624.0068	624.0653	0.0271	0.625
BSA [51]	623.9016	623.9757	624.0838	NR	NR
ACO [55]	623.9000	624.3500	624.7800	NR	8.35
GA_G [56]	623.8900	625.21	635.30	NR	NR
GA_MGC [56]	623.8900	624.72	626.94	NR	NR
GA_C [56]	623.8800	624.53	626.95	NR	NR
GA_BGC [56]	623.8800	624.14	626.51	NR	NR
QPSO [30]	623.8766	623.9639	624.4163	0.0688	0.315
DE_ALM [57]	623.8716	626.1298	642.7812	NR	12.375
CSA [58]	623.8684	623.9495	626.3666	0.2438	1.587
CSA_Cauchy [52]	623.8566	624.1160	626.3440	0.7395	2.1
CSA_Gauss [52]	623.8564	624.3618	626.3474	0.9826	2.2
GHS [40]	623.84914	624.1341	625.3157	NR	NR
CQPSO [30]	623.8476	623.8652	623.8885	0.0151	0.318
SFLA-GHS [40]	623.84065	623.9521	624.7804	NR	NR
DSPSO_TSA [7]	623.8375	623.8625	623.9001	0.0106	3.44
SQPSO [30]	623.8319	623.8440	623.8605	0.0107	0.324
IODPSO_G [59]	623.83	623.84	623.83	0.01	NR
IODPSO_L [59]	623.83	623.83	623.83	0.00	NR
SADE_ALM [57]	623.8278	624.7864	634.8313	NR	17.032
SDE	623.826575	623.833894	623.8412	3.62 × 10−3	~10

shows the comparison of the results obtained by SDE with other approaches of literature for all the power demands and

Table 12. Summary of simulation results achieved by SDE for both convex and non-convex PED.

Units	Pd = 2700 MW		Pd = 2600 MW		Pd = 2500 MW		Pd = 2400 MW
	Convex	Nonconvex	Convex	Nonconvex	Convex	Nonconvex	Convex	Nonconvex
1	218.249988	218.593998	216.544182	216.539998	206.519016	206.269999	189.740527	188.517831
2	211.662614	211.464175	210.905752	210.721482	206.457317	206.512887	202.342694	202.551856
3	280.722785	280.657064	278.544078	278.640638	265.739085	266.542078	253.895318	253.435305
4	239.631553	239.639428	239.096668	238.698832	235.953146	236.414526	233.045560	232.786510
5	278.497228	279.934520	275.519445	276.157152	258.017644	258.350235	241.829619	240.439406
6	239.631562	239.639428	239.096668	238.967574	235.953163	236.280155	233.045548	233.189623
7	288.584580	287.727493	285.717009	285.356480	268.863542	268.759386	253.275055	254.533306
8	239.631491	239.639428	239.096669	238.564461	235.953149	235.608300	233.045563	233.055252
9	428.521600	426.835856	343.493387	343.645968	331.487723	331.467106	320.383139	320.395414
10	274.866600	275.868609	271.986142	272.707417	255.056214	253.795328	239.396978	241.095497
TP (MW)	2700.00	2700.00	2600.00	2600.00	2500.00	2500.00	2400.00	2400.00
TC ($/h)	623.809154	623.826575	574.380823	574.387064	526.238760	526.245533	481.722624	481.734808

presents the summary of simulation results achieved by the proposed SDE while solving both convex and non-convex PED problems with four power demands of 2700 MW, 2600 MW, 2500 MW and 2700 MW separately.

6. Conclusions

In this research, SDE was mapped in a C++ programming environment and tested on standard test systems available in the literature. On the basis of the results achieved by computer implementation of the C++ SDE application, it can be seen that SDE has a reduced generation cost and it can be concluded that the proposed algorithm can effectively and efficiently explore the solution space and that SDE is one of the promising optimization techniques.

Thus, the following conclusions can be made:

• SDE is a potential solution methodology for the PED problem, as it addresses the convex and non-convex PED equally.
• Results obtained from SDE are better in comparison with the current research available, which indicates the promise of the approach.
• SDE can easily be further modified and hybridized with other optimization techniques because it has fewer control parameters.

The presented research work has been entirely computer oriented and the main motivation was to develop a software application using C++ based on SDE.