Risk Constrained Trading Strategies for Stochastic Generation with a Single-Price Balancing Market
Abstract
1. Introduction
2. Day-Ahead and Balancing Markets
3. Problem Formulation
3.1. Imbalance Minimisation
3.2. Categorical Assessment of System Length
3.3. Probabilistic Assessment of System Length
3.4. Risk Constrained Contracted Volume
3.4.1. Additive Adjustment
3.4.2. Multiplicative Adjustment
3.5. Quantile Offer
4. Forecasting
4.1. Probabilistic System Length Forecast
4.2. Price Forecasts
4.3. Wind Power Quantile Forecasts
5. Case Study and Results
5.1. System Length Forecast and Evaluation
5.2. Price Forecast Evaluation
5.3. Offer Strategy Results
6. Conclusions
Acknowledgments
Data Statement
Conflicts of Interest
Nomenclature
| Revenue from settlement period | |
| Imbalance cost in settlement period | |
| Forecast of made at time t | |
| Expectation operator | |
| Contracted volume for settlement period | |
| Actual energy delivered in settlement period | |
| Market participant’s imbalance | |
| Mean absolute imbalance volume | |
| Maximum deliverable volume in any single settlement period | |
| Price at which is contracted | |
| Imbalance price | |
| Imbalance price during periods of net up-regulation | |
| Imbalance price during periods of net down-regulation | |
| NIV | Net Imbalance Volume for settlement period ; a positive NIV is associated with up-regulation (‘the system is short’), negative NIV is associated with down-regulation (‘the system is long’) |
| Probability that the system will be short, | |
| The ratio | |
| The -quantile forecast of energy production | |
| Parameters of the additive, multiplicative and quantile trading strategies, respectively |
References
- Edwards, D.W. Energy Trading and Investing: Trading, Risk Management and Structuring Deals in the Energy Market; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Bessa, R.; Möhrlen, C.; Fundel, V.; Siefert, M.; Browell, J.; Haglund El Gaidi, S.; Hodge, B.M.; Cali, U.; Kariniotakis, G. Towards Improved Understanding of the Applicability of Uncertainty Forecasts in the Electric Power Industry. Energies 2017, 10, 1402. [Google Scholar] [CrossRef]
- Morales, J.; Conejo, A.; Madsen, H.; Pinson, P.; Zugno, M. Integrating Renewable in Electricity Markets; Springer: Heidelberg/Berlin, Germany, 2014. [Google Scholar]
- Pei, W.; Du, Y.; Deng, W.; Sheng, K.; Xiao, H.; Qu, H. Optimal Bidding Strategy and Intramarket Mechanism of Microgrid Aggregator in Real-Time Balancing Market. IEEE Trans. Ind. Inf. 2016, 12, 587–596. [Google Scholar] [CrossRef]
- Heydarian-Forushani, E.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K.; Shafie-khah, M.; Catalão, J.P.S. Risk-Constrained Offering Strategy of Wind Power Producers Considering Intraday Demand Response Exchange. IEEE Trans. Sustain. Energy 2014, 5, 1036–1047. [Google Scholar] [CrossRef]
- Fernandes, C.; Frías, P.; Reneses, J. Participation of intermittent renewable generators in balancing mechanisms: A closer look into the Spanish market design. Renew. Energy 2016, 89, 305–316. [Google Scholar] [CrossRef]
- Papakonstantinou, A.; Pinson, P. Information Uncertainty in Electricity Markets: Introducing Probabilistic Offers. IEEE Power Engi. Lett. 2016, 31, 5202–5203. [Google Scholar] [CrossRef]
- Bahrami, S.; Amini, M.H. A decentralized trading algorithm for an electricity market with generation uncertainty. Appl. Energy 2018, 218, 520–532. [Google Scholar] [CrossRef]
- Bathurst, G.; Weatherill, J.; Strbac, G. Trading wind generation in short term energy markets. IEEE Trans. Power Syst. 2002, 17, 782–789. [Google Scholar] [CrossRef]
- Bremnes, J.B. Probabilistic Wind Power Forecasts Using Local Quantile Regression. Wind Energy 2004, 7, 47–54. [Google Scholar] [CrossRef]
- Pinson, P.; Chevallier, C.; Kariniotakis, G. Trading wind generation from short-term probabilistic forecasts of wind power. IEEE Trans. Power Syst. 2007, 22, 1148–1156. [Google Scholar] [CrossRef]
- Bitar, E.; Rajagopal, R.; Khargonekar, P.; Poolla, K.; Varaiya, P. Bringing Wind Energy to Market. IEEE Trans. Power Syst. 2012, 27, 1225–1235. [Google Scholar] [CrossRef]
- Morales, J.M.; Conejo, A.J.; Pérez-Ruiz, J. Short-term trading for a wind power producer. IEEE Trans. Power Syst. 2010, 25, 554–564. [Google Scholar] [CrossRef]
- Skajaa, A.; Edlund, K.; Morales, J.M. Intraday Trading of Wind Energy. IEEE Trans. Power Syst. 2015, 30, 3181–3189. [Google Scholar] [CrossRef]
- Botterud, A.; Zhou, Z.; Wang, J.; Bessa, R.J.; Keko, H.; Sumaili, J.; Miranda, V. Wind Power Trading Under Uncertainty in LMP Markets. IEEE Trans. Power Syst. 2012, 27, 894–903. [Google Scholar] [CrossRef]
- Zugno, M.; Morales, J.M.; Pinson, P.; Madsen, H. Pool Strategy of a Price-Maker Wind Power Producer. IEEE Trans. Power Syst. 2013, 28, 3440–3450. [Google Scholar] [CrossRef]
- Delikaraoglou, S.; Papakonstantinou, A.; Ordoudis, C.; Pinson, P. Price-maker wind power producer participating in a joint day-ahead and real-time market. In Proceedings of the 12th International Conference on the European Energy Market, Lisbon, Portugal, 19–22 May 2015; pp. 1–5. [Google Scholar]
- Mazzi, N.; Pinson, P. 10—Wind power in electricity markets and the value of forecasting. In Renewable Energy Forecasting; Kariniotakis, G., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Sawston, UK, 2017; pp. 259–278. [Google Scholar]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Giebel, G.; Brownsword, R.; Kariniotakis, G.; Denhard, M.; Draxl, C. The State-Of-The-Art in Short-Term Prediction of Wind Power: A Literature Overview, 2nd ed.; ANEMOS.plus; European Commission: Brussels, Belgium, 2011. [Google Scholar]
- Foley, A.M.; Leahy, P.G.; Marvuglia, A.; McKeogh, E.J. Current methods and advances in forecasting of wind power generation. Renew. Energy 2012, 37, 1–8. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S.; Zareipour, H.; Troccoli, A.; Hyndman, R.J. Probabilistic energy forecasting: Global Energy Forecasting Competition 2014 and beyond. Int. J. Forecast. 2016, 32, 896–913. [Google Scholar] [CrossRef]
- Karakatsani, N.V.; Bunn, D.W. Forecasting electricity prices: The impact of fundamentals and time-varying coefficients. Int. J. Forecast. 2008, 24, 764–785. [Google Scholar] [CrossRef]
- Brijs, T.; Vos, K.D.; Jonghe, C.D.; Belmans, R. Statistical analysis of negative prices in European balancing markets. Renew. Energy 2015, 80, 53–60. [Google Scholar] [CrossRef]
- Andrade, J.; Filipe, J.; Reis, M.; Bessa, R. Probabilistic Price Forecasting for Day-Ahead and Intraday Markets: Beyond the Statistical Model. Sustainability 2017, 9, 1990. [Google Scholar] [CrossRef]
- Amini, M.H.; Kargarian, A.; Karabasoglu, O. ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation. Electr. Power Syst. Res. 2016, 140, 378–390. [Google Scholar] [CrossRef]
- Ziel, F.; Steinert, R.; Husmann, S. Efficient Modeling and Forecasting of the Electricity Spot Price. Energy Econ. 2015, 47, 98–111. [Google Scholar] [CrossRef]
- Olsson, M.; Söder, L. Modeling real-time balancing power market prices using combined SARIMA and Markov processes. IEEE Trans. Power Syst. 2008, 23, 443–450. [Google Scholar] [CrossRef]
- Jónsson, T.; Pinson, P.; Nielsen, H.A.; Madsen, H. Exponential Smoothing Approaches for Prediction in Real-Time Electricity Markets. Energies 2014, 7, 3710–3732. [Google Scholar] [CrossRef]
- Hirth, L.; Ziegenhagen, I. Balancing power and variable renewables: Three links. Renew. Sustain. Energy Rev. 2015, 50, 1035–1051. [Google Scholar] [CrossRef]
- Harris, C. Electricity Markets: Pricing, Structures and Economics; Wiley Finance: Hoboken, NJ, USA, 2006. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Hyndman, R.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008, 26, 1–22. [Google Scholar]
- Landry, M.; Erlinger, T.P.; Patschke, D.; Varrichio, C. Probabilistic gradient boosting machines for GEFCom2014 wind forecasting. Int. J. Forecast. 2016, 32, 1061–1066. [Google Scholar] [CrossRef]
- Ridgeway, G.; Southworth, H. gbm: Generalized Boosted Regression Models, R Package Version 2.1; 2014. Available online: https://CRAN.R-project.org/package=gbm (accessed on 20 April 2018).
- Brier, G. Verification of Forecasts Expressed in Terms of Probability. Mon. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Murphy, A.H. A new vector partition of the probability score. J. Appl. Meteorol. 1973, 12, 595–600. [Google Scholar] [CrossRef]
- Spackman, K.A. Signal detection theory: Valuable tools for evaluating inductive learning. In Proceedings of the Sixth International Workshop on Machine Learning, Ithaca, NY, USA, 26–27 June 1989; pp. 160–163. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Patt. Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
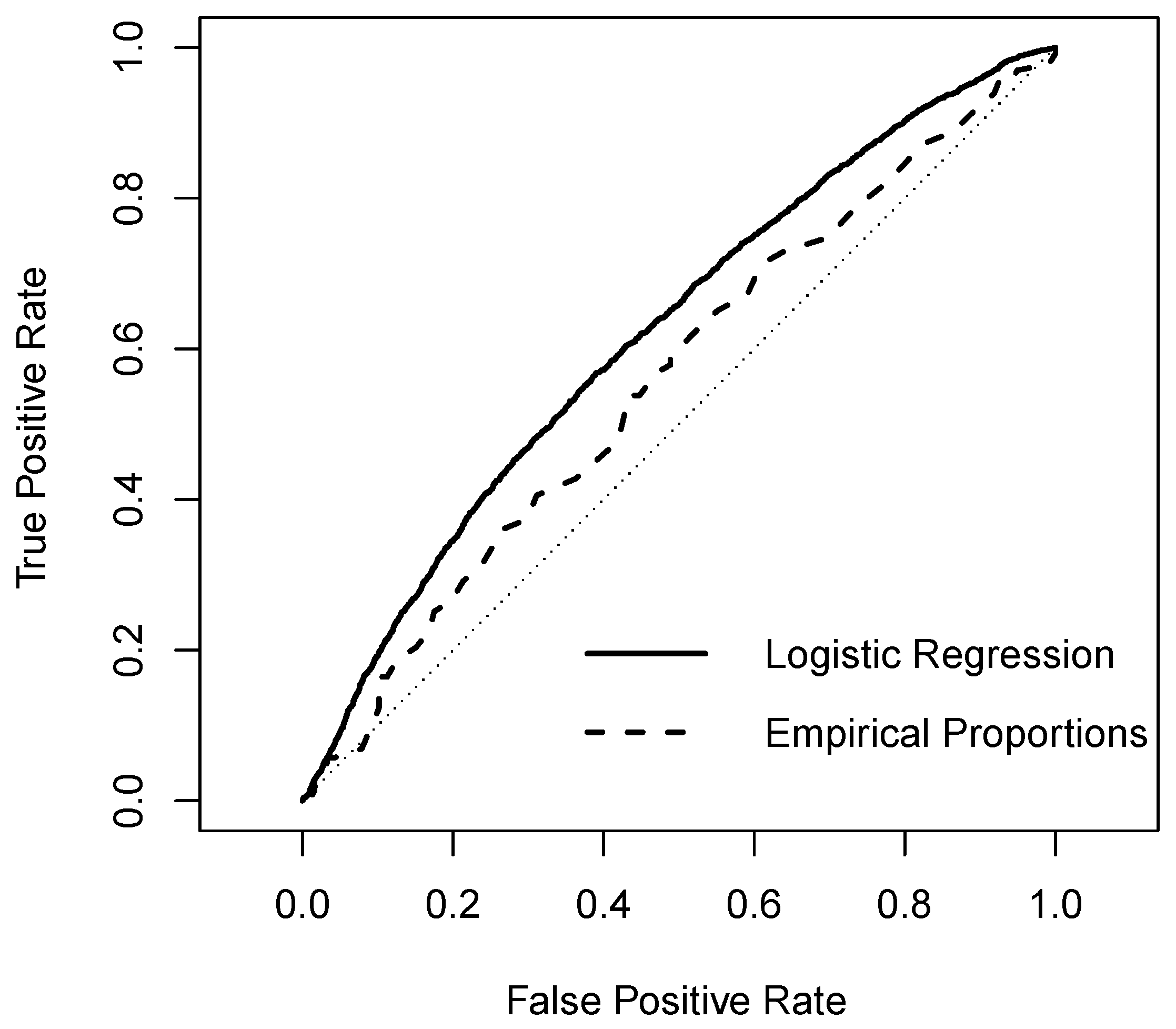
| Method | Brier Score | Reliability | Resolution |
|---|---|---|---|
| Empirical Proportions | 0.2318 | 0.0001 | 0.0029 |
| Logistic Regression | 0.2265 | 0.0030 | 0.0102 |
| Strategy | Forecast Method | ||
|---|---|---|---|
| Perfect | Simple | Advanced | |
| Minimise Imbalance | 34.66 | n/a | 34.81 |
| SL Forecast: Deterministic | 50.16 | 33.20 | 34.39 |
| SL Forecast: Empirical Proportion | 41.72 | 37.32 | 37.75 |
| SL Forecast: Logistic | 41.43 | 36.25 | 37.92 |
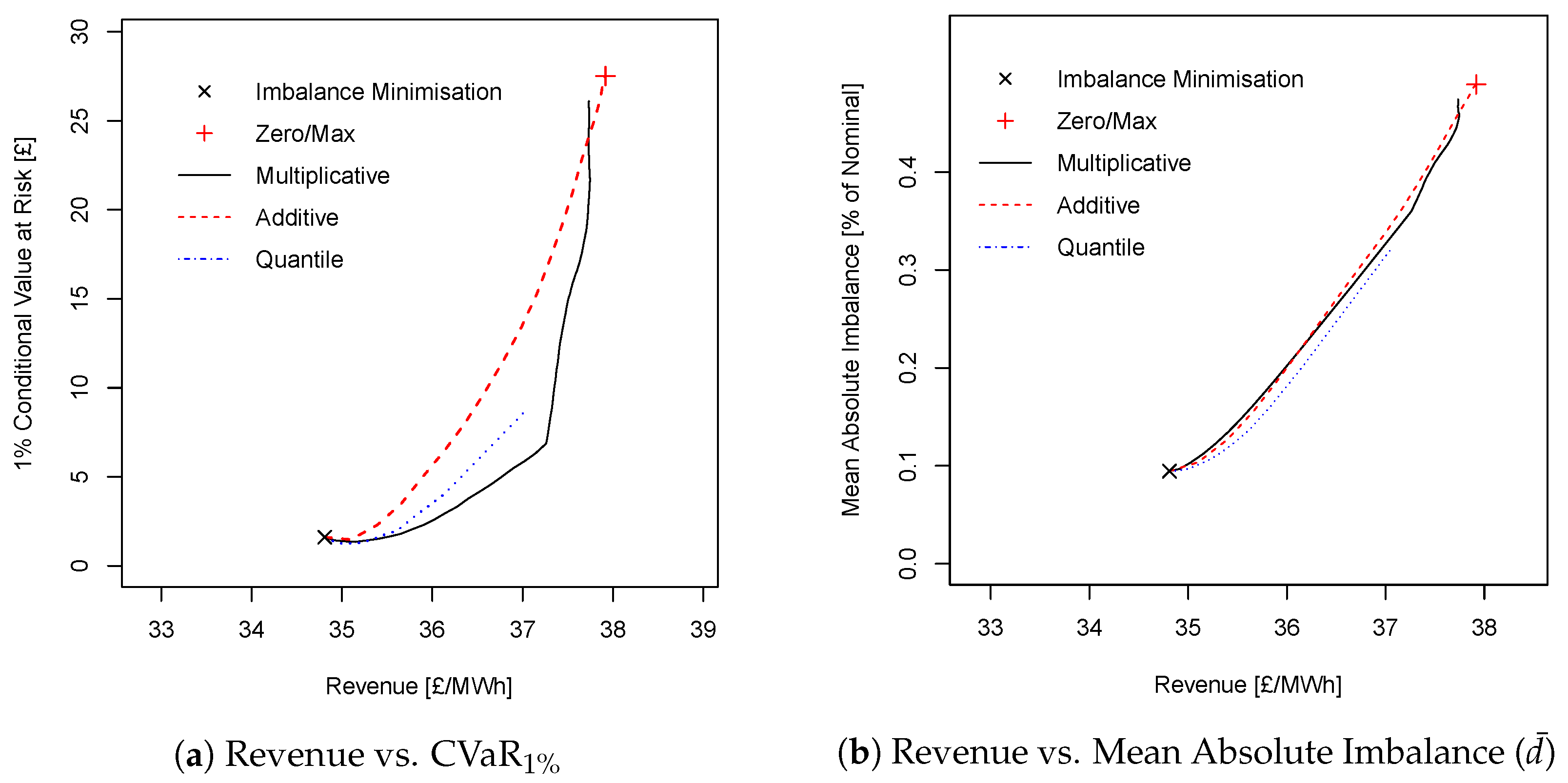
| Additive Adjustment | ||||
| Revenue | VaR | CVaR | ||
| 0 | 34.81 | 0.55 | 1.61 | 9% |
| 0.1 | 35.39 | 0.72 | 2.30 | 13% |
| 0.5 | 37.16 | 8.22 | 15.34 | 36% |
| 1 | 37.92 | 14.23 | 27.51 | 49% |
| Multiplicative Adjustment | ||||
| Revenue | VaR | CVaR | ||
| 0 | 34.81 | 0.55 | 1.61 | 9% |
| 0.1 | 35.02 | 0.43 | 1.38 | 10% |
| 0.5 | 36.02 | 0.82 | 2.60 | 20% |
| 1 | 37.26 | 2.57 | 6.87 | 36% |
| 5 | 37.72 | 11.13 | 19.71 | 45% |
| 10 | 37.73 | 14.14 | 26.11 | 47% |
| Quantile | ||||
| Revenue | VaR | CVaR | ||
| 0.55 | 34.90 | 0.45 | 1.38 | 10% |
| 0.65 | 35.09 | 0.47 | 1.27 | 10% |
| 0.75 | 35.32 | 0.45 | 1.46 | 11% |
| 0.95 | 36.14 | 1.73 | 4.07 | 20% |
| 0.99 | 37.05 | 3.75 | 8.77 | 32% |
| Units: | £/MWh | £ | % of | |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Browell, J. Risk Constrained Trading Strategies for Stochastic Generation with a Single-Price Balancing Market. Energies 2018, 11, 1345. https://doi.org/10.3390/en11061345
Browell J. Risk Constrained Trading Strategies for Stochastic Generation with a Single-Price Balancing Market. Energies. 2018; 11(6):1345. https://doi.org/10.3390/en11061345
Chicago/Turabian StyleBrowell, Jethro. 2018. "Risk Constrained Trading Strategies for Stochastic Generation with a Single-Price Balancing Market" Energies 11, no. 6: 1345. https://doi.org/10.3390/en11061345
APA StyleBrowell, J. (2018). Risk Constrained Trading Strategies for Stochastic Generation with a Single-Price Balancing Market. Energies, 11(6), 1345. https://doi.org/10.3390/en11061345





