Abstract
In this paper, we address the problem of minimizing the total daily energy cost in a smart residential building composed of multiple smart homes with the aim of reducing the cost of energy bills and the greenhouse gas emissions under different system constraints and user preferences. As the household appliances contribute significantly to the energy consumption of the smart houses, it is possible to decrease electricity cost in buildings by scheduling the operation of domestic appliances. In this paper, we propose an optimization model for jointly minimizing electricity costs and CO2 emissions by considering consumer preferences in smart buildings that are equipped with distributed energy resources (DERs). Both controllable and uncontrollable tasks and DER operations are scheduled according to the real-time price of electricity and a peak demand charge to reduce the peak demand on the grid. We formulate the daily energy consumption scheduling problem in multiple smart homes from economic and environmental perspectives and exploit a mixed integer linear programming technique to solve it. We validated the proposed approach through extensive experimental analysis. The results of the experiment show that the proposed approach can decrease both CO2 emissions and the daily energy cost.
1. Introduction
With the steadily rising electricity costs coupled with its impact on the environment, smart home energy efficiency has become one of the major issues that is necessary to improve the overall efficiency of power consumption in smart buildings. Smart grids (SGs) and micro-grids (MGs) have been developed to address the soaring electricity costs [1]. A microgrid (MG) encompasses a portion of an electric power distribution system that is located downstream of the distribution substation. It includes a variety of distributed energy resource (DER) units (such as solar panel and wind turbine [2]) and serves different types of end users of electricity and/or heat [3,4]. Each microgrid is able to supply power to local residents in a small geographical area in a cost-effective manner, by integrating a networked group of renewable generators and storage systems. A smart building with its own DER can be considered a microgrid because DERs provide local energy for the smart home residents.
In this paper, we address the problem of sustainable power usage in smart buildings composed of multiple smart homes. Since buildings contribute significantly to the overall power consumptions, recently, the question of optimal energy management of smart buildings has drawn significant attention. In smart homes, a considerable proportion of energy cost comes from smart home appliances. Therefore, there is significant potential for energy consumption and cost savings by minimizing the daily power cost of smart home appliances. Moreover, the relation between smart building residents’ comfort and power consumption has recently drawn much interest. Therefore, a smart energy management solution that will reduce energy wastage while meaningfully balancing between energy cost savings and smart home residents’ comfort level is necessary [5]. In addition, ways to reduce the impact of energy generation and consumption on the environment through minimization of greenhouse emission have drawn much interest. Therefore, the challenge is how to minimize the daily electricity cost of multiple smart homes with the aim of reducing resident energy costs and the CO2 emissions while simultaneously considering different system constraints and smart building resident preferences and comforts. In this paper, we address this problem in a simple and effective way by scheduling the operation of smart home appliances aiming at reducing energy costs and the environmental impact of the considered households with little or no effect on the comfort level of the smart home residents.
Although a variety of energy management systems for smart homes has been proposed [5,6,7,8,9,10,11,12,13], there are very few solutions that have considered a detailed energy management optimization problem that utilizes the energy cost savings and CO2 emission reduction as objectives without inconveniencing the smart home residents. Furthermore, existing solutions are based on changing the living habits of users to reduce energy costs and CO2 emissions by adjusting their demand according to time differentiated electricity pricing and making appropriate consumption scheduling decisions [14]. Unfortunately, the approaches that require end-users to manage their energy consumption manually will be time-consuming, require users to be available all the time and may not result in users’ satisfaction. Moreover, existing solutions consider only a single smart home while ignoring the states of its neighbours, which can lead to a problem known as peak rebound [15]. In addition, existing systems do not consider demand side management and a DER system in a smart home environment as tools to significantly reduce electricity consumption and CO2 emissions. Therefore, there is still room for novel energy management systems capable of reducing the energy bills for the smart building residents, as well as reducing environmental impacts [6]. The authors in [13] schedule deferrable appliances and energy resources in small buildings by using multi-time scale stochastic predictive control, the genetic algorithm and linear programming. In fact, this method includes uncertainty/time-varying of the power of the PV panels and model economic and technical constraints of the appliances and sources and schedules day-scale and hour-scale deferrable appliances using a combination of GA and LP. However, unlike our approach, we point out that: (i) the focus of [13] is on the stochastic predictive control of the considered loads for smart homes, so that the resulting scheduler does not support, by design, conflicting goals with operational constraints; (ii) the joint task (loads) and the PV rate mapping afforded in [13] are, by design, static; and (iii) the scheduler in [13] does not perform real-time user preferences and/or peak demand charge of the resources hosted by the serving request.
In this paper, we propose an energy management solution for a smart building, composed of multiple smart homes with its own DER as a microgrid. Specifically, we present a solution to the daily power consumption scheduling problem for household tasks over a finite time horizon. Besides, DER operation scheduling in a smart building composed of multiple smart homes is also investigated. We examine the validity of the proposed solution through numerical tests. The main contributions of this work can be summarized as follows:
- We present a solution to the daily power consumption scheduling problem for household tasks over a finite time horizon and DER operation scheduling in a smart building composed of multiple smart homes.
- A mathematical formulation of the scheduling problem, based on a combination of several single-objective MILP techniques, with the aim of minimizing the conflicting goals of reducing CO2 emissions and total electricity costs is presented.
- We show that adding a DER system in a smart home environment leads to a significant reduction in electricity consumption and CO2 emissions.
- Extensive experiments to validate the efficacy of the proposed approach are presented.
The remainder of this paper is organized as follows. In Section 2, the related works are presented. Section 3 presents the architecture for the system model. In Section 4, we develop the proposed optimization model and its constraints. The numerical results of performance tests are presented in Section 5, and some conclusions are drawn in Section 6.
2. Related Work
A wide range of energy management techniques in smart homes has recently been investigated. A mixed integer linear programming (MILP) model has been proposed by [8] to optimally coordinate both electrical and thermal units and household demands. Although this algorithm is a centralized energy-based scheduling that uses the predictive control model, it does not support the uncertainty of the electricity changes through the grid. The proposed solution is less scalable, and its communication requirements for the prediction and scheduling are limited. Besides, in our method, we offer different optimization solutions to the user, depending on their battery performance preferences. The problem of optimal smart home energy management considering energy savings and a comfortable lifestyle was discussed in [5]. Moreover, another work introduced new data measurement on seven households in Belgium, which can be used to acquire relationships to dimension storage packages for grid-connected PV panel installations [16]. The authors used high energy-density batteries, so they tended potentially utilize the batteries for residential energy storage since the energy density was less important for residential than for transportation applications. Furthermore, the distinction between controllable and non-controllable tasks and related appliances has been presented in [17]. This monitored the customers and actively managed their own energy usages. Furthermore, the authors in [18] presented an active demand-side management self-consumption system based on artificial neural networks, which employed microgrid and smart control to optimize the energy usage. The authors in [19] investigated the variability of electricity demand profiles, which often use common statistics such as the mean, standard deviation, variance and the coefficient of variation, and they claimed that they reduced household grid demand variation by 35%. In another work, the authors in [20] presented a smart home energy management model that jointly scheduled electrical and thermal appliances using various types of appliances considering the residents’ consumption behaviour, seasonal probability, a social random factor, the discomfort index and appliances’ starting probability functions. Recently, the author in [21] presented a new approach considering a pervasive information system in a retail environment. It helped to highlight the challenge of enhancing technical components with information systems as a smart grid solution. Besides such method being of interest, it neither gave details of the smart grid household power management, nor the current secure solutions, while our paper fills such gaps. A multi-objective mixed integer nonlinear programming model was developed for optimal energy use in a smart home. Through simulations performed under different scenarios using real data, the obtained results were compared in terms of total energy consumption cost, users’ convenience rates and thermal comfort level. The major drawback of this method falls into local energy and comfort management of the demand response (DR) problem and does not support dynamic pricing, intermittent renewable energy generation and other real-time technical aspects of energy saving.
A multi-objective genetic approach to domestic load scheduling in an energy management system was discussed in [7]. The management of controllable domestic loads was aimed at minimizing the electricity bill and the end-users’ dissatisfaction concerning two different aspects: the preferred time slots for load operation and the risk of interruption of the energy supply. This method was considered as an asset in DR scheduling; however, the scheduling on that demand side optimizing electricity consumption behaviours was more complex. In contrast, we present a solution to the daily power consumption scheduling problem for household tasks over a finite time horizon and DER operation scheduling in a smart building composed of multiple smart homes.
Residential appliance DR energy management with electricity privacy protection by online stochastic optimization was shown in [22]. This method requires knowledge of the statistics of the load requirements and the electricity prices, which may not be readily available. Moreover, dynamic programming was utilized; however, the approach was observed to be computationally difficult for a system with a large state space, hence suffering from the curse of dimensionality. An energy management solution for households with solar-assisted thermal load considering renewable energy and price uncertainty was discussed in [23]. In [9], the authors used artificial neural networks to predict the heat demand in a house based on several factors, to achieve a better match between demand and supply. Although these methods focused on one facet of the DR problem, which was energy-provisioning and load balancing, the proposed methods are incompatible with wide-area aggregation and intractable in large-scale problems. The studies in [12] addressed the demand side management problem with game theory and reached the optimal performance for minimizing energy costs under the Nash equilibrium constraints. This method has been prevalently used to respond to demand profile shaping of management objectives for energy saving and cost/price of the individual users in DR problem; however, it only considered one single snapshot on electricity prices and power consumptions of individual appliances within an hour.
The authors of [24] utilized a deterministic energy management system based on load forecasting and photovoltaic (PV) power predictions to enable a microgrid to perform day-ahead power scheduling. The drawback of this method is in its secondary control to ensure power sharing among sources, which is not generalized and depends on the characteristics of power flow within the microgrid network and cannot be used in generic cases. Besides, it is complicated by the ageing infrastructure of the existing power grid, which already causes problems for utilities and customers. This makes the system unreliable, with low power quality, and consequently, this increases cost and customer dissatisfaction.
To reduce energy costs and the peak-to-average ratio (PAR) among residents who share an energy resource, the authors in [25] proposed an algorithm to implement energy consumption scheduling devices inside smart meters in a smart grid. Particularly, that method considered only the minimization energy cost and did not address the management of loads at the network control centre level, while our method addresses both of these.
In [26], several types of controllable loads were considered to simulate a demand-side management strategy relying on a load shifting approach. Subsequently, the heuristic-based evolutionary algorithm was adopted to solve the minimization problem. Indeed, this method exploits modelling of consumer utility/disutility of demand shifting and can be of interest for the optimization of consumers’ consumption patterns within the framework.
The authors of [27] adapted an optimal residential load commitment architecture for a smart home to reduce the residential payment and PAR by determining the on/off statuses of flexible appliances and consuming the energy stored in a battery during high peaks, while selling the surplus back to the utility. In this method, DR behaves as an intermediate between buyers and sellers, but it neglects the impact of an extra peak, power-limiting strategy that is probably imposed by a load-serving entity. In order to maintain a balance between demand and supply in multiple residences, [28] designed a real-time coordinated home energy management model and handled the problem by dynamic programming. This method disregards the operational constraints of the DS infrastructure; however, this is highlighted in our method. The authors of [29] used an Android-based controller to remotely control appliances in a smart home to provide comfort and security for the residents. This method can be listed as flexible, scalable and expandable, but it needs to configure a new communication each time a there is a new way of interaction between Android-based technologies.
In [30], the authors used the non-dominated sorting genetic algorithm II (NSGA-II) to enhance the solution to multi-objective problems in smart grid systems. Although the idea is promising and appealing, it does not cover the operational cost motivated by DR and loads. Specifically, the objectives in [31] were to reduce cost and the end users’ dissatisfaction. The aim of the multi-objective problem in [30] was to minimize the total generation cost for the units and the total amount of pollution in multiple microgrids. The authors of [32] proposed energy consumption scheduling for a smart building of units with the same habits with the aim of reducing CO2 and cost saving without considering user preferences and renewable energy. They failed to analyse the uncontrollable DERs of such homogeneous buildings. To cover these limitations, the authors of [33] considered both economic and environmental issues in demand response and used a weighted sum technique to jointly investigate CO2 and cost reduction. The issue behind this method is that it does not consider electrical storage systems (ESS), while it would be more flexible and efficient for consumers to manage their energy use in response to time-varying electricity prices by storing energy and releasing it when it is more convenient, as our method.
In summary, there are very few works that have considered a detailed energy management optimization problem considering the energy cost savings and CO2 emission reduction as objectives without inconveniencing the smart home residents. Furthermore, approaches that require the end-users to manage their energy consumption may not result in users’ satisfaction. Moreover, existing solutions consider only a single smart home while ignoring the states of its neighbours. In addition, existing systems do not consider a DER system in a smart home environment as a tool to significantly reduce electricity consumption and CO2 emissions. Unlike existing works, this study investigates economic and environmental sustainability by the combination of several single-objective optimization models and solves the problem with an MILP approach. We are concerned with scheduling a number of user-specified smart appliances in their operation time windows (between the earliest starting time and the latest ending time) to minimize CO2 emissions and save daily energy costs.
3. System Model
Figure 1 shows the high level system model of interest. It consists of the main power grid with its own distribution network and a smart building with a number of smart homes and renewable energy sources (PV panels) and energy storage system (ESS). Furthermore, the building is equipped with a main energy management system to coordinate smart home appliances and DERs. The smart home appliances include deferrable loads such as electric vehicle (EV), washer/dryer, etc. We assume that the demand for energy in each smart home is different and is based on the residents’ living habits.
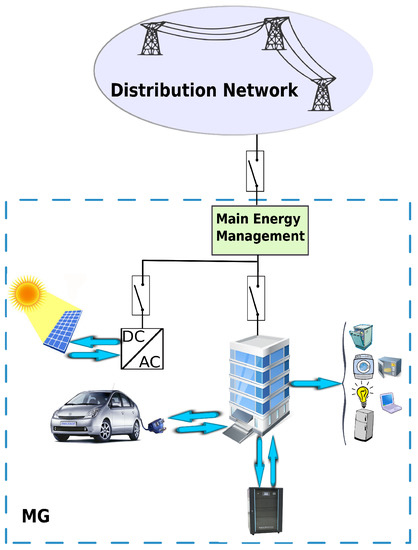
Figure 1.
System model.
The proposed model can export energy to the national grid during periods when solar energy production is greater than user demand. Conversely, when the locally generated energy is not sufficient for domestic demands, there is a possibility of obtaining electricity from the main grid. In this model, loads are divided into two categories: controllable and uncontrollable. Both controllable and uncontrollable appliances are assumed in our work. The uncertainty in renewable energy resources is considered, and we also assume that the solar radiation is provided through a Beta distribution. One-day ahead forecasted electricity prices and the emission intensity over time are taken into account in order to show the variation in these. In addition, two different tariff schemes are considered that rely on real-time price (RTP) and peak-demand charge (PDC). It is expected that users will buy electricity from the grid when the electricity tariff and CO2 emissions are low and will consume the locally generated energy otherwise.
4. Appliance Scheduling Optimization Problem Formulation
In this paper, the energy management problem in a smart building is modelled as an MILP over a specific prediction time horizon T with discrete time steps . The model is developed for 1oneday optimal scheduling that takes into account only operation and maintenance costs. Furthermore, the time resolution is considered to be 30 min over a single day, so that one day has 48 slots.
4.1. Optimization Constraints
In this subsection, we aim to specify the optimization constraints coming from the real environment.
4.1.1. Execution Time Window for Each Appliance
Mathematically, for the scheduling of two categories of smart appliances, the appliance execution time horizon is divided into H equal-length time slots (e.g., 30 min per slot). N denotes the number of appliances i in each home j (). For each domestic appliance, there is a starting time ST and a maximal ending time EN such for which the appliance’s task must be completed during this time window. The parameters for each appliance, including ST, ET, power consumption, the length of the time window and the duration of the task operation, are adopted from [34] and shown in Table 1. Furthermore, we limit ourselves to the case where each task is executed exactly once during the day in each home.

Table 1.
Household appliance parameters. ST: earliest starting time; and, ET: latest ending time [34].
We use a binary variable to indicate whether task i of home j is running (on/off) at time t. Furthermore, we limit each task i hat home j can execute once during its time window, expressed using Equation (1), where denotes the operation time for task i in home j.
Indeed, the starting time of each task should be after the given earliest starting time (ST) and must finish before the latest finishing time (ET).
4.1.2. Solar Panel
The building is equipped with a rooftop solar panel. Electricity generated by the PV system will be consumed in the building in order to minimize the overall costs for the users. The power generated by a PV module varies according to the solar radiation on the Earth’s surface, which mainly depends on the installation site and the weather conditions. Power systems are inherently uncertain. To deal with probabilistic data, appropriate probabilistic methods must be implemented. To model the solar power uncertainty, the first task is to generate solar irradiation samples by a Beta distribution function [35] and standard deviation (STD) value equal to 1000 W/m. The PV modules are tested in standard test conditions. The output power of the module is calculated as follows [36]:
where is solar radiation in the standard conditions, usually set to 1000 W/m2, is rated power of the PV (k), is a certain radiation point, usually set to 150 W/m2, and R is solar irradiance (W/m2).
4.1.3. Energy Storage System
The available energy in the energy storage system at time t, , is equal to the amount available at , , plus the electricity charged minus the electricity discharged:
where is the time interval duration, is the ESS charge/discharge efficiency, is the ESS charge rate at time t and is the ESS discharge rate at time t. At the beginning of the day, ESS has an initial value, denoted as . At the end of each day, the ESS must return electricity stored to the initial state in order to prevent net accumulation. Hence, the constraint is as follows:
where is the initial state of electricity storage.
In order to avoid damaging the ESS, the rates of electricity charge/discharge cannot exceed the energy storage limits [32], respectively, defined by the battery manufacturer:
where and are, respectively, the maximum charging rate and the maximum discharging rate for the ESS.
The output of the energy storage should not be more than its designed capacity, :
4.1.4. Energy Balances
One of the important conditions is to balance the energy consumption. The electricity demand must be met by the electricity generated by the PV, the ESS charge and power purchased from the external grid minus the electricity sold to the main grid and the ESS discharge. Therefore, the electricity balance is as follows:
where is the constant power consumption capacity of task i.
4.1.5. Peak Demand Charge
It is not economical to enhance the capacity of the connection between plants and the main grid to address an energy shortage during the peak demand period. To handle this problem, we introduce a further constraint to encourage residents to reduce their energy consumption. This method assumes an agreed-upon threshold () for each time interval. In this way, the appliance cannot be run outside of the time preference interval. Moreover, if the energy demand from the main grid is less than this threshold, users pay the normal electricity price; otherwise, they must pay an extra fee for the extra demand , as follows:
4.1.6. User Time Preferences
This constraint takes into account specific characteristics of users, namely their preferred time intervals for running their tasks. Household tasks must be finished within and cannot be run outside of their time preference ranges [37]:
where is the length of the load profile for an appliance.
4.2. Objective Functions
There are two important objectives to optimize in this work. The first objective is to minimize the total energy cost, which is based on the operation and maintenance () costs of the ESS and PV and the cost of buying/selling energy from/to the grid under the RTP tariff, as follows:
where (i.e., proportional to charge/discharge battery power) and are the operation and maintenance costs for the ESS (battery) and PV, respectively, and and are the price of buying/selling electricity from/to the grid, respectively, at time t.
The penalty part of the demand charge tariff adds to the overall daily energy cost. If the demand is below the threshold, the price scheme is RTP, and an extra cost is applied when it is over the threshold. Where is the difference between the real electricity tariff from the grid and PDC, the second scheme for the first objective is defined as follows:
The aim of the second objective is to minimize CO emissions. Accordingly, the objective that includes the CO emissions from the conventional electricity grid is defined as follows:
where is the CO intensity of the grid electricity at time t.
Given these two objective functions, the problem is a combination of several single-objective minimization problems with conflicting objectives regarding CO emissions and the electricity bill. Various methods have been proposed to handle this conflict and trade-off. We convert the combination of several objectives into a single object through a weighted sum approach using two factors, and , where is an (assigned) weight factor that tunes the desired trade-off between the cost of CO emissions and the electricity bill (i.e., in this paper, we give the same weight to both objectives, = ).
For the RTP scheme, the objective is to minimize the total energy cost and CO emissions’ cost under real-time electricity prices as shown in Equation (13), subject to Equations (1)–(9). For the PDC scheme, the objective is to minimize CO emissions and the total daily CO cost together with the extra cost charged for over-consumed electricity from the grid as shown in Equation (13), subject to Equations (1)–(10). The problems belong to the class of MILP formulations. Therefore, we have relied on solvers to find the solutions.
5. Performance Evaluation
In this section, we evaluate our proposed MILP model for scheduling energy (electricity) consumption with several numerical evaluations.
5.1. Experimental Setup
To run the simulation, we use the CVX solver, the state-of-the-art Stanford optimizing solver, running over MATLAB [38] on an Apple MacBook with a 2.6-GHz processor and 16-GB RAM to test our model for a smart building with 30 different numbers of homes that do not share the same living habits. Table 1 summarizes the appliance types and other features of households with 12 basic tasks that consume electricity. To simplify, it is assumed that all tasks have constant power consumption rates, despite in reality, for example, the dishwasher having a different power consumption rate. These tasks can be scheduled according to their earliest starting time, latest finishing time, duration and power requirements as presented in Table 1. All tasks have fixed power consumption rates.
Each building is equipped with a PV panel with a 10 kW capacity and a maintenance cost of 0.5 p/kWh. Each building also has one ESS with a 10 kW capacity [32], 98% charge/discharge efficiency, 20 kW discharge and charge limits and a maintenance cost of 0.1 p/kW. The grid connection has the ability to import/export energy to/from the main grid. The real electricity tariff [39] and CO intensity profiles [40] gathered from the U.K. for one day are shown in Figure 2. The real-time electricity prices at different times collected from the Balancing Mechanism Reporting Service in [39] are shown in Figure 2a, and the CO intensity rates for 15 January 2015 and 15 August 2015 are presented in Figure 2b [40]. The planning horizon for both examples is from 00.00 a.m. one day to 00.00 a.m. the next morning. From Figure 2, it can be seen that there is a conflict between CO emissions and the electricity tariff. For instance, in Hour 5 (summer), the electricity price is at its lowest point, while the opposite is the case for CO emissions, which are at their peak point. Each time interval is 30 min long; in total, we consider 48 time intervals for a single day.
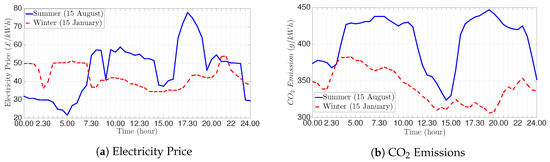
Figure 2.
Electricity tariff and CO emissions for the U.K. city of Bristol for the summer (15 August 2015; continuous line) and winter (15 January 2015; dashed line).
We consider two electricity pricing schemes: the PDC scheme and the RTP scheme, and we consider variations in CO intensity over time. For the peak demand charge tariff, the agreed-upon threshold is 30 kW [32]; the extra fee that must be paid above this threshold is 5 p/kWh; and the price for selling energy to the grid is 1 p/kWh. For the RTP scheme, the objective is to minimize CO emissions and the total daily CO cost under real-time electricity prices as shown in Equation (13), subject to Equations (1)–(9). For the PDC scheme, the objective is to minimize CO emissions and the total daily CO cost together with the extra cost charged for over-consumed electricity from the grid as shown in Equation (13), subject to Equations (1)–(10). We define several scenarios for the RTP and PDC schemes: (i) macrogrid earliest starting time (ME); (ii) macrogrid optimized scheduling (MO); (iii) microgrid earliest starting time (mE); (iv) microgrid optimized scheduling (mO), using the schemes PDC (P) and RTP (R) (e.g., RmO is the microgrid optimized scheduling scenario with the scheme RTP) (for simplicity, ‘xyz’ is used as the abbreviation, where ‘x’ represents real-time price scheme (R) or peak demand price scheme (P), ‘y’ represents the macrogrid (M) or microgrid (m) and ‘z’ represents earliest starting time (E) or optimized scheduling (O)). Macrogrid (M) shows that the electrical demand of the smart building is provided only by the main grid, whilst microgrid (m) indicates that the building considers DER and the storage system. Furthermore, in the “earliest starting time (E)” case, all appliances start operating as soon as they are available, whereas in the “optimized scheduling (O)” case, the proposed optimized power profiles are followed. Moreover, we test these scenarios on two days of the year: 15 January 2015 to represent the winter and 15 August 2015 to represent the summer (see Figure 2). We run our MILP problem to schedule appliances for the two different price schemes to simultaneously optimize CO emissions and the electricity bill.
5.2. Performance Results
In this subsection, we simulate our model for heterogeneous living habits.
For the first test, we run the solver and evaluate the resulting electrical power usage for the aforementioned scenarios. The optimal electricity balance cost for a day under the RTP scheme is shown in Figure 3. Hence, based on the numerical tests carried out, we have determined that: (i) the electricity cost (power) decreases using the solver for the optimization scenarios (see Figure 3b,d), and this rate is even higher with more components (Figure 3d) as the microgrid scenario is applied; and (ii) the solution can respond to the electricity demand using its storage, and even the rate of electricity that is sold is significant compared to the consumer demand (see the light blue bars in Figure 3d).
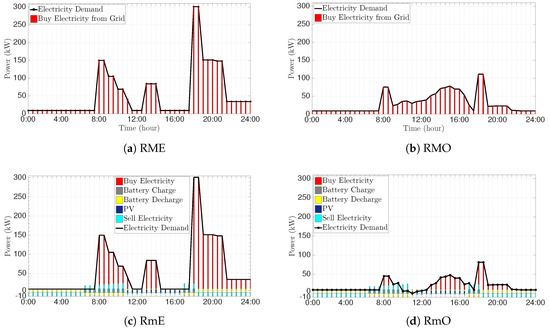
Figure 3.
Thirty homes: electricity balance cost under the real-time price (RTP) scheme for one day in the summer. (a) RME: macrogrid earliest starting time scenario; (b) RMO: macrogrid optimized scheduling scenario; (c) RmE: microgrid earliest starting time scenario; (d) RmO: microgrid optimized scheduling scenario.
Based on the given task operation time window in Table 1, most of the appliance start times are in the slots between 8:00 and 9:00 and between 18:00 and 19:00. Therefore, we have peaked during these time intervals, which can be deduced from Figure 3a,c. On the other hand, by using the optimization scheme (see Figure 3b,d), the electricity demand curves are made smoother than they are for the scheme without optimization (see Figure 3a,c). For the optimization scheme, the scheduler tries to move the execution of the demands with high electricity prices [39] and CO emissions [40] (8:00 and 18:00 in Figure 2a,b) to the lowest slots. Moreover, in the microgrid scenario, there is more energy from the PV between 12:00 and 16:00, and it can be seen from Figure 3d that in this time interval, there is a peak in the demand curve.
The optimal electricity balance cost for a day under the PDC scheme is shown in Figure 4. A significant point can be understood by comparing Figure 3 and Figure 4: when we apply the PDC scheme, the total energy cost in each scenario is higher than under the RTP scheme. When there is an extra charge for the over-consumed electricity from the grid, the peak demand is reduced through optimization. Figure 4 shows that under the PMO scenario, the tasks are scattered according to the peak demand extra charges. The total cost for the PME scenario is around 1.5 M£, but it decreases to 0.9 M£ when the optimized scheduling is applied in the PMO scenario and the peak demand from the grid is reduced from 300.4–192.6 kW. There are still peaks in the early morning and evening that cannot be avoided, mainly because of the inflexible time window requirement for specific tasks. This happens even in the PmO scenario (see Figure 4d), but we can declare that the electricity demand makes the plot smoother. Under the microgrid scenarios, the total cost is reduced to 0.6 M£in the PmO scenario, and the peak demand from the grid is reduced from 300.4 kW in the PmE scenario to 126.3 kW in the PmO scenario.
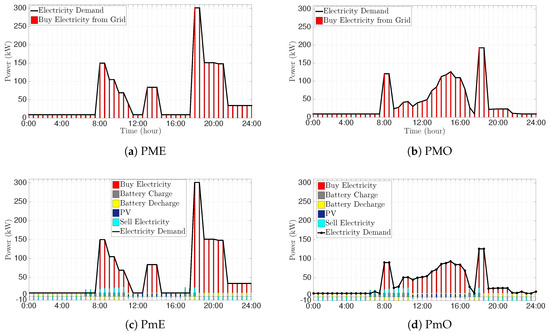
Figure 4.
Thirty homes: electricity balance cost under the peak-demand charge (PDC) scheme for one day in the summer. (a) PME: macrogrid earliest starting time scenario; (b) PMO: macrogrid optimized scheduling scenario; (c) PmE: microgrid earliest starting time scenario; (d) PmO: microgrid optimized scheduling scenario.
For the third test, we compared the total costs, the electricity bought and sold and the CO costs for the scenarios under the RTP and PDC schemes for two seasons: summer and winter. Note that the yellow bars indicate the electricity that is sold to the grid, which yields a negative cost (revenue). The results of this comparison are presented in Figure 5 and Figure 6. Based on these figures, we conclude that the total energy cost, CO emissions and imported electricity can be reduced by scheduling the appliances and exploiting the DERs. As shown, the total energy cost and imported electricity from the grid in the ‘m’ scenarios have been reduced significantly compared to the ‘M’ scenarios, which do not have DERs. Moreover, in the ‘O’ scenarios, there is more cost saving than in the ‘E’ scenarios and less demand from the grid due to the scheduling. As a result, the ‘ME’ scenarios are the most expensive scheduling plan, since we used neither the optimized solution nor DERs.
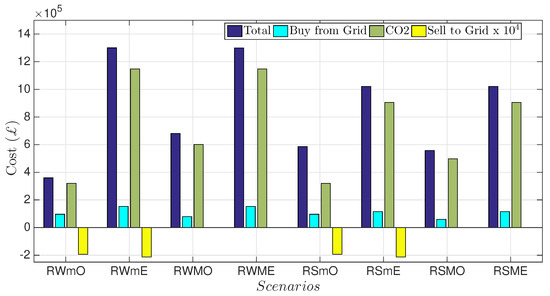
Figure 5.
Cost comparisons between the optimized and non-optimized scenarios for the real-time price scheme.
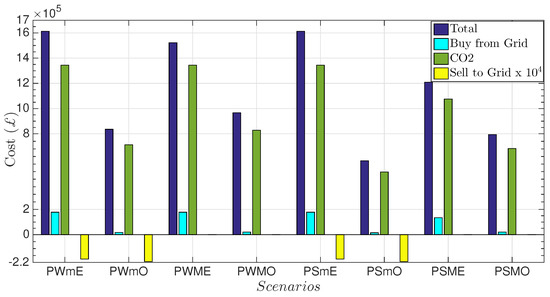
Figure 6.
Cost comparisons between the optimized and non-optimized scenarios with a threshold of 30 for the peak demand price scheme.
For the fourth test, we aimed to analyse the cost of each scenario and its savings, as well as to understand the peak/total demands in the RTP and PDC schemes. Table 2 and Table 3 present these outcomes. Specifically, Table 2 presents the peak/total demands with the total costs for the different scenarios in the winter and the summer for the U.K. data profiles. As indicated by the results in Table 2, we also tested the MILP problem using various thresholds () for the peak demands (see Equation (8)). We can see from Table 2 that: (i) when increases, the total demand for the threshold decreases for all peak demand scenarios, which confirms the constraints in Equation (9); in other words, the PDC price scheme targets minimizing the maximum power demand from the grid (kW); (ii) the maximum power demand from the grid is reduced while the total demand from the grid including the threshold is also reduced; in this case, the stress the smart home’s place on the grid is decreased; and (iii) when the PDC scenarios change from the ‘E’ mode to the ‘O’ mode, the total demand over the threshold savings increases, and they also increase when MGs are utilized.

Table 2.
Peak demand from the grid and total electricity for two price schemes and three thresholds (); TC: total cost; PD: peak demand; TD: total demand; TDo: total demand over thresholds.

Table 3.
Comparisons between optimized scenarios and their corresponding non-optimized scenarios in cost and peak demand savings.
Comparing the scenarios where all tasks start at their earliest possible starting time (i.e., scenarios with the ‘E’ mode), it is obvious that savings increase through task starting time scheduling in both examples under the RTP and PDC pricing schemes. Compared with the earliest starting time scenarios, the cost savings and total peak demand savings from the grid over the earliest starting scenarios by scheduling task starting times are presented in Table 3 for the different scenarios. In the RTP scheme, the two seasons have similar cost savings, while under the PDC scheme, the summer season demonstrates more cost savings, which was expected from Figure 2. Table 3 shows that for all scenarios, the winter season has a higher percentage of cost savings from the grid. In both seasons, when a microgrid is utilized, the lowest percentage of cost savings is 48% and the lowest percentage of peak demand savings is 58%. Thus, use of a microgrid is an important alternative solution for reducing costs and peak demands. Table 3 also shows that there are peak demand savings even when only the RTP scheme is used. However, the peak demands are accidentally reduced in that case, as the reduction results from the optimized task starting time schedule based on electricity’s RTP. When the PDC scheme is used, the total peak demands from the grid are minimized through the objective function, which provides similar savings for both seasons. In a nutshell, it is evident that the proposed MILP model can offer significant cost savings and peak demand savings with very modest computational complexity for smart buildings.
Finally, the model statistics for the microgrid-optimized scheduling scenarios under the two pricing schemes are presented in Table 4 for the two seasons, and the consumed CPU time is also presented. We can see that applying PDC with an optimality gap of 0.1% for the scheduling scenarios RmO and PmO in the summer season requires 7.6 CPU s and 8.0 CPU s, respectively.

Table 4.
Execution statistics for the CVX model.
6. Conclusions and Future Directions
In this work, a smart building with 30 homes in which user preferences and various types of appliances are considered has been used as an illustration to study the performance of the proposed optimization-based framework. An MILP-based model with three objectives was presented: minimizing the total emission cost, the total electricity cost and the peak demand charge. The building has its own microgrid (PV and ESS) to locally generate energy. As a consequence, when the electricity tariff and CO emissions are in peak periods, the scheduler tries to shift domestic appliances into the slots with the lowest price and CO densities based on their operation time windows. In addition, the uncertainty inherent in PV generation and two different price tariffs (RTP and PDC) were taken into account. Different scenarios were simulated in order to demonstrate the effectiveness of the proposed scheduling model, and the results for the different scenarios were analysed and compared. The simulation results demonstrated from both economic and environmental perspectives that the proposed home energy management model results in a lower total cost and CO emissions cost and also has the ability to shave the peak demand. An interesting outlook is to study the microgrid economic dispatching problem under various noisy predictions of future demand and renewable generation within a limited look-ahead window.
Supplementary Materials
The Source code of the paper is available at http://www.mdpi.com/1996-1073/11/6/1348/s1, To be precise, the required information for the PV/CO2 for various scenarios are the same name using csv format at which is extracted in txt format. The file cvx_Zahra_Smartgrid_differentload_dishwasher_updated_mutipleMM.m: The main file. Note that, to run the program you are requested to install Matlab and CVX toolbox. Also, The folders reflects the homogeneous and heterogeneous smart home scenario and their results.
Author Contributions
All authors together proposed, discussed and finalized the main idea of this work. Z.P. and V.P proposed the idea, conceptualization, formal analysis, calculated and plotted the feasible regions, and compared and classified the background and taxonomy presentation and evaluated their pros and cons. J.H.A. technically supported the content, verified the accuracy, writing-original draft preparation, and revised the clarity of the work as well as helping to write and organize the paper. Finally, M.C. helped in the paper preparations, English corrections, and submission.
Acknowledgments
Mauro Conti is supported by a Marie Curie Fellowship funded by the European Commission (Agreement PCIG11-GA-2012-321980). This work is also partially supported by the EU TagItSmart! Project (Agreement H2020-ICT30-2015-688061), the EU-India REACH Project (Agreement ICI+/2014/342-896) and by the projects “Physical-Layer Security for Wireless Communication”, “Content Centric Networking: Security and Privacy Issues”, and “Adaptive Failure and QoS-aware Controller over Cloud Data Center to Preserve Robustness and Integrity of the Incoming Traffic” funded by the University of Padua. This work is partially supported by Grant No. 2017-166478 (3696) from the Cisco University Research Program Fund and the Silicon Valley Community Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Binary Variables | |
| task i status of home j at time t | |
| Indices | |
| i | ask number |
| j | home number in the smart building |
| t | time interval |
| Parameters | |
| weighting factor of the multi-objective function | |
| weighting factor of the multi-objective function | |
| time interval duration h | |
| charge/discharge efficiency of the energy storage system | |
| intensity of the grid electricity at time t (kg CO/kWh) | |
| real-time price for buying electricity from the grid at time t (£/kWh) | |
| the difference between peak and base electricity demand price from the grid (£/kWh) | |
| C | operation and maintenance cost of the energy storage system (£/kWh) |
| operation and maintenance cost of photovoltaic panels (£/kWh) | |
| real-time price for selling electricity to the grid at time t (£/kWh) | |
| latest finishing time of task i in home j | |
| energy storage system capacity (kWh) | |
| energy storage system discharge limit (kW) | |
| processing time of task i in home j | |
| agreed electricity peak demand threshold from the grid (kW) | |
| earliest starting time of task i in home j | |
| Variables | |
| length of the load profile of an appliance | |
| daily electricity cost of a home (£) | |
| daily emissions (kg CO) | |
| energy storage system charge rate at time t (kW) | |
| energy storage system discharge rate at time t (kWh) | |
| electrical power bought from the grid at time t (kW) | |
| extra electrical load from the grid over the agreed threshold value (kW) | |
| initial state of the energy storage system (kW) | |
| electricity in the energy storage system at time t (kW) | |
| generated power by PV with solar irradiance R (kW) | |
| rated power of PV (kW) | |
| R | solar irradiance (W/m) |
| certain radiation point, usually set to 150 W/m | |
| solar radiation in the standard conditions, usually set to 1000 W/m |
References
- Rahimi, F.; Ipakchi, A. Demand response as a market resource under the smart grid paradigm. IEEE Trans. Smart Grid 2010, 1, 82–88. [Google Scholar] [CrossRef]
- Hajeforosh, S.F.; Pooranian, Z.; Shabani, A.; Conti, M. Evaluating the High Frequency Behavior of the Modified Grounding Scheme in Wind Farms. Appl. Sci. 2017, 7, 1323. [Google Scholar] [CrossRef]
- Katiraei, F.; Iravani, R.; Hatziargyriou, N.; Dimeas, A. Microgrids management. IEEE Power Energy Mag. 2008, 6, 54–65. [Google Scholar] [CrossRef]
- Fallah, S.N.; Deo, R.C.; Shojafar, M.; Conti, M.; Shamshirband, S. Computational Intelligence Approaches for Energy Load Forecasting in Smart Energy Management Grids: State of the Art, Future Challenges, and Research Directions. Energies 2018, 11, 596. [Google Scholar] [CrossRef]
- Moghaddam, A.A.; Rahimi-Kian, H.M. Optimal smart home energy management considering energy saving and a comfortable lifestyle. IEEE Trans. Smart Grid 2015, 6, 324–332. [Google Scholar] [CrossRef]
- Soares, A.; Álvaro Gomes, C.H.A. Categorization of residential electricity consumption as a basis for the assessment of the impacts of demand response actions. Renew. Sustain. Energy Rev. 2014, 30, 490–503. [Google Scholar] [CrossRef]
- Soares, A.; Antunes, C.H.; Gomes, C.O. A multi-objective genetic approach to domestic load scheduling in an energy management system. Energy 2014, 77, 144–152. [Google Scholar] [CrossRef]
- Kriett, P.O.; Salani, M. Optimal control of a residential microgrid. Energy 2012, 42, 321–330. [Google Scholar] [CrossRef]
- Molderink, A.; Bakker, V.; Bosman, M.G.; Hurink, J.L.; Smit, G.J. Management and control of domestic smart grid technology. IEEE Trans. Smart Grid 2010, 1, 109–119. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Dounis, A.I.; Yang, R. Multi-agent control system with information fusion based comfort model for smart buildings. Appl. Energy 2012, 99, 247–254. [Google Scholar] [CrossRef]
- Širokỳ, J.; Oldewurtel, F.; Cigler, J.; Prívara, S. Experimental analysis of model predictive control for an energy efficient building heating system. Appl. Energy 2011, 88, 3079–3087. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Wong, V.W.; Jatskevich, J.; Schober, R.; Leon-Garcia, A. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid. IEEE Trans. Smart Grid 2010, 1, 320–331. [Google Scholar] [CrossRef]
- Rahmani-Andebili, M. Scheduling deferrable appliances and energy resources of a smart home applying multi-time scale stochastic model predictive control. Sustain. Cities Soc. 2017, 32, 338–347. [Google Scholar] [CrossRef]
- Liu, Y.; Hassan, N.; Huang, S.; Yuen, C. Electricity cost minimization for a residential smart grid with distributed generation and bidirectional power transactions. In Proceedings of the IEEE Innovative Smart Grid Technol (ISGT), Sao Paulo, Brazil, 15–17 April 2013; pp. 1–63. [Google Scholar]
- Kishore, S.; Snyder, L.V. Control mechanisms for residential electricity demand in smart grids. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications (SmartGridComm), Gaithersburg, MD, USA, 4–6 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 443–448. [Google Scholar]
- Mulder, G.; De Ridder, F.; Six, D. Electricity storage for grid-connected household dwellings with PV panels. Sol. Energy 2010, 84, 1284–1293. [Google Scholar] [CrossRef]
- Gottwalt, S.; Ketter, W.; Block, C.; Collins, J.; Weinhardt, C. Demand side management—A simulation of household behaviour under variable prices. Energy Policy 2011, 39, 8163–8174. [Google Scholar] [CrossRef]
- Matallanas, E.; Castillo-Cagigal, M.; Gutiérrez, A.; Monasterio-Huelin, F.; Caamaño-Martín, E.; Masa, D.; Jiménez-Leube, J. Neural network controller for active demand-side management with PV energy in the residential sector. Appl. Energy 2012, 91, 90–97. [Google Scholar] [CrossRef]
- Purvins, A.; Papaioannou, I.T.; Debarberis, L. Application of battery-based storage systems in household-demand smoothening in electricity-distribution grids. Energy Convers. Manag. 2013, 65, 272–284. [Google Scholar] [CrossRef]
- Shirazi, E.; Zakariazadeh, A.; Jadid, S. Optimal joint scheduling of electrical and thermal appliances in a smart home environment. Energy Convers. Manag. 2015, 106, 181–193. [Google Scholar] [CrossRef]
- Brandt, T.; Feuerriegel, S.; Neumann, D. Modeling interferences in information systems design for cyberphysical systems: Insights from a smart grid application. Eur. J. Inf. Syst. 2018, 1–14. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, L. Residential appliance dr energy management with electric privacy protection by online stochastic optimization. IEEE Trans. Smart Grid 2013, 4, 1861–1869. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Le, L.B. Energy management for households with solar assisted thermal load considering renewable energy and price uncertainty. IEEE Trans. Smart Grid 2015, 6, 301–2173. [Google Scholar] [CrossRef]
- Kanchev, H.; Lu, D.; Colas, F.; Lazarov, V.; Francois, B. Energy management and operational planning of a microgrid with a PV-based active generator for smart grid applications. IEEE Trans. Ind. Electron. 2011, 58, 4583–4592. [Google Scholar] [CrossRef]
- Mohsenian-Rad, A.H.; Wong, V.W.; Jatskevich, J.; Schober, R. Optimal and autonomous incentive-based energy consumption scheduling algorithm for smart grid. In Proceedings of the Innovative Smart Grid Technologies (ISGT), Gaithersburg, MD, USA, 19–21 January 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand side management in smart grid using heuristic optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Rastegar, M.; Fotuhi-Firuzabad, M.; Aminifar, F. Load commitment in a smart home. Appl. Energy 2012, 96, 45–54. [Google Scholar] [CrossRef]
- Chang, T.H.; Alizadeh, M.; Scaglione, A. Real-time power balancing via decentralized coordinated home energy scheduling. IEEE Trans. Smart Grid 2013, 4, 1490–1504. [Google Scholar] [CrossRef]
- Baraka, K.; Ghobril, M.; Malek, S.; Kanj, R.; Kayssi, A. Low cost arduino/android-based energy-efficient home automation system with smart task scheduling. In Proceedings of the 2013 Fifth International Conference on Computational Intelligence, Communication Systems and Networks (CICSyN), Madrid, Spain, 5–7 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 296–301. [Google Scholar]
- Pooranian, Z.; Nikmehr, N.; Najafi-Ravadanegh, S.; Mahdin, H.; Abawajy, J. Economical and environmental operation of smart networked microgrids under uncertainties using NSGA-II. In Proceedings of the 2016 24th International Conference on Software, Telecommunications and Computer Networks (SoftCOM), Split, Croatia, 22–24 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Pal, S.; Singh, B.; Kumar, R.; Panigrahi, B. Consumer End Load Scheduling in DSM Using Multi-objective Genetic Algorithm Approach. In Proceedings of the 2015 IEEE International Conference on Computational Intelligence & Communication Technology (CICT), Ghaziabad, India, 13–14 February 2015; pp. 518–523. [Google Scholar]
- Zhang, D.; Evangelisti, S.; Lettieri, P.; Papageorgiou, L.G. Economic and environmental scheduling of smart homes with microgrid: DER operation and electrical tasks. Energy Convers. Manag. 2016, 110, 113–124. [Google Scholar] [CrossRef]
- Song, M.; Alvehag, K.; Widén, J.; Parisio, A. Estimating the impacts of demand response by simulating household behaviours under price and CO2 signals. Electric Power Syst. Res. 2014, 111, 103–114. [Google Scholar] [CrossRef]
- Domestic Electrical Energy Usage. Electropaedia. Available online: http://www.mpoweruk.com/electricity_demand.htm (accessed on 1 September 2015).
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]
- Aien, M.; Rashidinejad, M.; Fotuhi-Firuzabad, M. On possibilistic and probabilistic uncertainty assessment of power flow problem: A review and a new approach. Renew. Sustain. Energy Rev. 2014, 37, 883–895. [Google Scholar] [CrossRef]
- Qayyum, F.; Naeem, M.; Khwaja, A.; Anpalagan, A.; Guan, L.; Venkatesh, B. Appliance Scheduling Optimization in Smart Home Networks. IEEE Access 2015, 3, 2176–2190. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming; CVX Research, Inc.: Austin, TX, USA, 2014. [Google Scholar]
- Balancing Mechanism Reporting Service (BMRS). Available online: http://www.bmreports.com/bsp/SystemPricesHistoric.htm (accessed on 15 August 2016).
- UK/GB Grid Electricity CO2 Intensity with Time. Available online: http://www.earth.org.uk/note-on-UK-grid-CO2-intensity-variations.html (accessed on 15 August 2016).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).