Gear Ratio Optimization of a Multi-Speed Transmission for Electric Dump Truck Operating on the Structure Route
Abstract
:1. Introduction
2. Modeling and Analysis of Electric Dump Truck
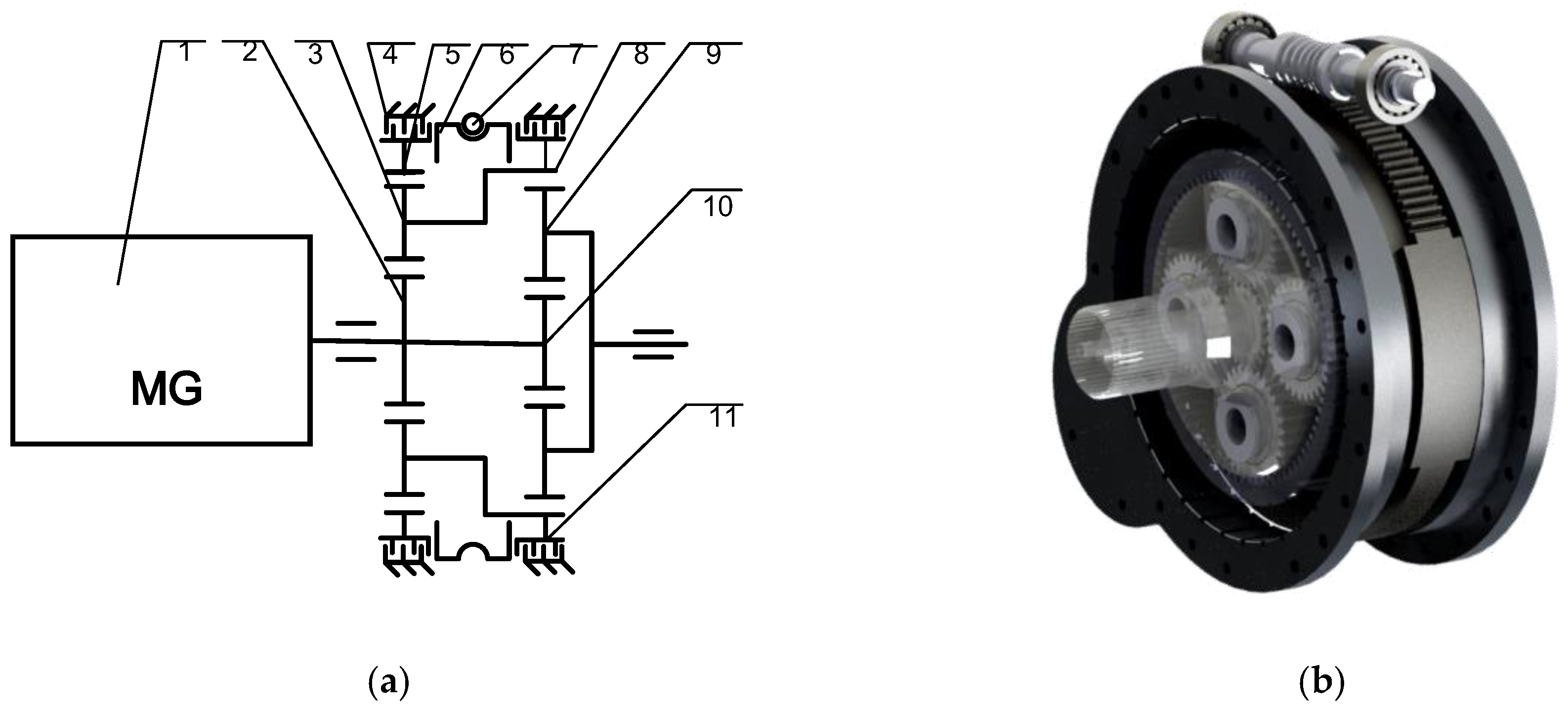
2.1. Dynamics of the Transmission
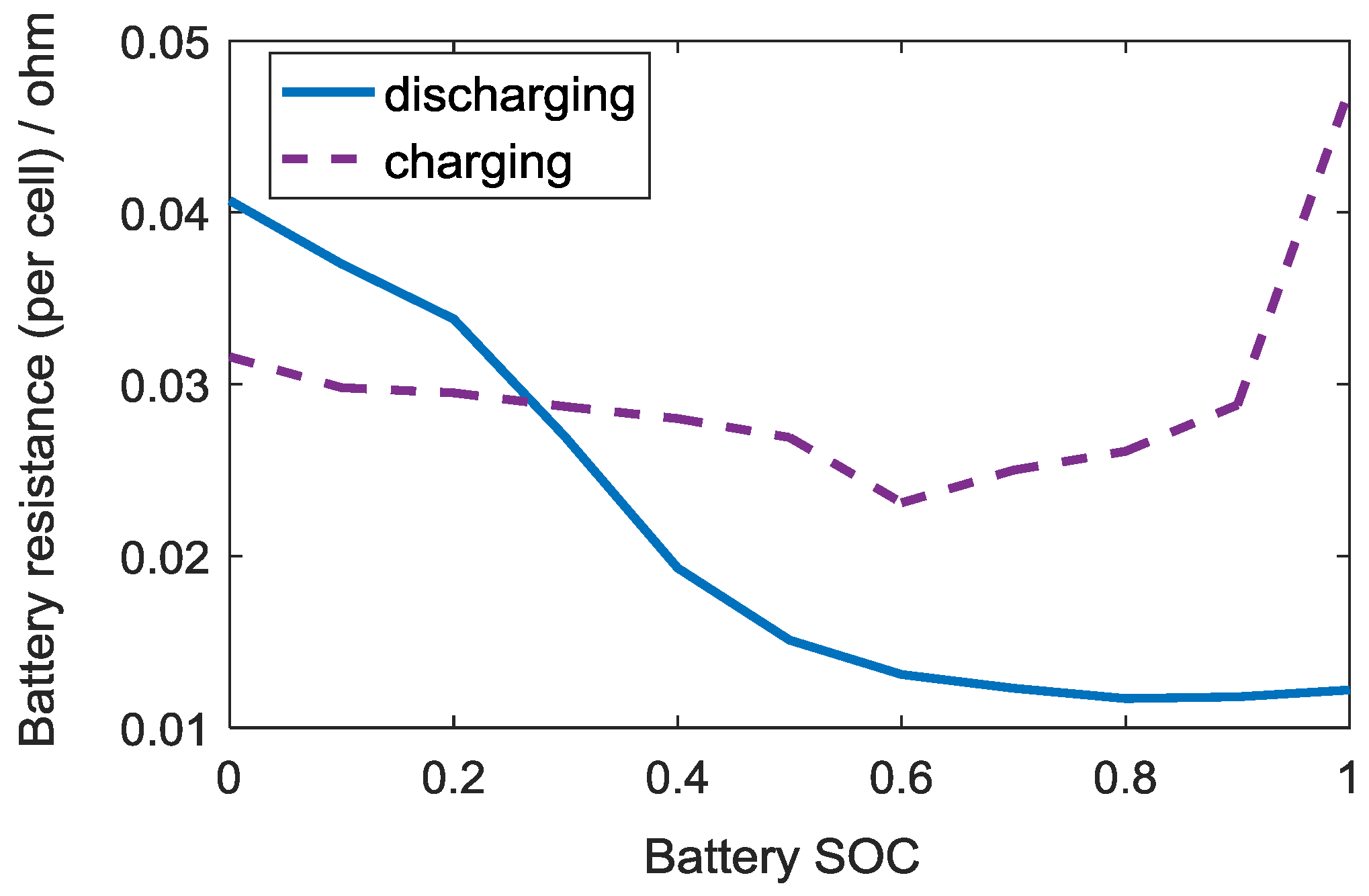
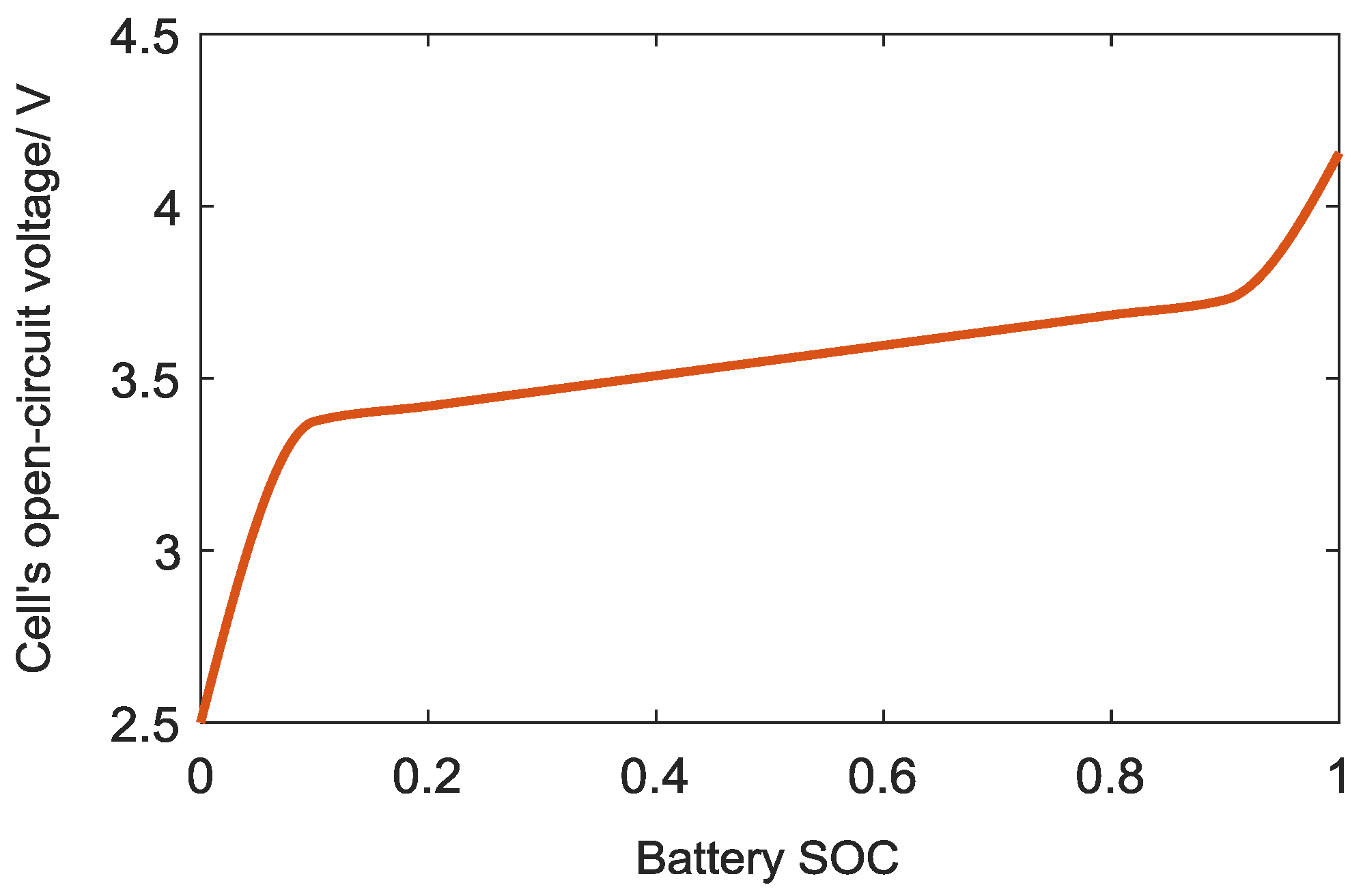
2.2. Battery Model
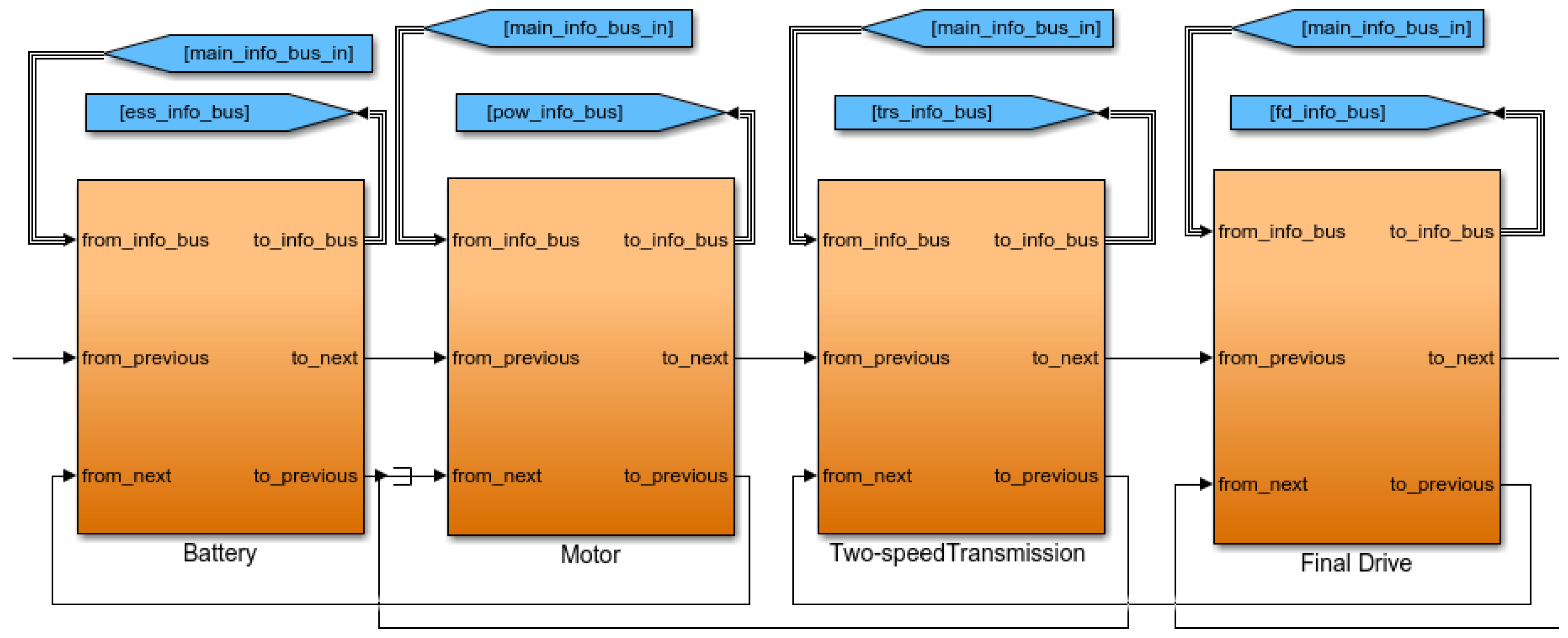
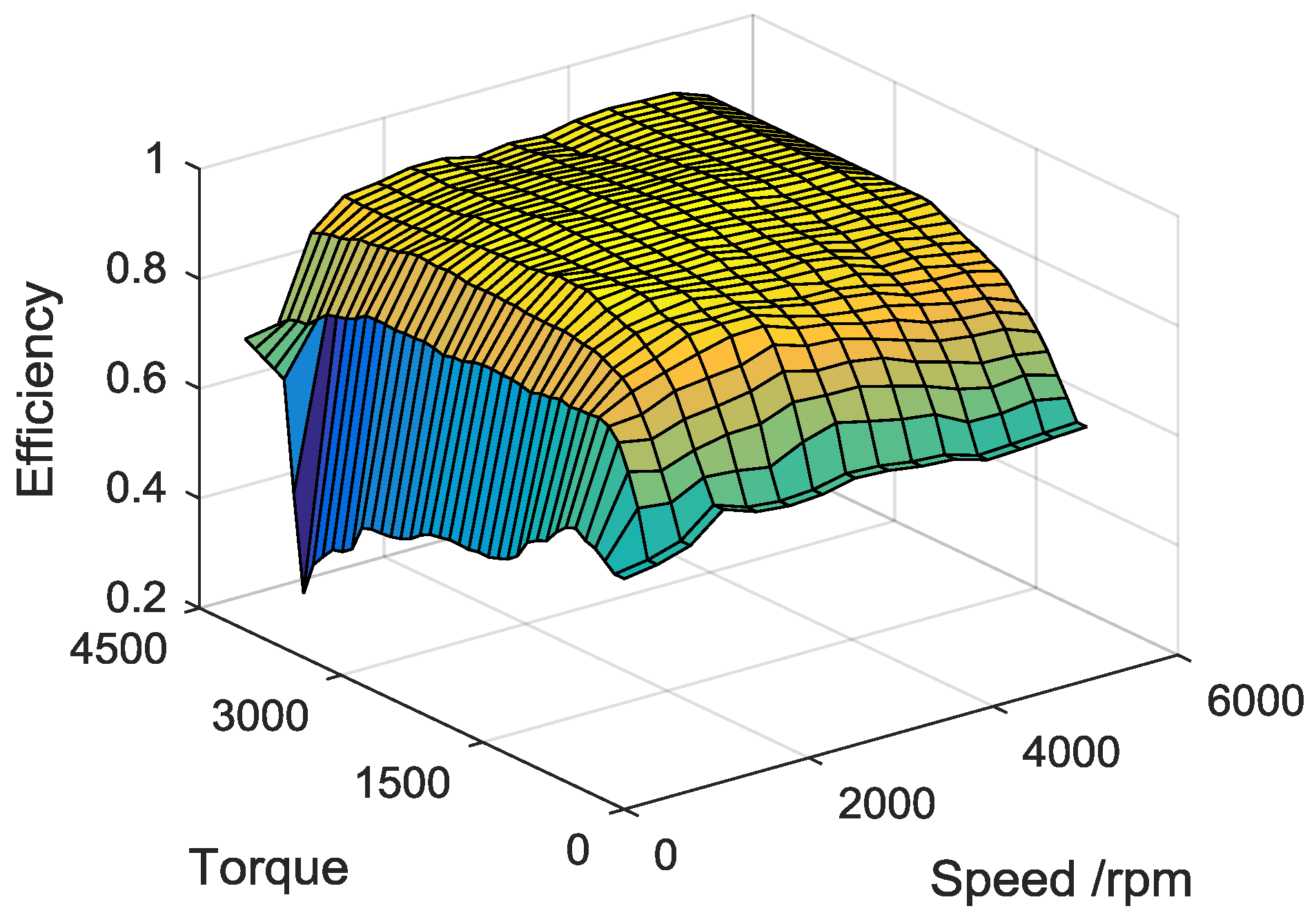
2.3. Powertrain System
3. Shift Schedule and Gear Ratio Optimization
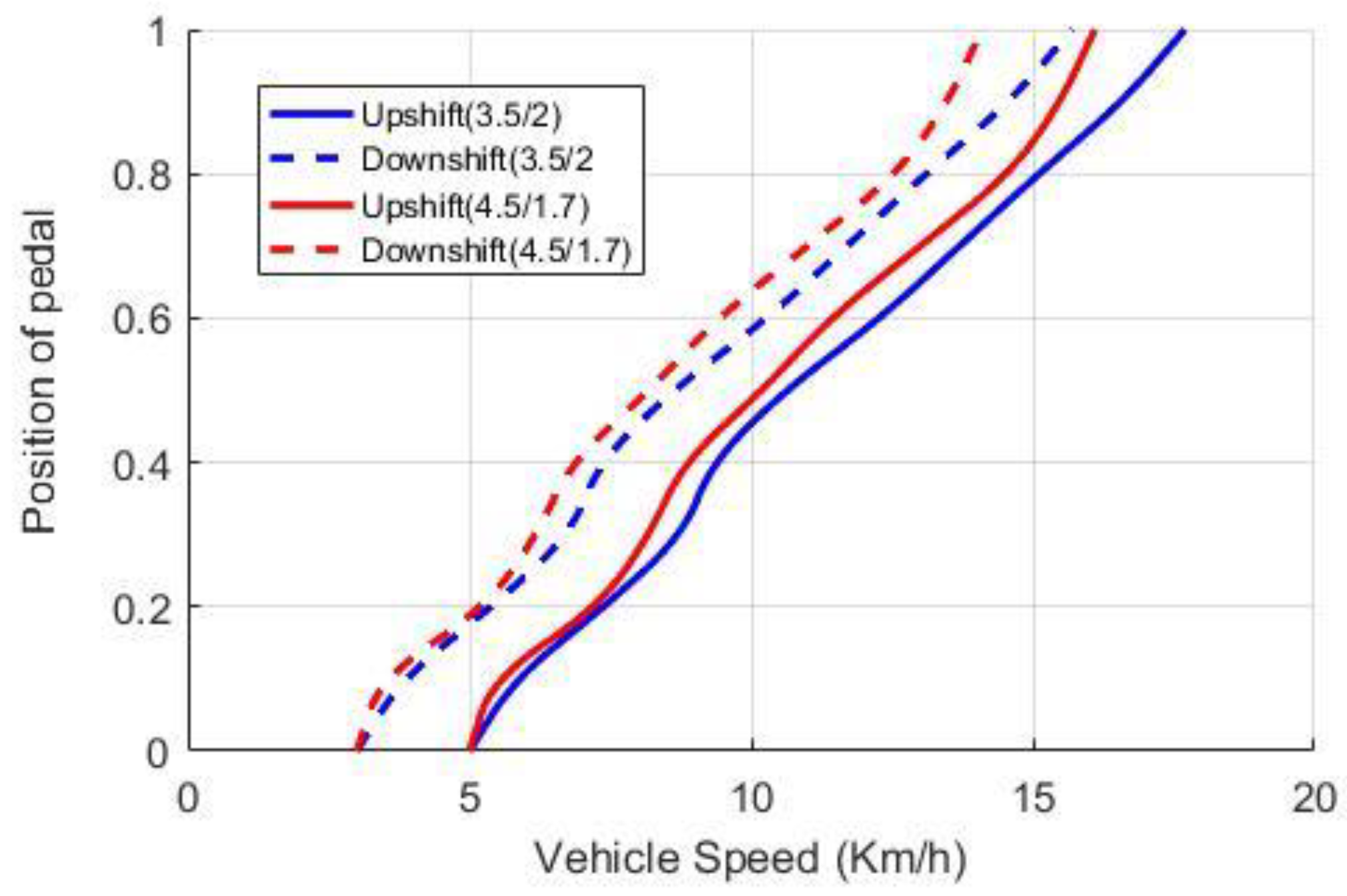
3.1. Shift Schedule
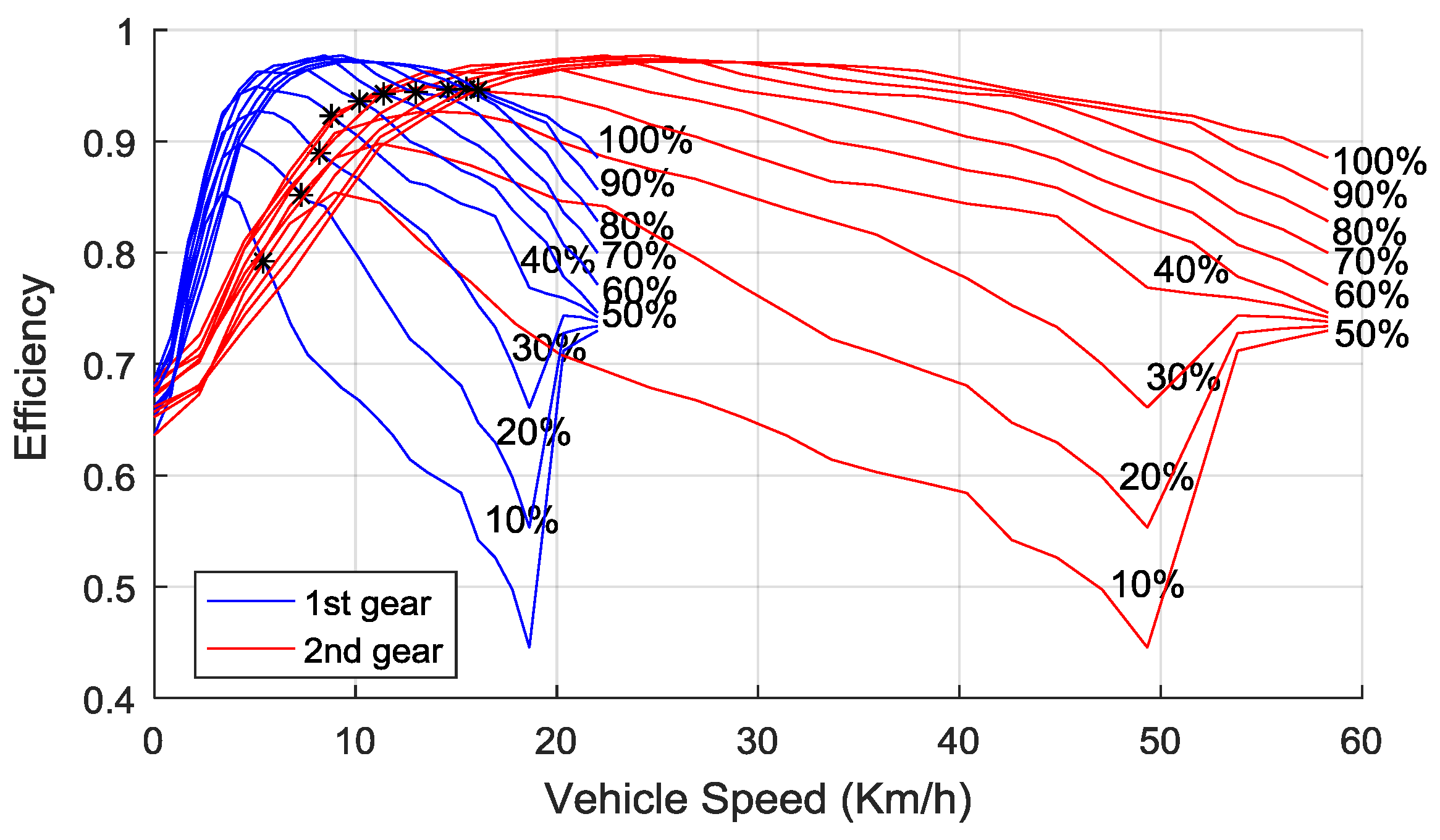
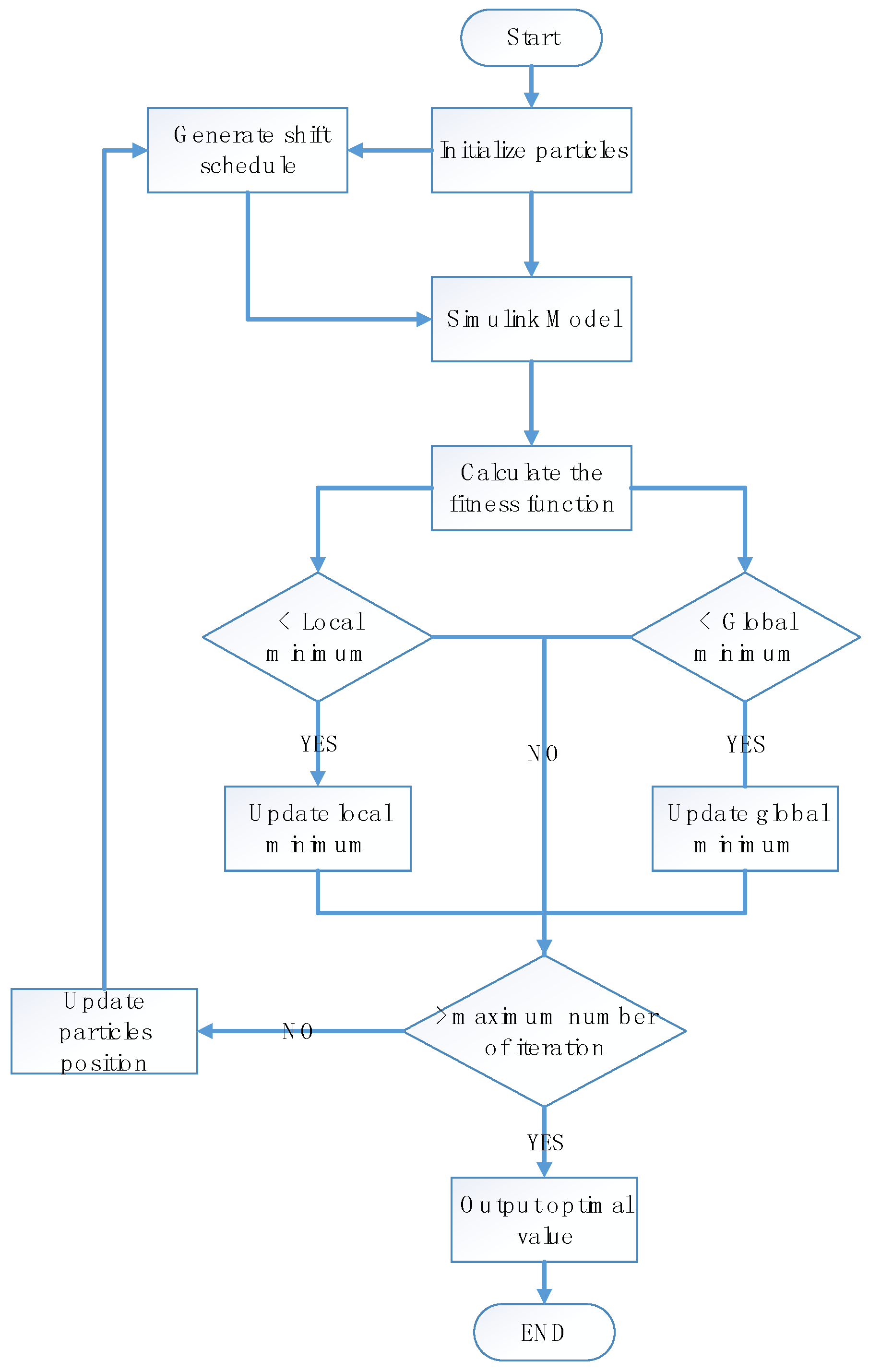
3.2. Gear Ratio Optimization
3.3. The Objective Function
3.4. Inequality Constraints
4. Simulation Results
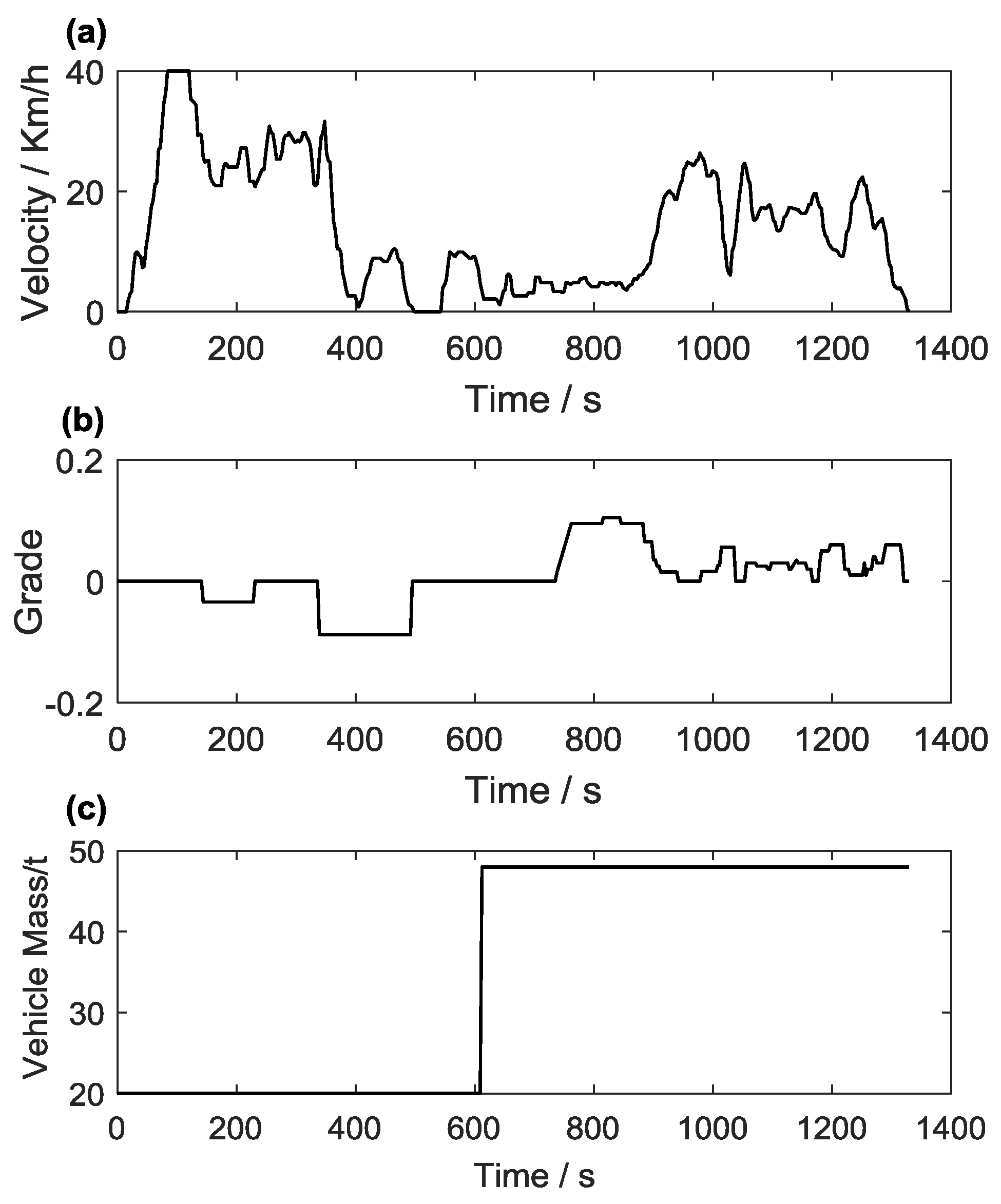
4.1. Driving Cycle Analysis
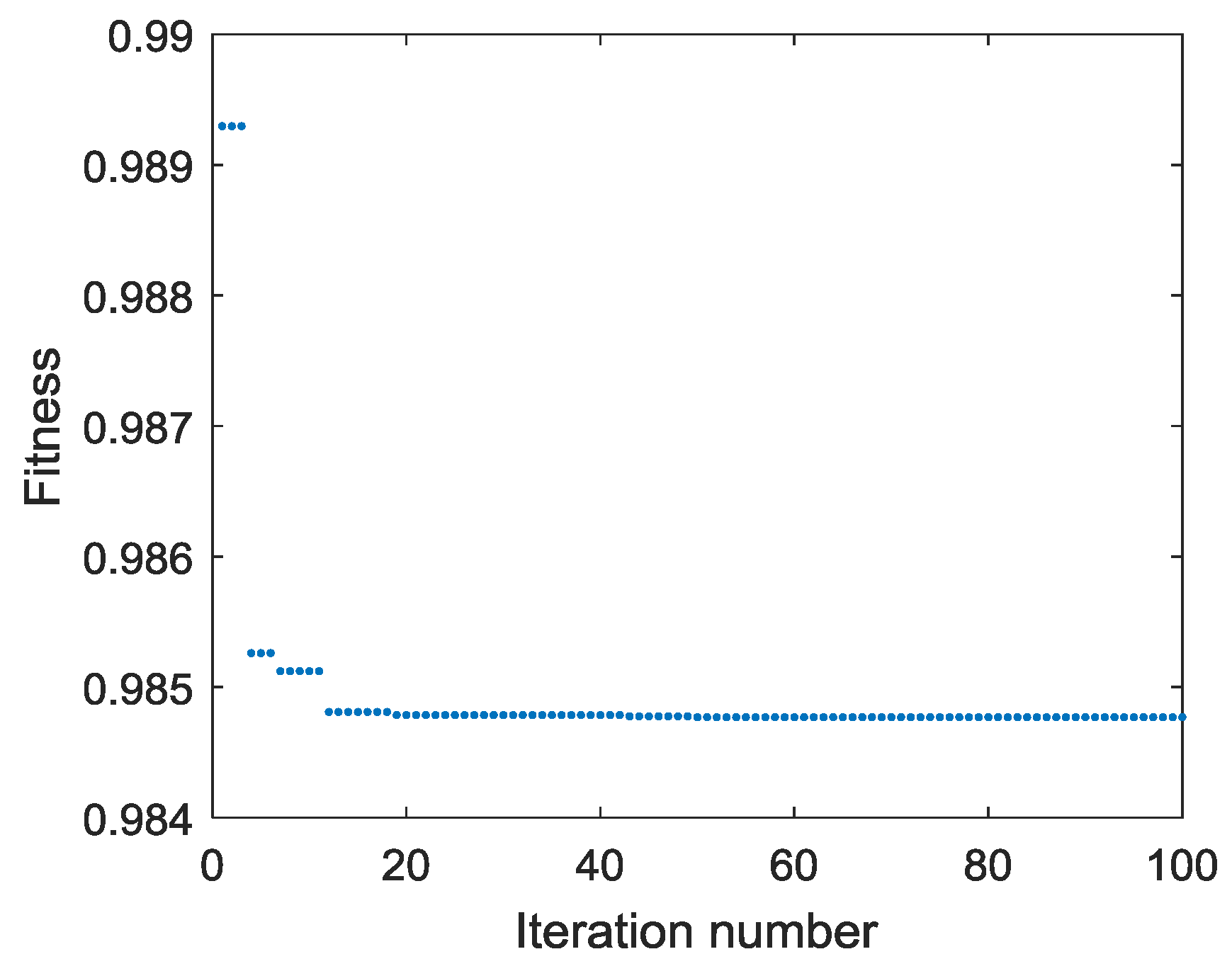
4.2. Optimization Results
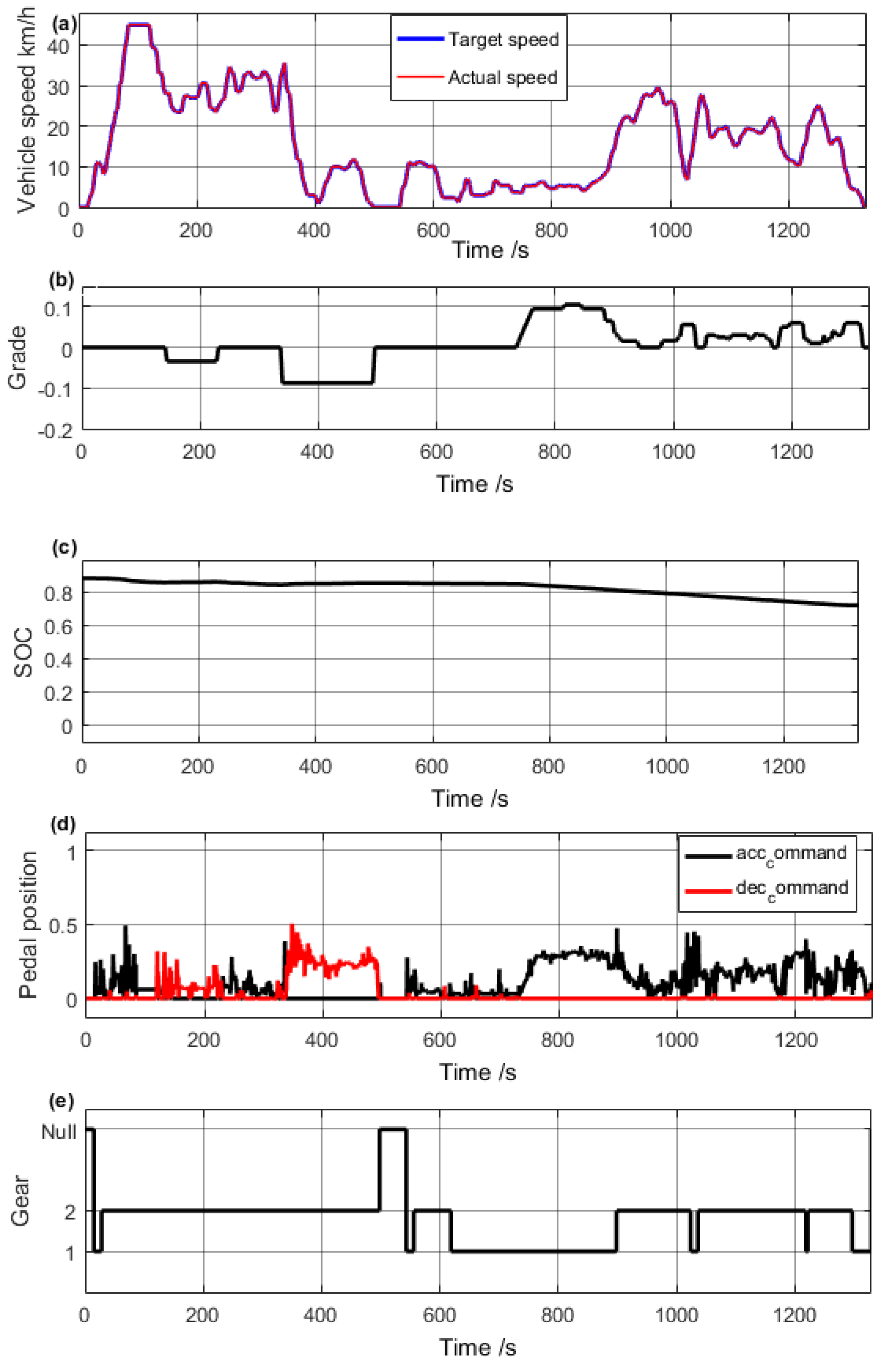
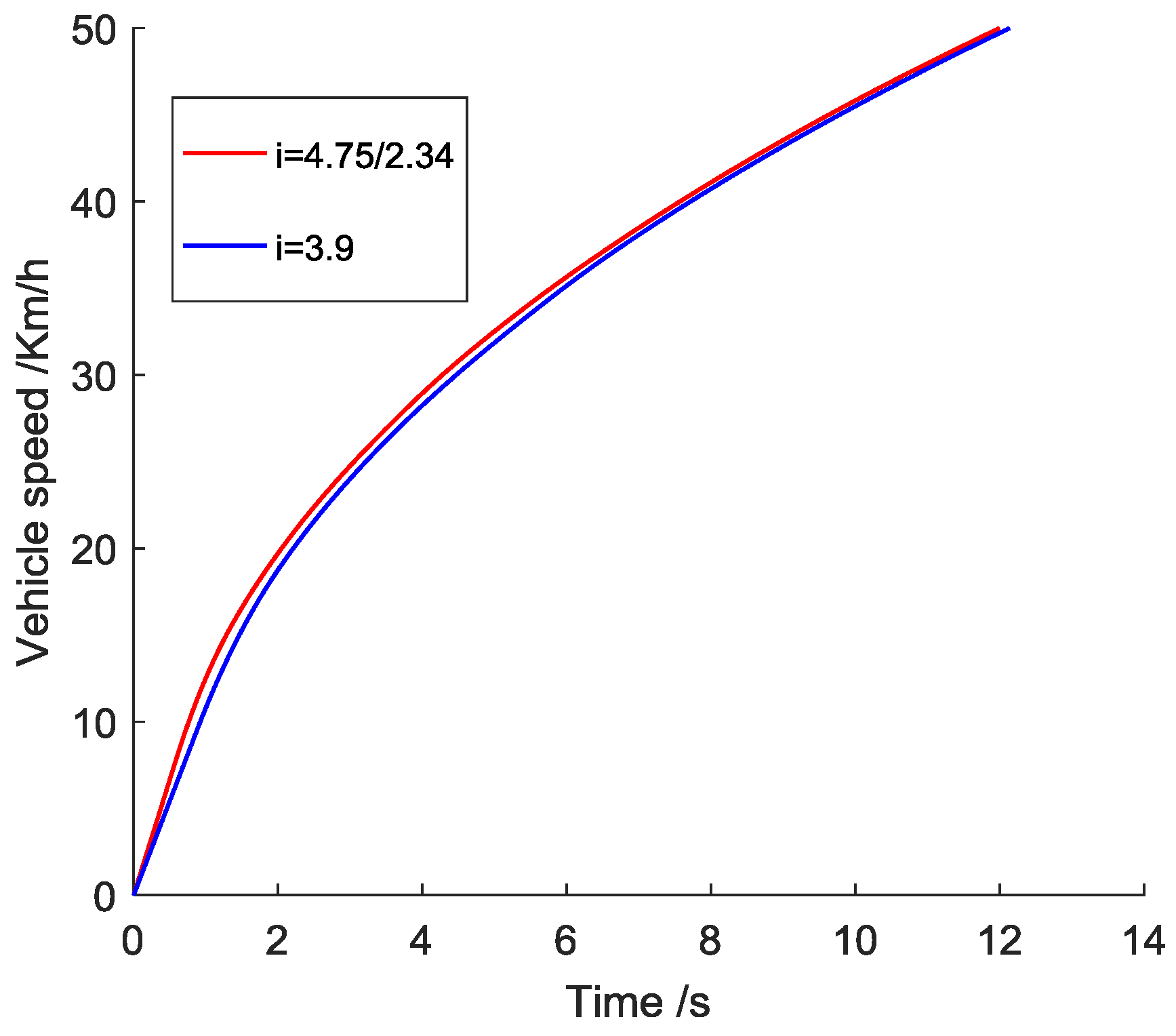
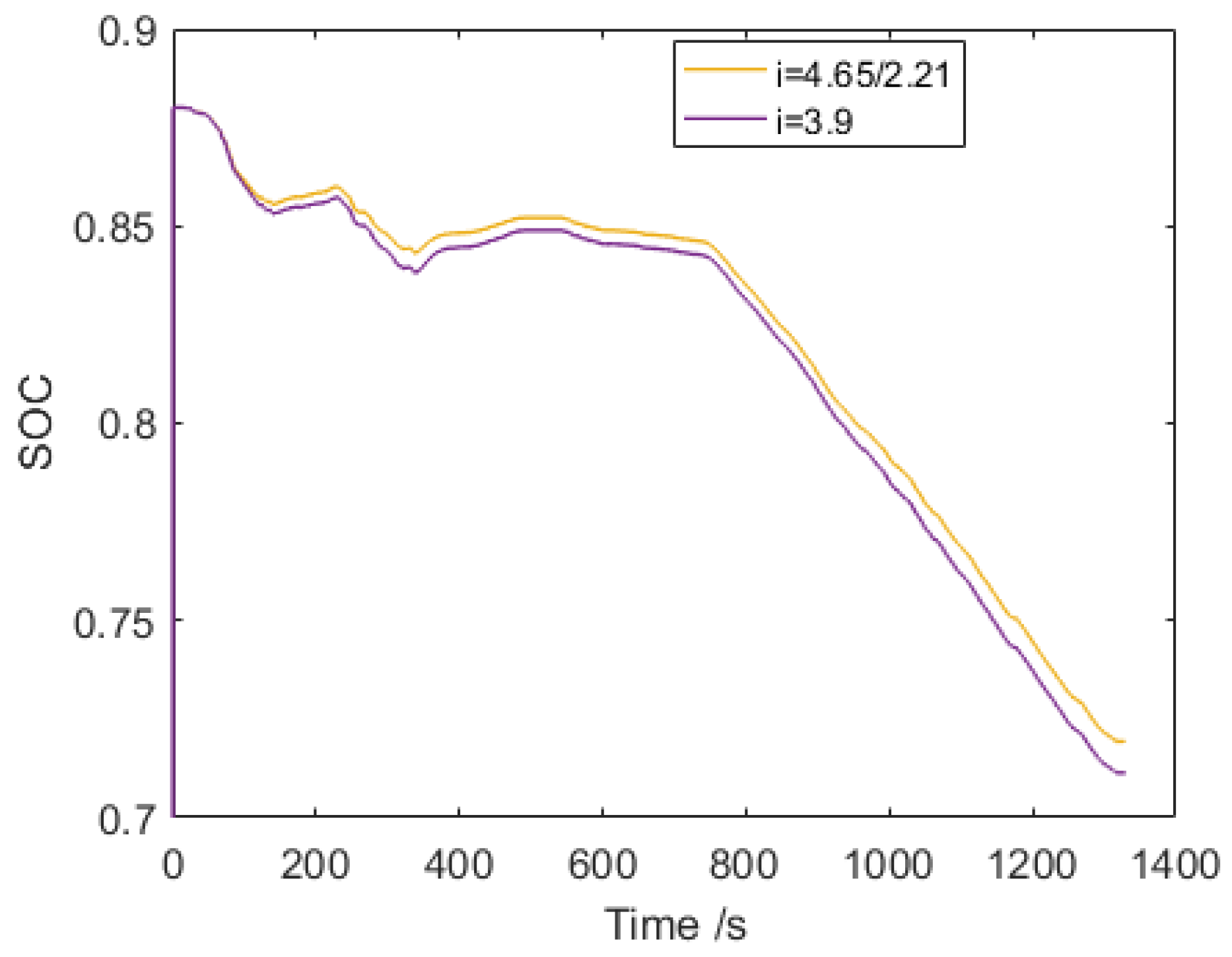
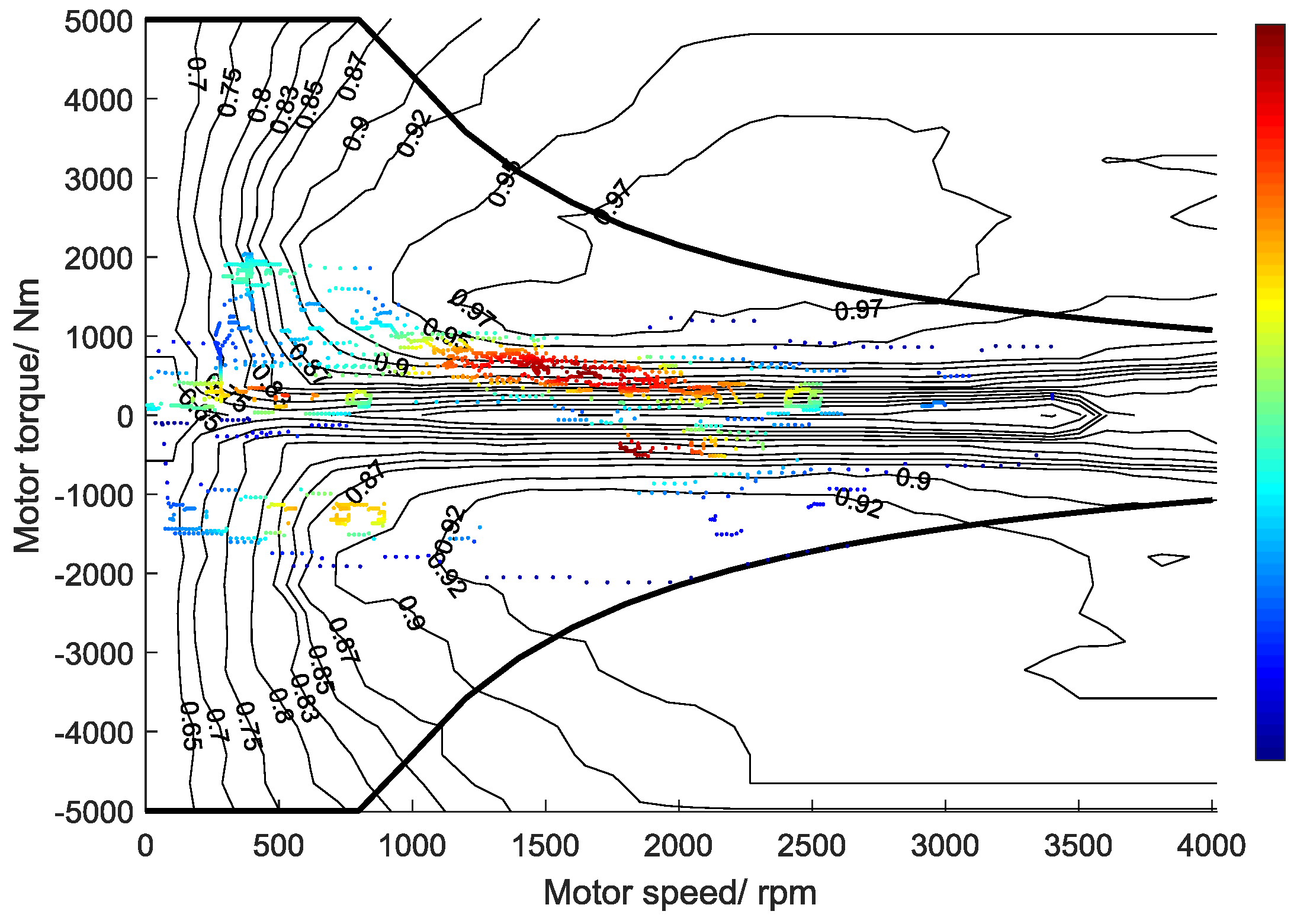
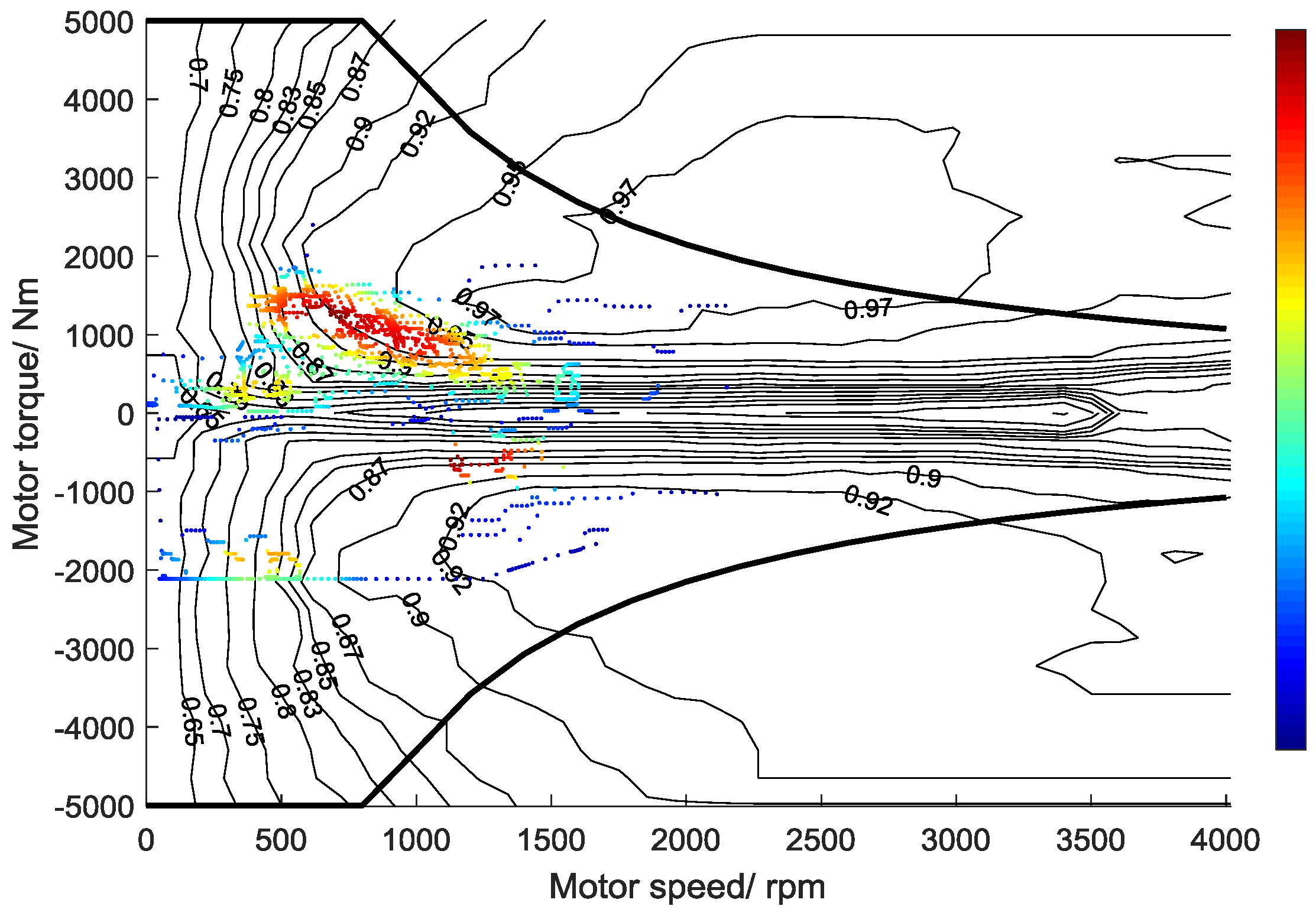
4.3. Performance Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mahmoudzadeh Andwari, A.; Pesiridis, A.; Rajoo, S.; Martinez-Botas, R.; Esfahanian, V. A review of Battery Electric Vehicle technology and readiness levels. Renew. Sustain. Energy Rev. 2017, 78, 414–430. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, X.; Dong, Z. Powertrain architectures of electrified vehicles: Review, classification and comparison. J. Frankl. Inst. 2015, 352, 425–448. [Google Scholar] [CrossRef]
- Ruan, J.; Walker, P.; Zhang, N. A comparative study energy consumption and costs of battery electric vehicle transmissions. Appl. Energy 2016, 165, 119–134. [Google Scholar] [CrossRef]
- Jayakumar, A.; Chalmers, A.; Lie, T.T. Review of prospects for adoption of fuel cell electric vehicles in New Zealand. IET Electr. Syst. Transp. 2017, 7, 259–266. [Google Scholar] [CrossRef]
- Sahoo, L.; Bandyopadhyay, S.; Banerjee, R. Energy Performance of Dump Trucks in Opencast Mine. In Proceedings of the 23th International Conference on Efficiency, Costs, Optimization, Simulation and Environmental Impact of Energy Systems ECOS 2010, Lausanne, Switzerland, 14–17 June 2010; pp. 1–8. [Google Scholar]
- Feng, Y.; Dong, Z.; Yang, J.; Cheng, R. Performance Modeling and Cost-benefit Analysis of Hybrid Electric Mining Trucks. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–6. [Google Scholar]
- Ballantyne, G.R.; Powell, M.S. Benchmarking comminution energy consumption for the processing of copper and gold ores. Miner. Eng. 2014, 65, 109–114. [Google Scholar] [CrossRef]
- Sahoo, L.K.; Bandyopadhyay, S.; Banerjee, R. Benchmarking energy consumption for dump trucks in mines. Appl. Energy 2014, 113, 1382–1396. [Google Scholar] [CrossRef]
- Oh, K.; Yun, S.; Ko, K.; Ha, S.; Kim, P.; Seo, J.; Yi, K. Gear ratio and shift schedule optimization of wheel loader transmission for performance and energy efficiency. Autom. Constr. 2016, 69, 89–101. [Google Scholar] [CrossRef]
- Yang, W.; Liang, J.; Yang, J.; Zhang, N. Investigation of a novel coaxial power-split hybrid powertrain for mining trucks. Energies 2018, 11, 172. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, H.; Xi, J.; Wang, J.; Fang, Z. Optimal speed synchronization control for clutchless AMT systems in electric vehicles with preview actions. In Proceedings of the American Control Conference (ACC), Portland, OR, USA, 4–6 June 2014; pp. 4611–4616. [Google Scholar] [CrossRef]
- Walker, P.; Zhu, B.; Zhang, N. Powertrain dynamics and control of a two speed dual clutch transmission for electric vehicles. Mech. Syst. Signal Process. 2017, 85, 1–15. [Google Scholar] [CrossRef]
- Roozegar, M.; Setiawan, Y.D.; Angeles, J. Design, modelling and estimation of a novel modular multi-speed transmission system for electric vehicles. Mechatronics 2017, 45, 119–129. [Google Scholar] [CrossRef]
- Sorniotti, A.; Holdstock, T.; Everitt, M.; Fracchia, M.; Viotto, F.; Cavallino, C.; Bertolotto, S. A novel clutchless multiple-speed transmission for electric axles. Int. J. Powertrains 2013, 2, 103–131. [Google Scholar] [CrossRef]
- Qin, D.; Wang, Y.; Hu, M. Powertrain parameter design for the electric vehicle considering driving cycle. J. Chongqing Univ. 2014, 37, 7–14. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, X.; Dong, Z. Impacts of Two-Speed Gearbox on Electric Vehicle’s Fuel Economy and Performance. SAE Tech. Pap. 2013, 2. [Google Scholar] [CrossRef]
- Sorniotti, A.; Subramanyan, S.; Turner, A.; Cavallino, C.; Viotto, F.; Bertolotto, S. Selection of the Optimal Gearbox Layout for an Electric Vehicle. SAE Int. J. Engines 2011, 4, 1267–1280. [Google Scholar] [CrossRef]
- Morozov, A.; Humphries, K.; Zou, T.; Martins, S.; Angeles, J. Design and optimization of a drivetrain with two-speed transmission for electric delivery step van. In Proceedings of the 2014 IEEE International Electric Vehicle Conference (IEVC), Florence, Italy, 17–19 December 2014. [Google Scholar] [CrossRef]
- Gao, B.; Liang, Q.; Xiang, Y.; Guo, L.; Chen, H. Gear ratio optimization and shift control of 2-speed I-AMT in electric vehicle. Mech. Syst. Signal Process. 2015, 50–51, 615–631. [Google Scholar] [CrossRef]
- Inalpolat, M.; Kahraman, A. Dynamic modelling of planetary gears of automatic transmissions. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2008, 222, 229–242. [Google Scholar] [CrossRef]
- Jiao, W.; Yang, J.; Ma, F.; Zhang, W. Equal strength optimal design of planetary gear transmission. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2015, 46, 1–7. [Google Scholar]
- Wei, X.L.; Wang, G.Q.; Feng, S.L. Aerodynamic characteristics about mining dump truck and the improvement of head shape. J. Hydrodyn. 2008, 20, 713–718. [Google Scholar] [CrossRef]
- Kahraman, A. Planetary gear train dynamics. J. Mech. Des. 1994, 11, 713–720. [Google Scholar] [CrossRef]
- Greenwood, D.T. Principles of Dynamics; Prentice Hall: Upper Saddle River, NJ, USA, 1965. [Google Scholar]
- Johnson, V. Battery performance models in ADVISOR. J. Power Sources 2002, 110, 321–329. [Google Scholar] [CrossRef]
- Szumanowski, A.; Yuhua, C. Battery management system based on battery nonlinear dynamics modeling. IEEE Trans. Veh. Technol. 2008, 57, 1425–1432. [Google Scholar] [CrossRef]
- Tsang, K.M.; Sun, L.; Chan, W.L. Identification and modelling of Lithium ion battery. Energy Convers. Manag. 2010, 51, 2857–2862. [Google Scholar] [CrossRef]
- Chen, T.Y.; Chi, T.M. On the improvements of the particle swarm optimization algorithm. Adv. Eng. Softw. 2010, 41, 229–239. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal power flow using particle swarm optimization. Int. J. Electr. Power Energy Syst. 2002, 24, 563–571. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value |
|---|---|---|
| Vehicle mass | 20,000 kg | |
| Load mass | 28,000 kg | |
| Full load mass | m | 48,000 kg |
| Wheel radius | r | 0.74 m |
| Maximum speed | 60 km/h | |
| Maximum ascendable grade | G | 40% |
| Coefficient of rolling resistance | 0.017 | |
| Coefficient of air resistance | 0.8 | |
| Main reducer ratio | 7.3 | |
| Face area | 5 m2 | |
| Battery capacity | 220 Ah | |
| Maximum motor speed | 4000 rpm | |
| Maximum motor torque | 5000 Nm |
| Gear | B1 | B2 |
|---|---|---|
| 1st gear | engaged | disengaged |
| 2nd gear | disengaged | engaged |
| Null | disengaged | disengaged |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, S.; Yang, J.; Zhao, X.; Hai, T.; Zhang, W. Gear Ratio Optimization of a Multi-Speed Transmission for Electric Dump Truck Operating on the Structure Route. Energies 2018, 11, 1324. https://doi.org/10.3390/en11061324
Tan S, Yang J, Zhao X, Hai T, Zhang W. Gear Ratio Optimization of a Multi-Speed Transmission for Electric Dump Truck Operating on the Structure Route. Energies. 2018; 11(6):1324. https://doi.org/10.3390/en11061324
Chicago/Turabian StyleTan, Senqi, Jue Yang, Xinxin Zhao, Tingting Hai, and Wenming Zhang. 2018. "Gear Ratio Optimization of a Multi-Speed Transmission for Electric Dump Truck Operating on the Structure Route" Energies 11, no. 6: 1324. https://doi.org/10.3390/en11061324
APA StyleTan, S., Yang, J., Zhao, X., Hai, T., & Zhang, W. (2018). Gear Ratio Optimization of a Multi-Speed Transmission for Electric Dump Truck Operating on the Structure Route. Energies, 11(6), 1324. https://doi.org/10.3390/en11061324





