Short-Term Forecasting of the Output Power of a Building-Integrated Photovoltaic System Using a Metaheuristic Approach

Abstract

The rapidly increasing use of renewable energy resources in power generation systems in recent years has accentuated the need to find an optimum and efficient scheme for forecasting meteorological parameters, such as solar radiation, temperature, wind speed, and sun exposure. Integrating wind power prediction systems into electrical grids has witnessed a powerful economic impact, along with the supply and demand balance of the power generation scheme. Academic interest in formulating accurate forecasting models of the energy yields of solar energy systems has significantly increased around the world. This significant rise has contributed to the increase in the share of solar power, which is evident from the power grids set up in Germany (5 GW) and Bavaria. The Spanish government has also taken initiative measures to develop the use of renewable energy, by providing incentives for the accurate day-ahead forecasting. Forecasting solar power outputs aids the critical components of the energy market, such as the management, scheduling, and decision making related to the distribution of the generated power. In the current study, a mathematical forecasting model, optimized using differential evolution and the particle swarm optimization (DEPSO) technique utilized for the short-term photovoltaic (PV) power output forecasting of the PV system located at Deakin University (Victoria, Australia), is proposed. A hybrid self-energized datalogging system is utilized in this setup to monitor the PV data along with the local environmental parameters used in the proposed forecasting model. A comparison study is carried out evaluating the standard particle swarm optimization (PSO) and differential evolution (DE), with the proposed DEPSO under three different time horizons (1-h, 2-h, and 4-h). Results of the 1-h time horizon shows that the root mean square error (RMSE), mean relative error (MRE), mean absolute error (MAE), mean bias error (MBE), weekly mean error (WME), and variance of the prediction errors (VAR) of the DEPSO based forecasting is 4.4%, 3.1%, 0.03, −1.63, 0.16, and 0.01, respectively. Results demonstrate that the proposed DEPSO approach is more efficient and accurate compared with the PSO and DE.

1. Introduction

Climate change, depletion of energy resources, increasing price and uncertainty about the availability of fossil fuels have invigorated the use of green or renewable resources in recent years. Primarily, interest in solar energy is more significant than those in other renewable resources as it is ubiquitous and freely available everywhere [1]. Despite the excessive energy demand worldwide, usage of fossil fuel resources for energy generation has become uncommon considering the environmental impact in terms of sustainable power generation. Global concern regarding the environmental impact of the usage of fossil fuels has also grown due to the factors associated with carbon emission [2]. The significance of the efficiency and conservation of energy has become the primary focus for many studies conducted worldwide. Effective and efficient habits for an energy-efficient lifestyle can be adopted by analyzing and reviewing the variations in global energy consumption patterns [3].

Meanwhile, the increase in population and the rapid depletion of fossil fuel reserves have created continued interest among researchers in various fields, such as engineering, hydrology, and meteorology, to design and develop power generation techniques using renewable resources like solar and wind energy [4,5]. Using renewable energy resources reduces the need for fossil fuels, thereby reducing carbon emission into the atmosphere. Moreover, renewable energy resources are available for free and can be harnessed efficiently through passive and active designs [6]. For example, solar-based renewable solutions have witnessed significant growth in their application after the introduction of various photovoltaic systems because solar energy is more abundant in comparison with any other renewable resources. Considering the random nature of solar radiation and the high cost of energy storage devices, forecasting the next-day outputs of the power generation systems is essential for decreasing the capital and operational costs of solar power generation systems.

However, the output of photovoltaic (PV) systems is dependent on meteorological parameters, such as solar irradiance and temperature, which are stochastic and unpredictable. Therefore, PV generation has become an unreliable source for power generation and may cause power imbalance and instability in the system. Few unique storage schemes are incorporated into the system to stabilize this problem. However, the inclusion of a storage system increases its capital cost, which is a major disadvantage. The ideal solution to dynamically control the operation of a power system is to accurately forecast the PV output generation power based on the random weather data. A sophisticated and reliable forecasting method in an energy management system not only minimizes the uncertainties of generated power but also enhances the power quality, reliability, and stability of a system. Owing to the exponential rise in the use of solar energy, efforts for the integration of a PV system into the power grid and the development of reliable forecasting techniques have considerably increased.

Currently, accuracy and complexity are the main problems associated with PV power forecasting systems. Hence, in this paper, we propose a mathematical forecasting model that uses the differential evolution and particle swarm optimization (DEPSO) technique addressing these issues [7]. This model is a combination of the differential evolution (DE) and particle swarm optimization (PSO) methods used for the short-term output power forecasting of a PV system. The proposed model is tranined and evaluated experimentally using the data obtained from the PV system located at Deakin University (Victoria, Australia) equipped with a self-energized data logger. The proposed technique offers an accurate and straightforward approach for forecasting the power output of a PV system on a system scale. The rest of the paper is organized as follows: Section 2 gives an overview of the existing literature; Section 3.1.1 and Section 3.1.2 present a brief overview of the DE and PSO, respectively; Section 3.1.3 describes the proposed hybrid algorithm of the DEPSO technique; Section 3.2 presents PV power forecasting and the proposed DEPSO technique; Section 3.3 and Section 3.4 explain the procedural steps for collecting information from the weather station and the PV system installed at Deakin University and the forecasting model used; Section 4 includes the empirical results of the proposed strategy; and Section 5 presents the conclusions of this study.

2. Related Works

The techniques used for forecasting the output power of a PV system remain inferior to those used in wind power generation systems in terms of robustness and reliability. The methods for forecasting PV systems are classified into two, namely, direct and indirect approaches. In the indirect methods, the environmental parameters like solar irradiance and temperature are first predicted by using historical data [8]. Then, the output power is calculated using relevant mathematical models. The main drawback of this method is the correlation between the meteorological data and the PV output power. Therefore, the forecasted meteorological data are merely converted into the relevant PV power output through the predefined mathematical models. However, other influential parameters, such as partial shading conditions, tilt angle, panel direction, meteorological factors, and inevitable power loss with converters and other axillary circuits of PV system, are disregarded in this approach. These parameters significantly affect the output power of a PV system and are thus indispensable when these type of forecasting approaches are used for the estimation of the power outputs. For this reason, the forecasting of the associated parameters is more stochastic and random.

An intelligent approach to estimate the PV power output using multiple meteorological data in order to solve the problem with the indirect method is another alternative [9]. However, this approach results in a complicated forecasting system. In addition, the substantial inaccuracy, which is associated with the indirect method, remains in the system to a certain degree. Considering all these factors, determining the exact relationship between output power and meteorological data is not feasible. In contrast, the direct approach presented in [10,11,12] and considered in this paper, forecasts the generated power using historical data for PV output and weather parameters. Therefore, addressing the issues of the direct forecasting results in an accurate and robust solution.

Numerous artificial intelligence (AI) based approaches has been investigated addressing the forecasting and power point tracking problem of the PV generation systems [13]. Out of the different AI approaches, the artificial neural network (ANN)-based forecasting systems have garnered great interest among researchers due to the high accuracy and performance of the ANN [14]. However, the ANN has high user dependency as the user identifies the parameters. The backpropagation (BP) neural network method is the most popular among the ANN-based methods used for the forecasting problem [10]. However, the BP-ANN method suffers from many issues, such as local optimum tracking, slow convergence speed, high computation cost and the unclear correlation between the input and output of the system [9].

The support vector machine (SVM) and wavelet analysis have also been used in solar forecasting systems [15]. These tools are extensively used in hybrid forecasting systems due to their capability of classifying problems and processing smooth and vividly changing signals. For instance, a two-stage forecasting system with the support vector regression (SVR) used for training and fuzzy logic approaches used in forecasting stages is highlighted in the work of C.M. Huang, Y.C. Huang and K.Y. Huang [16]. In [17], the SVM method was combined with other regression techniques in order to enhance the performance of solar power forecasting systems. A wavelet transformation (WT) method was used for the decomposition of the PV time series data using the ANN method [18]. In Macau and Shanghai (China), a novel method called diagonal recurrent wavelet neural network (DRWNN) was used for the hourly and daily forecasts of PV systems [19]. The hybrid methods were designed to enhance the forecasting system’s accuracy. However, the compound model structure and high computational cost of most hybrid methods, especially those combined with the WT technique, further emphasize the need for a robust forecasting method with less complexity and computational requirements.

To date, robust solar forecasting systems that provide information on the management and scheduling of power plants and appropriate decision making of energy consumption practices remain evasive [20]. Extensive reviews of various forecasting techniques are discussed in [21,22,23] highlighting the problems in solar forecasting caused due to the nonlinear pattern of solar irradiance caused by the complex and chaotic effect of cloud motion. In the short-term forecasting of PV power output, satellite data were analyzed to predict a temporal range of certain hour accuracy [24]. Meanwhile, the forecast must be two days ahead. Mesoscale methods, such as the numerical weather prediction (NWP) model with MM5 [25], weather research and forecasting (WRF) [26], and eta coordinate system to overcome the problem in calculating the force of the pressure gradient using sigma vertical coordinate, have been used for the numerical prediction of the changes in irradiance [27]. Then, data on the irradiance and other weather parameters are used to forecast the output power through the evaluation of the predicted changes [28]. In this work, a different approach is presented, which uses the ETA model built with multiple neural network approaches for environmental prediction, such as solar radiation forecast [21]. Similar to this, forecasting algorithms using NWP [11,29], PSO-ANN integrated NWP [30] for forecasting weather parameters is considered.

A solar radiation forecasting model was formulated by using information from the U.S. National Forecast Database [31]. The influence of aerosols on the forecasting of PV systems has also been investigated [32]. Different ANN based techniques [10,33], traditional evolutionary algorithms [34], support vector models [16], and few hybrid AI models [18,30,35] are used for forecasting the output power as illustrated in the comparison study listed below. In addition, the use of evolutionary algorithms like genetic algorithm (GA), DE, and PSO for addressing the optimization of forecasting is investigated [30]. In most of the solar power forecasting algorithms highlighted in the literature, the historical weather data used to train the system were obtained from a weather station situated far away from the actual PV system being studied. This is a major drawback considering places like Melbourne, where the experimental analysis of this proposed algorithm has been carried out. Thus, in the proposed system, we use a local weather station in order to reduce the inaccuracies of the forecasting algorithm.

This paper proposes a metaheuristic approach of forecasting solar output power in relation to the weather parameters (e.g., solar radiance and temperature), using a hybrid DEPSO approach. The key parameters for evaluating the proposed algorithm were identified by this initial study made on various forecasting approaches. This study mainly helped in determining the evaluation creations of the proposed approach, which included the root mean square error (RMSE), mean relative error (MRE), mean bias error (MBE), mean absolute error (MAE), variance error (VAR) and weekly mean error (WME). Other key components, such as time horizon and length of training dataset, were obtained from this study and highlighted in Table 1 above. From these inferences, the horizons of 1 h, 2 h, and 4 h were selected to be experimentally evaluated from a dataset of 1 year which is highlighted in Section 4.

Table 1. Overview of different forecasting algorithms.

Ref.	Year of Publication	Method Used	Location	Error Evaluated	Horizon	Training Data
[10]	2011	RBF	Online	MAPE, MAE, RMSE	24 h	1 year
[11]	2016	NWP	California, USA	MAE, MBE, RMSE	1 h, 3 h	18 months
[12]	2017	MLR, RT, SVM, NN	New South Wales, Australia	RMSE	2 h	3 years
[15]	2012	SVM	China	RMSE, MRE	15 m	~1 year
[16]	2014	SVR	Taiwan	MRE, RMSE	1 h	1 year
[18]	2012	BPNN, RBFNN, WT + BPNN, WT + RBFNN	Ashland, Oregon	MAPE, MAE, RMSE	1 h	30 days
[29]	2013	NWP	Ontario, Canada	RMSE, MBE, MAE	48 h	1 year
[30]	2017	PSO-ANN, NWP	Beijing, China	MAPE, RMSE, SDE	1 h	1 year
[33]	2014	ANN	Italy	SD, NRMSE, NMAE, NMBE, MSE	1 h	1 year
[34]	2010	GA, PSO, DE, ARIMA, NN, AWINN,	Canada	WME, VAR	1 day	4 weeks
[35]	2012	ARIMA, kNN, ANN, GA/ANN	Merced, California, USA	MAE, MBE, RMSE	1 h, 2 h	~2 years

3. Materials and Methods

3.1. Proposed Hybrid DEPSO Forecasting Method

3.1.1. Overview of the DE Algorithm

Theory

The process of finding the best-suited solution of a problem within a given constraint is called optimization. Storn and Price [36] proposed a particle-based global optimization algorithm called the differential evolution (DE). DE is a direct search approach for nonlinear and non-differentiable objectives and has many similarities with the genetic algorithm. DE is a population based stochastic meta-heuristic global optimization algorithm used in continuous domain. The DE is one of the most powerful optimization algorithms among various population-based optimizers due to its stochastic and relatively simple approach. The implication of the DE algorithm when it addresses optimization issues is through the creation of a new candidate solution using different mathematical blueprints. Given that the total size of the population remains constant, the replacement of an existing solution with a new one in the search space depends on the best fitness history of the individual. Then, based on the history of the best fitness of each individual, the optimization algorithm decides whether to replace the new solution over a weaker one in the search space. The method is applicable for problems involving several local optima [37]. DE is efficient, simple, fast, and robust. It is also inherently parallel in nature. The mutation scaling factor (F), crossover constant (CR), and dimension of the search space (D) are considered as the input/control parameters that require minimal tuning, and the number of candidate solutions/population size (NP) is one other parameter that determines the performance of the optimizer.

DE is mainly used for the minimization of non-continuous, nonlinear, and nondifferential space functions, along with noisy, flat, multidimensional, time-dependent objective functions and constraint optimization issues. Figure 1 indicates the operational flow of the DE algorithm, which mainly consists of three main operation sections, namely, mutation, crossover, and selection.

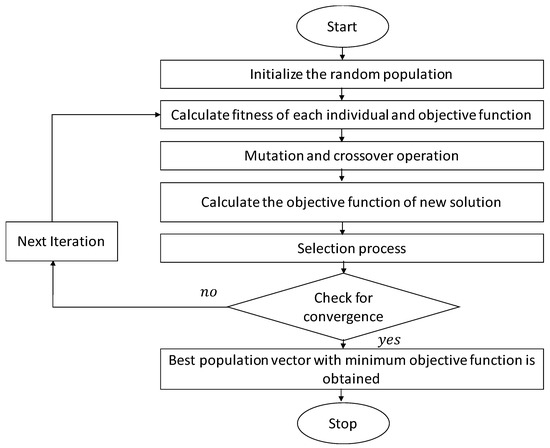
Figure 1. Flowchart of the DE algorithm.

Initialization

DE searches for an optimum global point in the search space and begins to randomly initialize the population NP. The initial locations of the particles in the search space are assigned to the target vector also known as “genome/chromosome”, thus forming the candidate solution to the multidimensional optimization problem. The initial vectors of the candidate solution are selected randomly in order to optimize the search process by benefiting from the stochastic nature of this method [38]. Each candidate’s solutions are likely to be changed in each generation, and so we represent the i-th particle in the G-th iteration or generation as illustrated in Equation (1):

$$\begin{gathered} \overrightarrow{X_{i,G}}=\left[x_{1,i,G},x_{2,i,G},x_{3,i,G}, \dots \dots \dots , x_{D,i,G}\right], \mathrm{where} \\ {x}_{j,i}=x_{j,min}+rn{d}_{i,j}\left[0,1\right]·\left(x_{j,max}-x_{j,min}\right). \end{gathered}$$

(1)

Each parameter of the candidate solution is restricted within a range as specified below, f(Xi). $G=0,1,\dots .G_{max}$, $\overrightarrow{X_{min}}=\left\{ X_{1,min},X_{2,min},X_{3,min}, \dots \dots , X_{D,min}\right\}$ and $\overrightarrow{X_{max}}=\{ X_{1,max},X_{2,max},X_{3,max},$ $\dots \dots , X_{D,max}\}$. The initial population covers the search space with uniformly random individuals constrained with the abovementioned restrictions, thus forming the candidate solution distributed randomly as illustrated in Figure 2.

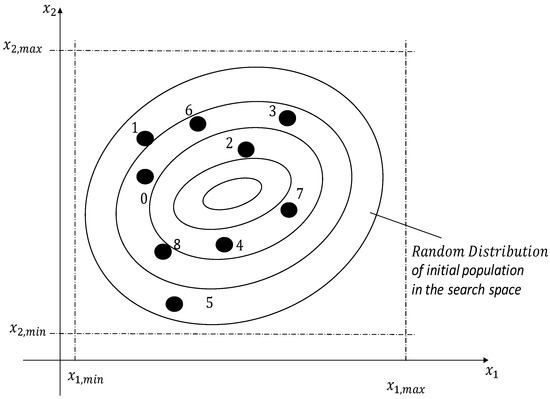
Figure 2. Random distribution of initial population in the search space of the DE algorithm.

Mutation

After initialization, a change or a perturbation occurs with a random element. The DE consists of a parent vector from the current generation (i.e., the target vector), a mutant vector obtained from the differential mutation process (i.e., the donor vector), and the resultant offspring vector obtained from the recombination of the target and mutant vector, which is called the trial vector. In general, the donor vector $\overrightarrow{V_{i,G}}$ of the DE algorithm can be expressed in Equation (2) where F is a mutation control parameter with its value between 0 and 2 and $r_1$, $r_2$ and $r_3$ are randomly chosen numbers within the population size:

$$\overrightarrow{V_{i,G}}=\overrightarrow{ X_{{\mathrm{r}}_1,G}}+F·\left(\overrightarrow{ X_{{\mathrm{r}}_2,G}}-\overrightarrow{ X_{{\mathrm{r}}_3,G}}\right).$$

(2)

Crossover

After generating the mutation vectors, they are combined with the target vectors through a non-uniform crossover operation for the formation of trial vectors. Equation (3) shows the crossover operation and illustrates the successful combinations that enable the optimization algorithm to recommend improved solutions of the optimized search process:

$$\overrightarrow{U_{i,G}}=\{\begin{array}{c}\overrightarrow{v_{i,G} } if\left(rn{d}_j\le CR\right) \mathrm{or} j=r{n}_i\\ \overrightarrow{x_{i,G}} if\left(rn{d}_j>CR\right) \mathrm{or} j\ne r{n}_i\end{array},$$

(3)

where $rn{d}_j$ is a random number within the range [0, 1], and $r{n}_i$ is a random number from the domain $j ϵ \left\{1, 2,\dots , \mathrm{D}\right\}$, in which D denotes the maximum dimension of the search space.

The DE algorithm is rotationally invariant in terms of the recombination process, in which the new trial vector generated is replaced by either a binomial crossover operator, which generates a trial vector $\overrightarrow{ U_{i,,G}}$ by linearly combining the target vector $\overrightarrow{ X_{i,,G}}$ and the corresponding donor vector $\overrightarrow{ V_{i,,G}} ,$ or an exponential crossover as highlighted in Equation (3). The variables $r_1,r_2, \mathrm{and} r_3$ represent the randomness of the system and have a range of $\left(1, 2, 3,\dots \dots ,NP\right)$. Figure 3 indicates the process through which the trial vector is obtained with respect to the DE search algorithm, as shown in Equations (4) and (5):

$$\overrightarrow{U_{i,G}}=\overrightarrow{ X_{i,G}}+K·\left(\overrightarrow{ V_{i,G}}-\overrightarrow{ X_{i,G}}\right)$$

(4)

$$\overrightarrow{U_{i,G}} =\overrightarrow{ X_{i,G}}+K·\left(\overrightarrow{ X_{r_1,G}}+\overrightarrow{ X_{i,G}}\right)+F\prime ·\left(\overrightarrow{ X_{r_2,G}}-\overrightarrow{ X_{r_3,G}}\right) .$$

(5)

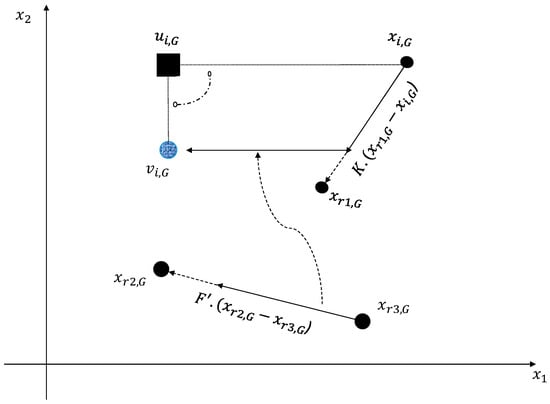
Figure 3. Process of obtaining the trial vector in the DE algorithm.

Additionally, the scaling and combination factors are considered, and are given by $F^{\prime }=K·F$ and $K,$ respectively; they have values within the range of [0, 2]. In the metaheuristic methods, DE parameters have a considerable effect on system performance. Thus, selecting parameters is an important consideration, especially for applications with a high degree of uncertainty, such as a forecasting system. A commonly known parameter selection method used for DE optimization is a rule of thumb formulated by Storn [39].

CR refers to the crossover constant used in the condition statement shown in Equation (3). The value of the variable CR is within the range [0, 1]. Based on the value of the crossover constant, a trial value follows the mutation or the target value in the following relationships: if the value of CR is greater than or equal to the random number $rn{d}_j$, then the trial value will follow the mutation value; if it is lower than $rn{d}_j$, then the trial value follows the target value. Figure 4 illustrates these relationships.

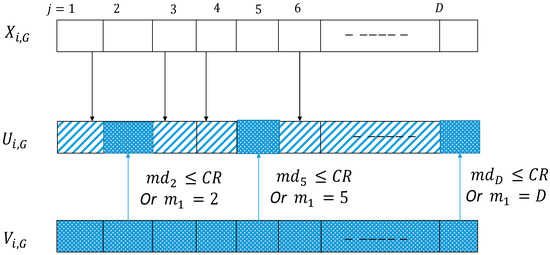
Figure 4. Generation of D-dimensional trial vector after crossover operation in DE algorithm.

Selection

The next optimization process of the DE algorithm is selected to determine whether the target or trial vector survives for the next generation. In the case of the trial vectors generated through mutation or crossover, a certain level of consideration is involved in the evolution of the fitness function along with the parent target vectors.

The parent vectors are considered to have better fitness values than their child vectors in the population of the search space. When this condition fails, the selection process replaces the trial or newly created trial vector with a suitable fitness value, as illustrated in Equation (6). Note that in Equation (6), the target vector is replaced with the trial vector even if both yield the same value of the objective function. This feature enables DE vectors to move over with generations. Minimizing the objective function corresponds to a high fitness:

$$X_{i,G+1}=\{\begin{array}{c}{u}_{i,G}, if f\left(u_{i,G}\right) \ge f\left(x_{i,G}\right)\\ x_{i,G}, otherwise\end{array}.$$

(6)

3.1.2. Overview of the PSO Algorithm

Theory

PSO is a metaheuristic search optimization algorithm that is used across a wide range of engineering applications. PSO is inspired by nature’s bird flocking behavior and was first introduced by Kennedy and Eberhart in 1995 [40]. PSO, a swarm-based evolutionary algorithm, investigates the search space and determines the parameter settings required to optimize the objective function. In PSO, possible solutions within the search space are randomly selected. Each individual within the search space moves throughout the space in search of an optimal solution. The optimal solution and modification of the fitness coefficient of the individual particles within the swarm are made based on the previous experiences of the individual and adjacent elements stored in the memory. Figure 5 depicts the flowchart of the PSO algorithm.

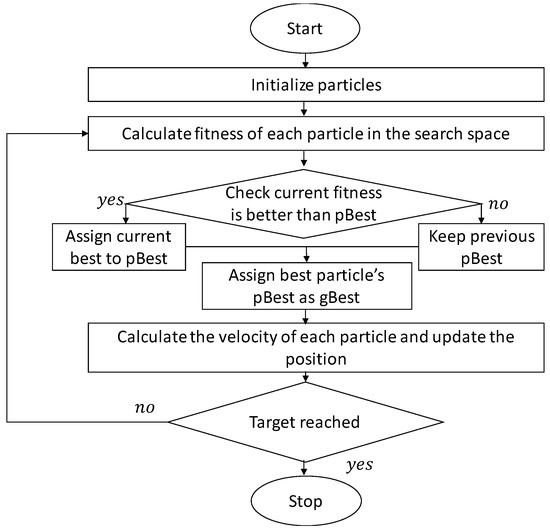
Figure 5. Flowchart of the PSO algorithm.

PSO involves initialization, movement, and evaluation. Initialization starts with a random selection of particles and then continues with the search for optimal solutions in past iterations. Next, the quality of the particle according to the fitness function is evaluated [41]. These steps are defined in a broad perspective in the subsequent sections. The PSO algorithm is simple and features high tracing accuracy with a good convergence profile.

Initialization

In the initialization process of PSO, the algorithm hires a certain number of particles (N) of the search space. PSO has only two parameters, namely, particles’ position and velocity. Moreover, it is a fast convergent and global solution solver for most scientific and engineering optimization problems. Each particle is assigned to a distinct location represented by $X_i$ within the search space. These particles move in a pattern within the search space.

Movement

Each particle moves from its current location, $X_{ik}$, to the global optimum position ($G_b$) with velocity $V_{ik}$ in the search space. Such movement helps the particle to stochastically explore the entire search space until it finds the best optimum solution. The movement of the particle within the search space is based on the personal best position $P_{bi}$ of the $i\mathrm{th}$ iteration and the global best position ($G_b$) obtained by comparing the particles in the previous iteration. Figure 6 indicates the transformation of the particle position and velocity in a three-dimensional search space; here, the blue star represents the global best position.

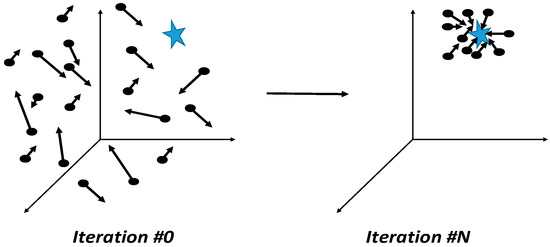
Figure 6. Pictorial representation of PSO algorithm in a three-dimensional search space.

During optimization, the particles communicate with one another and update the best fitness of every individual particle with every other particle in the search space on the basis of the objective function. Accordingly, the values of the best position of each particle in the swarm are recorded and used to select the random components of the optimization problem. The following equation defines how the next position of the particle is calculated:

$$V_i^{k+1}=w\times V_i^k+ r_1\times c_1\times \left(P_{bi}-X_i^k\right)+ r_2\times c_2\times \left(G_b-X_i^k\right)$$

(7)

$$X_i^{k+1}=X_i^k+V_i^k,$$

(8)

where $i$ represents the respective particle in the search space; $k$ is the iteration of the optimization sequence; $V_{ik}$ denotes the velocity of the particle; $X_{ik}$ denotes the current position of the particle in iteration $k$; $w$ is the inertia coefficient or the inertia weighting factor; $c_1$ and $c_2$ are the acceleration coefficients of the cognitive and social components of the particles, respectively; and $r_1$ and $r_2$ correspond to the random values chosen from a uniform distribution from 0 to 1. The primary objective of this randomness is to maintain the stochastic movement throughout the iterations specified in the optimization cycle. For the maintenance of the search space within a specified area, the velocity values are set with a bound between $\left[0, V_{max}\right]$. Figure 7 shows the representation of the fitness function used to evaluate the particle position and velocity through the PSO algorithm.

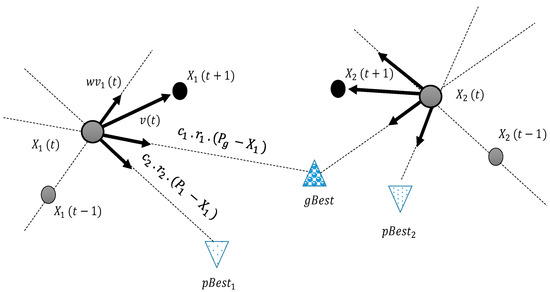
Figure 7. Representation of the fitness function to evaluate particle position and velocity using PSO algorithm.

Modifications made to the values of $w$, $c_1$, and $c_2$ affect the accuracy and speed of the algorithm. Appropriately selecting $c_1$ and $c_2$ is important to prevent the settling for a local extreme position. The selection of appropriate values for the inertia weight of a particle is important because the convergence of particles is slow when their inertia weight is high and the search space becomes narrow when the inertia weight is low. Changes in the inertia coefficient or weight w cause particles to diffuse at the initial condition and then gradually limit the search space in the final iteration and optimize the swarm. Figure 8 depicts the behavior of the inertia weight during the iterations of the optimization.

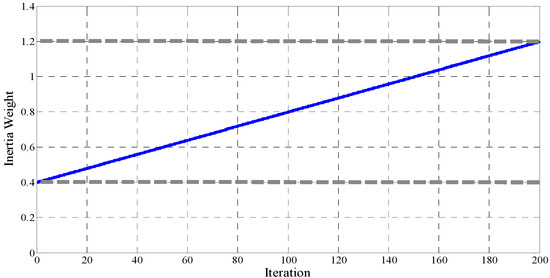
Figure 8. Behavior of inertia weight during all iterations.

Evaluation

To improve the particle movement within the search space in the subsequent iterations, we use a fitness function to find the new location of the particle and save it for every iteration. The best position $P_{bi}$ is achieved by the particle till date and subsequently updated to the memory when Equation (9) is satisfied.

Meanwhile, $G_b$ represents the global best position achieved through the comparison of the personal bests $P_{bi}$ of an individual particle for each iteration. Additionally, we update the condition for $G_b$ and $P_{bi}$, as illustrated in Equations (8) and (9), when the condition is true:

$$P_{bi} =X_i^k if f\left(X_i^k\right)\ge f\left(P_i\right),$$

(9)

$$G_b =P_{bi} if f\left(P_{bi} \right)\ge f\left(G_b\right).$$

(10)

$P_{bi}$ and $G_b$ are updated throughout the optimization process in each iteration. To do so, we define a fitness function to evaluate the location of each particle at each step. The mathematical form of obtaining the velocity and updating the location of each particle is shown in Equations (7) and (8), respectively. Particle optimization continues until the stopping conditions formulated according to several factors, such as system complexity, accuracy required, and response time.

3.1.3. DEPSO Algorithm

In PSO, the diversity of particles decreases significantly [42], and the likelihood that these particles will be trapped at the local optima increases as iterations continue. By contrast, the DE algorithm successfully explores the local optima by utilizing differential information. However, its ability to find the global optima is compromised [36]. The DEPSO combines the DE operator with the PSO algorithm to prevent individual particles from being trapped at the local optima, thereby improving the overall capability of the PSO technique [43]. Applications of DEPSO to training, clustering, and optimization have been presented in the literature and demonstrate improved solution quality and convergence speed relative to PSO and DE [7,44].

The global position $G_b$ and personal best position $P_{bi}$ are two key factors considered in the search process of the PSO algorithm. The optimization algorithm adds a thrust component to an individual particle such that the particle is pushed toward the global optimum position. For this action, the position of each individual in the swarm is considered. Nonetheless, the unfavorable weighted velocity of each particle in the swarm reduces the capability of the swarm to converge.

The DE in DEPSO comes into the picture here as it adds a feature to the conventional PSO algorithm to explore and exploit the search space efficiently and avoid individual particles stuck in the local optima [43]. Therefore, the proposed system uses the PSO and DE algorithms efficiently by using a PSO-based optimization for each odd iteration and DE-based optimization strategy for each even iteration. Figure 9 depicts the flowchart or the state diagram to illustrate the DEPSO algorithm, where $ff$ represents its fitness function.

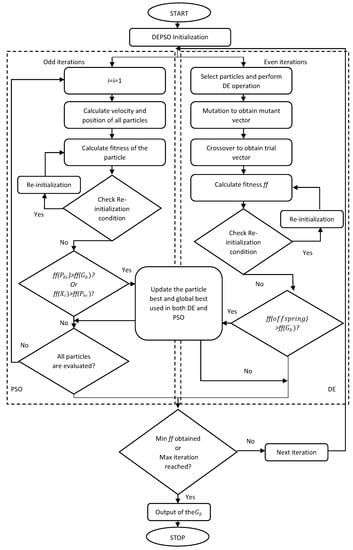
Figure 9. Flowchart of the forecasting strategy based on the DEPSO technique.

3.2. Implementation of DEPSO in Forecasting

The fitness function $\left(ff\right)$ for the $i\mathrm{th}$ particle of the proposed DEPSO process is expressed in Equation (11), where $N$ represents the hourly samples of the weather data used, true$\left(m\right)$ corresponds to the actual data collected, and $forecas{t}_i\left(m\right)$ denotes the proposed forecast model output:

$$fitness function\left(i\right)=ff\left(i\right)={{\displaystyle \sum }}_{m=1}^N{\left(forecas{t}_i\left(m\right)-true\left(m\right)\right)}^2,$$

(11)

The search space consists of six dimensions, which are represented as parameters $a_3$ to $a_0$ and $b_1$ to $b_2$, as expressed in Equation (13). The respective values for these parameters are used to construct the forecast model after the evaluation of the location of each particle in the search space. The values are then evaluated with the fitness function. The best way to show the sequences and priorities of an implemented DEPSO algorithm is through a flowchart, such as that shown in Figure 9. The figure shows that the stoppage condition occurs when it reaches the maximum number of generations considered. Table 2 shows the parameter selection of the DEPSO algorithm based on successful experiments in the literature [45].

Table 2. Parameter selection of the proposed DEPSO algorithm.

C1	C2	W	CR	F	K
2	1.5	1.2	0.8	0.7	0.5

3.3. Data Collection

One of the most critical steps in the forecasting system is providing reliable and trustable data collected on-site. Poor data collection and inaccuracy in the meteorological and PV power undoubtedly lead to inaccurate and unreliable forecasting outputs, even with a sophisticated forecasting system. As highlighted above, one of the key points of this research includes the local weather monitoring station, which collects data from the same site where the actual PV system is located. This feature contributes to the increased accuracy of the proposed DESPO forecasting algorithm relative to that proposed in the literature [15]. Moreover, the output of the PV system is significantly affected by irradiance intensity and direction, temperature, and shading conditions on-site. Therefore, the difference in locations for the imported weather and collected historical PV power data causes further inaccuracy in the forecasting system. The weather station in this project is installed close to the PV system on the rooftop of the School of Engineering, Deakin University (Victoria, Australia).

Figure 10 presents the geographical location of the system used to validate the proposed forecasting algorithm. Figure 11 highlights the average solar irradiance specific to the region where the system is situated. This information is critical in identifying the data used to test the forecasting algorithm.

Figure 10. Geographical location of the test location [46].

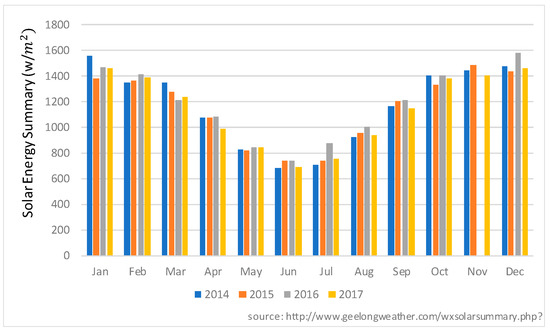
Figure 11. Distribution of solar energy generation during the period of observation.

Figure 12 illustrates the location on the rooftop. The collected dataset includes hourly weather data collected from the installed Envirodata-WeatherMaster-2000 weather station and historical PV power from the data obtained from the PV system. Table 3 tabulates the technical specifications of the PV array.

Figure 12. Weather station and PV system located at Deakin University, Australia.

Table 3. PV array—Technical Specifications.

Parameter	Value
Solar module type	CS6P-250M
Number of modules	12
Module rated power output	250 W
Open circuit voltage ($V_{oc}$)	37.5 V
Short Circuit Current	8.74 A
Optimum operating voltage ($V_{mp}$)	30.4 V
Optimum operating current ($I_{mp}$)	8.22 A

Note: All parameters are based on the standard testing condition, in which the ambient temperature is 25 °C and the irradiance level is 1000 W/m².

The PV system has a peak power of nearly 3 kW and comprises 12 PV modules at approximately 250 W each. The logged climate data are solar irradiance, air temperature, and relative humidity. An intensive impact analysis of the weather data was carried out during the study. Solar irradiance and temperature were considered as the primary input variables due to the insignificant impact of relative humidity deemed in this study. The generated output power of the PV system was also recorded using a self-sufficient data acquisition system, which acted as a self-energized data logger connected to the output terminal of the inverters in the PV system. Data collection was carried out for a period of about 15 months from the 1 July 2014 to the 30 September 2015. Due to the power interruption of the data logger, the overall data were collected for 293 days and then used in the training and validation processes of the proposed forecasting technique in the later stages. Figure 13 shows the system’s hourly weather data and power output during this period as recorded in the self-energized data logger system. Figure 14 shows the relationship of measured solar irradiance and air temperature during the data collection period as a function of hourly sampled time.

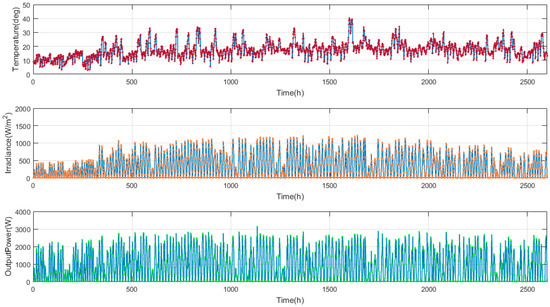
Figure 13. System’s hourly weather data recorded in the local data logger system.

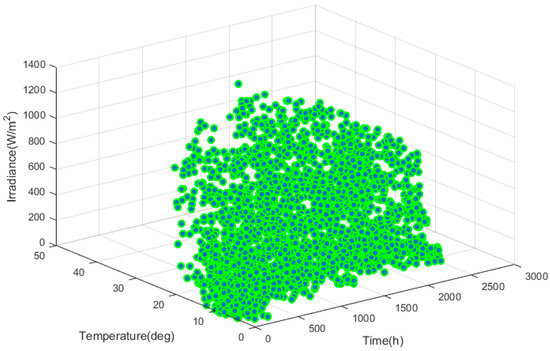
Figure 14. Evolution of the measured solar irradiance and air temperature during the data collection period with an hourly time scale.

3.4. Forecast Model

Two types of input are typically considered when forecasting the output power of PV arrays. A polynomial mathematical model is assumed as the forecasting model consisting of two stochastic weather inputs; the output provides the forecast value for the output power. This model has several benefits, such as simplicity and ease of implementation. The proposed system is comprehensive because every mathematical function can be expressed as a polynomial form on the basis of the Maclaurin series expansion given in Equation (12) [47]:

$$f\left(x\right)=f\left(0\right)+f^{\prime }\left(0\right)x+\frac{f^{″}\left(0\right)}{2!}{x}^2+\frac{f^{\left(3\right)}\left(0\right)}{3!}{x}^3+\cdots +\frac{f^{\left(n\right)}\left(0\right)}{n!}{x}^n+\cdots .$$

(12)

Therefore, all possible nonlinear functions can be included by considering a polynomial function as the representative model. On the basis of the above explanation, the following forecast model, which evaluates particle locations, is expressed as the fitness function of the optimization process proposed in this research. Equation (13) illustrates the forecast model consisting of a six-dimensional search space:

$$forecast\left(i\right)=a_3{x}^3+a_2{x}^2+a_1{x}^1+b_2{y}^2+b_1{y}^1+a_0,$$

(13)

where $i$ denotes the $i\mathrm{th}$ particle in the search space of the algorithm and variables $x \mathrm{and} y$ represent the values of the irradiation and ambient temperature, respectively. Parameters $a_3$ to $a_0$ and $b_1 \mathrm{to} b_2$ are the factors that need to be conventionally set on the basis of the proposed technique to obtain the most suitable fitting curve for the proposed forecasting algorithm.

4. Experimental Forecasting Results

The forecasting model was formulated and trained with an input dataset of hourly intervals of the historic PV output power to obtain improved forecasting results. The ambient temperature and solar irradiation values of 2100 hourly samples were used in the training process, whereas the remaining 530 hourly samples from the 293-day dataset were used to evaluate the forecasting model based on the results obtained from the sensitivity experiments conducted on optimizing the sample length of the proposed model. The daily recorded data varied according to the availability of solar irradiance during the day because the generated PV power was used as the energy source of the data logger. The model output was the hourly PV output power forecasting results of the same day. The DEPSO technique was applied to the forecasting model for 15 runs, in which the constant coefficients in Equations (14) and (15) were selected on the basis of the average objective value presented by the objective function. Table 4 presents the optimized values for the parameters, as well as the parameters of the DEPSO algorithm.

Table 4. Optimized values for the parameters of the forecasting model.

Parameter	Value
Number of particles	100
Number of iterations	1000
Number of algorithm run	20
$a_3$	4.7 × 10−5
$a_2$	3.1 × 10−3
$a_1$	−9.2 × 10−3
$a_0$	9.4 × 10−4
$b_2$	−1.4 × 10−3
$b_1$	2.5 × 10−3

Figure 13 represents the complete data of the hourly samples of the PV system and the weather data. Figure 15 presents the zoomed version of the forecasted output of the DEPSO approach in relation to the actual value. The comparison revealed the quality of the proposed forecasting model after the actual data were traced. As shown in Figure 15 and Figure 17, the proposed forecasting model could track the correct power output even when the variations were severe and intense between days. The accuracy of the system is evident in the detailed visualization expressed in Figure 18, which shows a comparison of the DE, PSO, and DEPSO with the actual data of the five-day period in August 2015. The MAE, MBE, MRE, RMSE, VAR, and WME were used to evaluate the accuracy of the forecasting algorithm proposed in this research which is calculated using the entire forecast result whereas the figure highlighted below are showing a zoomed view of the forecasted output. The mathematical representations of these evaluation criterions are expressed in Equations (14)–(19) where $forecas{t}_i\left(m\right)$ represents the forecasted and $true\left(m\right)$ represents the current value used in the forecasting system and $total$ represents the total number of data samples:

$$MRE=\frac{1}{N}{\displaystyle \sum }_{m=1}^N\frac{forecas{t}_i\left(m\right)-true\left(m\right)}{total}\times 100\text{\%}$$

(14)

$$RMSE=\sqrt{\frac{1}{N}{{\displaystyle \sum }}_{m=1}^N{\left(forecas{t}_i\left(m\right)-true\left(m\right)\right)}^2}.$$

(15)

$$MAE=\frac{1}{N}{{\displaystyle \sum }}_{m=1}^N\left|forecas{t}_i\left(m\right)-true\left(m\right)\right|.$$

(16)

$$MBE=\frac{1}{N}{\displaystyle \sum }_{m=1}^{N}forecas{t}_i\left(m\right)-true\left(m\right).$$

(17)

$$WME=\frac{1}{N}{\displaystyle \sum }_{m=1}^N\frac{\left|true\left(m\right)-forecas{t}_i\left(m\right)\right|}{true\left(m\right)}.$$

(18)

$$VAR=\frac{1}{N}{\displaystyle \sum }_{m=1}^N{\left(\frac{\left|true\left(m\right)-forecas{t}_i\left(m\right)\right|}{true\left(m\right)}-WME\right)}^2.$$

(19)

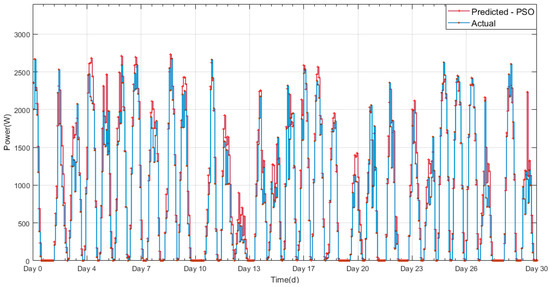
Figure 15. PSO-forecasted and actual values of PV output power.

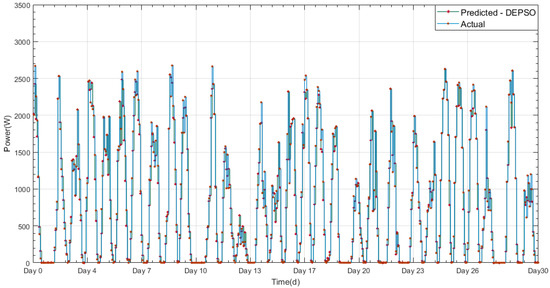
Figure 17. DEPSO-forecasted and actual values of PV output power.

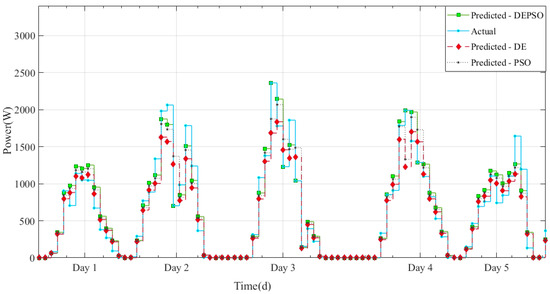
Figure 18. Comparison of DE-, PSO-, and DEPSO-forecasted values with actual value of PV output power.

For comparison, separate simulations were performed for the DE and PSO algorithms with the same parameter adjustments and conditions with three different time horizons of the training data being used (1, 2, and 4 h) for the day-ahead forecasting. The parameters of the PSO algorithm were set as those used in [43], and the DE parameters were the same as those in [36]. The best results out of 15 runs for the DE, PSO, and DEPSO algorithms were selected according to the values tabulated in Table 5. The simulation was carried out in MATLAB 2017a, and a COREi7-6600 @ 2.6 GHz with 16.00 GB RAM laptop computer was used to simulate the algorithms. A fair comparison between the proposed method and the standard DE- or PSO-based forecasting method was conducted over all algorithms by using an identical training dataset.

Table 5. Calculated error values for the DE, PSO, and proposed DEPSO methods.

Technique	1 h	2 h	4 h	1 h	2 h	4 h
	RMSE (%)			MRE (%)
PSO	14.2	15.8	21.9	9.2	11.5	13.3
DE	9.4	21.2	19.8	6.3	13.7	9.7
DEPSO	4.4	5.2	3.5	3.1	3.17	1.6
	MAE			MBE
PSO	0.05	0.26	0.25	−3.67	−7.45	−3.82
DE	0.06	0.23	0.19	−8.25	−14.25	−2.15
DEPSO	0.03	0.03	0.01	−1.63	5.19	−1.2
	WME			VAR
PSO	0.19	0.65	0.66	0.03	0.222	0.18
DE	0.2	0.68	1.18	0.064	1.24	0.21
DEPSO	0.16	0.28	0.16	0.01	0.79	0.12

The results presented in Table 5 showed that the proposed DEPSO performed better than the PSO and DE techniques. The MRE value for the DEPSO technique for the 1 h time horizon was 3.1%, demonstrating that the presented algorithm accurately forecasted the output power of the PV system. The average RMSE value of the proposed DEPSO method was 4.4%, which satisfies the industrial requirement of RMSE less than 20% [48].

The forecasting results of the proposed DEPSO, DE, and PSO methods are presented individually for a month in Figure 15, Figure 16 and Figure 17. We plotted the hourly forecasting power for five consecutive days in August 2015, along with the actual observed output power and the forecasted output from the other two evaluated algorithms (DE and PSO), to show the accuracy of DEPSO in a visually satisfying way in Figure 18. As expected, the proposed DEPSO algorithm was highly accurate in imitating the observed PV output power in comparison with the other two algorithms. Figure 19 shows the unit error deviation calculated according to the forecasted value over the actual value. As shown in this figure, the high error values are related to the low power values in which the denominator is extremely small and causes a surge in error value.

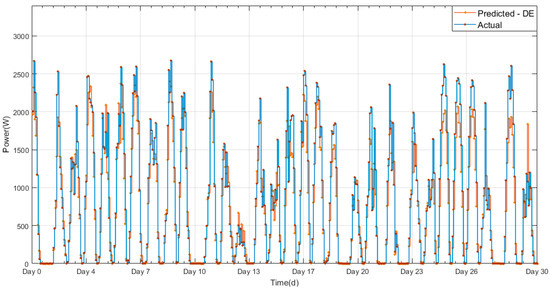
Figure 16. DE-forecasted and actual values of PV output power.

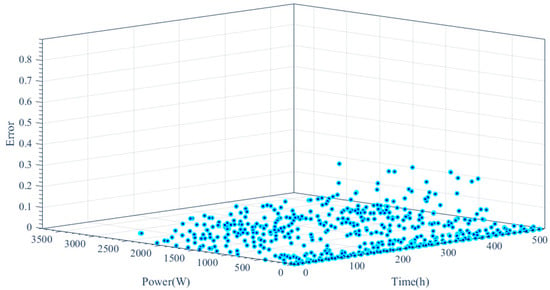
Figure 19. Error deviation calculated based on the forecasted over actual value.

5. Conclusions

This paper presents a forecasting model optimized by the DEPSO technique used for short-term PV power output forecasting of a PV system stationed at Deakin University (Victoria, Australia). DEPSO is a new metaheuristic swarm-based algorithm that efficiently and rapidly addresses global optimization problems. The stochastic nature of the DEPSO algorithm makes the system purely independent of its power output. Furthermore, the existence of the randomness of the system in the search process keeps the metaheuristic nature of the algorithm robust, reliable, efficient, and straightforward for short-term power forecasting. The limitations of the DE and PSO algorithms, such as the slow convergence rate of PSO and the lack of randomness in DE, are adequately addressed in the hybrid DEPSO technique. The comparison made among the DE, PSO, and DEPSO algorithms proves that the combinational evolutionary algorithm outperforms the two algorithms. The RMSE, MAE, MBE, VAR, WME, and MRE values of the forecasting algorithm are reduced to 4.4%, 0.03, −1.63, 0.01, 0.16, and 3.1%, respectively, when DEPSO is used under a 1 h time horizon. Meanwhile, these values reach 14.2%, 0.05, −3.67, 0.03, 0.19, and 9.2% for PSO and 9.4%, 0.06, −8.25, 0.064, 0.2, and 6.3% for DE under a 1 h time horizon. A comparison under different time horizons is highlighted in Table 5. Traditional methods like regression model and autoregressive moving average models have drawbacks of non-linear fitting capabilities which is addressed in the proposed model. Finally, the use of the DEPSO hybrid metaheuristic algorithm in short-term forecasting is supported by its simplicity, robustness, and novelty of implementation. DEPSO is also more computationally efficient than other optimization algorithms. Given the stochastic nature of the dependent parameters, such as temperature and solar irradiance, which are used to forecast a system’s power output, DEPSO is a suitable approach that addresses the research gap in the short-term forecasting of PV power output owing to its capacity to address uncertainties and its fast convergence rate.