Nonlinear Robust Control for Low Voltage Direct-Current Residential Microgrids with Constant Power Loads
Abstract
:1. Introduction
- Robust stability against arbitrary (bounded) changes in source voltage, output power, inductance and capacitance on the desired operating-point.
- Flexibility for use with the basic converters and even in a reconfigurable scheme.
- Low implementation time and cost.
- Easy tuning for a certain desired response.
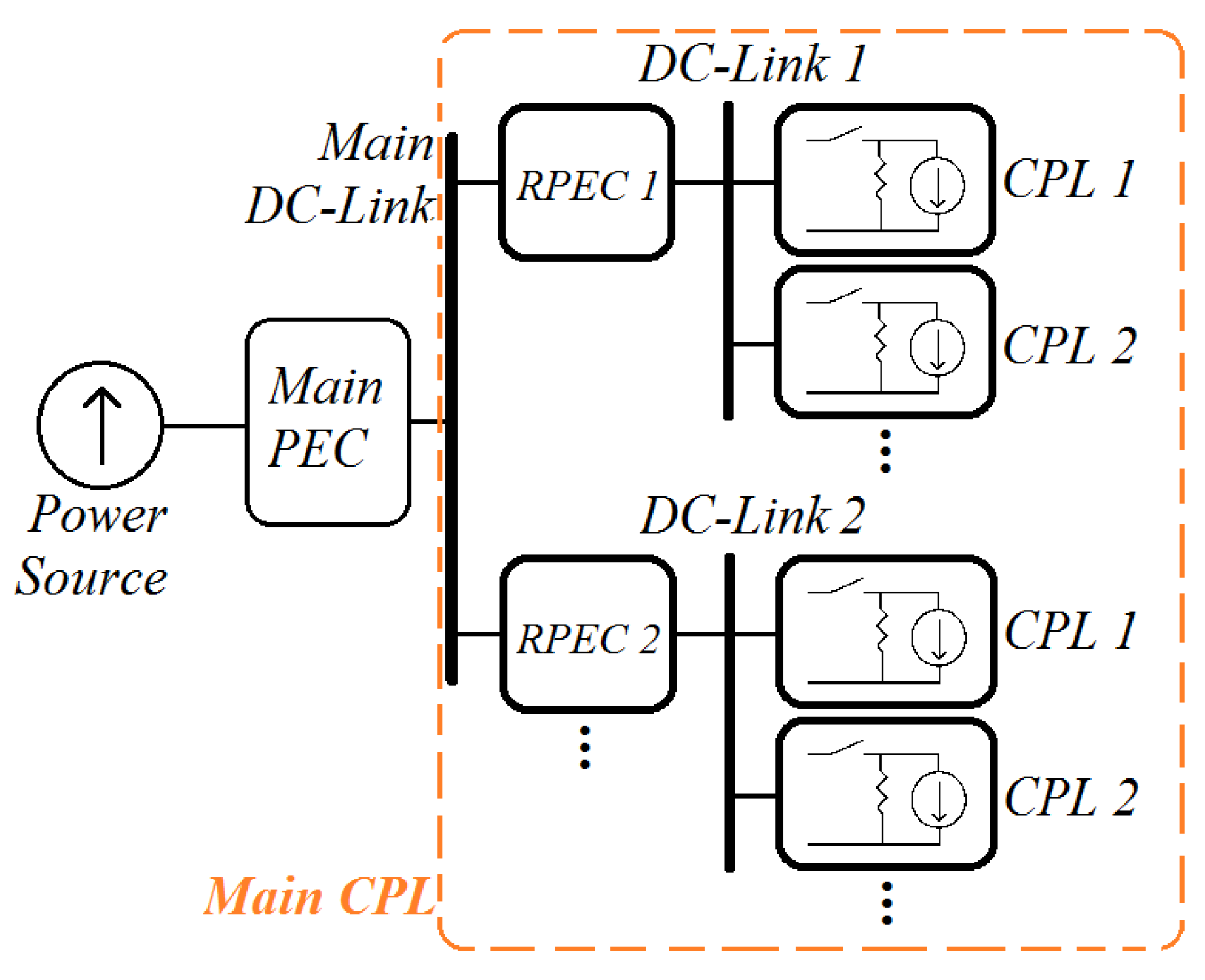
2. Modeling
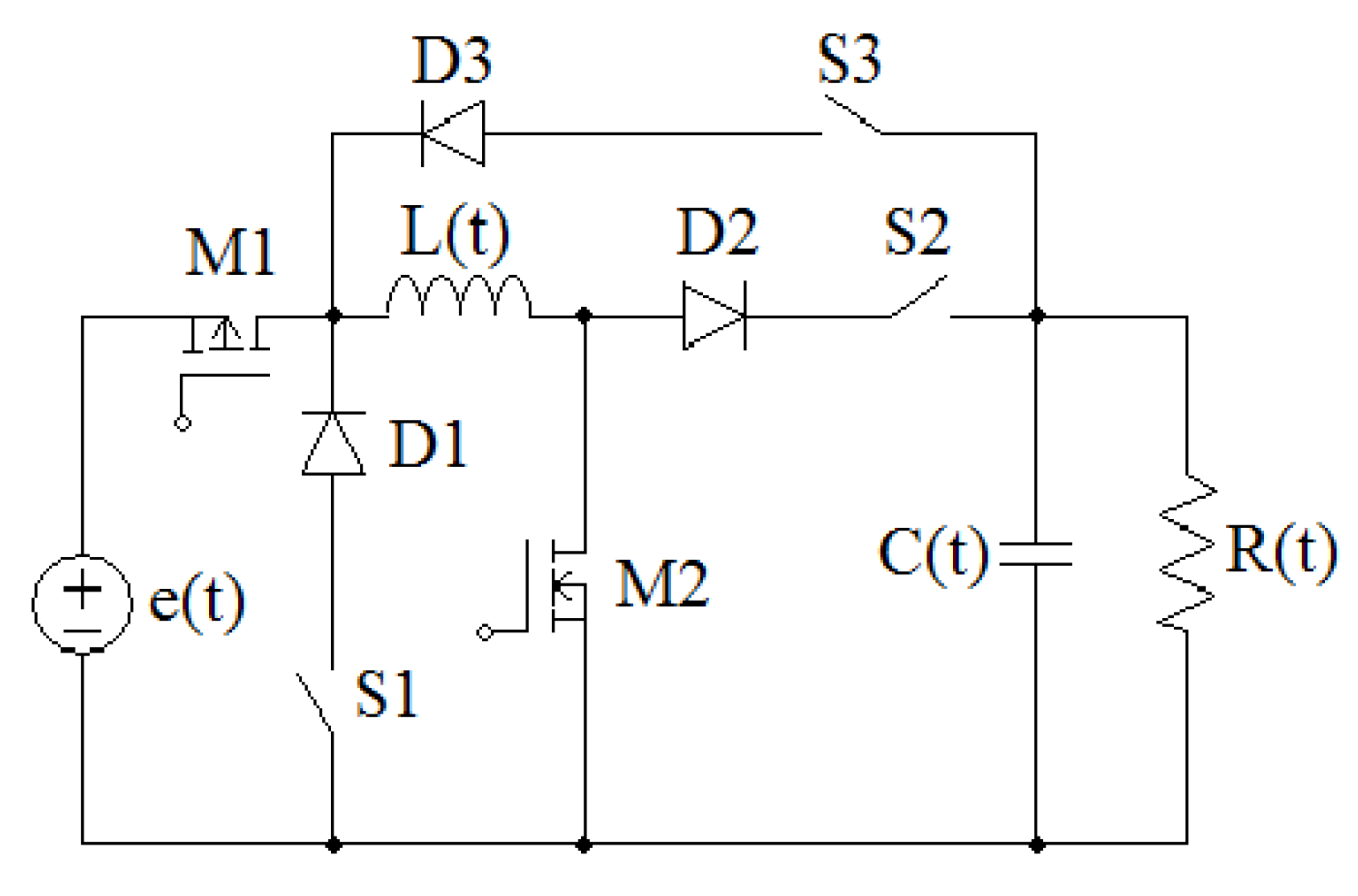
2.1. Voltage-Mode Modeling
- S1, S2 closed, S3, M2 open and PWM switching on M1, buck.
- M1, S2 closed, S1, S3 open and PWM switching on M2, boost.
- M2, S3 closed, S1, S2 open and PWM switching on M1, buck-boost.
- a buck PEC if
- a boost PEC if
- a buck-boost PEC if
- buck duty-cycle for is
- boost duty-cycle for is
- buck-boost duty-cycle for is
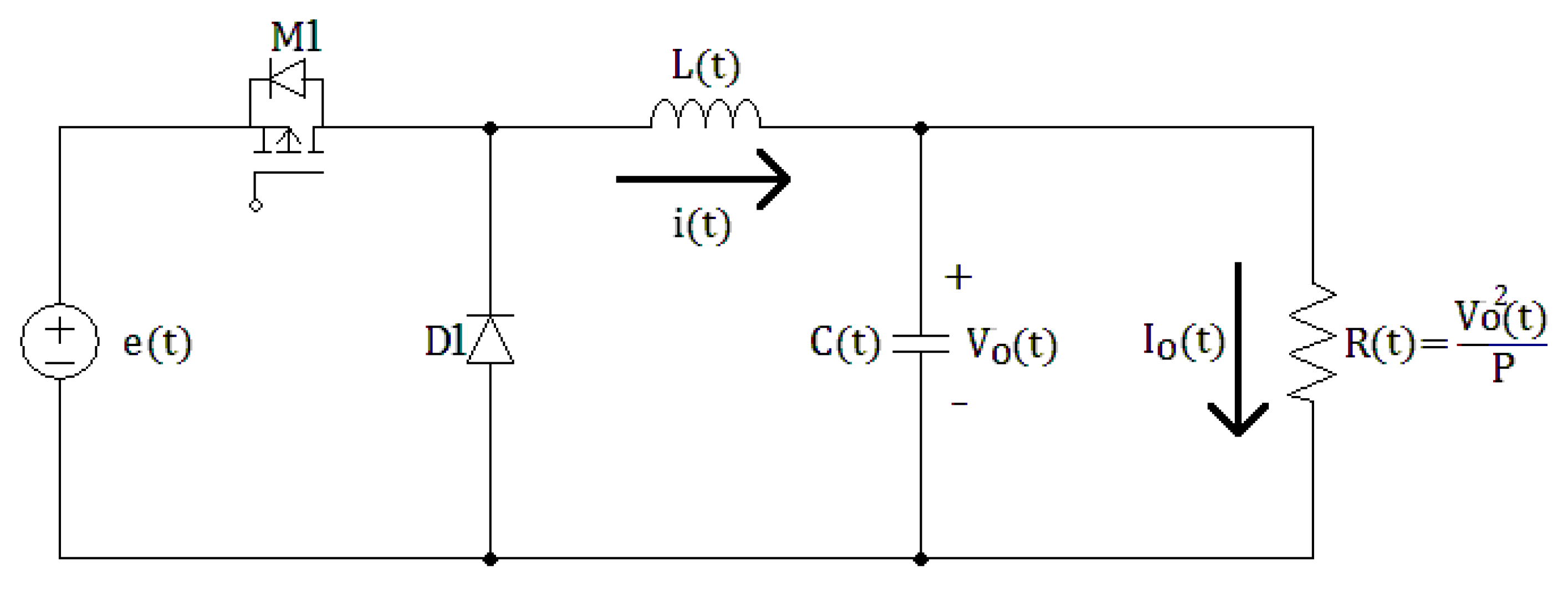
2.2. Current-Mode Modeling
3. Controller Design and Stability
3.1. Feedback Linearization for Voltage-Mode Controller
3.2. Taylor Series Linearization for Voltage-Mode Controller
3.3. Taylor Series Linearization for Current-Mode Controller
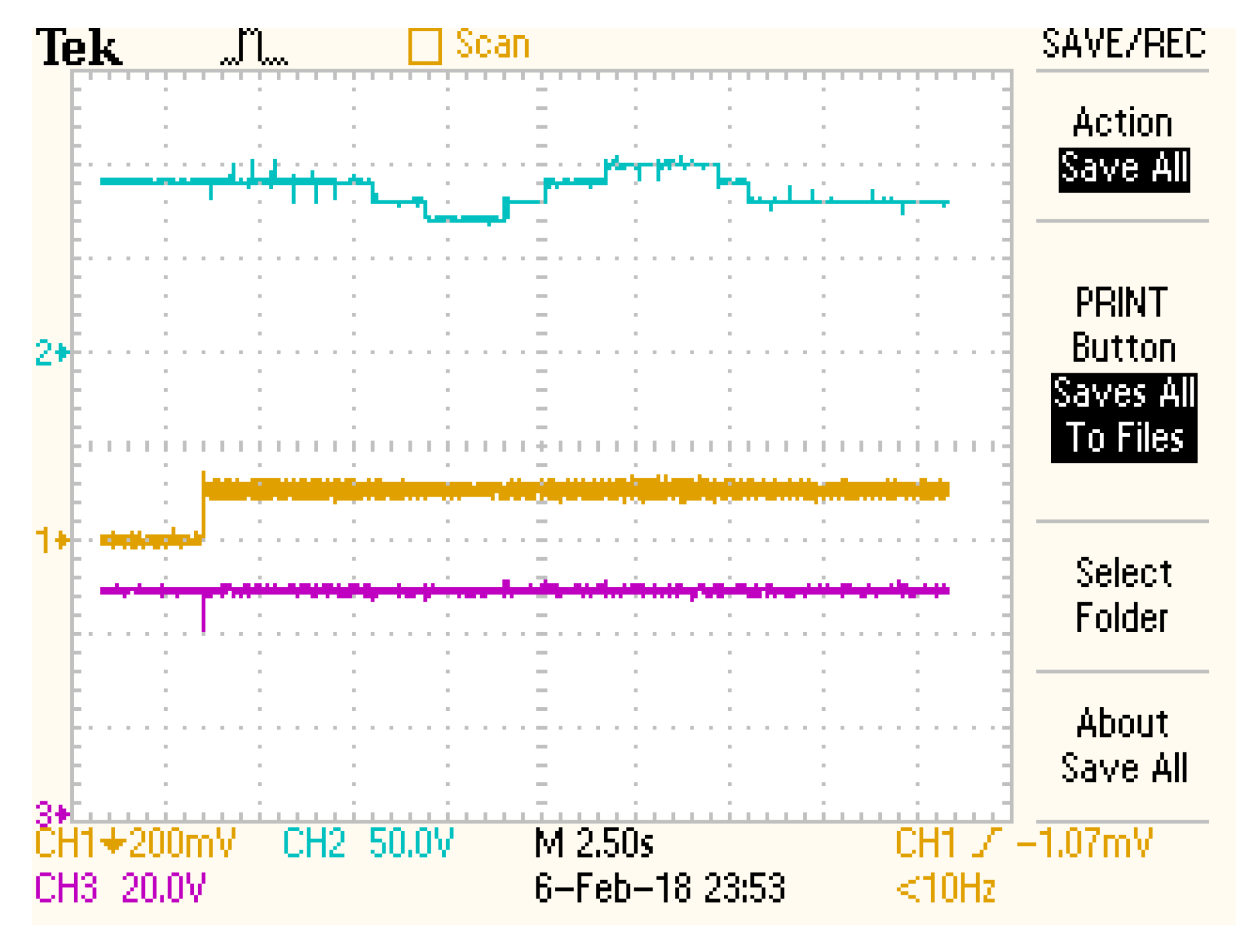
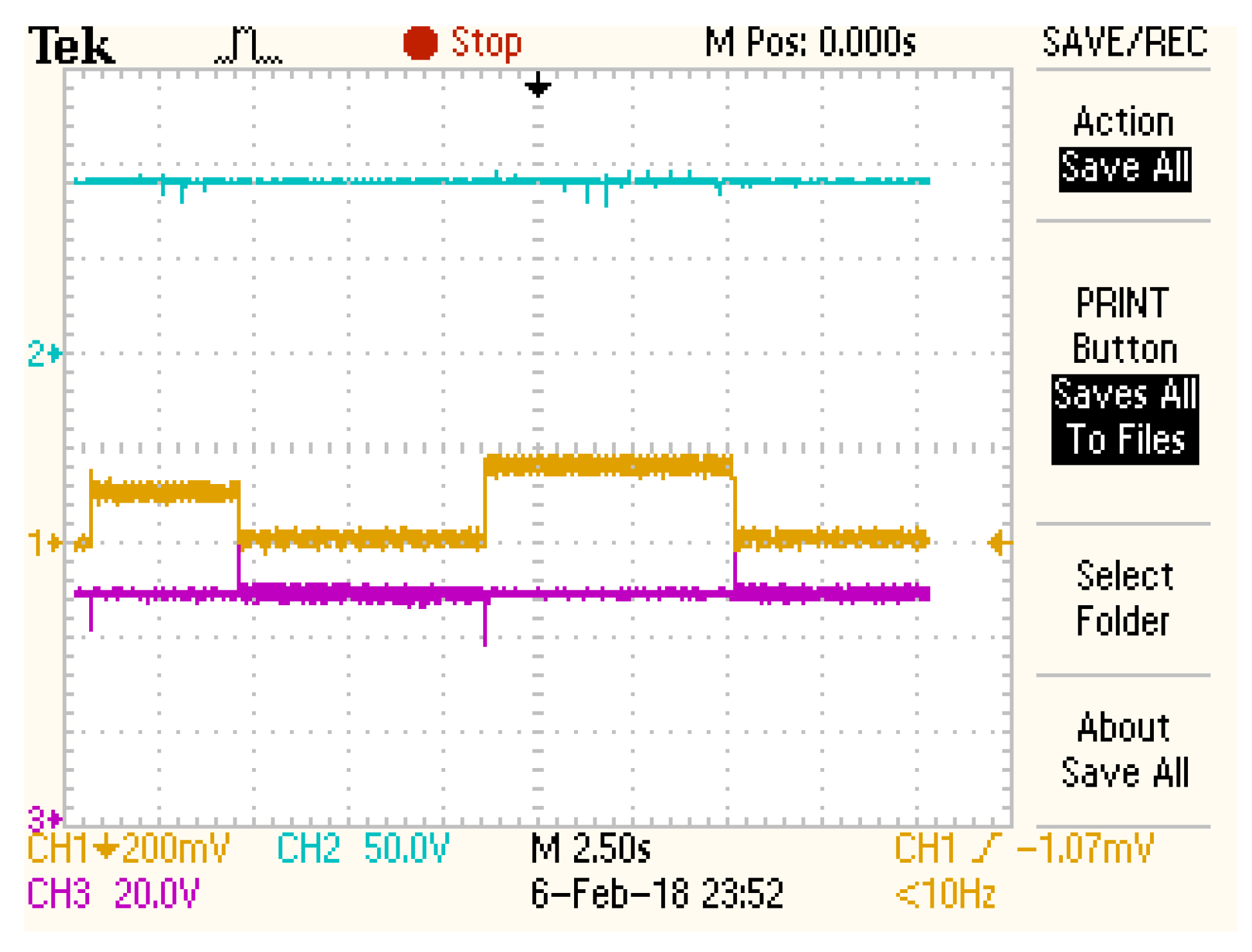
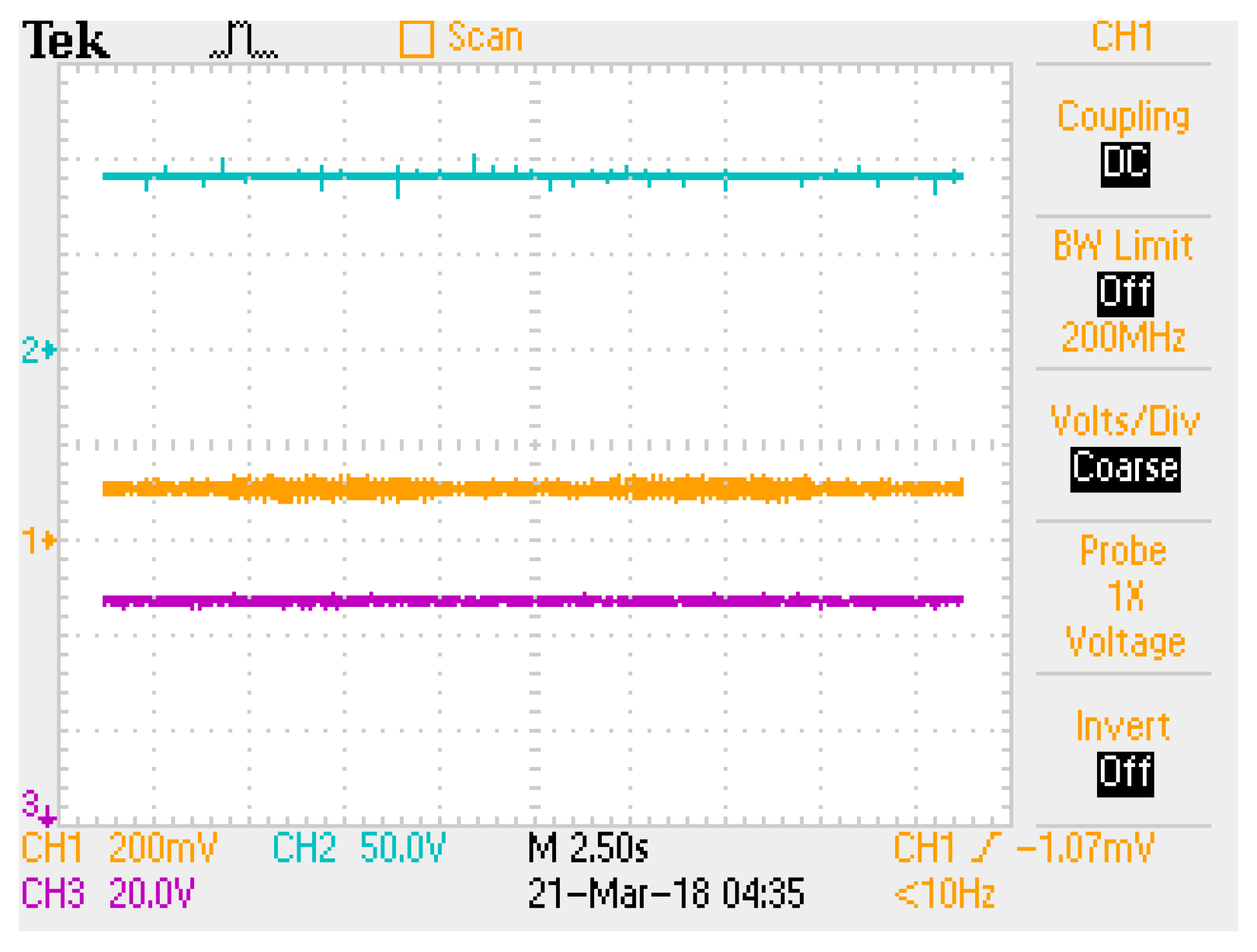
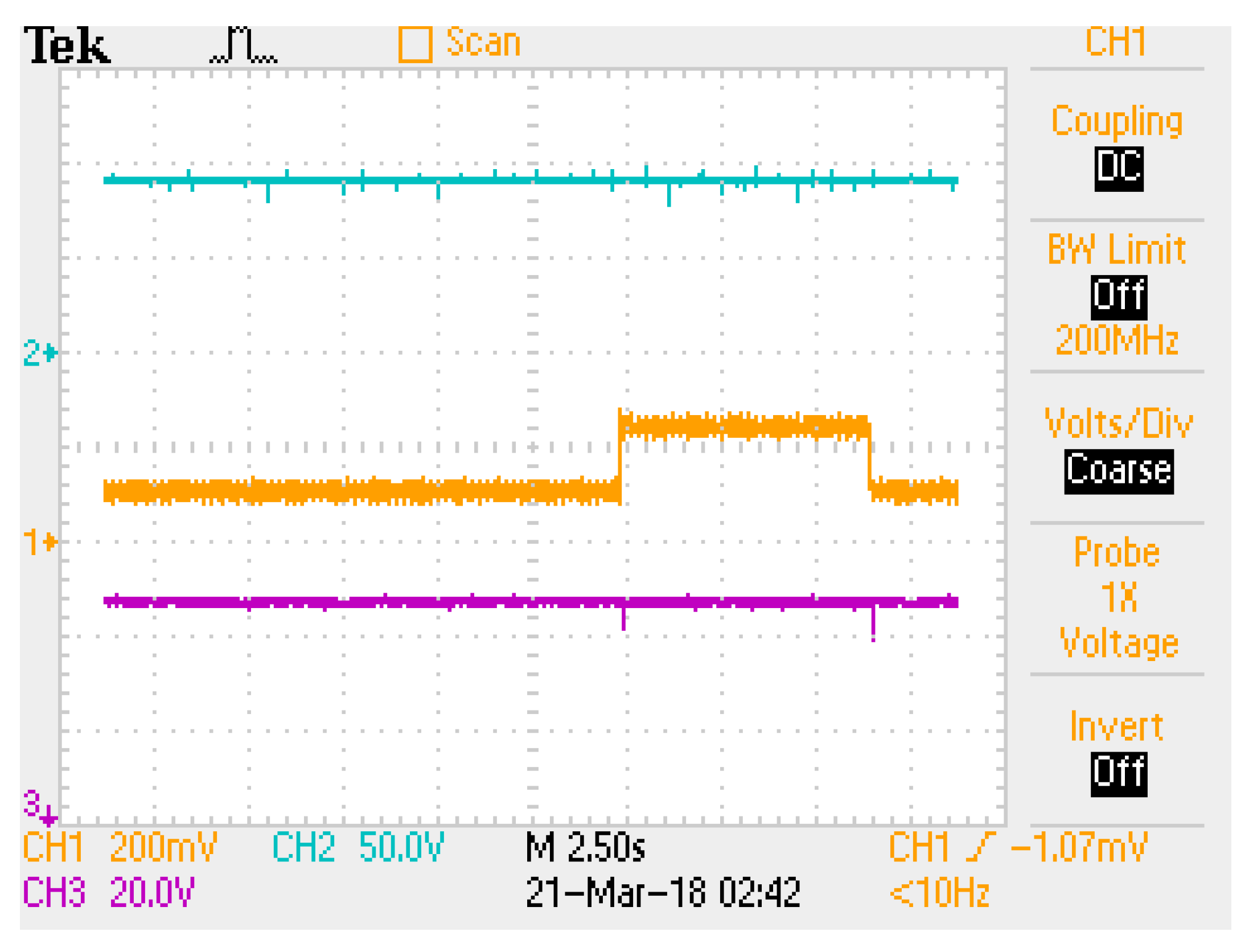
4. Experimental Behavior
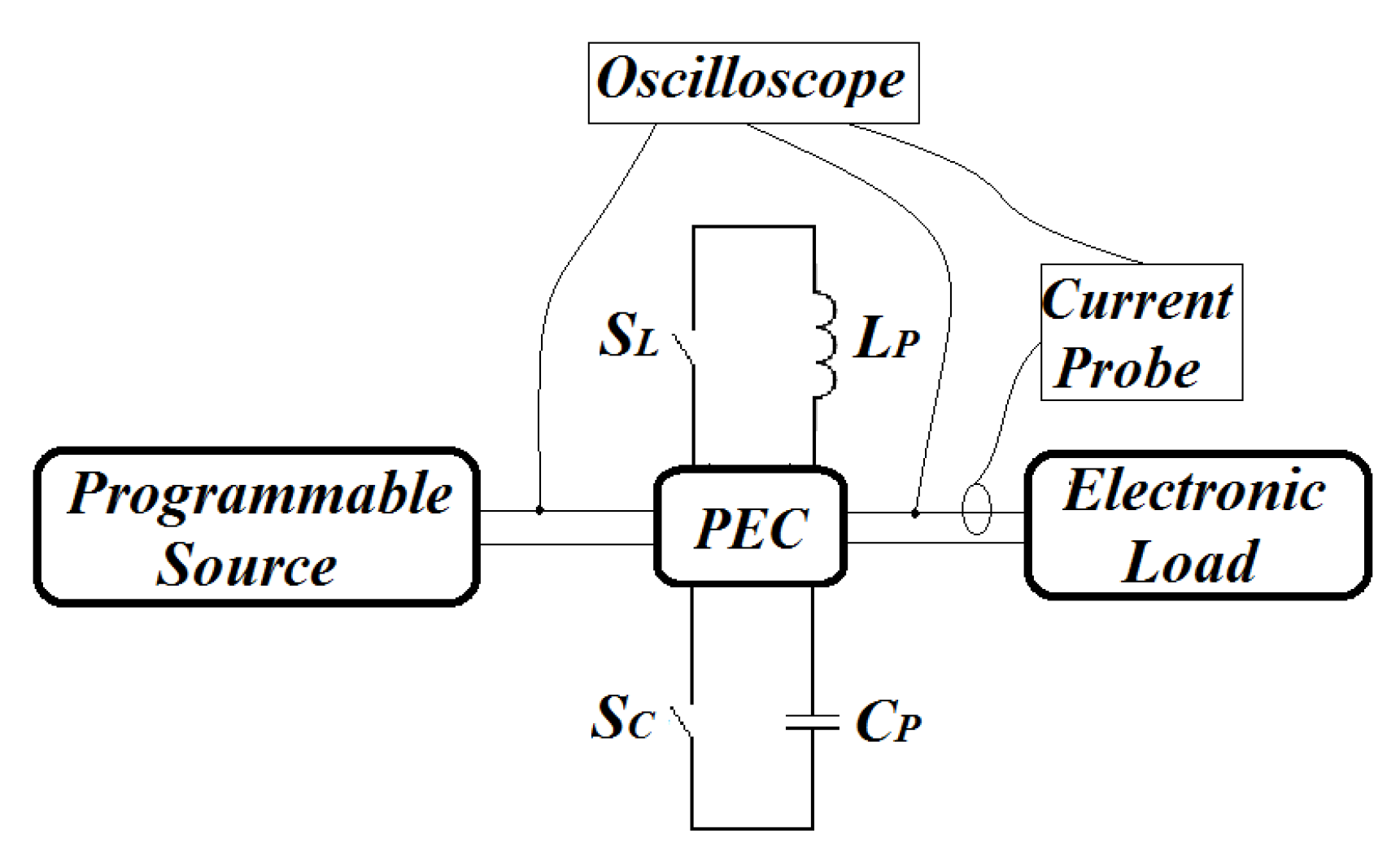
4.1. Equipment
4.2. Procedure
4.3. Discussion of the Results
4.4. Brief Comparison with Other Proposals
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Wang, P.; Goel, L.; Liu, X.; Choo, F.H. Harmonizing AC and DC: A hybrid AC/DC future grid solution. IEEE Power Energy Mag. 2013, 11, 76–83. [Google Scholar] [CrossRef]
- Kakigano, H.; Nomura, M.; Ise, T. Loss evaluation of DC distribution for residential houses compared with AC system. In Proceedings of the International Power Electronics Conference (IPEC), Sapporo, Japan, 21–24 June 2010; pp. 480–486. [Google Scholar]
- Wang, B.; Sechilariu, M.; Locment, F. Intelligent DC microgrid with smart grid communications: Control strategy consideration and design. IEEE Trans. Smart Grid 2012, 3, 2148–2156. [Google Scholar] [CrossRef]
- Hart, D.W. Power Electronics; Tata McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- Rodriguez-Diaz, E.; Chen, F.; Vasquez, J.C.; Guerrero, J.M.; Burgos, R.; Boroyevich, D. Voltage-level selection of future two-level LVdc distribution grids: A compromise between grid compatibiliy, safety, and efficiency. IEEE Electr. Mag. 2016, 4, 20–28. [Google Scholar] [CrossRef]
- AL-Nussairi, M.K.; Bayindir, R.; Padmanaban, S.; Mihet-Popa, L.; Siano, P. Constant power loads (cpl) with microgrids: Problem definition, stability analysis and compensation techniques. Energies 2017, 10, 1656. [Google Scholar] [CrossRef]
- Singh, S.; Gautam, A.R.; Fulwani, D. Constant power loads and their effects in DC distributed power systems: A review. Renew. Sustain. Energy Rev. 2017, 72, 407–421. [Google Scholar] [CrossRef]
- Zadeh, M.K.; Gavagsaz-Ghoachani, R.; Martin, J.P.; Nahid-Mobarakeh, B.; Pierfederici, S.; Molinas, M. Discrete-time modeling, stability analysis, and active stabilization of dc distribution systems with multiple constant power loads. IEEE Trans. Ind. Appl. 2016, 52, 4888–4898. [Google Scholar] [CrossRef]
- Chang, X.; Li, Y.; Li, X.; Chen, X. An active damping method based on a supercapacitor energy storage system to overcome the destabilizing effect of instantaneous constant power loads in dc microgrids. IEEE Trans. Energy Convers. 2017, 32, 36–47. [Google Scholar] [CrossRef]
- Arocas-Pérez, J.; Griño, R. A local stability condition for dc grids with constant power loads. IFAC-PapersOnLine 2017, 50, 7–12. [Google Scholar] [CrossRef]
- Herrera, L.; Yao, X. Computation of stability metrics in DC power systems using sum of squares programming. In Proceedings of the IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 9–12 July 2017; pp. 1–5. [Google Scholar]
- Van der Blij, N.H.; Ramirez-Elizondo, L.M.; Spaan, M.T.; Bauer, P. Stability of DC Distribution Systems: An Algebraic Derivation. Energies 2017, 10, 1412. [Google Scholar] [CrossRef]
- Hossain, E.; Perez, R.; Padmanaban, S.; Siano, P. Investigation on the development of a sliding mode controller for constant power loads in microgrids. Energies 2017, 10, 1086. [Google Scholar] [CrossRef]
- Srinivasan, M.; Kwasinski, A. European Conference on Power Electronics and Applications. In Proceedings of the International Power Electronics Conference (IPEC), Warsaw, Poland, 11–14 Sptember 2017; pp. 1–10. [Google Scholar]
- Garces, A. Uniqueness of the power flow solutions in low voltage direct current grids. Electr. Power Syst. Res. 2017, 151, 149–153. [Google Scholar]
- Zhao, Z.; Hu, J.; Xue, H.; Huang, R.; Li, X.; Zhang, X. Large signal stability analysis of DC microgrid under droop control with constant power load. In Proceedings of the Chinese Automation Congress, Jinan, China, 20–22 October 2017; pp. 1046–1051. [Google Scholar]
- Asghar, M.; Khattak, A.; Rafiq, M.M. Comparison of integer and fractional order robust controllers for DC/DC converter feeding constant power load in a DC microgrid. Sustain. Energy Grids Netw. 2017, 12, 1–9. [Google Scholar]
- Chen, Y.; Petras, I.; Xue, D. Fractional order control-a tutorial. In Proceedings of the American Control Conference (ACC’09), St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar]
- Liu, J.; Zhang, W.; Rizzoni, G. Robust stability analysis of dc microgrids with constant power loads. IEEE Trans. Power Syst. 2018, 33, 851–860. [Google Scholar] [CrossRef]
- Momayyezan, M.; Hredzak, B.; Agelidis, V.G. A Load-Sharing Strategy for the State of Charge Balancing Between the Battery Modules of Integrated Reconfigurable Converter. IEEE Trans. Power Electron. 2017, 32, 4056–4063. [Google Scholar] [CrossRef]
- Momayyezan, M.; Hredzak, B.; Agelidis, V.G. Integrated Reconfigurable Converter Topology for High-Voltage Battery Systems. IEEE Trans. Power Electron. 2016, 31, 1968–1979. [Google Scholar] [CrossRef]
- Rizzo, R.; Spina, I.; Tricoli, P. A single input dual buck-boost output reconfigurable converter for distributed generation. In Proceedings of the International Conference on Clean Electrical Power (ICCEP), Taormina, Italy, 16–18 June 2015; pp. 767–774. [Google Scholar]
- Grigore, V.; Hatonen, J.; Kyyra, J.; Suntio, T. Dynamics of a buck converter with a constant power load. In Proceedings of the 29th Annual IEEE Power Electronics Specialists Conference, (PESC’98), Fukuoka, Japan, 22–22 May 1998; Volume 1, pp. 72–78. [Google Scholar]
- Licea, M.A.R.; Pinal, F.J.P.; Gutiérrez, A.I.B.; Ramírez, C.A.H.; Perez, J.C.N. A Reconfigurable buck, boost, and buck-boost Converter: Unified Model and Robust Controller. Math. Prob. Eng. 2018, 2018, 6251787. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.J.; Silva-Ortigoza, R. Control Design Techniques in Power Electronics Devices; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Khalil, H. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Lay, S.R. Convex sets and their applications. In Pure and Applied Mathematics; John Wiley and Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Licea, M.R.; Cervantes, I. Robust indirect-defined envelope control for rollover and lateral skid prevention. Control Eng. Pract. 2017, 61, 149–162. [Google Scholar] [CrossRef]



| Type of Controller | Theory Difficulty | Implementation Complexity | Dynamic Response | Remarks |
|---|---|---|---|---|
| Active stabilizer [8] | High | High | Good | Good performance and a digital platform is used, in this case, a dSPACE. |
| Active damping [9] | Medium | Medium | Good | Good performance and a digital platform is used, in this case a pair of DSPs. |
| Linear [10] | High | High | Good | Good performance and only numerical results are reported. |
| Sum of squares [11] | High | High | Medium | Medium performance and only numerical results are reported. |
| Algebraic [12] | Medium | Medium | Medium | Medium performance and only numerical results are reported. |
| Sliding mode [13] | Medium | High | Good | Good performance and only numerical results are reported. |
| Linear damping [14] | Medium | High | Good | Good performance and a digital platform is used, in this case a DSP. |
| Robust stability [15] | High | High | Medium | Medium performance and only numerical results are reported. |
| Drop control [16] | High | High | Good | Good performance and only numerical results are reported. |
| Fractional order controller [17] | High | High | Medium | Medium performance and only numerical results are reported. |
| Robust stability [19] | High | High | Medium | Medium performance and only numerical results are reported. |
| Proposed approach | Medium | Low | High | Good performance and a low cost digital platform is used, in this case, a microcontroller. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez-Licea, M.-A.; Pérez-Pinal, F.-J.; Nuñez-Perez, J.-C.; Herrera-Ramirez, C.-A. Nonlinear Robust Control for Low Voltage Direct-Current Residential Microgrids with Constant Power Loads. Energies 2018, 11, 1130. https://doi.org/10.3390/en11051130
Rodríguez-Licea M-A, Pérez-Pinal F-J, Nuñez-Perez J-C, Herrera-Ramirez C-A. Nonlinear Robust Control for Low Voltage Direct-Current Residential Microgrids with Constant Power Loads. Energies. 2018; 11(5):1130. https://doi.org/10.3390/en11051130
Chicago/Turabian StyleRodríguez-Licea, Martín-Antonio, Francisco-Javier Pérez-Pinal, Jose-Cruz Nuñez-Perez, and Carlos-Alonso Herrera-Ramirez. 2018. "Nonlinear Robust Control for Low Voltage Direct-Current Residential Microgrids with Constant Power Loads" Energies 11, no. 5: 1130. https://doi.org/10.3390/en11051130
APA StyleRodríguez-Licea, M.-A., Pérez-Pinal, F.-J., Nuñez-Perez, J.-C., & Herrera-Ramirez, C.-A. (2018). Nonlinear Robust Control for Low Voltage Direct-Current Residential Microgrids with Constant Power Loads. Energies, 11(5), 1130. https://doi.org/10.3390/en11051130








