Abstract
From an environment perspective, the increased penetration of wind and solar generation in power systems is remarkable. However, as the intermittent renewable generation briskly grows, electrical grids are experiencing significant discrepancies between supply and demand as a result of limited system flexibility. This paper investigates the optimal sizing and control of the hydrogen energy storage system for increased utilization of renewable generation. Using a Finnish case study, a mathematical model is presented to investigate the optimal storage capacity in a renewable power system. In addition, the impact of demand response for domestic storage space heating in terms of the optimal sizing of energy storage is discussed. Finally, sensitivity analyses are conducted to observe the impact of a small share of controllable baseload production as well as the oversizing of renewable generation in terms of required hydrogen storage size.
1. Introduction
The integration of wind generation and utility-scale solar generation in electrical grids has seen a surge in recent years. In 2016, more than 75 GW of solar generation have been added to the grid all over the world [1]. In the EU, approximately 50% of the newly installed capacity (12.5 GW) is composed of wind generation [2]. However, the intermittent and uncertain nature of solar and wind generation has led to considerable uncertainty as to how to balance energy demand with production [3]. For instance, 16 GWh of solar generation and 358 GWh of wind generation was curtailed in Germany in 2012 [4]. Curtailment is a natural response to preserve the capability of the system at times of excess production. However, as a result, a large amount of renewable generation is wasted, which not only undermines stakeholders’ assurance regarding the feasibility of renewable generation technologies but also contributes to sub-optimal system performance [5].
Among the various options to integrate intermittent renewable generation into power systems, energy storages have the highest potential in terms of flexibility. As the integration of large-scale storage into a system can significantly improve renewable generation usage, it recently has been the focus of considerable scholarly attention [6,7,8,9]. Although energy storage appears to be a feasible option with which to increase system flexibility for the accommodation of large-scale intermittent renewable generation, the high upfront costs of this advanced storage technology merit consideration.
Electric storage space heating systems are widely used in Finland to satisfy the demand for both space heating and hot water. When they are accompanied by a home energy management system, they can shift the heating demand profile of a household by storing heat during off-peak hours. In Nordic countries, space heating comprises the largest portion of total annual energy usage in buildings [10]. It is conceivable that an aggregation of the large number of domestic electric storage heaters as well as collaboration with centralized energy storage can provide additional capacity (increased power and energy limits) to accommodate largescale renewable generation.
Accordingly, some studies have focused on innovative tools and frameworks that exploit demand-side resources and technologies. For example, Ali et al. [11] assessed the joint flexibility of electric vehicles and heating loads to integrate wind generation in the system. In 2017, Ali et al. [12] proposed a framework to evaluate the potential of electric storage heating as a means by which excess generation could be addressed. In a 2015 study by Ali et al. [13], the value of flexible domestic heating demand was highlighted as a method by which higher penetration of wind generation in the system could be accommodated. Studies by Lund et al. [14] and Guille et al. [15] emphasized that, during generation hours, the controlled charging of electric vehicles can provide ample benefits.
In this paper, a framework is presented for the optimal sizing of hydrogen energy storage for balancing the volatility of renewable integration in power systems. Hydrogen energy storage technology is considered in particular because of its versatility and scalability. The opportunities for renewable integration in terms of domestic storage space heating demand response in coordination with centralized hydrogen energy storage is thoroughly assessed. Additionally, this paper discusses the effect of increasing domestic thermal storage capacity and hydrogen energy storage round-trip efficiency on the optimal capacity of centralized storage. The results are highlighted by means of a Finnish case study.
The rest of the paper is structured as follows. Section 2 describes the preliminary basis of the work, which includes a detailed representation of renewable generation modeling in the power system and space heating estimation methodology. Section 3 presents the methodology to assess the optimal hydrogen energy storage capacity for intermittent renewable generation integration. Case study and results are presented in Section 4. Conclusion of the work is stated in Section 5.
2. Methodology
This section constitutes a methodology of intermittent renewable generation modeling in Section 2.1 as well as the basis for modeling the thermal dynamic behaviors of domestic heat pumps as integrated with thermal storage in Section 2.2. The space heating model, a two capacity thermal model, has already been introduced by Ali et al. [16] and does not constitute an original contribution of this work. However, the thermodynamic model is repeated for the sake of completeness.
2.1. Renewable Generation Modelling
The analyses of this paper require the production of several realistic intermittent renewable generation time series, accounting for different wind and photovoltaic (PV) penetrations for each scenario. Wind power generation can be modelled utilizing a statistical methodology developed for modelling wind power generation scenarios with new generation locations without any measurement data. The methodology is presented in detail in Ekström et al. [17]. On the other hand, the required PV generation can be modelled with a statistical methodology designed for the simulation of new PV generation scenarios, as presented in Ekström et al. [18]. This approach is also suitable for modelling new PV plants in locations without measurement data.
To capture the effect of the temporal and spatial dependency structures between wind and PV generation on the aggregated intermittent renewable generation, a joint modelling of both generation types was utilized in the simulations. This approach combines the simulation methodologies presented for wind and PV generation in studies by Ekström et al. in 2015 and 2016 [17,18] and as shown in a paper by Ekström et al. in 2017 [19]. The methodology was designed for long-term simulation studies of new intermittent renewable generation scenarios using Monte Carlo simulations and produces both synthetic wind and PV generation time series. These time series can be combined into aggregated intermittent renewable generation time series, which can be utilized in the case studies.
The wind power generation structure for the simulations were built according to the actual wind generation structure in Finland at the beginning of 2016, which took into account existing wind farms and their geographical locations. Depending on the intermittent renewable generation penetration in each scenario, the existing wind farms were expanded with new turbines to achieve the required installed capacity. For the PV generation, the installed capacity was always divided equally into 12 locations throughout Southern Finland. The average capacity factor for the aggregated wind generation was 0.2796 and 0.1181 for the PV.
One year from the 100 simulated years of aggregated intermittent renewable generation was selected to be used in the analyses; however, a sensitivity analysis on optimal storage sizing with respect to multiple renewable generation runs is also presented. The single simulated year for each case was chosen as a representation of a good year in terms of hourly average aggregated intermittent renewable generation. However, to avoid the most extreme (i.e., too optimistic) cases, the best year within the 95th percentile was selected for each case.
2.2. Electric Storage Space Heating System
The structure of the considered heating system is shown in Figure 1. In Finland, this system is ubiquitous in the household sector. These installations have a large thermal storage tank (with typical storage units around 300–500 L) to store hot water which can be used for both space heating and domestic hot water.
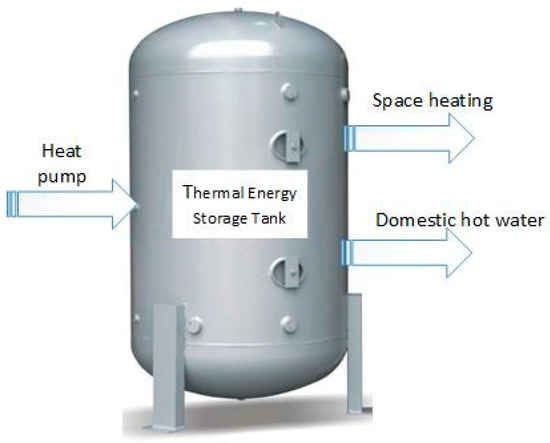
Figure 1.
Schematic of electric storage space heating system.
Space Heating Estimation
In this paper, a comprehensive two capacity building model, as illustrated in Figure 2, is utilized to estimate the space heating requirement.
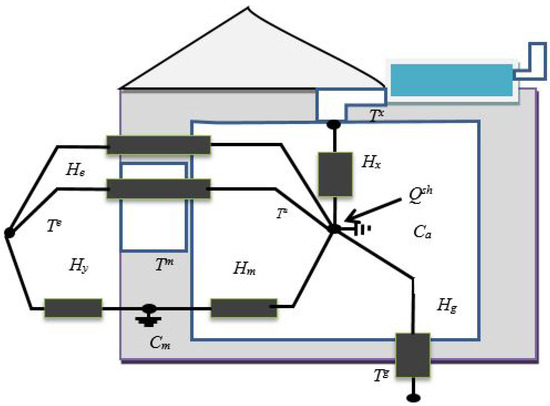
Figure 2.
Two capacity building model.
This model is reasonably accurate for the assessment of the heating/cooling requirement in a dynamic situation for multi-zone buildings. The thermal mass of the building structure is driven by the heat capacity, Cm, which is located in the depth of the building. The dynamic response was modelled through a state space equation given the following:
The state space equation can be transformed into an approximately equivalent discrete time model to estimate the space heating requirement.
3. Sizing Energy Storage to Firm up Intermittent Renewable Generation
This section presents an optimization model to determine the minimum hydrogen energy storage capacity to mitigate the daily variability of renewable generation. It can be mathematically represented as follows:
The objective function is subjected to the following constraints:
Constraint (5) ascertains that the system demand and generation is balanced every hour. Notably, there is no option for load curtailment; however, renewable generation curtailment is possible. A non-negative constraint is added in (6) to determine the degree of curtailment, if any. The dynamics of the state of charge of hydrogen energy storage is expressed in (7) with round-trip efficiency of . The maximum charging/discharging power of hydrogen energy storage is bounded in (8), while constraint (9) restricts the permissible state of charge limits of energy storage. The total system demand is determined in (10), which is the summation of critical and flexible demand. The flexible demand is a demand response through domestic thermal energy storages. Note that the flexible demand depends on the input of the case study. The evolution of heat stored in thermal storage is described in (11) by a simplified linear equation. The constraint (12) includes the upper and lower limit of energy stored in thermal storage. Rated power of thermal storage unit is bounded by (13). Constraint (14) accounts for the non-ideality of thermal storage. The constraint (15) determines the total demand response.
The input data of the model are solar generation, wind generation time series data, building thermal model parameters, a customer’s temperature preferences, and critical load. The optimal decisions from this framework include energy storage capacity, demand response and total renewable generation curtailment, and charging/discharging time series of hydrogen energy storage. The above model is formulated as a linear programming problem and can be solved using the CPLEX solver via GAMS.
4. Case Studies and Results
4.1. Input Data
In this paper, we considered a renewable generation-based power system over a horizon of one year. The hourly level demand time series are given in Figure 3, which correspond to the Finnish electrical demand in 2015. The electrical demand was approximately 82 TWh.
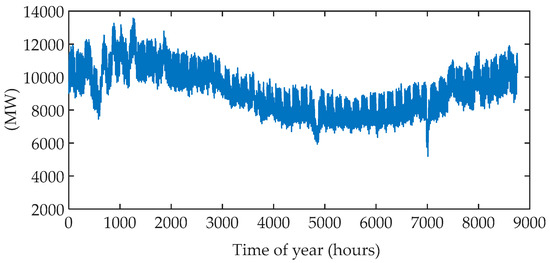
Figure 3.
Hourly level demand data.
The renewable generation profiles (70% wind and 30% solar) are simulated as described by Section 2 with a total generation of 87 TWh. The single run used in the simulation is shown in Figure 4. The base-load generation was assumed to be 25% of annual generation; the time series is given in Figure 5. The base-load time series are from Finnish nuclear production in 2015. The storage technology is hydrogen storage with a power to gas efficiency of 75% and fuel cell efficiency of 65%. It was assumed that the final level of centralized energy storage needs to be within ±20% of the initial level of storage.
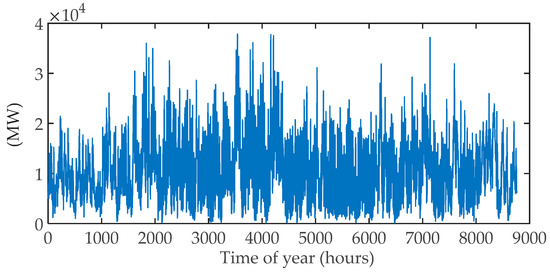
Figure 4.
Renewable generation (70% wind and 30% PV) time series.
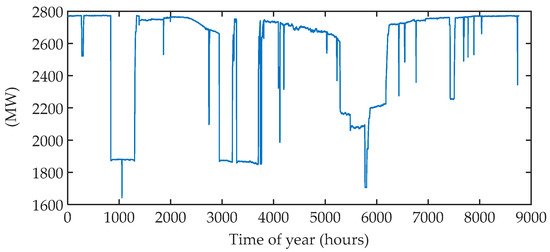
Figure 5.
Hourly base-load generation time series used in the simulation.
For the storage space heating system, it was assumed that 300,000 customers were equipped with 60 kWh and 8 kW domestic thermal storage, with storage losses of 1%. Space heating load was estimated using the model described in Section 2.2, taking into account different building components in Finland as well as outside temperature profiles. The domestic hot water load was aggregated into critical demand as it represented a fraction of household annual consumption.
This case study examined the size of hydrogen energy storage for the following scenarios.
- Case 1
- This represents a base case, in which hydrogen energy storage capacity is optimized to accommodate renewable generation without coordinating with demand response.
- Case 2
- This represents a case of hydrogen energy storage sizing in the presence of demand response through domestic thermal storages. Demand response enrollment was considered to be 100%.
- Case 3
- This represents a case of hydrogen energy storage sizing in the presence of 25% of base-load generation in the system.
The above cases were simulations and corresponding results are discussed henceforth. In addition to the above cases, intensive sensitivity analyses were performed on the results to investigate the impact of the increasing amount of renewable generation.
4.2. Simulation Results
Taking the case studies mentioned above into consideration, the proposed model optimized the size of the hydrogen energy storage in order to balance both generation and demand as well as to better integrate renewable generation into the power system.
Case 1 Hydrogen Energy Storage Sizing without Demand Response
For the base case scenario, it was assumed that the system was renewable generation-based with 70% wind and 30% solar. However, in this case, no system-wide demand response was activated and the case served as a benchmark against the other cases.
According to the optimization results, the hydrogen storage capacity of approximately 67 TWh (82% of system annual demand) was needed to balance the system demand to avoid any curtailment. Figure 6 shows the energy time series of the centralized storage and residual load. As such, it is evident from Figure 6 that hydrogen storage operation was more demanding during the spring season because of high renewable generation. Despite the over-generation hours, there was no curtailment, as storage capacity was adequate to absorb any excess renewable generation.
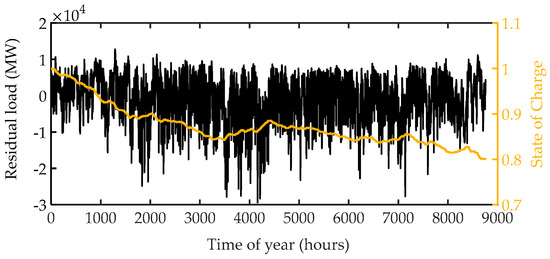
Figure 6.
Residual load and energy time series of the energy system in Case 1.
The obtained optimum storage capacity was based on a single run of a renewable generation time series. However, given the variability and uncertainty of the renewable generation, it was important to determine the most relevant statistics for the observed results. To do this, we simulated the basic study for multiple runs (100) and calculated the mean value, the standard deviation, and the lower and upper 95% confidence intervals for the mean. The overview of basic results are given in Table 1.

Table 1.
Case 1 Results Stats.
Case 2 Hydrogen Energy Storage Sizing with Demand Response through Domestic Thermal Storages
The hydrogen energy storage system size in Case 2, in which demand response was activated to minimize the storage requirement, resulted in 58 TWh (0.71 p.u.). The result exhibited a superior performance when compared to Case 1, as the hydrogen energy storage capacity reduced by 14% in a renewable generation system. Figure 7 presents the hourly residual load and the state of charge of the hydrogen energy storage.
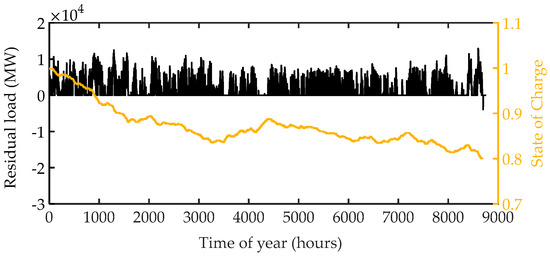
Figure 7.
Residual load and energy time series of the energy system in Case 2.
Notably, the domestic thermal storages, in coordination with the hydrogen energy storage, smoothed the volatility; consequently, it reduced the size of hydrogen storage needed. However, 13 GWh of generation curtailment was observed in this case.
Next, the opportunities of demand response through increased thermal storage size to minimize the required hydrogen storage capacity were assessed. The evolution of the optimal hydrogen storage capacity, with respect to domestic thermal storages capacity, is presented in Figure 8. Notably, there was a clear difference in the results with the integration of thermal energy storage. The figure clearly shows that an increase in domestic thermal storage size from one day (60 kWh) to two days (120 kWh), resulted in an approximately 10% reduction in required hydrogen storage capacity. However, when increasing from a two-day storage capacity to three-day storage, the reduction was marginal, as the benefits of demand response saturated very quickly.
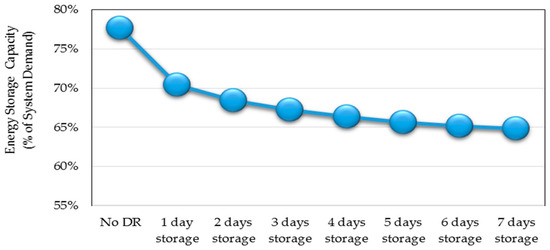
Figure 8.
Influence of domestic demand response on hydrogen energy storage sizing.
Case 3 Energy Storage Sizing in the Presence of Base-Load Generation
The effect of base-load generation on energy storage size is presented in Case 3. Base-load generation comprised 25% of total generation, with the remaining generation deriving from wind and solar. According to the obtained result, to keep the system balanced, an energy storage size of 46 TWh (0.56 p.u.) was required as well as 18 GWh of curtailment. The hydrogen storage size decreased 31% and 20% when compared with Case 1 and Case 2, respectively. The storage energy time series and residual load in this case is shown in Figure 9. Notably, the base-load generation significantly to the renewable generation power system balance.
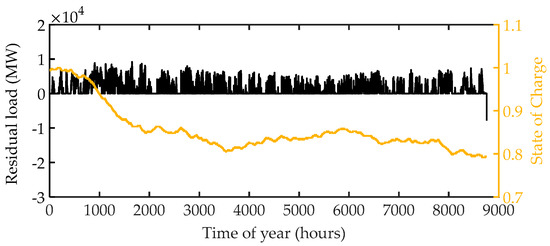
Figure 9.
Residual load and energy time series of the energy system in Case 3.
Sensitivity Analyses
In this sub-section, a sensitivity analysis was conducted to determine the influence of increasing renewable generation on hydrogen energy storage capacity size. Figure 10 demonstrates the evolution of sizes of energy storage systems with respect to the increasing generation in the system.
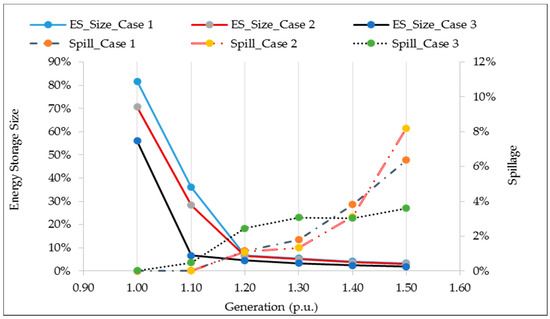
Figure 10.
Hydrogen energy storage size (% of demand) and spillage (% of generation) in different cases.
Notably, in Case 3, base-load generation was fixed (25% of annual generation in the base case), while renewable generation capacity was increased. As can be observed from the result, the storage capacity requirement decreased drastically as the renewable generation was oversized to 110–120% of the energy demand in the system. The storage capacity was reduced by approximately 55%, 60%, and 62%, with an increase of 10% of renewable generation in the system in Case 1, Case 2, and Case 3, respectively. However, the spillage of renewable generation increased as the amount of renewable increased in the system. This clear trend was observable from the model’s attempt to minimize the energy storage capacity; accordingly, over-generation resulted in spillage.
It is clear from Figure 10 that the base-load generation appeared to drastically decrease the storage capacity requirement when compared with the other cases; simultaneously, it increased the spillover of renewable generation. A summary of the sensitivity results are given in Table 2.

Table 2.
Overview of Sensitivity Analysis Results.
5. Conclusions
Wind and solar generation are increasingly found in worldwide power systems. However, they pose huge integration challenges in the current power system. This paper addresses the sizing issue of large-scale hydrogen energy storage from the perspective of power systems to mitigate the balancing issue of renewable generation. The second contribution of this paper is an analysis of the opportunities for demand response in optimal energy storage size within a renewable generation-based power system. Accordingly, a framework is presented for the optimal sizing of energy storage in a highly renewable generation power system, as applied to a case study in Finland. Results indicate that a significant amount of the balancing needs should be served from large-scale energy storage; however, it was also found that demand response, controllable generation, and energy storage could play complementary roles, supporting each other to economically meet energy-balancing needs. Oversizing of renewable energy generation effectively reduces the required size of hydrogen storage. However, this also has a negative result of an increased spillage of power.
Author Contributions
Mubbashir Ali proposed the framework and performed simulations. Jussi Ekström performed the renewable generation time series modelling, and Matti Lehtonen supervised the work.
Acknowledgments
This work was supported by Aalto University’s Sustainable Transition of European Energy Markets (STEEM) Project.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Indices and Sets | |
| n, N | Index and set of customers |
| t, T | Index and set of time e.g., hours |
| Parameters and Constants | |
| Ca | Heat capacity of the indoor air (MJ/°C) |
| Cm | Heat capacity of the building fabric (MJ/°C) |
| He | Summation of the infiltration heat capacity flow and house’s window heat conductance (W/°C) |
| Hg | Floor heat conductance (W/°C) |
| Hm | Thermal conductance which allows Cm to be lumped in the mass node point (W/°C) |
| Hx | Ventilation air heat conductance (W/°C) |
| Hy | Heat conductance in the solid walls and convection of surface (W/°C) |
| Power rating of thermal storage (kW) | |
| Power of all critical appliances at time t of customer n (kW) | |
| Domestic hot water consumption of customer n at time t | |
| Maximum allowable state of charge of thermal storage (of customer n) | |
| Minimum allowable state of charge of thermal storage (of customer n) | |
| Temperature of dwelling at time t (of customer n) (°C) | |
| Outside temperature at time t (°C) | |
| Ground temperature at time t (°C) | |
| Ventilation supply air temperature (°C) | |
| Renewable generation at time t (kW) | |
| Conventional generation at time t (kW) | |
| Duration of time slot (hours) | |
| Charging/Discharging efficiency of hydrogen energy storage | |
| Demand limit (kW) | |
| Internal temperature dead-band (of customer n) (°C) | |
| Maximum thermal energy storage capacity (kWH) | |
| Space heating load at time t | |
| Domestic heating load at time t | |
| Thermal energy storage heat loss rate | |
| Thermal energy storage heat loss coeff. | |
| Functions and Variables | |
| Critical demand at time t (kW) | |
| Heating demand at time t (kW) | |
| Total demand at time t (kW) | |
| Electrical power supplied to storage space heating unit at time t (of customer n) (kW) | |
| HVAC thermal output power at time t (of customer n) (kW) | |
| State of charge of Energy storage at time t | |
| Indoor ambient temperature of dwelling at time t (of customer n) (°C) | |
| Thermal mass temperature at time t (°C) | |
| Thermal Storage losses at time t (of customer n) (kWh) | |
| Variable to regulate renewable generation | |
| Charging rate of thermal energy storage | |
| Power of energy storage at time t | |
| Charge level of thermal energy storage at time t | |
| Maximum power capacity of hydrogen energy storage | |
| Maximum energy capacity of hydrogen energy storage | |
References
- IEA PVPS. Available online: http://www.iea-pvps.org/fileadmin/dam/public/report/statistics/IEA-PVPS_-_A_Snapshot_of_Global_PV_-_1992-2016__1_.pdf (accessed on 1 July 2017).
- WindEurope. Available online: https://windeurope.org/about-wind/statistics/european/wind-in-power-2016/ (accessed on 10 March 2017).
- NREL. Available online: https://www.nrel.gov/docs/fy14osti/61721.pdf (accessed on 1 July 2017).
- Bird, L.; Lew, D.; Milligan, M.; Carlini, E.M.; Estanqueiro, A.; Flynn, D.; Gomez-Lazaro, E.; Holttinen, H.; Menemenlis, N.; Orths, A.; et al. Wind and solar energy curtailment: A review of international experience. Renew. Sustain. Energy Rev. 2016, 65, 577–586. [Google Scholar] [CrossRef]
- Burke, D.J.; O’Malley, M.J. Factors Influencing Wind Energy Curtailment. IEEE Trans. Sustain. Energy 2011, 2, 185–193. [Google Scholar] [CrossRef]
- Alnaser, S.W.; Ochoa, L.F. Optimal Sizing and Control of Energy Storage in Wind Power-Rich Distribution Networks. IEEE Trans. Power Syst. 2016, 31, 2004–2013. [Google Scholar] [CrossRef]
- Ke, X.; Lu, N.; Jin, C. Control and size energy storage systems for managing energy imbalance of variable generation resources. IEEE Trans. Sustain. Energy 2015, 6, 70–78. [Google Scholar] [CrossRef]
- Cleary, B.; Duffy, A.; OConnor, A.; Conlon, M.; Fthenakis, V. Assessing the economic benefits of compressed air energy storage for mitigating wind curtailment. IEEE Trans. Sustain. Energy 2015, 6, 1021–1028. [Google Scholar] [CrossRef]
- Makarov, Y.V.; Du, P.; Kintner-Meyer, M.C.W.; Jin, C.; Illian, H.F. Sizing Energy Storage to Accommodate High Penetration of Variable Energy Resources. IEEE Trans. Sustain. Energy 2012, 3, 34–40. [Google Scholar] [CrossRef]
- Fazeli, R.; Davidsdottir, B.; Hallgrimsson, J.H. Residential energy demand for space heating in the Nordic countries: Accounting for interfuel substitution. Renew. Sustain. Energy Rev. 2016, 57, 1210–1226. [Google Scholar] [CrossRef]
- Ali, M.; Ekström, J.; Alahäivälä, A.; Lehtonen, M. Assessing the Upward Demand Response Potential for Mitigating the Wind Generation Curtailment: A Case Study. In Proceedings of the 14th International Conference on the European Energy Market, Dresden, Germany, 6–9 June 2017. [Google Scholar]
- Ali, M.; Ekström, J.; Lehtonen, M. Assessing the Potential Benefits and Limits of Electric Storage Heaters for Wind Curtailment Mitigation: A Finnish Case Study. Sustainability 2017, 9, 836. [Google Scholar]
- Ali, M.; Humayun, M.; Safdarian, A.; Degefa, M.; Lehtonen, M. A Framework for activating residential HVAC demand response for wind generation balancing. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Asia, Bangkok, Thailand, 4–6 November 2015. [Google Scholar]
- Lund, H.; Kempton, W. Integration of renewable energy into the transport and electricity sectors through V2G. Energy Policy 2008, 36, 3578–3587. [Google Scholar] [CrossRef]
- Guille, C.; Gross, G. A conceptual framework for the vehicle-to-grid (V2G) implementation. Energy Policy 2009, 37, 4379–4390. [Google Scholar] [CrossRef]
- Ali, M.; Safdarian, A.; Lehtonen, M. Demand Response Potential of HVAC Load Considering User Preferences. In Proceedings of the ISGT Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Ekström, J.; Koivisto, M.; Mellin, I.; Millar, J.; Saarijärvi, E.; Haarla, L. Assessment of Large Scale Wind Power Generation with New Generation Locations without Measurement Data. Renew. Energy 2015, 83, 362–374. [Google Scholar] [CrossRef]
- Ekström, J.; Koivisto, M.; Millar, J.; Mellin, I.; Lehtonen, M. A Statistical Approach for Hourly Photovoltaic Power Generation Modeling with Generation Locations without Measured Data. Sol. Energy 2016, 132, 173–187. [Google Scholar] [CrossRef]
- Ekström, J.; Koivisto, M.; Mellin, I.; Millar, J.; Lehtonen, M. A Statistical Model for Hourly Large-Scale Wind and Photovoltaic Generation in New Locations. IEEE Trans. Sustain. Energy 2017, 8, 1383–1393. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).