Maximum Power Point Tracking for Brushless DC Motor-Driven Photovoltaic Pumping Systems Using a Hybrid ANFIS-FLOWER Pollination Optimization Algorithm
Abstract
:1. Introduction
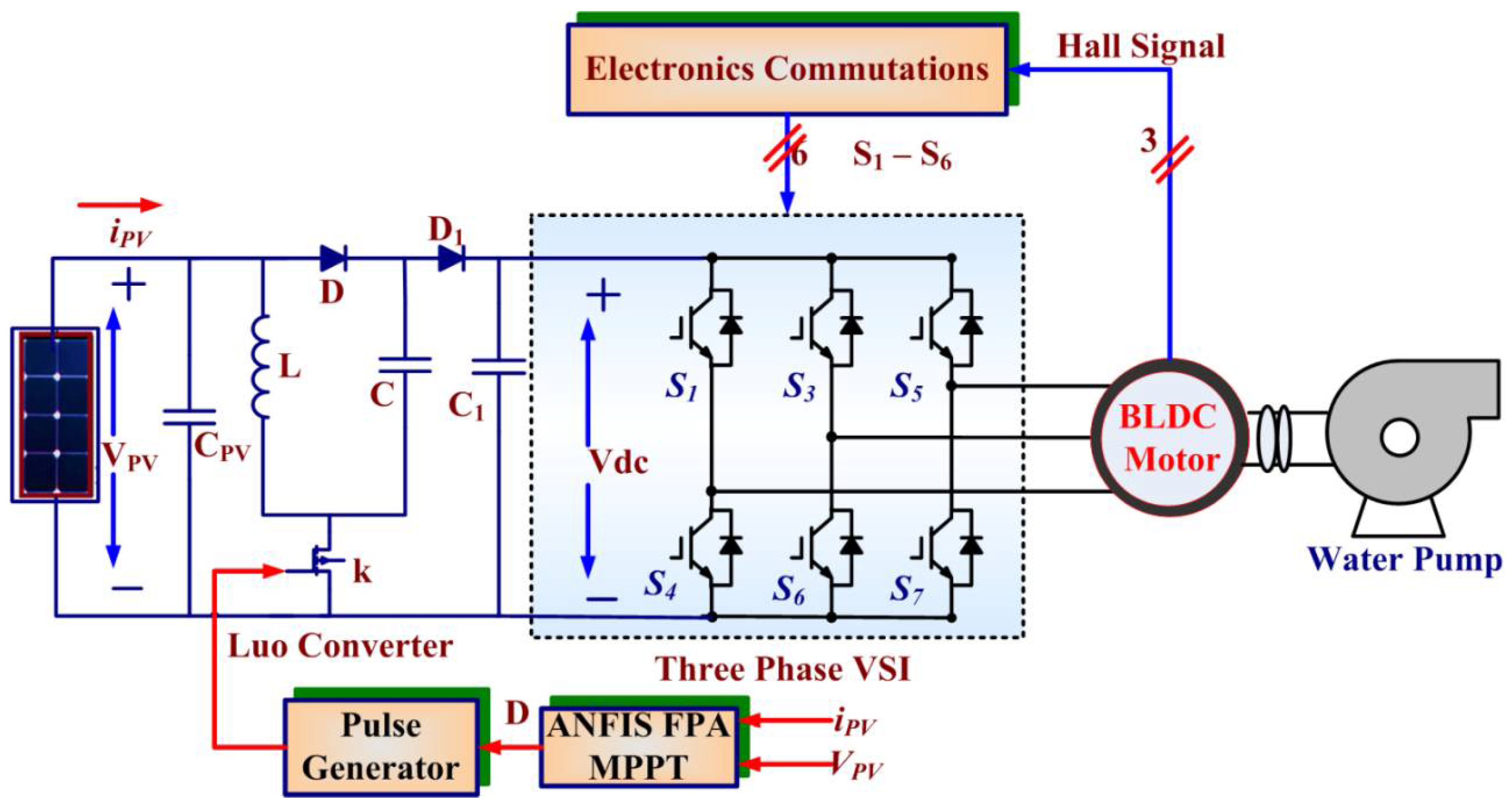
2. Complete System Formation
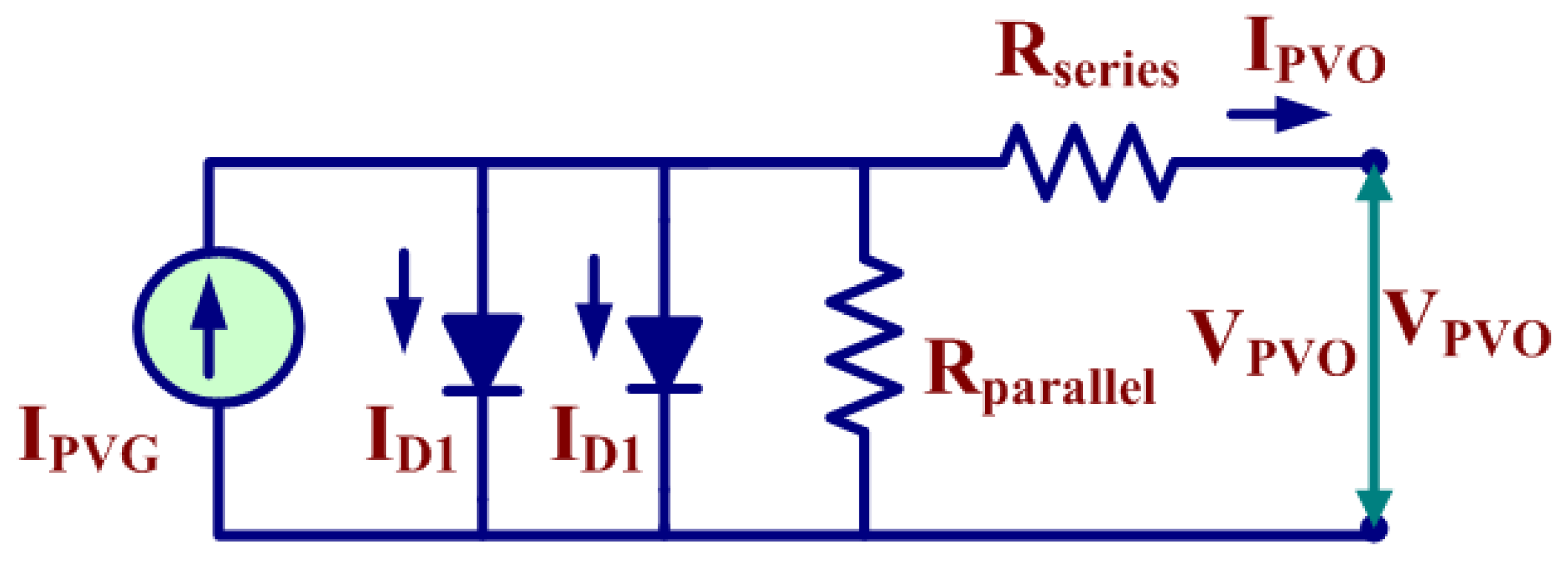
2.1. PV Generator
- IPVG = Photo Current
- IRSC = Diode reverse saturation current
- IPVo = Output PV current
- VPVo = PV output voltage
- Rseries = Resistance in series
- RParallel = Resistance in parallel
- VThermal = PV module thermal voltage
- A = Ideality constant of diode
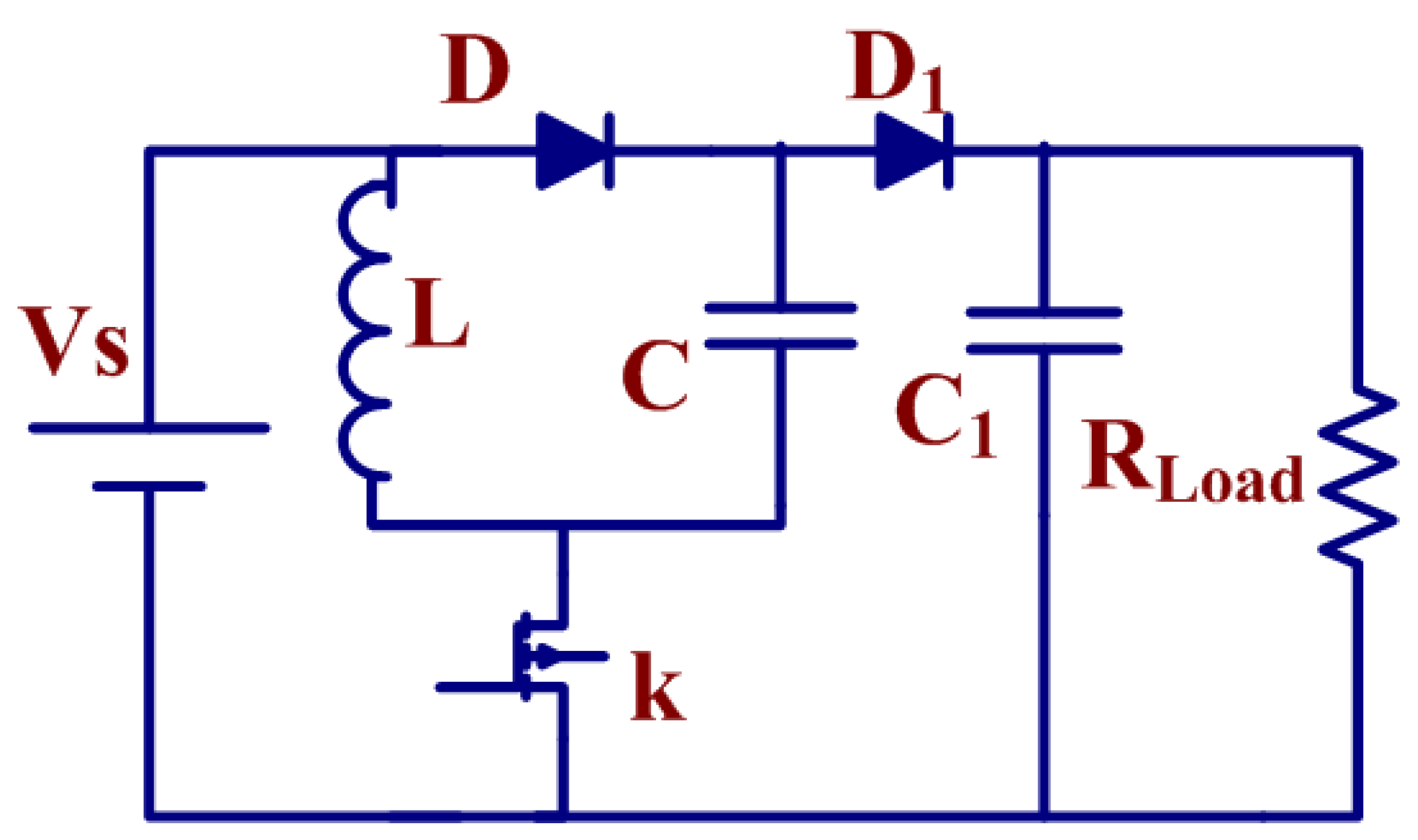
2.2. Luo Converter Mathematical Modeling
- dduty = Duty ratio
- fPulse = Frequency of Switched pulse
- V0 = Output Voltage of Luo Converter
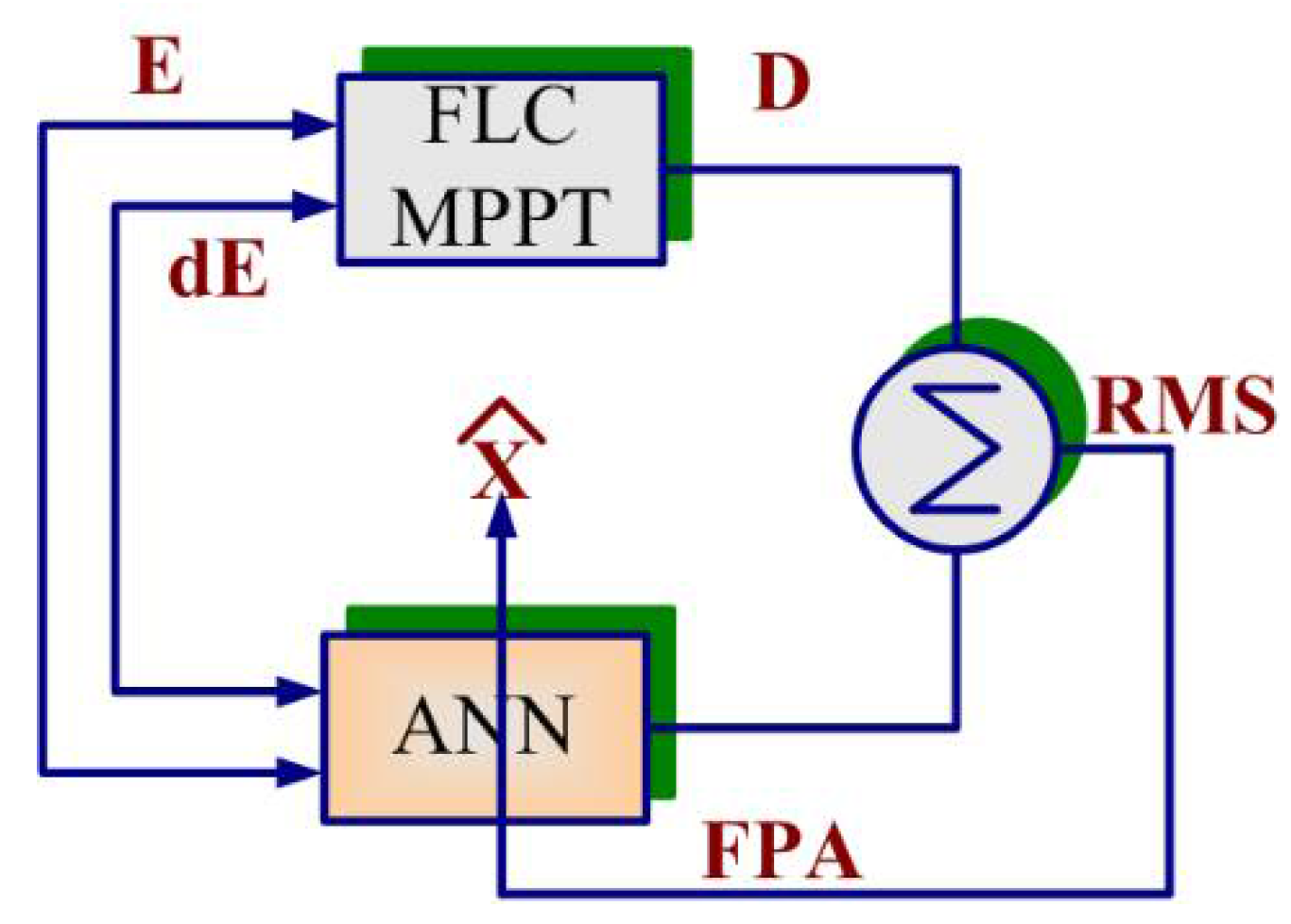
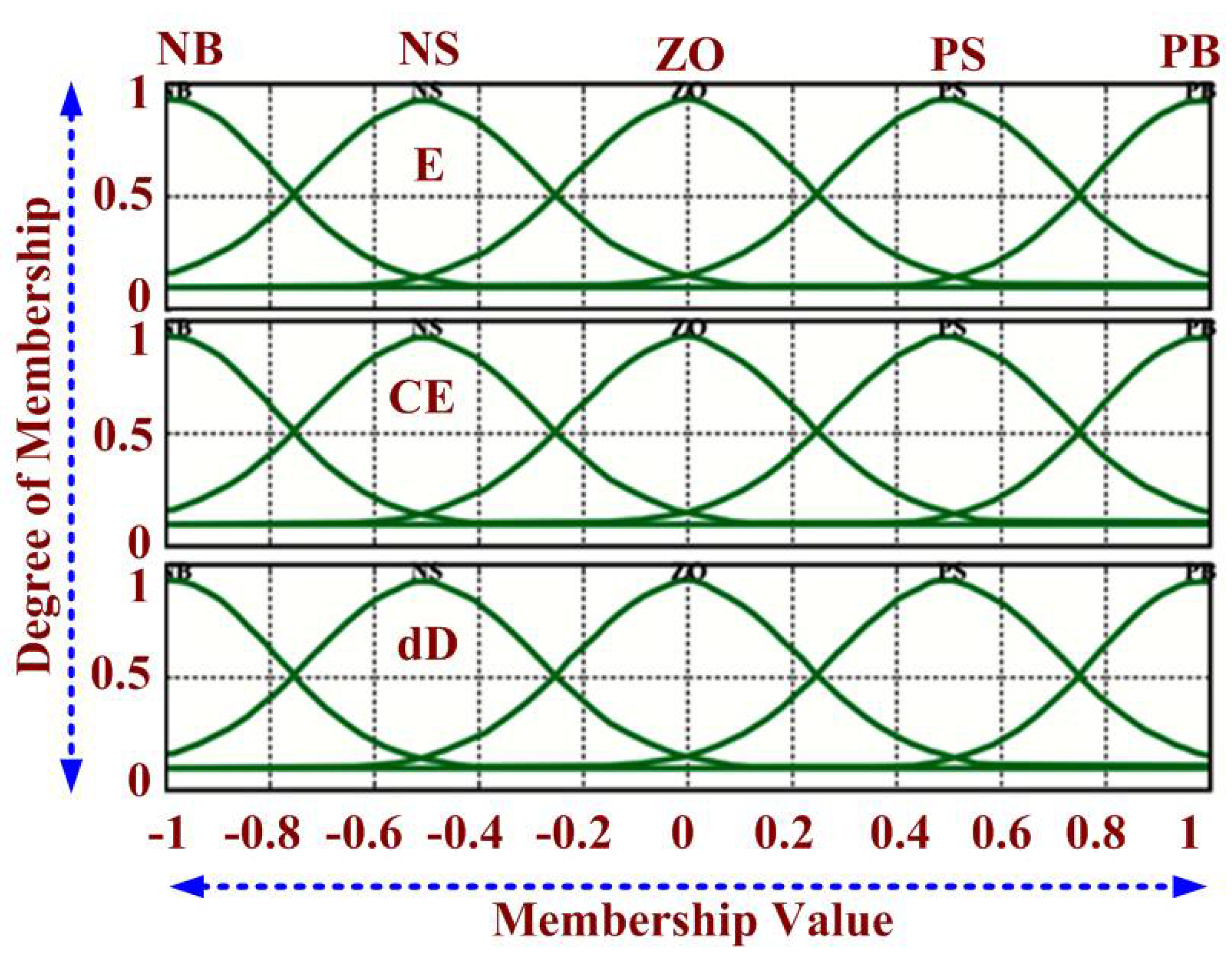
2.3. A Hybrid Proposed FLC-ANN Tuned FPA MPPT
- = Membership function of P fuzzy set in X Universe of discourse
- = Membership function of Q fuzzy set in Y Universe of discourse
- x, y variables defined in Universe X and Y, respectively
- = Crisp output
- = Membership function (Aggregated)
- D = Fuzzy output
- S = Subarea/Universe of discourse
- = Membership function of fuzzy set A in E universe of discourse
- = Membership function of fuzzy set B in dE universe of discourse
- WLi = Weight of consequent ith layer
- P = Total sample
- D = Fuzzy output
- = Neural network output
- = Vector representing solution
- T = No. of iteration
- Lf = Levy flight factor
- = Scaling factor
- Gbest = Global best solution
- and = two unlike pollen in the species
- Pf = Switched probability
- =nth iteration PV voltage
- =nth iteration PV current
- = change in PV voltage (nth and (n − 1)th iteration)
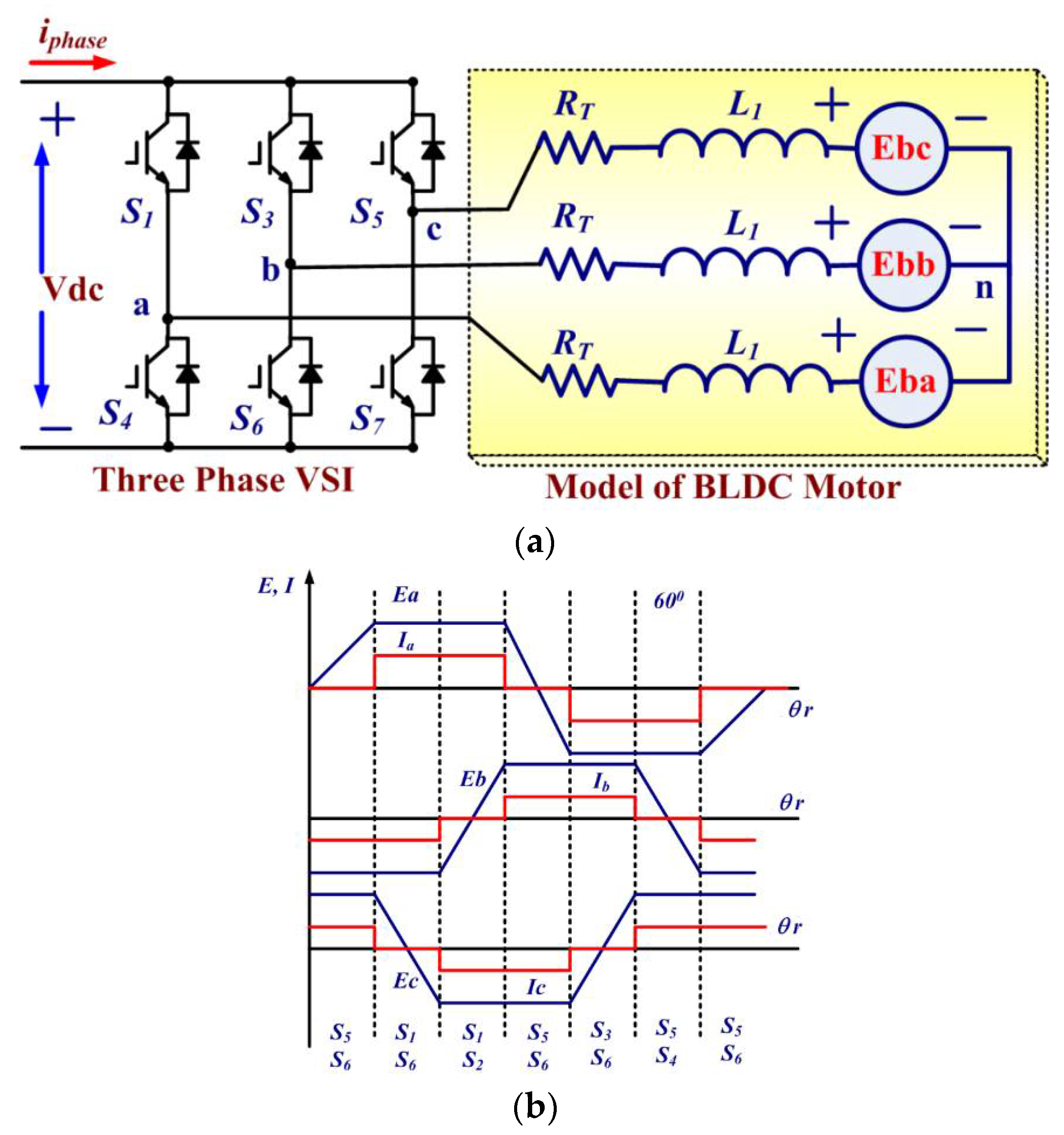
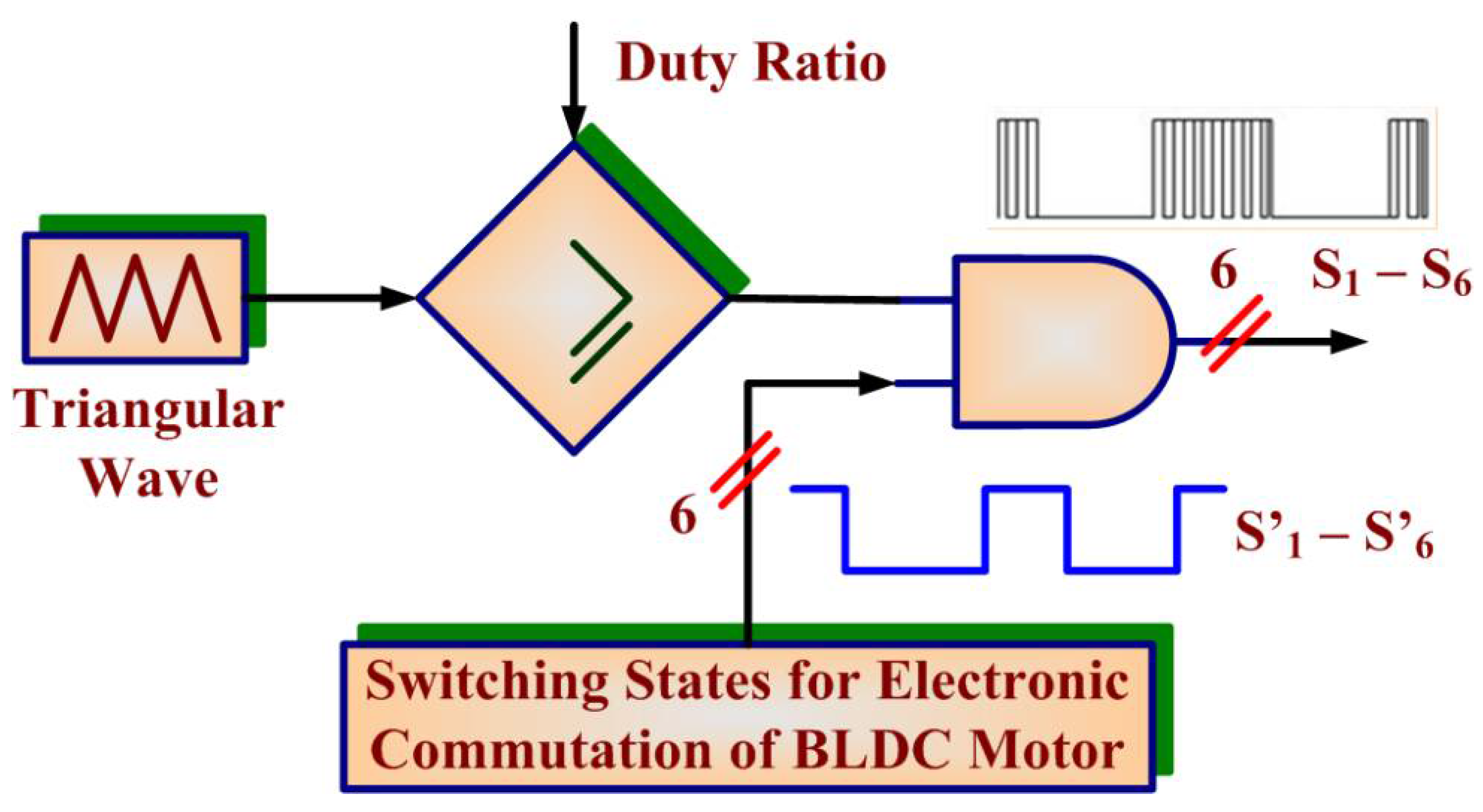
2.4. Electronic BLDC Commutator and VSI Switching
- Vap, Vbp, Vcp = Phase voltage of a 3-Phase BLDC motor
- Iap, Ibp, Icp = Phase Currents
- Eba, Ebb, Ebc = Phase Back EMF of BLDC motor
- L1 = Each Phase self-inductance
- M1 = Two phase’s mutual inductance
- TEM = Developed Electromagnetic torque of BLDC motor
- ωRotor = Rotor Speed
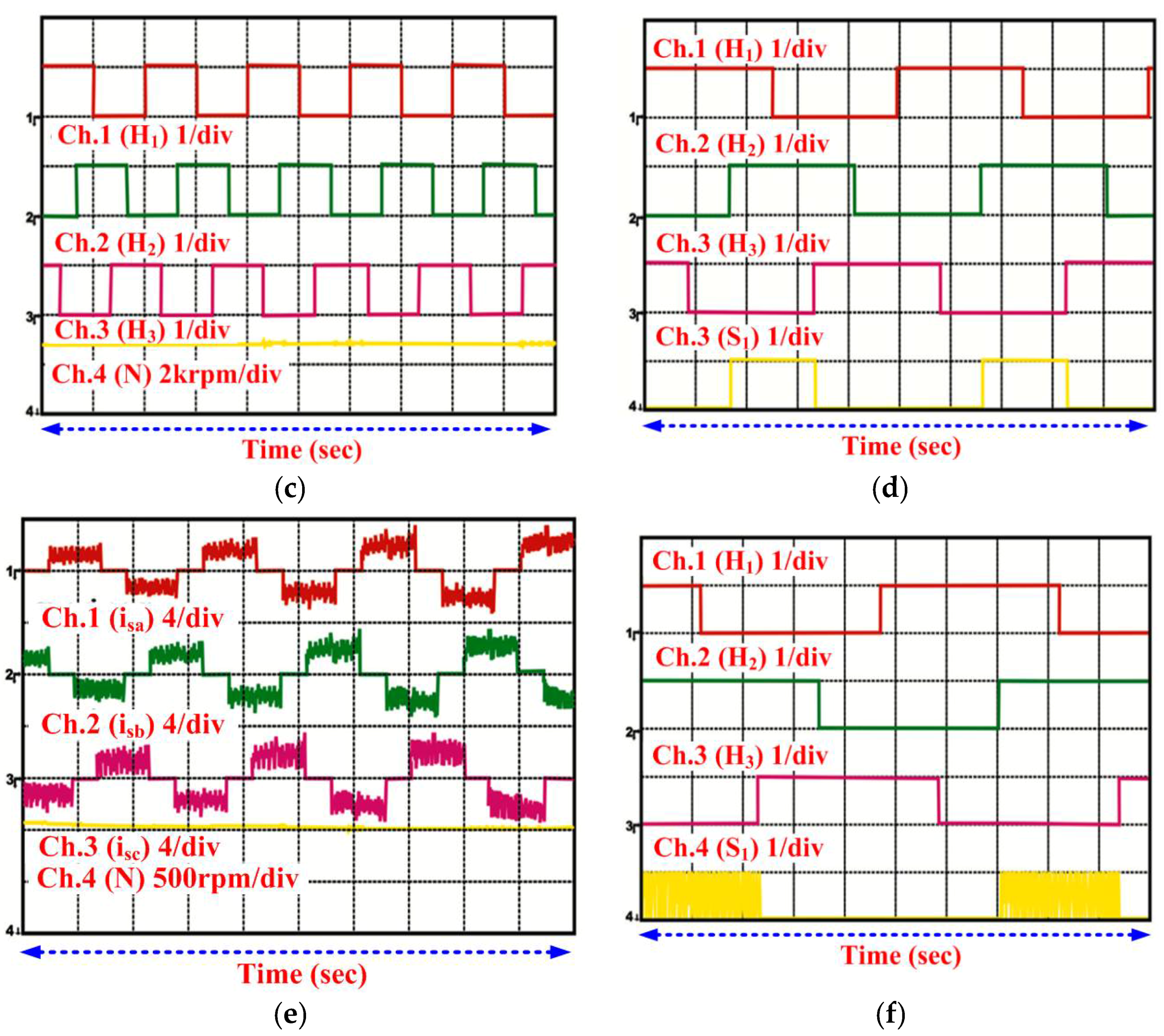
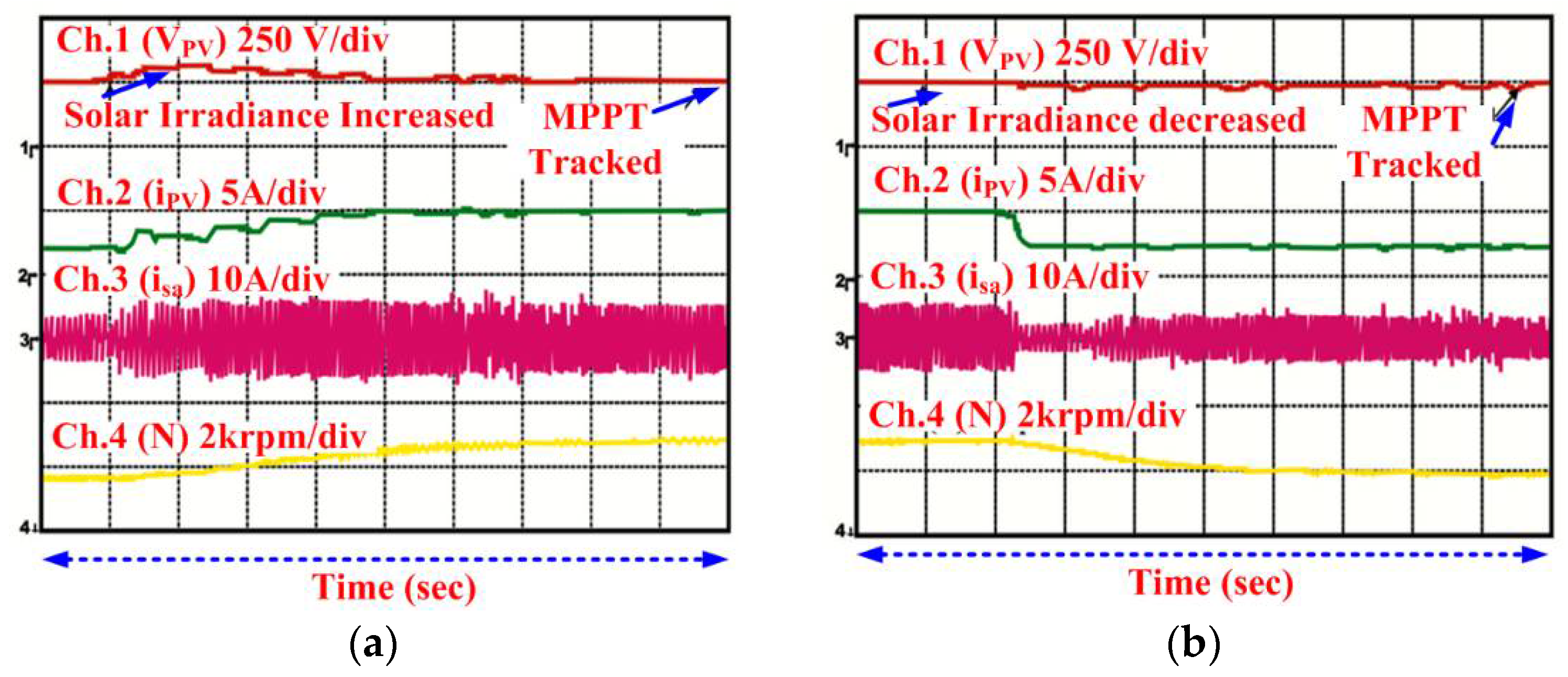
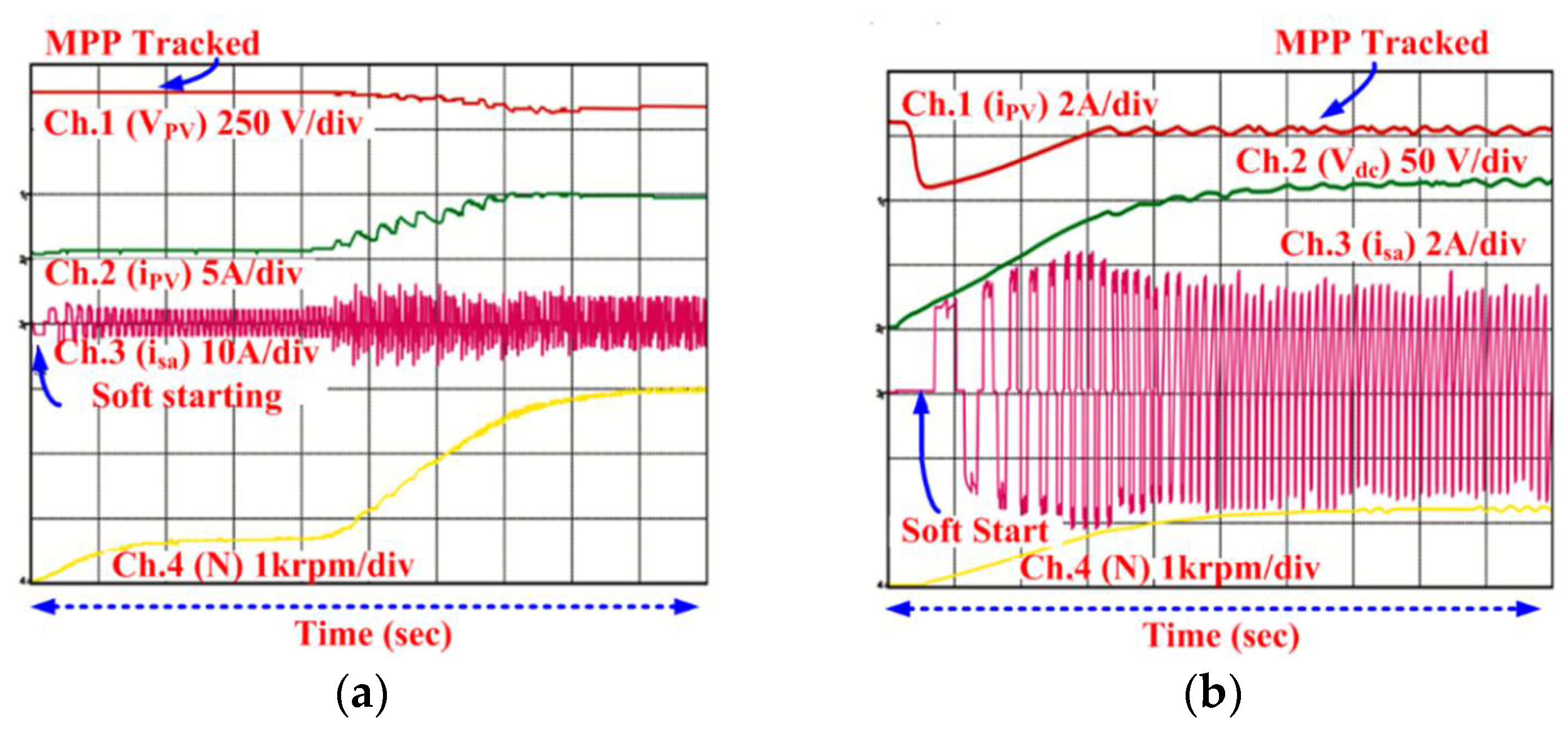
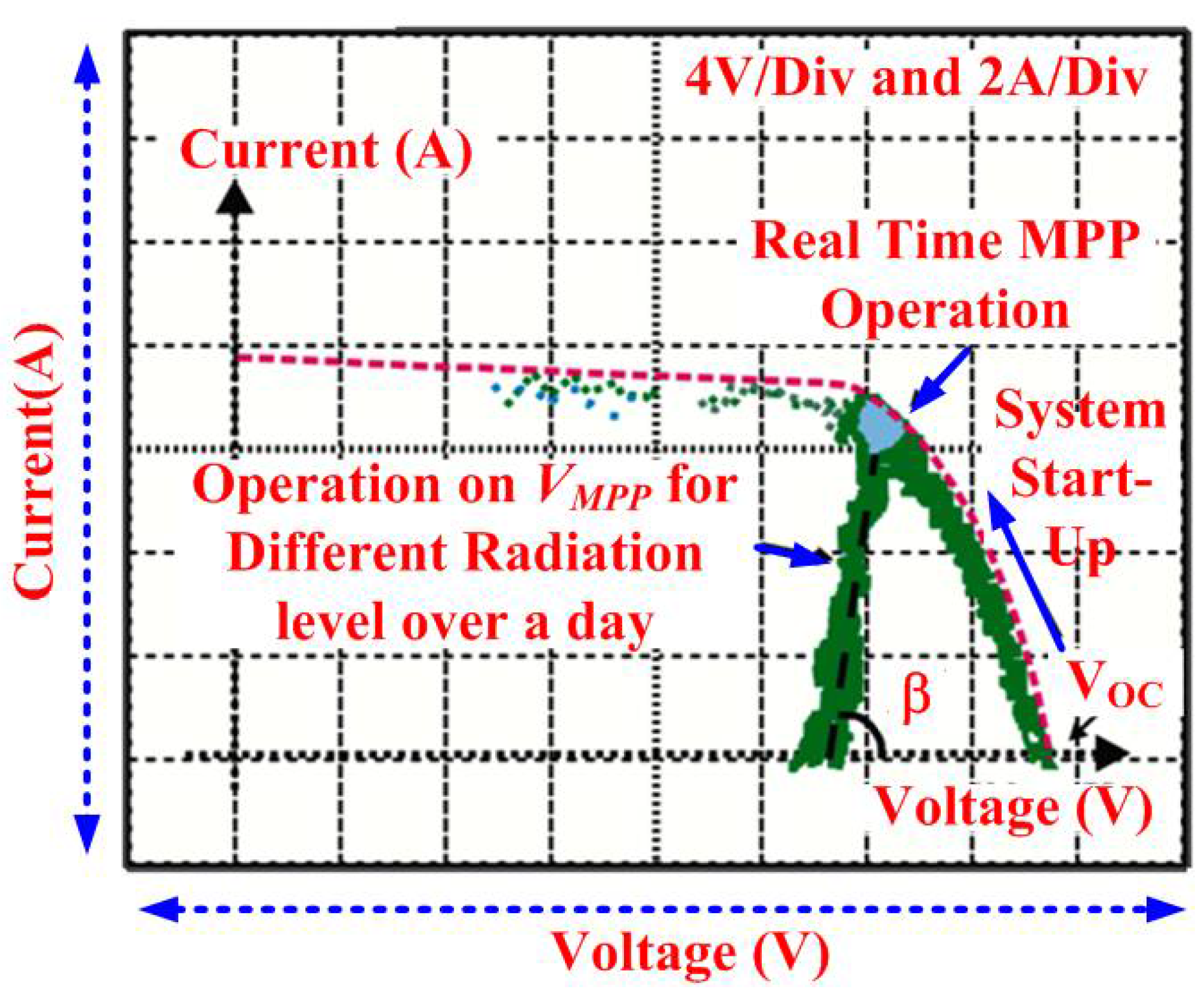
3. Experimental Results
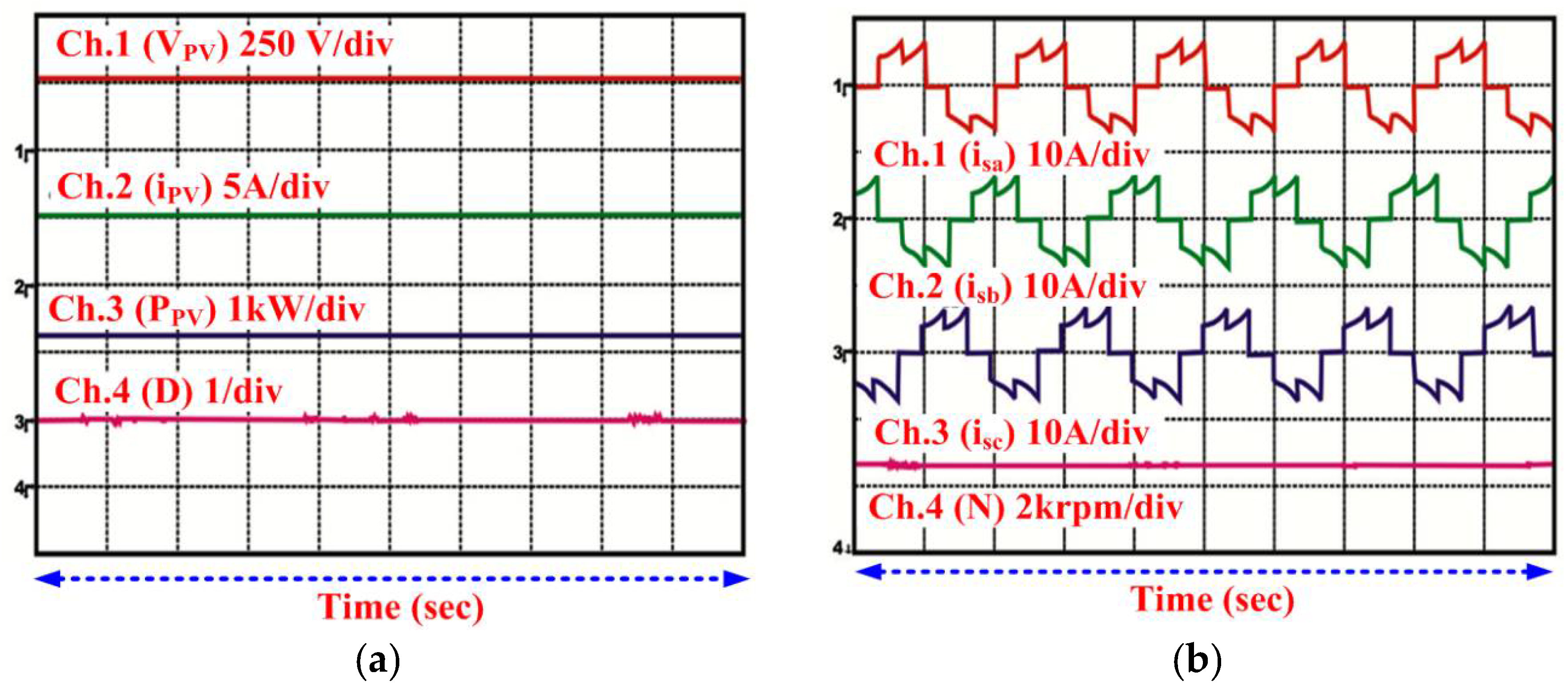
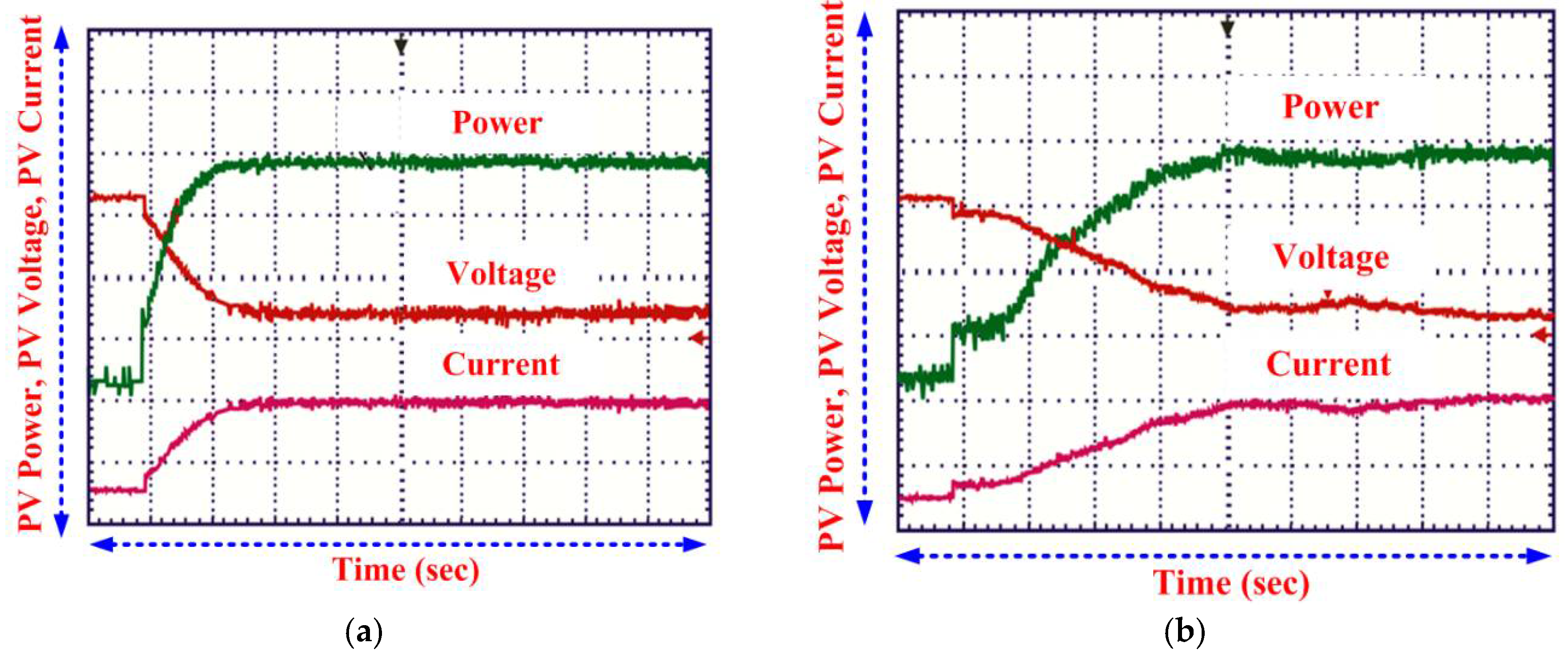
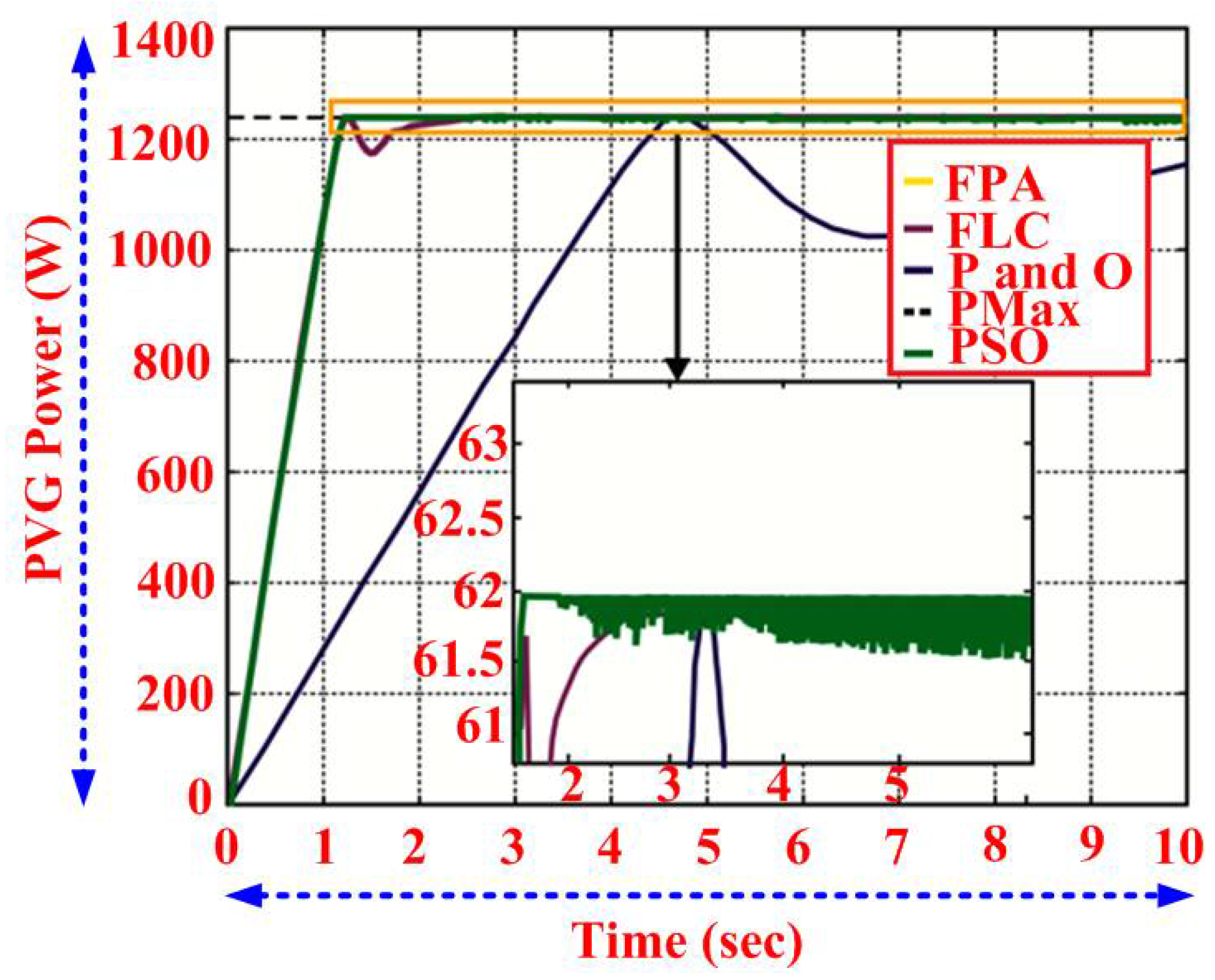
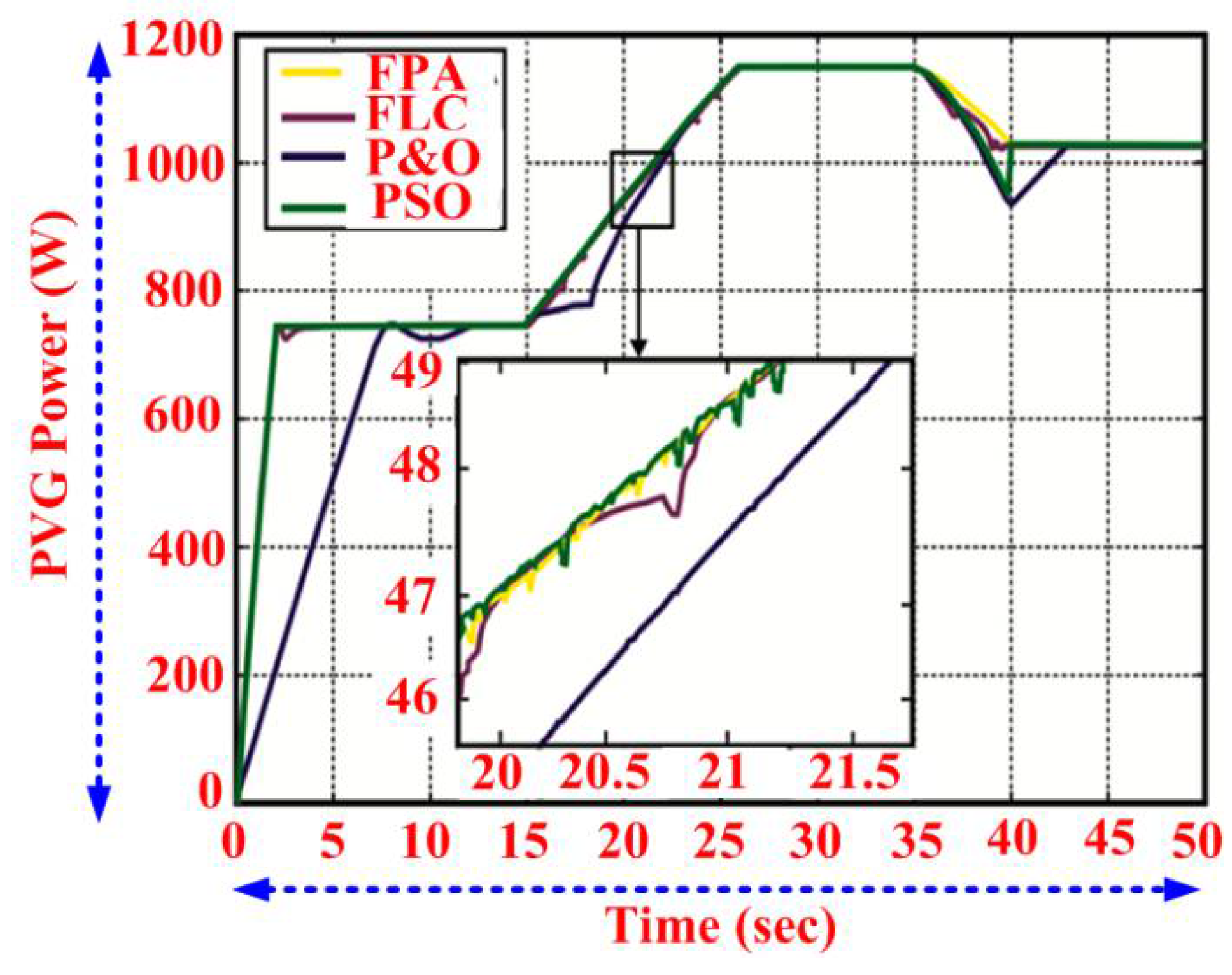
3.1. Steady-State Performance
3.2. Dynamic Behavior of PV System
3.3. Behavior at Starting
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Priyadarshi, N.; Sanjeevikumar, P.; Maroti, P.K.; Sharma, A. An Extensive Practical Investigation of FPSO based MPPT for Grid Integrated PV System under Variable Operating Conditions with Anti Islanding Protection. IEEE Syst. J. 2018. [Google Scholar] [CrossRef]
- Lakshman, N.P.; Palanisamy, K.; Babu, N.M.; Sanjeevikumar, P. Photovoltaic- STATCOM with Low Voltage Ride-Through Strategy and Power Quality Enhancement in Grid Integrated Wind-PV System. Electronics 2018, 7, 51. [Google Scholar]
- Jain, S.; Ramulu, C.; Sanjeevikumar, P.; Ojo, O.; Ertas, A.H. Dual MPPT Algorithm for Dual PV Source Fed Open-End Winding Induction Motor Drive for Pumping Application. Eng. Sci. Technol. 2016, 19, 1771–1780. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B. BLDC Motor Driven Solar PV Array Fed Water Pumping System Employing Zeta Converter. IEEE Trans. Ind. Appl. 2016, 52, 2315–2322. [Google Scholar] [CrossRef]
- Montorfano, M.; Sbarbaro, D.; Mor’an, L. Economic and technical evaluation of solar assisted water pump stations for mining applications: A case of study. IEEE Trans. Ind. Appl. 2016, 52, 4454–4459. [Google Scholar] [CrossRef]
- Alghuwainem, S.M. Speed Control of a PV Powered DC Motor Driving a Self- Excited 3-Phase Induction Generator for Maximum Utilization Efficiency. IEEE Trans. Energy Convers. 1996, 11, 768–773. [Google Scholar] [CrossRef]
- Jain, S.; Thopukara, A.K.; Karampuri, R.; Somasekhar, V.T. A Single-Stage Photo Voltaic System for a Dual- Inverter fed Open-End Winding Induction Motor Drive for Pumping Applications. IEEE Trans. Power Electron. 2015, 30, 4809–4818. [Google Scholar] [CrossRef]
- Sashidhar, S.; Fernandes, B.G. A Novel Ferrite SMDS Spoke-Type BLDC Motor for PV Bore-Well Submersible Water Pumps. IEEE Trans. Power Electron. 2017, 64, 104–114. [Google Scholar] [CrossRef]
- Killi, M.; Samanta, S. An Adaptive Voltage Sensor Based MPPT for Photovoltaic Systems with SEPIC Converter including Steady State and Drift Analysis. IEEE Trans. Power Electron. 2015, 62, 7609–7619. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Kumar, V.; Yadav, K.; Vardia, M. An Experimental Study on Zeta buck-boost converter for Application in PV system. In Handbook of Distributed Generation; Springer: Cham, Switzerland, 2017; pp. 393–406. [Google Scholar]
- Priyadarshi, N.; Anand, A.; Sharma, A.K.; Azam, F.; Singh, V.K.; Sinha, R.K. An Experimental Implementation and Testing of GA based Maximum Power Point Tracking for PV System under Varying Ambient Conditions Using dSPACE DS 1104 Controller. Int. J. Renew. Energy Res. 2017, 7, 255–265. [Google Scholar]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Framework of Maximum Power Extraction from Solar PV Panel using Self Predictive Perturb and Observe Algorithm. IEEE Trans. Sustain. Energy 2017, 9, 895–903. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of the Incremental Conductance Maximum Power Point Tracking Algorithm. IEEE Trans. Sustain. Energy 2013, 4, 108–117. [Google Scholar] [CrossRef]
- Zamora, A.C.; Vazquez, G.; Sosa, J.M.; Rodriguez, P.R.M.; Juarez, M.A. Efficiency Based Comparative Analysis of Selected Classical MPPT Methods. In Proceedings of the IEEE International Autumn Meeting on Power, Electronics and Computing, Ixtapa, Mexico, 8–10 November 2017; pp. 1–6. [Google Scholar]
- Abu-Rub, H.; Iqbal, A.; Ahmed, SK.M.; Peng, F.Z.; Li, Y.; Baoming, G. Quasi-Z-Source Inverter-Based Photovoltaic Generation System With Maximum Power Tracking Control Using ANFIS. IEEE Trans. Sustain. Energy 2013, 4, 11–20. [Google Scholar] [CrossRef]
- Mohamed, A.A.S.; Berzoy, A.; Mohammed, O. Design and Hardware Implementation of FL-MPPT Control of PV Systems Based on GA and Small-Signal Analysis. IEEE Trans. Sustain. Energy 2017, 8, 279–290. [Google Scholar] [CrossRef]
- Wang, L.; Singh, C. Population-Based Intelligent Search in Reliability Evaluation of Generation Systems with Wind Power Penetration. IEEE Trans. Power Syst. 2008, 23, 1336–1345. [Google Scholar] [CrossRef]
- Koad, R.B.A.; Zobaa, A.F.; El-Shahat, A. A Novel MPPT Algorithm Based on Particle Swarm Optimisation for Photovoltaic Systems. IEEE Trans. Sustain. Energy 2017, 8, 468–476. [Google Scholar] [CrossRef]
- Priyadarshi, N.; Sharma, A.K.; Azam, F. A Hybrid Firefly-Asymmetrical Fuzzy Logic Controller based MPPT for PV-Wind-Fuel Grid Integration. Int. J. Renew. Energy Res. 2017, 7, 1546–1560. [Google Scholar]
- Sundareswaran, K.; Sankar, P.; Nayak, P.S.R.; Simon, S.P.; Palani, S. Enhanced Energy Output From a PV System Under Partial Shaded Conditions Through Artificial Bee Colony. IEEE Trans. Sustain. Energy 2015, 6, 198–209. [Google Scholar] [CrossRef]
- Kalaam, R.N.; Muyeen, S.M.; Al-Durra, A.; Hasanien, H.N.; Al-Wahedi, K. Optimisation of controller parameters for grid tied photovoltaic system at faulty network using artificial neural network-based cuckoo search algorithm. IET Renew. Power Gen. 2017, 11, 1517–1526. [Google Scholar] [CrossRef]
- Ram, J.P.; Rajasekar, N. A novel Flower Pollination based Global Maximum Power Point method for Solar Maximum Power Point Tracking. IEEE Trans. Power Electron. 2017, 32, 8486–8499. [Google Scholar]
- Abouzeid, M.; Sood, V.; Youssef, M. A Comparative Study of a PV-MPPT grid-integrated system under Different Control Techniques. In Proceedings of the IEEEElectrical Power and Energy Conference (EPEC), London, ON, Canada, 26–28 October 2015; pp. 256–261. [Google Scholar]
- Pansare, C.; Sharma, S.K.; Jain, C.; Saxena, R. Analysis of a Modified Positive Output Luo Converter and its application to Solar PV system. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–6. [Google Scholar]
- Pachauri, R.K.; Chauhan, Y.K. Modeling and Simulation Analysis of PV Fed Cuk, Sepie, Zeta and Luo DC-DC Converter. In Proceedings of the IEEE1st International Conference on Power Electronics. Intelligent Control and Energy Systems (ICPEICES-2016), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar]
- Kaced, K.; Larbes, C.; Ait-Chikha, S.M.; Bounabi, M.; Dahmane, Z.E. FPGA implementation of PSO based MPPT for PV systems under partial shading conditions. In Proceedings of the IEEE6th International Conference on Systems and Control, Batna, Algeria, 7–9 May 2017; pp. 150–155. [Google Scholar]
- Niapoor, S.A.KH.M.; Danyali, S.; Sharifian, M.B.B. PV Power System Based MPPT Z-Source Inverter to Supply a Sensorless BLDC Motor. In Proceedings of the 1st Power Electronic & Drive Systems & Technologies Conference, Tehran, Iran, 17–18 February 2010; pp. 111–116. [Google Scholar]
- Saponara, S.; Gabriele, C.; Groza, V.Z. Design and Experimental Measurement of EMI Reduction Techniques for Integrated Switching DC/DC Converters. IEEE Can. J. Electr. Comput. Eng. 2017, 40, 116–127. [Google Scholar]

| S.N | Parameters | Values |
|---|---|---|
| 1. | Inductor (L) | 0.02 mH |
| 2. | Capacitor (C and C1) | 20 µF, 15 µF |
| 3. | Switching Frequency (fpulse) | 10 KHz |
| 4. | Duty Ratio (dduty) | 0.58 |
| S.N | Parameters | Value |
|---|---|---|
| 1 | Total fuzzy rule base fired | 25 |
| 2 | Total number of Epoch | 740 |
| 3 | Types of membership function | Gaussian type |
| 4 | Total layer (neural network) | 5 |
| 5 | Total neural network training data sets | 200 |
| S.N | Parameters | Values |
|---|---|---|
| 1. | Switched Probability (Pf) | 0.7 |
| 2. | Scaling Factor | 1.25 |
| 3. | No of Epoch | 740 |
| 4. | RMSE (Obtained) | 106 × 10−6 |
| 5. | Total Rule Based Fired | 25 |
| 6. | ANFIS Obtained (Training Error) | 0.6255 × 10−6 |
| Angle | Hall Signals | Switching States | |||||||
|---|---|---|---|---|---|---|---|---|---|
| H1 | H2 | H3 | |||||||
| 0–π/3 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| π/3–2π/3 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 2π/3–π | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| π–4π/3 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 4π/3–5π/3 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 5π/3–2π | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| S.N | Parameters | Value |
|---|---|---|
| 1 | Resistance of stator | 4.16 Ω |
| 2 | Inductance value of stator | 2.2 mH |
| 3 | Speed rating | 1500 rpm |
| 4 | Number of Pole pair | 2 |
| 5 | Constants(Voltage & torque) | 86 VLL/KRPM & 0.85 Nm/Ampere |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Priyadarshi, N.; Padmanaban, S.; Mihet-Popa, L.; Blaabjerg, F.; Azam, F. Maximum Power Point Tracking for Brushless DC Motor-Driven Photovoltaic Pumping Systems Using a Hybrid ANFIS-FLOWER Pollination Optimization Algorithm. Energies 2018, 11, 1067. https://doi.org/10.3390/en11051067
Priyadarshi N, Padmanaban S, Mihet-Popa L, Blaabjerg F, Azam F. Maximum Power Point Tracking for Brushless DC Motor-Driven Photovoltaic Pumping Systems Using a Hybrid ANFIS-FLOWER Pollination Optimization Algorithm. Energies. 2018; 11(5):1067. https://doi.org/10.3390/en11051067
Chicago/Turabian StylePriyadarshi, Neeraj, Sanjeevikumar Padmanaban, Lucian Mihet-Popa, Frede Blaabjerg, and Farooque Azam. 2018. "Maximum Power Point Tracking for Brushless DC Motor-Driven Photovoltaic Pumping Systems Using a Hybrid ANFIS-FLOWER Pollination Optimization Algorithm" Energies 11, no. 5: 1067. https://doi.org/10.3390/en11051067
APA StylePriyadarshi, N., Padmanaban, S., Mihet-Popa, L., Blaabjerg, F., & Azam, F. (2018). Maximum Power Point Tracking for Brushless DC Motor-Driven Photovoltaic Pumping Systems Using a Hybrid ANFIS-FLOWER Pollination Optimization Algorithm. Energies, 11(5), 1067. https://doi.org/10.3390/en11051067








