Non-Equal Voltage Cell Balancing for Battery and Super-Capacitor Source Package Management System Using Tapped Inductor Techniques
Abstract
1. Introduction
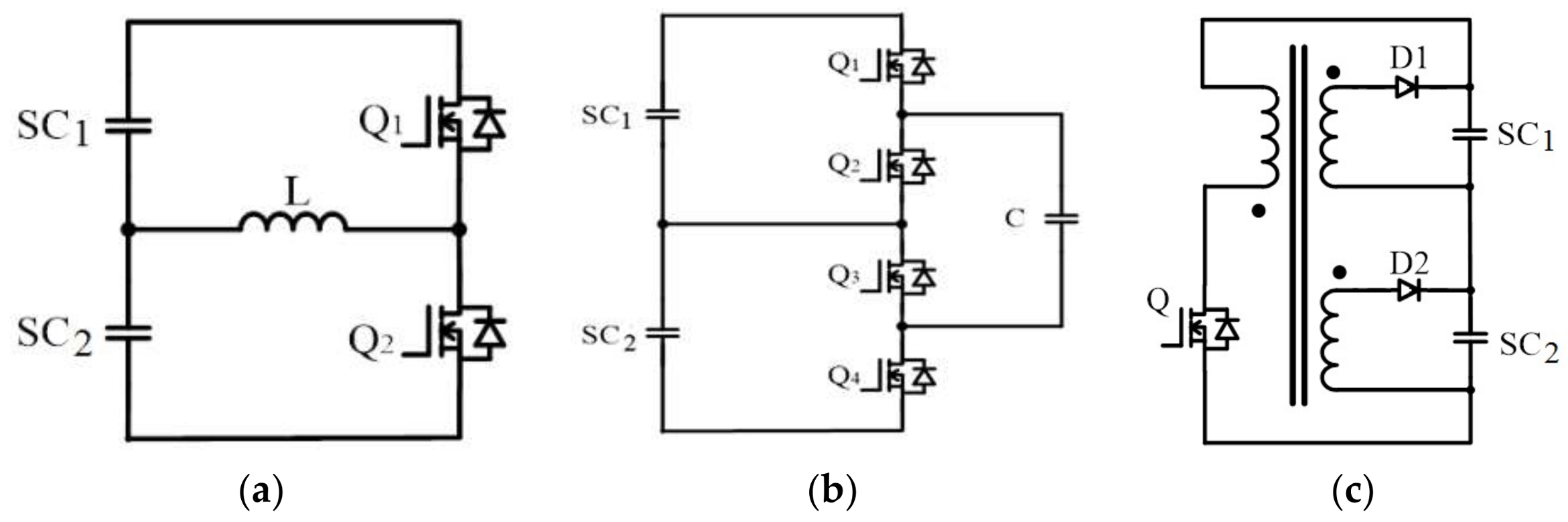
2. Tapped Inductor Basic Circuit
2.1. Conventional Buck-Boost Balancing
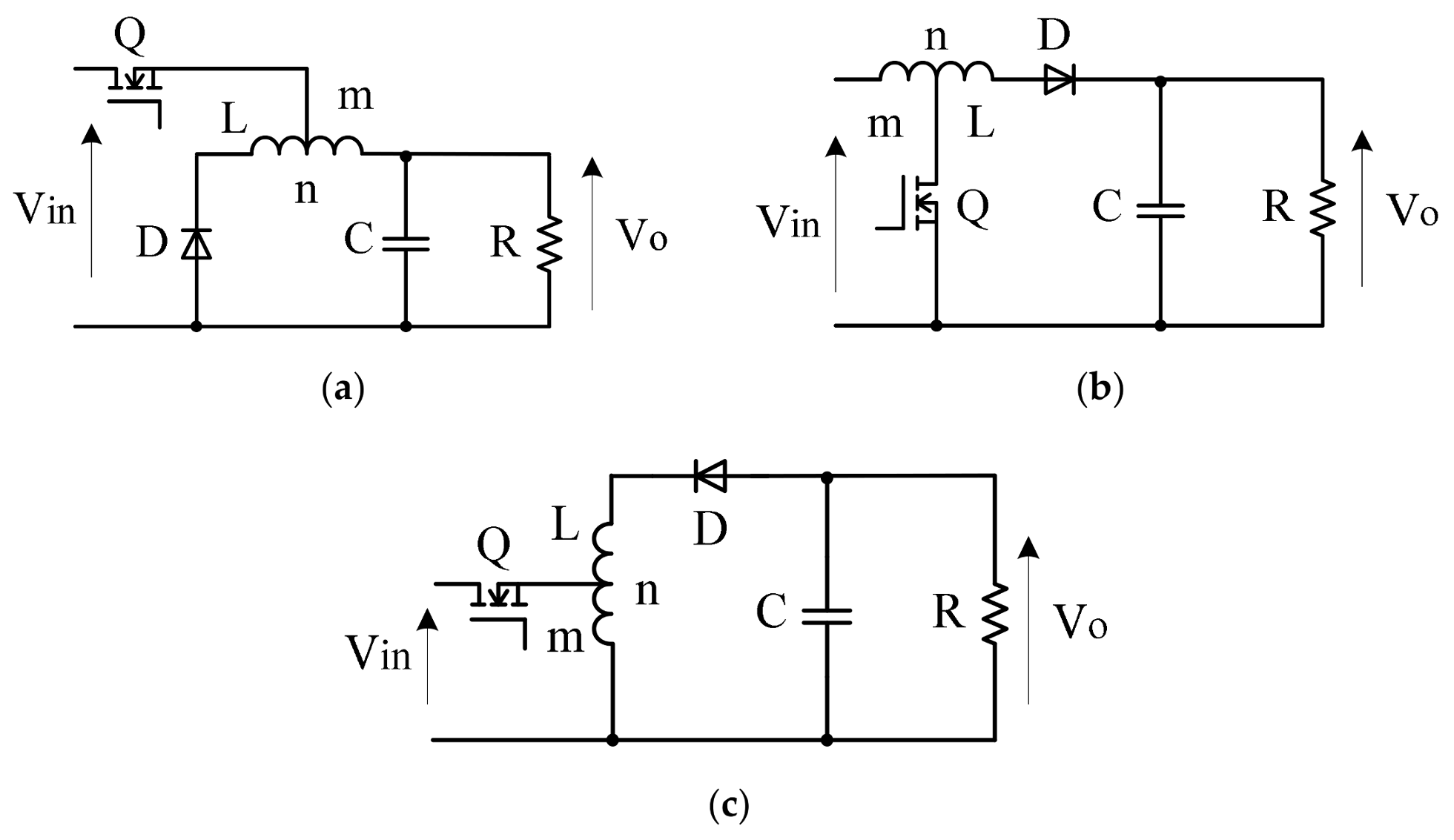
2.2. The Tapped Inductor Basic Theory
3. The Tapped Inductor Balancing
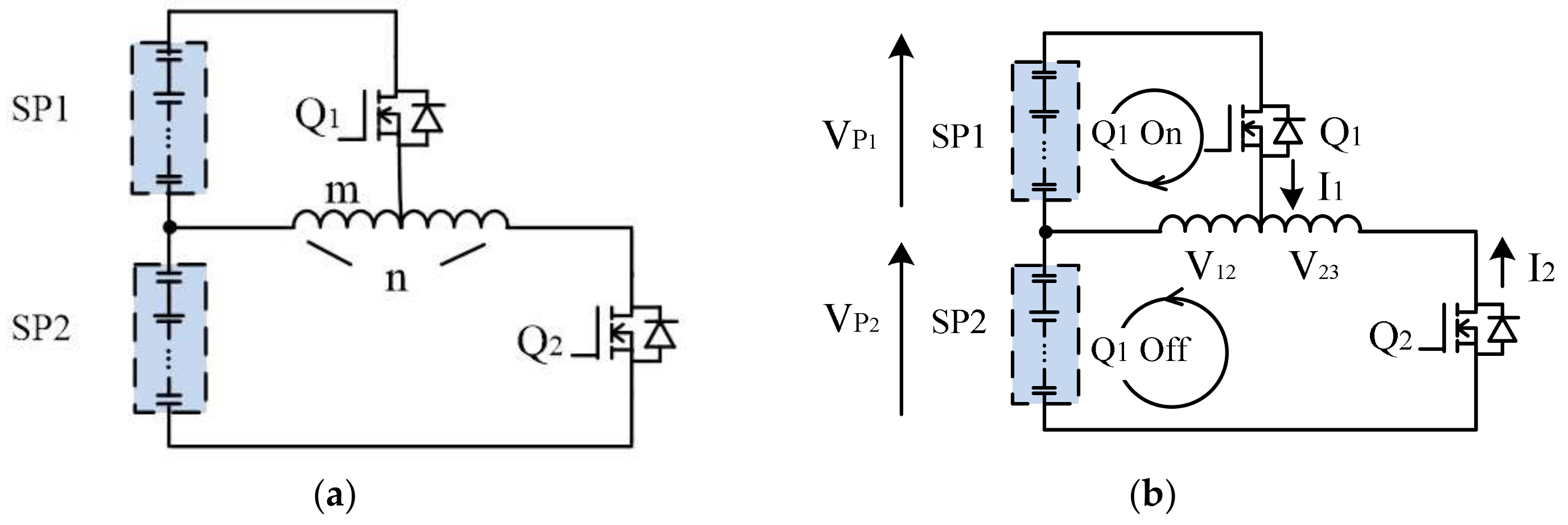
3.1. Basic Cell Equalization
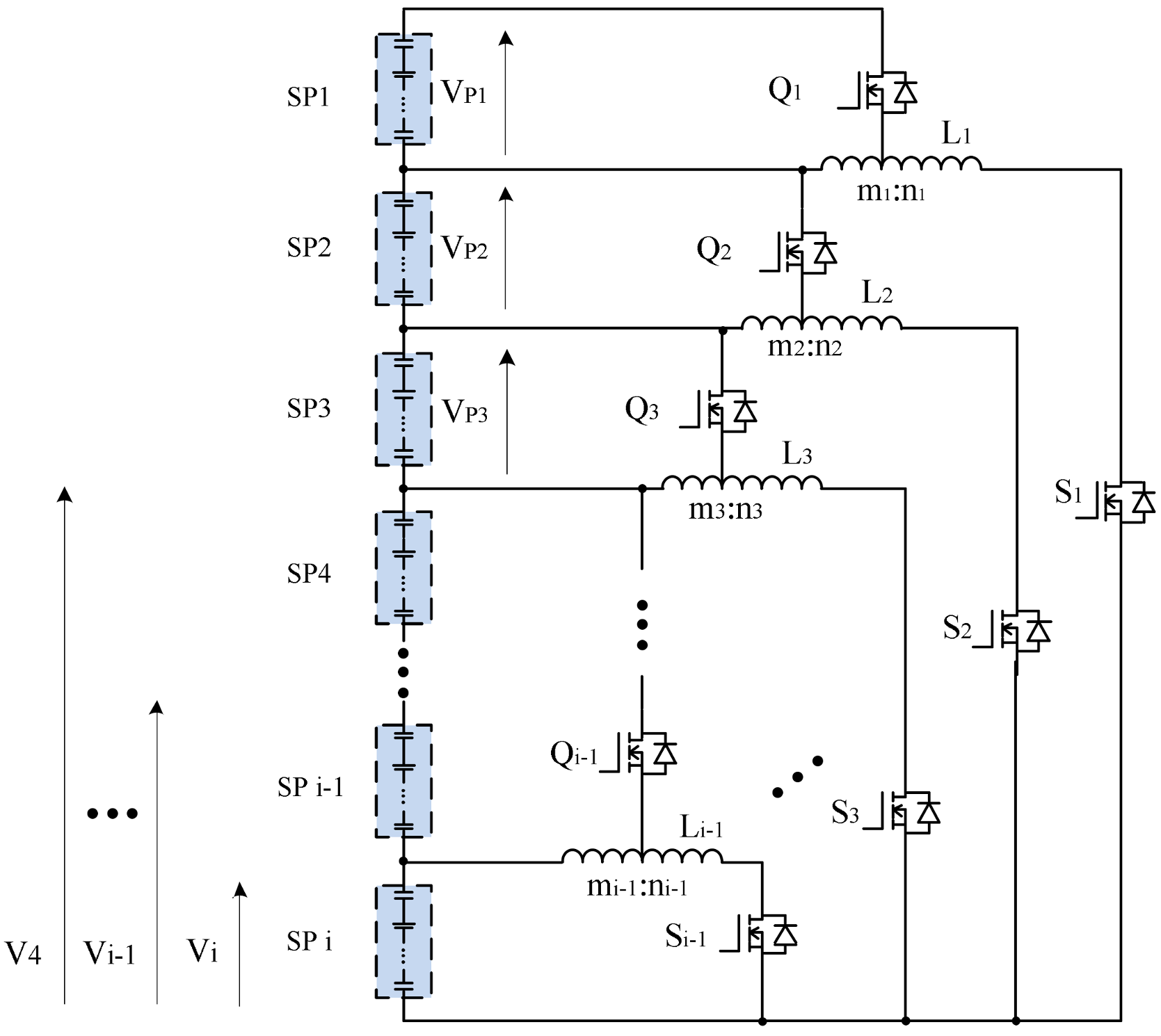
3.2. Generalized Cell Equalization
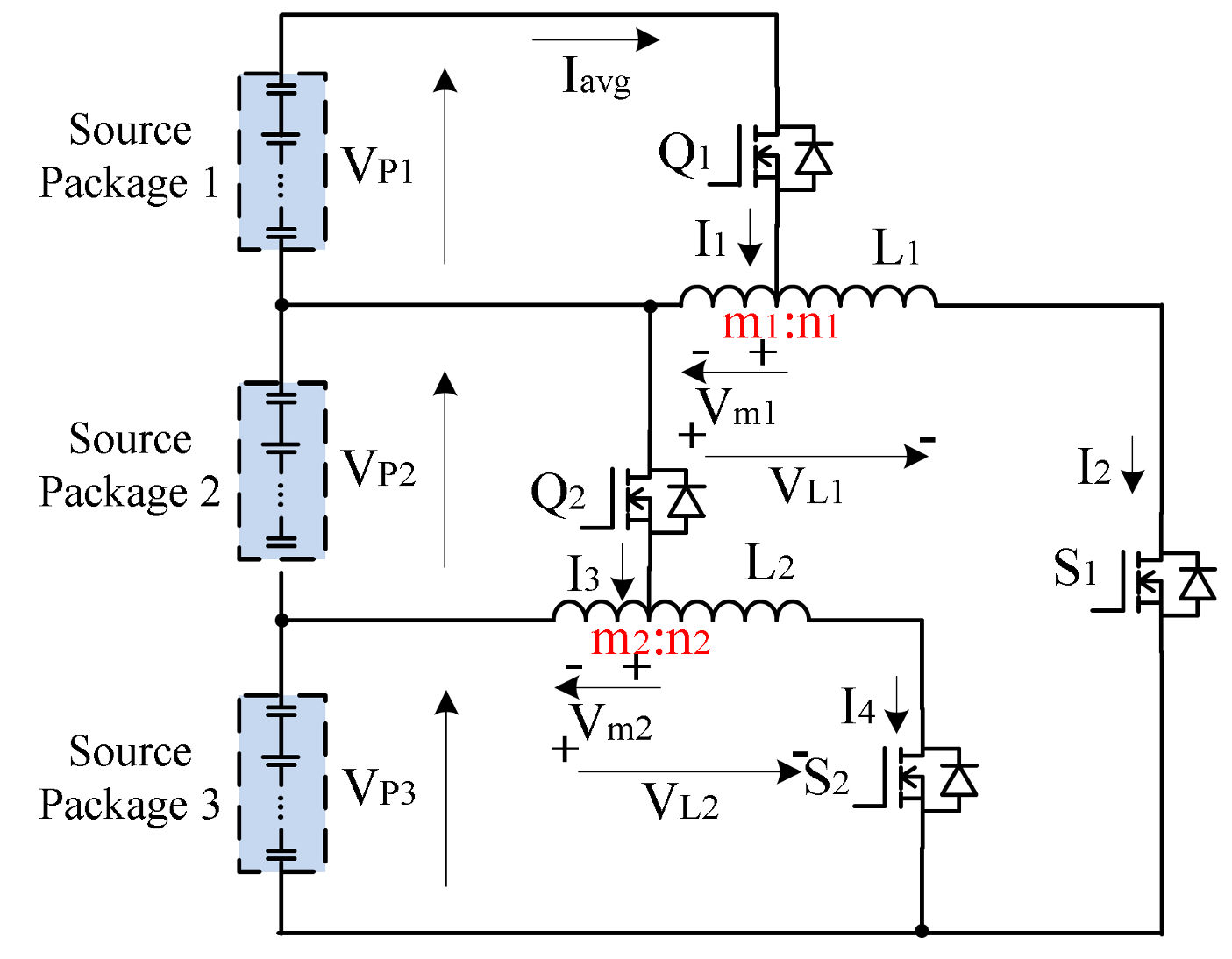
4. Modeling of Tapped Inductor Voltage Equalizer
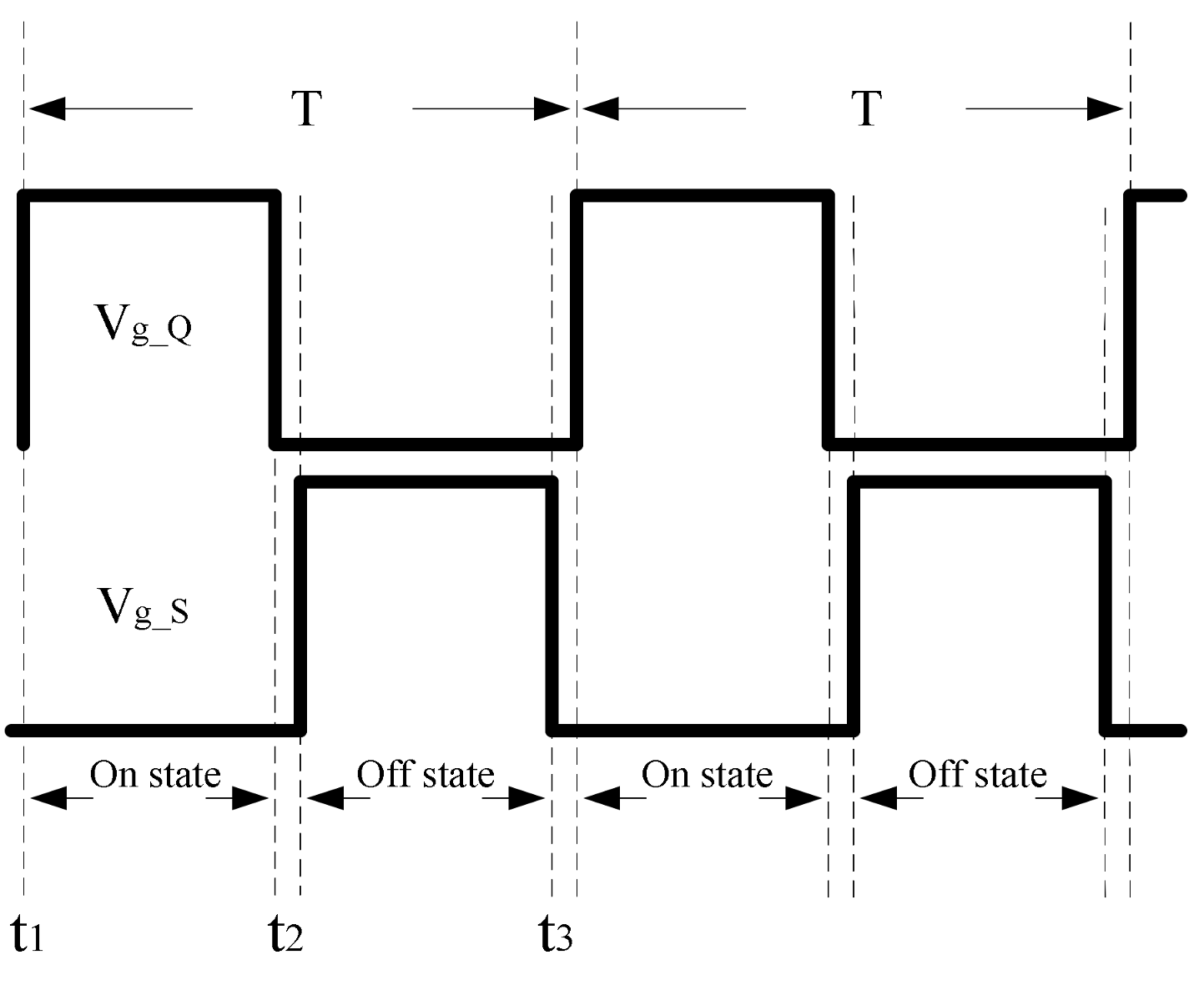
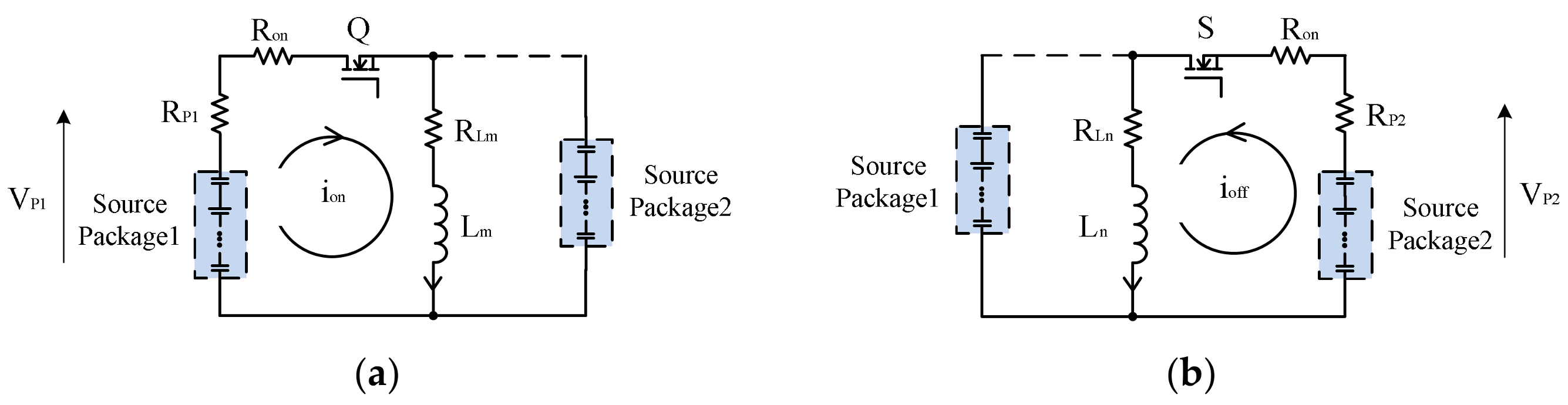
4.1. Operation Principle and Average Current Analysis
4.2. Energy Conversion Loss Analysis
5. Simulation Study
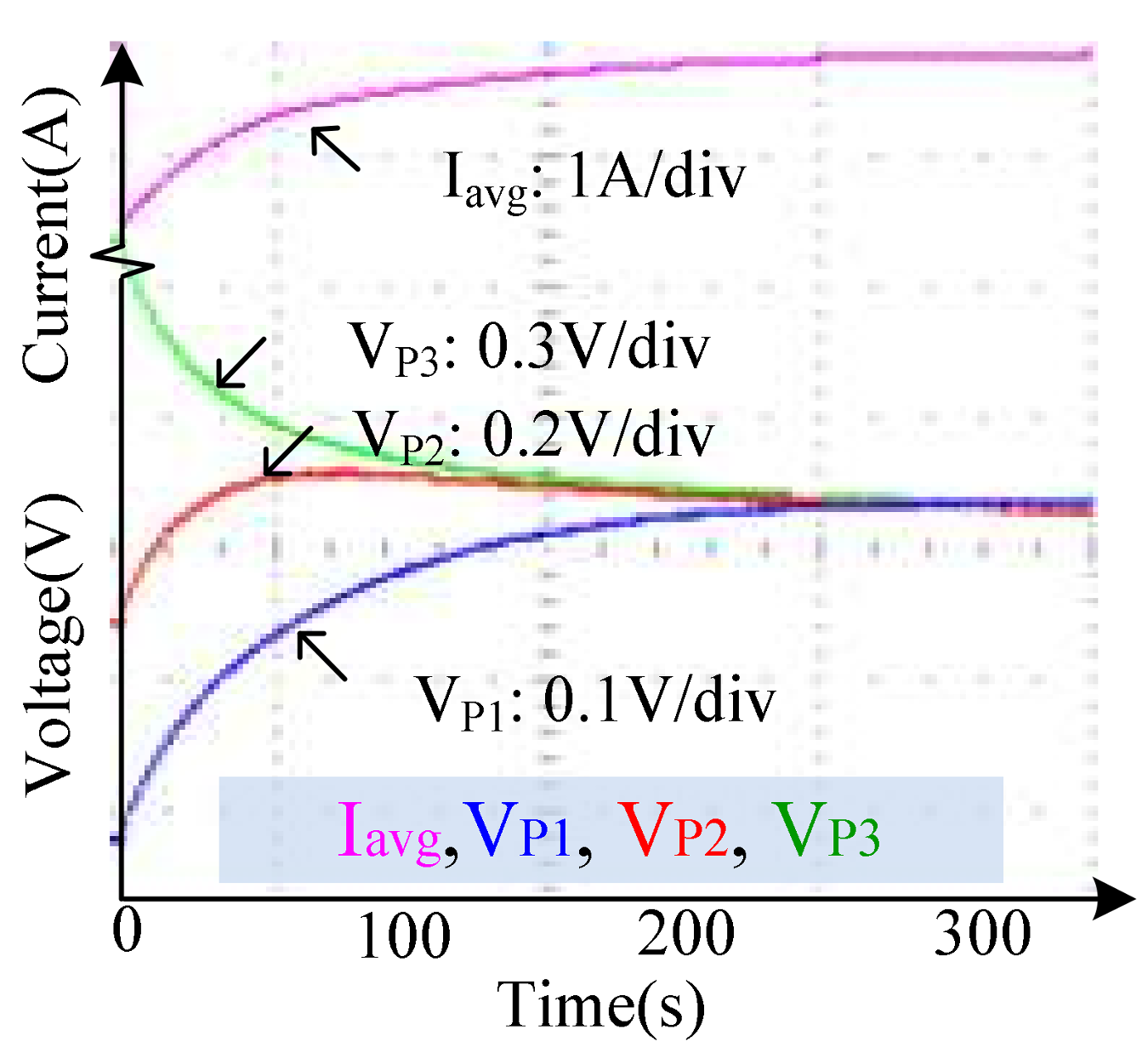
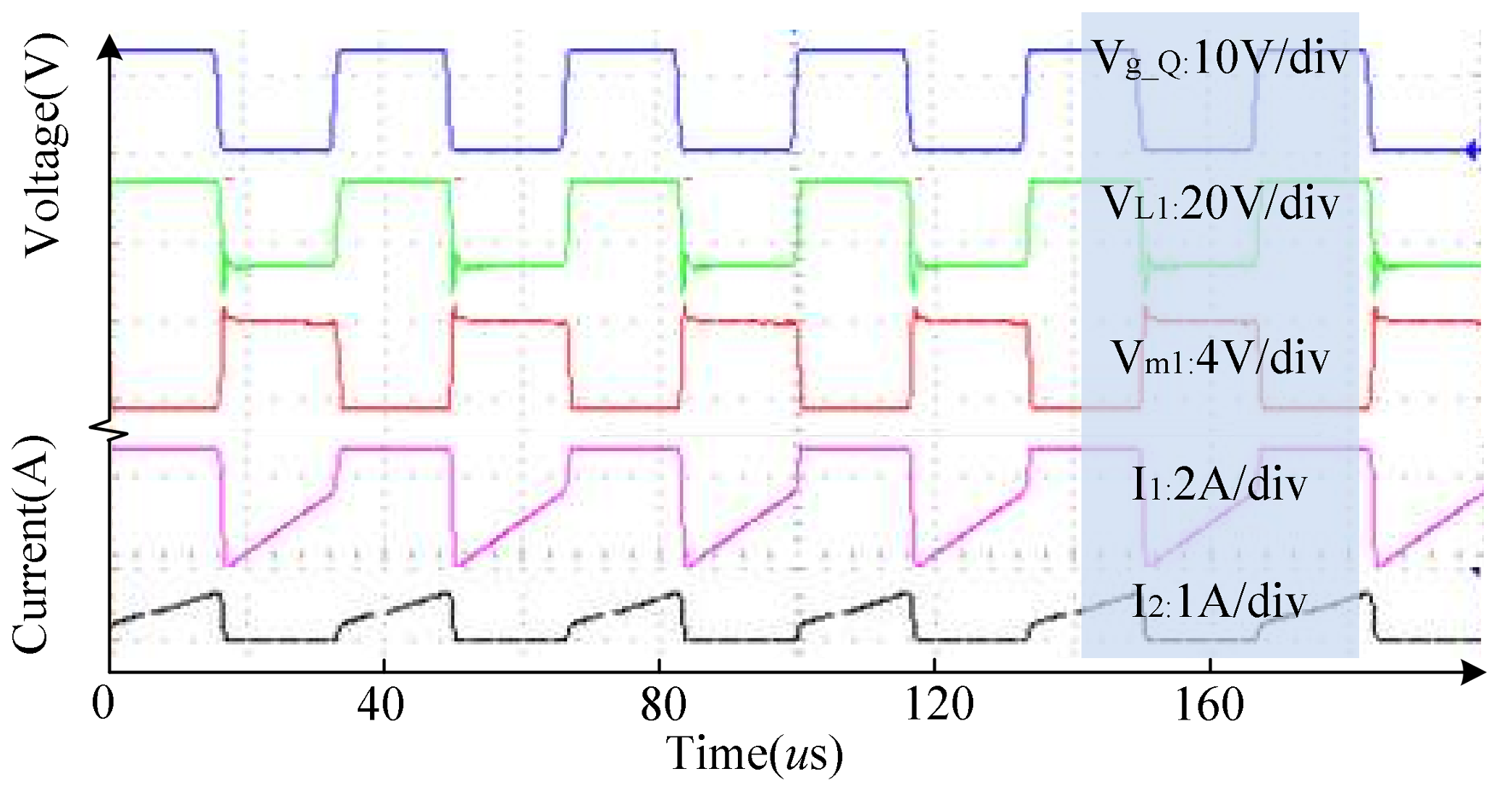
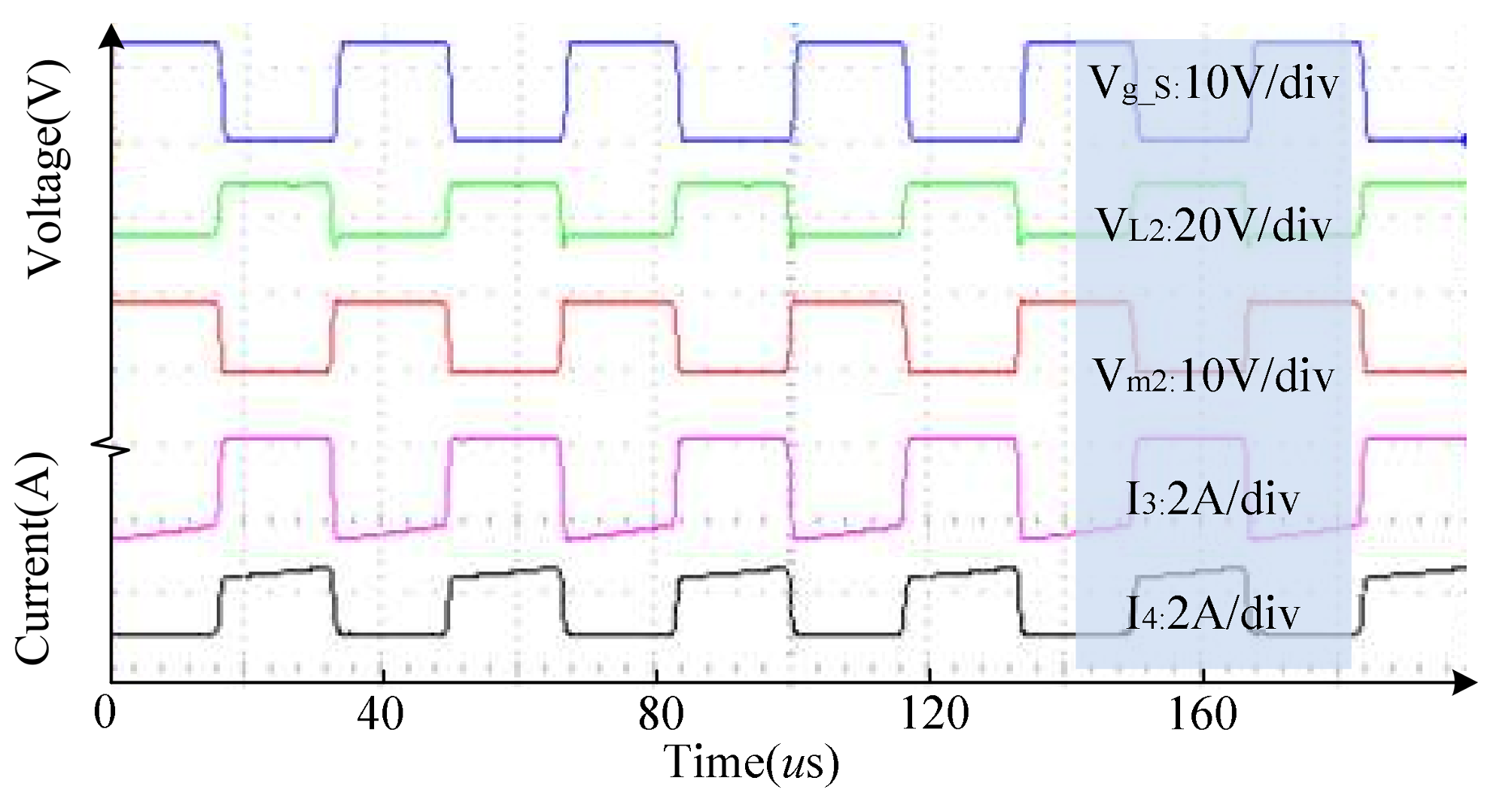
6. Experimental Results
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gao, Z.C.; Chin, C.S.; Chiew, J.; Jia, J.B.; Zhang, C.Z. Design and Implementation of Smart Lithium-ion Battery System with Real-time Fault Diagnosis Capability for Electric Vehicles. Energies 2017, 10, 1503. [Google Scholar] [CrossRef]
- Gao, Z.C.; Chin, C.S.; Woo, W.L.; Jia, J.B. Integrated Equivalent Circuit and Thermal Model for Simulation of Temperature-Dependent LiFePO4 Battery in Actual Embedded Application. Energies 2017, 10, 85. [Google Scholar] [CrossRef]
- Cheng, K.W.E.; Divakar, B.P.; Wu, H.; Ding, K.; Ho, H.F. Battery-Management System (BMS) and SOC Development for Electrical Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 76–88. [Google Scholar] [CrossRef]
- Peng, X.; He, X.; Han, P.; Guo, A.; Shu, Z.; Gao, S. Smooth switching technique for voltage balance management based on three-level neutral point clamped cascaded rectifier. Energies 2016, 9, 803. [Google Scholar] [CrossRef]
- Park, S.H.; Park, K.B.; Kim, S.H.; Moon, G.W.; Youn, M.J. Single-Magnetic Cell-to-Cell Charge Equalization Converter With Reduced Number of Transformer Windings. IEEE Trans. Power Electron. 2012, 27, 2900–2911. [Google Scholar] [CrossRef]
- Gao, Z.C.; Chin, C.S.; Toh, W.D.; Chiew, J.; Jia, J. State-of-Charge Estimation and Active Cell Pack Balancing Design of Lithium Battery Power System for Smart Electric Vehicle. J. Adv. Transp. 2017. [Google Scholar] [CrossRef]
- Daowd, M.; Antoine, M.; Omar, N.; Bossche, P.V.D.; Mierlo, J.V. Single switched capacitor battery balancing system enhancements. Energies 2013, 6, 2149–2174. [Google Scholar] [CrossRef]
- Law, K.K.; Cheng, K.W.E. Examination of the frequency modulation and lifting techniques for the generalized power factor correction switched-capacitor resonant converter. Int. J. Circuit Theory Appl. 2008, 7, 839–855. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E.; Fong, Y.C. Topology, Modeling, and Design of Switched-Capacitor-Based Cell Balancing Systems and Their Balancing Exploration. IEEE Trans. Power Electron. 2017, 32, 4444–4454. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Zhu, C. Equalisation strategy for serially connected LiFePO4 battery cells. IET Electr. Syst. Transp. 2016, 6, 246–252. [Google Scholar]
- Lambert, S.M.; Pickert, V.; Atkinson, D.J.; Zhan, H. Transformer-Based Equalization Circuit Applied to n-Number of High Capacitance Cells. IEEE Trans. Power Electron. 2016, 31, 1334–1343. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Cui, Y.; Zou, J.; Yang, S. A MultiWinding Transformer Cell-to-Cell Active Equalization Method for Lithium-Ion Batteries With Reduced Number of Driving Circuits. IEEE Trans. Power Electron. 2016, 31, 4916–4929. [Google Scholar]
- Liu, M.; Fu, M.; Wang, Y.; Ma, C. Battery Cell Equalization via Megahertz Multiple-Receiver Wireless Power Transfer. IEEE Trans. Power Electron. 2018, 33, 4135–4144. [Google Scholar] [CrossRef]
- Cheng, K.W.E. Review of battery management systems for electric vehicles. In Energy Systems for Electric and Hybrid Vehicles; IET: London, UK, 2016; ISBN 978-1-78561-008-0. [Google Scholar]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Online estimation of peak power capability of Li-ion batteries in electric vehicles by a hardware-in-loop approach. Energies 2012, 5, 1455–1469. [Google Scholar] [CrossRef]
- Choe, J.M.; Choe, G.H.; Lai, J.S. System for load levelling control and operation of an energy storage system. IET Power Electron. 2017, 10, 739–745. [Google Scholar] [CrossRef]
- Casals, L.C.; Garca, B.A. Communications concerns for reused electric vehicle batteries in smart grids. IEEE Commun. Mag. 2016, 54, 120–125. [Google Scholar] [CrossRef]
- Monem, M.A.; Hegazy, O.; Omar, N.; Trad, K.; Breucker, S.D.; Bossche, P.V.D. Design and analysis of generic energy management strategy for controlling second-life battery systems in stationary applications. Energies 2016, 9, 889. [Google Scholar] [CrossRef]
- Mukherjee, N.; Strickland, D. Control of Second-Life Hybrid Battery Energy Storage System Based on Modular Boost-Multilevel Buck Converter. IEEE Trans. Ind. Electron. 2015, 62, 1034–1046. [Google Scholar] [CrossRef]
- Mukherjee, N.; Strickland, D. Analysis and Comparative Study of Different Converter Modes in Modular Second-Life Hybrid Battery Energy Storage Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 547–563. [Google Scholar] [CrossRef]
- Chan, H.L.; Cheng, K.W.E.; Sutanto, D. Bidirectional phase-shifted DC-DC converter. IEE Electron. Lett. 1999, 35, 523–524. [Google Scholar] [CrossRef]
- Cheng, K.W.E.; Evans, P.D. Parallel-mode extended-period quasiresonant convertor. IEE Proc. B 1991, 138, 243–251. [Google Scholar] [CrossRef]
- Shi, Z.H.; Cheng, K.W.E.; Ho, S.L. Static performance and parasitic analysis of tapped-inductor converters. IET Power Electron. 2014, 7, 366–375. [Google Scholar] [CrossRef]
- Li, S.; Cheng, K.W.E.; Ye, Y.; Shi, Z. Wide input and wide output topology analysis for tapped-inductor converters with consideration of parasitic elements. IET Power Electron. 2016, 9, 1952–1961. [Google Scholar] [CrossRef]
- Grant, D.A.; Darroman, Y. Watkins-Johnson converter completes tapped inductor converter matrix. Electron. Lett. 2003, 39, 271–272. [Google Scholar] [CrossRef]
| LiCoO2 | LiMn2O4 | LiNi ⅓Mn ⅓Co ⅓O2 | LiFePO4 | Li4Ti5O12 | |
|---|---|---|---|---|---|
| Name | Lithium Cobalt | Lithium Manganese | NMC | Lithium Iron Phosphate | LTO |
| Energy Density (Wh/kg) | 180 | 100 | 180 | 140 | 100 |
| Cell Voltage (V) | 3.7 | 3.8 | 3.8 | 3.2 | 2.2 |
| Voltage Ratio | 1:2:3 | 1:2:4 | 1:3:9 |
|---|---|---|---|
| Voltage Balance Waveform | 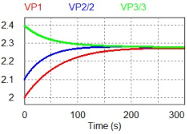 | 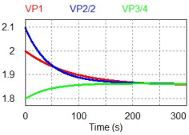 | 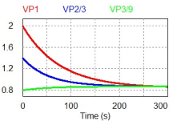 |
| X: Time (s); Y: Voltage (V) | |||
| Average Current Waveform | 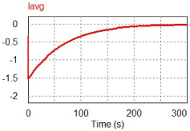 |  | 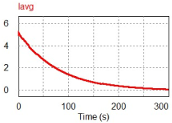 |
| X: Time (s); Y: Current (A) | |||
| Units | Quantity |
|---|---|
| Supercapacitor (DRL357S0TQ60SC) | 6 |
| Capacitance of SCs | 350 F |
| ESR of SCs | 6 mΩ |
| MOSFET (IRFR3607PBF) | 4 |
| On-state resistance of MOSFETS | 7.34 mΩ |
| Inductance of L1 | 390.4 µH |
| Turns ratio of L1 | 1:5 |
| Inductance of L2 | 386.9 µH |
| Turns ratio of L2 | 2:3 |
| Switching frequency | 30 kHz |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cheng, K.W.E.; Fong, Y.C. Non-Equal Voltage Cell Balancing for Battery and Super-Capacitor Source Package Management System Using Tapped Inductor Techniques. Energies 2018, 11, 1037. https://doi.org/10.3390/en11051037
Wang X, Cheng KWE, Fong YC. Non-Equal Voltage Cell Balancing for Battery and Super-Capacitor Source Package Management System Using Tapped Inductor Techniques. Energies. 2018; 11(5):1037. https://doi.org/10.3390/en11051037
Chicago/Turabian StyleWang, Xiaolin, Ka Wai Eric Cheng, and Yat Chi Fong. 2018. "Non-Equal Voltage Cell Balancing for Battery and Super-Capacitor Source Package Management System Using Tapped Inductor Techniques" Energies 11, no. 5: 1037. https://doi.org/10.3390/en11051037
APA StyleWang, X., Cheng, K. W. E., & Fong, Y. C. (2018). Non-Equal Voltage Cell Balancing for Battery and Super-Capacitor Source Package Management System Using Tapped Inductor Techniques. Energies, 11(5), 1037. https://doi.org/10.3390/en11051037






