Intrinsic Variability in the Degradation of a Batch of Commercial 18650 Lithium-Ion Cells
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Conditioning and Cell-Aging Protocols
2.2. Half-Cell Preparation and Testing
3. Results
3.1. Initial Characterization
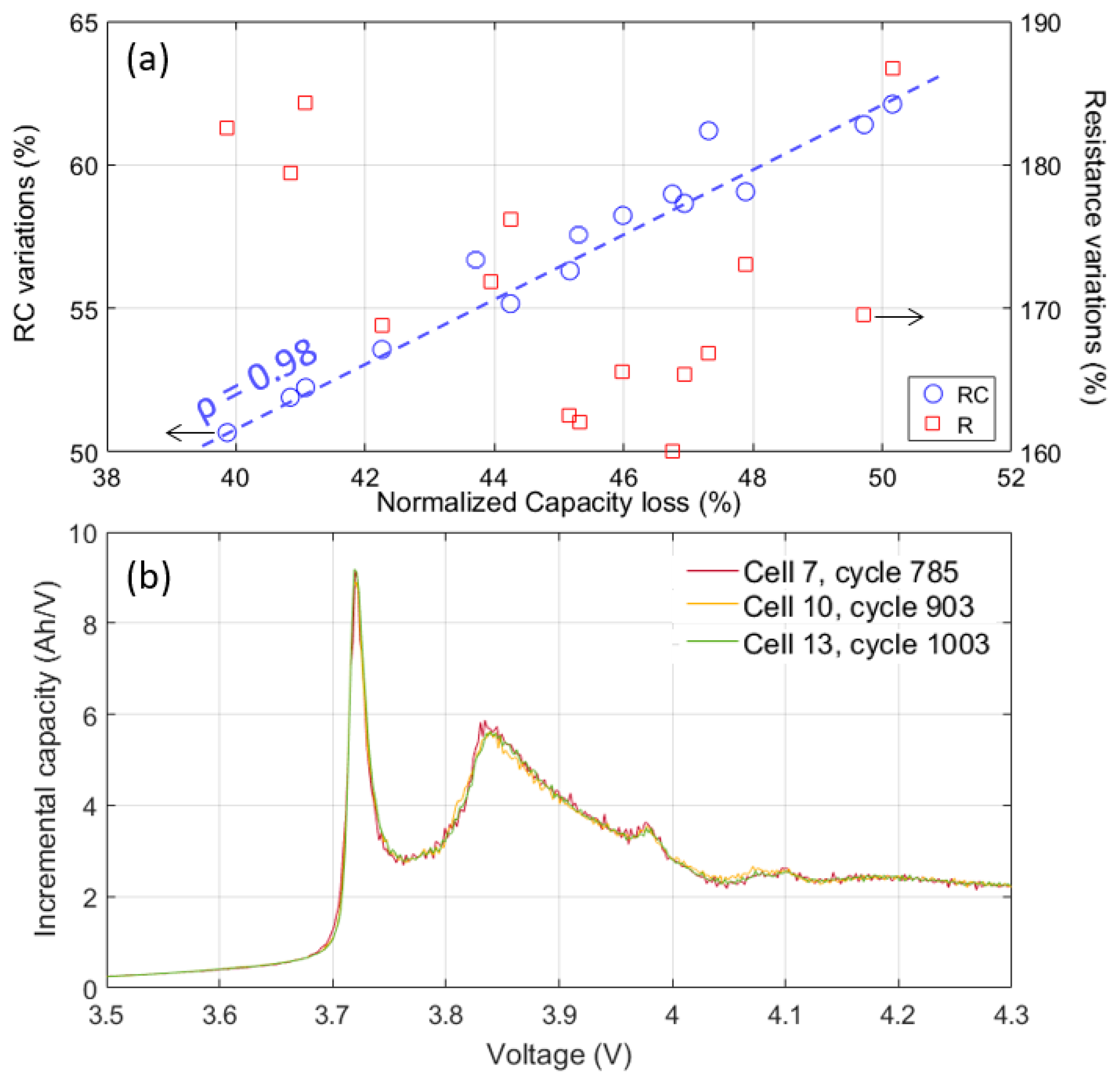
3.2. Cycle Aging Characterization
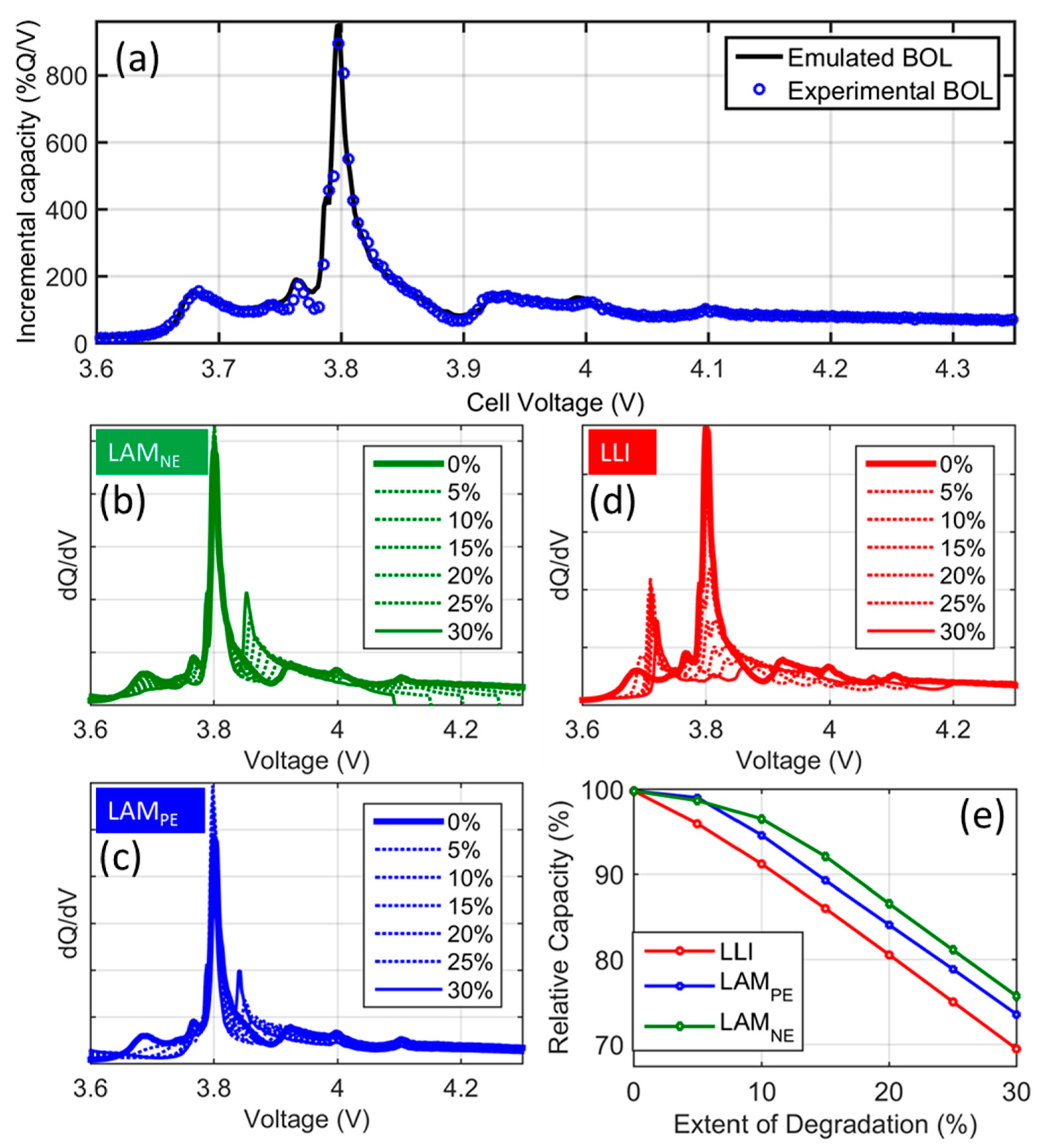
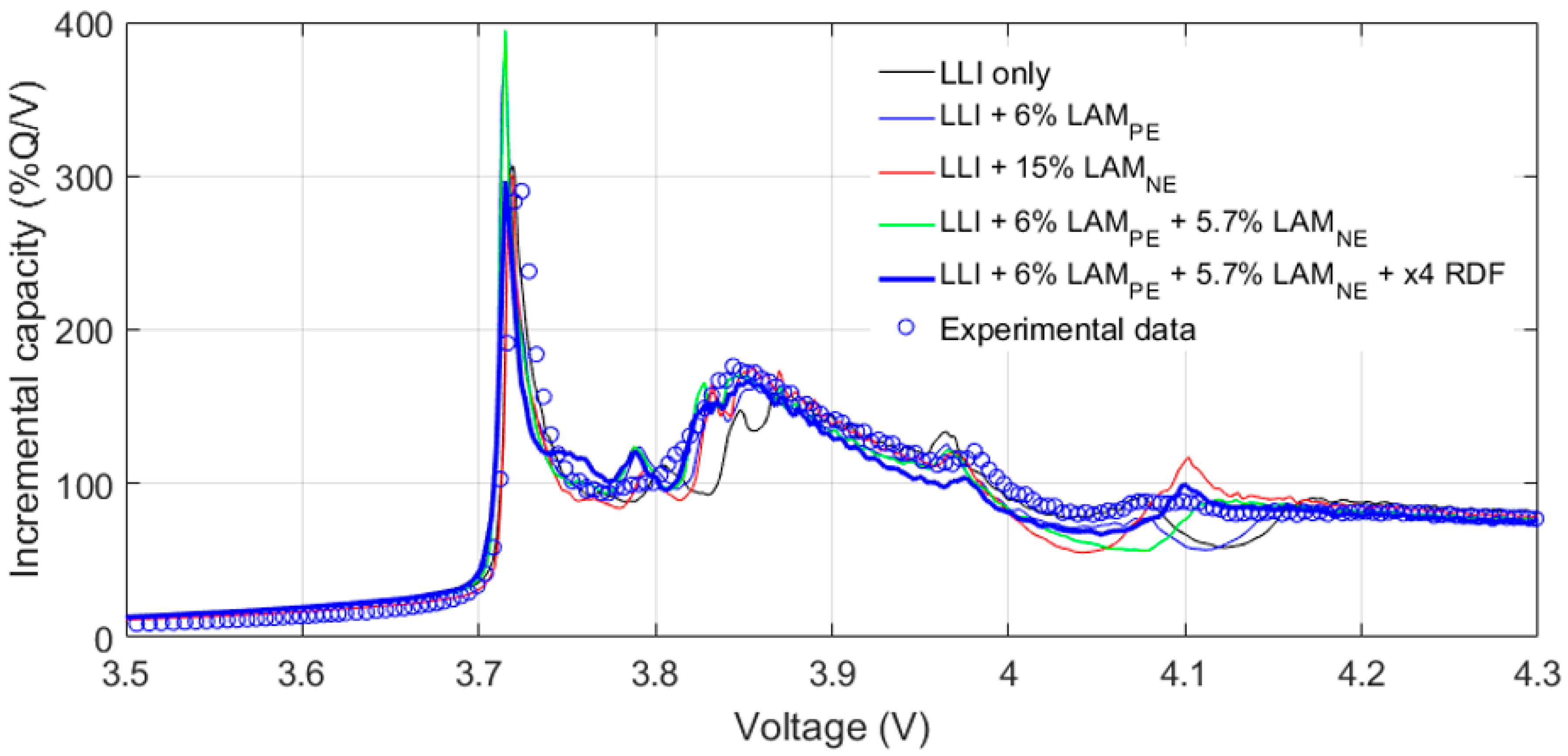
3.3. Full Cell Emulation
4. Discussion
4.1. Cell-to-Cell Variations
4.2. Degradation Mechanisms
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Sripad, S.; Viswanathan, V. Evaluation of Current, Future, and Beyond Li-Ion Batteries for the Electrification of Light Commercial Vehicles: Challenges and Opportunities. J. Electrochem. Soc. 2017, 164, E3635–E3646. [Google Scholar] [CrossRef]
- Hesse, H.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-Ion Battery Storage for the Grid—A Review of Stationary Battery Storage System Design Tailored for Applications in Modern Power Grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef]
- Rohr, S.; Müller, S.; Baumann, M.; Kerler, M.; Ebert, F.; Kaden, D.; Lienkamp, M. Quantifying Uncertainties in Reusing Lithium-Ion Batteries from Electric Vehicles. Procedia Manuf. 2017, 8, 603–610. [Google Scholar] [CrossRef]
- Harris, S.J.; Harris, D.J.; Li, C. Failure statistics for commercial lithium ion batteries: A study of 24 pouch cells. J. Power Sources 2017, 342, 589–597. [Google Scholar] [CrossRef]
- Baumhöfer, T.; Brühl, M.; Rothgang, S.; Sauer, D.U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 2014, 247, 332–338. [Google Scholar] [CrossRef]
- Cripps, E.; Pecht, M. A Bayesian nonlinear random effects model for identification of defective batteries from lot samples. J. Power Sources 2017, 342, 342–350. [Google Scholar] [CrossRef]
- Velho, R.; Beirao, M.; Calado, M.D.; Pombo, J.; Fermeiro, J.; Mariano, S. Management System for Large Li-Ion Battery Packs with a New Adaptive Multistage Charging Method. Energies 2017, 10, 605. [Google Scholar] [CrossRef]
- Rumpf, K.; Naumann, M.; Jossen, A. Experimental investigation of parametric cell-to-cell variation and correlation based on 1100 commercial lithium-ion cells. J. Energy Storage 2017, 14, 224–243. [Google Scholar] [CrossRef]
- An, F.; Chen, L.; Huang, J.; Zhang, J.; Li, P. Rate dependence of cell-to-cell variations of lithium-ion cells. Sci. Rep. 2016, 6, 35051. [Google Scholar] [CrossRef] [PubMed]
- Schuster, S.F.; Brand, M.J.; Berg, P.; Gleissenberger, M.; Jossen, A. Lithium-ion cell-to-cell variation during battery electric vehicle operation. J. Power Sources 2015, 297, 242–251. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Quantifying Cell-to-Cell Variations in Lithium Ion Batteries. Int. J. Electrochem. 2012, 2012, 395838. [Google Scholar] [CrossRef]
- Kim, J.; Shin, J. Screening Process of Li-Ion Series Battery Pack for Improved Voltage SOC Balancing. In Proceedings of the 2010 International Power Electronics Conference, Sapporo, Japan, 21–24 June 2010. [Google Scholar]
- He, X. A Facile Consistency Screening Approach to Select Cells with Better Performance Consistency for Commercial 18650 Lithium Ion Cells. Int. J. Electrochem. Sci. 2017, 12, 10239–10258. [Google Scholar] [CrossRef]
- Miyatake, S.; Susuki, Y.; Hikihara, T.; Itoh, S.; Tanaka, K. Discharge characteristics of multicell lithium-ion battery with nonuniform cells. J. Power Sources 2013, 241, 736–743. [Google Scholar] [CrossRef]
- Gogoana, R.; Pinson, M.B.; Bazant, M.Z.; Sarma, S.E. Internal resistance matching for parallel-connected lithium-ion cells and impacts on battery pack cycle life. J. Power Sources 2014, 252, 8–13. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Cugnet, M.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of commercial lithium-ion cells based on composite positive electrode for plug-in hybrid electric vehicle applications. Part I: Initial characterizations. J. Power Sources 2011, 196, 10328–10335. [Google Scholar] [CrossRef]
- Zheng, Y.; Han, X.; Lu, L.; Li, J.; Ouyang, M. Lithium ion battery pack power fade fault identification based on Shannon entropy in electric vehicles. J. Power Sources 2013, 223, 136–146. [Google Scholar] [CrossRef]
- Dubarry, M.; Vuillaume, N.; Liaw, B.Y. Origins and accommodation of cell variations in Li-ion battery pack modeling. Int. J. Energy Res. 2010, 34, 216–231. [Google Scholar] [CrossRef]
- Dubarry, M.; Devie, A.; McKenzie, K. Durability and reliability of electric vehicle batteries under electric utility grid operations: Bidirectional charging impact analysis. J. Power Sources 2017, 358, 39–49. [Google Scholar] [CrossRef]
- Campestrini, C.; Keil, P.; Schuster, S.F.; Jossen, A. Ageing of lithium-ion battery modules with dissipative balancing compared with single-cell ageing. J. Energy Storage 2016, 6, 142–152. [Google Scholar] [CrossRef]
- Paul, S.; Diegelmann, C.; Kabza, H.; Tillmetz, W. Analysis of ageing inhomogeneities in lithium-ion battery systems. J. Power Sources 2013, 239, 642–650. [Google Scholar] [CrossRef]
- Devie, A.; Dubarry, M. Durability and Reliability of Electric Vehicle Batteries under Electric Utility Grid Operations. Part 1: Cell-to-Cell Variations and Preliminary Testing. Batteries 2016, 2, 28. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, Y.; Ouyang, M.; Lu, L. A study on parameter variation effects on battery packs for electric vehicles. J. Power Sources 2017, 364, 242–252. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, Y.; Jiang, J.; Cheng, G.; Diao, W.; Zhang, W. Study on battery pack consistency evolutions and equilibrium diagnosis for serial-connected lithium-ion batteries. Appl. Energy 2017, 207, 510–519. [Google Scholar] [CrossRef]
- Berdichevsky, G.K.K.; Straubel, J.B.; Toomre, E. The Tesla Roadster Battery System; Tesla Motors: Palo Alto, CA, USA, 2007; pp. 1–5. [Google Scholar]
- Bloom, I.; Jansen, A.N.; Abraham, D.P.; Knuth, J.; Jones, S.A.; Battaglia, V.S.; Henriksen, G.L. Differential voltage analyses of high-power, lithium-ion cells. 1. Technique and Applications. J. Power Sources 2005, 139, 295–303. [Google Scholar] [CrossRef]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Incremental capacity analysis and close-to-equilibrium OCV measurements to quantify capacity fade in commercial rechargeable lithium batteries. Electrochem. Solid-State Lett. 2006, 9, A454–A457. [Google Scholar] [CrossRef]
- HNEI Alawa Central. Available online: https://www.soest.hawaii.edu/HNEI/alawa/ (accessed on 23 April 2018).
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Kassem, M.; Delacourt, C. Postmortem analysis of calendar-aged graphite/LiFePO4 cells. J. Power Sources 2013, 235, 159–171. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Tran, H.Y.; Richter, J.; Ivers-Tiffée, E.; Wohlfahrt-Mehrens, M. Analysis and prediction of the open circuit potential of lithium-ion cells. J. Power Sources 2013, 239, 696–704. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Anseán, D.; Dubarry, M.; Devie, A.; Liaw, B.Y.; García, V.M.; Viera, J.C.; González, M. Operando lithium plating quantification and early detection of a commercial LiFePO4 cell cycled under dynamic driving schedule. J. Power Sources 2017, 356, 36–46. [Google Scholar] [CrossRef]
- Dubarry, M.; Baure, G.; Devie, A. Durability and Reliability of EV Batteries under Electric Utility Grid Operations: Path Dependence of Battery Degradation. J. Electrochem. Soc. 2018, 165, A773–A783. [Google Scholar] [CrossRef]
- Devie, A.; Dubarry, M.; Wu, H.-P.; Wu, T.-H.; Liaw, B.Y. Overcharge Study in Li4Ti5O12 Based Lithium-Ion Pouch Cell II. Experimental Investigation of the Degradation Mechanism. J. Electrochem. Soc. 2016, 163, A2611–A2617. [Google Scholar] [CrossRef]
- Devie, A.; Dubarry, M.; Liaw, B.Y. Overcharge Study in Li4Ti5O12 Based Lithium-Ion Pouch Cell: I. Quantitative Diagnosis of Degradation Modes. J. Electrochem. Soc. 2015, 162, A1033–A1040. [Google Scholar] [CrossRef]
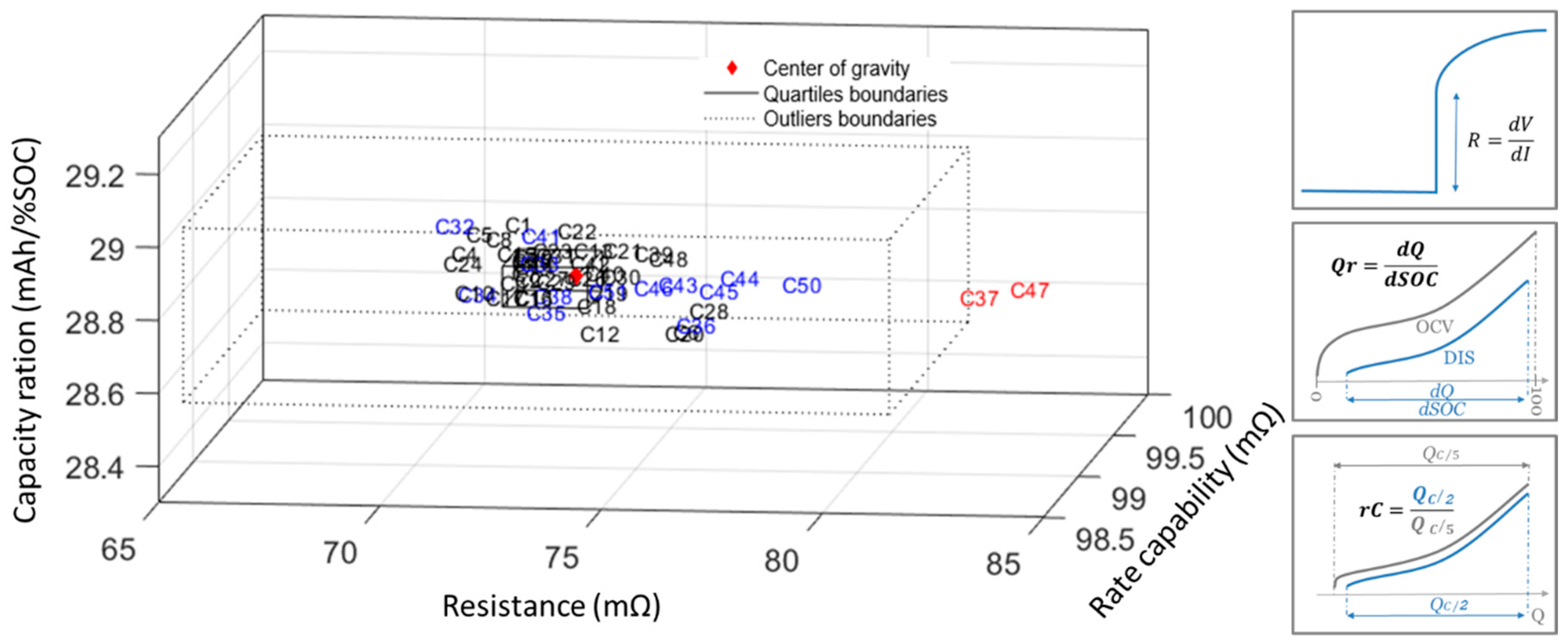
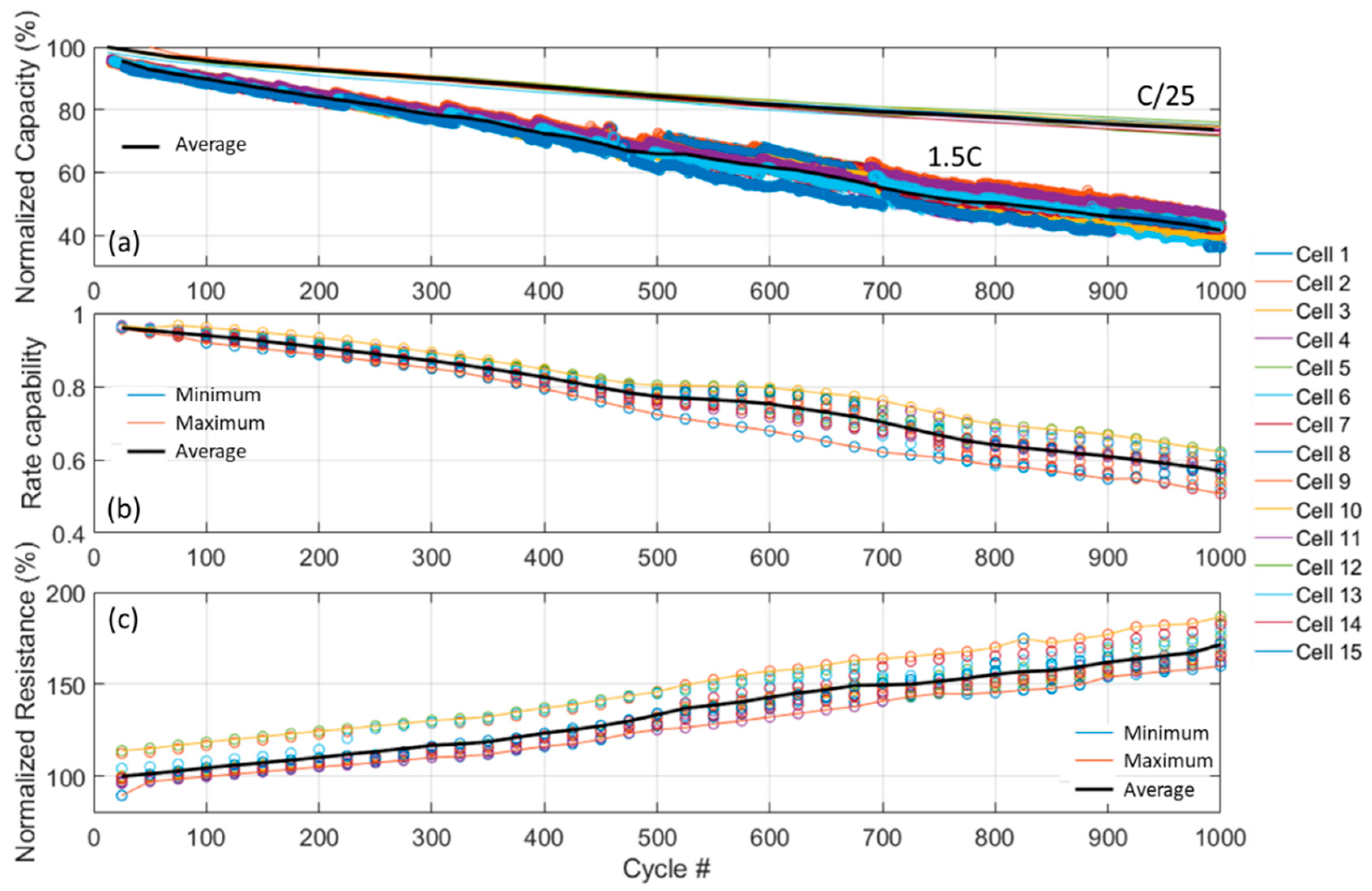
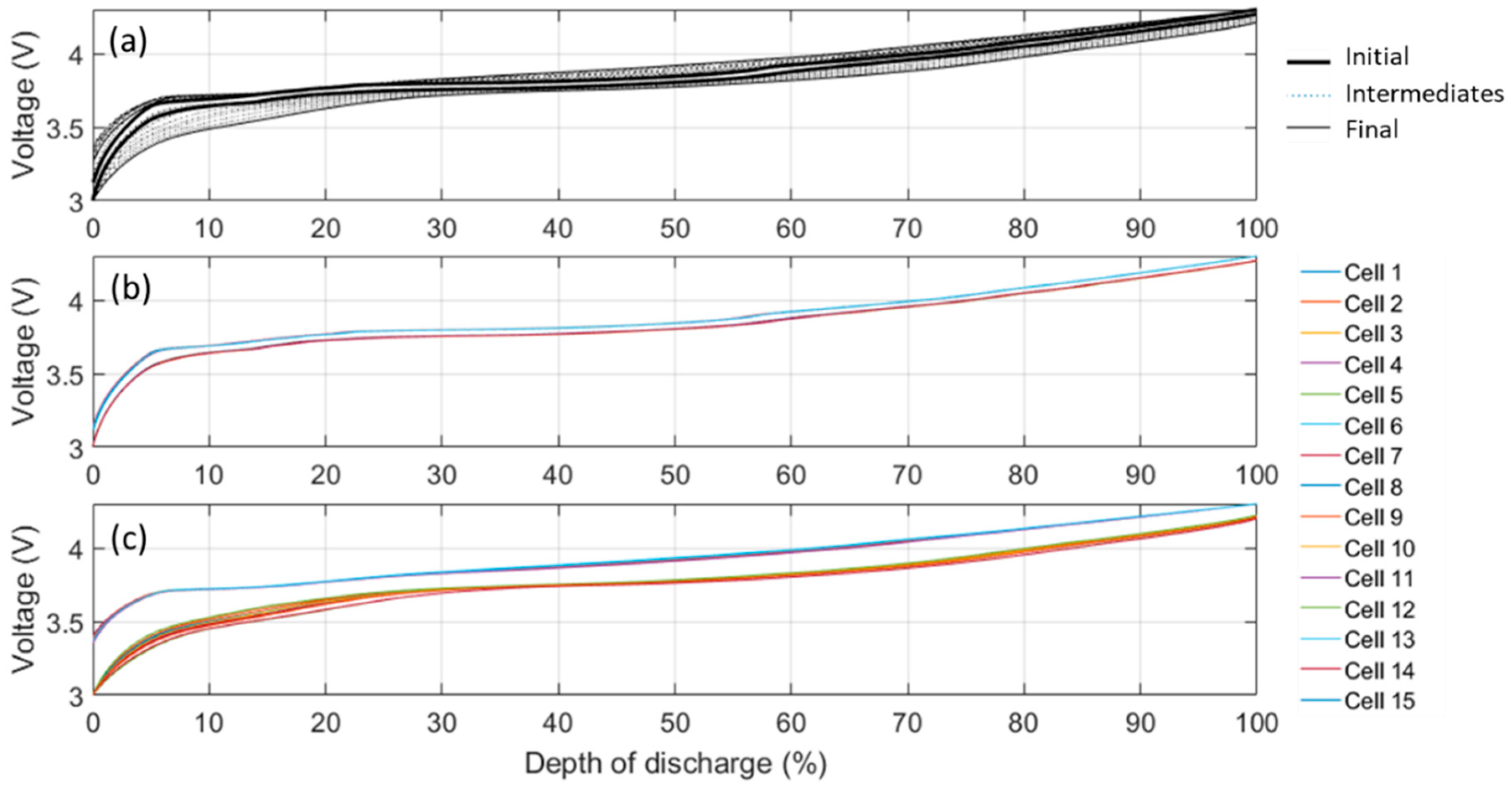
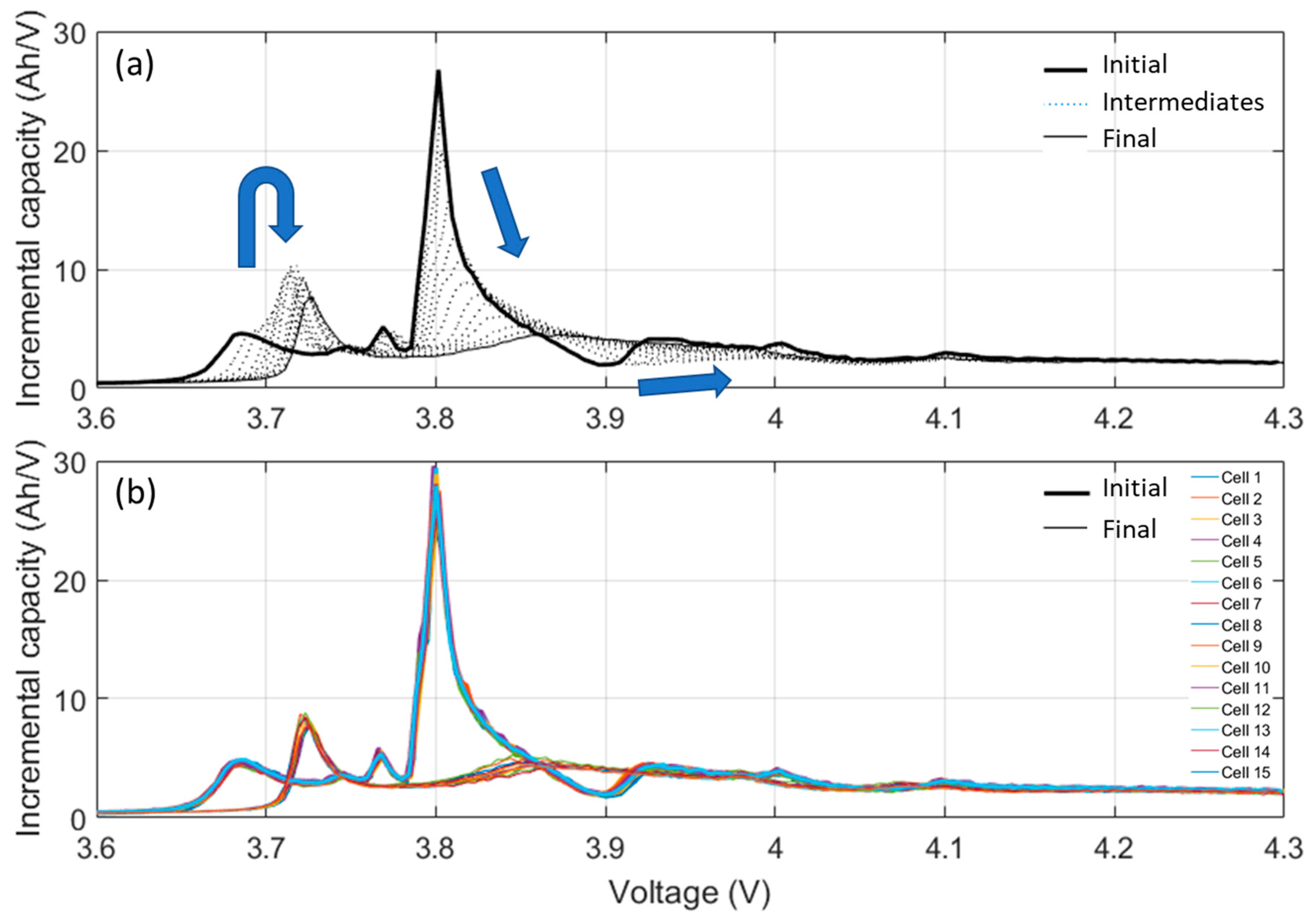

| Result | Mean | Standard Deviation (%) | Minimum | Maximum |
|---|---|---|---|---|
| Weight (g) | 45.8 | 0.2 | 45.7 | 45.9 |
| As received OCV (V) | 3.726 | 4.8 | 3.088 | 3.785 |
| As received SOC (%) | 26.7 | 31.1 | 0.5 | 34.7 |
| C/5 capacity (Ah) | 2.863 | 0.4 | 2.890 | 2.836 |
| C/2 capacity (Ah) | 2.842 | 0.3 | 2.863 | 2.824 |
| C/5 beginning-of-discharge voltage (V) | 4.331 | 0.02 | 4.328 | 4.332 |
| C/5 end-of-discharge (EOD) voltage (V) | 3.231 | 0.3 | 3.208 | 3.253 |
| C/2 beginning-of-discharge voltage (V) | 4.330 | 0.02 | 4.327 | 4.332 |
| C/2 EOD voltage (V) | 3.287 | 0.5 | 3.258 | 3.316 |
| Resistance (mΩ) | 73.2 | 3.6 | 70.1 | 83.1 |
| Rate capability (%) | 99.3 | 0.2 | 98.9 | 99.7 |
| Capacity ration (mAh/%SOC) | 28.7 | 0.3 | 28.6 | 29.0 |
| Observation | Mean | Standard Deviation (%) | Minimum | Maximum |
|---|---|---|---|---|
| C/5 capacity (Ah) | 1.862 | 2.8 | 1.767 | 1.928 |
| Resistance (mΩ) | 112.5 | 5.0 | 105.1 | 122.6 |
| Rate capability (%) | 56.9 | 6.8 | 50.7 | 62.1 |
| Capacity ration (mAh/%SOC) | 22.3 | 1.7 | 21.7 | 23.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devie, A.; Baure, G.; Dubarry, M. Intrinsic Variability in the Degradation of a Batch of Commercial 18650 Lithium-Ion Cells. Energies 2018, 11, 1031. https://doi.org/10.3390/en11051031
Devie A, Baure G, Dubarry M. Intrinsic Variability in the Degradation of a Batch of Commercial 18650 Lithium-Ion Cells. Energies. 2018; 11(5):1031. https://doi.org/10.3390/en11051031
Chicago/Turabian StyleDevie, Arnaud, George Baure, and Matthieu Dubarry. 2018. "Intrinsic Variability in the Degradation of a Batch of Commercial 18650 Lithium-Ion Cells" Energies 11, no. 5: 1031. https://doi.org/10.3390/en11051031
APA StyleDevie, A., Baure, G., & Dubarry, M. (2018). Intrinsic Variability in the Degradation of a Batch of Commercial 18650 Lithium-Ion Cells. Energies, 11(5), 1031. https://doi.org/10.3390/en11051031






