Conducted EMI Prediction and Mitigation Strategy Based on Transfer Function for a High-Low Voltage DC-DC Converter in Electric Vehicle
Abstract
:1. Introduction
2. EMI Test and Modeling Analysis for Isolated Full-Bridge DC-DC Converter
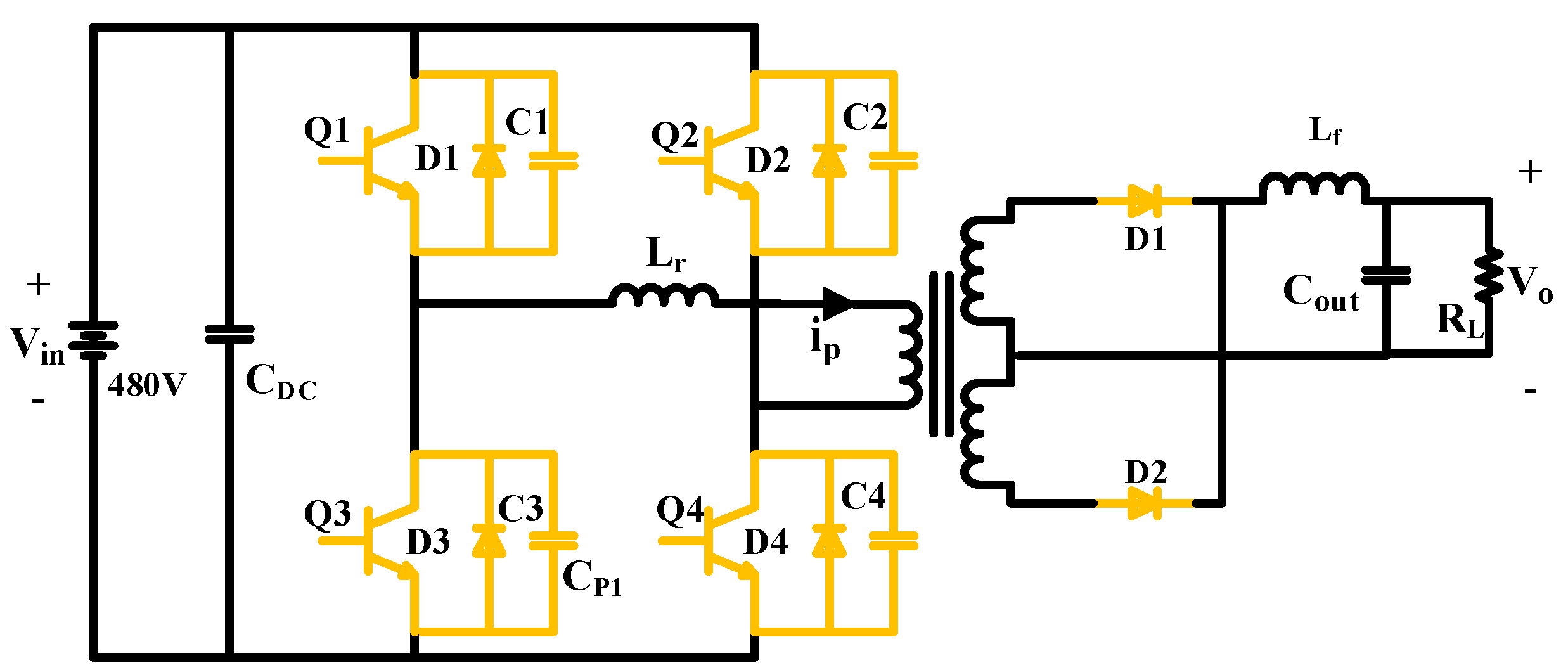
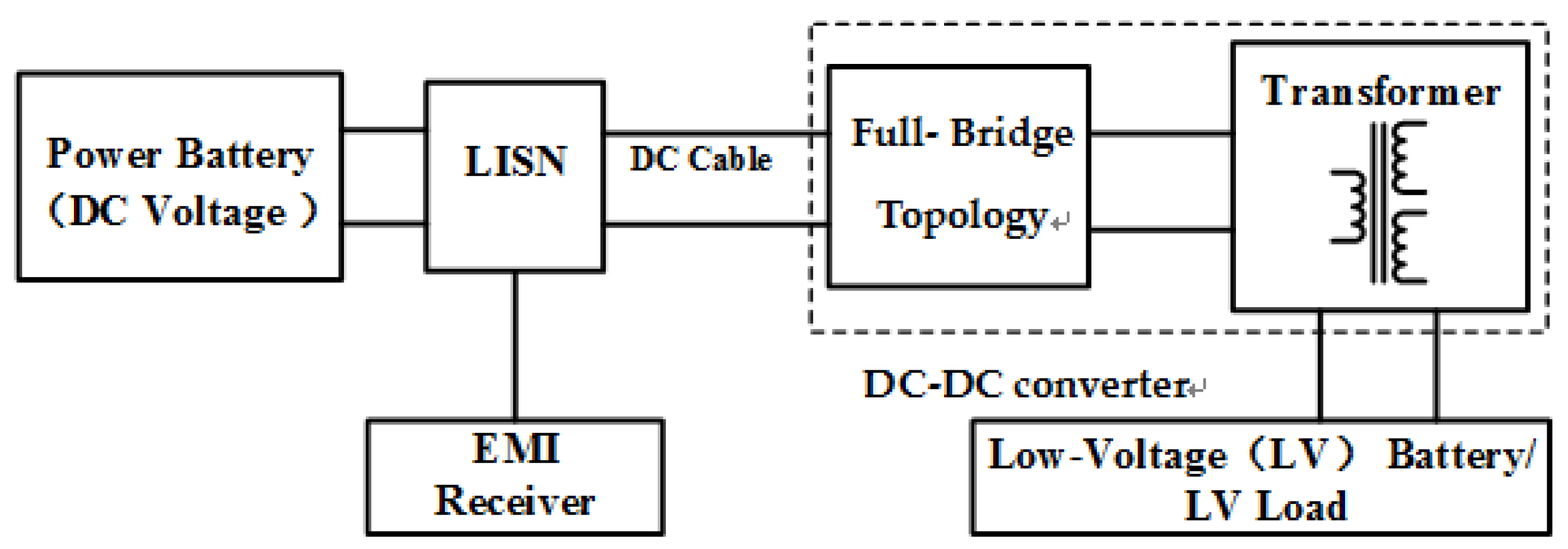
2.1. The Construction of the Onboard DC-DC Converter System
2.2. Setup for Conducted-EMI Emission Test
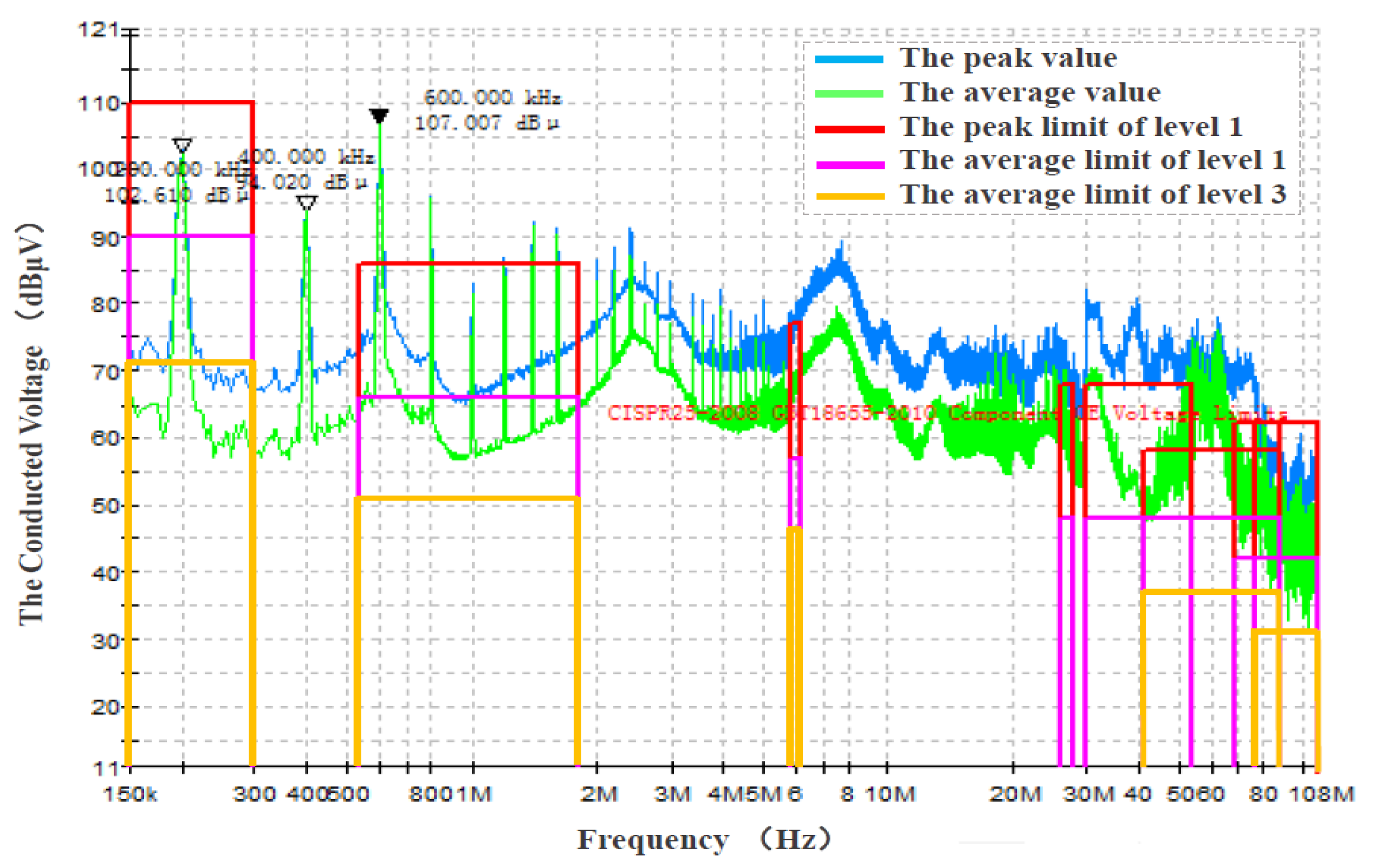
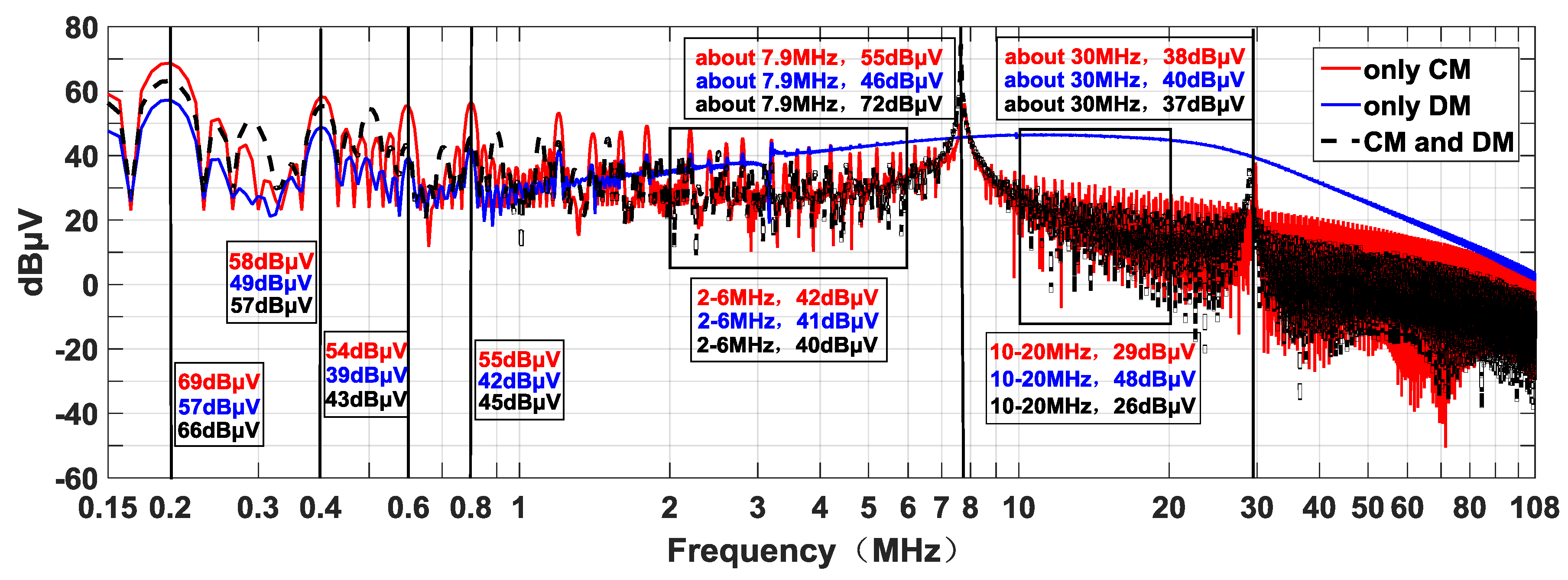
2.3. Experiment Results of the Conducted EMI
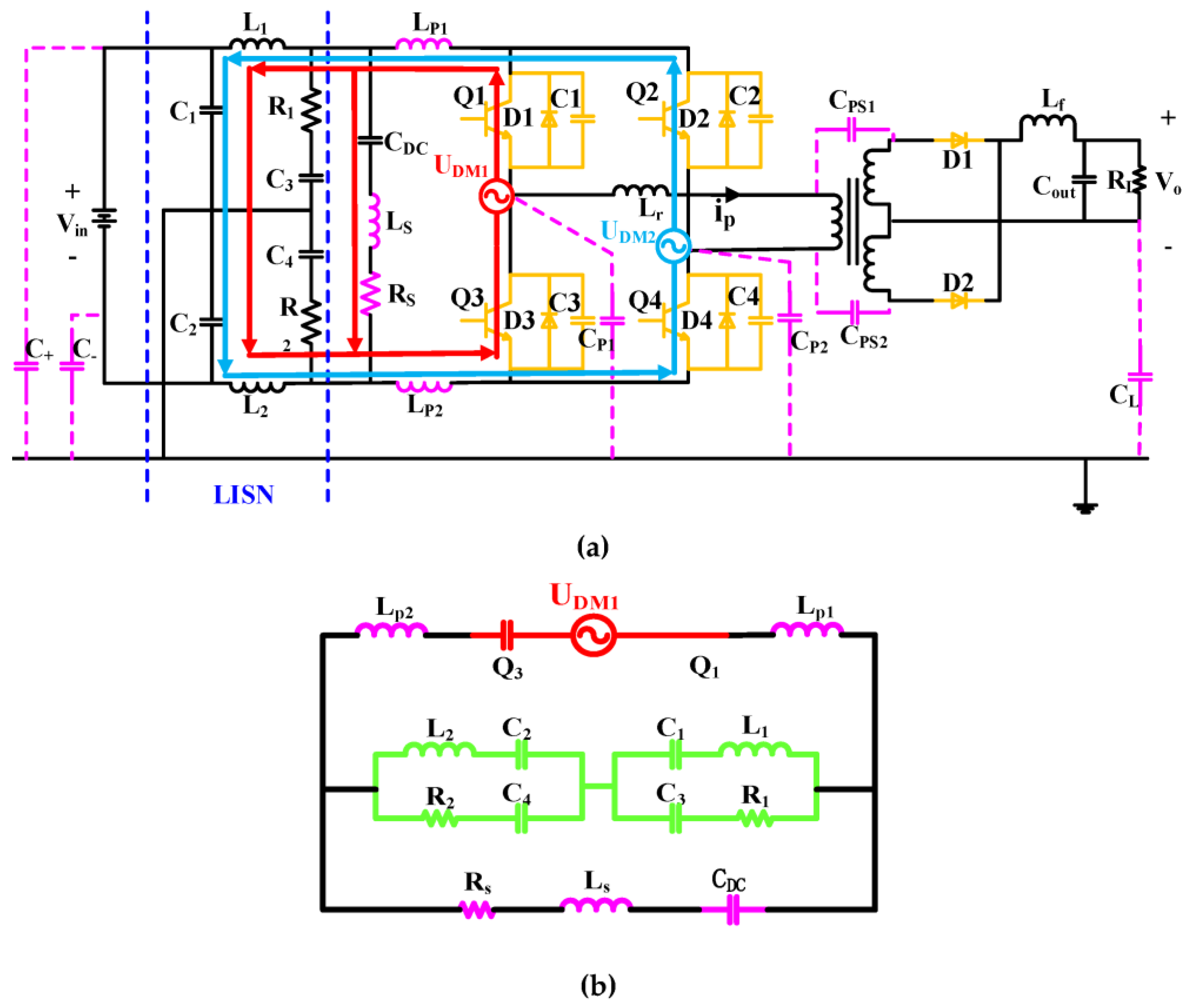
2.4. Modeling Analysis of the Onboard DC-DC Converter System
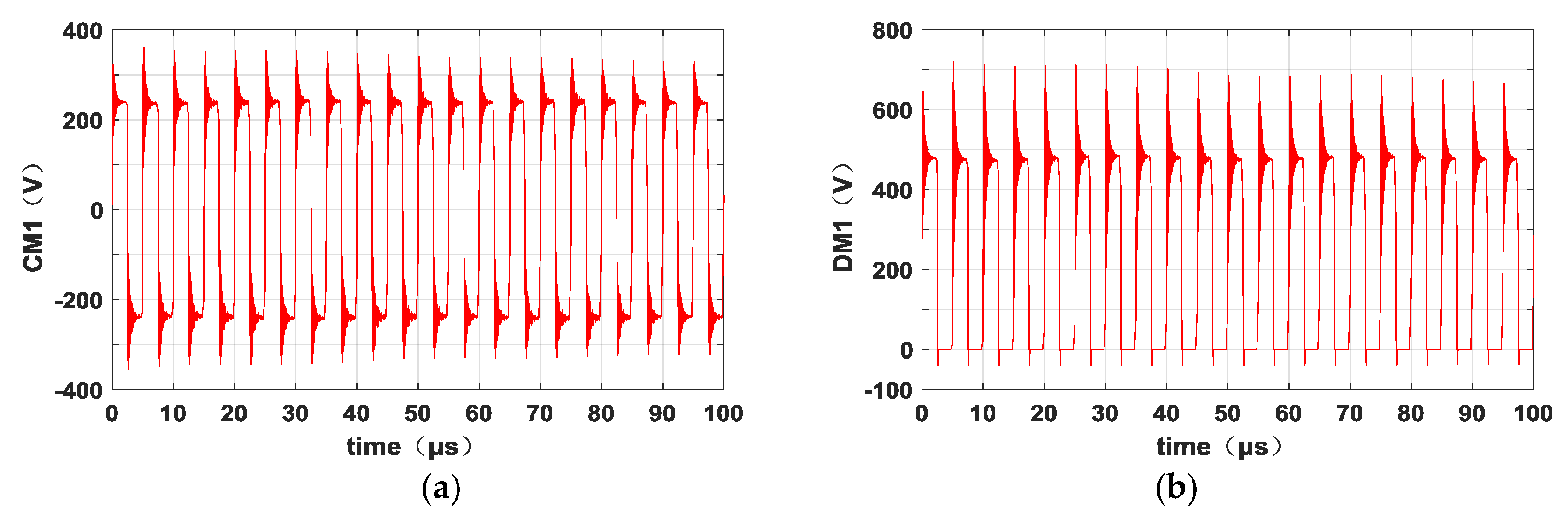
2.4.1. Noise Source
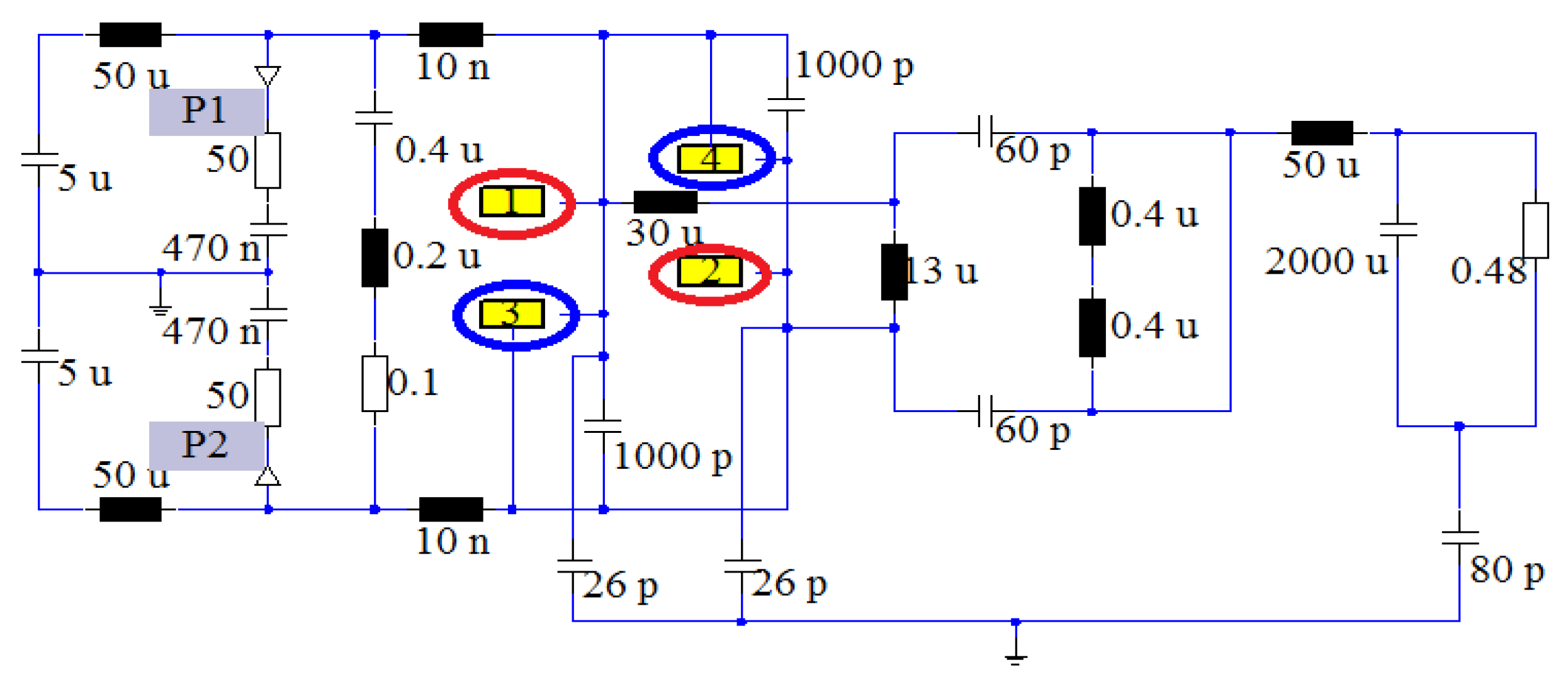
2.4.2. Main Parasitic Parameter
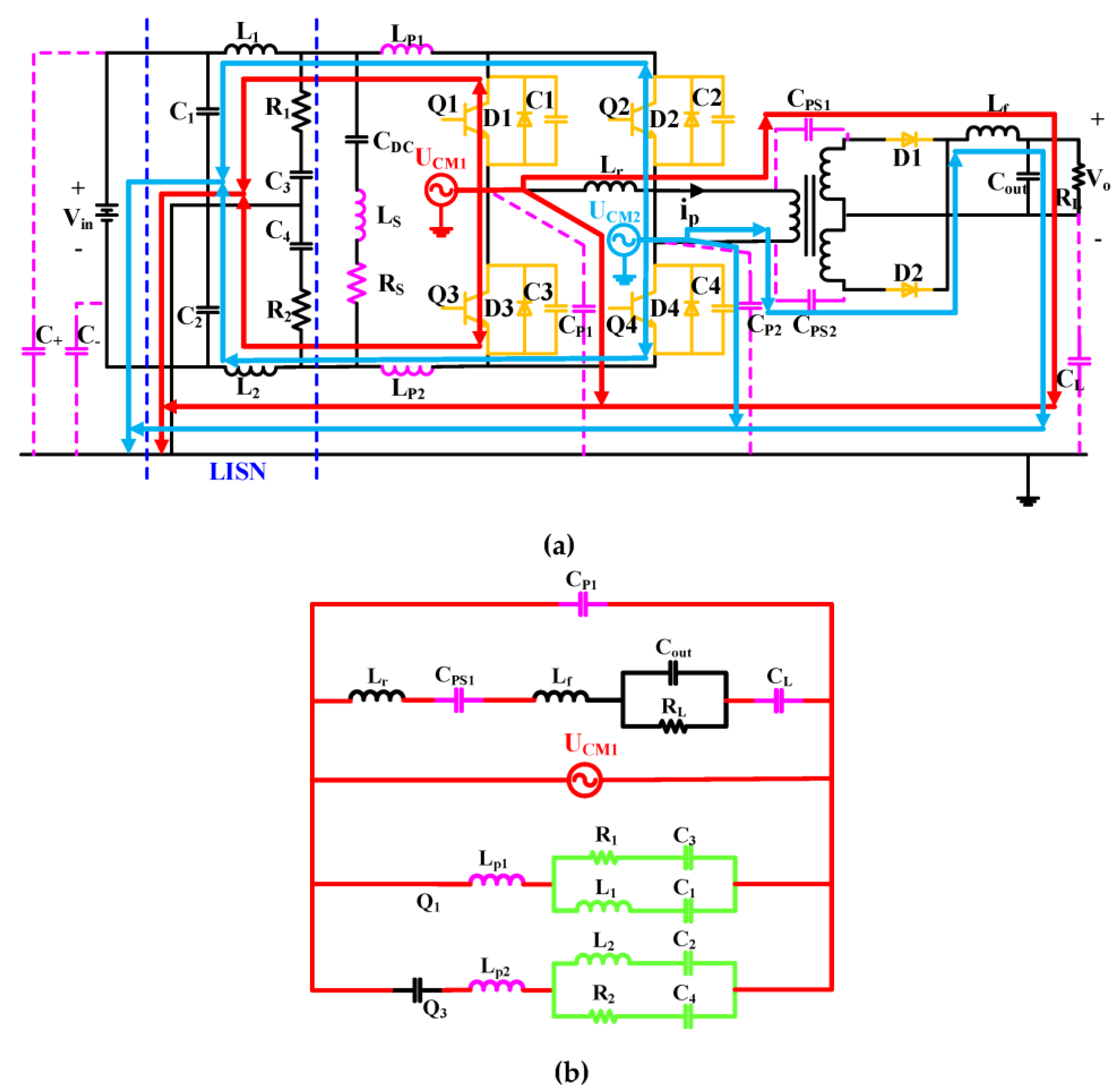
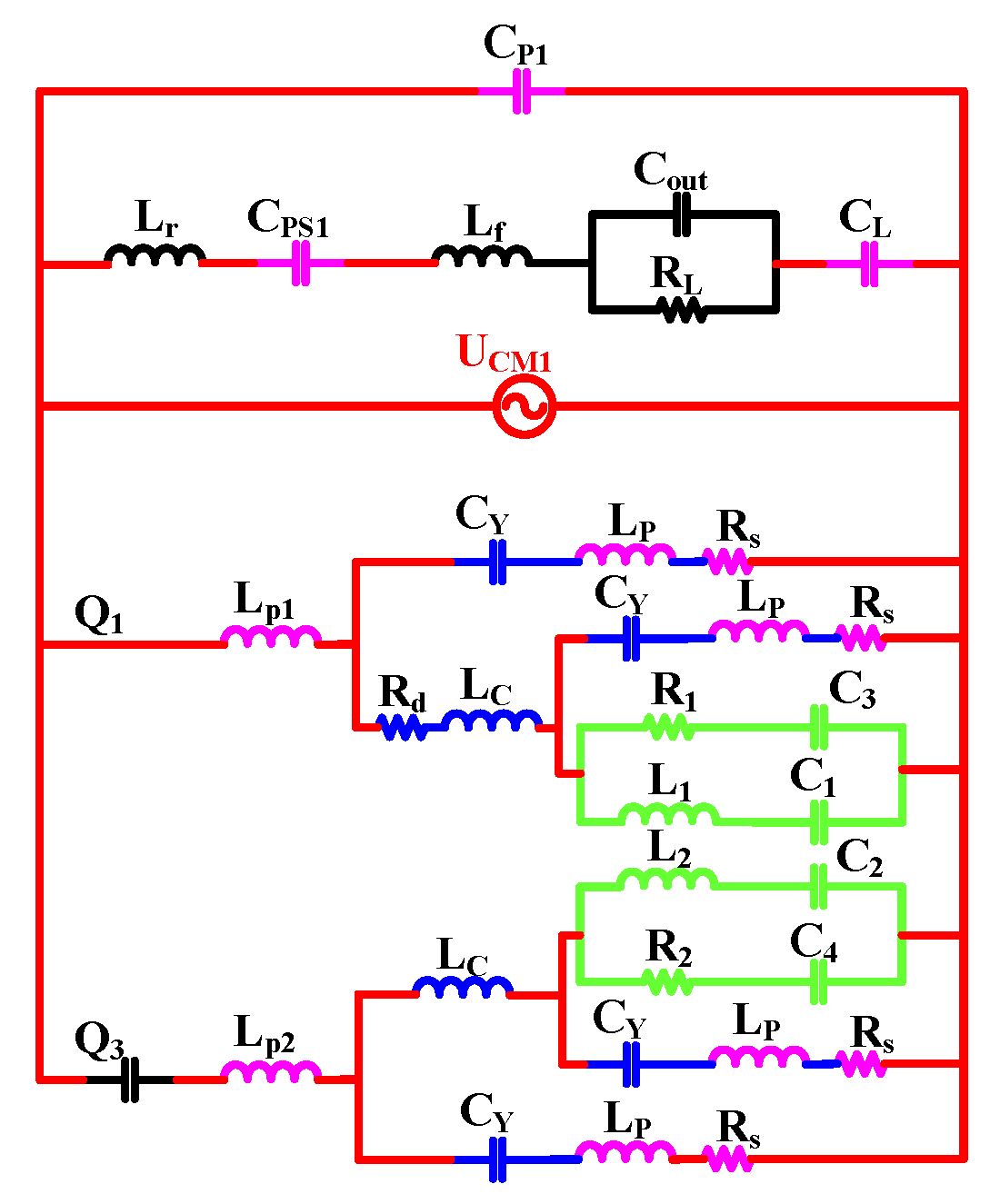
2.4.3. High Frequency Parasitic Parameters of Common Mode EMI
- Loop 1 for CM1: UCM1→Cp1→UCM1
- Loop 1 for CM2: UCM2→Cp2→UCM2
- Loop 2 for CM1: UCM1→CL→→Lf→Cps1→Lr→UCM1
- Loop 2 for CM2: UCM2→CL→→Lf→Cps2→UCM2
- Loop 3 for CM1: UCM1→→Lp1→UCM1
- Loop 3 for CM2: UCM2→→Lp2→UCM2
- Loop 4 for CM1: UCM1→→CQ3→Lp2→UCM1
- Loop 4 for CM2: UCM2→→Lp1→CQ3→UCM2
2.4.4. High Frequency Parasitic Parameters of Differential Mode EMI
- Loop 1 for DM1: UDM1→Lp1→→→Lp2→CQ3→UDM1
- Loop 1 for DM2: UDM2→CQ1→Lp1→→→Lp2→UDM2
- Loop 2 for DM1: UDM1→Lp1→CDC→Ls→Rs→Lp2→CQ3→UDM1
- Loop 2 for DM2: UDM2→CQ2→Lp1→CDC→Ls→Rs→Lp2→UDM2
3. Characteristics Analysis and Simulation Prediction for the Conduction Interference
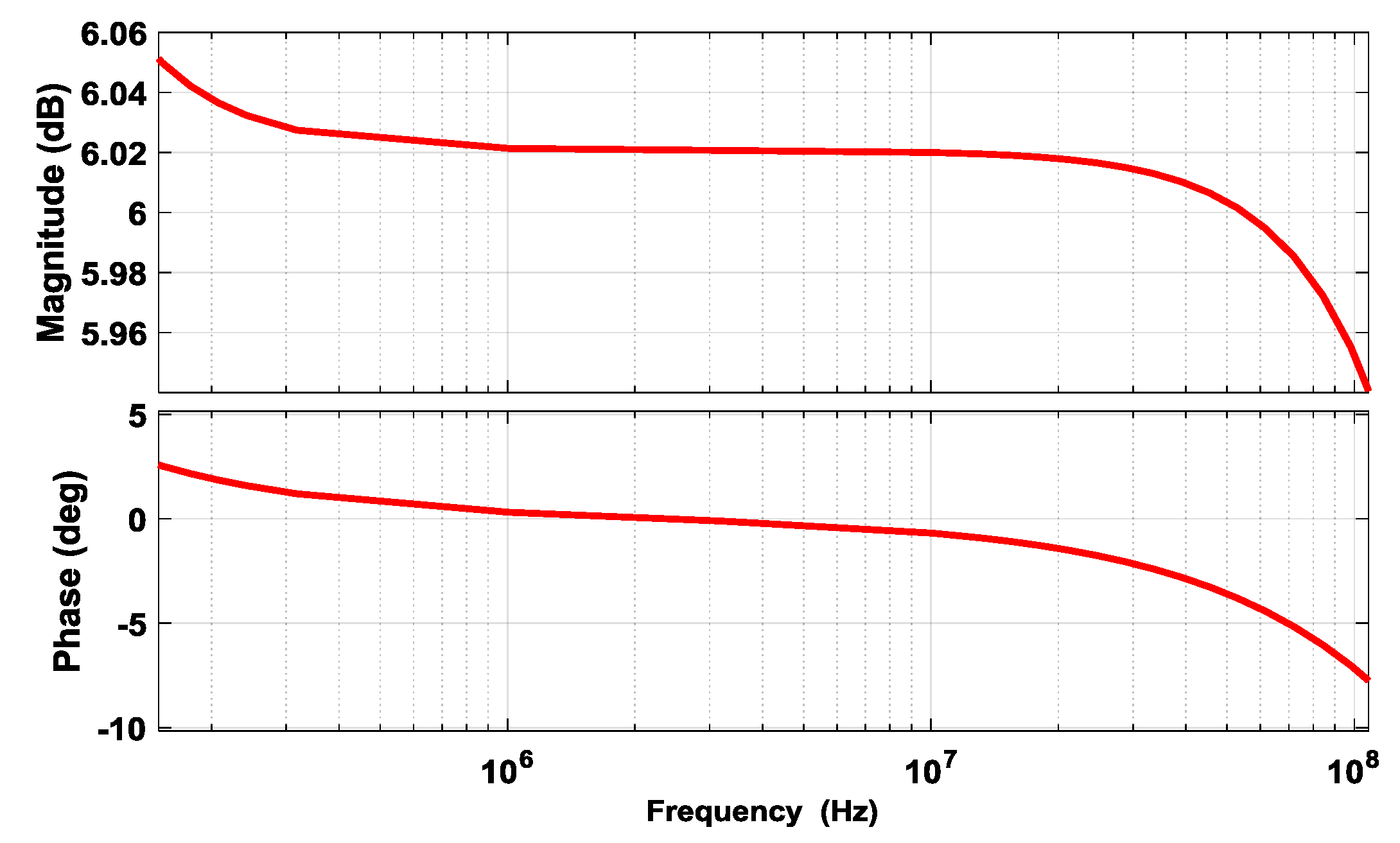
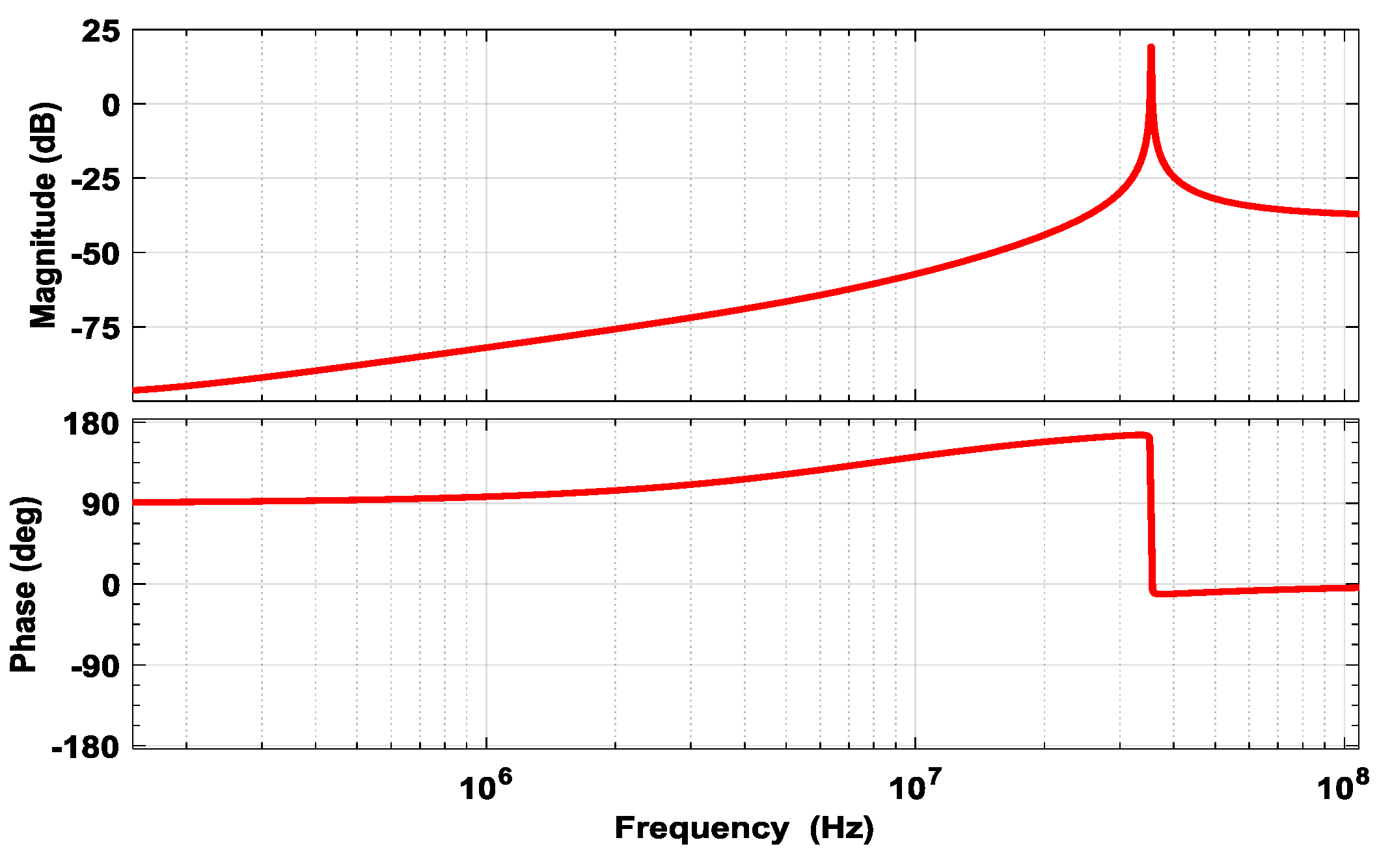
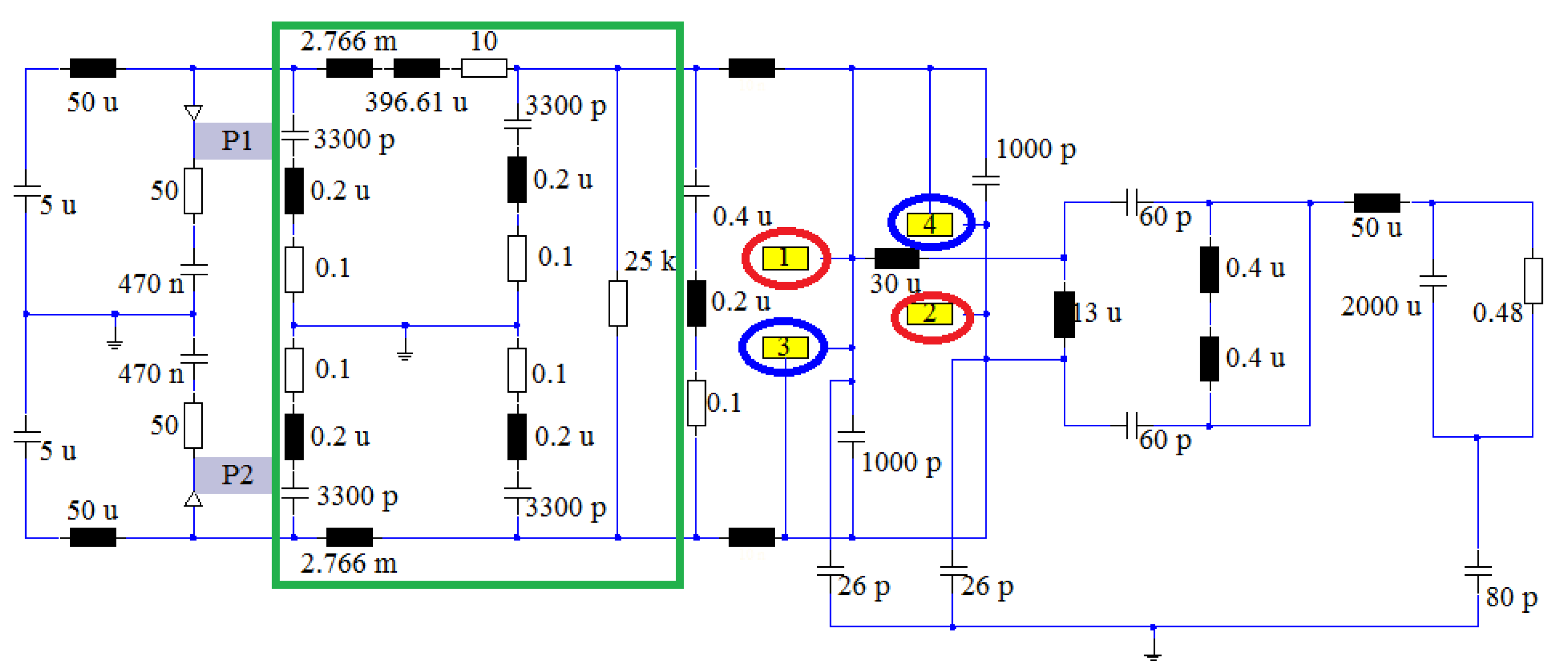
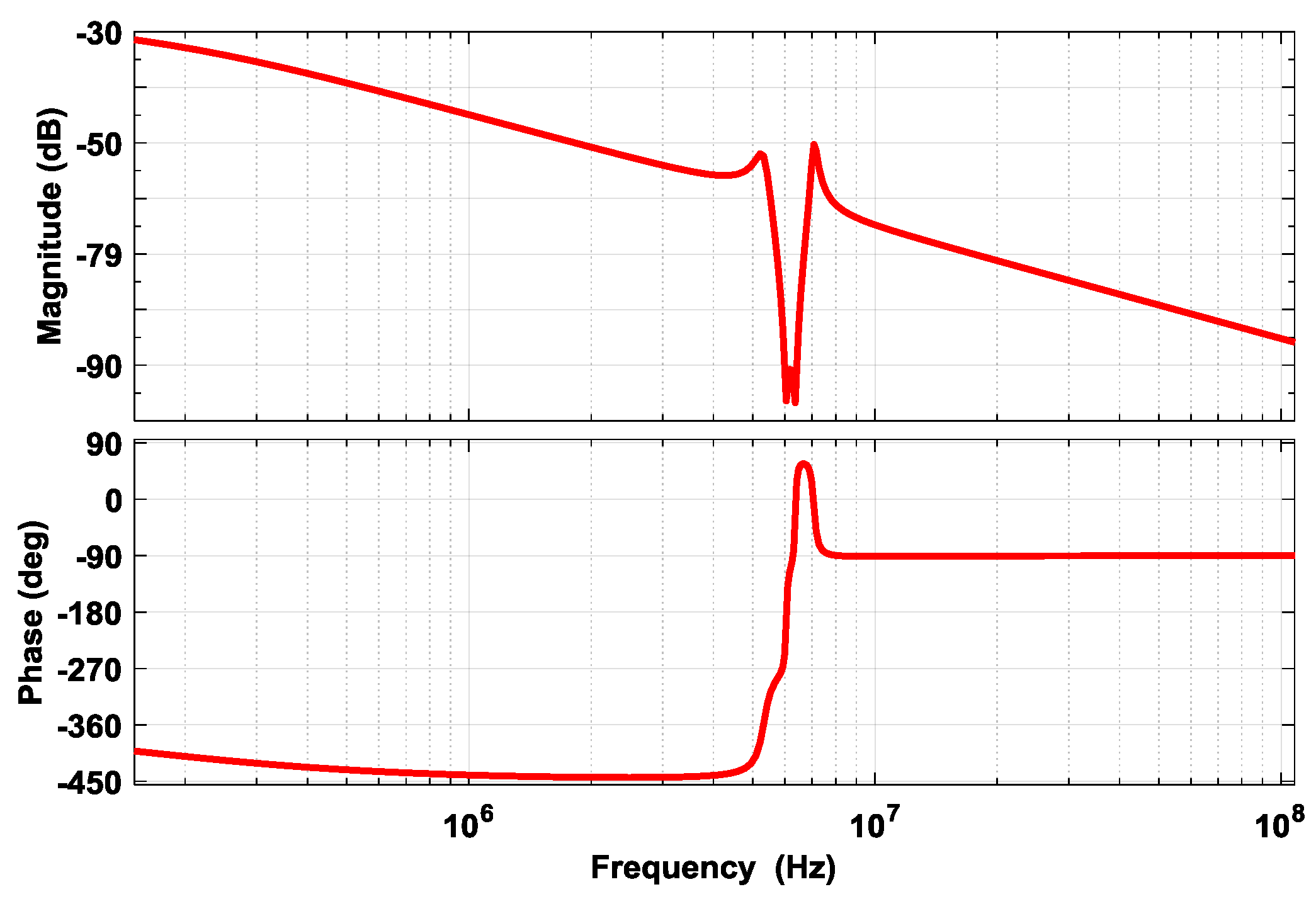
3.1. The Establishment of Transfer Functions
3.2. Extraction of the Noise Sources
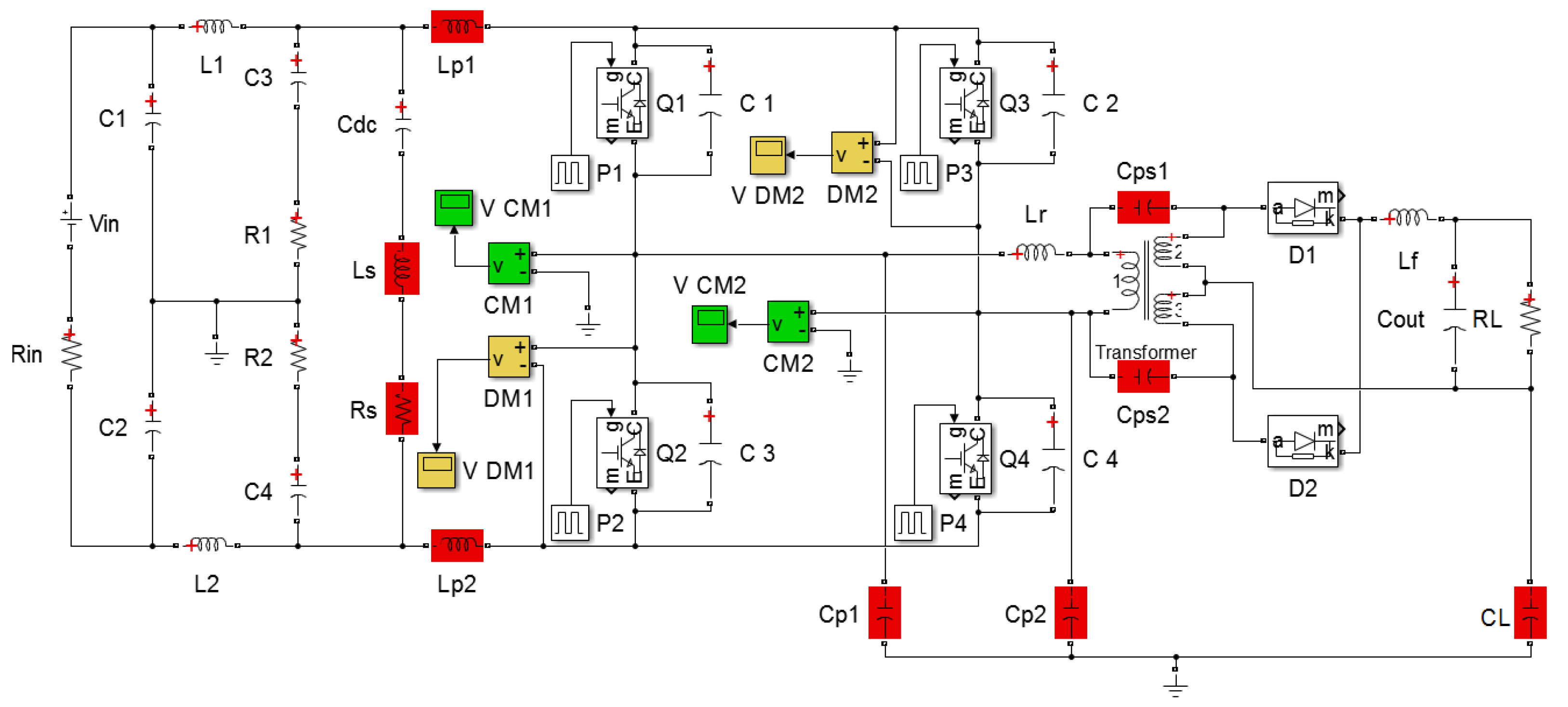
3.3. Simulation for the Conducted Interference
4. Design of High Frequency EMI Filter
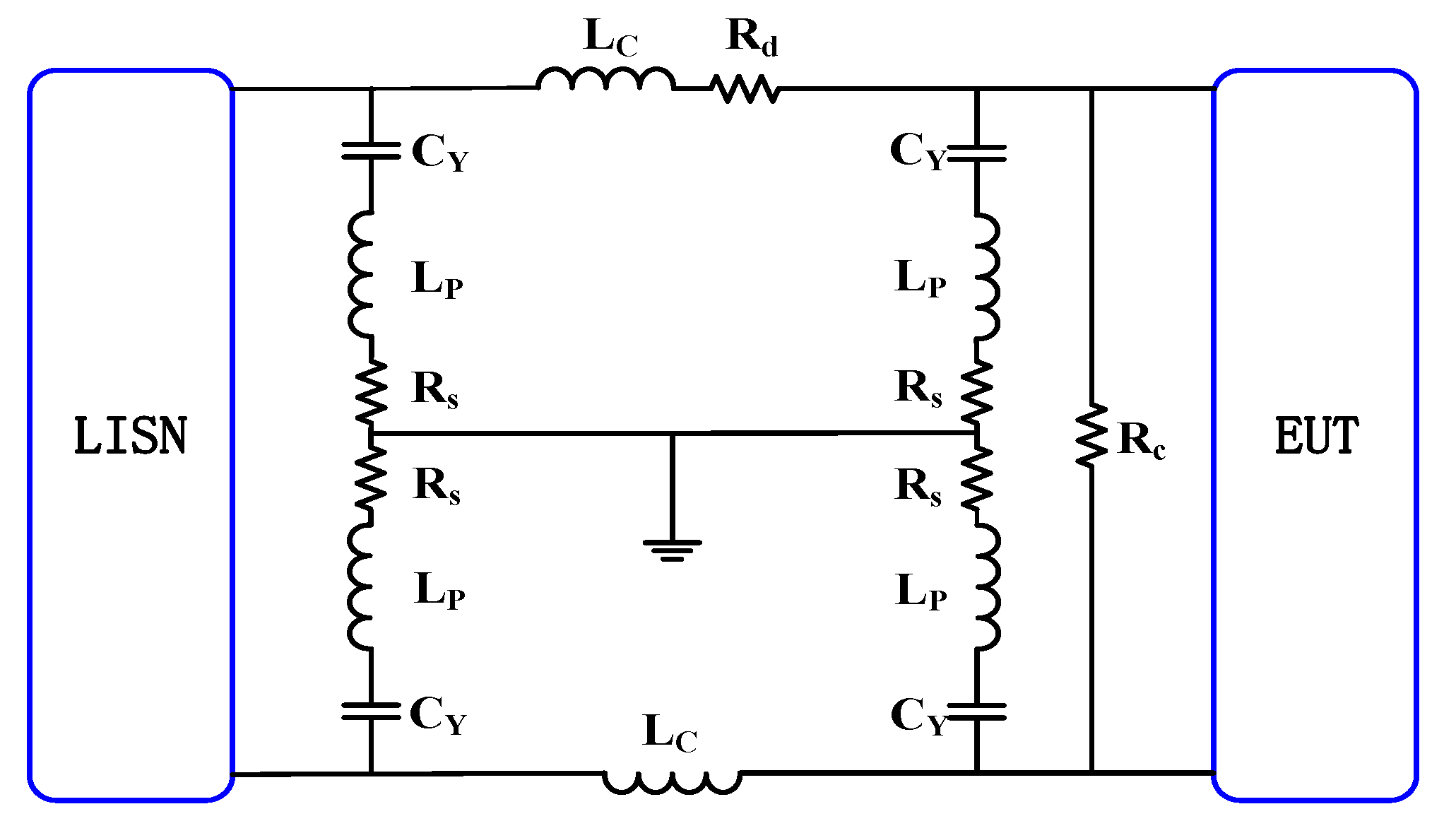
4.1. Parameters Calculation of CM EMI Filter
4.2. Topology Selection of CM Filter
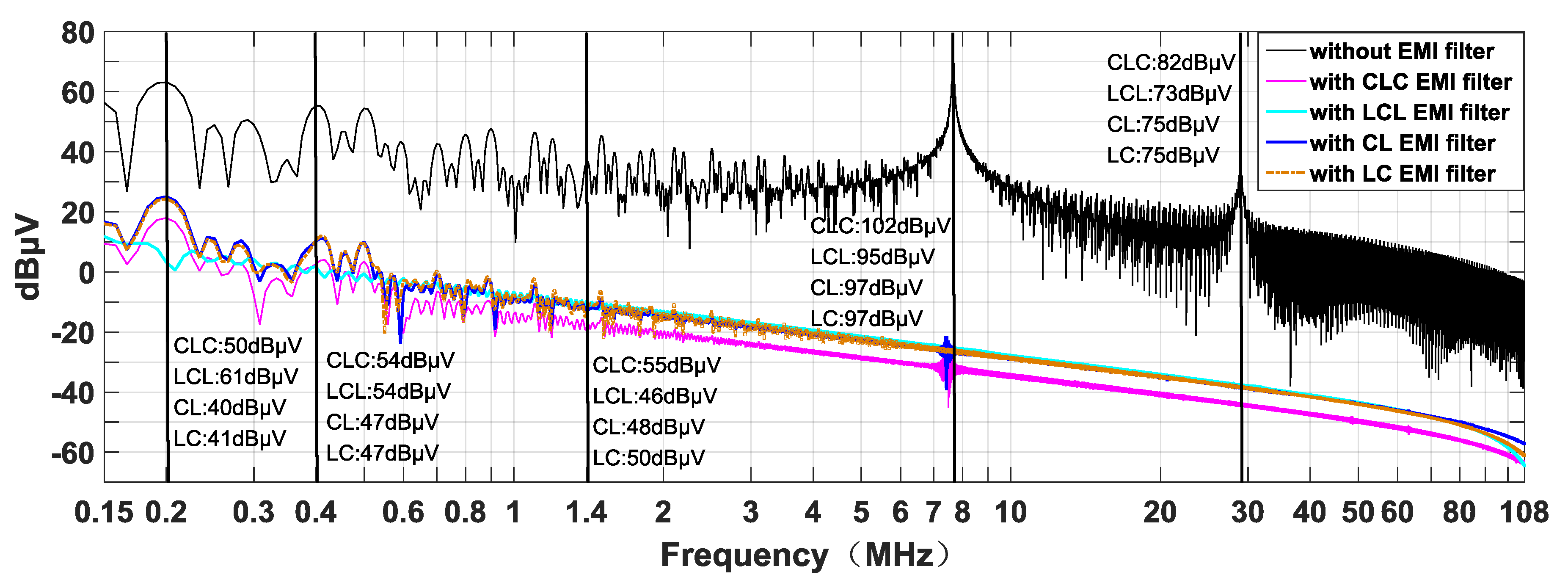
4.3. Mitigation Effect and Stability Analysis of the High Frequency EMI Filter
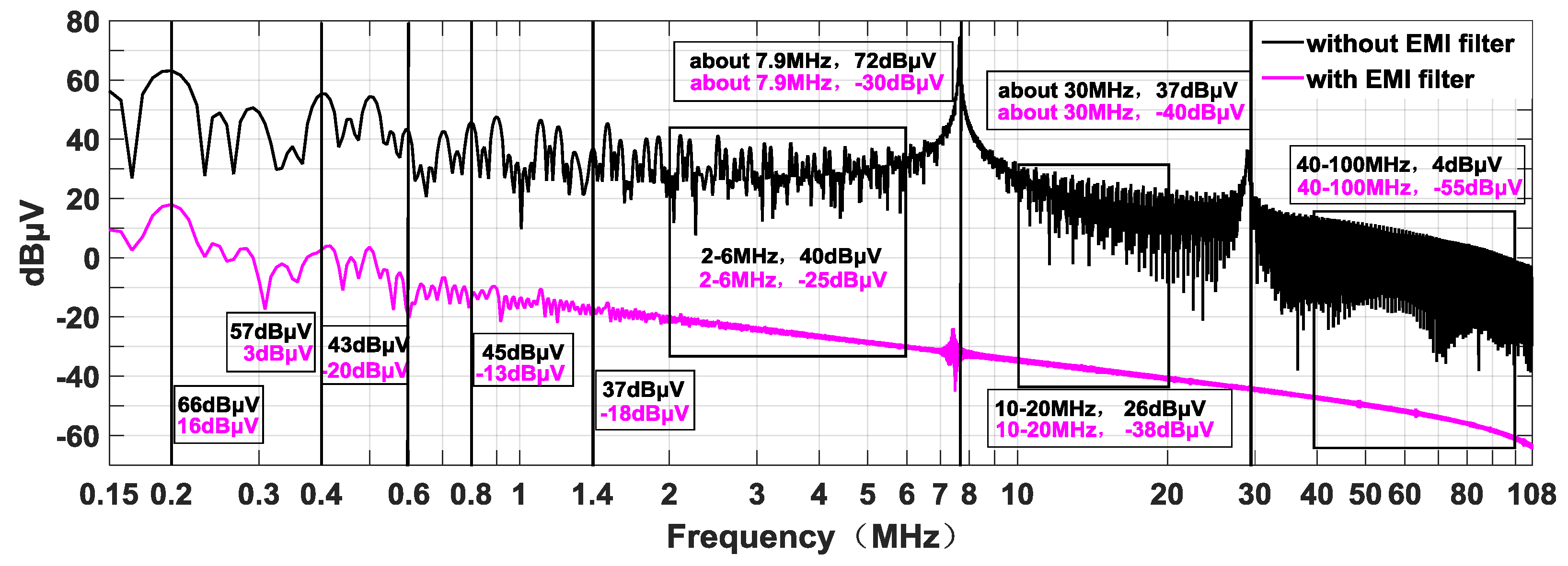
5. Experimental Verification
Comparison and Analysis for the EMI Experimental Result and EMI Simulation Result
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ferrero, E.; Alessandrini, S.; Balanzino, A. Impact of the electric vehicles on the air pollution from a highway. Appl. Energy 2016, 169, 450–459. [Google Scholar] [CrossRef]
- Zhai, L.; Zhang, X.; Bondarenko, N.; Loken, D.; Van Doren, T.P.; Beetner, D.G. Mitigation Emission Strategy Based on Resonances from a Power Inverter System in Electric Vehicles. Energies 2016, 9, 419. [Google Scholar] [CrossRef]
- Zhai, L.; Lin, L.; Zhang, X.; Song, C. The Effect of Distributed Parameters on Conducted EMI from DC-Fed Motor Drive Systems in Electric Vehicles. Energies 2016, 10, 1. [Google Scholar] [CrossRef]
- Xue, J.; Wang, F. Modeling and design of common-mode inductor for conductive EMI noise suppression in DC-fed motor drive system. In Proceedings of the Energy Conversion Congress and Exposition, Raleigh, NC, USA, 15–20 September 2012; pp. 645–651. [Google Scholar]
- Kahoul, R.; Marchal, P.; Azzouz, Y.; Mazari, B. HF model of DC motor impedance EMC problems in automotive applications. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Detroit, MI, USA, 18–22 August 2008; pp. 1–5. [Google Scholar]
- Song, B.; Tao, Y. The suppression of conducted EMI for the motor controller in a battery electric vehicle. Automot. Eng. 2013, 35, 996–999. [Google Scholar]
- Kahoul, R.; Azzouz, Y.; Ravelo, B.; Mazari, B. New Behavioral Modeling of EMI for DC Motors Applied to EMC Characterization. IEEE Trans. Ind. Electron. 2013, 60, 5482–5496. [Google Scholar] [CrossRef]
- He, H.; Qu, B.; Chen, C.; Bai, B. Research on the EMI suppression methods of the integrative motor system. In Proceedings of the International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–4. [Google Scholar]
- Diouf, F.; Leferink, F.; Duval, F.; Bensetti, M. Wideband Impedance Measurements and Modeling of DC Motors for EMI Predictions. IEEE Trans. Electromagn. Compat. 2014, 57, 180–187. [Google Scholar] [CrossRef]
- Kubik, Z.; Skala, J. Industrial DC/DC converters in terms of EMC. In Proceedings of the Compatibility and Power Electronics, Tallinn, Estonia, 1–3 June 2011; pp. 295–298. [Google Scholar]
- Ali, M.; Labouré, E.; Costa, F.; Revol, B. Design of a Hybrid Integrated EMC Filter for a DC–DC Power Converter. IEEE Trans. Power Electron. 2012, 27, 4380–4390. [Google Scholar] [CrossRef]
- Ali, M.; Laboure, E.; Costa, F.; Revol, B.; Gautier, C. Hybrid Integrated EMC filter for CM and DM EMC Suppression in a DC-DC Power converter. In Proceedings of the International Conference on Integrated Power Electronics Systems, Nuremberg, Germany, 6–8 March 2012; pp. 1–6. [Google Scholar]
- Grobler, I.; Gitau, M.N. Conducted EMC modeling for accreditation in DC-DC converters. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 002329–002335. [Google Scholar]
- Huynh, H.A.; Joo, S.; Kim, S. An experimental study of EMI reduction of DC-DC converter with frequency hopping technique. In Proceedings of the Electrical Design of Advanced Packaging and Systems, Honolulu, HI, USA, 14–16 Decemebr 2016; pp. 107–109. [Google Scholar]
- Ales, A.; Schanen, J.L.; Moussaoui, D.; Roudet, J. Impedances Identification of DC/DC Converters for Network EMC Analysis. IEEE Trans. Power Electron. 2014, 29, 6445–6457. [Google Scholar] [CrossRef]
- Koo, K.; Kim, J.; Kim, M.; Kim, J. Impact of PCB design on switching noise and EMI of synchronous DC-DC buck converter. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Fort Lauderdale, FL, USA, 25–30 July 2010; pp. 67–71. [Google Scholar]
- Luo, F.L.; Ye, H. Investigation of EMI, EMS and EMC in power DC/DC converters. In Proceedings of the International Conference on Power Electronics and Drive Systems, Singapore, 17–20 November 2003; Volume 1, pp. 572–577. [Google Scholar]
- Mukharjee, I.; Gadoura, I.A. Simple, low EMI-noise input-filter design for DC/DC power regulators. In Proceedings of the Industrial Electronics and Applications, Singapore, 18–20 July 2012; pp. 948–953. [Google Scholar]
- Karvonen, A.; Astrom, J. Simulating the EMI characteristics of step-down DC/DC converters. In Proceedings of the Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–6. [Google Scholar]
- Wang, Q.; An, Z.; Zheng, Y.; Yang, Y. Parameter extraction of conducted electromagnetic interference prediction model and optimisation design for a DC-DC converter system. IET Power Electron. 2013, 6, 1449–1461. [Google Scholar] [CrossRef]
- Gao, X.; Su, D.; Li, Y. Study on electromagnetic interference of DC/DC converter used in the EV. In Proceedings of the 2015 Asia-Pacific Symposium on Electromagnetic Compatibility (APEMC), Taipei, Taiwan, 26–29 May 2015; pp. 258–261. [Google Scholar]
- Kotny, J.L.; Duquesne, T.; Idir, N. Design of EMI filters for DC-DC converter. In Proceedings of the Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar]
- Makda, I.A.; Nymand, M. Differential mode EMI filter design for isolated DC-DC boost converter. In Proceedings of the European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–8. [Google Scholar]
- Wei, T.Y.; Shen, Y.Z.; Zhang, Y.C.; Yao, Y.T. EMI Analysis and EMC Design of DC/DC Converter Used in Electric Vehicle. Low Volt. Appar. 2005, 5, 13–25. [Google Scholar]
- Bondarenko, N.; Zhai, L.; Xu, B. A Measurement-Based Model of the Electromagnetic Emissions from a Power Inverter. IEEE Trans. Power Electron. 2015, 30, 5522–5531. [Google Scholar] [CrossRef]


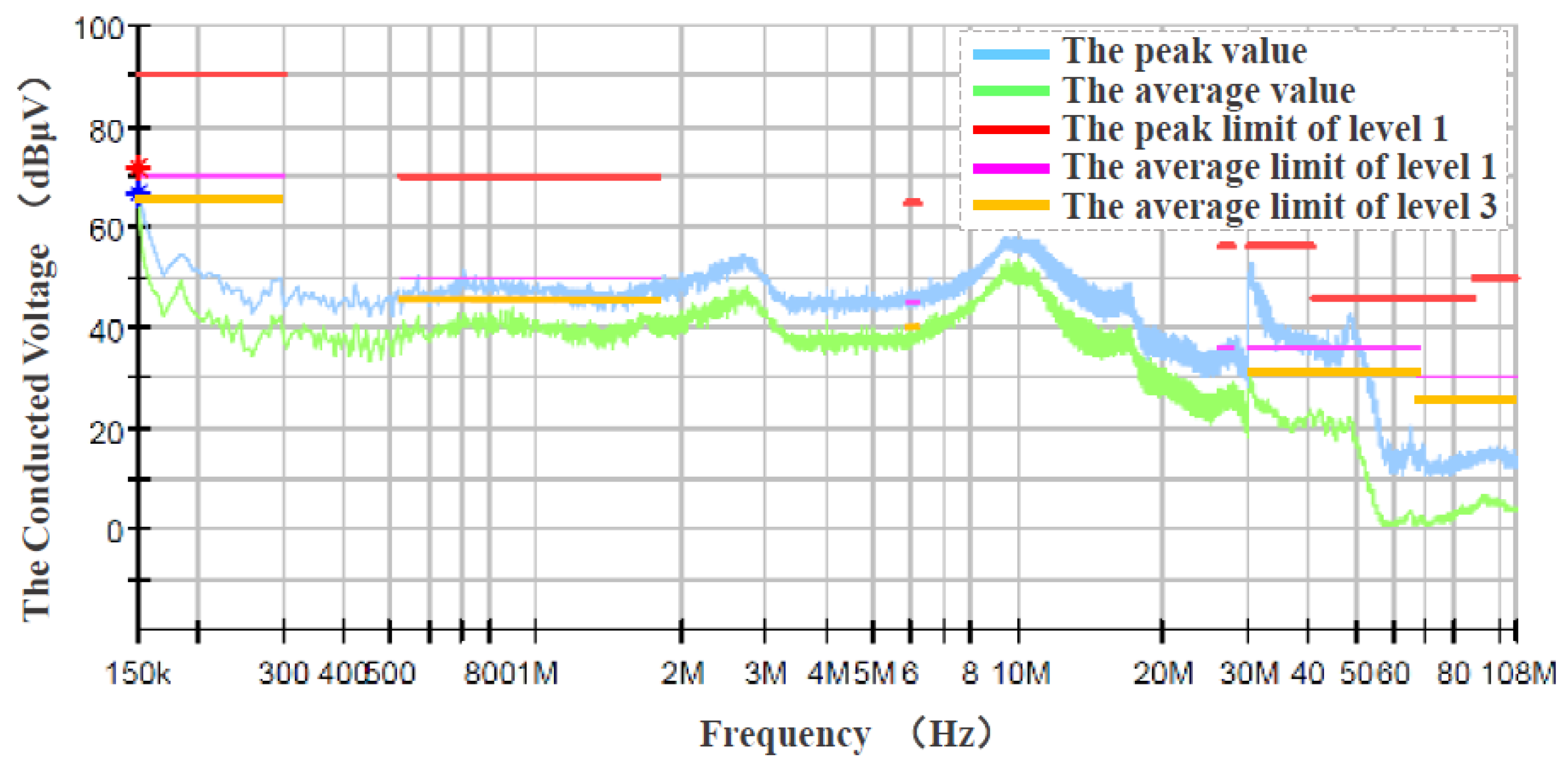
| Band | Frequency/MHz | Electrical Level/dB(μV) |
|---|---|---|
| LW | 0.15–0.30 | 70 |
| MW | 0.53–1.8 | 50 |
| SW | 5.9–6.2 | 45 |
| FW | 76–108 | 30 |
| TV Band I | 41–88 | 36 |
| Circuit Element | Value | Circuit Element | Value | Parameter | Value |
|---|---|---|---|---|---|
| CQ2 | 1000 pF | R2 | 50 Ω | Cp1 | 26 pF |
| CQ3 | 1000 pF | L1 | 50 μH | Cps1 | 60 pF |
| Lr | 30 μH | L2 | 50 μH | CL | 80 pF |
| Lf | 50 μH | C1 | 5 μF | Ls | 0.2 μH |
| RL | 0.48 Ω | C2 | 5 μF | Rs | 0.1 Ω |
| Cout | 2000 μF | C3 | 470 nF | Lp1 | 10 nH |
| R1 | 50 Ω | C4 | 470 nF | Lp2 | 10 nH |
| Frequency | Simulation Results (dBμV) | ||
|---|---|---|---|
| without Filter | with Filter | Attenuation | |
| 200 kHz | 66 | 16 | 50 |
| 400 kHz | 57 | 3 | 54 |
| 600 kHz | 43 | −20 | 63 |
| 800 kHz | 45 | −13 | 58 |
| 1.4 MHz | 37 | −18 | 55 |
| 2–6 MHz | 40 | −25 | 65 |
| 7.8 MHz | 72 | −30 | 102 |
| 10–20 MHz | 26 | −38 | 64 |
| 30 MHz | 37 | −40 | 77 |
| 50 MHz | 8 | −50 | 58 |
| Frequency | Attenuation (dBμV) | ||
|---|---|---|---|
| Measurement | Simulation | Error (dBμV) | |
| 200 kHz | 58 | 50 | 8 |
| 400 kHz | 55 | 54 | 1 |
| 600 kHz | 65 | 63 | 2 |
| 800 kHz | 54 | 58 | −4 |
| 1.0 MHz | 42 | 42 | 0 |
| 1.4 MHz | 53 | 55 | −2 |
| 2.0 MHz | 42 | 49 | −7 |
| 50 MHz | 54 | 58 | −4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, L.; Zhang, T.; Cao, Y.; Yang, S.; Kavuma, S.; Feng, H. Conducted EMI Prediction and Mitigation Strategy Based on Transfer Function for a High-Low Voltage DC-DC Converter in Electric Vehicle. Energies 2018, 11, 1028. https://doi.org/10.3390/en11051028
Zhai L, Zhang T, Cao Y, Yang S, Kavuma S, Feng H. Conducted EMI Prediction and Mitigation Strategy Based on Transfer Function for a High-Low Voltage DC-DC Converter in Electric Vehicle. Energies. 2018; 11(5):1028. https://doi.org/10.3390/en11051028
Chicago/Turabian StyleZhai, Li, Tao Zhang, Yu Cao, Sipeng Yang, Steven Kavuma, and Huiyuan Feng. 2018. "Conducted EMI Prediction and Mitigation Strategy Based on Transfer Function for a High-Low Voltage DC-DC Converter in Electric Vehicle" Energies 11, no. 5: 1028. https://doi.org/10.3390/en11051028
APA StyleZhai, L., Zhang, T., Cao, Y., Yang, S., Kavuma, S., & Feng, H. (2018). Conducted EMI Prediction and Mitigation Strategy Based on Transfer Function for a High-Low Voltage DC-DC Converter in Electric Vehicle. Energies, 11(5), 1028. https://doi.org/10.3390/en11051028





