Classification Method to Define Synchronization Capability Limits of Line-Start Permanent-Magnet Motor Using Mesh-Based Magnetic Equivalent Circuit Computation Results
Abstract
:1. Introduction
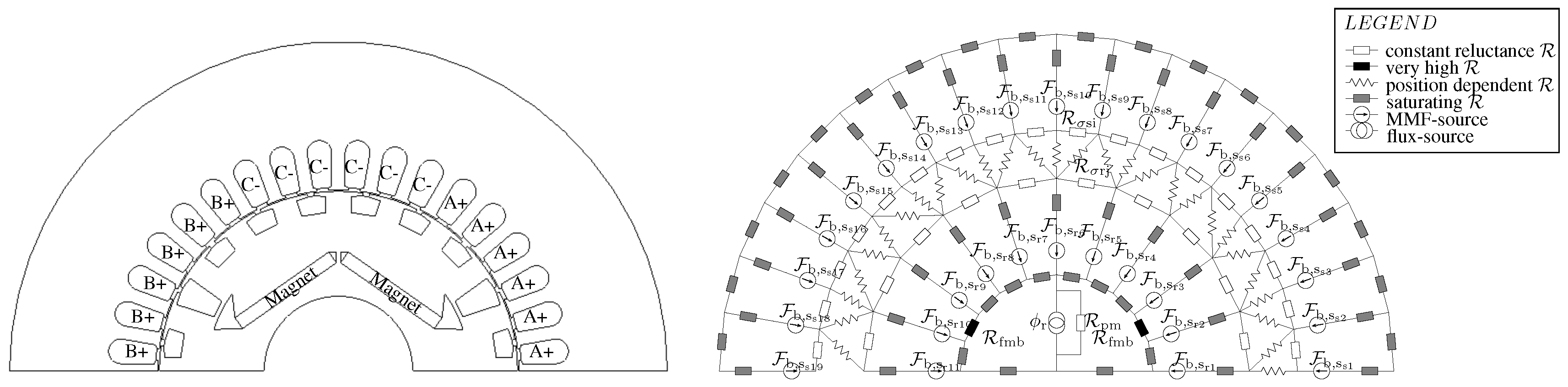
2. Magnetic Network Algorithm
2.1. Constant Reluctances
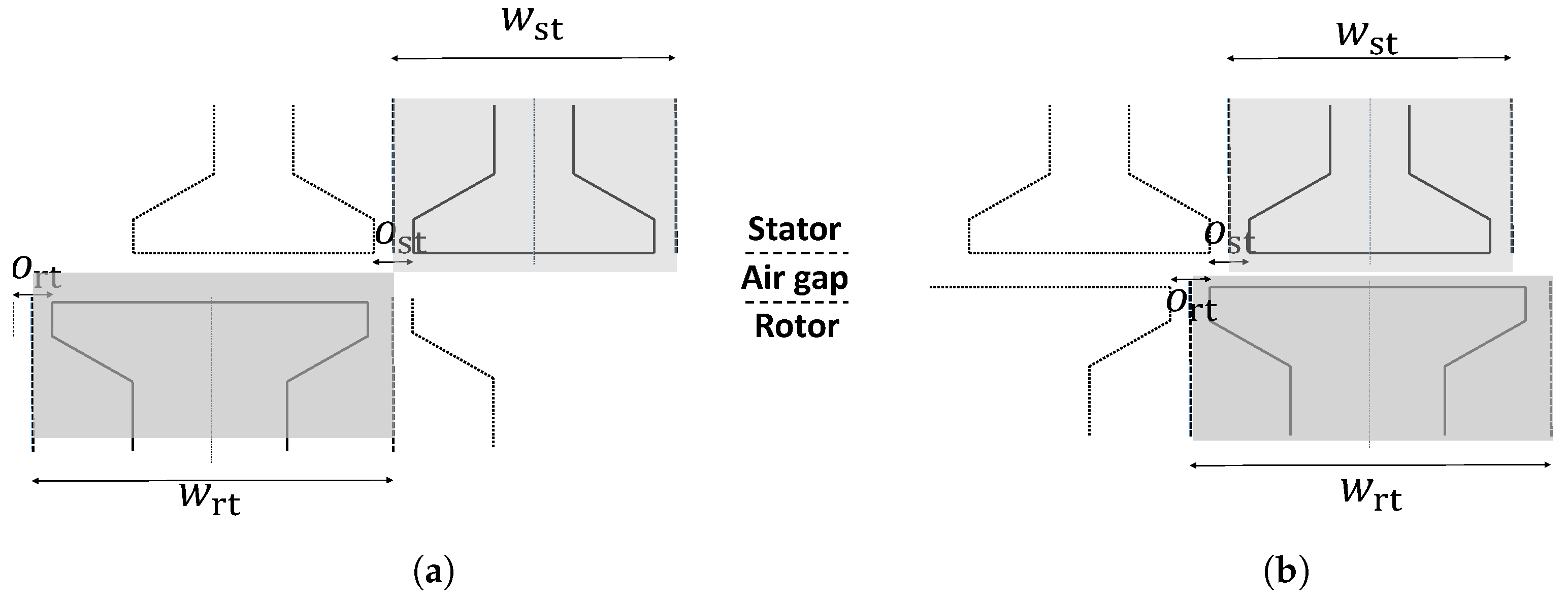
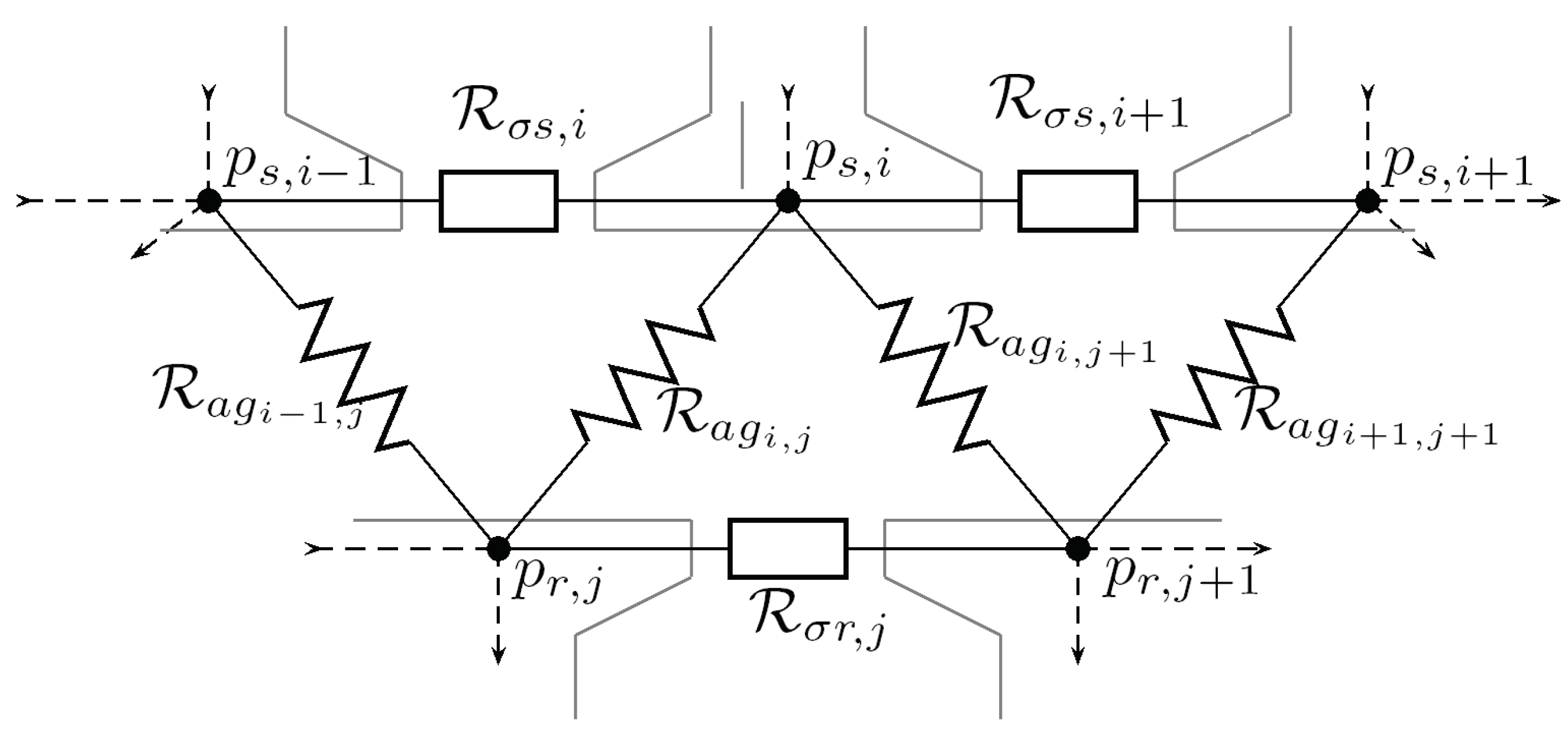
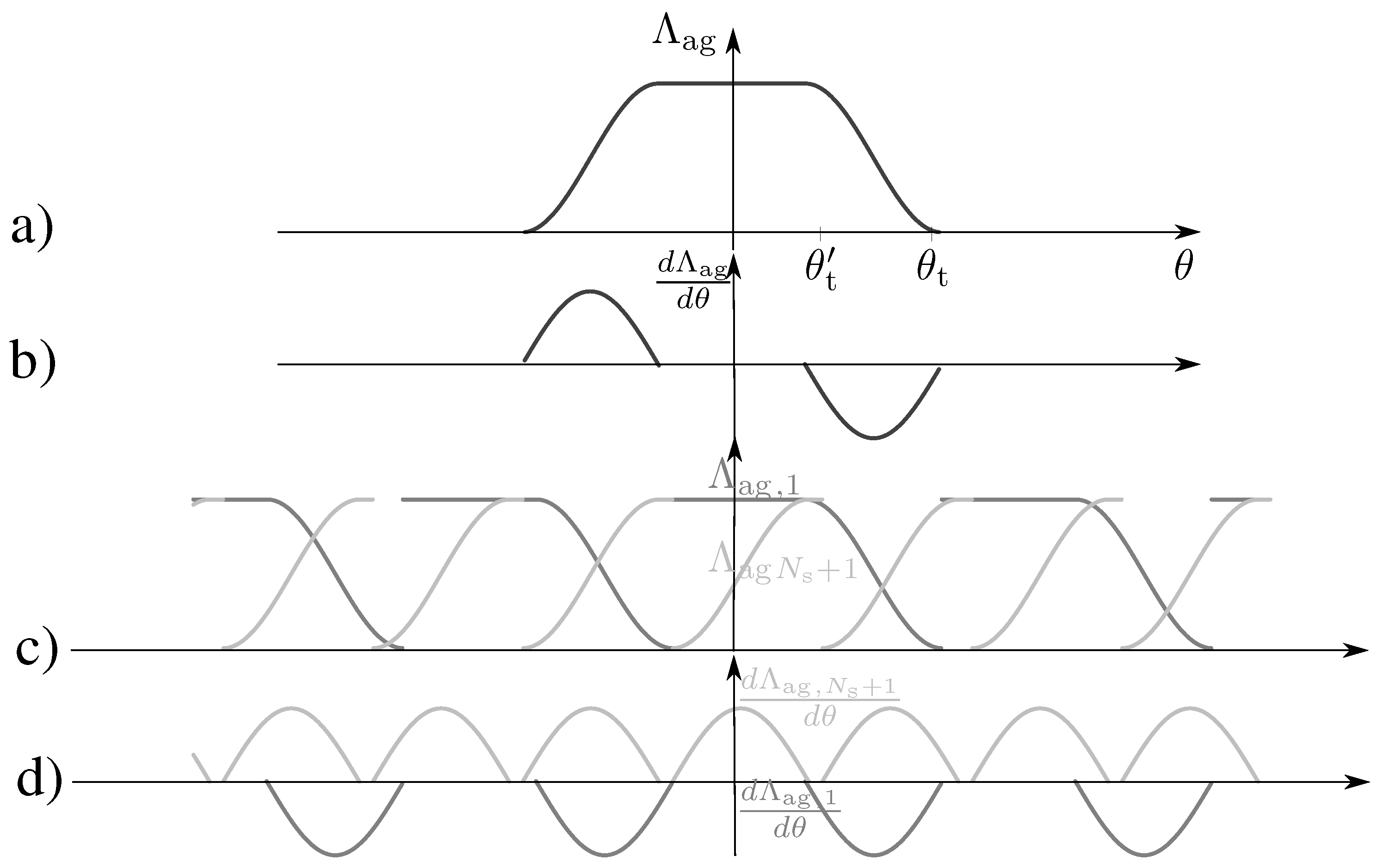
2.2. Position-Dependent Reluctances
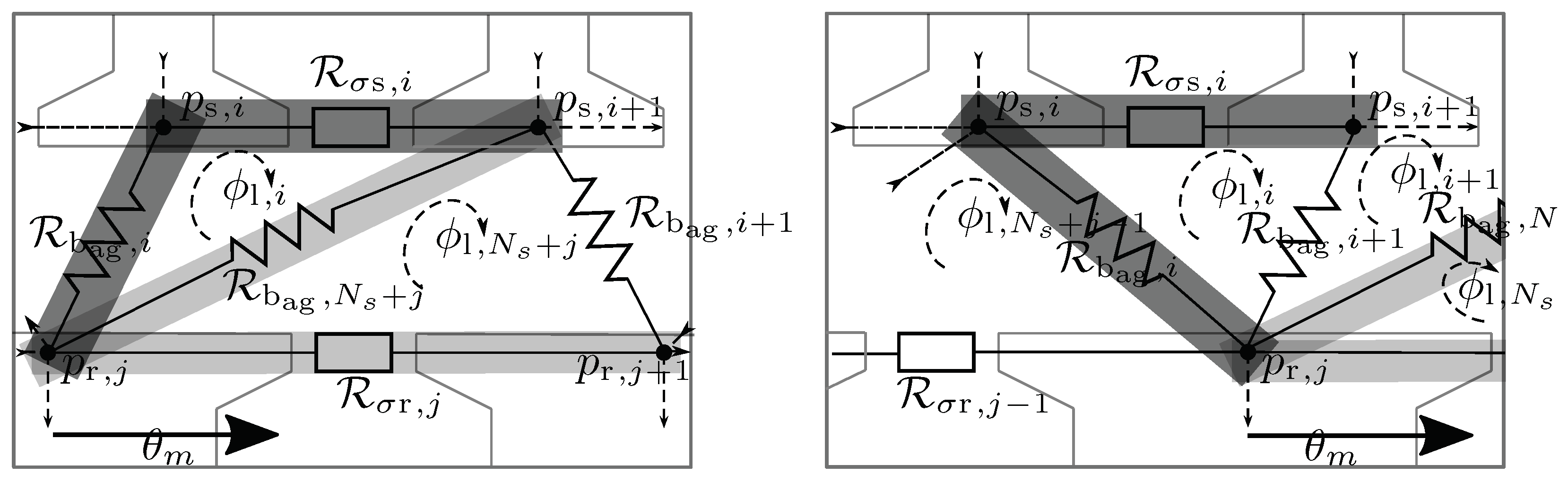
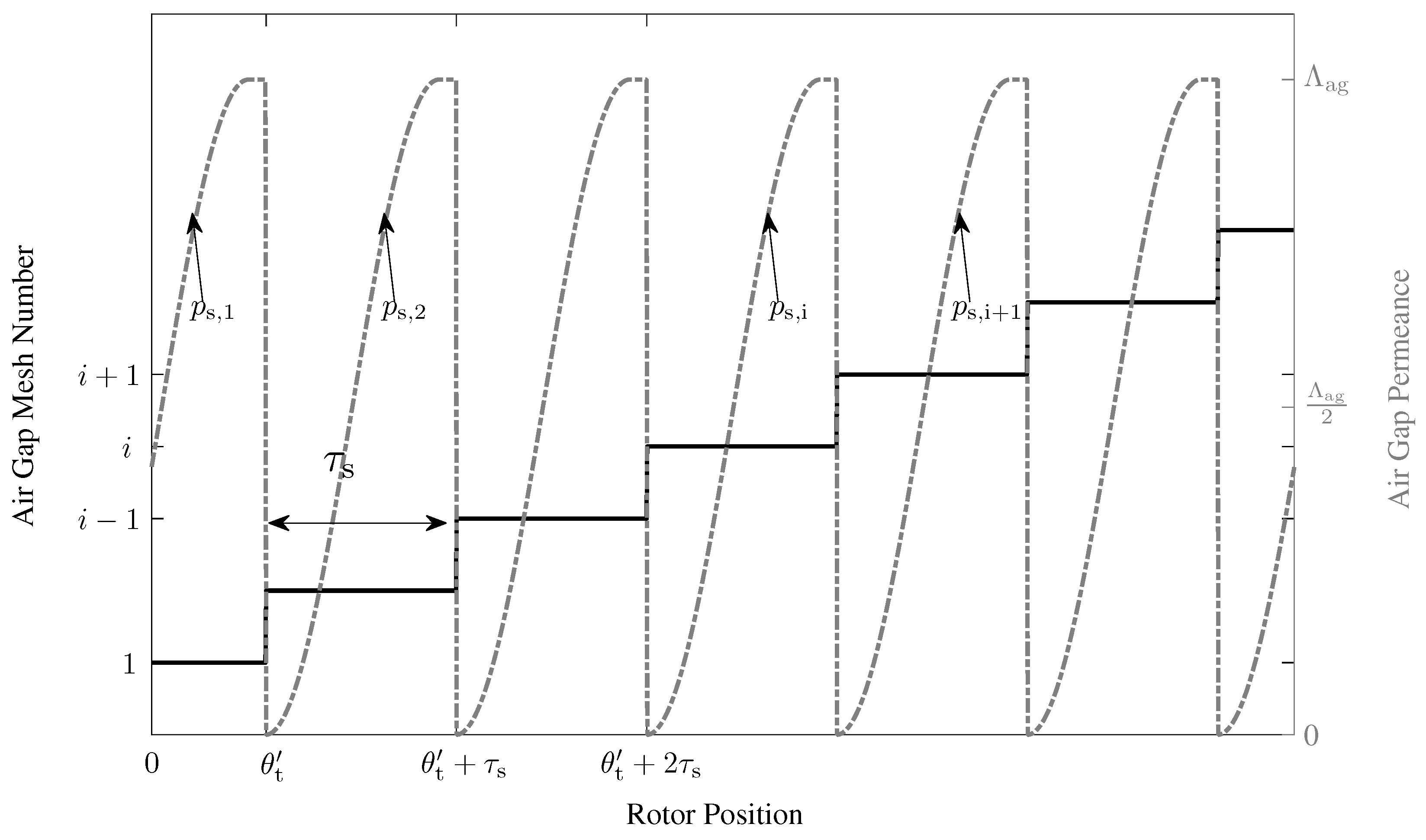
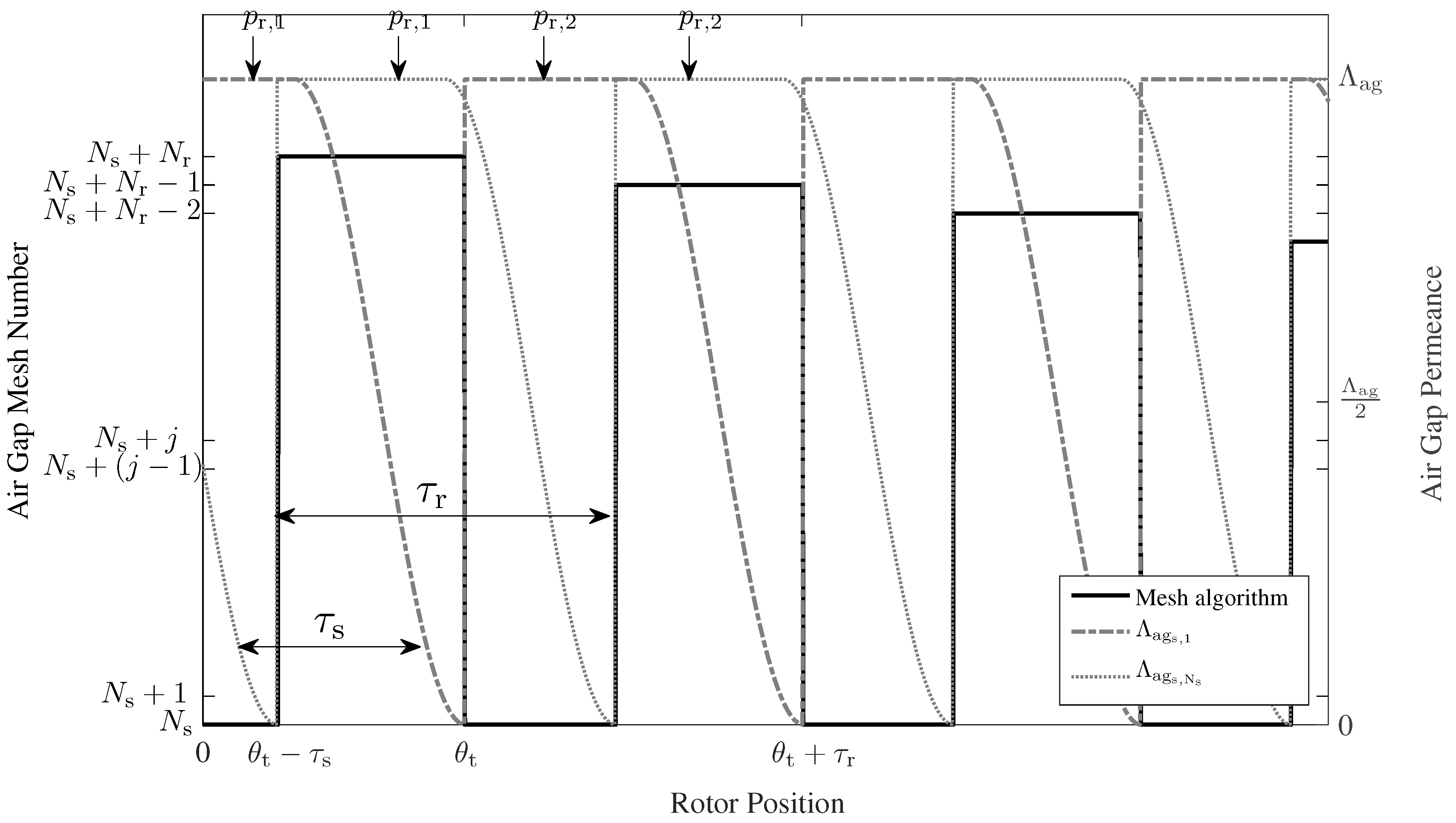
Air Gap Reluctances
2.3. Nonlinear Reluctances
2.4. Active Elements
2.4.1. Magnet MMF Source
2.4.2. Stator and Rotor MMF
2.5. MEC Network
3. Analysis of an LS-PMSM by Using MEC-Based Time Simulations
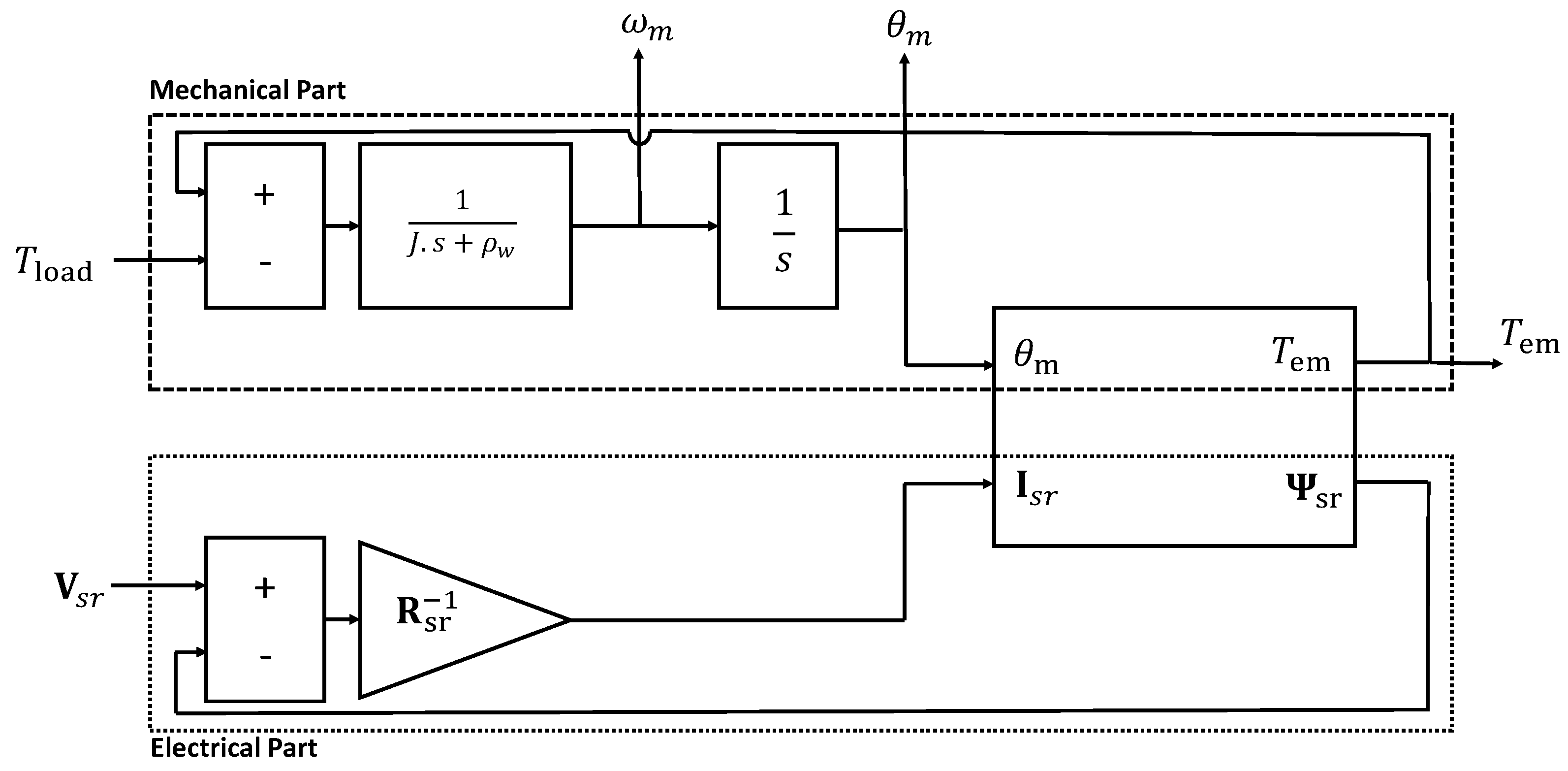
3.1. Dynamical Model of the LS-PMSM
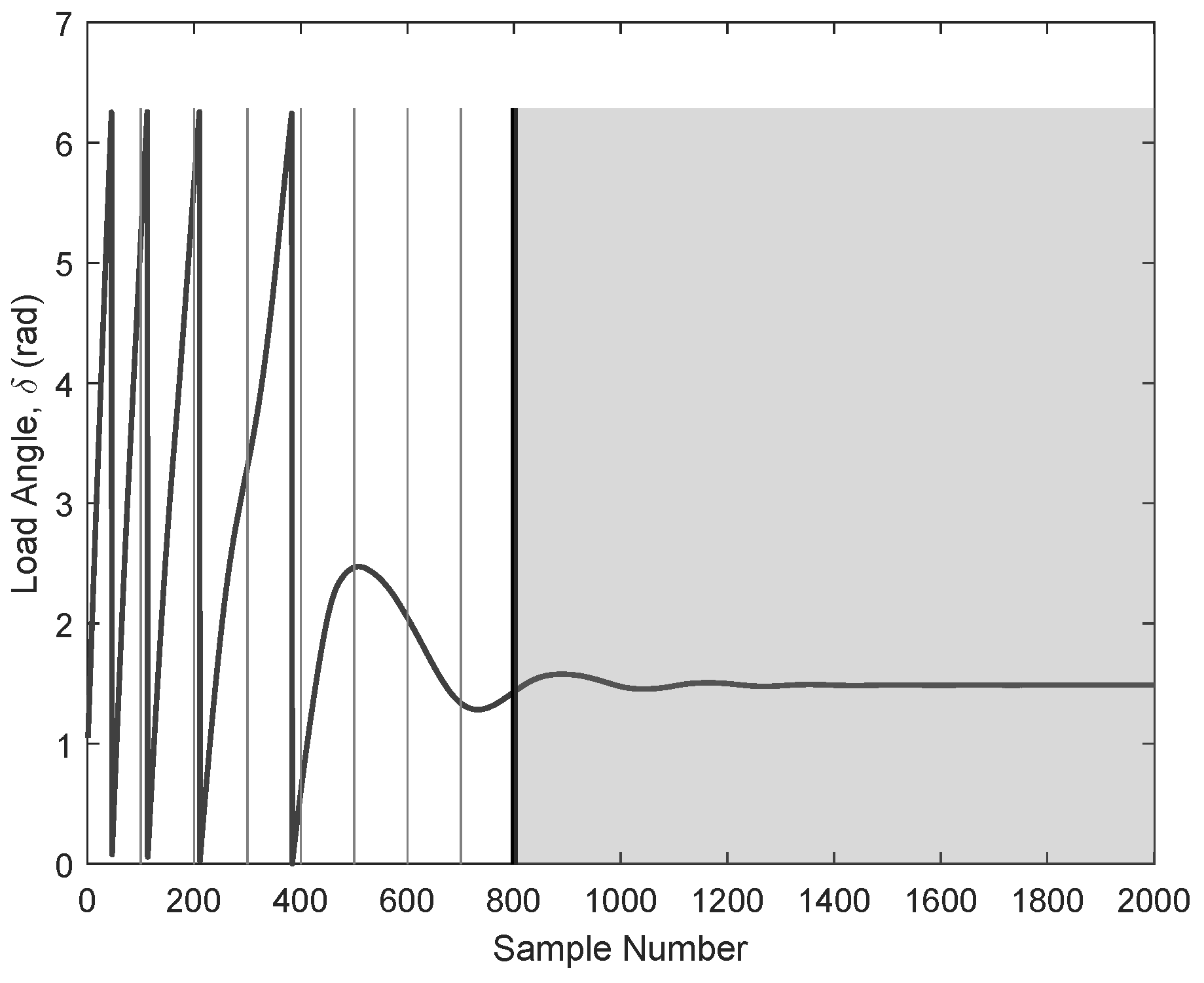
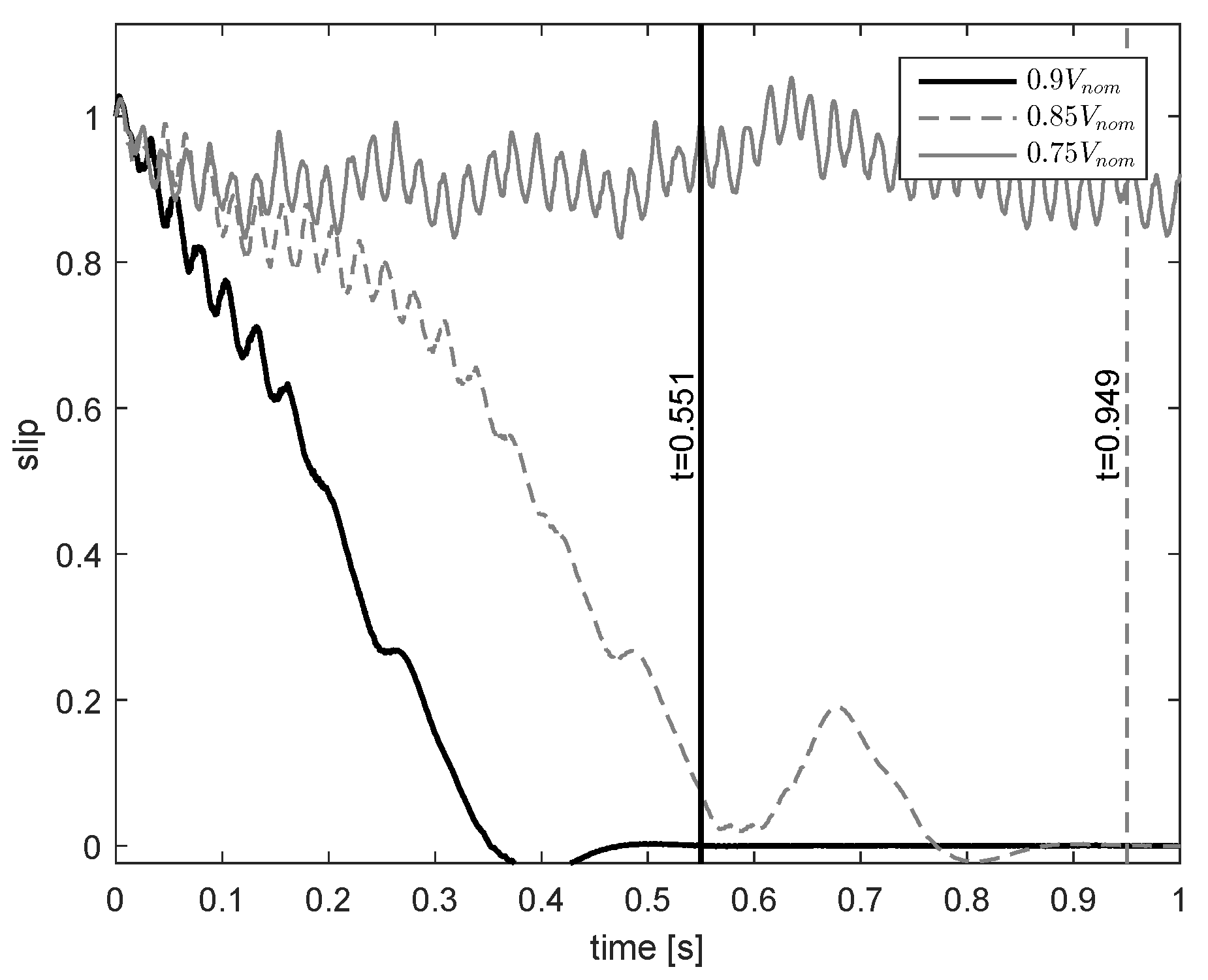
3.2. Synchronization Capability
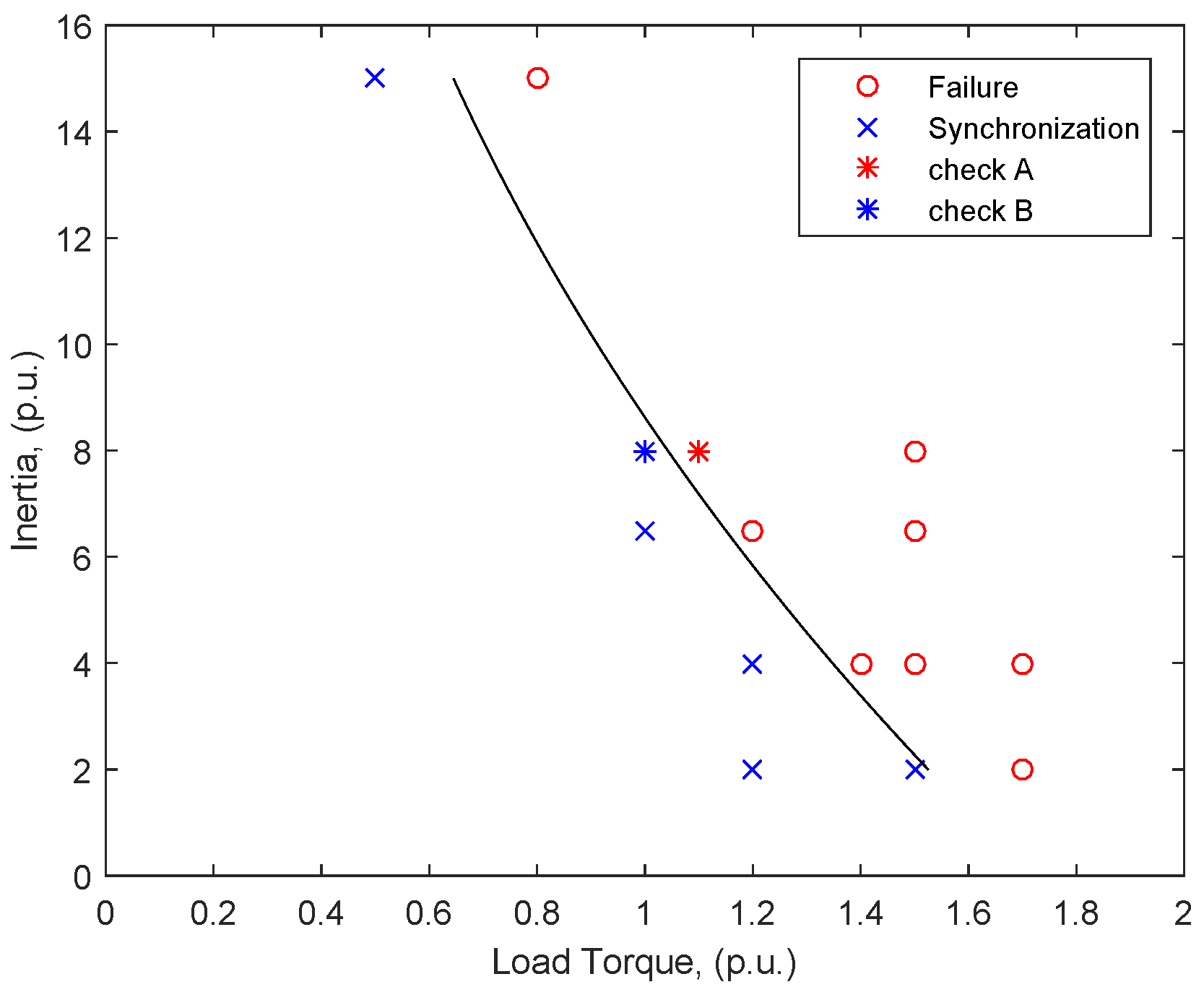
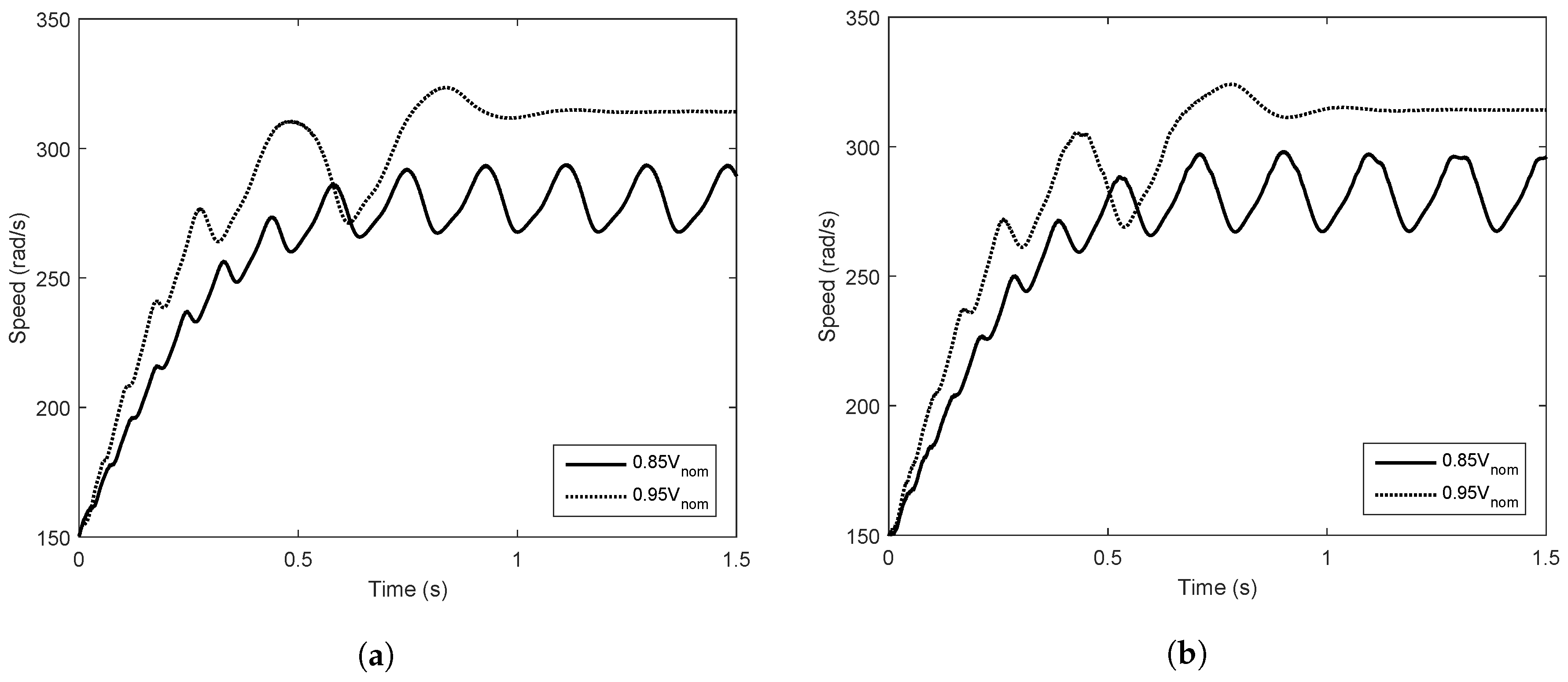
3.3. Results
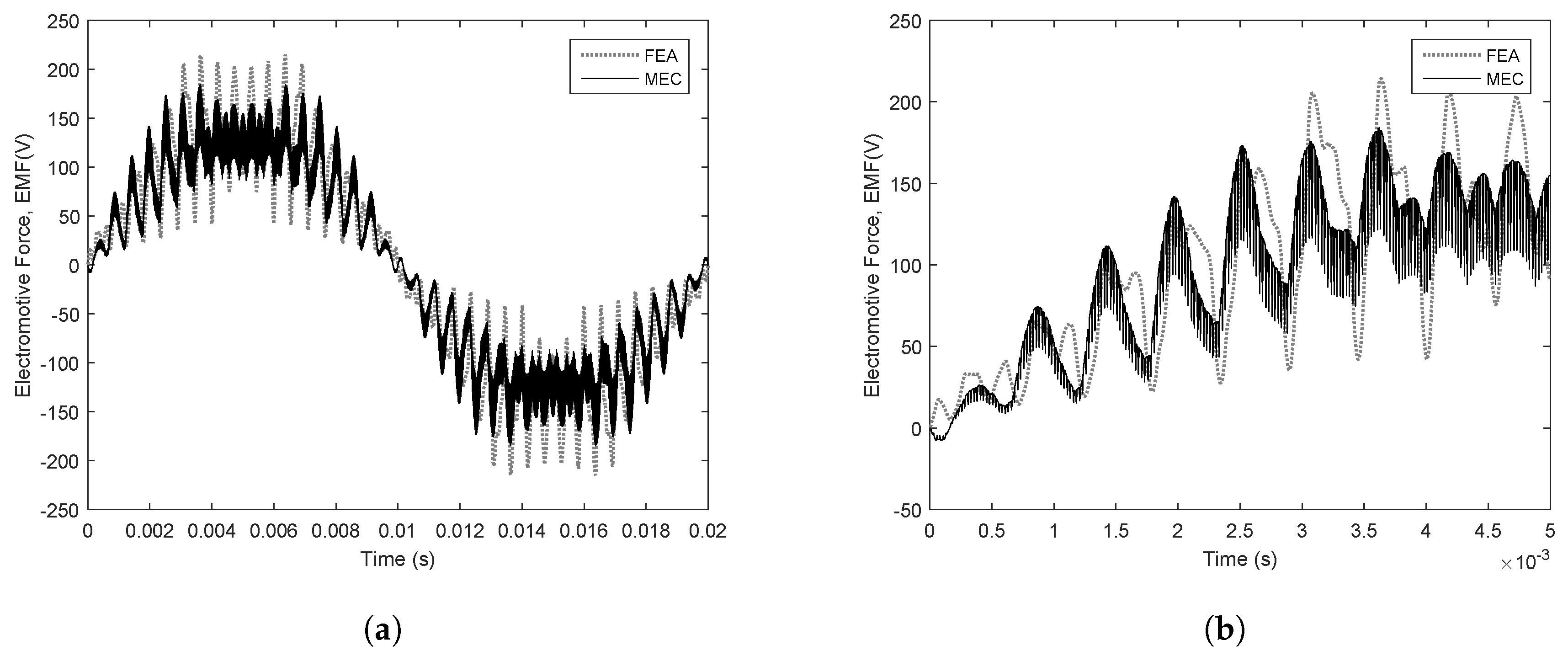
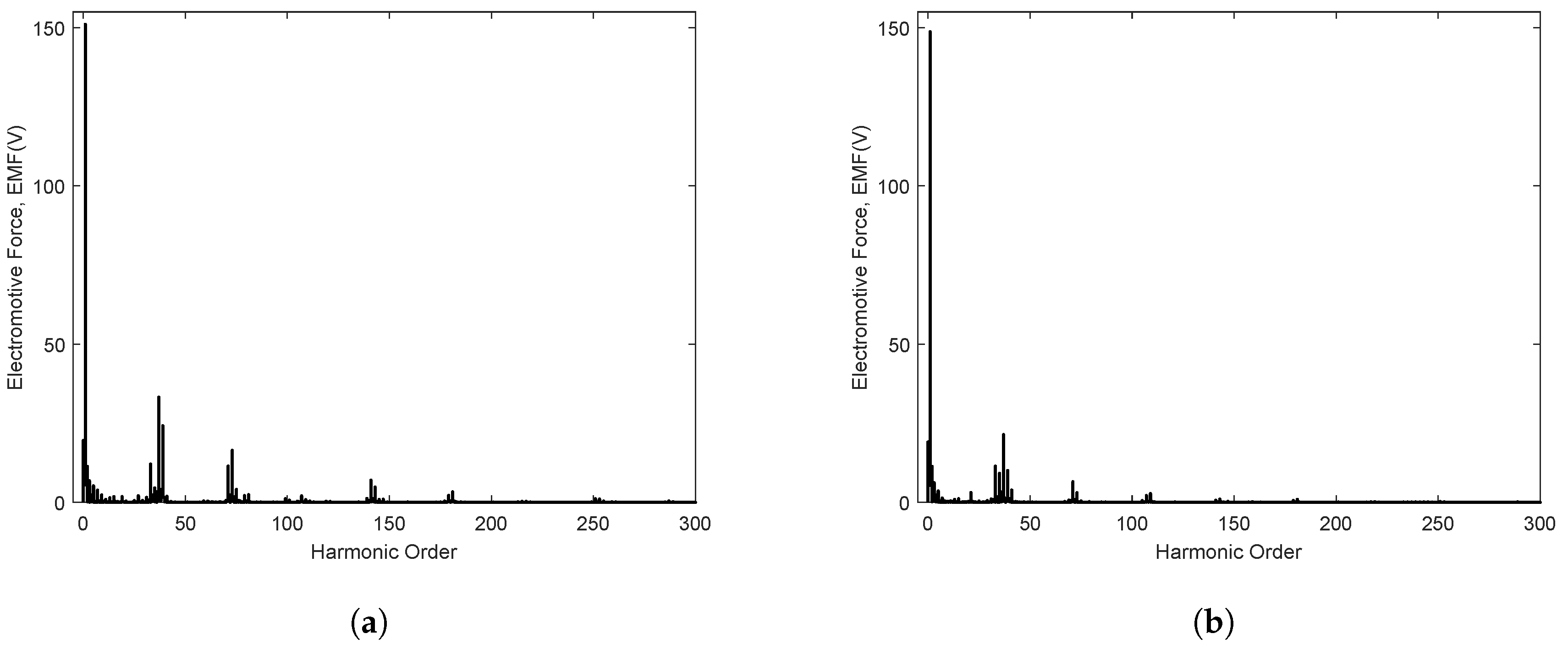
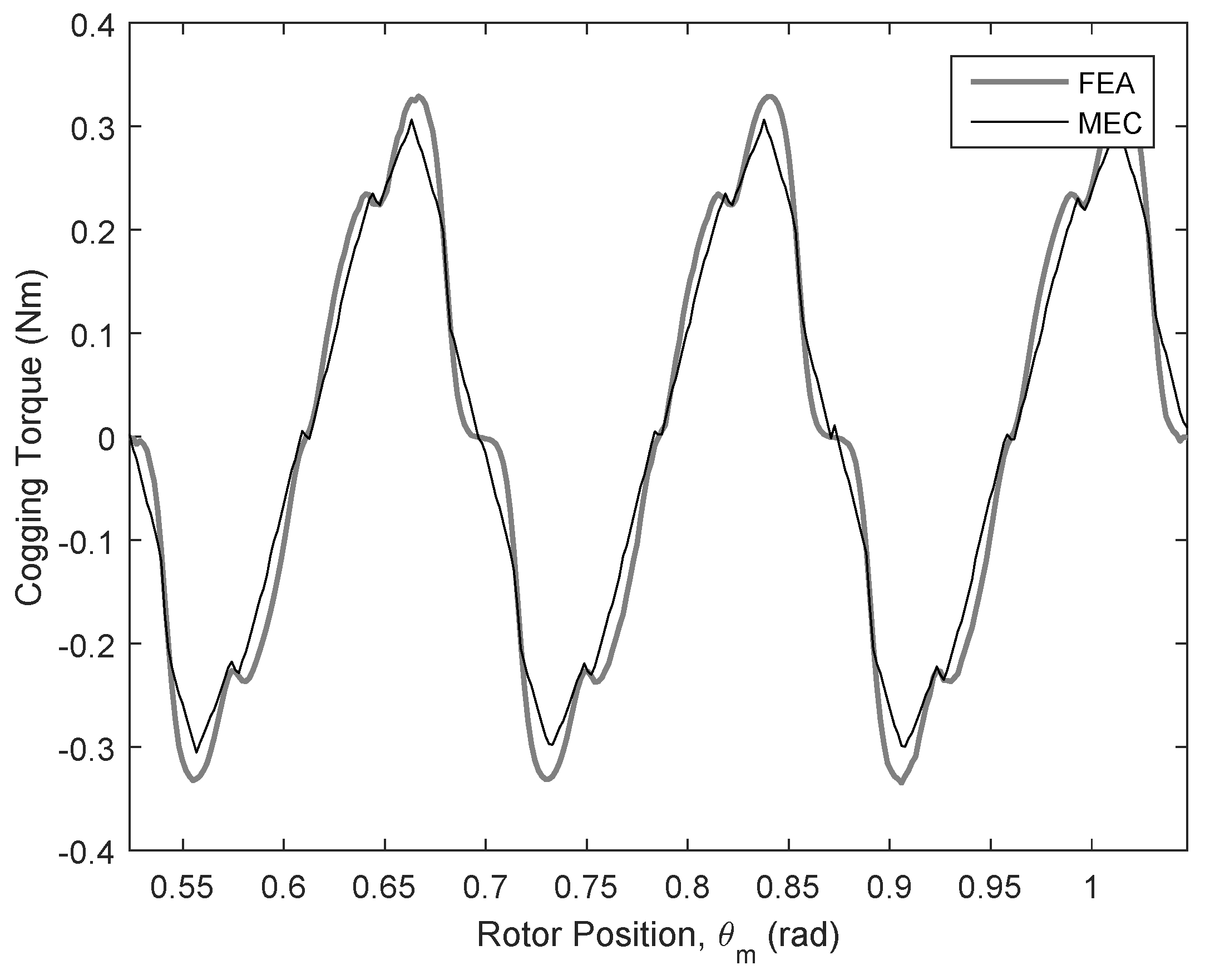
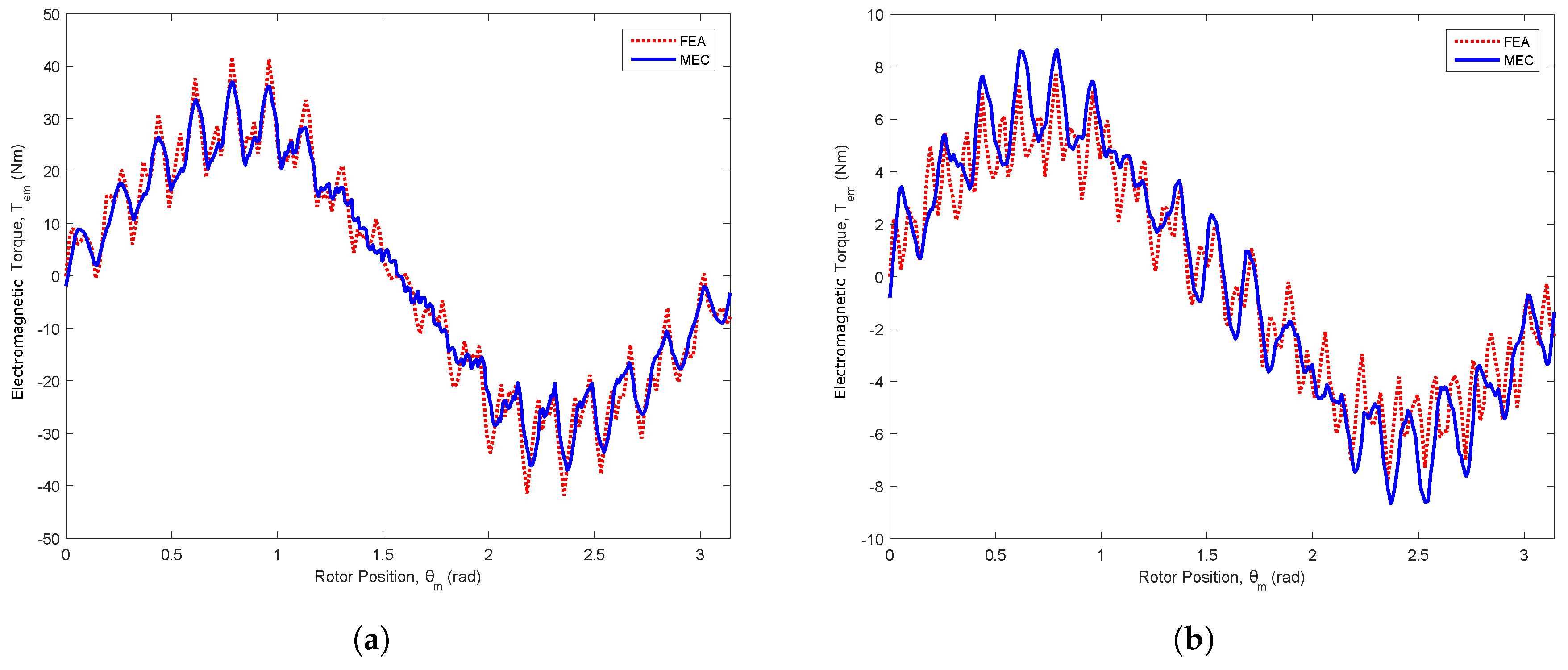
3.3.1. Simulation Results
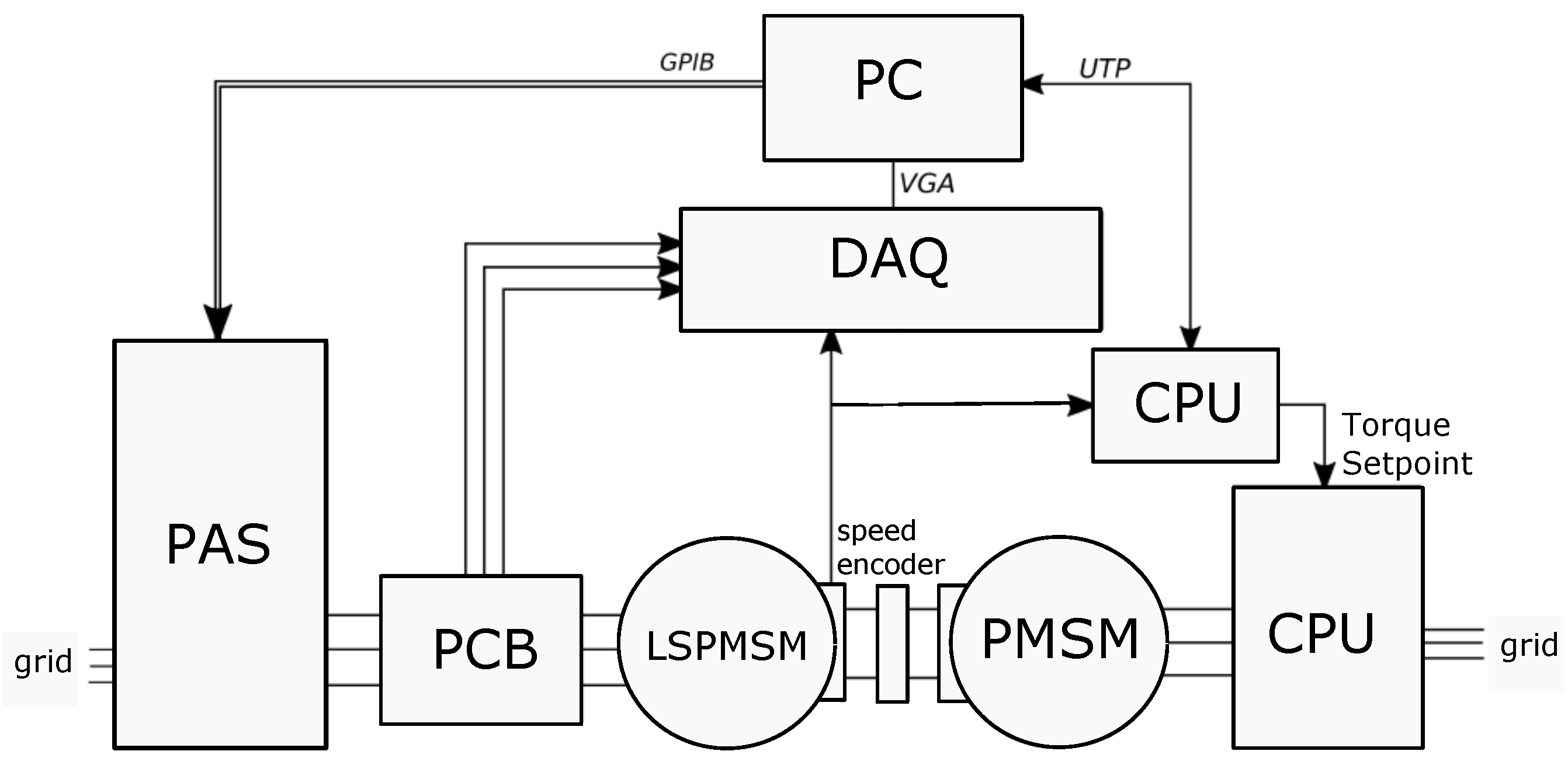
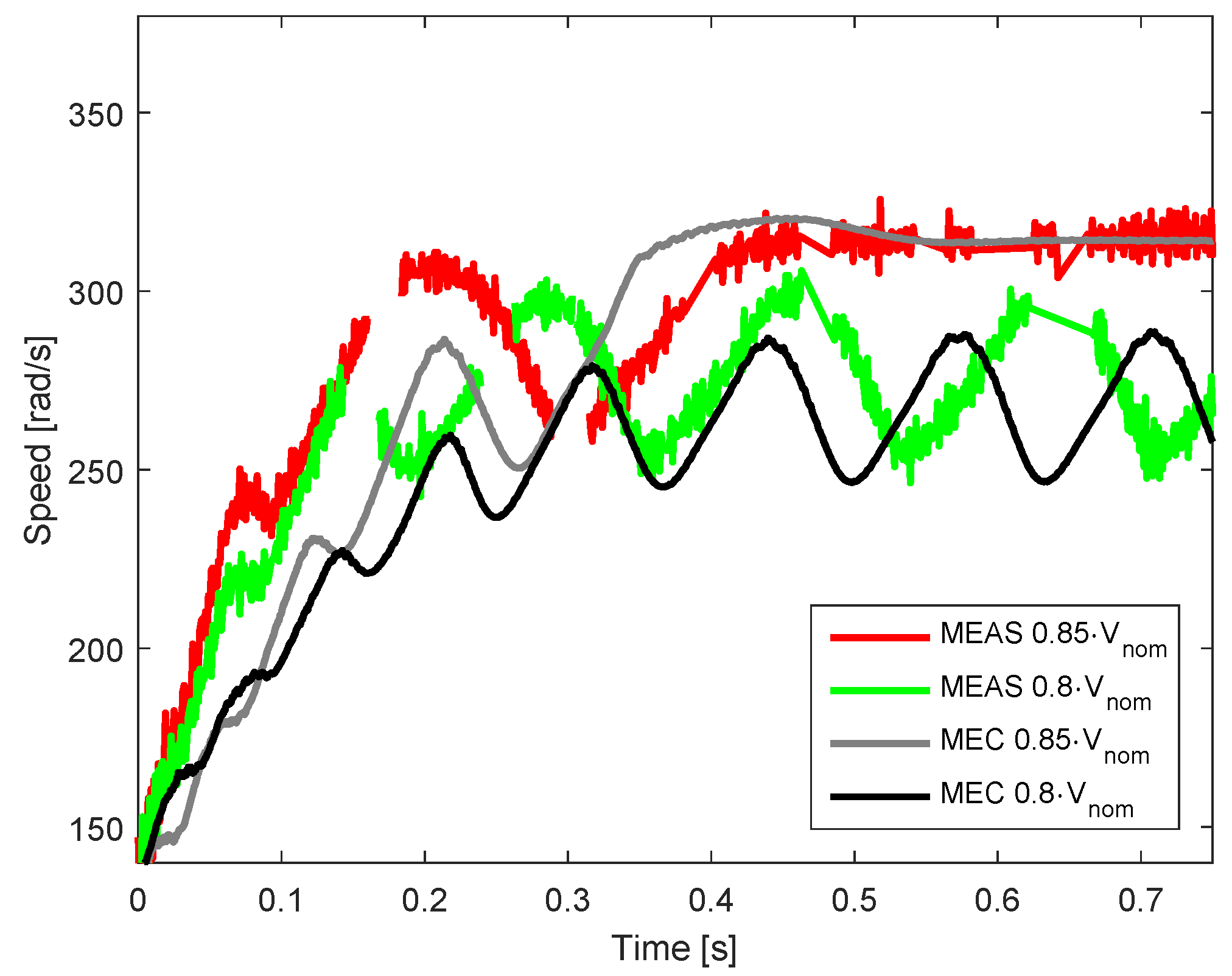
3.3.2. Experimental Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- De Almeida, A.T.; Ferreira, F.J.T.E.; Fong, J.A.C. Standards for Super-Premium Efficiency class for electric motors. In Proceedings of the Record 2009 IEEE Industrial Commercial Power Systems Technical Conference, Calgary, AB, Canada, 3–7 May 2009. [Google Scholar]
- Miller, T.J.E. Synchronization of Line-Start Permanent-Magnet AC Motors. IEEE Power Eng. Rev. 1984, PER-4, 57–58. [Google Scholar] [CrossRef]
- Rahman, M.A.; Little, T.A. Dynamic Performance Analysis of Permanet Magnet Synchronous Motors Magnet Synchronous Motors. IEEE Trans. Power Appar. Syst. 1984, PAS-103, 1277–1282. [Google Scholar] [CrossRef]
- Hendershot, J.R.; Miller, T.J.E. Design of Brushless Permanent-Magnet Machines; Motor Design Books LLC: Venice, FL, USA, 2010. [Google Scholar]
- Isfahani, A.H.; Vaez-Zadeh, S. Effects of Magnetizing Inductance on Start-Up and Synchronization of Line-Start Permanent-Magnet Synchronous Motors. IEEE Trans. Magn. 2011, 47, 823–829. [Google Scholar] [CrossRef]
- Wymeersch, B.J.; De Belie, F.; Rasmussen, C.B.; Jensen, F.; Vandevelde, L. Influence of ferromagnetic bridges in dq-equivalent-circuit modeling of interior permanent-magnet machines. In Proceedings of the International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1238–1242. [Google Scholar]
- Lu, X.; Iyer, K.L.V.; Mukherjee, K.; Kar, N.C. Development of a Novel Magnetic Circuit Model for Design of Premium Efficiency Three-Phase Line Start Permanent Magnet Machines With Improved Starting Performance. IEEE Trans. Magn. 2013, 49, 3965–3968. [Google Scholar] [CrossRef]
- Niazazari, M.; Mirsalim, M.; Mohammadi, S. Analytical framework for analysis and demagnetization study of a slotted solid-rotor line-start permanent-magnet synchronous motor. In Proceedings of the 2014 5th Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Tehran, Iran, 5–6 February 2014; pp. 494–499. [Google Scholar]
- Wymeersch, B.; De Belie, F.; Rasmussen, C.B.; Jensen, F.; Vandevelde, L. Mutual-inductance modeling in line-start permanent-magnet synchronous machines based on winding-function theory. In Proceedings of the IEEE International Electric Machines Drives Conference (IEMDC), Chicago, IL, USA, 12–15 May 2013; pp. 607–611. [Google Scholar]
- Naderi, P.; Shiri, A. Rotor/Stator Inter-Turn Short Circuit Fault Detection for Saturable Wound-Rotor Induction Machine by Modified Magnetic Equivalent Circuit Approach. IEEE Trans. Magn. 2017, 53, 1–13. [Google Scholar] [CrossRef]
- Takahashi, A. Dynamic and Steady-State Characteristics of Line-Starting Permanent Magnet Motors (Berichte aus der Elektrotechnik); Shaker Verlag GmbH: Herzogenrath, Germany, 2010. [Google Scholar]
- Kemmetmüller, W.; Faustner, D.; Kugi, A. Modeling of a Permanent Magnet Synchronous Machine with Internal Magnets Using Magnetic Equivalent Circuits. IEEE Trans. Magn. 2014, 50, 1–14. [Google Scholar]
- Rabbi, S.F.; Rahman, M.A. Critical Criteria for Successful Synchronization of Line-Start IPM Motors. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 348–358. [Google Scholar] [CrossRef]
- Chama, A.; Sorgdrager, A.J.; Wang, R.J. Analytical synchronization analysis of line-start permanent magnet synchronous motors. Prog. Electromagn. Res. M 2016, 48, 183–193. [Google Scholar] [CrossRef]
- Jędryczka, C.; Knypiński, Ł.; Demenko, A.; Sykulski, J.K. Methodology for Cage Shape Optimization of a Permanent Magnet Synchronous Motor Under Line Start Conditions. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Miller, T.J.E.; McGilp, M.; Wearing, A. Motor design optimisation using SPEED CAD software. In Proceedings of the IEE Seminar Practical Electromagnetic Design Synthesis, London, UK, 11 February 1999; pp. 2/1–2/5. [Google Scholar]
- Tariq, A.R.; Nino-Baron, C.E.; Strangas, E.G. Iron and Magnet Losses and Torque Calculation of Interior Permanent Magnet Synchronous Machines Using Magnetic Equivalent Circuit. IEEE Trans. Magn. 2010, 46, 4073–4080. [Google Scholar] [CrossRef]
- De Belie, F.; Melkebeek, J.; Vandevelde, L.; Geldhof, K.; Boel, R. A discrete-time model including cross-saturation for surface permanent-magnet synchronous machines. Int. J. Comput. Math. Electr. Electron. Eng. (COMPEL) 2006, 25, 766–778. [Google Scholar] [CrossRef]
- Bash, M.L.; Williams, J.M.; Pekarek, S.D. Incorporating Motion in Mesh-Based Magnetic Equivalent Circuits. IEEE Trans. Energy Convers. 2010, 25, 329–338. [Google Scholar] [CrossRef]
- Wang, R.; Pekarek, S.; Bash, M.L.; Larson, A.; Maaren, R.V. Incorporating Dynamics in a Mesh-Based Magnetic Equivalent Circuit Model of Synchronous Machines. IEEE Trans. Energy Convers. 2015, 30, 821–832. [Google Scholar] [CrossRef]
- Sudhoff, S.D. Magnetics and Magnetic Equivalent Circuits; Wiley-IEEE Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- Gyselinck, J.; Sabariego, R. Airgap reluctance identification for the magnetic equivalent circuit modeling of induction machines. In Proceedings of the Conference on the Computation of Electromagnetic Fields (COMPUMAG), Budapest, Hungary, 30 June–4 July 2013; Volume 4, pp. 2820–2827. [Google Scholar]
- Ostovic, V. Computation of Saturated Permanent-Magnet AC Motor Performance by Means of Magnetic Circuits. IEEE Trans. Ind. Appl. 1987, IA-23, 836–841. [Google Scholar] [CrossRef]
- Derbas, H.W.; Williams, J.M.; Koenig, A.C.; Pekarek, S.D. A Comparison of Nodal- and Mesh-Based Magnetic Equivalent Circuit Models. IEEE Trans. Energy Convers. 2009, 24, 388–396. [Google Scholar] [CrossRef]
- Bash, M.; Pekarek, S. Modeling of salient-pole wound-rotor synchronous machines for population-based design. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Bash, M.L.; Pekarek, S.D. Modeling of Salient-Pole Wound-Rotor Synchronous Machines for Population-Based Design. IEEE Trans. Energy Convers. 2011, 26, 381–392. [Google Scholar] [CrossRef]
- Liu, G.; Chen, L.; Zhao, W.; Jiang, Y.; Qu, L. Internal Model Control of Permanent Magnet Synchronous Motor Using Support Vector Machine Generalized Inverse. Trans. Ind. Inform. 2013, 9, 890–898. [Google Scholar] [CrossRef]
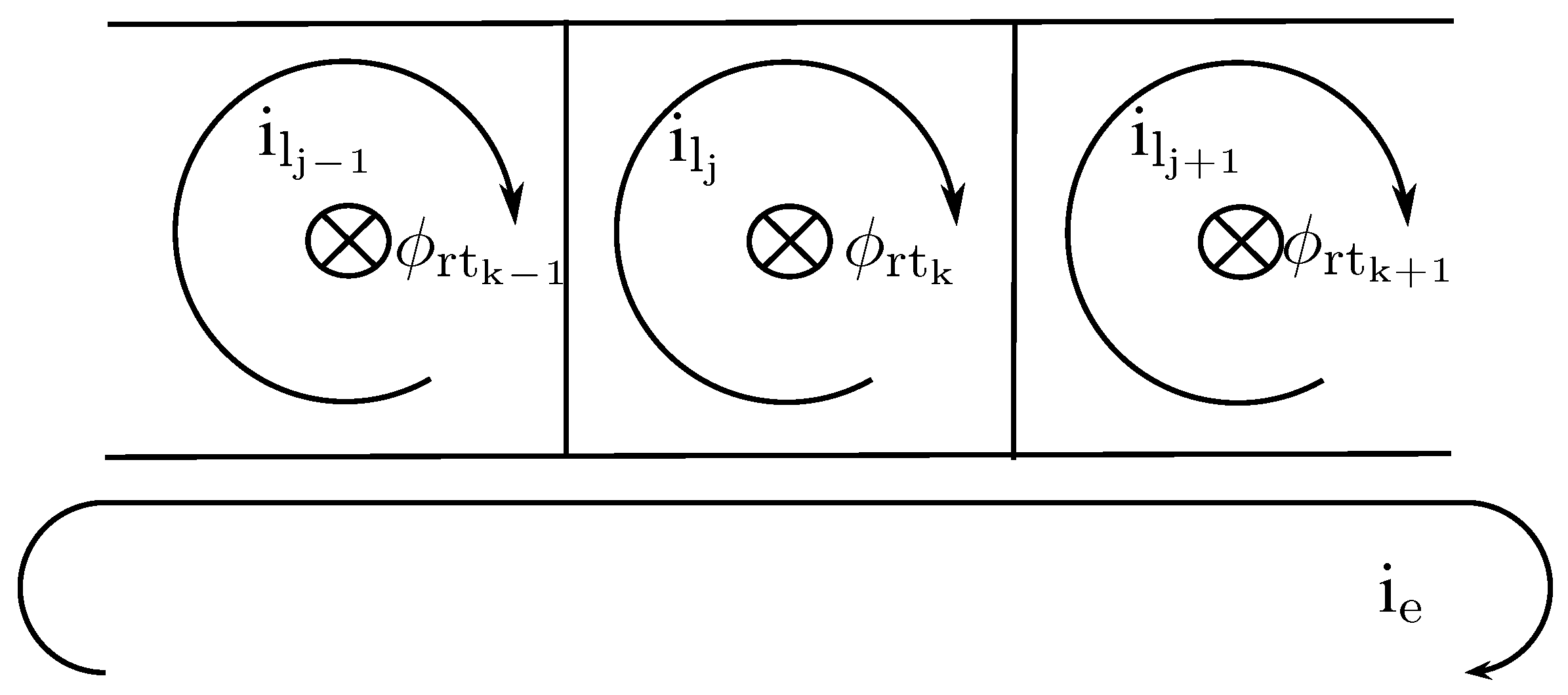

| Symbol | Parameter | Value |
|---|---|---|
| nominal voltage | 380 V | |
| nominal power | 3 kW | |
| nominal frequency | 50 Hz | |
| nominal speed | 3000 rpm | |
| nominal torque | 9.55 Nm | |
| motor inertia | 0.0053 kg·m | |
| number of phases | 3 | |
| number of poles | 2 | |
| N | number of stator teeth | 36 |
| number of rotor teeth | 20 | |
| g | air gap length | 0.3 mm |
| rotor stack length | 103 mm | |
| rotor radius | 42.2 mm | |
| permanent magnet width | 27 mm | |
| permanent magnet length | 103 mm | |
| permanent magnet thickness | 3 mm | |
| permanent magnet remanent induction | 1.1 T |
| Setting | Value |
|---|---|
| Relative precision () for NR | |
| Absolute precision () for NR | |
| Relaxation | no |
| Material Properties | MEC | FEA |
|---|---|---|
| linear | 0.007 s | 1.6 s |
| nonlinear | 0.014 s | 3.67 s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wymeersch, B.; De Belie, F.; Rasmussen, C.B.; Vandevelde, L. Classification Method to Define Synchronization Capability Limits of Line-Start Permanent-Magnet Motor Using Mesh-Based Magnetic Equivalent Circuit Computation Results. Energies 2018, 11, 998. https://doi.org/10.3390/en11040998
Wymeersch B, De Belie F, Rasmussen CB, Vandevelde L. Classification Method to Define Synchronization Capability Limits of Line-Start Permanent-Magnet Motor Using Mesh-Based Magnetic Equivalent Circuit Computation Results. Energies. 2018; 11(4):998. https://doi.org/10.3390/en11040998
Chicago/Turabian StyleWymeersch, Bart, Frederik De Belie, Claus B. Rasmussen, and Lieven Vandevelde. 2018. "Classification Method to Define Synchronization Capability Limits of Line-Start Permanent-Magnet Motor Using Mesh-Based Magnetic Equivalent Circuit Computation Results" Energies 11, no. 4: 998. https://doi.org/10.3390/en11040998
APA StyleWymeersch, B., De Belie, F., Rasmussen, C. B., & Vandevelde, L. (2018). Classification Method to Define Synchronization Capability Limits of Line-Start Permanent-Magnet Motor Using Mesh-Based Magnetic Equivalent Circuit Computation Results. Energies, 11(4), 998. https://doi.org/10.3390/en11040998






