Wide-Area Measurement—Based Model-Free Approach for Online Power System Transient Stability Assessment
Abstract
:1. Introduction
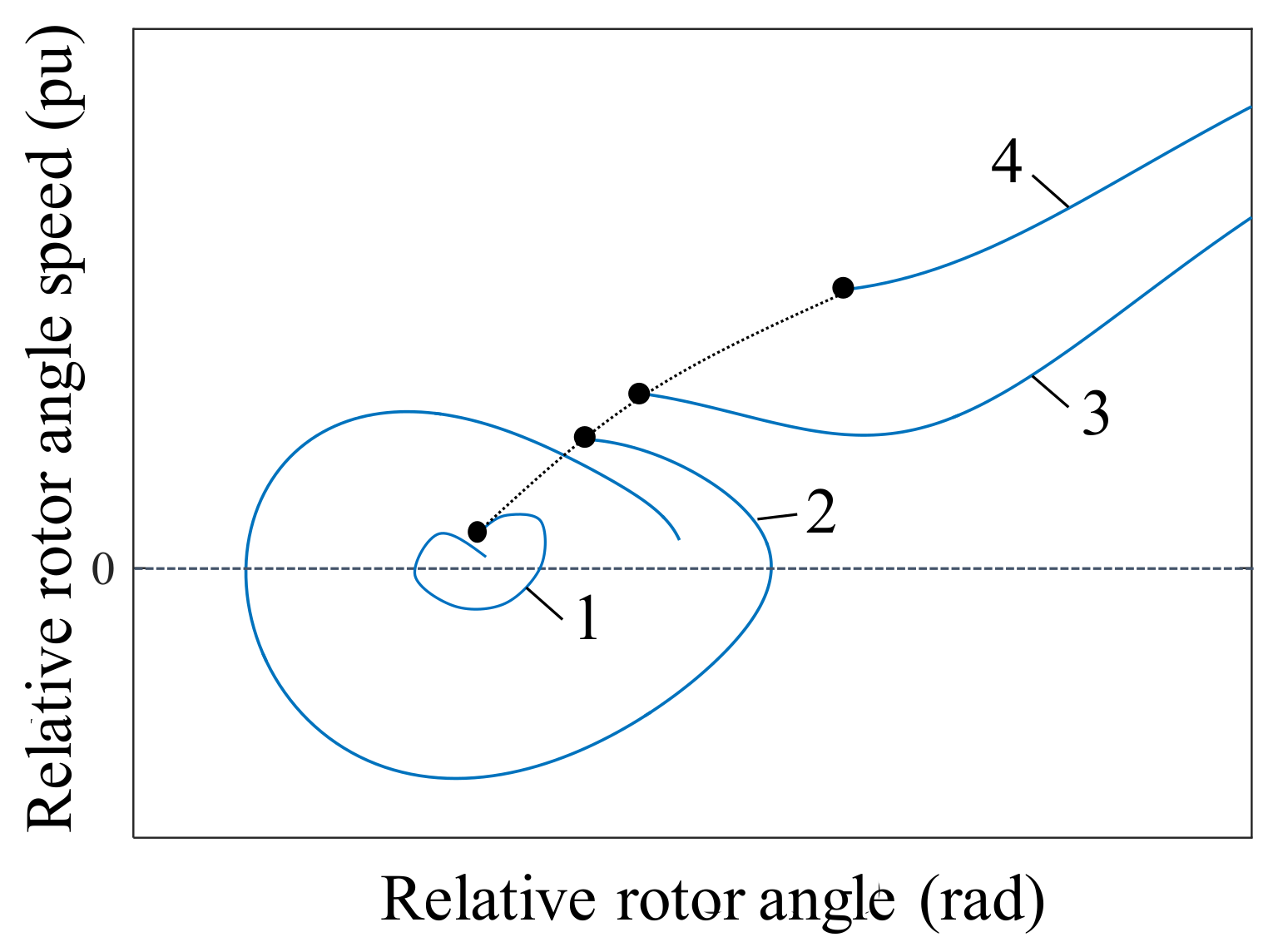
2. Transient Rotor Angle Stability Analysis Based on Post-Fault Phase-Plane Trajectories
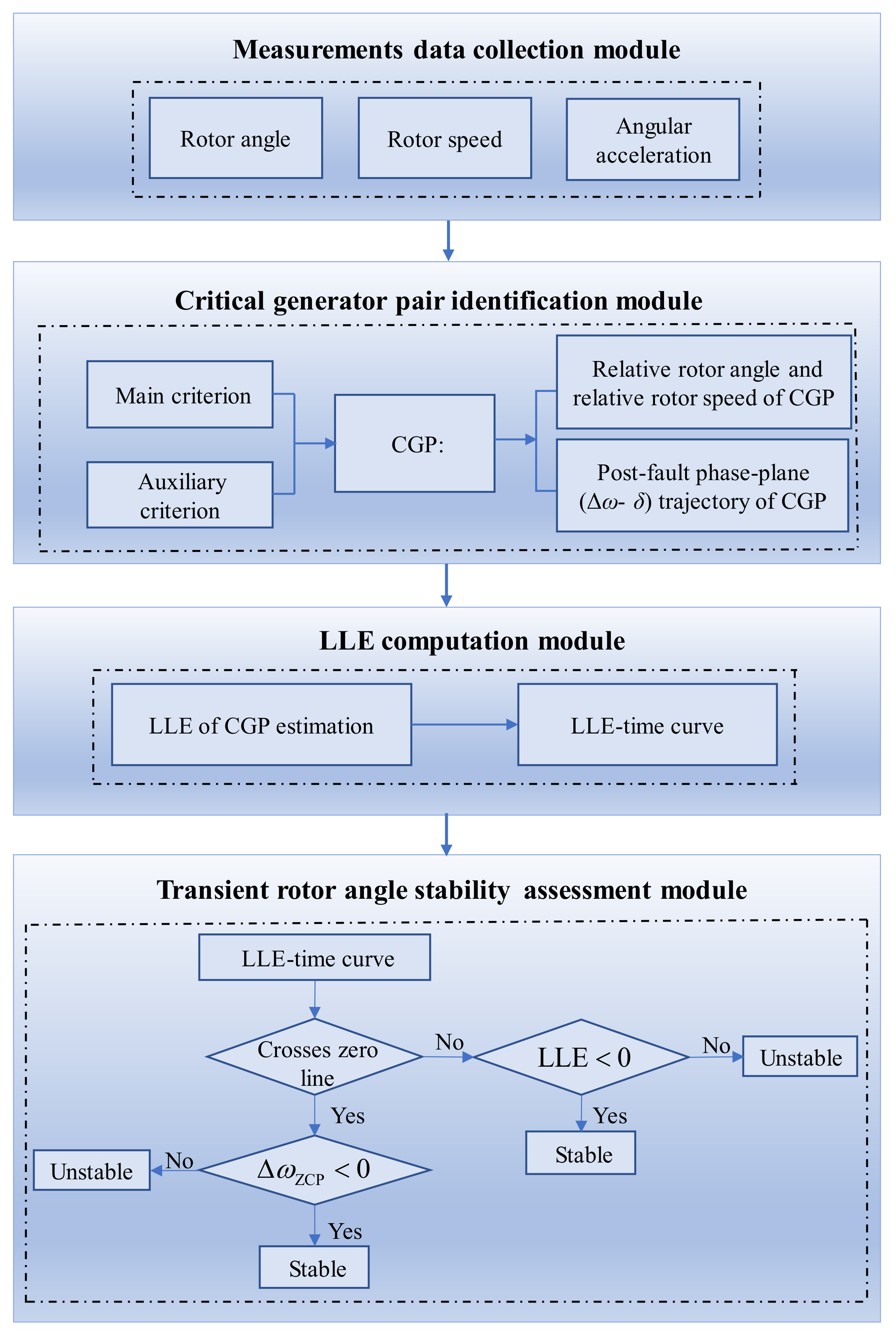
3. Online Rotor Angle Stability Assessment Scheme
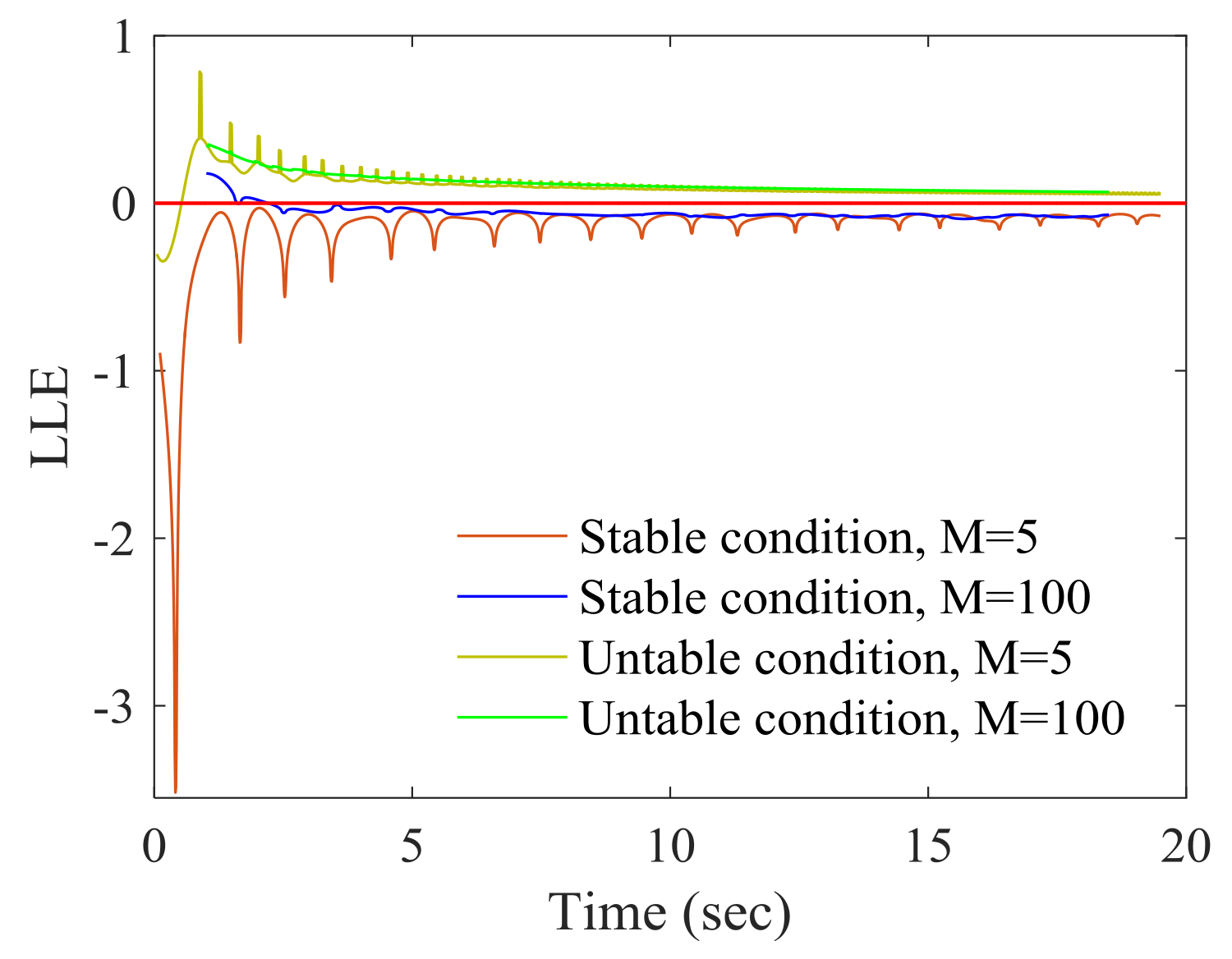
3.1. LLE Calculation from Time Series
- (1)
- Get the rotor angle time series data of the generators from WAMS. Suppose that n is the number of generators in the power grid, and θi(t) is a rotor angle vector of the generator i (i = 1, 2, 3, …, n) valued time series data for t = 0, ∆t, 2∆t, …, N∆t, where ∆t is the sampling period. Take one of the rotor angles denoted by θR(t) as the reference and define the relative rotor angle with respect to as:, i ≠ R.
- (2)
- Choose M initial conditions, and calculate the LLE of δi(t) by Equation (3):where m = 1, 2, …, M, M < k. The basic idea of Equation (3) is to take M initial conditions and study their evolution over time.
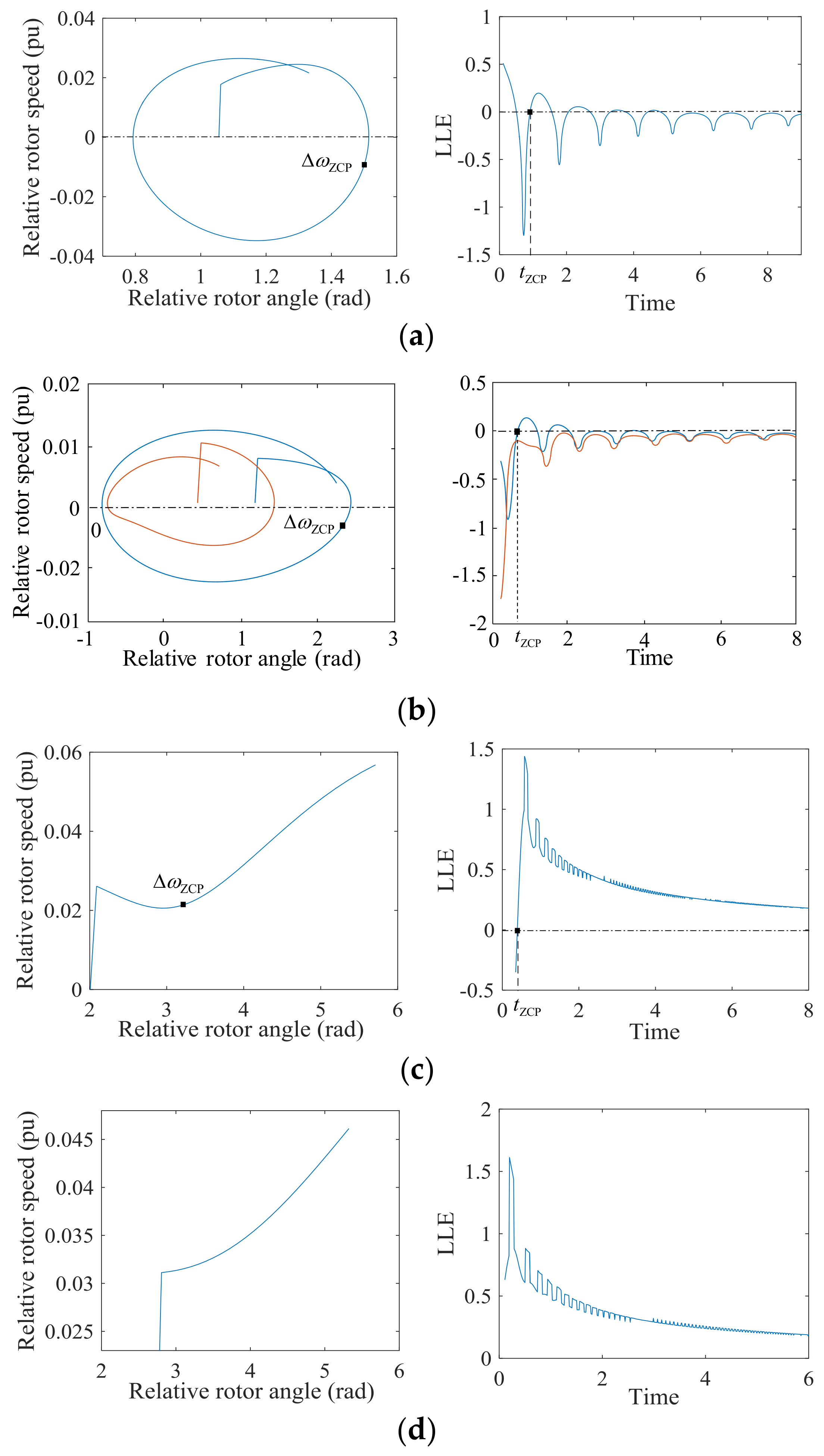
3.2. Rotor Angle Stability Criterion Based on the LLE and Rotor Speed
- (1)
- Proof of stable conditions
- (2)
- Proof of unstable conditions
3.3. Critical Generator Pair Identification
- (1)
- Get the initial Ωcr and Ωncr by using the main criterion.
- (2)
- Judge whether there is an intersection between Ωcr and Ωncr. If the intersection exists, Ωcr and Ωncr is renewed by using the auxiliary criterion.
- (3)
- Judge whether there exists an empty set for Ωcr and Ωncr. If it exists, repeat Steps (1) and (2) on the other generators.
- (4)
- Form the set of CGPs using the above steps as:
3.4. Online Rotor Angle Stability Assessment Scheme
- (1)
- When a fault is detected, the measurement data collection module is started to identify the CGPs. The relative rotor angle and rotor speed data of the CGPs are obtained in real time and the phase-plane trajectories of the CGPs are generated. It should be noted that the generator belonging to Ωncr is selected as the reference for the relative rotor angle and the rotor speed of the CGPs.
- (2)
- The LLE sequences for the relative rotor angle of the CGPs are calculated by the algorithm in Section 3.1.
- (3)
- The system rotor angle stability can be assessed by Criterion 1 and Criterion 2 proposed in Section 3.2. Note that the system is unstable if one of the CGPs is identified as unstable, and the system is stable if all of the CGPs are identified as stable.
4. Simulation Results
4.1. IEEE-39 Bus System
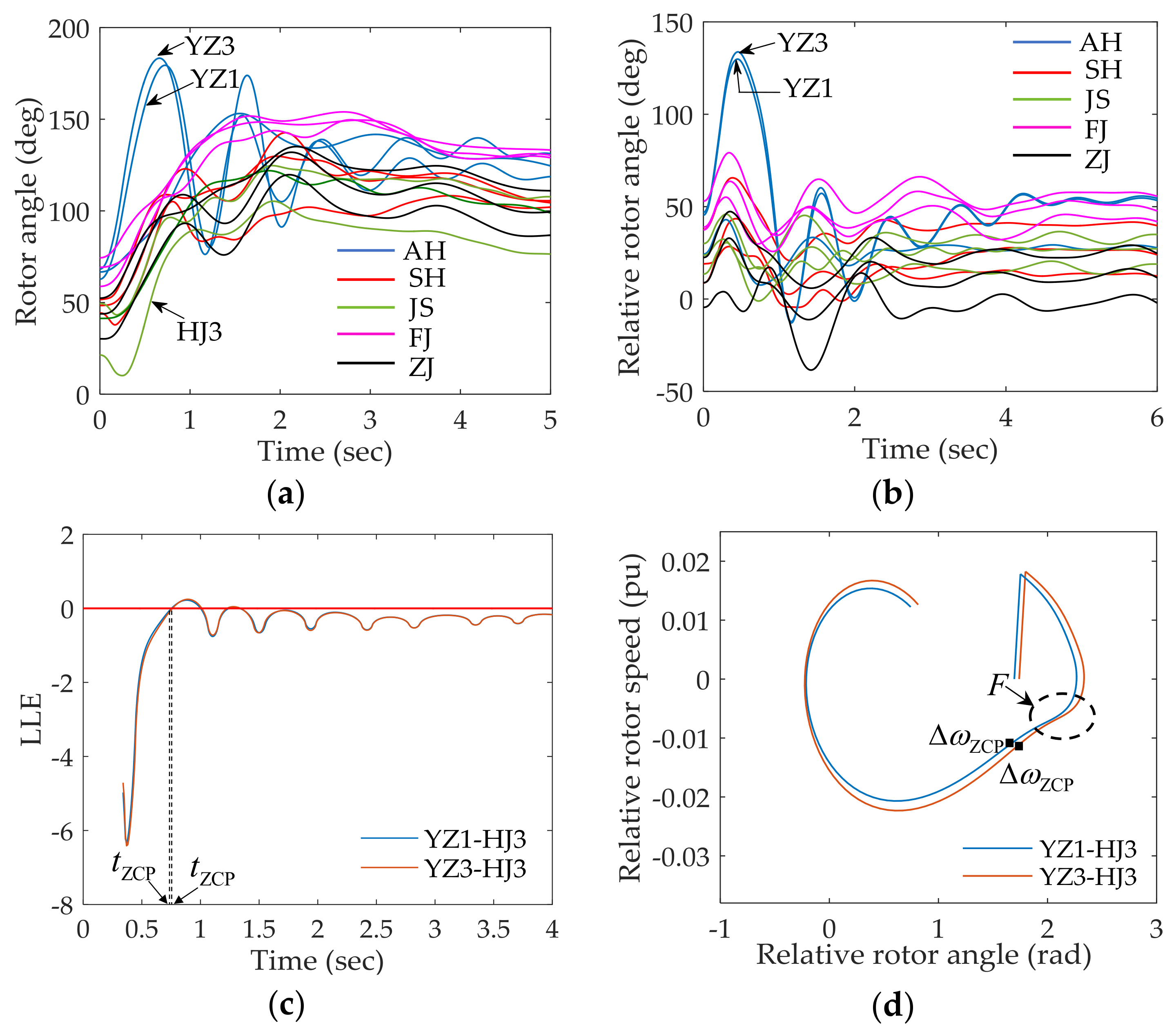
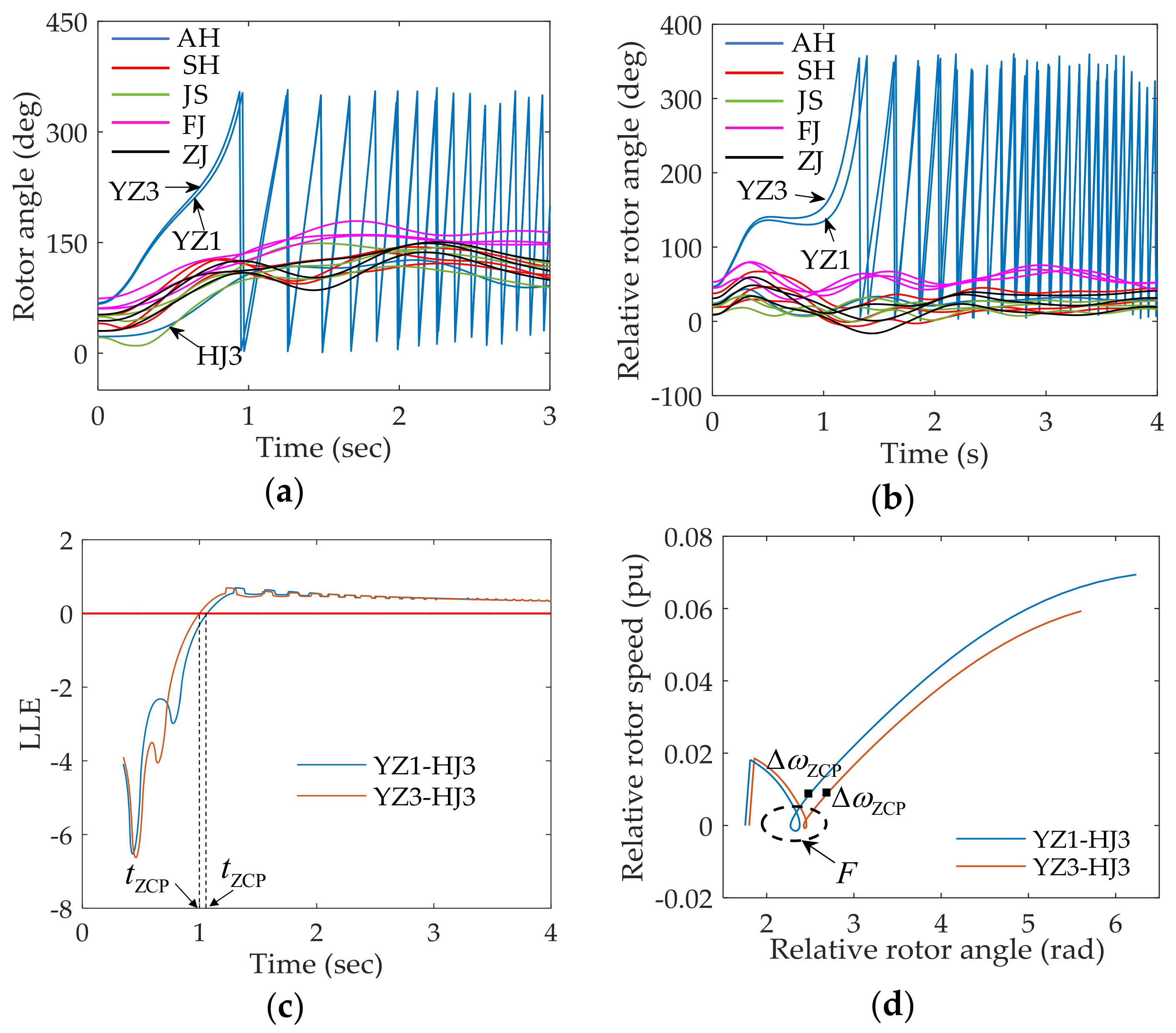
4.2. Real-World Power System
5. Discussions
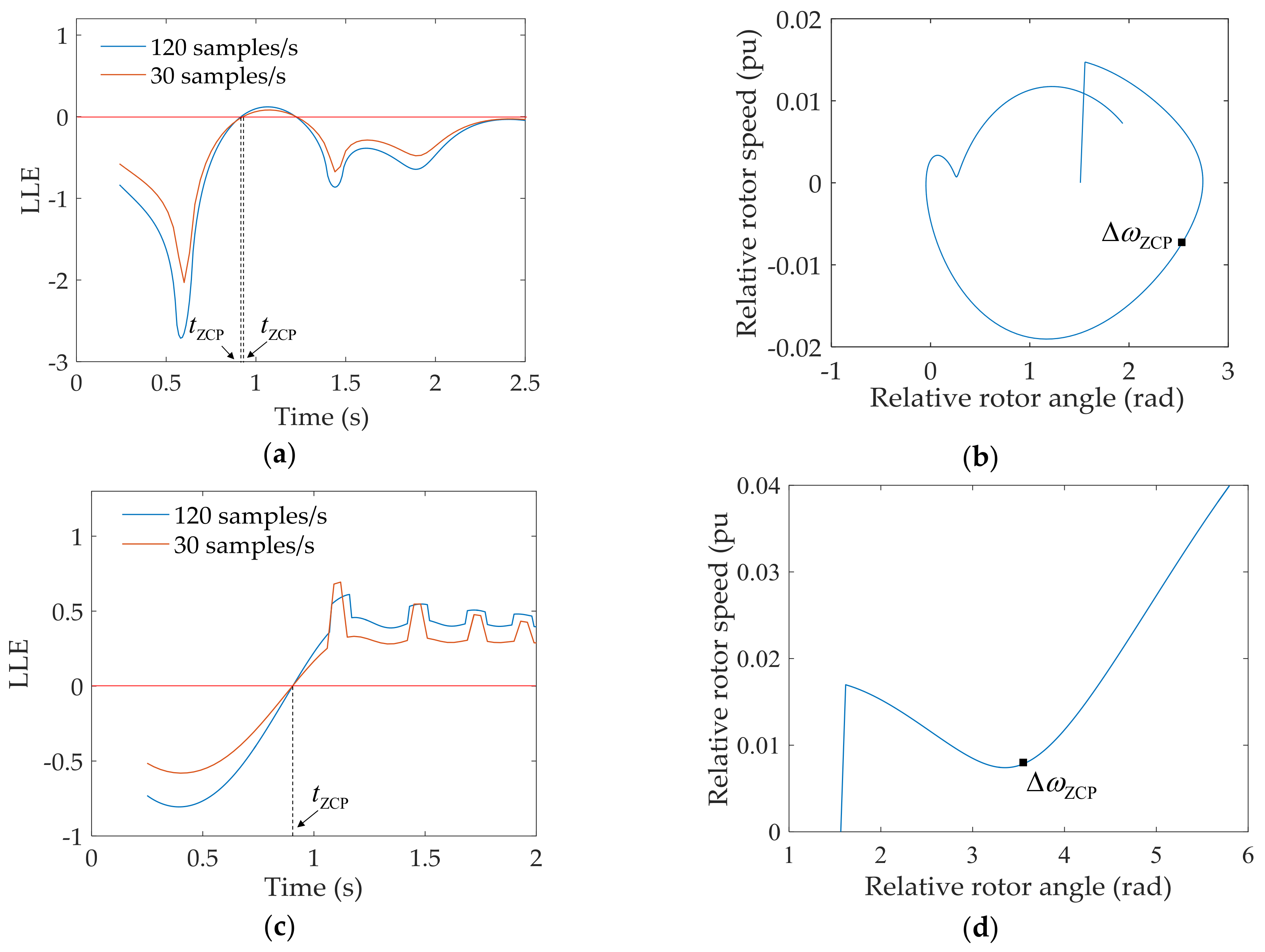
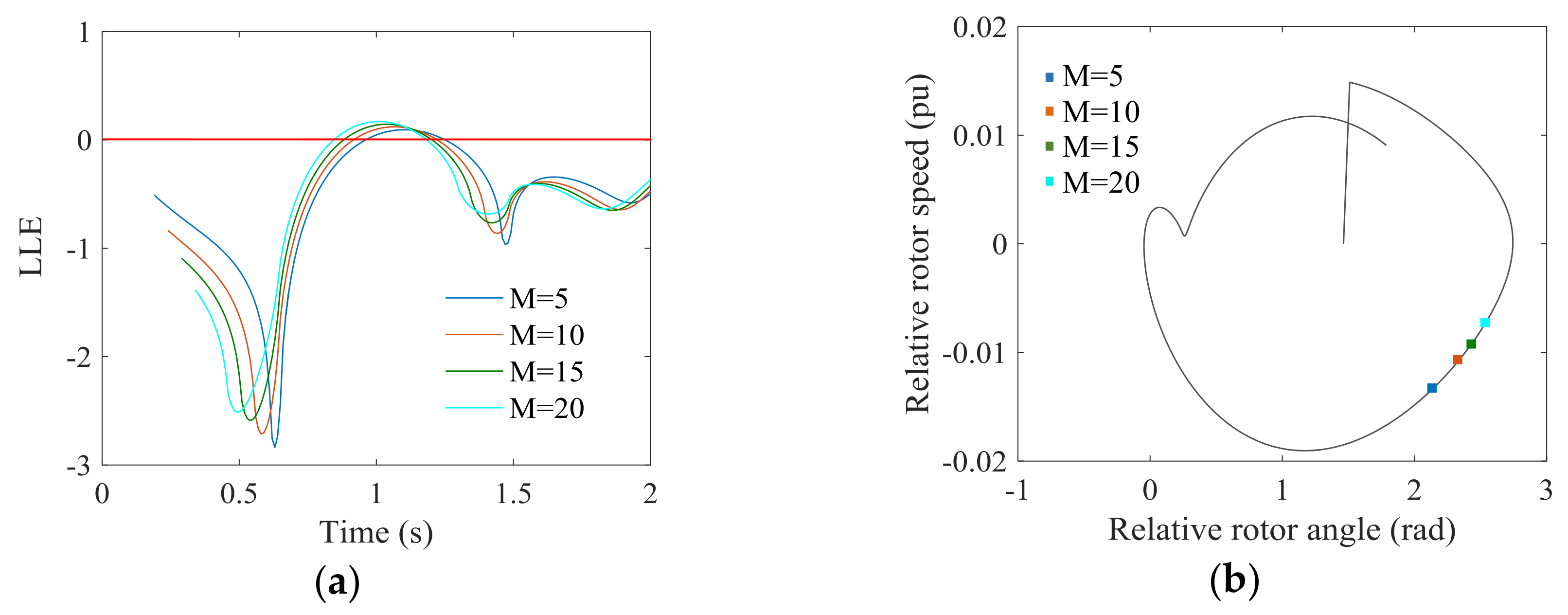
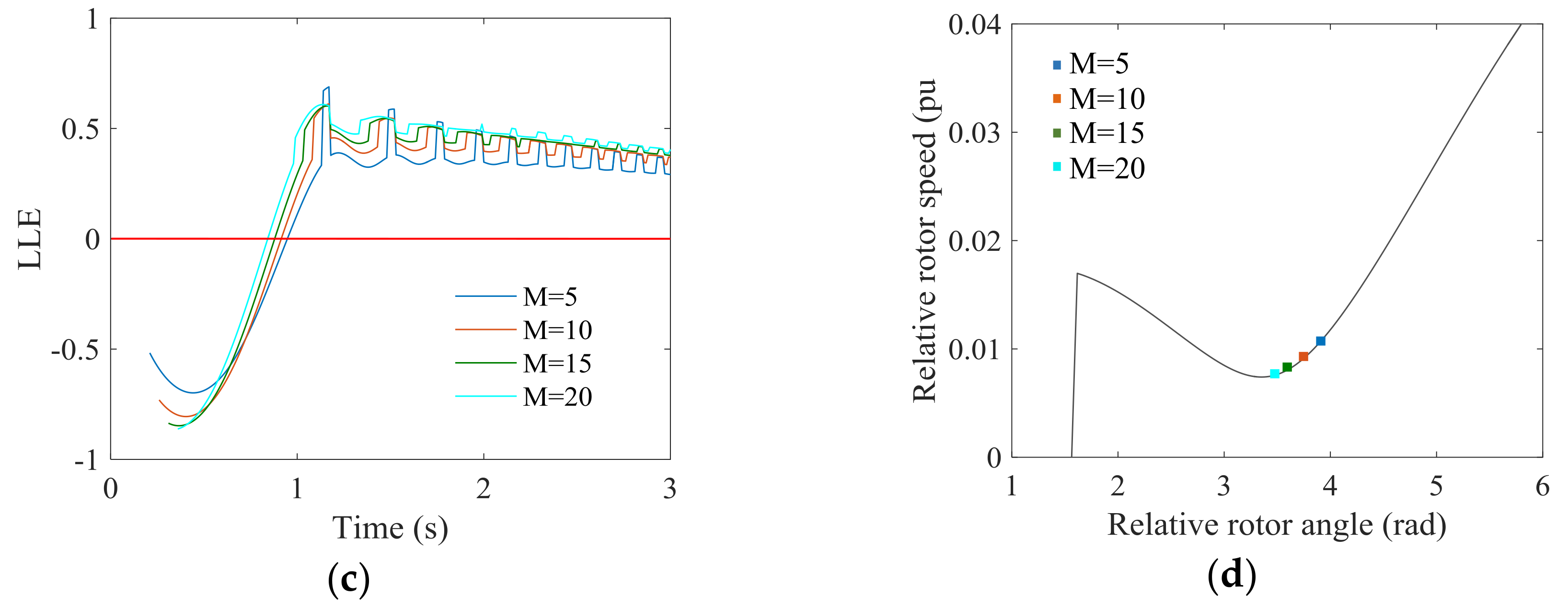
5.1. Effect of Sampling Rate
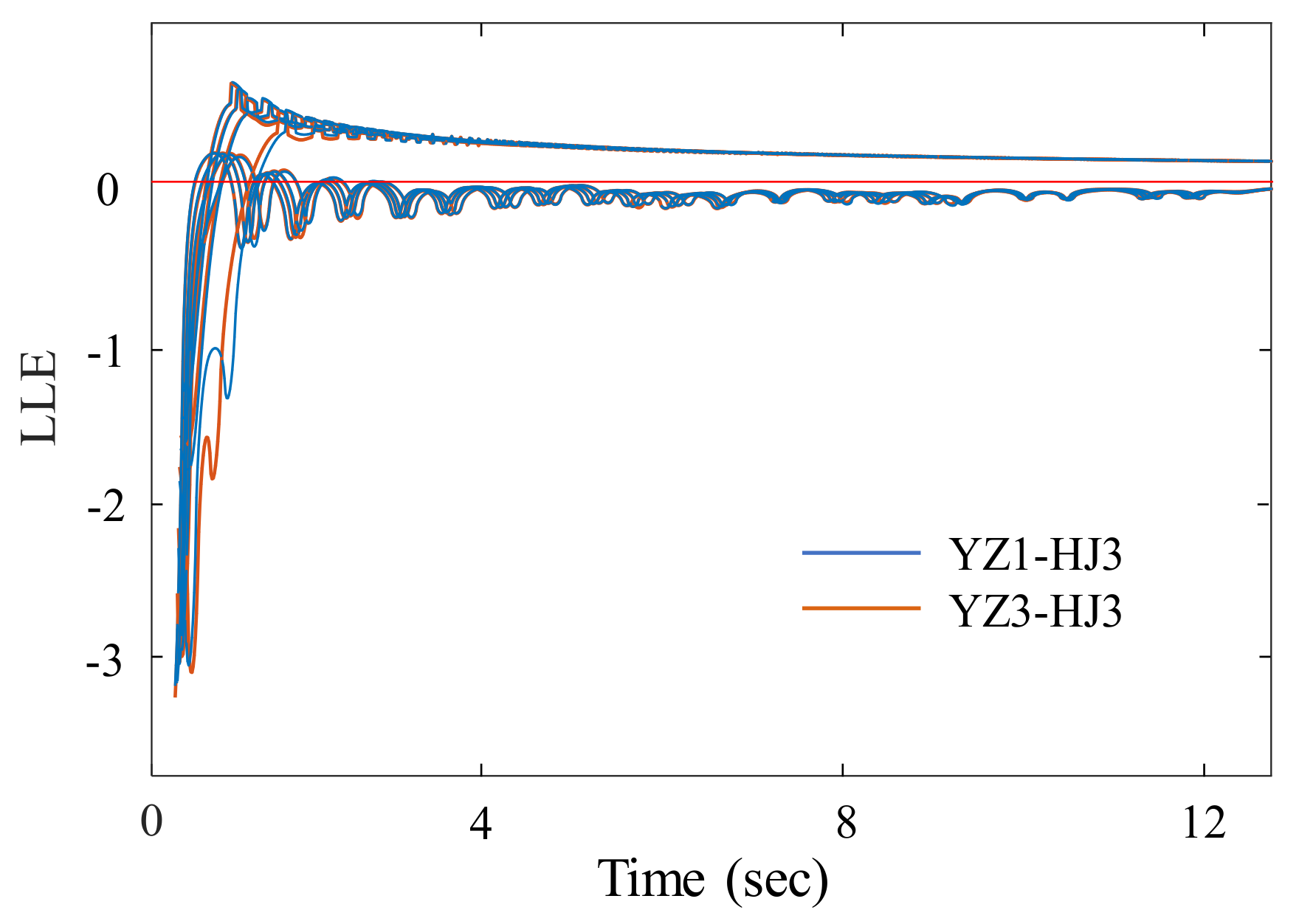
5.2. Effect of Initial Conditions
5.3. Discussions on the Differences from the Traditional LLE-Based Approach
- (1)
- Reference [22] requires the LLE–time curves of the relative rotor angles for all possible GPs. Instead, our proposed approach needs only the LLE–time curves of the CGPs.
- (2)
- Reference [22] requires sufficient length of calculation time because the LLE estimated by the algorithm usually fluctuates between negative and positive values for quite a long time. In this paper, the calculation time length for each GGP is usually less than 1 s because the rotor angle stability can be assessed when the LLE–time curve crosses the zero line from negative to positive for the first time.
- (3)
- In this paper, the mathematical model between the LLE value and the rotor speed is established, and the proposed stability criterion combines the mathematical model with the dynamic characteristics of the phase-plane trajectory to guarantee the accuracy and the rapidity of the proposed stability criterion. However, Reference [22] only considers the signs of the LLE evolution as stability criterion. As a result, the stability assessment time is long, and the assessment results may be inaccurate because the calculation window and the sampling rates have a great effect on the LLE estimation.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Van Cutsem, T.; et al. Definition and classification of power system stability IEEE/CIGRE joint task force on stability terms and definitions. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar]
- Su, H.Y.; Liu, T.Y. GECM-based voltage stability assessment using wide-area synchrophasors. Energies 2017, 10, 1601. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, G.; Das, K.; Korres, G.N.; Manousakis, N.M.; Sinha, A.K.; He, Z. Power system real-time monitoring by using PMU-based robust state estimation method. IEEE Trans. Smart Grid 2016, 7, 300–309. [Google Scholar] [CrossRef]
- Vu, T.L.; Turitsyn, K. Lyapunov functions family approach to transient stability assessment. IEEE Trans. Power Syst. 2016, 31, 1269–1277. [Google Scholar] [CrossRef]
- Reddy, S.S.; Prathipati, K.; Lho, Y.H. Transient stability improvement of a system connected with wind energy generators. Int. J. Emerg. Electr. Power Syst. 2017, 18, 1–15. [Google Scholar] [CrossRef]
- Zadkhast, S.; Jatskevich, J.; Vaahedi, E. A multi-decomposition approach for accelerated time-domain simulation of transient stability problems. IEEE Trans. Power Syst. 2015, 30, 2301–2311. [Google Scholar] [CrossRef]
- Fang, D.Z.; Chung, T.S.; Zhang, Y.; Song, W. Transient stability limit conditions analysis using a corrected transient energy function approach. IEEE Trans. Power Syst. 2000, 15, 804–810. [Google Scholar] [CrossRef]
- Wang, B.; Fang, B.; Wang, Y.; Liu, H.; Liu, Y. Power system transient stability assessment based on big data and the core vector machine. IEEE Trans. Smart Grid 2016, 7, 2561–2570. [Google Scholar] [CrossRef]
- Reddy, S.S.; Rathnam, C.S. Optimal power flow using glowworm swarm optimization. Int. J. Electr. Power Energy Syst. 2016, 80, 128–139. [Google Scholar] [CrossRef]
- Gurusinghe, D.R.; Rajapakse, A.D. Post-disturbance transient stability status prediction using synchrophasor measurements. IEEE Trans. Power Syst. 2016, 31, 3656–3664. [Google Scholar] [CrossRef]
- Bhui, P.; Senroy, N. Real-time prediction and control of transient stability using transient energy function. IEEE Trans. Power Syst. 2017, 32, 923–934. [Google Scholar] [CrossRef]
- Oluic, M.; Ghandhari, M.; Berggren, B. Methodology for rotor angle transient stability assessment in parameter space. IEEE Trans. Power Syst. 2017, 32, 1202–1211. [Google Scholar]
- Amraee, T.; Ranjbar, S. Transient instability prediction using decision tree technique. IEEE Trans. Power Syst. 2013, 28, 3028–3037. [Google Scholar] [CrossRef]
- AL-Masri, A.N.; Ab Kadir, M.Z.A.; Hizam, H.; Mariun, N. A novel implementation for generator rotor angle stability prediction using an adaptive artificial neural network application for dynamic security assessment. IEEE Trans. Power Syst. 2013, 28, 2516–2525. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, J.; Ji, L.; Hao, L. A hierarchical method for transient stability prediction of power systems using the confidence of a SVM-based ensemble classifier. Energies 2016, 9, 778. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z. Application of EOS-ELM with binary Jaya-based feature selection to real-time transient stability assessment using PMU Data. IEEE Access 2017, 25, 23092–23101. [Google Scholar] [CrossRef]
- James, J.Q.; Hill, D.J.; Lam, A.Y.; Gu, J.; Li, V.O. Intelligent time-adaptive transient stability assessment system. IEEE Trans. Power Syst. 2018, 33, 1049–1058. [Google Scholar]
- Liu, C.W.; Thorp, J.S.; Lu, J.; Thomas, R.J.; Chiang, H.D. Detection of transiently chaotic swings in power systems using real-time phasor measurements. IEEE Trans. Power Syst. 1994, 9, 1285–1292. [Google Scholar]
- Khaitan, S.K.; McCalley, J.D. VANTAGE: A Lyapunov exponents based technique for identification of coherent groups of generators in power systems. Electr. Power Syst. Res. 2013, 105, 33–38. [Google Scholar] [CrossRef]
- Yan, J.; Liu, C.C.; Vaidya, U. PMU-based monitoring of rotor angle dynamics. IEEE Trans. Power Syst. 2011, 26, 2125–2133. [Google Scholar] [CrossRef]
- Wadduwage, D.P.; Wu, C.Q.; Annakkage, U.D. Power system transient stability analysis via the concept of Lyapunov Exponents. Electr. Power Syst. Res. 2013, 104, 183–192. [Google Scholar] [CrossRef]
- Dasgupta, S.; Paramasivam, M.; Vaidya, U.; Ajjarapu, V. PMU-based model-free approach for real-time rotor angle monitoring. IEEE Trans. Power Syst. 2015, 30, 2818–2819. [Google Scholar] [CrossRef]
- Dasgupta, S.; Paramasivam, M.; Vaidya, U.; Ajjarapu, V. Real-time monitoring of short-term voltage stability using PMU data. IEEE Trans. Power Syst. 2013, 28, 3702–3711. [Google Scholar] [CrossRef]
- Skokos, C.H.; Gottwald, G.A.; Laskar, J. Chaos Detection and Predictability; Springer: Berlin/Heidelberg, Germany, 2016; pp. 123–135. [Google Scholar]
- Pai, M.A. Energy Function Analysis for Power System Stability; Kluwer Academic Publishers: Boston, MA, USA, 1989. [Google Scholar]
- Wang, L.; Girgis, A.A. A new method for power system transient instability detection. IEEE Trans. Power Deliv. 1997, 12, 1082–1089. [Google Scholar] [CrossRef]
- Haque, M.H.; Rahim, A.H.M.A. Determination of first swing stability limit of multimachine power systems through taylor series expansions. IEE Proc. C 1989, 136, 373–380. [Google Scholar] [CrossRef]
- He, M.; Vittal, V.; Zhang, J. Online dynamic security assessment with missing PMU measurements: A data mining approach. IEEE Trans. Power Syst. 2013, 28, 1969–1977. [Google Scholar] [CrossRef]
- Sun, K.; Qi, J.; Kang, W. Power system observability and dynamic state estimation for stability monitoring using synchrophasor measurements. Control Eng. Pract. 2016, 53, 160–172. [Google Scholar] [CrossRef]
- Zhou, N.; Meng, D.; Huang, Z.; Welch, G. Dynamic state estimation of a synchronous machine using PMU data: A. comparative study. IEEE Trans. Smart Grid. 2015, 6, 450–460. [Google Scholar] [CrossRef]
- Ariff, M.A.; Pal, B.C.; Singh, A.K. Estimating dynamic model parameters for adaptive protection and control in power system. IEEE Trans. Power Syst. 2015, 30, 829–839. [Google Scholar] [CrossRef]
- Qi, J.; Sun, K.; Kang, W. Optimal PMU placement for power system dynamic state estimation by using empirical observability gramian. IEEE Trans. Power Syst. 2015, 30, 2041–2054. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Hao, Z. Response based emergency control system for power system transient stability. Energies 2015, 8, 13508–13520. [Google Scholar] [CrossRef]
- Gu, Z.Y.; Yong, T.; Sun, H. An identification method for power system transient angle stability based on the trend of rotor speed difference-rotor angle difference. Proc. CSEE 2013, 33, 65–72. [Google Scholar]
- Jones, K.D.; Pal, A.; Thorp, J.S. Methodology for performing synchrophasor data conditioning and validation. IEEE Trans. Power Syst. 2015, 30, 1121–1130. [Google Scholar] [CrossRef]
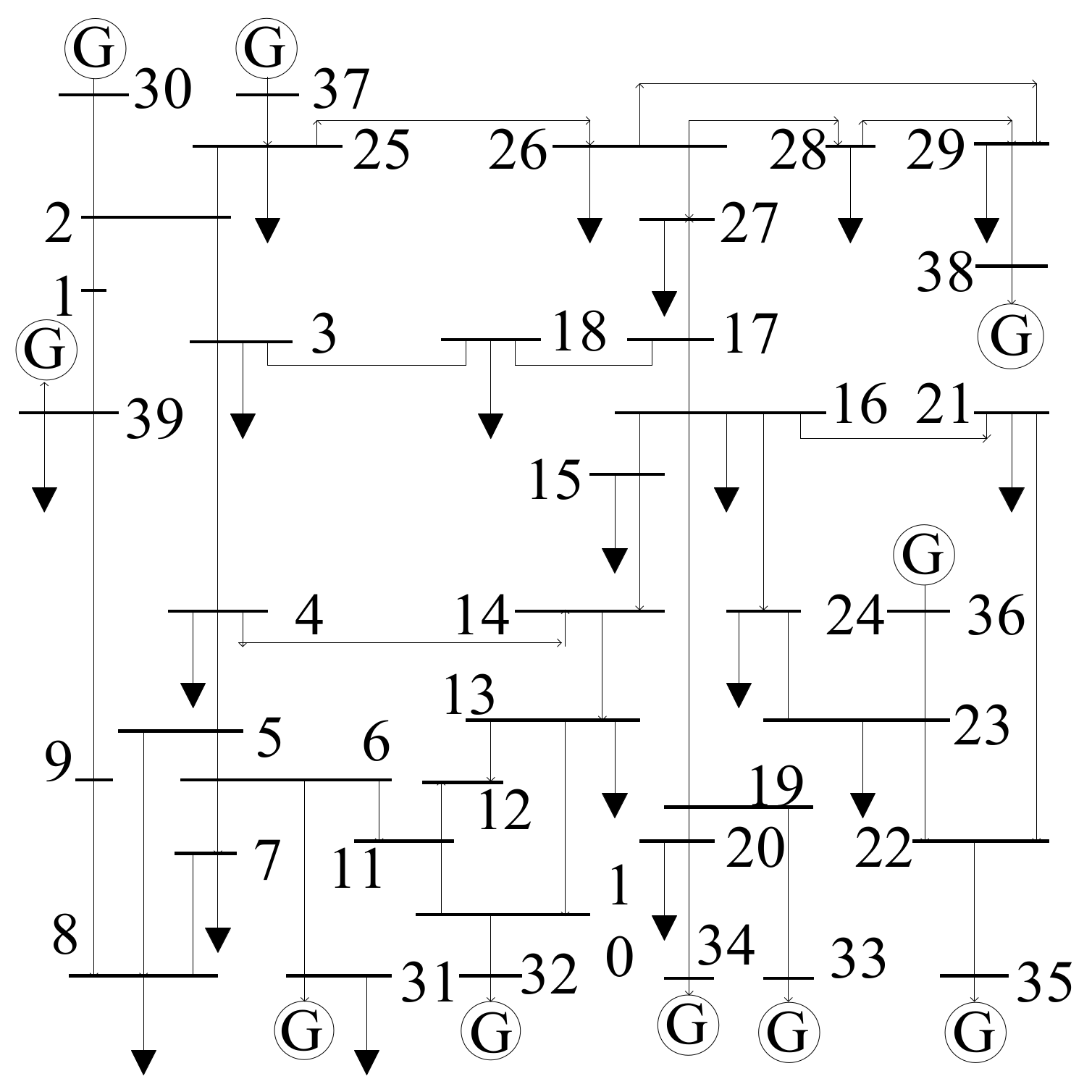

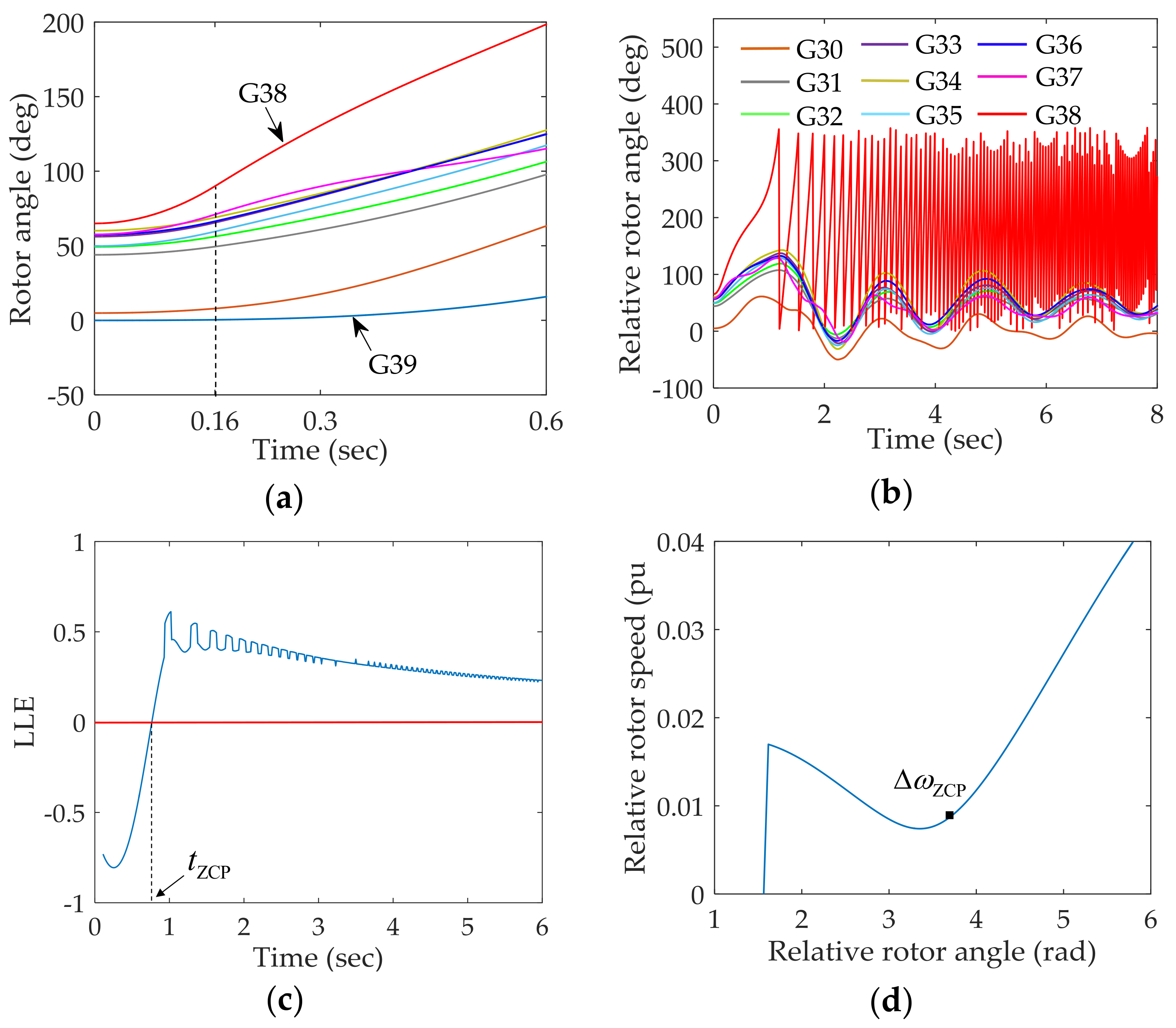
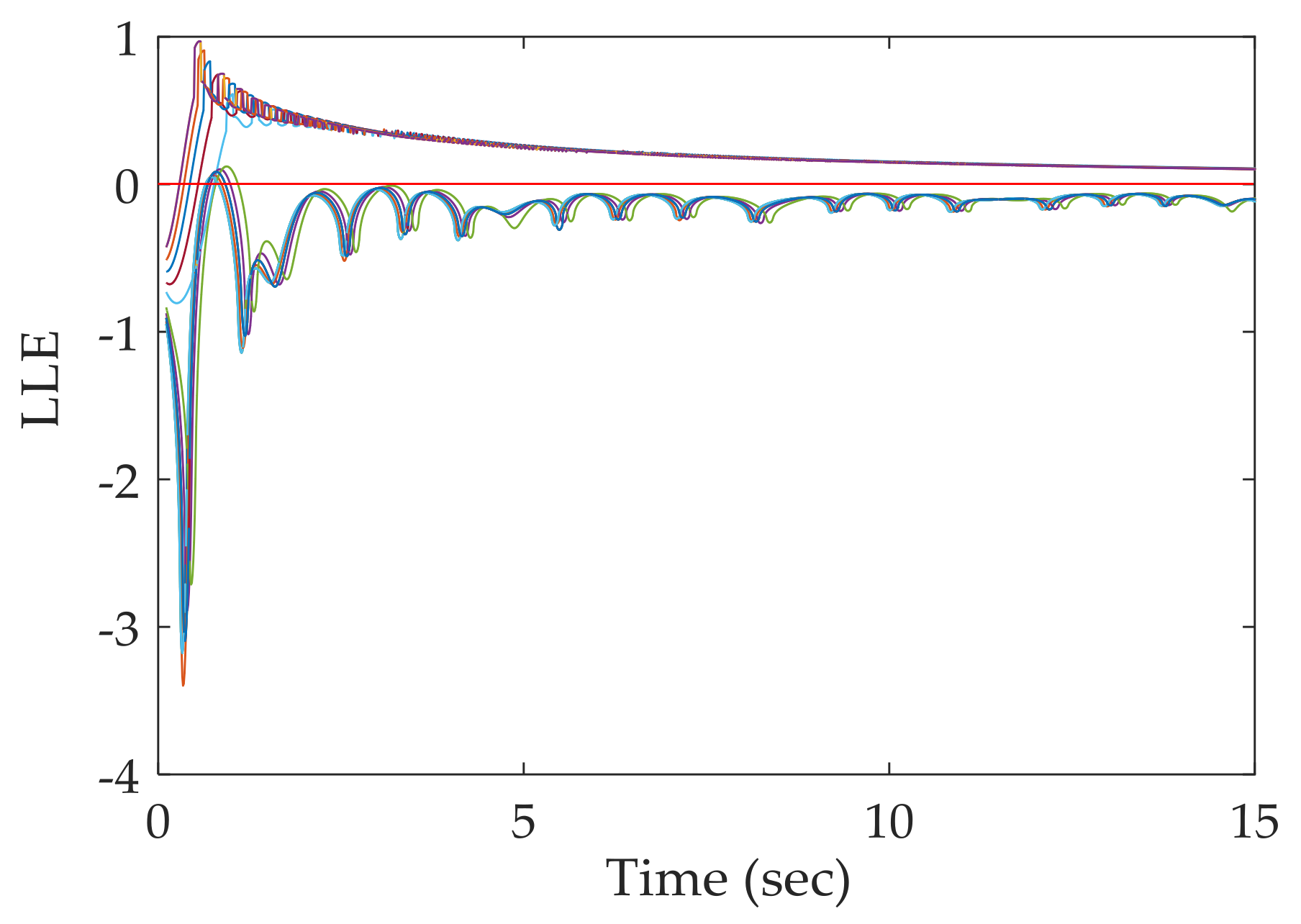
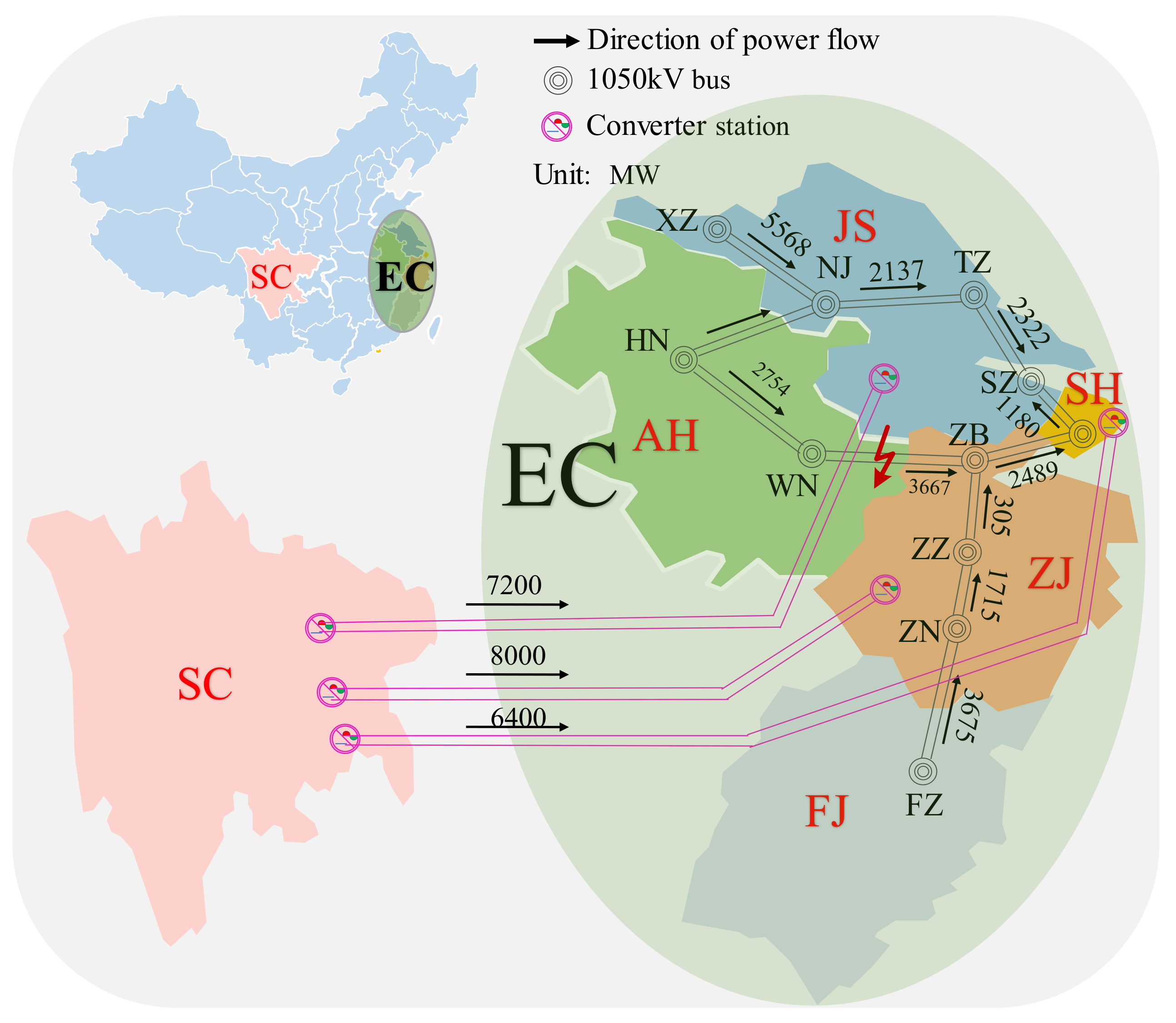
| Tc 1 (cycles) | CGP | TDS | The Proposed Approach | Only by LLE–t Curve | |||
|---|---|---|---|---|---|---|---|
| Stability Assessment Results | tac 2 (s) | ΔωZCP (rad) | Stability Assessment Results | LLE at t = 4 s | |||
| 5.5 | G38-G39 | stable | stable | 0.54 | −0.0054 | stable | −0.0560 |
| 6 | G38-G39 | stable | stable | 0.56 | −0.0056 | stable | −0.0076 |
| 6.5 | G38-G39 | stable | stable | 0.58 | −0.0057 | stable | −0.0631 |
| 7 | G38-G39 | stable | stable | 0.62 | −0.0061 | unstable | 0.0075 |
| 7.5 | G38-G39 | stable | stable | 0.73 | −0.0086 | unstable | 0.0141 |
| 8 | G38-G39 | unstable | unstable | 0.71 | 0.0089 | unstable | 0.1069 |
| 8.5 | G38-G39 | unstable | unstable | 0.55 | 0.0114 | unstable | 0.0947 |
| 9 | G38-G39 | unstable | unstable | 0.44 | 0.0135 | unstable | 0.1064 |
| 9.5 | G38-G39 | unstable | unstable | 0.36 | 0.0156 | unstable | 0.0937 |
| 10 | G38-G39 | unstable | unstable | 0.29 | 0.0176 | unstable | 0.1054 |
| Tc (cycles) | CGP | TDS | The Proposed Approach | Only by LLE–t Curve | |||
|---|---|---|---|---|---|---|---|
| Stability Assessment Results | tac (s) | ΔωZCP (rad) | Stability Assessment Results | LLE at t = 5 s | |||
| 10 | YZ1-HJ3 | stable | stable | 0.28 | −0.0094 | stable | −0.2229 |
| YZ3-HJ3 | stable | stable | 0.29 | −0.0101 | stable | −0.2238 | |
| 10.5 | YZ1-HJ3 | stable | stable | 0.31 | −0.0105 | stable | −0.2228 |
| YZ3-HJ3 | stable | stable | 0.32 | −0.0111 | stable | −0.2235 | |
| 11 | YZ1-HJ3 | stable | stable | 0.37 | −0.0111 | stable | −0.2240 |
| YZ3-HJ3 | stable | stable | 0.38 | −0.0115 | stable | −0.2246 | |
| 11.5 | YZ1-HJ3 | stable | stable | 0.44 | −0.0115 | unstable | 0.0028 |
| YZ3-HJ3 | stable | stable | 0.44 | −0.0114 | unstable | 0.0033 | |
| 12 | YZ1-HJ3 | stable | stable | 0.53 | −0.0111 | unstable | 0.0087 |
| YZ3-HJ3 | stable | stable | 0.54 | −0.0112 | unstable | 0.0090 | |
| 12.5 | YZ1-HJ3 | unstable | unstable | 0.73 | 0.0087 | unstable | 0.1653 |
| YZ3-HJ3 | unstable | unstable | 0.71 | 0.0090 | unstable | 0.1642 | |
| 13 | YZ1-HJ3 | unstable | unstable | 0.50 | 0.0090 | unstable | 0.1673 |
| YZ3-HJ3 | unstable | unstable | 0.48 | 0.0092 | unstable | 0.1661 | |
| 13.5 | YZ1-HJ3 | unstable | unstable | 0.40 | 0.0091 | unstable | 0.1668 |
| YZ3-HJ3 | unstable | unstable | 0.39 | 0.0096 | unstable | 0.1656 | |
| 14 | YZ1-HJ3 | unstable | unstable | 0.34 | 0.0095 | unstable | 0.1641 |
| YZ3-HJ3 | unstable | unstable | 0.33 | 0.0098 | unstable | 0.1630 | |
| 14.5 | YZ1-HJ3 | unstable | unstable | 0.30 | 0.0104 | unstable | 0.1653 |
| YZ3-HJ3 | unstable | unstable | 0.28 | 0.0106 | unstable | 0.1642 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Chen, Q.; Ma, S.; Zhang, Y.; Chen, S. Wide-Area Measurement—Based Model-Free Approach for Online Power System Transient Stability Assessment. Energies 2018, 11, 958. https://doi.org/10.3390/en11040958
Huang D, Chen Q, Ma S, Zhang Y, Chen S. Wide-Area Measurement—Based Model-Free Approach for Online Power System Transient Stability Assessment. Energies. 2018; 11(4):958. https://doi.org/10.3390/en11040958
Chicago/Turabian StyleHuang, Dan, Qiyu Chen, Shiying Ma, Yichi Zhang, and Shuyong Chen. 2018. "Wide-Area Measurement—Based Model-Free Approach for Online Power System Transient Stability Assessment" Energies 11, no. 4: 958. https://doi.org/10.3390/en11040958
APA StyleHuang, D., Chen, Q., Ma, S., Zhang, Y., & Chen, S. (2018). Wide-Area Measurement—Based Model-Free Approach for Online Power System Transient Stability Assessment. Energies, 11(4), 958. https://doi.org/10.3390/en11040958




