Dynamic Wireless Power Transfer for Logistic Robots
Abstract
:1. Introduction
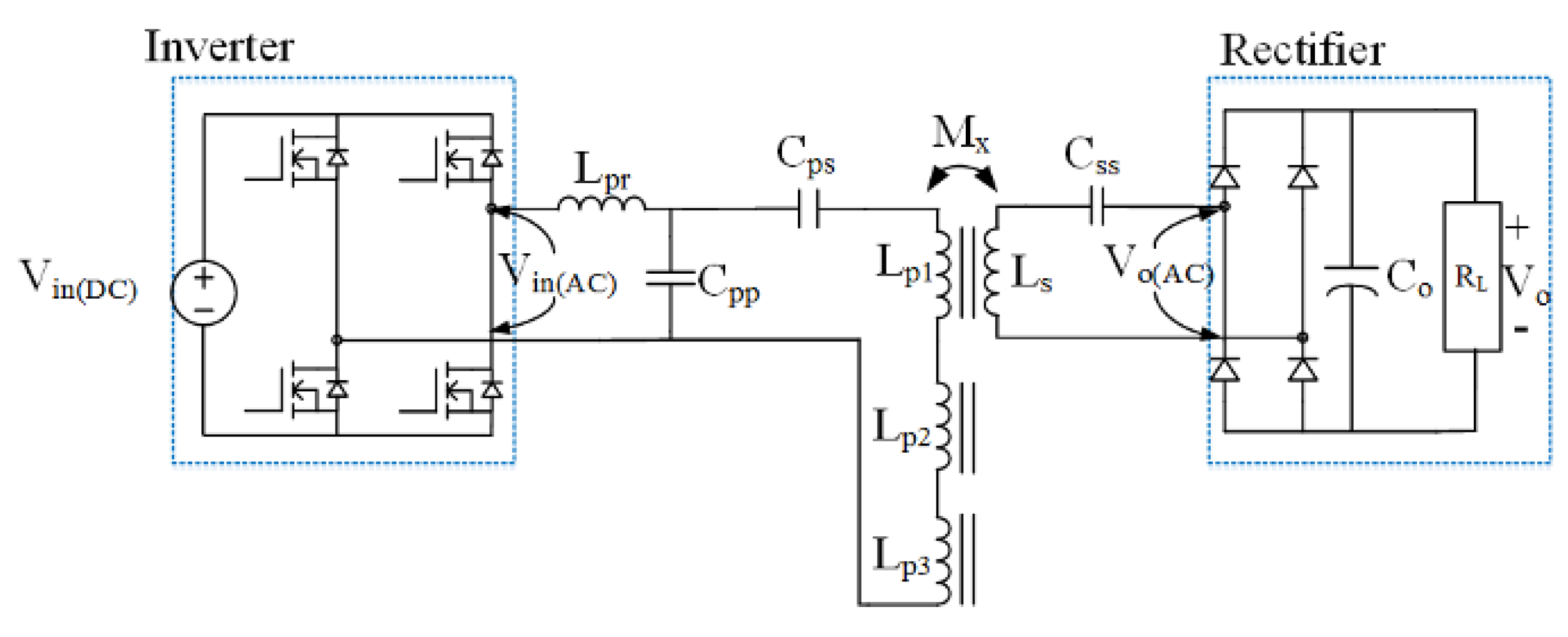
2. Analysis and Characteristic of LCC-S DWPT
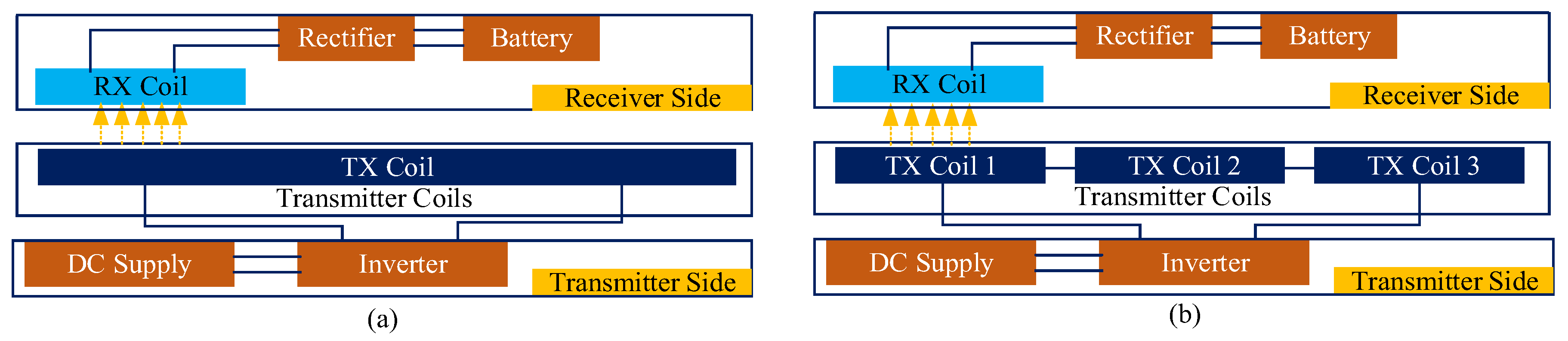
3. Coils and Compensation Design
3.1. Coils Design
3.2. Compensation Circuit Design
4. Simulation and Experimental Verifications
4.1. Simulation
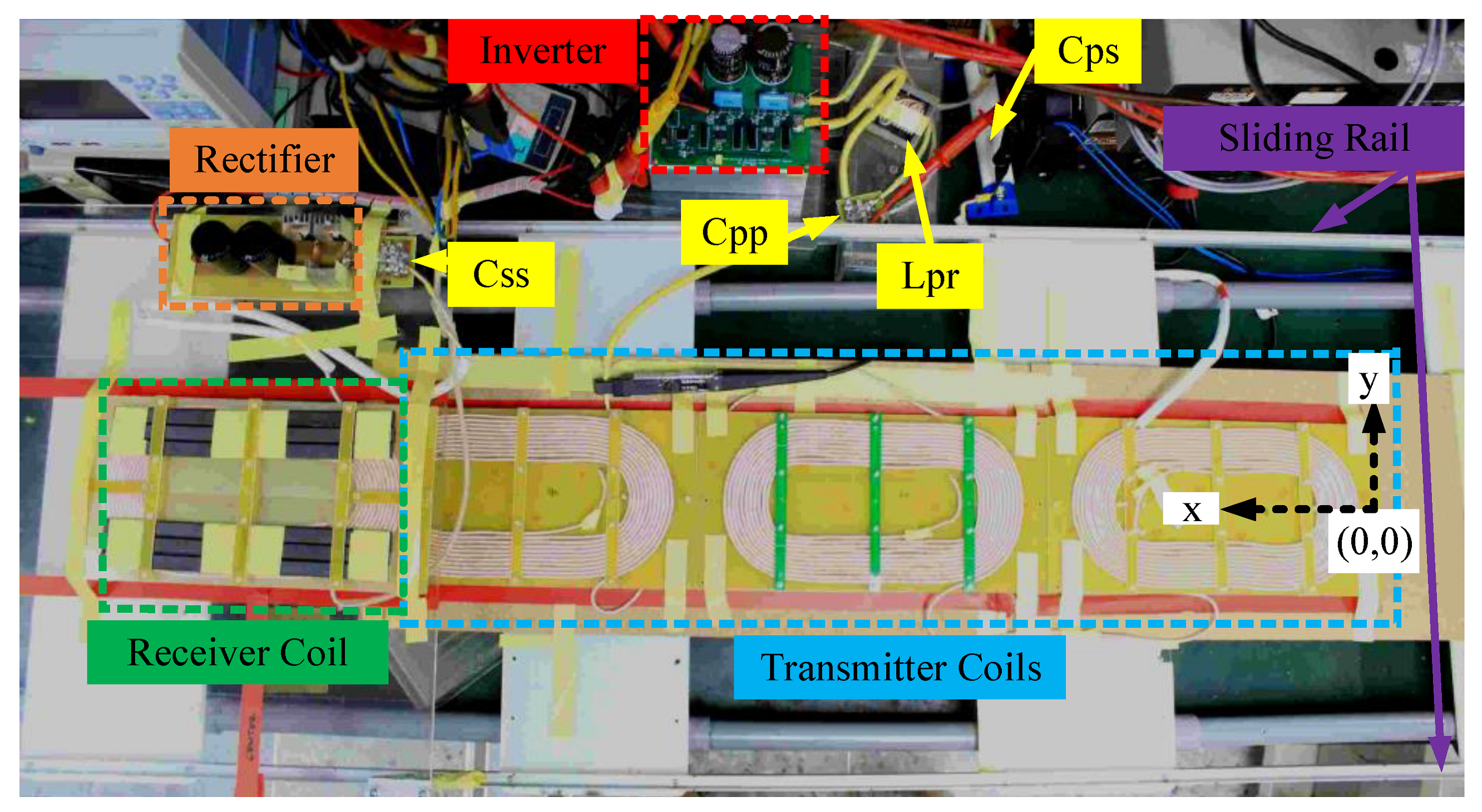
4.2. Hardware Implementation
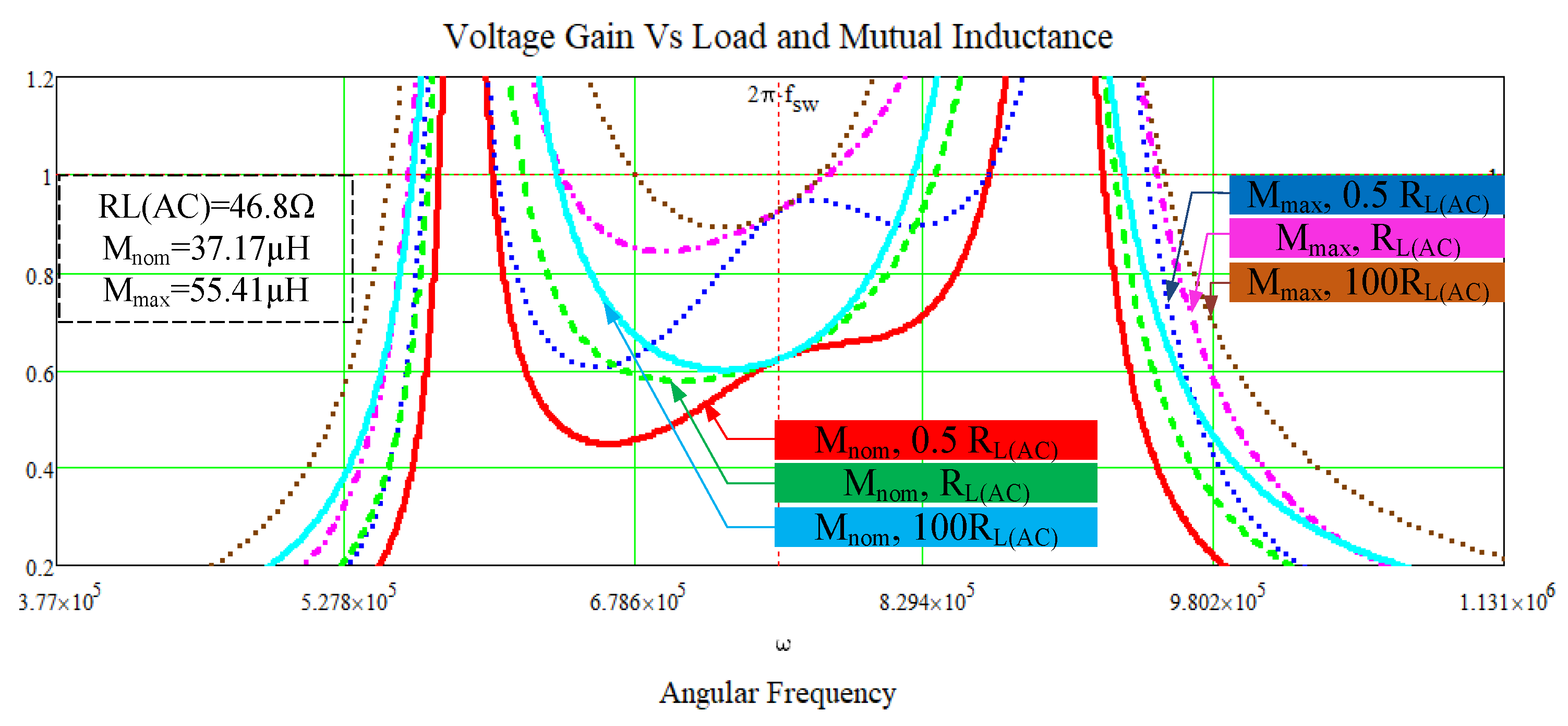
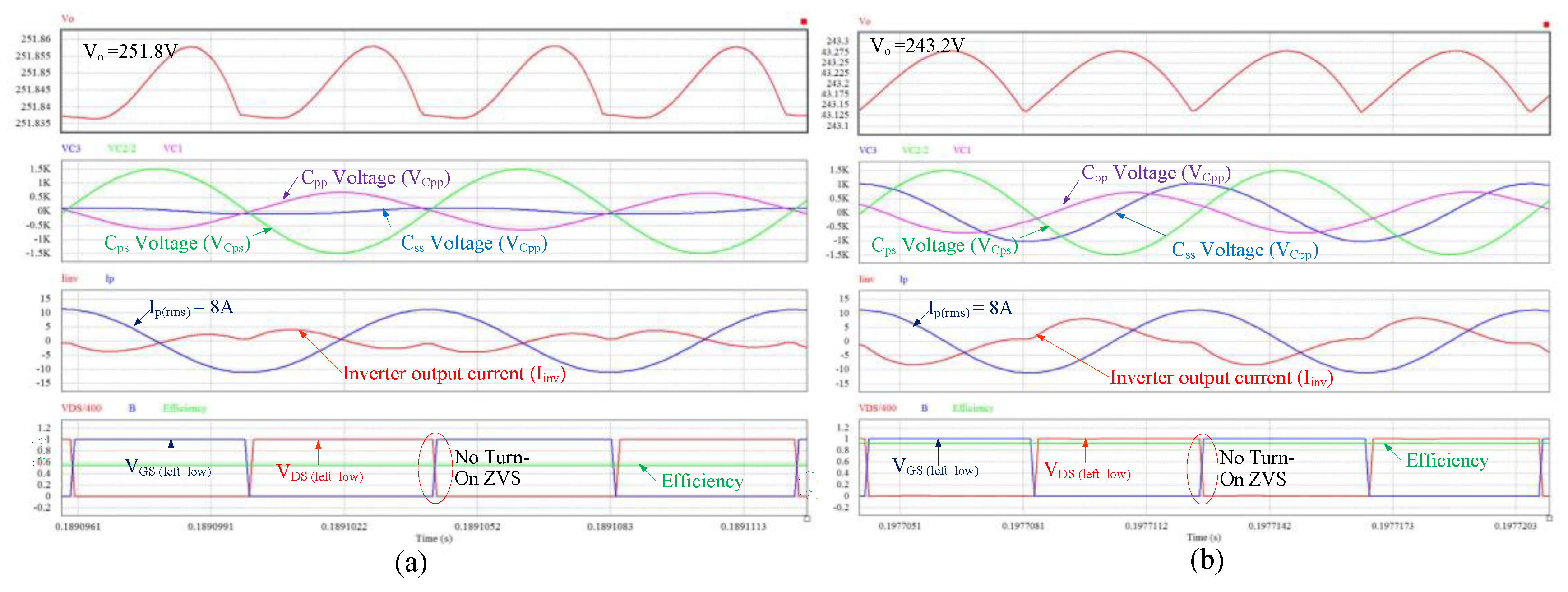
4.3. Performance at the Maximum Coupling Coefficient
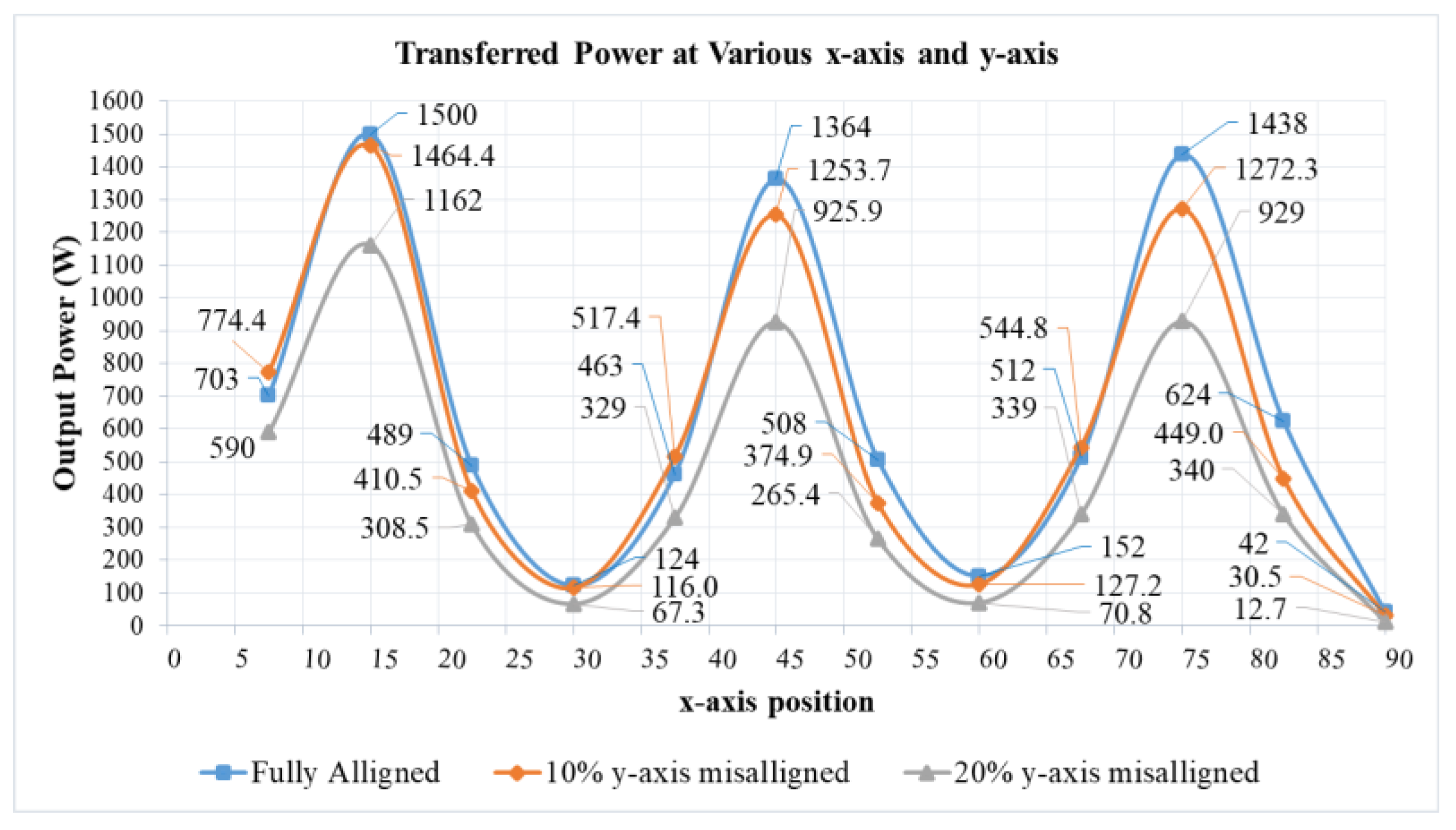
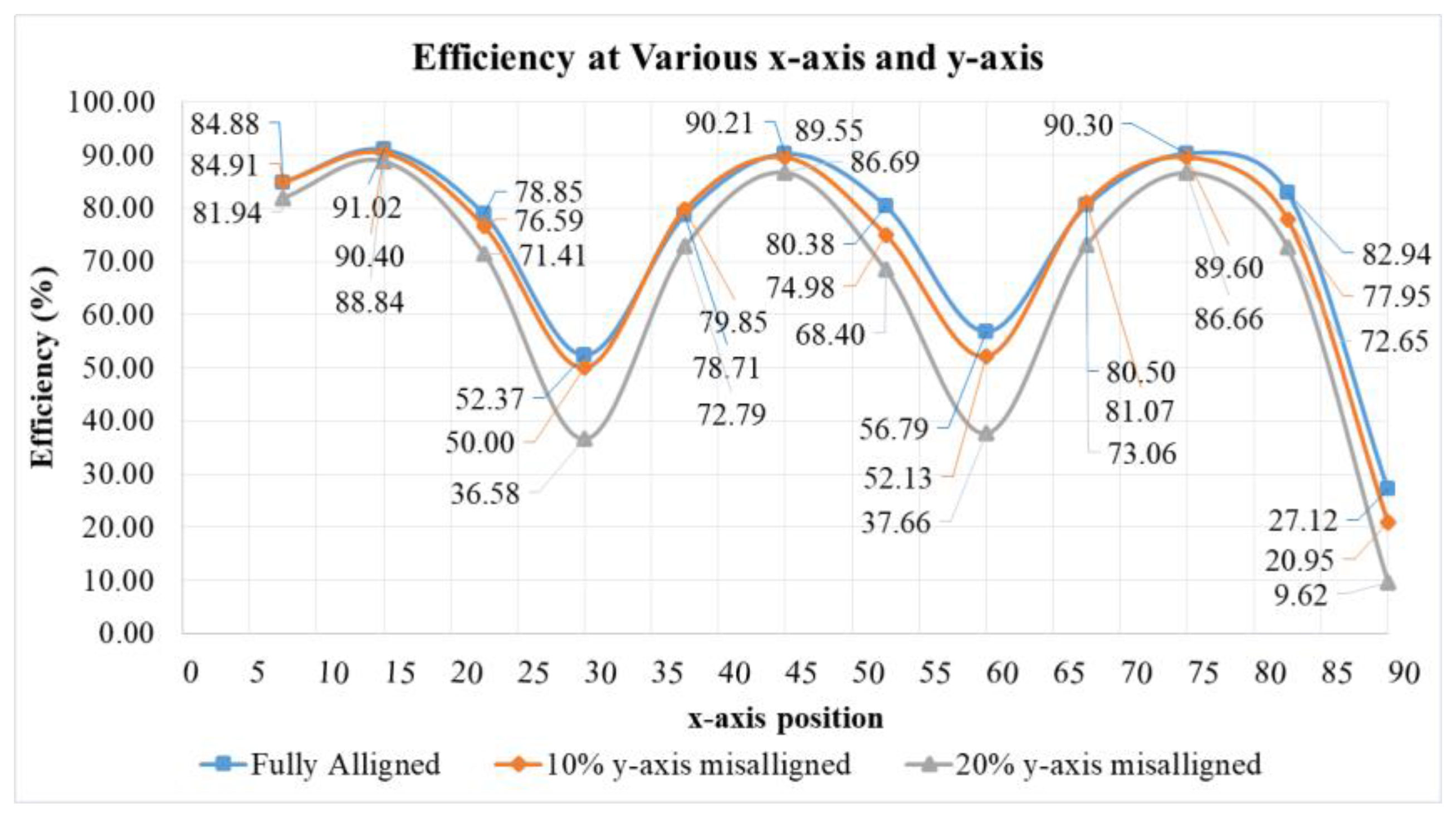
4.4. Dynamic Performance
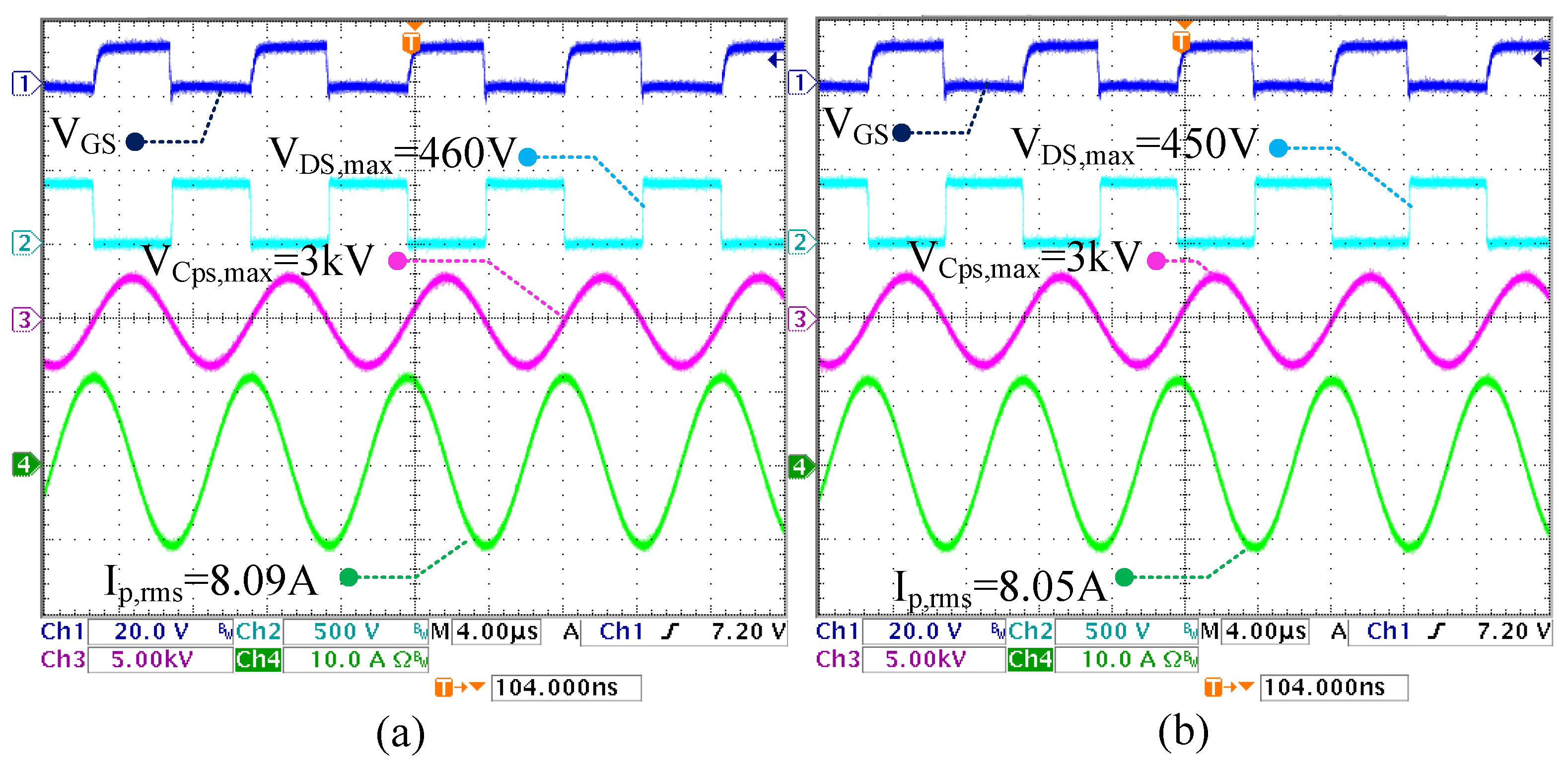
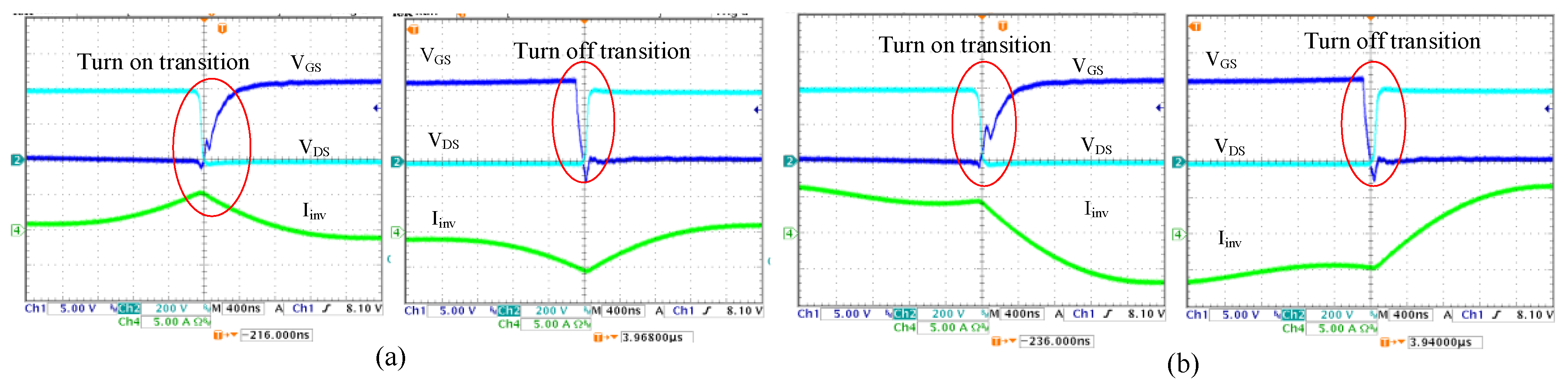
4.5. Zero-Voltage Switching Transition
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bonkenburg, T. Robotics in Logistics: A DPDHL Perspective on Implications and Use Cases for the Logistics Industry; DHL Customer Solutions & Innovation: Bonn, Germany, 2016; p. 4. [Google Scholar]
- Bhasin, K.; Clark, P. How Amazon Triggered a Robot Arms Race. Available online: http://fromm.usfca.edu/Spring2017Handouts/Levy%20Week%203.4.pdf (accessed on 27 July 2017).
- Robotics, L. Collaborative, Autonomous Robots That Just Work. Available online: http://www.locusrobotics.com/features/autonomous-robots/ (accessed on 25 July 2017).
- Boys, J.T.; Covic, G.A.; Green, A.W. Stability and control of inductively coupled power transfer systems. IEE Proc. Electr. Power Appl. 2000, 147, 37–43. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Modern Trends in Inductive Power Transfer for Transportation Applications. IEEE J. Emerg. Sel. Top. Power Electr. 2013, 1, 28–41. [Google Scholar] [CrossRef]
- Li, T.; Wang, X.; Zheng, S.; Liu, C. An Efficient Topology for Wireless Power Transfer over a Wide Range of Loading Conditions. Energies 2018, 11, 141. [Google Scholar] [CrossRef]
- Obayashi, S.; Tsukahara, H. EMC Issues on Wireless Power Transfer. In Proceedings of the 2014 International Symposium on Electromagnetic Compatibility, Tokyo, Japan, 12–16 May 2014; IEICE: Tokyo, Japan, 2014; pp. 601–604. [Google Scholar]
- Wen, F.; Huang, X. Optimal Magnetic Field Shielding Method by Metallic Sheets in Wireless Power Transfer System. Energies 2016, 9, 733. [Google Scholar] [CrossRef]
- Suzuki, S.-N.; Ishihara, M.; Kobayashi, Y. The Improvement of the Noninvasive Power-Supply System Using Magnetic Coupling for Medical Implants. IEEE Trans. Magn. 2011, 47, 2811–2814. [Google Scholar] [CrossRef]
- Lu, Y.; Ma, D. Wireless Power Transfer System Architectures for Portable or Implantable Applications. Energies 2016, 9, 1087. [Google Scholar] [CrossRef]
- Junaid, A.; Konoiko, A.; Zweiri, Y.; Sahinkaya, M.; Seneviratne, L. Autonomous Wireless Self-Charging for Multi-Rotor Unmanned Aerial Vehicles. Energies 2017, 10, 803. [Google Scholar] [CrossRef]
- Campi, T.; Cruciani, S.; Feliziani, M. Wireless Power Transfer Technology Applied to an Autonomous Electric UAV with a Small Secondary Coil. Energies 2018, 11, 352. [Google Scholar] [CrossRef]
- Lee, S.-H.; Kim, J.-H.; Lee, J.-H. Development of a 60 kHz, 180 kW, Over 85% Efficiency Inductive Power Transfer System for a Tram. Energies 2016, 9, 1075. [Google Scholar] [CrossRef]
- Kobayashi, D.; Imura, T.; Hori, Y. Real-time coupling coefficient estimation and maximum efficiency control on dynamic wireless power transfer using secondary DC-DC converter. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 004650–004655. [Google Scholar]
- Lovison, G.; Imura, T.; Hori, Y. Secondary-side-only simultaneous power and efficiency control by online mutual inductance estimation for dynamic wireless power transfer. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 4553–4558. [Google Scholar]
- Angelis, A.D.; Dionigi, M.; Wang, Q.; Che, W.; Mastri, F.; Monti, G. Resonant inductive wireless power transfer links operating in a coupling-independent regime: Theory and experiments. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Torino, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar]
- Feng, H.; Cai, T.; Duan, S.; Zhao, J.; Zhang, X.; Chen, C. An LCC-Compensated Resonant Converter Optimized for Robust Reaction to Large Coupling Variation in Dynamic Wireless Power Transfer. IEEE Trans. Ind. Electr. 2016, 63, 6591–6601. [Google Scholar] [CrossRef]
- Systems Control Technology, Inc. Roadway Powered Electric Vehicle Project Track Construction And Testing Program Phase 3D; Systems Control Technology, Inc.: Palo Alto, CA, USA, 1994. [Google Scholar]
- Chou, C.-Y.; Tampubolon, M.; Lin, J.-Y.; Hsieh, Y.-C.; Chiu, H.-J. Study on LCC-C Wireless Power Transfer. In Proceedings of the 2017 IEEE Wireless Power Transfer Conference (WPTC), Taipei, Taiwan, 10–12 May 2017; pp. 1–4. [Google Scholar]
- Pantic, Z.; Bai, S.; Lukic, S.M. ZCS LCC Compensated Resonant Inverter for Inductive-Power-Transfer Application. IEEE Trans. Ind. Electr. 2011, 58, 3500–3510. [Google Scholar] [CrossRef]
- Waters, B.H.; Mahoney, B.J.; Lee, G.; Smith, J.R. Optimal coil size ratios for wireless power transfer applications. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, Australia, 1–5 June 2014; pp. 2045–2048. [Google Scholar]
- Fujita, T.; Yasuda, T.; Akagi, H. A Dynamic Wireless Power Transfer System Applicable to a Stationary System. IEEE Trans. Ind. Appl. 2017, 53, 3748–3757. [Google Scholar] [CrossRef]


| Components | Units | Values |
|---|---|---|
| Transmitter inductance (Lp) | µH | 410.4 |
| Receiver inductance (Ls) | µH | 143.9 |
| Mutual inductance (M) | µH | 24.93 |
| Series resonant inductor (Lpr) | µH | 60 |
| Parallel primary resonant capacitor (Cpp) | nF | 29.4 |
| Series primary resonant capacitor (Cps) | nF | 5 |
| Series primary resonant capacitor (Css) | nF | 12.2 |
| AC equivalent output resistance (RL(AC)) | Ω | 48.634 |
| Parameters | Units | Values |
|---|---|---|
| Self-inductance of transmitter coil 1 Lp1 | µH | 137.3 |
| Self-inductance of transmitter coil 2 Lp2 | µH | 143.3 |
| Self-inductance of transmitter coil 3 Lp3 | µH | 141.4 |
| Self-inductance of receiver coil 4 Ls | µH | 143.9 |
| Total transmitter inductance Lp | µH | 410.4 |
| Minimum coupling coefficient (kmin) | - | 0.102 |
| Maximum coupling coefficient (kmax) | - | 0.228 |
| Nominal coupling coefficient (knom) | - | 0.153 |
| DC resistance/coil | mΩ | 50 |
| Number of turn/coil | - | 22 |
| Ferrite bar size | mm | 14 × 5 × 120 |
| Component | Unit | Value | ESR |
|---|---|---|---|
| Primary Series Resonant Inductor (Lp) | µH | 60 | 6 mΩ |
| Primary Series Resonant Capacitor (Cps) | nF | 5 | 15 mΩ |
| Primary Parallel Resonant Capacitor (Cpp) | nF | 29.4 | 19 mΩ |
| Secondary Series Resonant Capacitor (Css) | nF | 12.2 | 9.7 mΩ |
| Designed Switching Frequency (fsw) | kHz | 120 | |
| k | Power (W) | Vo (V) | VC2,max (kV) | Ip,rms (A) | η (%) |
|---|---|---|---|---|---|
| 0.1026 | 150 | 165.5 | 2.99 | 8.08 | 59.7 |
| 1500 | 151.15 | 2.98 | 8.1 | 87.29 | |
| 0.153 | 150 | 251.8 | 2.99 | 8.1 | 56.4 |
| 1500 | 243.2 | 2.98 | 8 | 92.2 | |
| 0.228 | 150 | 393 | 2.99 | 8.05 | 48.1 |
| 1500 | 367.2 | 2.99 | 8.06 | 92.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tampubolon, M.; Pamungkas, L.; Chiu, H.-J.; Liu, Y.-C.; Hsieh, Y.-C. Dynamic Wireless Power Transfer for Logistic Robots. Energies 2018, 11, 527. https://doi.org/10.3390/en11030527
Tampubolon M, Pamungkas L, Chiu H-J, Liu Y-C, Hsieh Y-C. Dynamic Wireless Power Transfer for Logistic Robots. Energies. 2018; 11(3):527. https://doi.org/10.3390/en11030527
Chicago/Turabian StyleTampubolon, Marojahan, Laskar Pamungkas, Huang-Jen Chiu, Yu-Chen Liu, and Yao-Ching Hsieh. 2018. "Dynamic Wireless Power Transfer for Logistic Robots" Energies 11, no. 3: 527. https://doi.org/10.3390/en11030527
APA StyleTampubolon, M., Pamungkas, L., Chiu, H.-J., Liu, Y.-C., & Hsieh, Y.-C. (2018). Dynamic Wireless Power Transfer for Logistic Robots. Energies, 11(3), 527. https://doi.org/10.3390/en11030527






