1. Introduction
The random variability of atmospheric phenomena affects the available irradiance intensity for photovoltaic (PV) generators. During the clear days an analytic expression for the solar irradiance can be defined, whereas this is not possible for cloudy days. The effects of the environmental conditions are studied in [
1,
2,
3,
4,
5]. After the installation of a PV plant, a system for monitoring the energy performance in every environmental condition is needed. As the modules are main components of a PV plant, deep attention is focused on their state of health [
6]. For this reason, techniques commonly used to verify the presence of typical defects in PV modules are based on infrared analysis [
7,
8], eventually supported by unmanned aerial vehicles [
9], on luminescence imaging [
10], or on their combination [
11], while automatic procedures to extract information using thermograms are proposed in [
12,
13]. Nevertheless, these approaches regard single modules of the PV plants. When there is no information about the general operation of the PV plant, other techniques can be considered to prevent failures and to enhance the energy performance of the PV system, such as artificial neural networks [
3,
14], statistics [
15,
16,
17], and checking the electrical variables [
18,
19,
20]. More in detail, some of the PV fault detection algorithms are based on electrical circuit simulation of the PV generator [
21,
22], while other researchers use approaches based on the electrical signals [
23,
24]. Moreover, predictive model approaches for PV system power production based on the comparison between measured and modeled PV system outputs are discussed in [
15,
25,
26,
27]. Standard benchmarks [
28], called
final PV system yield, reference yield and
Performance Ratio (PR), are currently used to assess the overall system performance in terms of energy production, solar resource, and system losses. These benchmarks have been recently used to review the energy performance of 993 residential PV systems in Belgium [
29] and 6868 PV installations in France [
30]. Unfortunately, these indices have two drawbacks: they only supply rough information about the performance of the overall PV plant and they do not allow any assessment of the behavior of single PV plant parts. Moreover, when important faults such as short circuits or islanding occur, the electrical variables and the produced energy have fast and not negligible variations, so they are easily detected. These events produce drastic changes and can be classified as high-intensity anomalies. On the other hand, low-intensity anomalies such as the ageing of the components or minimal partial shading produce minimal variations on the electrical variables and on the produced energy, so they are not easily detectable. Moreover, these minor anomalies can evolve into failures or faults, so their timely identification can avoid more serious failures and limit the occurrence of out of order states. With respect to the configuration defined in the design stage, any PV plant can be single-array or multi-array, being an array a set of connected PV modules, for which the electrical variables and the produced energy are measured. Moreover, PV plants with only two arrays are not common: the alternatives are between one-array PV plant—this is the case of small nominal peak power PV plant—and multiple-array PV plant for higher nominal peak power PV plant. The multiple-array solution is very common, because it has several advantages, thanks to the partition of the produced energy: lower current for each array (thus reduced section of the solar cables), high flexibility in the choice of the components (inverter, switches, electrical boxes, etc.), O&M services on each single array, avoiding situations where the whole plant is out of order, and so on. Moreover, the large PV plants, having a nominal peak power higher than 100 kWp are usually equipped with a weather station, able to measure and store the environmental parameters, which affect the energy production, i.e., the solar irradiance, temperature and wind. Frequently, the large PV plants with nominal peak power higher than 1 MWp are equipped with more than one weather station, because of the large occupied area, typically about 2 ha/MWp. Obviously, these last ones are solar farms and are located in extra-urban territory. Instead, the PV plants usually installed in a urban context have a nominal peak power that ranges between 3÷50 kWp; the minimum value refers, for example, to a PV plant on the roof of a residential building, while the maximum value corresponds to a PV plant of a small company that locates it on the roof of its industrial building or in a free private area. These PV plants are usually multi-array and are not equipped with a weather station, because the costs of an advanced monitoring system are not negligible with respect to the initial investment as well as to the costs of a yearly O&M service, so these medium size PV plants are usually equipped with a simplified monitoring system, which stores the total produced energy, the electrical variables on the AC and DC side, having also the possibility to send alerts to the owner via SMS or email. This system does not perform any analysis of the produced energy, so it cannot detect any anomaly before it becomes a failure, and it can only alert when the failure is already happened. In these cases, valid support is provided by the PhotoVoltaic Geographical Information System (PVGIS) [
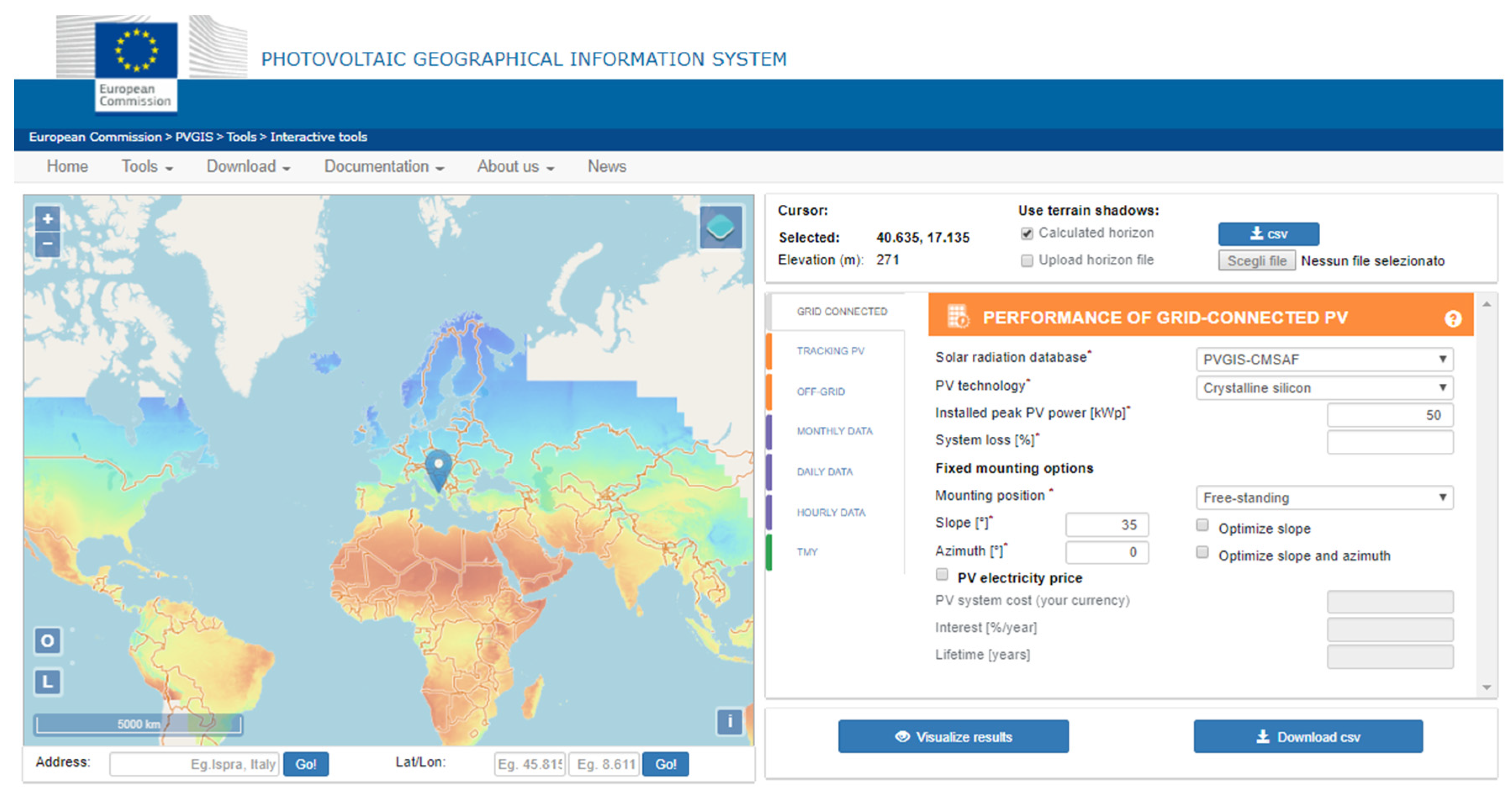
31] of the European Commission Joint Research Centre (EC-JRC) that is based on the historical data of the solar irradiance.
Figure 1 is a screenshot of the website. On the left hand-side, a colored map with the solar radiation is reported and the user can select the location of the PV plant, whereas, on the right hand-side, the user can insert the information on the typology of the PV plant (off-grid, grid-connected, tracking-based), the specifications of the PV plant (module technology, slope, rated power, etc.), and the required energy production data (monthly, daily, hourly). In this way, it is possible to estimate the productivity of the PV plant under investigation and to compare it with the real energy production. This can represent a preliminary check of the operation of the PV plant and will be used later, in the
Section 3 and
Section 4. Nevertheless, it is extremely important to prevent a failure, detecting any anomaly in a timely way for two reasons. Firstly, when an anomaly is present, the energy production is already lower than the expected one and this implies an economic loss. Secondly, a timely action of the O&M service allows restoring the damaged parts of the PV systems with minimum costs and minimum time out of order, reducing either the Mean Time To Repair (MTTR)—because the damage is limited—or the Mean Down Time (MDT), because the restore action is planned while the PV plant is still operating. This strategy, evidently, greatly increases the availability of the PV plant and its yearly energy performance.
With this in mind, this paper proposes a methodology to detect an anomaly in the operation of a PV system; this methodology can be easily applied to any multi-array PV plant, but it is particularly useful for PV plants not equipped with a weather station. This is often the situation of the PV plants in urban contexts, as previously explained. The proposed methodology, in fact, compares the energy distributions of the arrays with each other, on the basis of a statistical algorithm that does not consider the environmental parameters as inputs. This is possible because the area occupied by the PV modules of a PV plant in the urban context is limited and then the average environmental conditions can be considered to affect the identical arrays in the same way. The proposed procedure is completely based on several hypothesis tests and is a cheap and fast approach to monitor the energy performance of a PV system, because no additional hardware is required. The procedure also allows continuous monitoring because it is cumulative and new data can be added to the initial dataset, as they are acquired by the measurement system. The methodology is based on an algorithm, which suggests the user, step by step, the suitable statistical tool to use. The first one is the Hartigan’s Dip Test (HDT) that is able to discriminate an unimodal distribution from a multimodal one. The verification of the unimodality can be also done on the basis of a relationship between the values of skewness and kurtosis [
32,
33]; nevertheless, in this paper only HDT will be used, because it is usually more sensitive than other methods. The check on the unimodality is very important to decide whether a parametric test can be used to compare the energy distributions of the arrays or not, because the parametric tests, being based on known distributions, are more performing than the nonparametric ones. Nevertheless, the parametric tests can be applied, only if specific assumptions are satisfied. A powerful parametric test to compare more than two statistical distributions is the well-known ANalysis Of VAriance (ANOVA) [
34] that is based on three assumptions. The proposed algorithm suggests using the Jarque-Bera’s test and the Bartlett’s test to verify the assumptions. In the negative case, the procedure suggests to use the Kruskal-Wallis test or the Mood’s median test, in absence or in presence of outliers in the dataset, respectively. As a last step, Tukey’s test is run to do a multi-comparison one-by-one between the mean values of the distributions, in order to determine which estimates are significantly different.
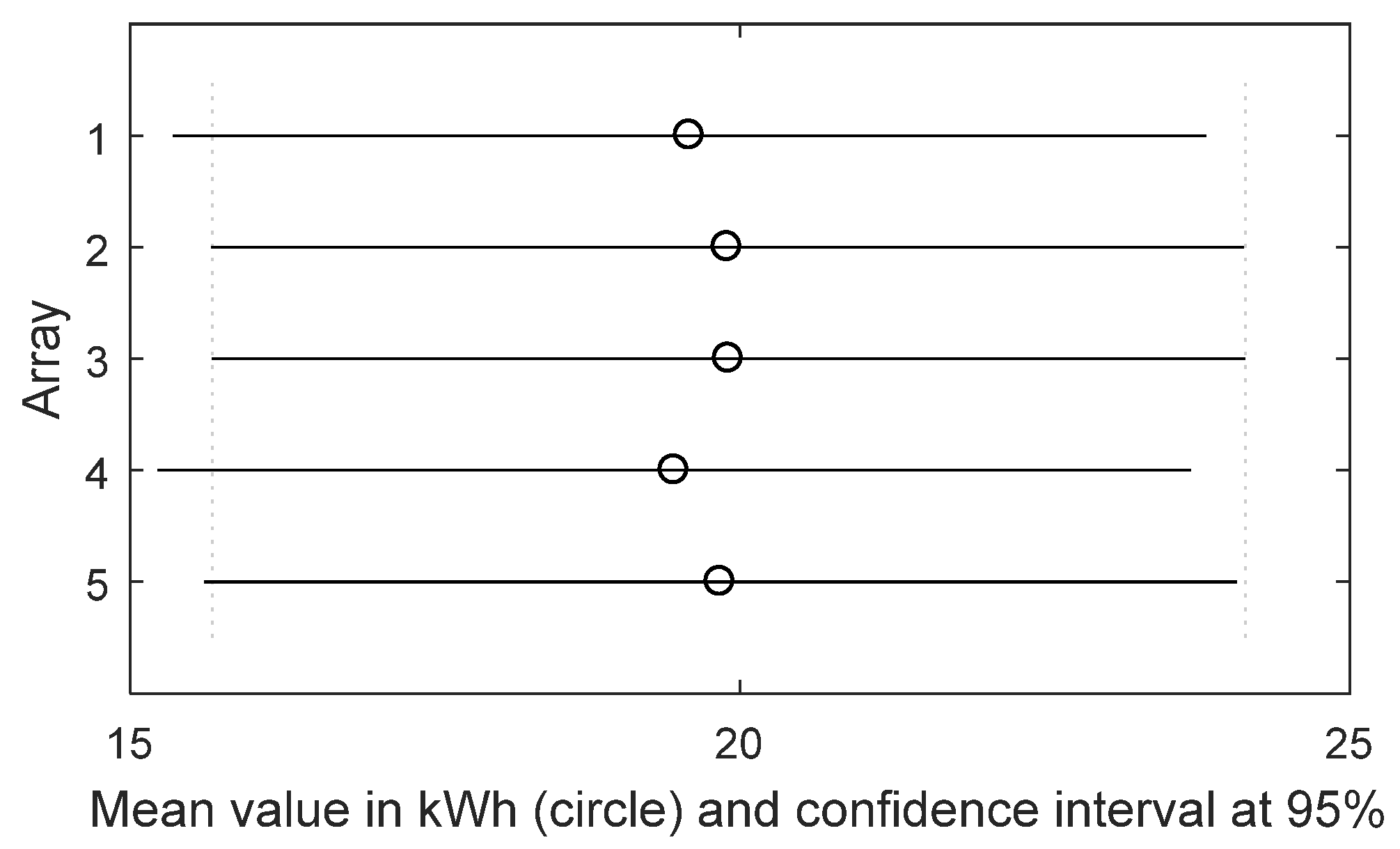
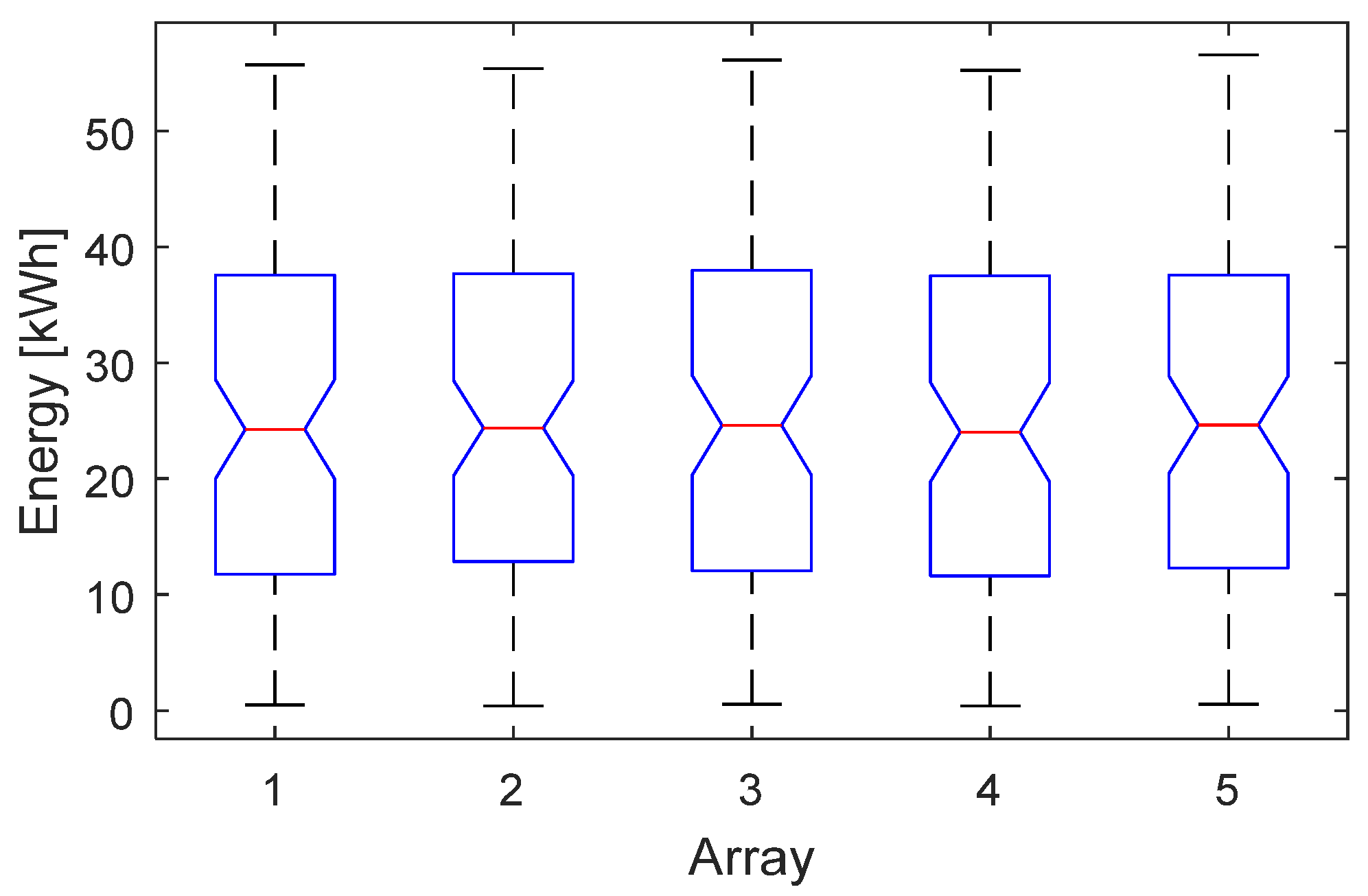
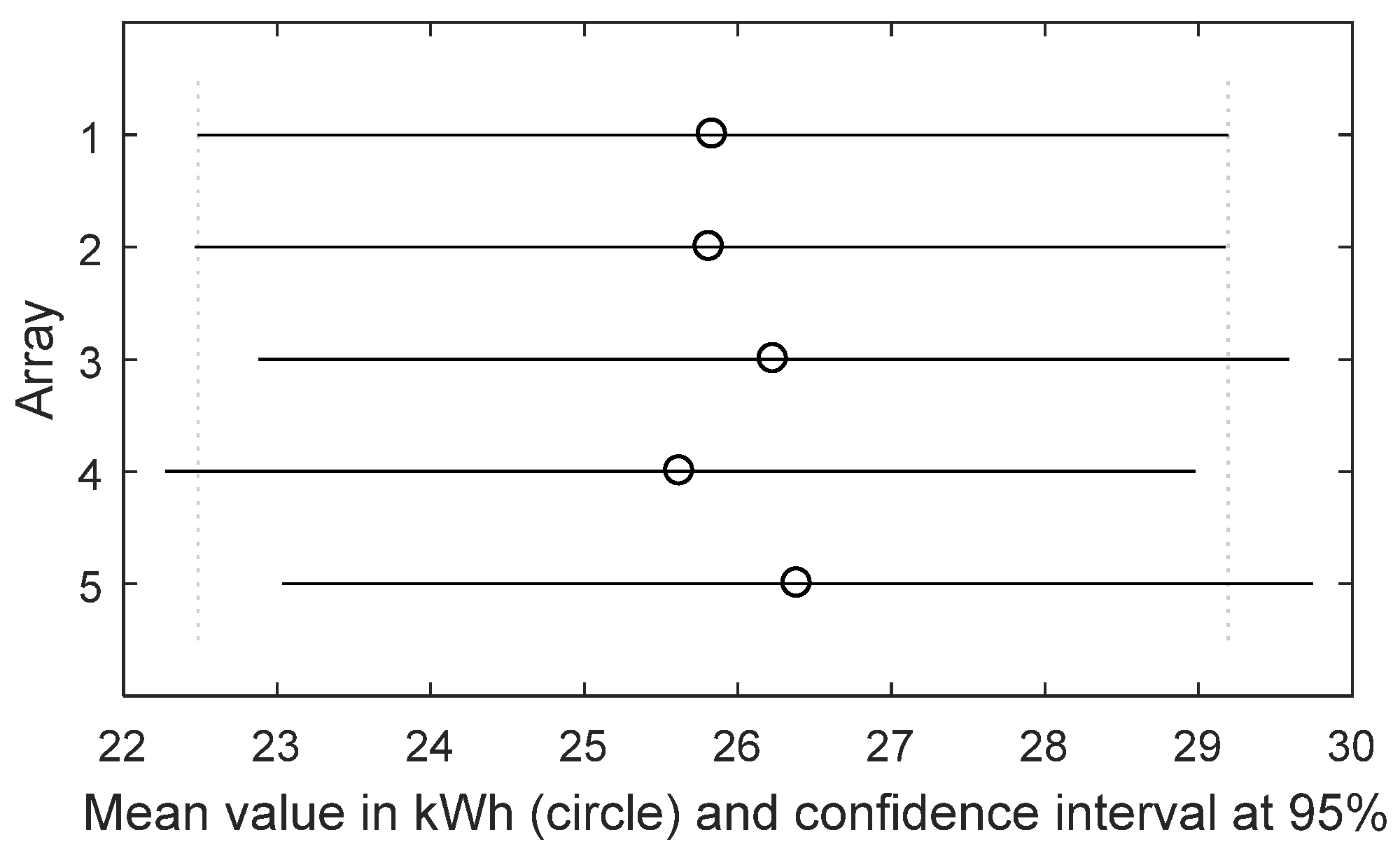
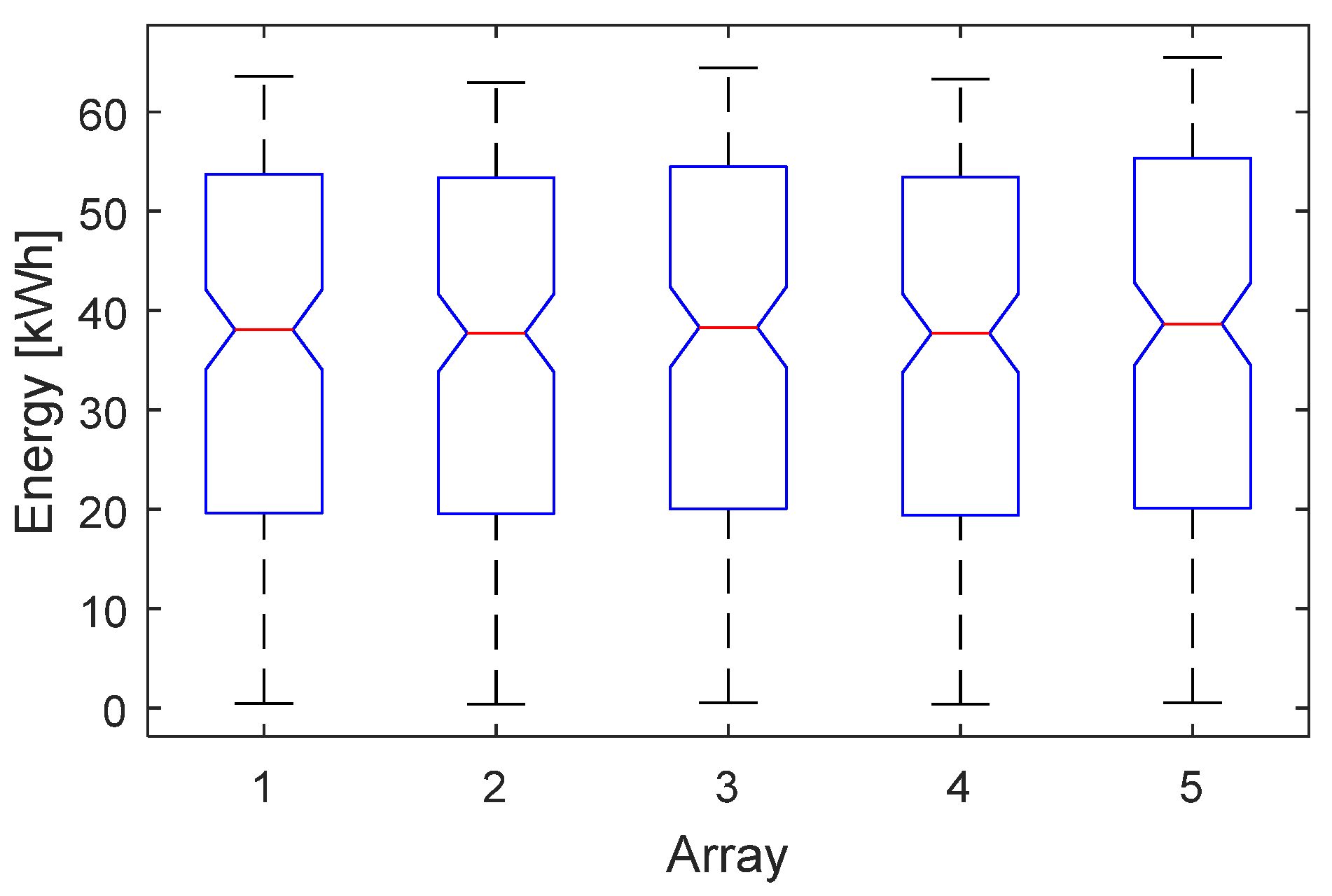
A case-study is discussed in the paper. The algorithm is applied to a real operating PV plant and the methodology is run four times: the first one, based on the energy dataset of one month; the second one, based on the energy dataset of three months; the third one, based on the energy dataset of six months; the last one, based on the energy dataset of the whole year. The paper is structured as follows:
Section 2 describes the proposed algorithm,
Section 3 describes the PV system under examination,
Section 4 discusses the results, and the Conclusions end the paper.
2. Statistical Methodology
In this paper, it is consider that the PV plant is composed of
A identical arrays, with
A > 2 for the reasons already explained in the Introduction. This constraint is mandatory for the proposed methodology, because it is based on the comparison among the energy distributions of the arrays constituting the PV system. Each array is usually equipped with a measurement system that measures the values of the produced energy in AC, other than the values of voltage and current of both the DC and AC sides of the inverter, with a fixed sampling time, ∆
t. At the generic time-instant
t =
q∆
t of the
j-th day, the
q-th sample vector of the
k-th array is defined as
, for
,
(being
D the number of the investigated days),
, where
q = 1 characterizes the first daily sample at the analysis time
and
q =
Q defines the last daily sample, acquired at the time
For our aims, let us consider only the dataset constituted by the energy values
. Thus, the proposed methodology can be applied to any PV plant, having a measurement system that measures at least the produced energy, no matter which are the other measured variables. The
k-th array, at the end of the
j-th day, has produced the energy
, therefore the complete dataset of the energy produced by the PV plant in a fixed investigated period can be represented in a matrix form:
The columns of the matrix (1) are independent each other, because the values of each array are acquired by devoted acquisition units, so no inter-dependence exists among the values of the columns, which can be considered as separate statistical distributions. The flow chart in
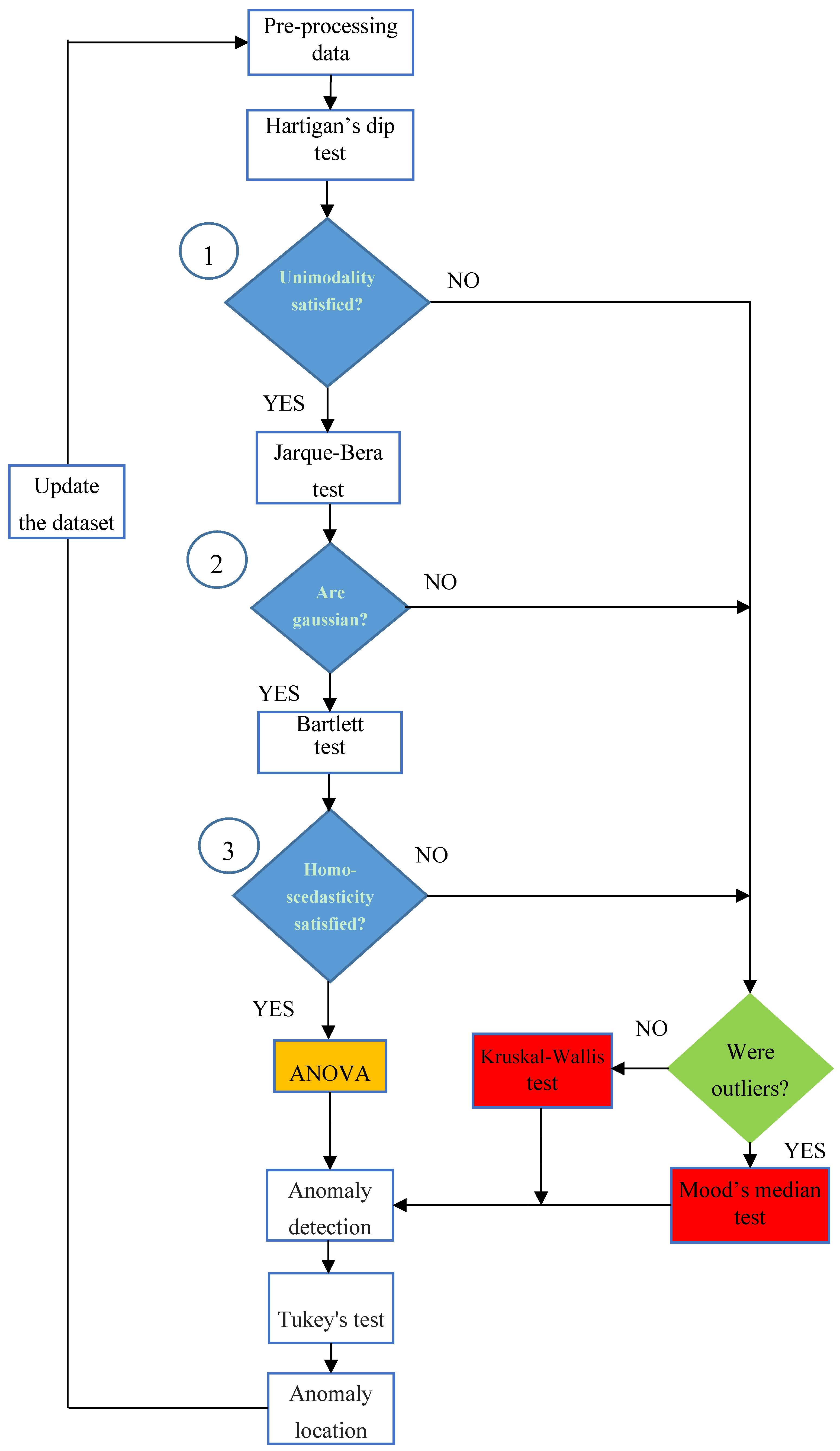
Figure 2 proposes the methodology to detect and locate any anomaly, before it becomes a fault.
It is based on the mutual comparison among the energy distributions of the arrays; therefore the environmental data are not necessary. Obviously, this approach is valid only if the arrays are identical (same PV modules, same number of modules for each array, same slope, same tilt, same inverter, and so on); in fact, under this assumption, the energy produced by any array must be almost equal to the energy produced by any other array of the same PV plant, in each period as well as in the whole year (the changing environmental conditions affect the arrays in the same way, if they are installed next to each other without any specific obstacle).
Thus, the comparative and cumulative monitoring of the energy performance of identical arrays allows one to determine, within the uncertainty defined by the value of the significance level α, if the arrays are producing the same energy or not. The first step of
Figure 2 is the pre-processing of the energy dataset collected as previously explained, in order to check if outliers are present; the information about the presence or not of the outliers will be also useful later (green block). By default, an outlier is a value that is more than three scaled Median Absolute Deviations (MAD) away from the median. For a random dataset
, the scaled MAD is defined as:
where
F is the scaling factor and is approximately 1.4826 for a normal distribution.
After the data pre-processing, it is necessary to verify if the arrays have produced the same amount of energy. This goal can be pursued by using parametric tests or non-parametric tests. As the parametric tests are based on a known distribution of the dataset, they are more reliable than the non-parametric ones, which are, instead, distribution-free. For this reason, it is advisable to use always the parametric tests, provided that all the needed assumptions are satisfied.
In particular, the parametric test known as ANOVA calculates the ratio between the variance
among the arrays’ distributions (divided by the freedom degree) and the variance
within each array distribution (divided by the freedom degree). In other words, ANOVA evaluates whether the differences of the mean values of the different groups are statistically significant or not. For this aim, ANOVA calculates the following Fisher’s statistic,
F, [
35]:
where
is the mean value of the
k-th distribution,
the global mean,
the
j-th occurrence of the
k-th distribution. The cumulative distribution function F allows to determine a
p-value, which has to be compared with the significance level α, as later explained.
ANOVA is based on the null hypothesis
H0 (Equation (4)) that the means of the distributions,
, are equal:
versus the alternative hypothesis that the mean value of at least one distribution is different from the others. The output of the ANOVA test, as any other hypothesis test, is the
p-value, which has to be compared with the pre-fixed significance value α. Usually, α = 0.05, so, if
p-value < α then the null hypothesis is rejected, considering acceptable to have a 5% probability of incorrectly rejecting the null hypothesis (this is known as type I error).
Smaller values of α are not advisable to study the data of a medium-large PV plant, because the complexity of the whole system requires a larger uncertainty to be accepted. Nevertheless, ANOVA can be used only under the following assumptions:
- (a)
all the observations are mutually independent;
- (b)
all the distributions are normally distributed;
- (c)
all the distributions have equal variance.
Finally, ANOVA can be applied also for limited violations of the assumptions (b) and (c), whereas the assumption (a) is always verified, if the measures come from independent local measurement units. So, before applying ANOVA test, several verifications are needed and they are represented by the three blue blocks of
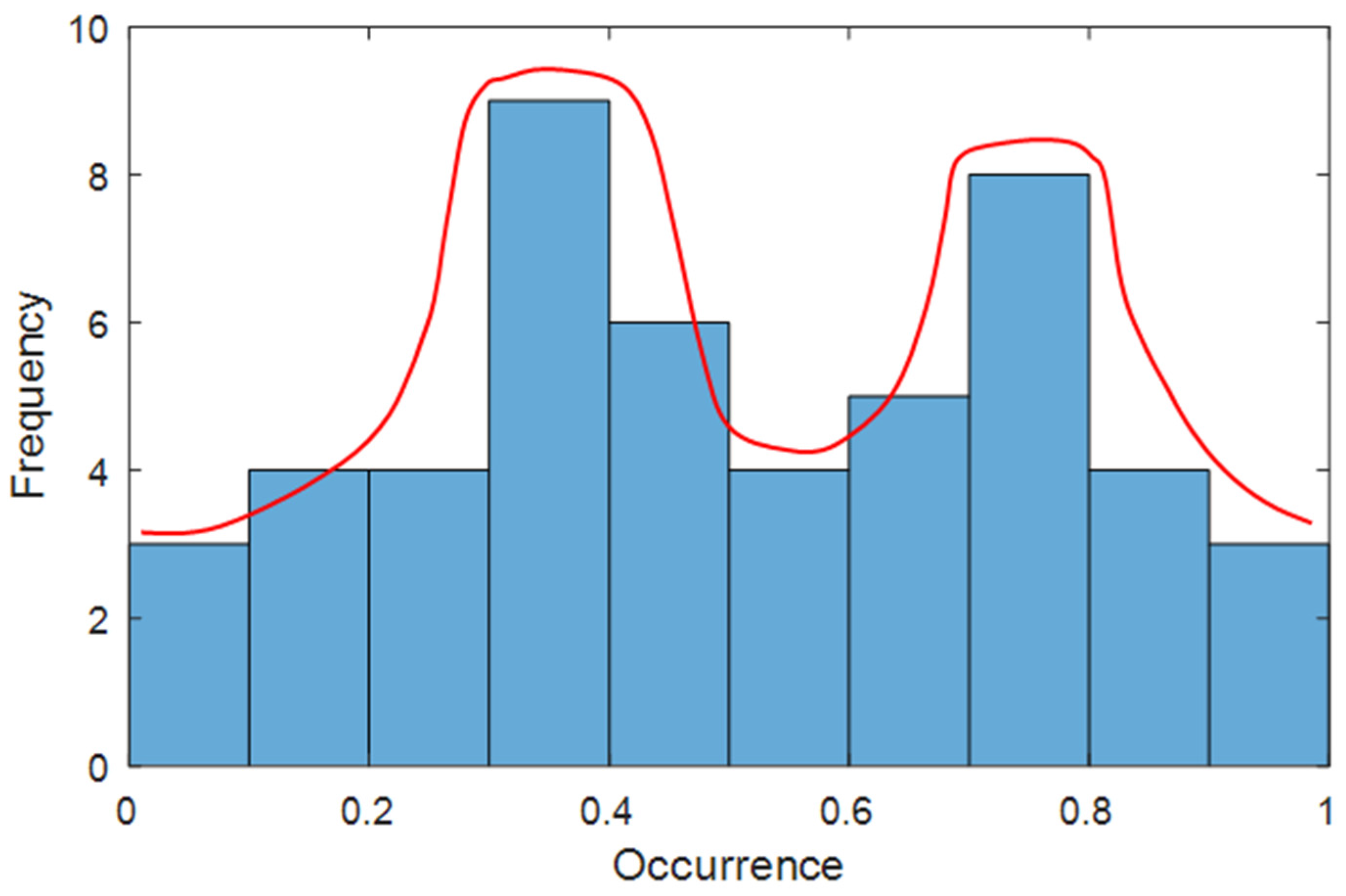
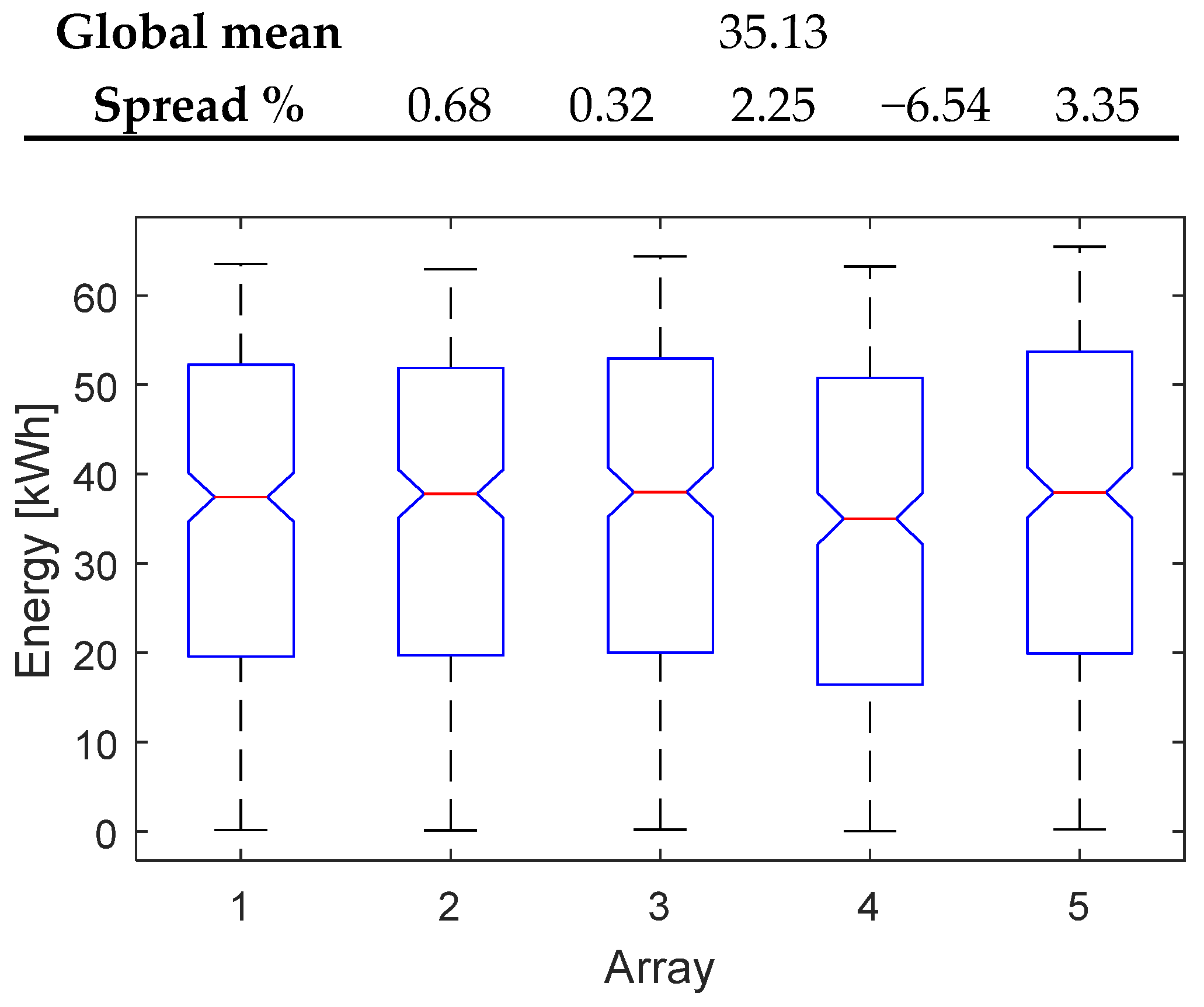
Figure 2. The first check (blue block 1) regards the unimodality of the dataset of each array, because a multimodality distribution, e.g., the bimodal distribution in
Figure 3, is surely not Gaussian and violates the condition (b). Moreover, the daily-based energy distribution of an array of a well-working PV system is unimodal, because the daily solar radiation has the typical Gaussian waveform, which is unimodal; therefore, the multimodality of a daily-based energy distribution is a clear alert of a high-intensity anomaly. The Hartigan’s Dip Test (HDT) is able to check the unimodality [
36] and is based on the null hypothesis that the distribution is unimodal versus the alternative one that it is at least bi-modal. The HDT is a non-parametric test, so it is distribution-free. HDT return a
p-value
HDT. By fixing the significance value α = 0.05, if
p-value
HDT < α is satisfied, the null hypothesis of the unimodality is rejected, the distribution is surely not Gaussian, ANOVA cannot be applied and a nonparametric test has to be used.
In the general case of
A arrays, with
A > 2, the nonparametric test has to be chosen between Kruskal-Wallis test (K-W) [
37,
38] and Mood’s Median test (MM), under the constraint of the green block; both K-W and MM do not require that the distributions are Gaussian, but only that the distributions are continuous.
In the presence of outliers (detected, if present, in the first block), MM performs better than K-W, otherwise K-W is a good choice. Both K-W and MM are based on the null hypothesis that the median values of all the distributions are equal versus the alternative one that at least one distribution has a median value different from the others. As K-W as MM returns a p-valueK-W(MM) that has to be compared with the significance value α = 0.05. If p-valueK-W(MM) < α is satisfied, the null hypothesis is rejected and the arrays have not produced the same energy; otherwise, they have. Instead, if the unimodality is satisfied, other checks are needed, before deciding whether ANOVA can be applied. In fact, it is needed to verify the previous assumptions (b) and (c). Only if both of them are satisfied (blue blocks 2 and 3, respectively), ANOVA can be applied.
To check the condition (b), an effective statistical tool is the Jarque-Bera’s Test (JBT). The JBT is distribution-free and based on independent random variable. It is a hypothesis test, whose null hypothesis is that the distribution is gaussian. Then, it calculates a statistical parameter, called JB, and returns a
p-value
JBT. By fixing the significance value α = 0.05, if
p-value
JBT < α is satisfied, the null hypothesis is rejected and the distribution is not gaussian, otherwise it is. It results:
Being
D the sample size,
the skewness and
the Pearson’s kurtosis less 3 (also known as excess kurtosis). The skewness is defined as:
Being D the sample size, the mean value, and the variance. The skewness is the third standardized moment and measures the asymmetry of the data around the mean value. Only for the distribution is symmetric; this is a necessary but not sufficient condition for a gaussian distribution. In fact, while the Gaussian distribution is surely symmetric, nevertheless there exist also symmetric but not gaussian distributions.
The excess kurtosis, instead, is defined as:
with the previous meaning of the parameters. The kurtosis is the fourth standardized moment and measures the tailedness of the distribution. Only for
, the distribution is mesokurtic, which is the necessary but not sufficient condition for a Gaussian distribution. If the check of the blue block 2 is not passed, a non-parametric test (K-W or MM) has to be used, in accordance with the green block. Instead, if this verification is passed, it needs to test the assumption (c) of ANOVA, i.e., the homoscedasticity (blue block 3). This assumption can be verified by means of the Bartlett’s Test (BT), which is again a hypothesis test that returns a
p-value
BT. The BT is effective for Gaussian distributions; in fact, in the flow-chart of
Figure 2 it is used only if the distributions are Gaussian. Also in this case, it is possible to fix the common significance value α = 0.05 and to compare it with the
p-value
BT. If the inequality
p-value
JBT < α is satisfied, the null hypothesis is rejected and the variances of the distributions of the arrays are different, then the condition (c) is violated, and ANOVA cannot be applied. In this case, it is necessary to use K-W or MM, in accordance with the green block. Otherwise, ANOVA can be applied and it return another
p-value
AN that must be compared with the significance level α = 0.05. If the inequality
p-value
AN < α = 0.05 is satisfied, then the null hypothesis (
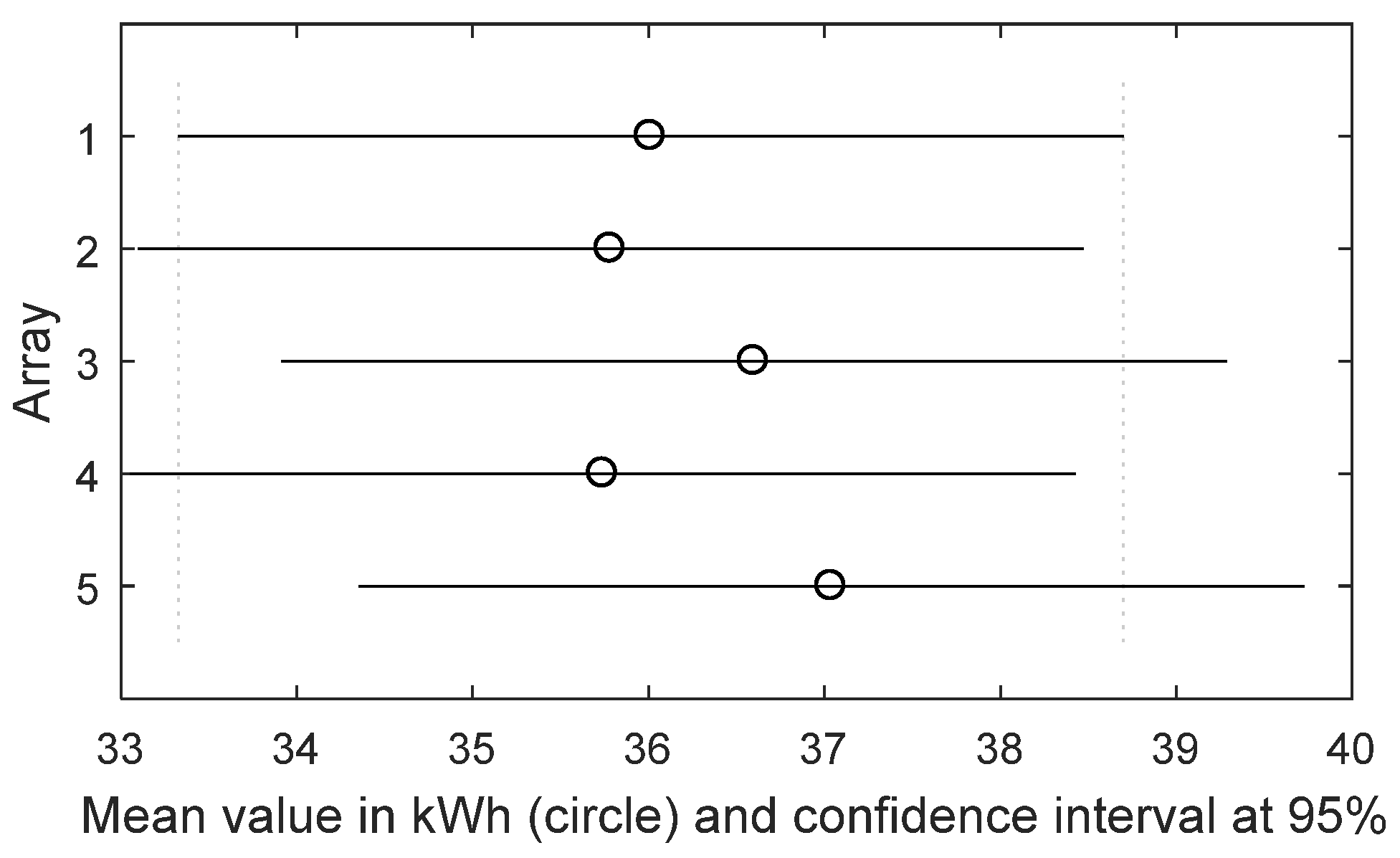
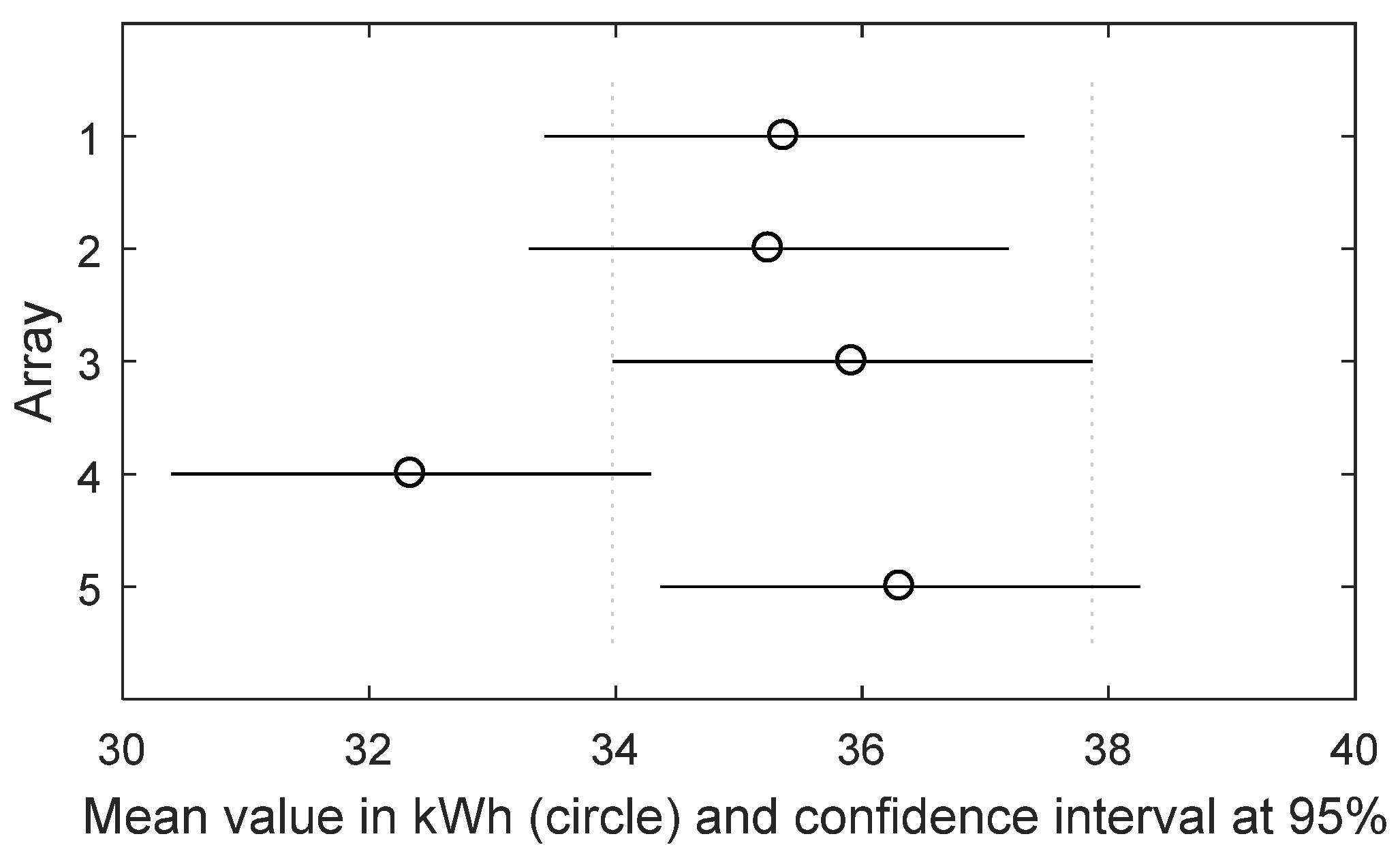
) is rejected and the conclusion is that the identical arrays have not produced the same amount of energy; so, a low-intensity anomaly is present and it is located in the array that has the mean value different from the other ones. To detect it, a multi-comparison analysis—one-to-one—between the distributions is done by means of the Tukey’s Test (TT), which is a modified version of the well-known
t-test and returns a
p-value
TT, which states whether the means between two distributions are equal or not. For a small sample size (about 20 samples) the TT is reliable only for normal distribution, instead, for a lager sample size it is valid also for not normal distributions, because of the central limit theorem. Otherwise, no criticality is present and the dataset can be updated with new data to continue the monitoring of the PV plant. As the energy dataset increases, the monitoring becomes more accurate.