Determining the U-Value of Façades Using the Thermometric Method: Potentials and Limitations
Abstract
1. Introduction
2. Theory
- Mounting the interior and exterior environmental temperature probes 30 cm away from the wall as well as at the same height as the internal surface temperature probes.
- No direct solar radiation.
- Measurements should be carried out during the night.
3. Quality Control, Data Post-Processing, and Uncertainty Quantification of the Method
3.1. Test Conditions
- For at least 24 h before starting the test, the external air temperature must not vary more than ±10 °C from the existing temperature at the moment of starting the inspection.
- During the inspection, the outdoor air temperature must not vary more than ±5 °C and the indoor air temperature should vary no more than ±2 °C with respect to their initial values.
- Taking an infrared thermal image should be avoided in these three cases: when it is detected that the wall surface is not dry, if it is raining at the moment of performing the test, or if the wind speed is higher than 8 m/s.
3.2. Selecting and Installing the Equipment
- Thermocouples measuring the internal surface temperature should be mounted with a space of 10 cm between them, as well as 20 mm away from the mortar joints of the pieces of brick of the internal side of the wall [31,37] at a height of 1.5 m above the floor [19]. The test described in ISO 6781 may be useful to determine the position of the mortar joints. According to the indications of Meng et al. [37], when the mortar joints cannot be determined, probes must be mounted without being vertically or horizontally aligned. A fixed mastic can also be used to achieve good contact with the wall [31]. In addition, it is important to avoid mounting the sensors in the corners, since the temperature is usually higher there than in the rest of the wall [23].
- Moreover, the internal and external air temperature sensors should be placed as horizontally aligned as possible, at a distance of 30 cm from the wall in order to avoid convective effects [31].
- In the case of those devices which directly measure air temperature, they should be placed at a distance of 30 cm from the internal side of the wall to prevent being affected by convective effects, with a height difference of 20 cm from the rest of the probes to avoid significant differences in temperature measurement.
- The weather station should be installed as near as possible to the wall under study, avoiding its installation towards other orientations.
3.3. Data Acquisition and Post-Processing
3.4. Estimating the Uncertainty
4. Experimental Campaign
5. Analysis and Results
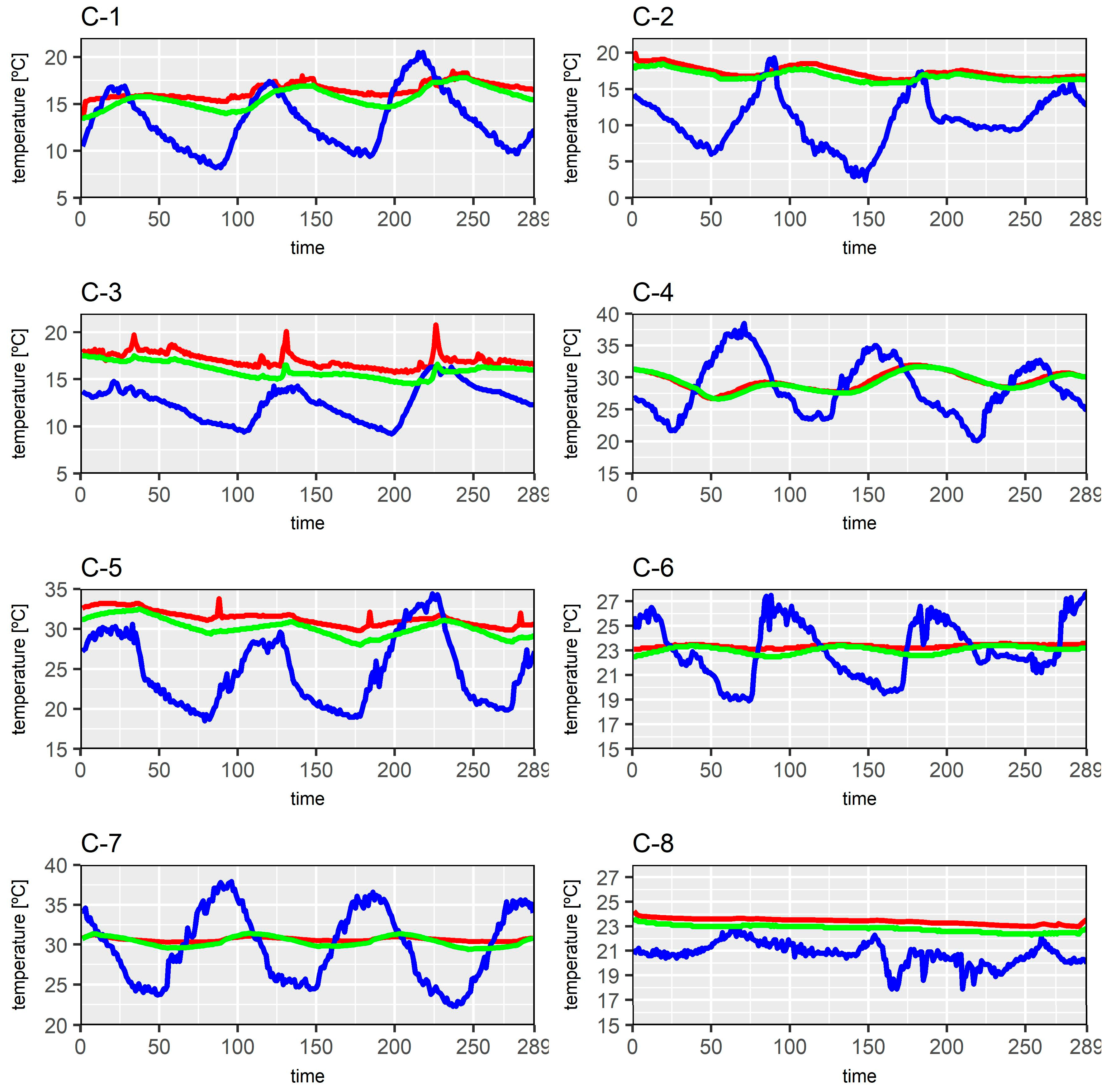
- As can be observed, there were difficulties in the case studies (except in C-2 and C-5) to find observations with a difference higher than 10 °C between indoor and outdoor air temperatures. Also, in the case studies carried out during winter (C-1 and C-3), the largest temperature difference between the outdoor and the indoor air temperature was 7.2 °C, with values of the maximum temperature reaching up to 20.5 °C, which are records more commonly found in spring than in winter. For C-6 and C-8, there were few instances of a temperature difference registered higher than 5 °C.
- In most case studies, the value of the indoor air temperature was constant but with slight variations.
- In C-2 and C-4, the external temperature sensor of data logger B, connected by radio, stopped emitting a signal shortly after the beginning of the test, so data could not be obtained from this equipment.
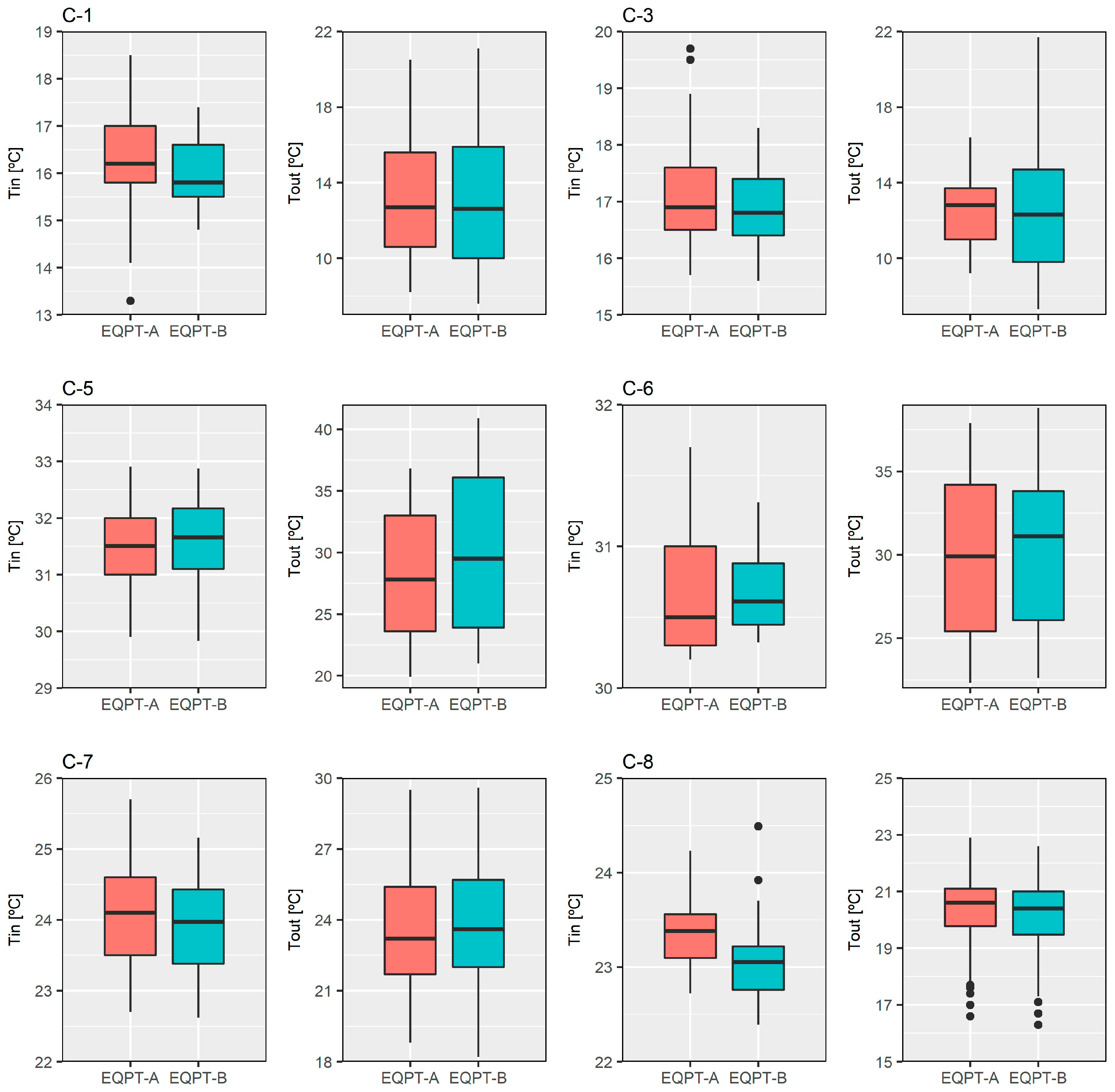
- Regarding the difference between the measures recorded by both data loggers, meaningful variations in the measurement of the internal surface temperature were not detected, with average deviations of ±0.1 °C. However, there were significant differences between the indoor and outdoor air temperatures (see Figure 5).
- During the performance of the tests, no rainfall occurred and the wind speed was always lower than 1 m/s.
6. Conclusions
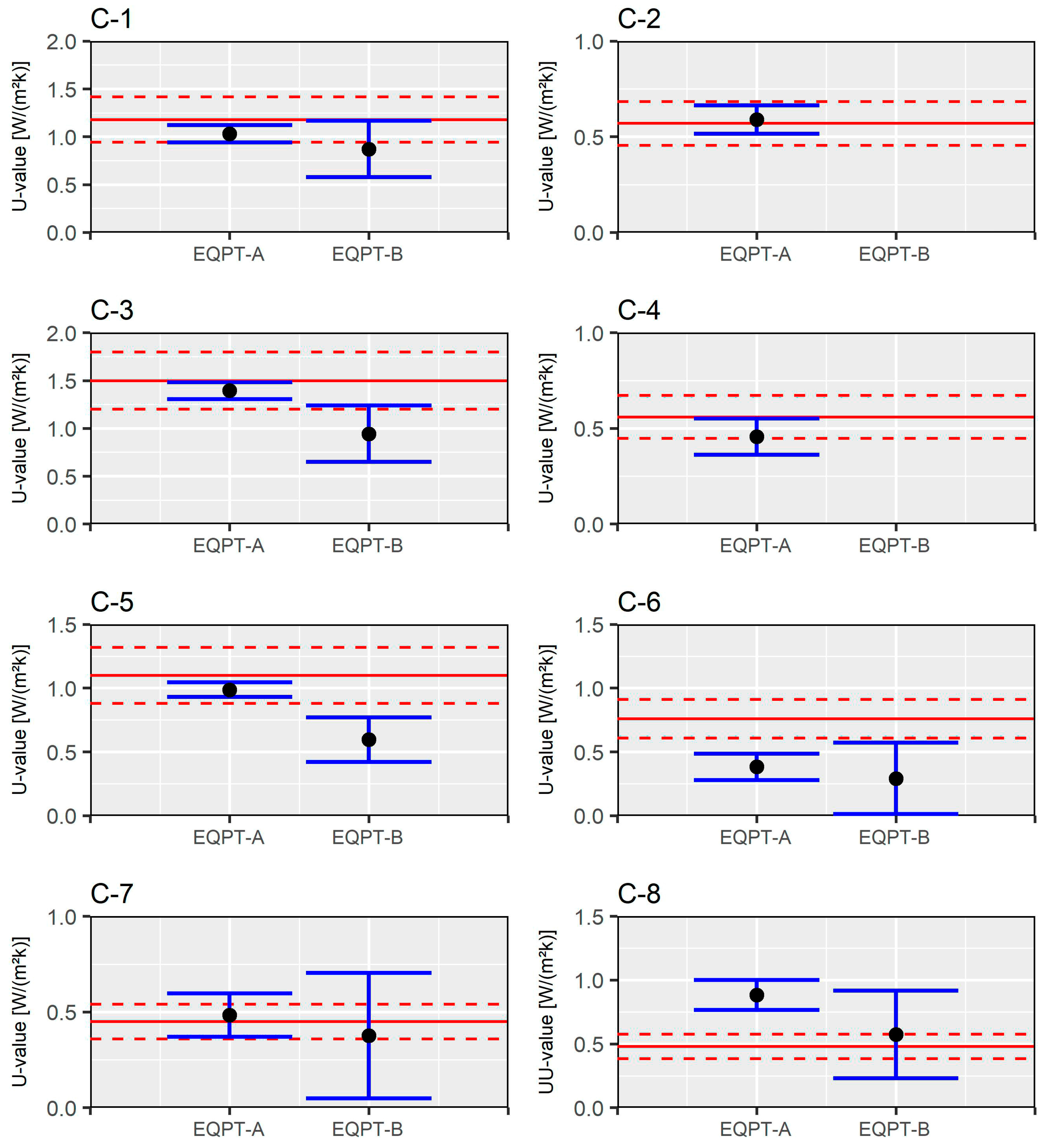
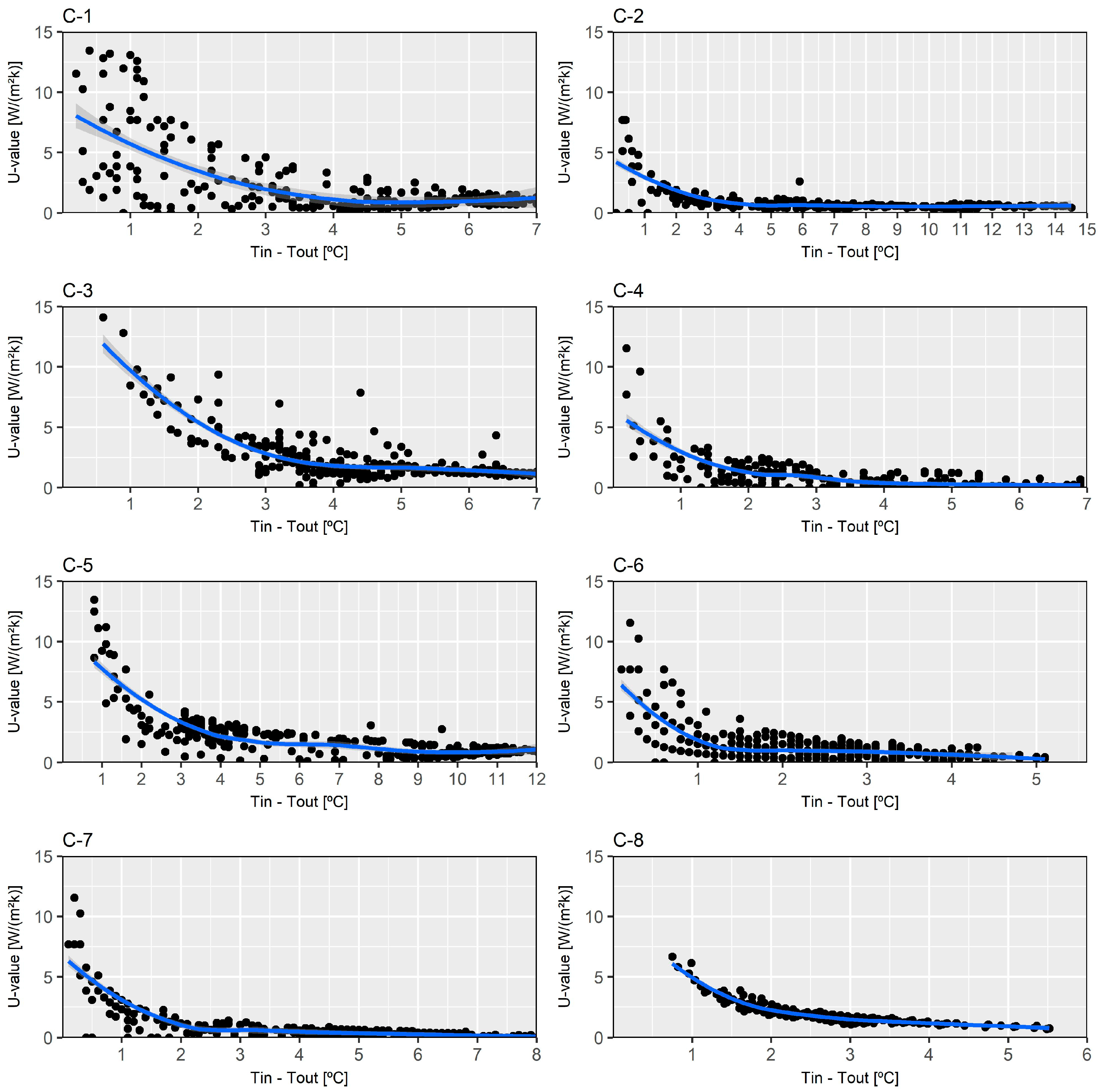
- THM shows a more optimal behaviour in winter than in summer, with relative uncertainties between 6% and 13%.
- With respect to the environmental conditions in summer and autumn, despite obtaining average values with a difference lower than 20% regarding the estimated value of thermal transmittance, the associated uncertainty for the tests is unacceptable. Only in C-5 was an optimal value acquired, as temperature records with a difference higher than 10 °C were obtained.
- Differences in the average values as well as uncertainty according to the technical characteristics of the employed equipment were revealed. In this sense, the data logger which has probes with better features used for the tests obtained acceptable average results as well as adequate levels of uncertainty. However, the same cannot be said for the other equipment setup, because there were differences in the distribution of the measured temperature values.
- The typical characteristics of the Mediterranean climate (class Csa according to Köppen and Geiger’s climate classification) notably causes some difficulties in obtaining records with a temperature difference higher than 10 °C between the interior and exterior environments. In this regard, the results show that measurements with a high number of observations with a temperature difference higher than 5 °C were able to obtain representative results. Therefore, a thermal gradient of 5 °C can be considered for tests which are carried out in warm climate regions, although a higher difference would guarantee a decrease in the uncertainty and the achievement of more representative values.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Tin | Internal air temperature (K) |
| Tout | External air temperature (K) |
| Ts,in | Internal surface temperature (K) |
| hin | Internal convective heat transfer coefficient (W/(m2·K)) |
| q | Heat flux (W/m2) |
| s | Thickness (m) |
| λ | Thermal conductivity (W/(m·K)) |
| R | Thermal resistance ((m2·K)/W) |
| Rs,in | Internal surface thermal resistance ((m2·K)/W) |
| Rs,out | External surface thermal resistance ((m2·K)/W) |
| U | Thermal transmittance (W/(m2·K)) |
| CCF | Conductivity correction factor (dimensionless) |
References
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- European Environment Agency. Final Energy Consumption by Sector and Fuel (2017); European Environment Agency: Copenhagen, Denmark, 2017. [Google Scholar]
- European Academy of Bolzano. European Project iNSPiRe Report; European Academy of Bolzano: Bolzano, Italy, 2015. [Google Scholar]
- Andalusian Energy Agency. Energy Data of Andalusia; Andalusian Energy Agency: Seville, Spain, 2015.
- Ecology and Development Foundation (ECODES). Archive ECODES. City and Building: Environmental Impacts; Ecology and Development Foundation: Bend, Oregon, 2009. [Google Scholar]
- Institute for the Energy Diversification and Saving. Balance of the Final Energy Consumption in Year 2015; Institute for the Energy Diversification and Saving: Seville, Spain, 2016. (In Spain) [Google Scholar]
- Sánchez-García, D.; Sánchez-Guevara, C.; Rubio-Bellido, C. The adaptive approach to thermal comfort in Seville. An. Edif. 2016, 2, 38–48. [Google Scholar] [CrossRef]
- Gangolells, M.; Casals, M.; Forcada, N.; MacArulla, M.; Cuerva, E. Energy mapping of existing building stock in Spain. J. Clean. Prod. 2016, 112, 3895–3904. [Google Scholar] [CrossRef]
- Kurtz, F.; Monzón, M.; López-Mesa, B. Energy and acoustics related obsolescence of social housing of Spain’s post-war in less favoured urban areas. The case of Zaragoza. Inf. Constr. 2015, 67, m021. [Google Scholar] [CrossRef]
- The Government of Spain. Royal Decree 314/2006. Approving the Spanish Technical Building Code CTE-DB-HE-1; The Government of Spain: Madrid, Spain, 2013.
- Moyano Campos, J.J.; Antón García, D.; Rico Delgado, F.; Marín García, D. Threshold Values for Energy Loss in Building Façades Using Infrared Thermography. In Sustainable Development and Renovation in Architecture, Urbanism and Engineering; Springer International Publishing: Basel, Switzerland, 2017; pp. 427–437. [Google Scholar]
- Mortarotti, G.; Morganti, M.; Cecere, C. Thermal analysis and energy-efficient solutions to preserve listed building façades: The INA-Casa building heritage. Buildings 2017, 7, 56. [Google Scholar] [CrossRef]
- Park, K.; Kim, M. Energy Demand Reduction in the Residential Building Sector: A Case Study of Korea. Energies 2017, 10, 1506. [Google Scholar] [CrossRef]
- Battista, G.; Evangelisti, L.; Guattari, C.; Basilicata, C.; de Lieto Vollaro, R. Buildings Energy Efficiency: Interventions Analysis under a Smart Cities Approach. Sustainability 2014, 6, 4694–4705. [Google Scholar] [CrossRef]
- Suárez, R.; Fragoso, J. Passive strategies for energy optimisation of social housing in the Mediterranean climate. Inf. Constr. 2016, 68, e136. [Google Scholar] [CrossRef]
- Serrano Lanzarote, B.; Sanchis Cuesta, A. The Technical Inspection of Buildings as an instrument for the energy improvement of existing buildings. Inf. Constr. 2015, 67, nt003. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 6946:2007—Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Method; International Organization for Standardization: Geneva, Switzerland, 2007. [Google Scholar]
- International Organization for Standardization. ISO 9869-1:2014—Thermal Insulation—Building Elements—In Situ Measurement of Thermal Resistance and Thermal Transmittance. Part 1: Heat Flow Meter Method; International Organization for Standardization: Geneva, Switzerland, 2014. [Google Scholar]
- Albatici, R.; Tonelli, A.M. Infrared thermovision technique for the assessment of thermal transmittance value of opaque building elements on site. Energy Build. 2010, 42, 2177–2183. [Google Scholar] [CrossRef]
- Madding, R. Finding R-values of stud-frame constructed houses with IR thermography. Proc. InfraMation 2008, 2008, 261–277. [Google Scholar]
- Dall’O, G.; Sarto, L.; Panza, A. Infrared screening of residential buildings for energy audit purposes: Results of a field test. Energies 2013, 6, 3859–3878. [Google Scholar] [CrossRef]
- Fokaides, P.A.; Kalogirou, S.A. Application of infrared thermography for the determination of the overall heat transfer coefficient (U-Value) in building envelopes. Appl. Energy 2011, 88, 4358–4365. [Google Scholar] [CrossRef]
- Tejedor, B.; Casals, M.; Gangolells, M.; Roca, X. Quantitative internal infrared thermography for determining in-situ thermal behaviour of façades. Energy Build. 2017, 151, 187–197. [Google Scholar] [CrossRef]
- Evangelisti, L.; Guattari, C.; Gori, P.; De Lieto Vollaro, R. In situ thermal transmittance measurements for investigating differences between wall models and actual building performance. Sustainability 2015, 7, 10388–10398. [Google Scholar] [CrossRef]
- Ficco, G.; Iannetta, F.; Ianniello, E.; D’Ambrosio Alfano, F.R.; Dell’Isola, M. U-value in situ measurement for energy diagnosis of existing buildings. Energy Build. 2015, 104, 108–121. [Google Scholar] [CrossRef]
- Choi, D.S.; Ko, M.J. Comparison of Various Analysis Methods Based on Heat Flowmeters and Infrared Thermography Measurements for the Evaluation of the In Situ Thermal Transmittance of Opaque Exterior Walls. Energies 2017, 10, 1019. [Google Scholar] [CrossRef]
- Nardi, I.; Paoletti, D.; Ambrosini, D.; De Rubeis, T.; Sfarra, S. U-value assessment by infrared thermography: A comparison of different calculation methods in a Guarded Hot Box. Energy Build. 2016, 122, 211–221. [Google Scholar] [CrossRef]
- Regional Government of Andalusia. Catalog of Services Offered by Quality Control Laboratories of the Regional Government of Andalusia—January 2017; Regional Government of Andalusia: Sevilla, Spain, 2017.
- The Government of Spain. 5th Registry, Entities and Quality Control Laboratories of Building; Ther Government of Spain: Madrid, Spain, 2017.
- KIMO Instruments. Determination of U Coefficient; KIMO Instruments: Montpon-Menesterol, France, 2010. [Google Scholar]
- Testo AG. U-Value Measurement; Testo AG: Lenzkirch, Germany, 2014. [Google Scholar]
- Trethowen, H. Measurement errors with surface-mounted heat flux sensors. Build. Environ. 1986, 21, 41–56. [Google Scholar] [CrossRef]
- Desogus, G.; Mura, S.; Ricciu, R. Comparing different approaches to in situ measurement of building components thermal resistance. Energy Build. 2011, 43, 2613–2620. [Google Scholar] [CrossRef]
- Cesaratto, P.G.; De Carli, M.; Marinetti, S. Effect of different parameters on the in situ thermal conductance evaluation. Energy Build. 2011, 43, 1792–1801. [Google Scholar] [CrossRef]
- Peng, C.; Wu, Z. In situ measuring and evaluating the thermal resistance of building construction. Energy Build. 2008, 40, 2076–2082. [Google Scholar] [CrossRef]
- Cucumo, M.; De Rosa, A.; Ferraro, V.; Kaliakatsos, D.; Marinelli, V. A method for the experimental evaluation in situ of the wall conductance. Energy Build. 2006, 38, 238–244. [Google Scholar] [CrossRef]
- Meng, X.; Yan, B.; Gao, Y.; Wang, J.; Zhang, W.; Long, E. Factors affecting the in situ measurement accuracy of the wall heat transfer coefficient using the heat flow meter method. Energy Build. 2015, 86, 754–765. [Google Scholar] [CrossRef]
- Pérez-Bella, J.M.; Domínguez-Hernández, J.; Cano-Suñén, E.; Del Coz-Díaz, J.J.; Álvarez Rabanal, F.P. A correction factor to approximate the design thermal conductivity of building materials. Application to Spanish façades. Energy Build. 2015, 88, 153–164. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 6781:1983—Thermal Insulation—Qualitative Detection of Thermal Irregularities in Building Envelopes—Infrared Method; International Organization for Standardization: Geneva, Switzerland, 1983. [Google Scholar]
- International Electrotechnical Commission. IEC 60584-1:2013—Thermocouples—Part 1: EMF Specifications and Tolerances; International Electrotechnical Commission: Geneva, Switzerland, 2013. [Google Scholar]
- Meng, X.; Gao, Y.; Wang, Y.; Yan, B.; Zhang, W.; Long, E. Feasibility experiment on the simple hot box-heat flow meter method and the optimization based on simulation reproduction. Appl. Therm. Eng. 2015, 83, 48–56. [Google Scholar] [CrossRef]
- Ihaka, R.; Gentleman, R. R: A Language for Data Analysis and Graphics. J. Comput. Graph. Stat. 1996, 5, 299–314. [Google Scholar]
- Eduardo Torroja Institute for Construction Science. Constructive Elements Catalogue of the CTE; Eduardo Torroja Institute for Construction Science: Madrid, Spain, 2010. [Google Scholar]
- International Organization for Standardization. ISO 10456:2007—Building Materials and Products—Hygrothermal Properties—Tabulated Design Values and Procedures for Determining Declared and Design Thermal Values; International Organization for Standardization: Geneva, Switzerland, 2007. [Google Scholar]
- International Organization for Standardization. ISO/IEC Guide 98-3:2008—Uncertainty of Measurement—Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995); International Organization for Standardization: Geneva, Switzerland, 2008. [Google Scholar]
- Rubel, F.; Kottek, M. Observed and projected climate shifts 1901–2100 depicted by world maps of the Köppen-Geiger climate classification. Meteorol. Z. 2010, 19, 135–141. [Google Scholar] [CrossRef]


| Type | Description | Estimation |
|---|---|---|
| Measurement equipment and procedure | Thermocouples in poor contact with the surface | 1–5% a |
| Non-uniformity of temperature due to heterogeneities in the wall or impacts of internal/external radiation | 1–5% b | |
| Installation of thermocouples near to the mortar joints of the pieces of brick of the internal side of the wall | 2–6% c | |
| Thermocouple linearity and sensitivity | 0.1–0.2 °C b | |
| A/D converter resolution and data transmission | 1–2% b | |
| Environment | Temperature instability due to environmental climatic variations | 3–10% a |
| Influence of external and internal radiation from the sun or lighting equipment | 1–2% b | |
| Influence of high speed wind | 1–2% | |
| Influence of moisture in measurements (i.e., moisture condensation) | 1–2% b |
| # | Component C-1 | s (mm) | λ (W/(m·K)) a | R ((m2·K)/W) | Sketch |
| 1 | Cement mortar | 15 | 1.30 | - | 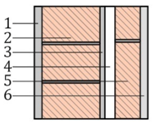 |
| 2 | Perforated brick | 115 | 0.35 | - | |
| 3 | Cement mortar | 10 | 1.30 | - | |
| 4 | Air gap | 20 | - | 0.17 c | |
| 5 | Hollow brick | 50 | 0.32 | - | |
| 6 | Gypsum plaster | 15 | 0.57 | - | |
| = 0.13 (m2·K)/W b | = 0.04 (m2·K)/W b | = 1.0385 d | |||
| # | Component C-2 | s (mm) | λ (W/(m·K)) a | R ((m2·K)/W) | Sketch |
| 1 | Cement mortar | 15 | 1.30 | - | 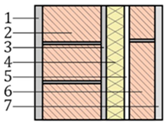 |
| 2 | Perforated brick | 115 | 0.35 | - | |
| 3 | Cement mortar | 10 | 1.30 | - | |
| 4 | Extruded polystyrene (XPS) insulation | 35 | 0.036 | - | |
| 5 | Air gap | 10 | - | 0.15 c | |
| 6 | Hollow brick | 50 | 0.32 | - | |
| 7 | Gypsum plaster | 15 | 0.57 | - | |
| = 0.13 (m2·K)/W b | = 0.04 (m2·K)/W b | = 1.0385 d | |||
| # | Component C-3 | s (mm) | λ (W/(m·K)) a | R ((m2·K)/W) | Sketch |
| 1 | Cement mortar | 15 | 1.30 | - | 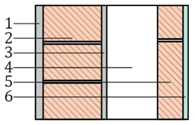 |
| 2 | Solid brick | 115 | 0.85 | - | |
| 3 | Cement mortar | 10 | 1.30 | - | |
| 4 | Air gap | 100 | - | 0.18 c | |
| 5 | Hollow brick | 50 | 0.32 | - | |
| 6 | Cement mortar | 15 | 1.30 | - | |
| 7 | Ceramic tiles | 10 | 1.30 | - | |
| = 0.13 (m2·K)/W b | = 0.04 (m2·K)/W b | = 1.0385 d | |||
| # | Component C-4 | s (mm) | λ (W/(m·K)) a | R ((m2·K)/W) | Sketch |
| 1 | Perforated brick | 115 | 0.35 | - | 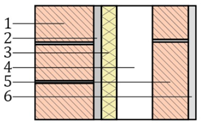 |
| 2 | Cement mortar | 15 | 1.30 | - | |
| 3 | Extruded polystyrene (XPS) insulation | 30 | 0.036 | - | |
| 4 | Air gap | 70 | - | 0.18 c | |
| 5 | Hollow brick | 70 | 0.32 | - | |
| 6 | Gypsum plaster | 15 | 0.57 | - | |
| = 0.13 (m2·K)/W b | = 0.04 (m2·K)/W b | = 1.0385 d | |||
| # | Component C-5 | s (mm) | λ (W/(m·K)) a | R ((m2·K)/W) | Sketch |
| 1 | Perforated brick | 115 | 0.35 | - | 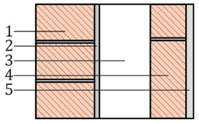 |
| 2 | Cement mortar | 10 | 1.30 | - | |
| 3 | Air gap | 100 | - | 0.18 c | |
| 4 | Hollow brick | 70 | 0.32 | - | |
| 5 | Gypsum plaster | 15 | 0.57 | - | |
| =0.13 (m2·K)/W b | =0.04 (m2·K)/W b | = 1.0385 d | |||
| # | Component C-6 | s (mm) | λ (W/(m·K)) a | R ((m2·K)/W) | Sketch |
| 1 | Cement mortar | 20 | 1.30 | - | 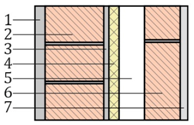 |
| 2 | Perforated brick | 115 | 0.35 | - | |
| 3 | Cement mortar | 10 | 1.30 | - | |
| 4 | Mineral wool (MW) insulation | 20 | 0.05 | - | |
| 5 | Air gap | 50 | - | 0.18 c | |
| 6 | Hollow brick | 70 | 0.32 | - | |
| 7 | Gypsum plaster | 15 | 0.57 | - | |
| = 0.13 (m2·K)/W b | = 0.04 (m2·K)/W b | = 1.0385 d | |||
| # | Component C-7 | s (mm) | λ (W/(m·K)) a | R ((m2·K)/W) | Sketch |
| 1 | Cement mortar | 25 | 1.30 | - |  |
| 2 | Perforated brick | 115 | 0.35 | - | |
| 3 | Cement mortar | 10 | 1.30 | - | |
| 4 | Polyurethane (PUR) insulation | 40 | 0.028 | - | |
| 5 | Air gap | 100 | - | 0.18 c | |
| 6 | Hollow brick | 40 | 0.32 | - | |
| 7 | Gypsum plaster | 15 | 0.57 | - | |
| = 0.13 (m2·K)/W b | = 0.04 (m2·K)/W b | = 1.0403 d | |||
| # | Component C-8 | s (mm) | λ (W/(m·K)) a | R ((m2·K)/W) | Sketch |
| 1 | Cement mortar | 15 | 1.30 | - | 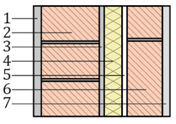 |
| 2 | Perforated brick | 115 | 0.35 | - | |
| 3 | Cement mortar | 10 | 1.30 | - | |
| 4 | Polyurethane (PUR) insulation | 35 | 0.028 | - | |
| 5 | Air gap | 10 | - | 0.15 c | |
| 6 | Hollow brick | 70 | 0.32 | - | |
| 7 | Gypsum plaster | 15 | 0.57 | - | |
| = 0.13 (m2·K)/W b | = 0.04 (m2·K)/W b | = 1.0403 d | |||
| Equipment | Measuring Range | Resolution | Accuracy | |
|---|---|---|---|---|
| Data logger A | ||||
| with thermocouples K | Temperature | −10 °C to 105 °C | 0.1 K | ±0.05 K ±0.05% |
| with thermocouples K | Temperature | −200 °C to 205 °C | 0.1 K | ±0.05 K ±0.05% |
| Data logger B | ||||
| with thermocouples K | Temperature | −20 °C to 70 °C | 0.1 °C | ±0.1 °C |
| with thermohygrometer | Temperature | −20 °C to 70 °C | 0.1 °C | ±0.3 °C |
| Infrared camera FLIR E60bx (FLIR systems, Portland, OR, USA) | Field of view (FOV) | 25° × 19° | ||
| Spectral range | 7.5 µm to 13 µm | |||
| Thermal sensitivity | <0.05 °C to 30 °C | |||
| Infrared camera Fluke TiR1 (Fluke Corporation, Everett, WA, USA) | Field of view (FOV) | 23° × 17° | ||
| Spectral range | 7.5 to 14 µm | |||
| Thermal sensitivity | <0.07 °C to 30 °C | |||
| Weather station PCE-FWS20 (PCE Instruments, Southampton, UK) | Temperature | −40 °C to 65 °C | 0.1 °C | ±1 °C |
| Wind speed | 0 km/h to 180 km/h | 0.07 m/s | ±10% | |
| Precipitation | 0 mm to 9.99 mm | 0.1 mm | ±1 mm |
| Case of Study | (W/(m2·K)) | ||
|---|---|---|---|
| a | b | c | |
| C-1 | 1.18 | 1.03 ± 0.09 | 0.87 ± 0.29 |
| C-2 | 0.57 | 0.59 ± 0.07 | Fail |
| C-3 | 1.50 | 1.39 ± 0.08 | 0.94 ± 0.29 |
| C-4 | 0.56 | 0.45 ± 0.09 | Fail |
| C-5 | 1.10 | 0.98 ± 0.06 | 0.59 ± 0.17 |
| C-6 | 0.76 | 0.38 ± 0.10 | 0.29 ± 0.37 |
| C-7 | 0.45 | 0.48 ± 0.11 | 0.37 ± 0.32 |
| C-8 | 0.48 | 0.88 ± 0.10 | 0.57 ± 0.33 |
| Case of Study | (W/(m2·K)) | ||||
|---|---|---|---|---|---|
| a | |||||
| b | c | b | c | ||
| C-2 | 0.57 | 0.59 ± 0.07 | Fail | 0.54 ± 0.05 | Fail |
| C-5 | 1.10 | 0.98 ± 0.06 | 0.59 ± 0.24 | 1.04 ± 0.05 | 0.59 ± 0.24 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bienvenido-Huertas, D.; Rodríguez-Álvaro, R.; Moyano, J.J.; Rico, F.; Marín, D. Determining the U-Value of Façades Using the Thermometric Method: Potentials and Limitations. Energies 2018, 11, 360. https://doi.org/10.3390/en11020360
Bienvenido-Huertas D, Rodríguez-Álvaro R, Moyano JJ, Rico F, Marín D. Determining the U-Value of Façades Using the Thermometric Method: Potentials and Limitations. Energies. 2018; 11(2):360. https://doi.org/10.3390/en11020360
Chicago/Turabian StyleBienvenido-Huertas, David, Roberto Rodríguez-Álvaro, Juan José Moyano, Fernando Rico, and David Marín. 2018. "Determining the U-Value of Façades Using the Thermometric Method: Potentials and Limitations" Energies 11, no. 2: 360. https://doi.org/10.3390/en11020360
APA StyleBienvenido-Huertas, D., Rodríguez-Álvaro, R., Moyano, J. J., Rico, F., & Marín, D. (2018). Determining the U-Value of Façades Using the Thermometric Method: Potentials and Limitations. Energies, 11(2), 360. https://doi.org/10.3390/en11020360







