Comparative Study of Different Methods for Estimating Weibull Parameters: A Case Study on Jeju Island, South Korea
Abstract
:1. Introduction
2. Sites and Wind Data
3. Methods for Estimating Weibull Parameters
3.1. Empirical Method
3.2. Moment Method
3.3. Graphical Method
3.4. Energy Pattern Factor Method
3.5. Maximum Likelihood Method (MLM)
3.6. Modified Maximum Likelihood Method (MMLM)
4. Assessment of Method Accuracy
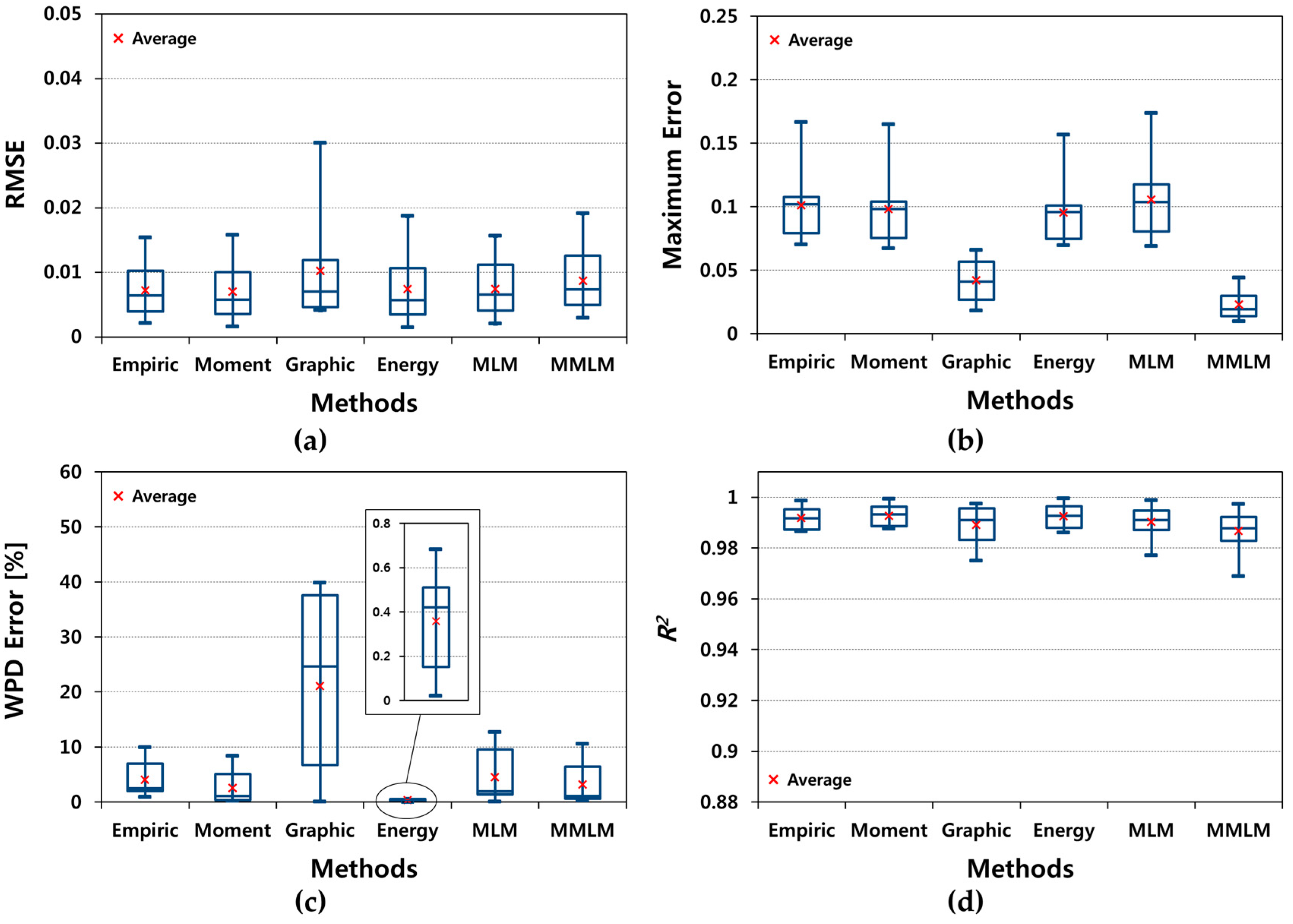
4.1. RMSE
4.2. Maximum Error
4.3. Wind Power Density (WPD) Error
- The average WPD of the Weibull distribution obtained using each method:where ρ is the air density.
- The average WPD of the observed wind speeds:
4.4. Analysis of Variance (R2)
5. Consideration of Bin Interval
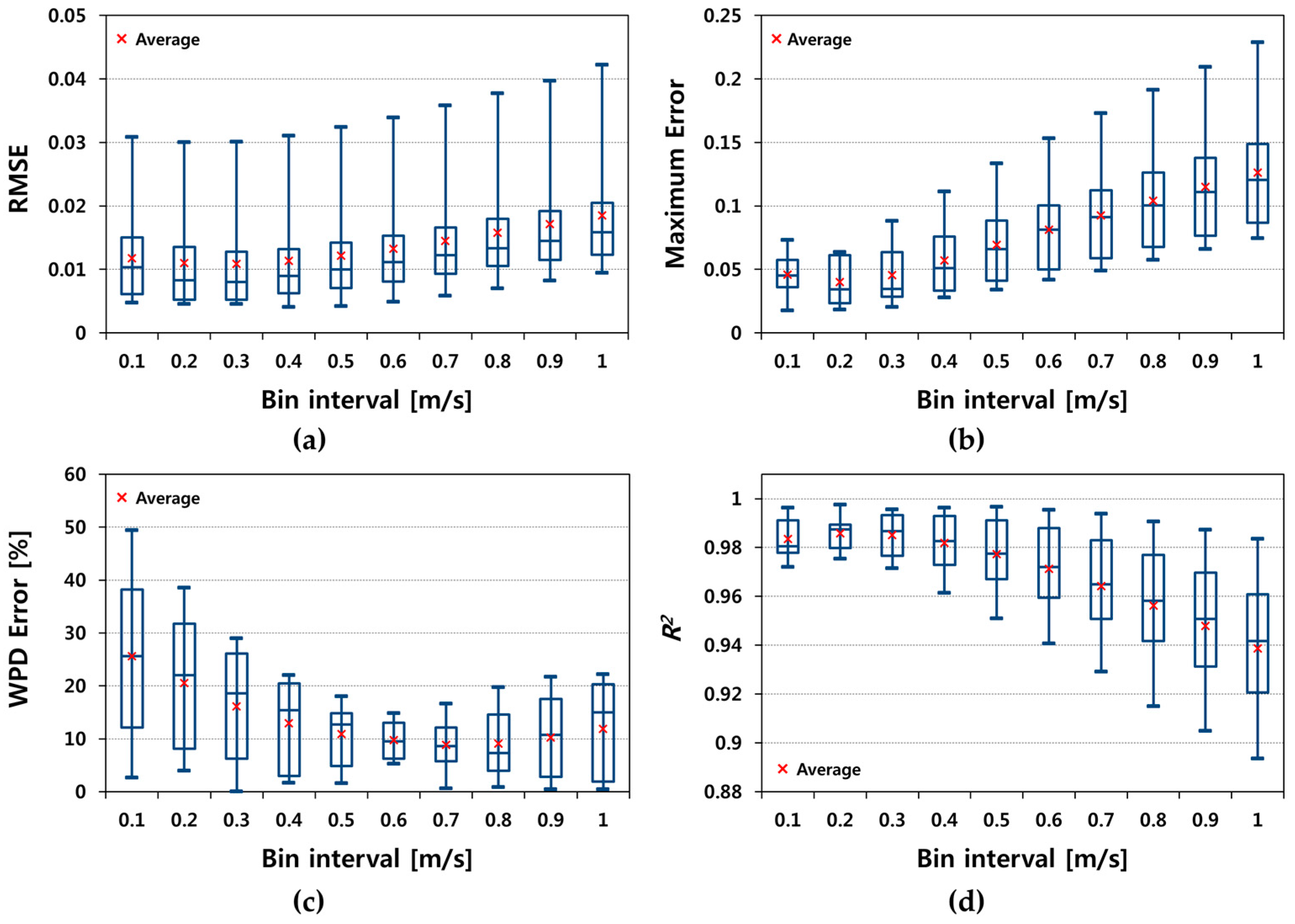
5.1. Graphical Method
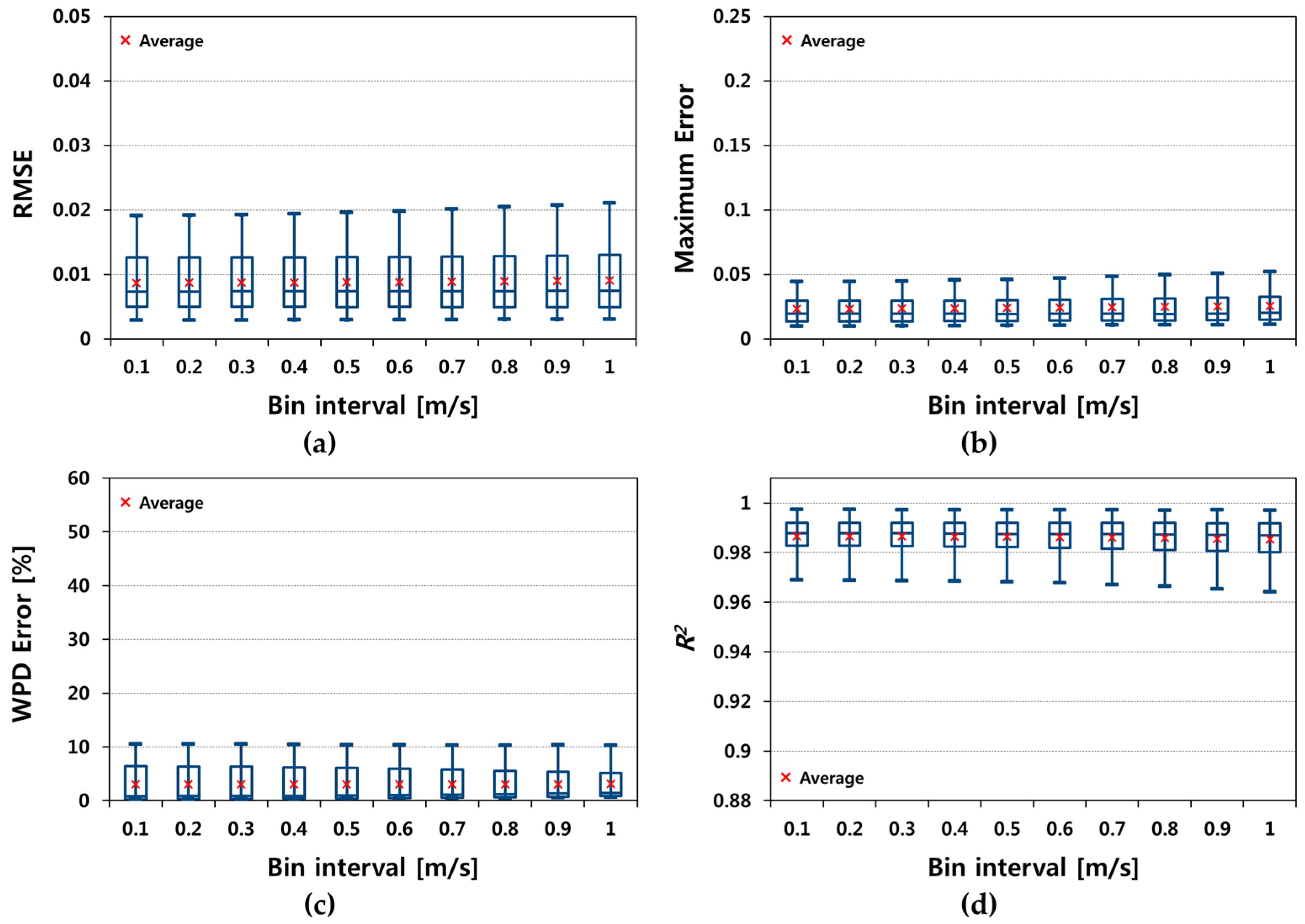
5.2. MMLM Method
6. Results and Discussion
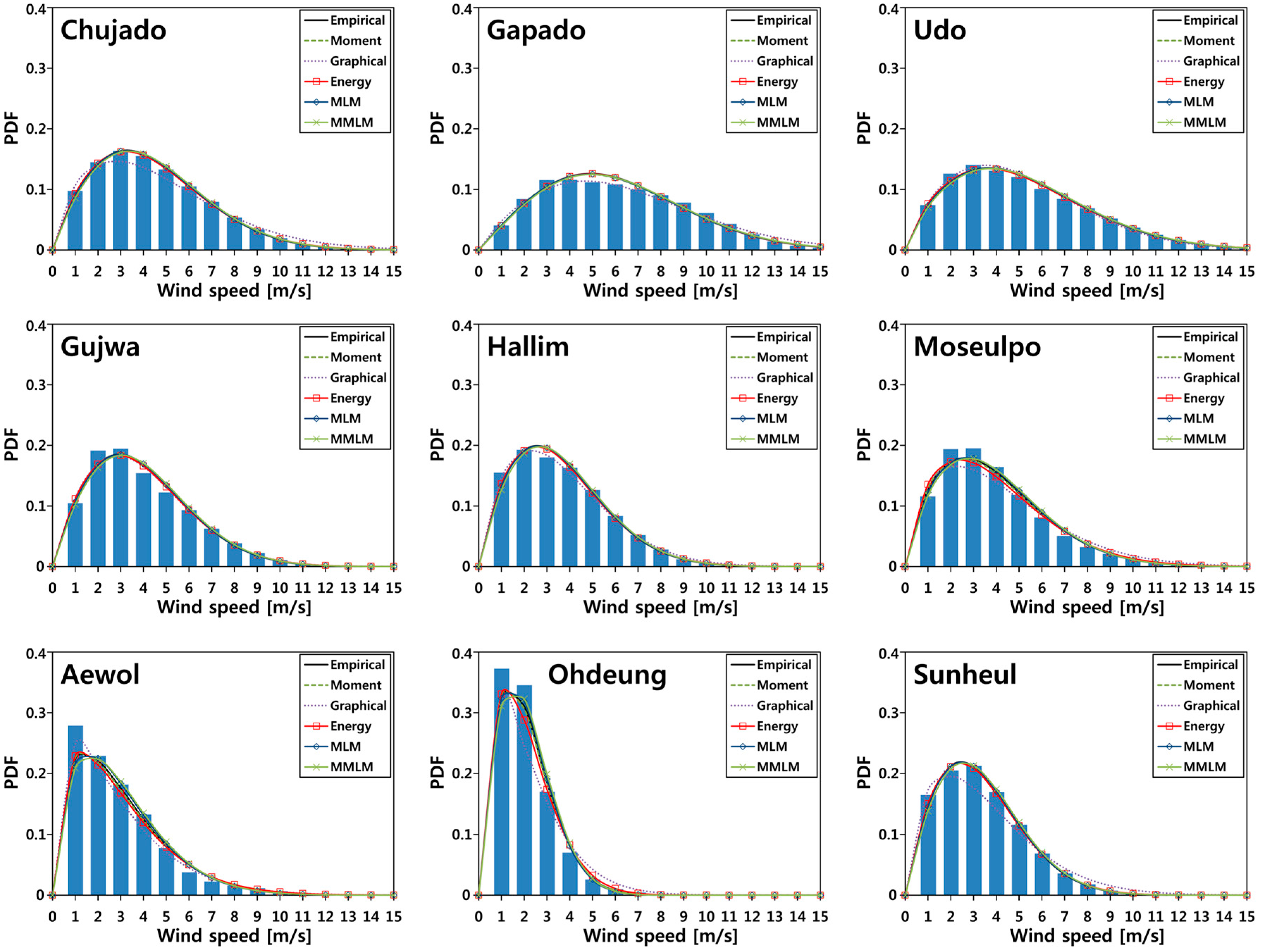
6.1. Comparison of the Methods
6.2. Impact of Topographical Conditions on the Performance of the Methods
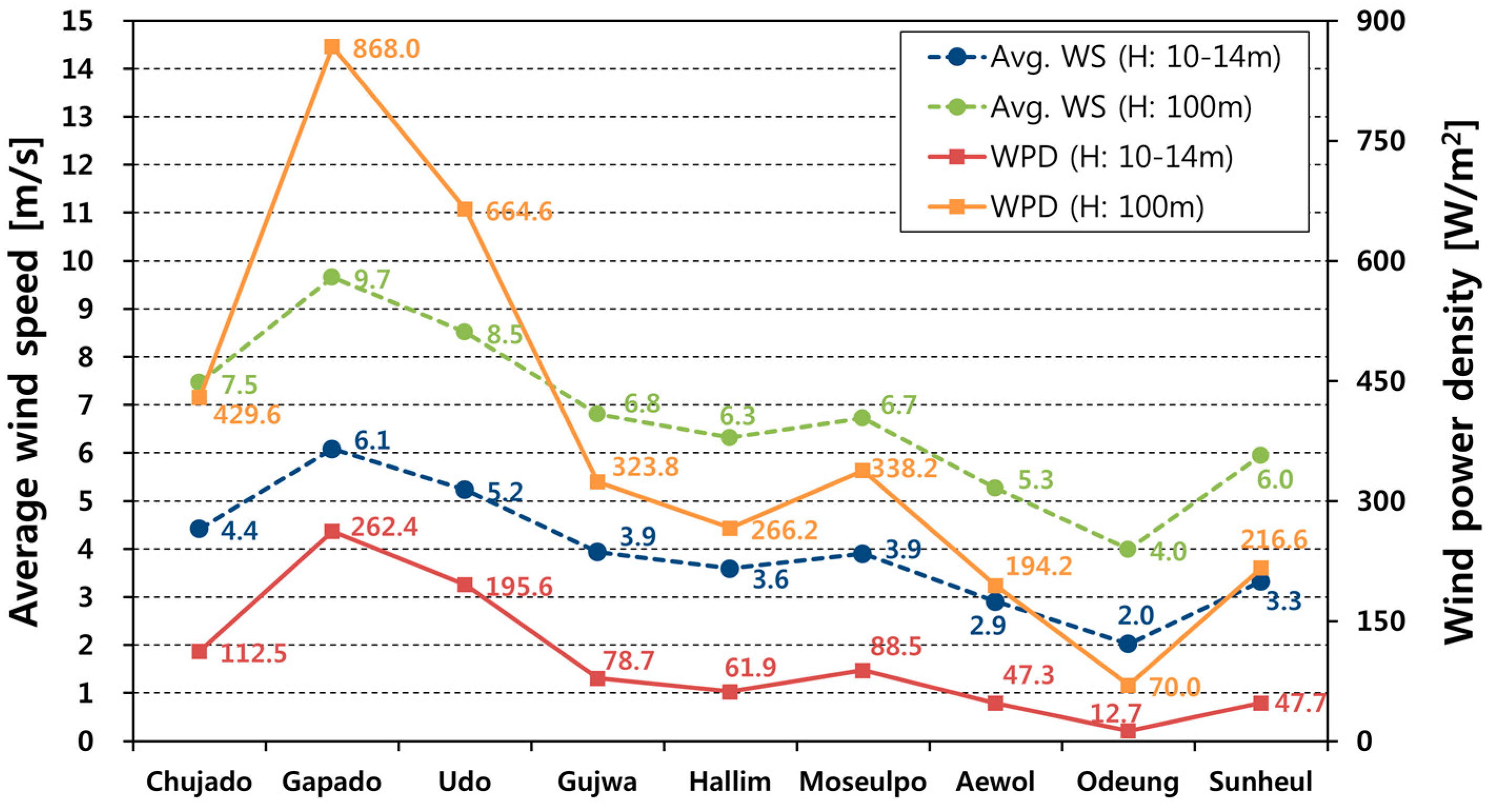
6.3. Wind Resource Extrapolation
7. Conclusions
- (1)
- When applying the MMLM, the bin interval did not significantly affect the performance of the estimation whereas for the graphical method, the performance depended on the bin interval. The graphical method suggested a better performance as bin interval decreased in the accuracy tests of RMSE, maximum error, and R2.
- (2)
- The variation in topographical conditions did not affect the accuracy ranking of the methods and there were no better methods relying on specific terrain condition.
- (3)
- As terrain complexity increased, the estimation uncertainty for Weibull parameters also increased. Therefore, in order to evaluate the economic feasibility, future wind farm developers should take into account different estimation uncertainties for the Weibull distribution based on the variation in topographical conditions.
- (4)
- The moment method performed the best and was the most accurate for all topographical conditions among the six methods. The energy pattern factor and empirical methods were ranked next best.
- (5)
- The graphical method performed the worst among the six methods in this study.
- (6)
- The observed distribution containing values close to zero in both skewness and kurtosis shows the best performance of the WPD error.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| c | Scale parameter of Weibull distribution (m/s) |
| Epf | Energy pattern factor, dimensionless |
| f(v) | Probability density function |
| F(v) | Cumulative distribution function |
| h | Height (m) |
| k | Shape parameter of Weibull distribution, dimensionless |
| n | Number of observations performed |
| v | Wind speed (m/s) |
| Average wind speed (m/s) | |
| Average of wind speed cubed (m3/s3) | |
| vi | Observed wind speed in stage, i, (m/s) |
| Greek Letters | |
| α | Power law exponent, dimensionless |
| ρ | Air density (kg/m3) |
| σ | Standard deviation of wind speed (m/s) |
Abbreviation
| AWS | Automatic weather system |
| CDF | Cumulative distribution function |
| C.V. | Coefficient of variation |
| MLM | Maximum likelihood method |
| MMLM | Modified maximum likelihood method |
| Probability density function | |
| RIX | Ruggedness index |
| RMSE | Root mean square error |
| S.D. | Standard deviation |
| WPD | Wind power density |
References
- Global Wind Energy Council (GWEC). Global Wind Report 2016; GWEC: Brussels, Belgium, 2017; pp. 12–19. [Google Scholar]
- Korea Wind Energy Industry Association (KWEIA). Korean Wind Energy Statistics Report. Available online: http://www.kweia.or.kr/ (accessed on 20 December 2017).
- Azad, A.K.; Rasul, M.G.; Yusaf, T. Statistical diagnosis of the best weibull methods for wind power assessment for agricultural applications. Energies 2014, 7, 3056–3085. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Akpinar, S. Determination of the wind energy potential for Maden-Elazig, Turkey. Energy Convers. Manag. 2004, 45, 2901–2914. [Google Scholar] [CrossRef]
- Arslan, T.; Bulut, Y.M.; Altın Yavuz, A. Comparative study of numerical methods for determining Weibull parameters for wind energy potential. Renew. Sustain. Energy Rev. 2014, 40, 820–825. [Google Scholar] [CrossRef]
- Ali, S.; Lee, S.; Jang, C. Techno-economic assessment of wind energy potential at three locations in South Korea using long-term measured wind data. Energies 2017, 10, 1442. [Google Scholar] [CrossRef]
- Shu, Z.R.; Li, Q.S.; Chan, P.W. Investigation of offshore wind energy potential in Hong Kong based on Weibull distribution function. Appl. Energy 2015, 156, 362–373. [Google Scholar] [CrossRef]
- Kadhem, A.A.; Wahab, I.N.; Aris, I.; Jasni, J.; Abdalla, N.A. Advanced wind Speed prediction model based on a combination of Weibull distribution and an artificial neural network. Energies 2017, 10, 1744. [Google Scholar] [CrossRef]
- Herrero-Novoa, C.; Pérez, I.A.; Sánchez, M.L.; García, M.Á.; Pardo, N.; Fernández-Duque, B. Wind speed description and power density in northern Spain. Energy 2017, 138, 967–976. [Google Scholar] [CrossRef]
- Akdağ, S.A.; Bagiorgas, H.S.; Mihalakakou, G. Use of two-component Weibull mixtures in the analysis of wind speed in the Eastern Mediterranean. Appl. Energy 2010, 87, 2566–2573. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramírez, P. Analysis of two-component mixture Weibull statistics for estimation of wind speed distributions. Renew. Energy 2007, 32, 518–531. [Google Scholar] [CrossRef]
- Gómez-Lázaro, E.; Bueso, M.; Kessler, M.; Martin-Martinez, S.; Zhang, J.; Hodge, B.; Molina-Garcia, A. Probability Density Function Characterization for Aggregated Large-Scale Wind Power Based on Weibull Mixtures. Energies 2016, 9, 91. [Google Scholar] [CrossRef]
- Justus, C.G.; Hargraves, W.R.; Mikhail, A.; Graber, D. Methods for estimating wind speed frequency distributions. J. Appl. Meteorol. 1978, 17, 350–353. [Google Scholar] [CrossRef]
- Stevens, M.J.M.; Smulders, P.T. Estimation of the parameters of the Weibull wind speed distribution for wind energy utilization purposes. Wind Eng. 1979, 3, 132–145. [Google Scholar]
- Deaves, D.M.; Lines, I.G. On the fitting of low mean wind speed data to the Weibull distribution. J. Wind Eng. Ind. Aerodyn. 1997, 66, 169–178. [Google Scholar] [CrossRef]
- Akdag, S.A.; Dinler, A. A new method to estimate Weibull parameters for wind energy applications. Energy Convers. Manag. 2009, 50, 1761–1766. [Google Scholar] [CrossRef]
- Seguro, J.V.; Lambert, T.W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. Wind Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar] [CrossRef]
- Chang, T.P. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application. Appl. Energy 2011, 88, 272–282. [Google Scholar] [CrossRef]
- Saleh, H.; Abou El-Azm Aly, A.; Abdel-Hady, S. Assessment of different methods used to estimate Weibull distribution parameters for wind speed in Zafarana wind farm, Suez Gulf, Egypt. Energy 2012, 44, 710–719. [Google Scholar] [CrossRef]
- Mohammadi, K.; Alavi, O.; Mostafaeipour, A.; Goudarzi, N.; Jalilvand, M. Assessing different parameters estimation methods of Weibull distribution to compute wind power density. Energy Convers. Manag. 2016, 108, 322–335. [Google Scholar] [CrossRef]
- Alavi, O.; Sedaghat, A.; Mostafaeipour, A. Sensitivity analysis of different wind speed distribution models with actual and truncated wind data: A case study for Kerman, Iran. Energy Convers. Manag. 2016, 120, 51–61. [Google Scholar] [CrossRef]
- Jeju Special Self-Governing Province. Administrative Statistics Information. Available online: http://www.jeju.go.kr/ (accessed on 20 December 2017).
- Bowen, A.J.; Mortensen, N.G. WAsP Prediction Errors Due to Site Orography; Risø National Laboratory: Roskilde, Denmark, 2004; ISBN 87-550-2320-7. [Google Scholar]
- Taylor, P.A.; Walmsley, J.L.; Salmon, J.R. A simple model of neutrally stratified boundary-layer flow over real terrain incorporating wavenumber-dependent scaling. Bound-Layer Meteorol. 1983, 26, 169–189. [Google Scholar] [CrossRef]
- Brower, M.C. Wind Resource Assessment; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 117–144. ISBN 978-1118022320. [Google Scholar]
- Measnet. Evaluation of Site-Specific Wind Conditions, version 1; Measnet: Madrid, Spain, 2009; pp. 14–18. [Google Scholar]
- Takle, E.S.; Brown, J.M. Note on the use of Weibull Statistics to characterize wind-speed data. J. Appl. Meteorol. Climatol. 1978, 17, 556–559. [Google Scholar] [CrossRef]
- Carrillo, C.; Cidrás, J.; Díaz-Dorado, E.; Obando-Montaño, A.F. An Approach to determine the Weibull parameters for wind energy analysis: The case of Galicia (Spain). Energies 2014, 7, 2676–2700. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramírez, P.; Velázquez, S. A review of wind speed probability distributions used in wind energy analysis: Case studies in the Canary Islands. Renew. Sustain. Energy Rev. 2009, 13, 933–955. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 1st ed.; John Wiley & Sons, Inc.: Chichester, UK, 2002; pp. 46–62. ISBN 978-0-470-01500-1. [Google Scholar]
- Jain, P. Wind Energy Engineering; McGraw-Hill Companies, Inc.: New York, NY, USA, 2011; pp. 26–37. ISBN 978-0071714778. [Google Scholar]
- Basumatary, H.; Sreevalsan, E.; Sasi, K.K. Weibull parameter estimation—A comparison of different methods. Wind Eng. 2005, 29, 309–316. [Google Scholar] [CrossRef]
- Justus, C.G.; Mikhail, A. Height variation of wind speed and wind distributions statistics. Geophys. Res. Lett. 1976, 3, 261–264. [Google Scholar] [CrossRef]
- Dorvlo, A.S.S. Estimating wind speed distribution. Energy Convers. Manag. 2002, 43, 2311–2318. [Google Scholar] [CrossRef]
- Gebizlioglu, O.L.; Şenoğlu, B.; Kantar, Y.M. Comparison of certain value-at-risk estimation methods for the two-parameter Weibull loss distribution. J. Comput. Appl. Math. 2011, 235, 3304–3314. [Google Scholar] [CrossRef]
- Lun, I.Y.F.; Lam, J.C. A study of Weibull parameters using long-term wind observations. Renew. Energy 2000, 20, 145–153. [Google Scholar] [CrossRef]
- Costa Rocha, P.A.; de Sousa, R.C.; de Andrade, C.F.; da Silva, M.E.V. Comparison of seven numerical methods for determining Weibull parameters for wind energy generation in the northeast region of Brazil. Appl. Energy 2012, 89, 395–400. [Google Scholar] [CrossRef]
- De Andrade, C.F.; Maia Neto, H.F.; Costa Rocha, P.A.; Vieira da Silva, M.E. An efficiency comparison of numerical methods for determining Weibull parameters for wind energy applications: A new approach applied to the northeast region of Brazil. Energy Convers. Manag. 2014, 86, 801–808. [Google Scholar] [CrossRef]
- Dahbi, M.; Benatiallah, A.; Sellam, M. The Analysis of Wind Power Potential in Sahara Site of Algeria-an Estimation Using the ‘Weibull’ Density Function. Energy Procedia 2013, 36, 179–188. [Google Scholar] [CrossRef]
- Garcia, A.; Torres, J.L.; Prieto, E.; de Francisco, A. Fitting wind speed distributions: A case study. Sol. Energy 1998, 62, 139–144. [Google Scholar] [CrossRef]
- Ko, K.; Kim, K.; Huh, J. Characteristics of wind variations on Jeju Island, Korea. Int. J. Energy Res. 2010, 34, 36–45. [Google Scholar] [CrossRef]
- Ko, K.; Kim, K.; Huh, J. Variations of wind speed in time on Jeju Island, Korea. Energy 2010, 35, 3381–3387. [Google Scholar] [CrossRef]
- Gualtieri, G.; Secci, S. Methods to extrapolate wind resource to the turbine hub height based on power law: A 1-h wind speed vs. Weibull distribution extrapolation comparison. Renew. Energy 2012, 43, 183–200. [Google Scholar] [CrossRef]
- Fortuna, L.; Nunnari, G.; Nunnari, S. A new fine-grained classification strategy for solar daily radiation patterns. Pattern Recognit. Lett. 2016, 81, 110–117. [Google Scholar] [CrossRef]
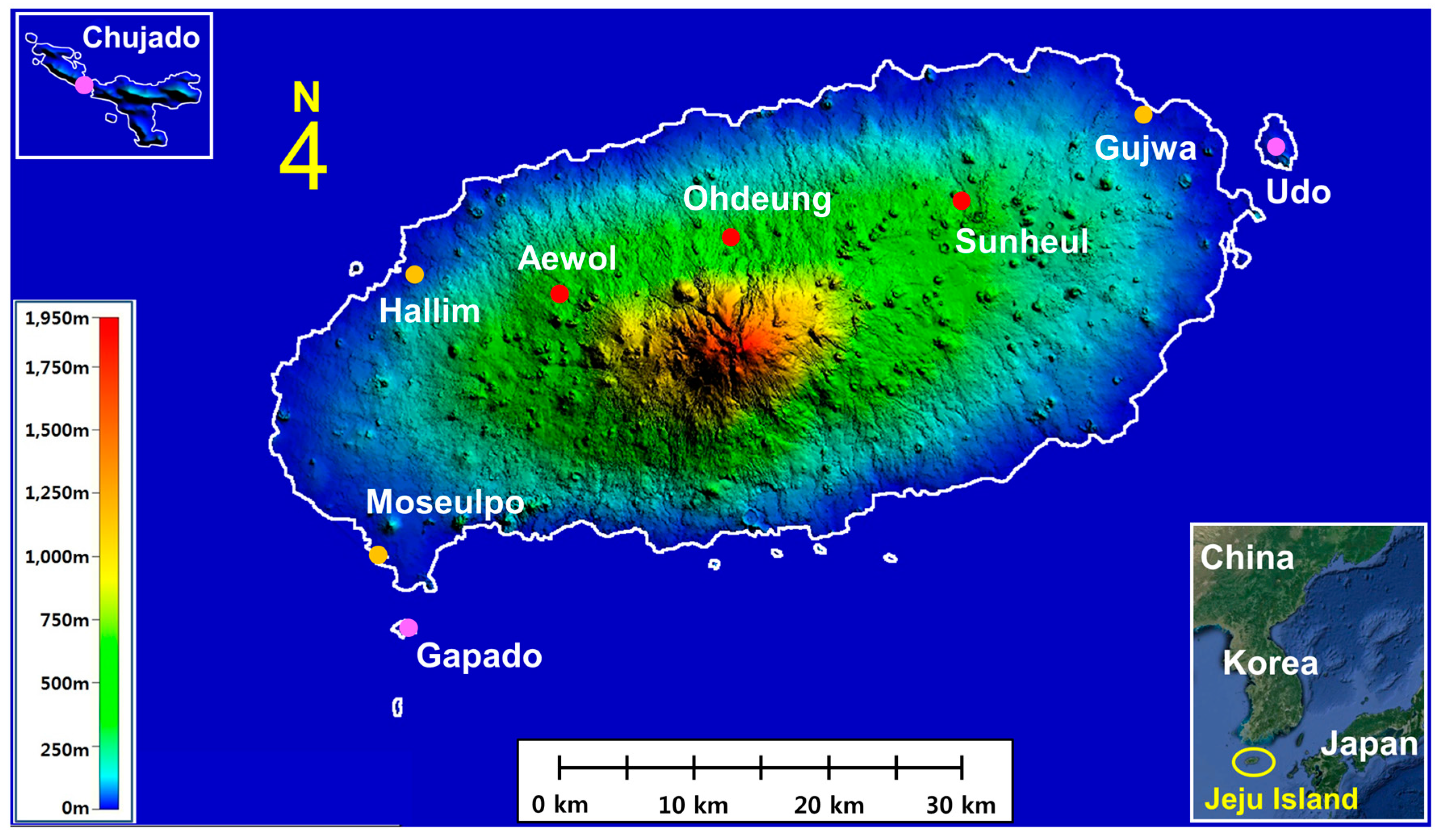
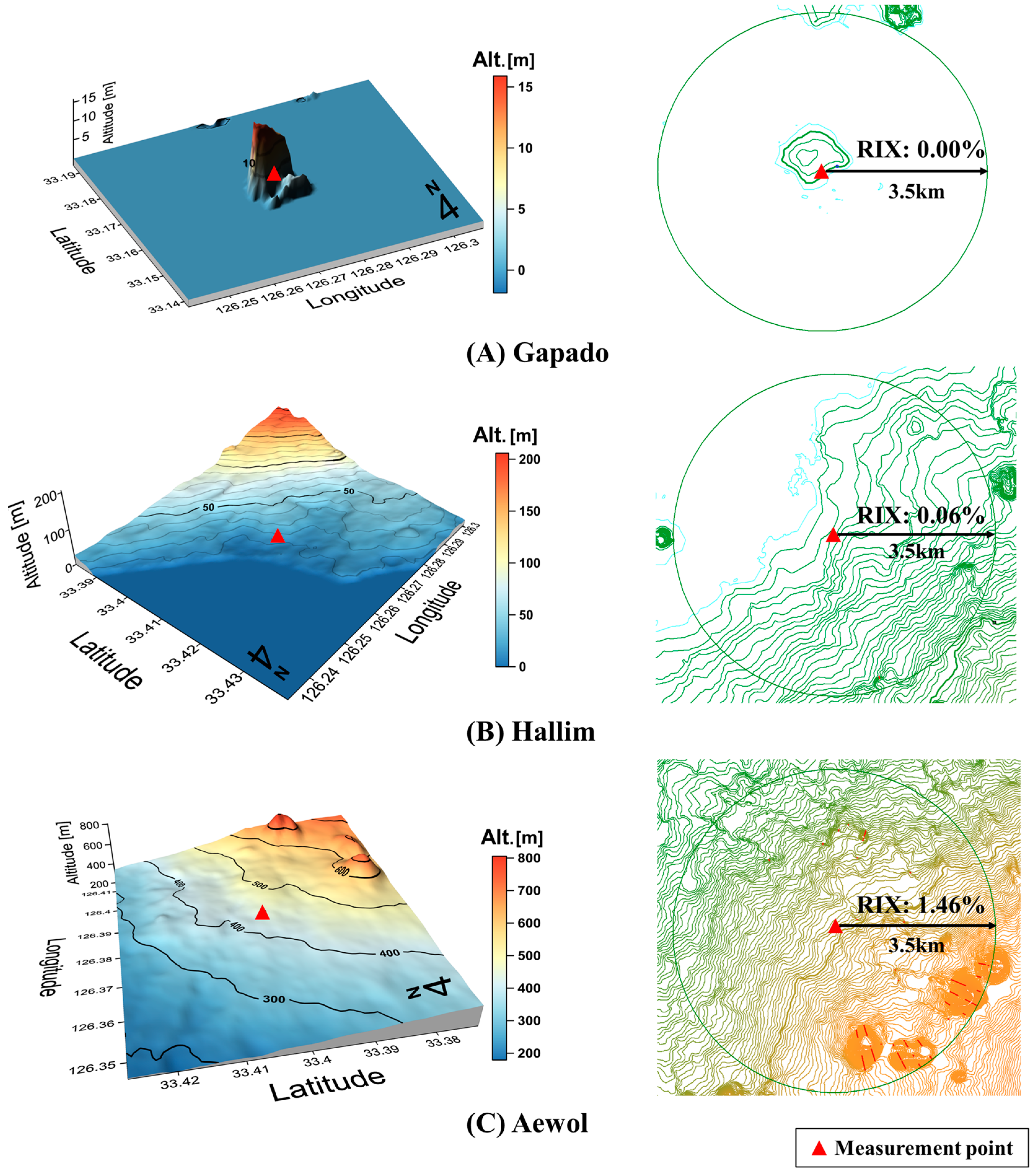
| Sites | Position | Altitude (m) | Data Recovery Rate (%) | Time of 0–0.5 m/s (h/Year) (Freq.) | RIX (%) | Topographical Condition |
|---|---|---|---|---|---|---|
| Chujado | 126°18′02″ E | 18 | 95.0 | 404.8 (4.6%) | 0.00 | Islet |
| 33°57′16″ N | ||||||
| Gapado | 126°16′24″ E | 13 | 97.6 | 165.3 (1.9%) | 0.00 | |
| 33°09′58″ N | ||||||
| Udo | 126°57′12″ E | 39 | 98.6 | 93.3 (1.1%) | 0.31 | |
| 33°30′23″ N | ||||||
| Gujwa | 126°51′06″ E | 25 | 98.2 | 137.6 (1.6%) | 0.00 | Coastal |
| 33°31′21″ N | ||||||
| Hallim | 126°16′02″ E | 22 | 94.7 | 439.8 (5.0%) | 0.06 | |
| 33°24′37″ N | ||||||
| Moseulpo | 126°14′60″ E | 12 | 96.8 | 259.8 (3.0%) | 0.14 | |
| 33°13′00″ N | ||||||
| Aewol | 126°22′48″ E | 447 | 93.9 | 502.9 (5.8%) | 1.46 | Inland |
| 33°23′60″ N | ||||||
| Ohdeung | 126°32′38″ E | 513 | 89.8 | 876.7 (10.0%) | 3.53 | |
| 33°25′25″ N | ||||||
| Sunheul | 126°42′42″ E | 341 | 93.1 | 575.7 (6.6%) | 4.21 | |
| 33°27′30″ N |
| Items | Specification |
|---|---|
| Model | WM-4-WS |
| Measuring range | 0–70 m/s |
| Sampling rate | 4 Hz |
| Threshold | Below 0.3 m/s |
| Resolution | 0.1 m/s |
| Accuracy | 0–10 m/s: <0.3 m/s Over 10 m/s: <3% |
| Operation temperature | −40–+80 °C |
| Type | 3-cup anemometer |
| Bin Interval (1 m/s) | Bin Interval (0.5 m/s) | Bin Interval (0.1 m/s) | ||||||
|---|---|---|---|---|---|---|---|---|
| Bin (m/s) | Freq. (%) | Cum. Freq. (%) | Bin (m/s) | Freq. (%) | Cum. Freq. (%) | Bin (m/s) | Freq. (%) | Cum. Freq. (%) |
| 0.5–1.5 | 4.03 | 4.03 | 0.5–1.0 | 1.65 | 1.65 | 0.5–0.6 | 0.29 | 0.29 |
| 1.5–2.5 | 8.38 | 12.41 | 1.0–1.5 | 2.38 | 4.03 | 0.6–0.7 | 0.29 | 0.58 |
| 2.5–3.5 | 11.51 | 23.92 | 1.5–2.0 | 3.58 | 7.60 | 0.7–0.8 | 0.33 | 0.91 |
| 3.5–4.5 | 11.56 | 35.48 | 2.0–2.5 | 4.80 | 12.41 | 0.8–0.9 | 0.34 | 1.25 |
| 4.5–5.5 | 11.15 | 46.62 | 2.5–3.0 | 5.68 | 18.08 | 0.9–1.0 | 0.40 | 1.65 |
| 5.5–6.5 | 10.80 | 57.43 | 3.0–3.5 | 5.83 | 23.92 | 1.0–1.1 | 0.39 | 2.03 |
| 6.5–7.5 | 9.97 | 67.40 | 3.5–4.0 | 5.87 | 29.79 | 1.1–1.2 | 0.45 | 2.48 |
| 7.5–8.5 | 9.02 | 76.42 | 4.0–4.5 | 5.69 | 35.48 | 1.2–1.3 | 0.47 | 2.95 |
| 8.5–9.5 | 7.79 | 84.21 | 4.5–5.0 | 5.63 | 41.10 | 1.3–1.4 | 0.51 | 3.46 |
| 9.5–10.5 | 6.07 | 90.28 | 5.0–5.5 | 5.52 | 46.62 | 1.4–1.5 | 0.56 | 4.03 |
| ≥10.5 | 9.72 | 100 | ≥5.5 | 53.38 | 100 | ≥1.5 | 95.97 | 100 |
| Methods | Bin Interval (m/s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Chujado | Gapado | Udo | Gujwa | Hallim | Moseulpo | Aewol | Odeung | Sunheul | |
| Graphical | 0.1 | 0.1 | 0.4 | 0.3 | 0.2 | 0.3 | 0.5 | 0.2 | 0.1 |
| MMLM | 0.1 | 1 | 1 | 1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| Sites | No. of Data | Average (m/s) | Mode (m/s) | Speed Range (m/s) | S.D. (m/s) | C.V. (%) | Skew-Ness | Kurtosis | |
|---|---|---|---|---|---|---|---|---|---|
| Islet | Chujado | 249,708 | 4.4 | 3.1 | 28.3 | 2.5 | 56.6 | 0.9 | 1.5 |
| Gapado | 256,521 | 6.1 | 3.4 | 31.0 | 3.2 | 52.2 | 0.6 | 0.5 | |
| Udo | 259,337 | 5.2 | 2.8 | 20.9 | 3.1 | 59.3 | 0.8 | 0.5 | |
| Coastal | Gujwa | 258,246 | 3.9 | 2.6 | 17.2 | 2.2 | 56.3 | 0.8 | 0.5 |
| Hallim | 249,066 | 3.6 | 1.8 | 18.3 | 2.1 | 58.0 | 0.9 | 1.0 | |
| Moseulpo | 254,620 | 3.9 | 2.5 | 23.4 | 2.4 | 61.1 | 1.4 | 3.2 | |
| Inland | Aewol | 246,856 | 2.9 | 0.9 | 19.6 | 2.1 | 71.7 | 1.7 | 4.1 |
| Ohdeung | 236,021 | 2.0 | 1.3 | 14.8 | 1.2 | 60.4 | 1.8 | 6.6 | |
| Sunheul | 244,848 | 3.3 | 2.4 | 25.6 | 1.9 | 56.4 | 0.9 | 1.2 | |
| Parameters | Methods | Islet | Coastal | Inland | Avg. (Rank) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Chujado | Gapado | Udo | Gujwa | Hallim | Moseulpo | Aewol | Ohdeung | Sunheul | |||
| k | Empirical | 1.8547 | 2.0253 | 1.7652 | 1.8664 | 1.8085 | 1.7080 | 1.4357 | 1.7276 | 1.8622 | - |
| Moment | 1.8305 | 2.0025 | 1.7407 | 1.8422 | 1.7841 | 1.6836 | 1.4147 | 1.7032 | 1.8380 | - | |
| Graphical | 1.5987 | 1.8421 | 1.7672 | 1.8197 | 1.6688 | 1.5376 | 1.2660 | 1.3523 | 1.5283 | - | |
| Energy | 1.8204 | 2.0186 | 1.7418 | 1.8353 | 1.7808 | 1.6246 | 1.3718 | 1.5933 | 1.8257 | - | |
| MLM | 1.8504 | 2.0110 | 1.7695 | 1.8771 | 1.8111 | 1.7429 | 1.5092 | 1.7825 | 1.8664 | - | |
| MMLM | 1.8756 | 2.0281 | 1.7857 | 1.8984 | 1.8412 | 1.7671 | 1.5376 | 1.8243 | 1.8988 | - | |
| C (m/s) | Empirical | 4.9824 | 6.8656 | 5.8774 | 4.4357 | 4.0436 | 4.3757 | 3.1992 | 2.2749 | 3.7469 | - |
| Moment | 4.9797 | 6.8643 | 5.8727 | 4.4334 | 4.0409 | 4.3714 | 3.1923 | 2.2728 | 3.7450 | - | |
| Graphical | 5.1954 | 7.1691 | 5.6966 | 4.4237 | 4.0590 | 4.5490 | 2.9645 | 2.2676 | 3.8327 | - | |
| Energy | 4.9785 | 6.8652 | 5.8729 | 4.4327 | 4.0405 | 4.3591 | 3.1766 | 2.2606 | 3.7439 | - | |
| MLM | 4.9910 | 6.8704 | 5.8947 | 4.4513 | 4.0545 | 4.4011 | 3.2424 | 2.2921 | 3.7571 | - | |
| MMLM | 5.0510 | 6.9340 | 5.9581 | 4.5160 | 4.1148 | 4.4615 | 3.3059 | 2.3508 | 3.8166 | - | |
| RMSE | Empirical | 0.0021 | 0.0051 | 0.0041 | 0.0075 | 0.0065 | 0.0068 | 0.0130 | 0.0153 | 0.0039 | 0.0071 (2) |
| Moment | 0.0016 | 0.0048 | 0.0036 | 0.0072 | 0.0058 | 0.0072 | 0.0129 | 0.0157 | 0.0034 | 0.0069 (1) | |
| Graphical | 0.0067 | 0.0047 | 0.0040 | 0.0071 | 0.0045 | 0.0122 | 0.0117 | 0.0300 | 0.0103 | 0.0101 (6) | |
| Energy | 0.0014 | 0.0050 | 0.0037 | 0.0072 | 0.0057 | 0.0085 | 0.0128 | 0.0186 | 0.0033 | 0.0074 (3) | |
| MLM | 0.0020 | 0.0049 | 0.0042 | 0.0078 | 0.0066 | 0.0067 | 0.0146 | 0.0156 | 0.0040 | 0.0074 (4) | |
| MMLM | 0.0029 | 0.0050 | 0.0049 | 0.0088 | 0.0078 | 0.0074 | 0.0164 | 0.0190 | 0.0054 | 0.0086 (5) | |
| Maximum error | Empirical | 0.0815 | 0.0702 | 0.0771 | 0.1073 | 0.1030 | 0.0956 | 0.1080 | 0.1663 | 0.1020 | 0.1012 (5) |
| Moment | 0.0780 | 0.0672 | 0.0731 | 0.1042 | 0.0991 | 0.0922 | 0.1041 | 0.1646 | 0.0983 | 0.0979 (4) | |
| Graphical | 0.0411 | 0.0375 | 0.0278 | 0.0259 | 0.0182 | 0.0504 | 0.0658 | 0.0633 | 0.0478 | 0.0420 (2) | |
| Energy | 0.0765 | 0.0693 | 0.0732 | 0.1033 | 0.0986 | 0.0871 | 0.0957 | 0.1565 | 0.0964 | 0.0952 (3) | |
| MLM | 0.0818 | 0.0687 | 0.0789 | 0.1105 | 0.1044 | 0.1028 | 0.1246 | 0.1737 | 0.1038 | 0.1055 (6) | |
| MMLM | 0.0096 | 0.0180 | 0.0193 | 0.0296 | 0.0178 | 0.0303 | 0.0288 | 0.0439 | 0.0096 | 0.0230 (1) | |
| WPD error (%) | Empirical | 2.494 | 0.899 | 1.852 | 2.293 | 2.118 | 6.257 | 7.734 | 9.915 | 2.610 | 4.019 (4) |
| Moment | 1.048 | 0.218 | 0.192 | 0.867 | 0.565 | 4.551 | 5.553 | 8.315 | 1.182 | 2.499 (2) | |
| Graphical | 36.603 | 25.641 | 10.775 | 0.021 | 10.780 | 24.591 | 2.605 | 38.504 | 39.786 | 21.034 (6) | |
| Energy | 0.421 | 0.575 | 0.271 | 0.445 | 0.350 | 0.020 | 0.682 | 0.034 | 0.430 | 0.359 (1) | |
| MLM | 1.706 | 0.041 | 1.310 | 1.938 | 1.513 | 7.310 | 12.693 | 11.723 | 2.083 | 4.480 (5) | |
| MMLM | 0.223 | 1.950 | 0.681 | 1.037 | 0.822 | 5.249 | 10.508 | 7.584 | 0.553 | 3.179 (3) | |
| R2 | Empirical | 0.9986 | 0.9865 | 0.9934 | 0.9879 | 0.9917 | 0.9909 | 0.9865 | 0.9929 | 0.9970 | 0.9917 (3) |
| Moment | 0.9992 | 0.9876 | 0.9948 | 0.9889 | 0.9934 | 0.9899 | 0.9884 | 0.9932 | 0.9977 | 0.9926 (1) | |
| Graphical | 0.9913 | 0.9909 | 0.9945 | 0.9896 | 0.9974 | 0.9749 | 0.9966 | 0.9805 | 0.9859 | 0.9891 (5) | |
| Energy | 0.9994 | 0.9869 | 0.9947 | 0.9891 | 0.9936 | 0.9861 | 0.9915 | 0.9927 | 0.9980 | 0.9924 (2) | |
| MLM | 0.9987 | 0.9873 | 0.9929 | 0.9869 | 0.9914 | 0.9910 | 0.9770 | 0.9905 | 0.9967 | 0.9903 (4) | |
| MMLM | 0.9973 | 0.9869 | 0.9903 | 0.9832 | 0.9878 | 0.9887 | 0.9689 | 0.9826 | 0.9941 | 0.9866 (6) | |
| Tests | Methods | Average | Rank | ||||
|---|---|---|---|---|---|---|---|
| Islet | Coastal | Inland | Islet | Coastal | Inland | ||
| RMSE | Empirical | 0.0037 | 0.0069 | 0.0107 | 4 | 2 | 2 |
| Moment | 0.0033 | 0.0067 | 0.0107 | 1 | 1 | 1 | |
| Graphical | 0.0052 | 0.0079 | 0.0173 | 6 | 5 | 6 | |
| Energy | 0.0034 | 0.0071 | 0.0116 | 2 | 4 | 4 | |
| MLM | 0.0037 | 0.0070 | 0.0114 | 3 | 3 | 3 | |
| MMLM | 0.0043 | 0.0080 | 0.0136 | 5 | 6 | 5 | |
| Maximum error | Empirical | 0.0763 | 0.1020 | 0.1255 | 5 | 5 | 5 |
| Moment | 0.0727 | 0.0985 | 0.1223 | 3 | 4 | 4 | |
| Graphical | 0.0355 | 0.0315 | 0.0590 | 2 | 2 | 2 | |
| Energy | 0.0730 | 0.0963 | 0.1162 | 4 | 3 | 3 | |
| MLM | 0.0765 | 0.1059 | 0.1340 | 6 | 6 | 6 | |
| MMLM | 0.0157 | 0.0259 | 0.0274 | 1 | 1 | 1 | |
| WPD error (%) | Empirical | 1.748 | 3.556 | 6.753 | 5 | 4 | 4 |
| Moment | 0.486 | 1.994 | 5.017 | 2 | 2 | 2 | |
| Graphical | 24.340 | 11.797 | 26.965 | 6 | 6 | 6 | |
| Energy | 0.422 | 0.272 | 0.382 | 1 | 1 | 1 | |
| MLM | 1.019 | 3.587 | 8.833 | 4 | 5 | 5 | |
| MMLM | 0.952 | 2.370 | 6.215 | 3 | 3 | 3 | |
| R2 | Empirical | 0.9928 | 0.9902 | 0.9921 | 4 | 2 | 3 |
| Moment | 0.9939 | 0.9908 | 0.9931 | 1 | 1 | 2 | |
| Graphical | 0.9922 | 0.9873 | 0.9876 | 5 | 5 | 5 | |
| Energy | 0.9937 | 0.9896 | 0.9941 | 2 | 4 | 1 | |
| MLM | 0.9930 | 0.9898 | 0.9881 | 3 | 3 | 4 | |
| MMLM | 0.9915 | 0.9866 | 0.9819 | 6 | 6 | 6 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, D.; Ko, K.; Huh, J. Comparative Study of Different Methods for Estimating Weibull Parameters: A Case Study on Jeju Island, South Korea. Energies 2018, 11, 356. https://doi.org/10.3390/en11020356
Kang D, Ko K, Huh J. Comparative Study of Different Methods for Estimating Weibull Parameters: A Case Study on Jeju Island, South Korea. Energies. 2018; 11(2):356. https://doi.org/10.3390/en11020356
Chicago/Turabian StyleKang, Dongbum, Kyungnam Ko, and Jongchul Huh. 2018. "Comparative Study of Different Methods for Estimating Weibull Parameters: A Case Study on Jeju Island, South Korea" Energies 11, no. 2: 356. https://doi.org/10.3390/en11020356
APA StyleKang, D., Ko, K., & Huh, J. (2018). Comparative Study of Different Methods for Estimating Weibull Parameters: A Case Study on Jeju Island, South Korea. Energies, 11(2), 356. https://doi.org/10.3390/en11020356





