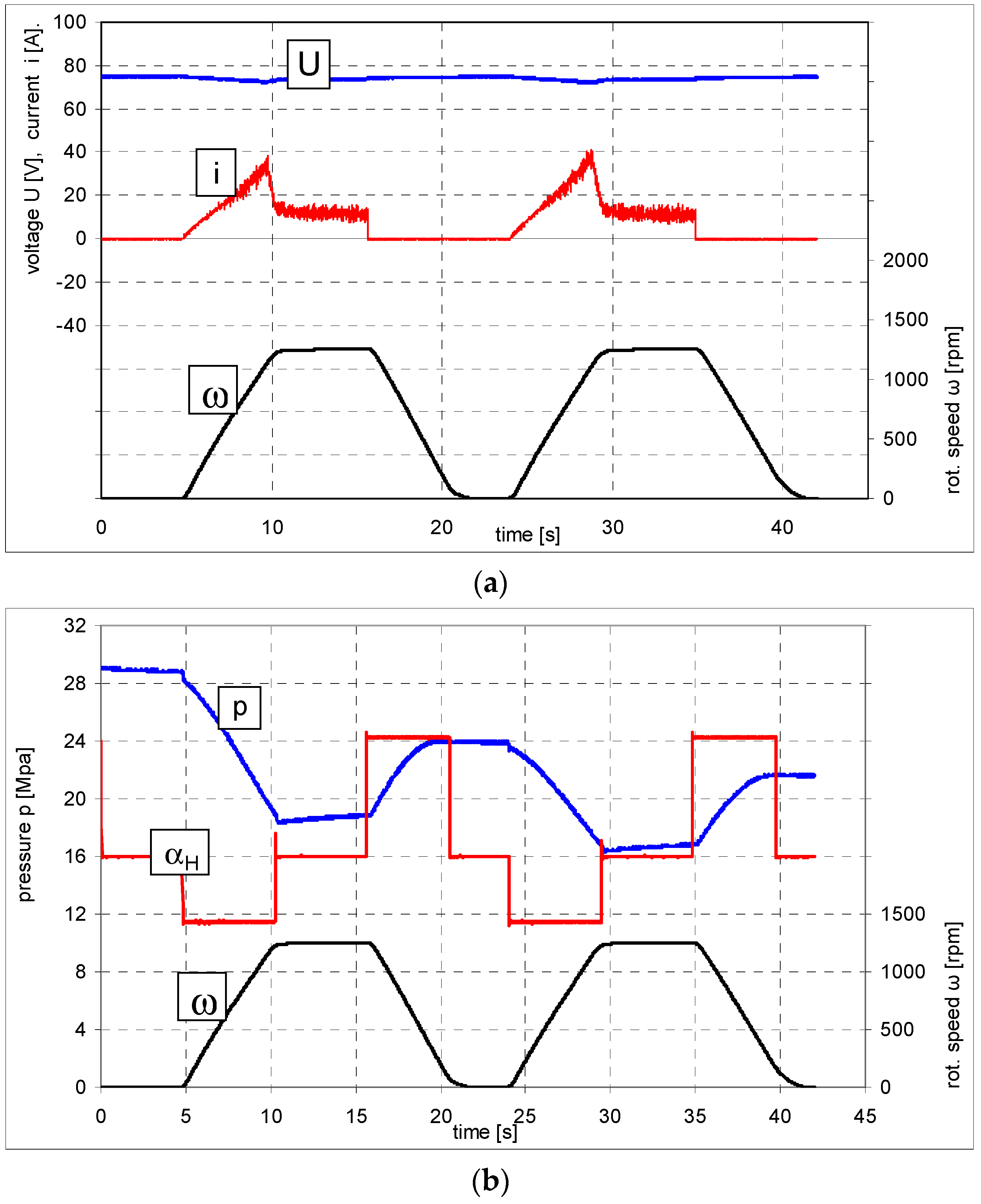
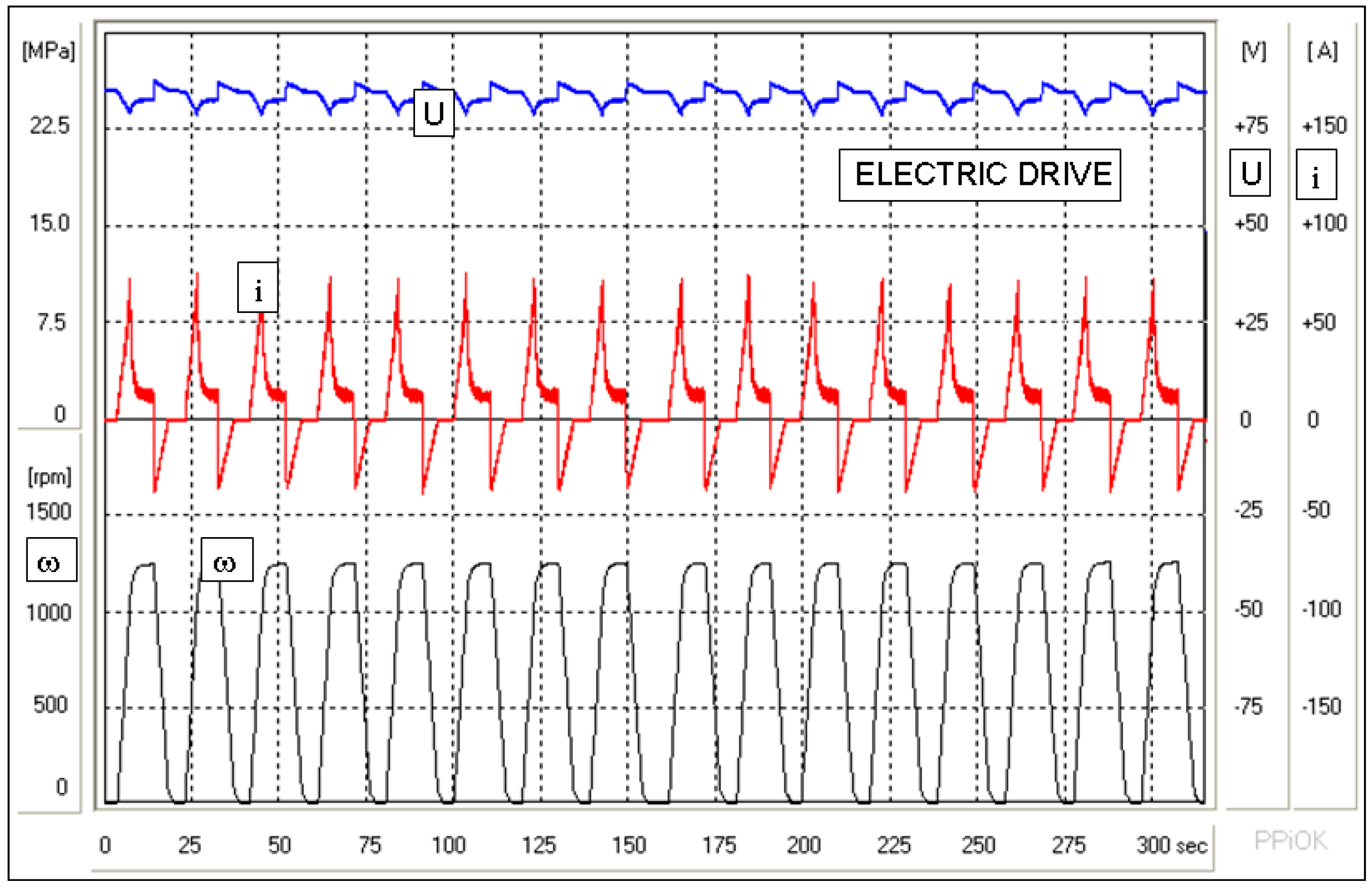
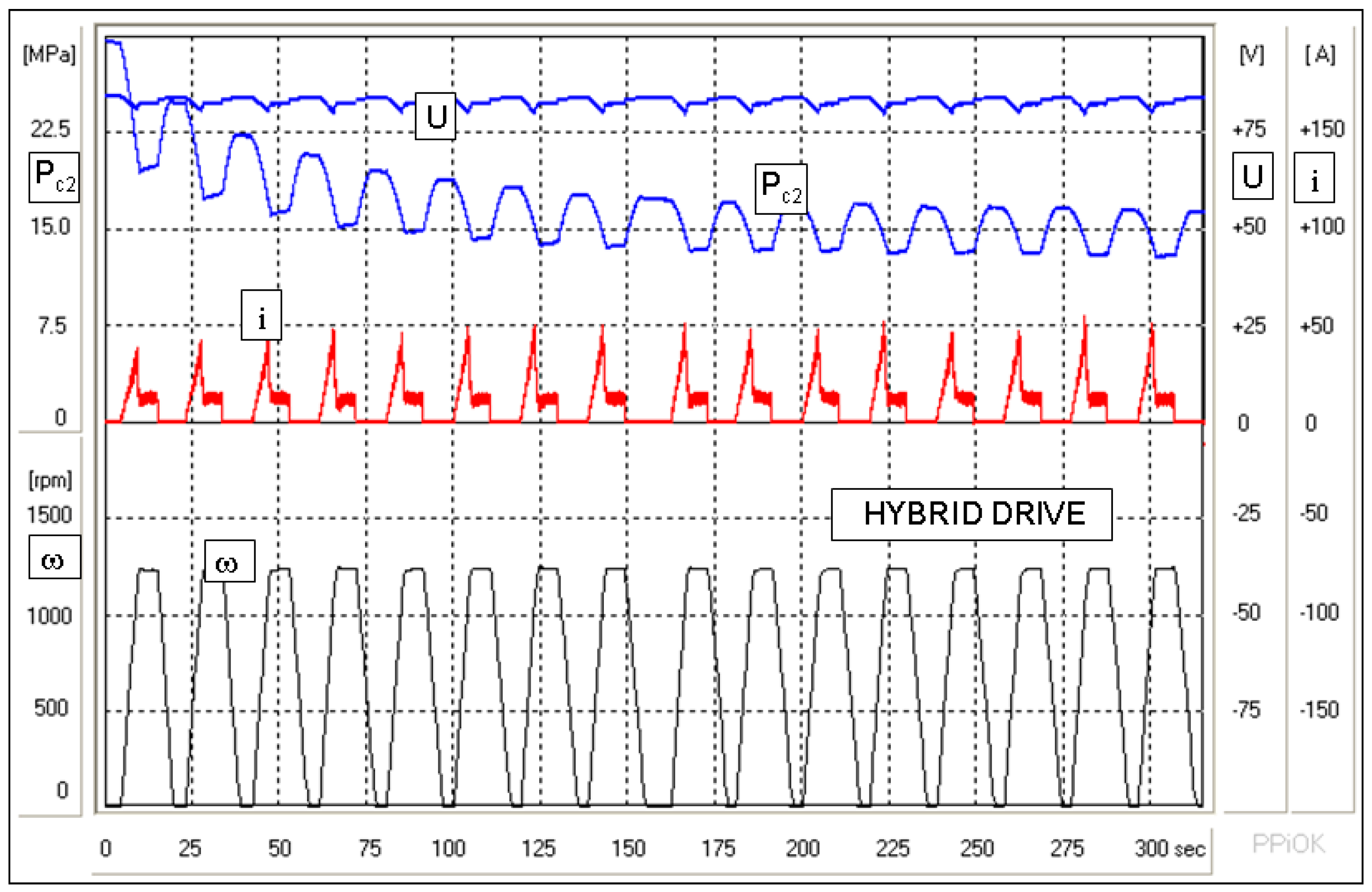
2.2. Mathematical Description of the Hydrostatic Drive
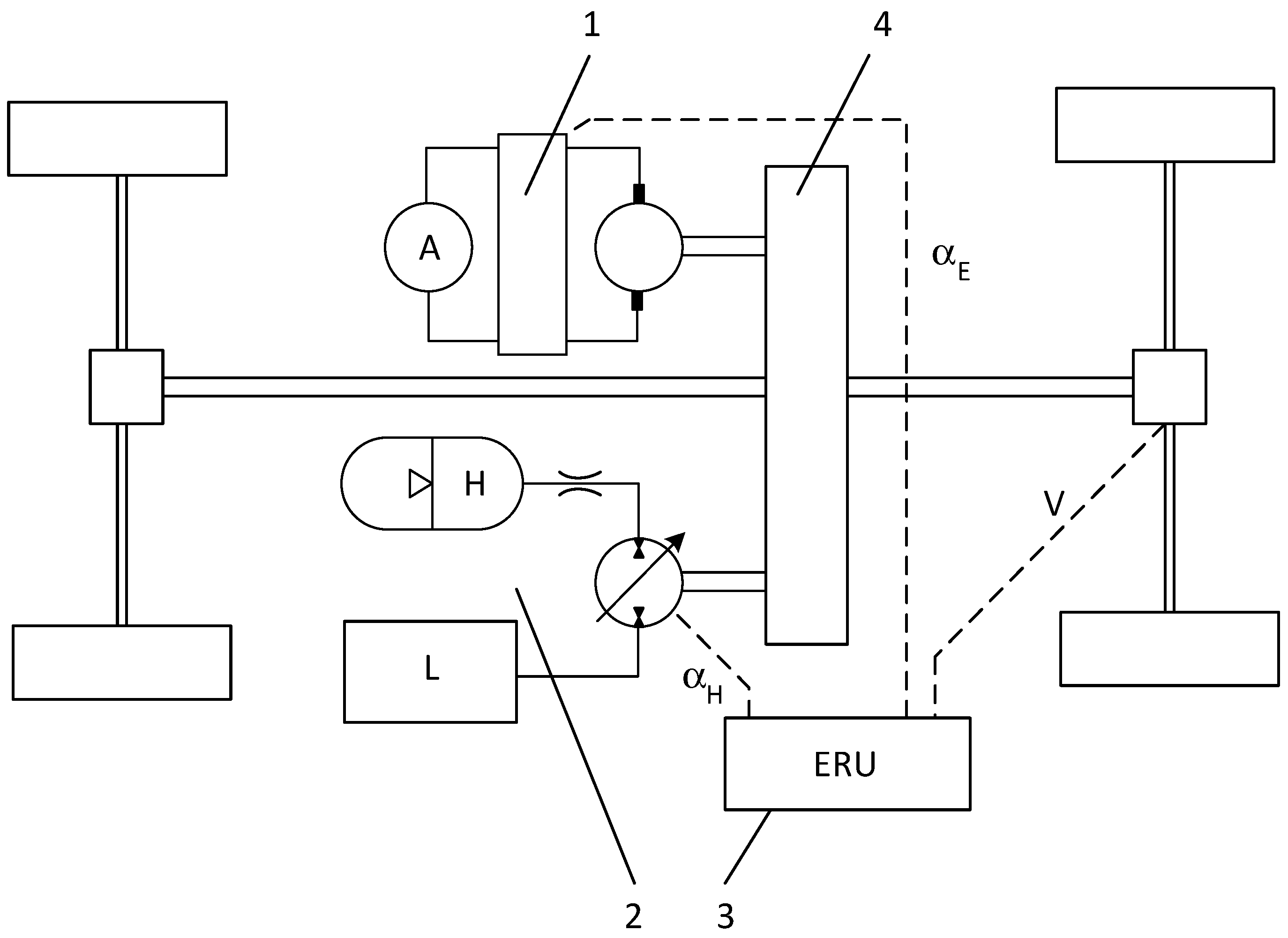
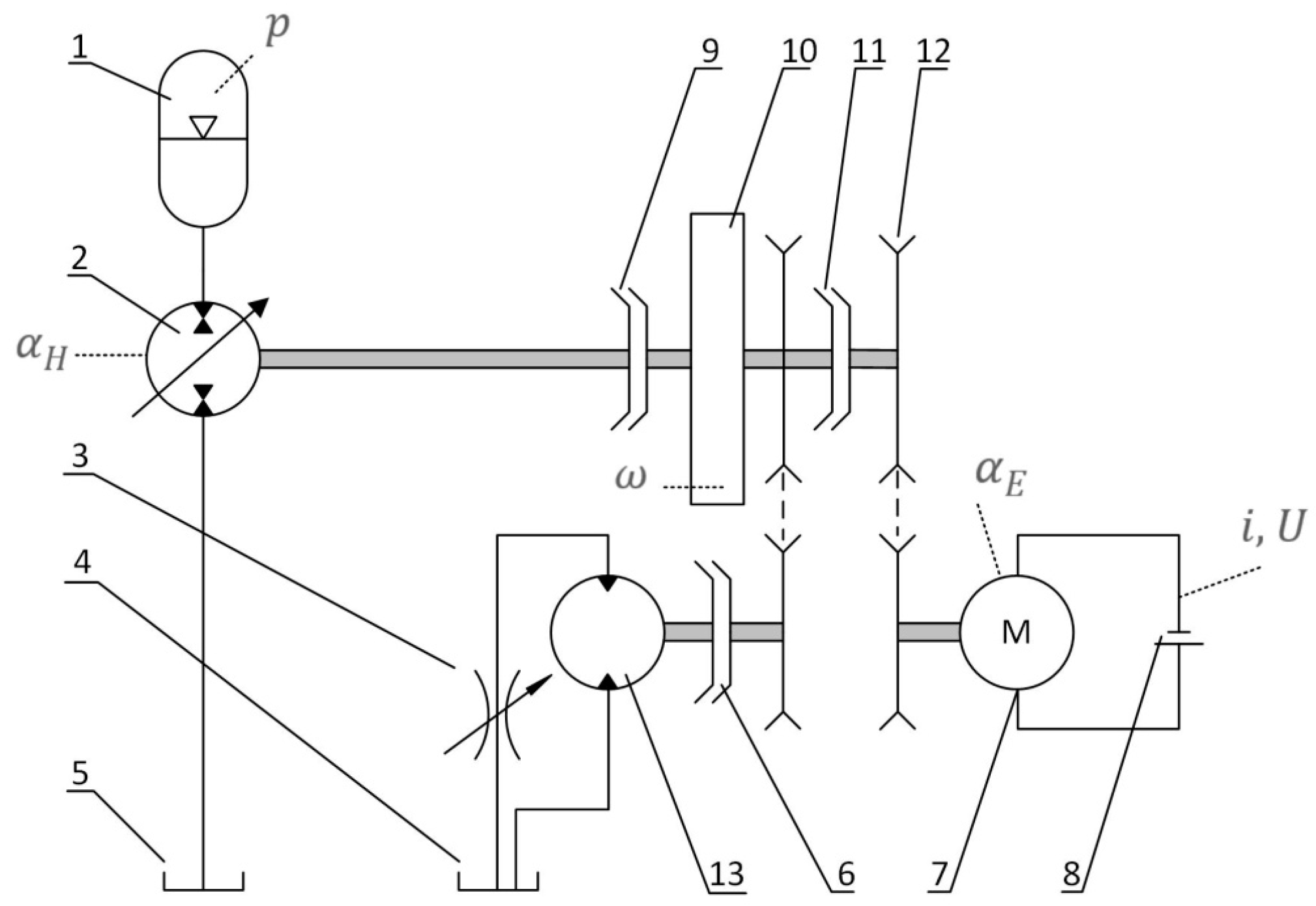
A scheme of the structure of the considered hydrostatic drive is shown in
Figure 2. The drive consists of: 1—hydro-pneumatic battery; 2—pump-motor with variable displacement, where the energy conversion occurs; 3—drive shaft; 4—oil tank with constant pressure; 5—reducer rendering hydraulic resistance in the pipeline connecting the battery with the pump-motor.
In the presented power transmission system, while the vehicle accelerates, the energy accumulated in the gas bladder 1 flows to the drive shaft 3. While the vehicle brakes, the direction of the energy flow is reverse. In the scheme of the hydrostatic drive (cf.
Figure 2), the symbols of physical quantities are shown, by means of which the energy flow process will be described. The symbols denote:
—specific volume of gas,
—gas pressure,
—specific entropy of gas,
—gas temperature,
—volume intensity of the oil flow through the pump-motor,
—signal controlling the pump-motor,
—pressure of hydraulic oil on the pump-motor terminals,
—angular velocity of the drive shaft,
—moment acting upon the drive shaft,
—pressure in the oil tank,
—ambient temperature of the hydro-pneumatic battery.
It is assumed that:
the hydro-pneumatic battery is filled with perfect gas,
in the hydraulic installation, between the battery 1 and the tank 4, there is incompressible oil
the principal resistance of the oil flow occurs in the ducts connecting the battery 1 to the pump-motor 2,
the pump-motor is treated as a perfect converter,
between the hydro-pneumatic battery and its environment, there is energy exchange in the form of heat conduction.
The amount of energy accumulated in the compressed gas is calculated as change in relation to the established reference state, according to the formula:
where:
—specific volume, specific entropy and temperature of gas determining the reference state,
—specific heat of gas,
—constant called isentropic exponent (adiabate),
—energy of gas in the reference state in relation to which the change is determined:
where:
—mass of gas included in the hydro-pneumatic battery bladder,
—volume of gas in the reference state.
As mentioned before, the crucial part of the operation of the considered hydrostatic drive is energy exchange, i.e., collecting it from the battery during acceleration and returning it during braking. Based on the Formula (1a), the power of the energy exchange is determined, assuming that the considered physical quantities change in time:
The first component of the right side of the Formula (2) determinates the power of energy exchange, connected with the change of gas volume, triggered by the operation of the hydraulic pump-motor. The second component defines the power of energy exchange between the gas and the environment, resulting from heat conduction.
Having performed the appropriate transformations, the Formula (2) can be written as follows:
if pressure
and temperature
are defined by the formulae:
As mentioned before, as a result of the operation of the pump-motor, the volume of gas changes; the rate of the change is defined by the formula resulting from the continuity of the oil flow in the hydraulic installation:
where:
—angular velocity of the rotor of hydraulic pump-motor,
—a constant characterizing the flow characteristics (volume capacity) of the pump-motor,
—signal controlling the capacity of the hydraulic pump-motor.
Expression of the right side of the Equation (5) determines the flow intensity in the hydraulic installation of the hydrostatic drive.
Usually, it is assumed, that the process of energy change in the battery occurs according to a specified thermodynamic transformation, e.g., isentropic transformation (adiabatic), in which or isothermal process, when .
While performing experimental studies it was noticed, that the patterns of variables defining the state of gas differ from the above-mentioned thermodynamic transformations. Hence, based on the results of experimental studies of isochoric transformation of gas in the battery a model of heat exchange between the gas and its environment was established. Mathematical description of this process looks as follows:
where:
—ambient temperature,
—the constant characterizing the process of heat exchange between the gas and the environment, established on the basis of the results of experiments.
In the hydraulic installation, through which the energy is transferred between the battery (1) and the pump-motor (2), the losses resulting from the resistances of oil flow occur. As a result of these losses, the difference in oil pressure in the battery occurs on the first terminal of the pump-motor (see
Figure 2). In the model, it was assumed that:
where:
As mentioned before, in the pipeline connecting the pump-motor 2 to the tank 4 the flow losses were omitted and it was assumed that there is constant pressure in the tank. Thus, the pressure on the second terminal of the pump-motor is the same as in the tank, i.e., .
From the assumption on the perfect energy conversion in the pump-motor, stems the equation of power balance:
and thus, the formula for the moment of forces acting upon the drive shaft is obtained:
Based on the above considerations, the description of the process of energy conversion in the hydrostatic drive, was formulated. The description consists of the following formulae: (4)–(7) and (9).
2.3. Mathematical Description of the Electric Drive
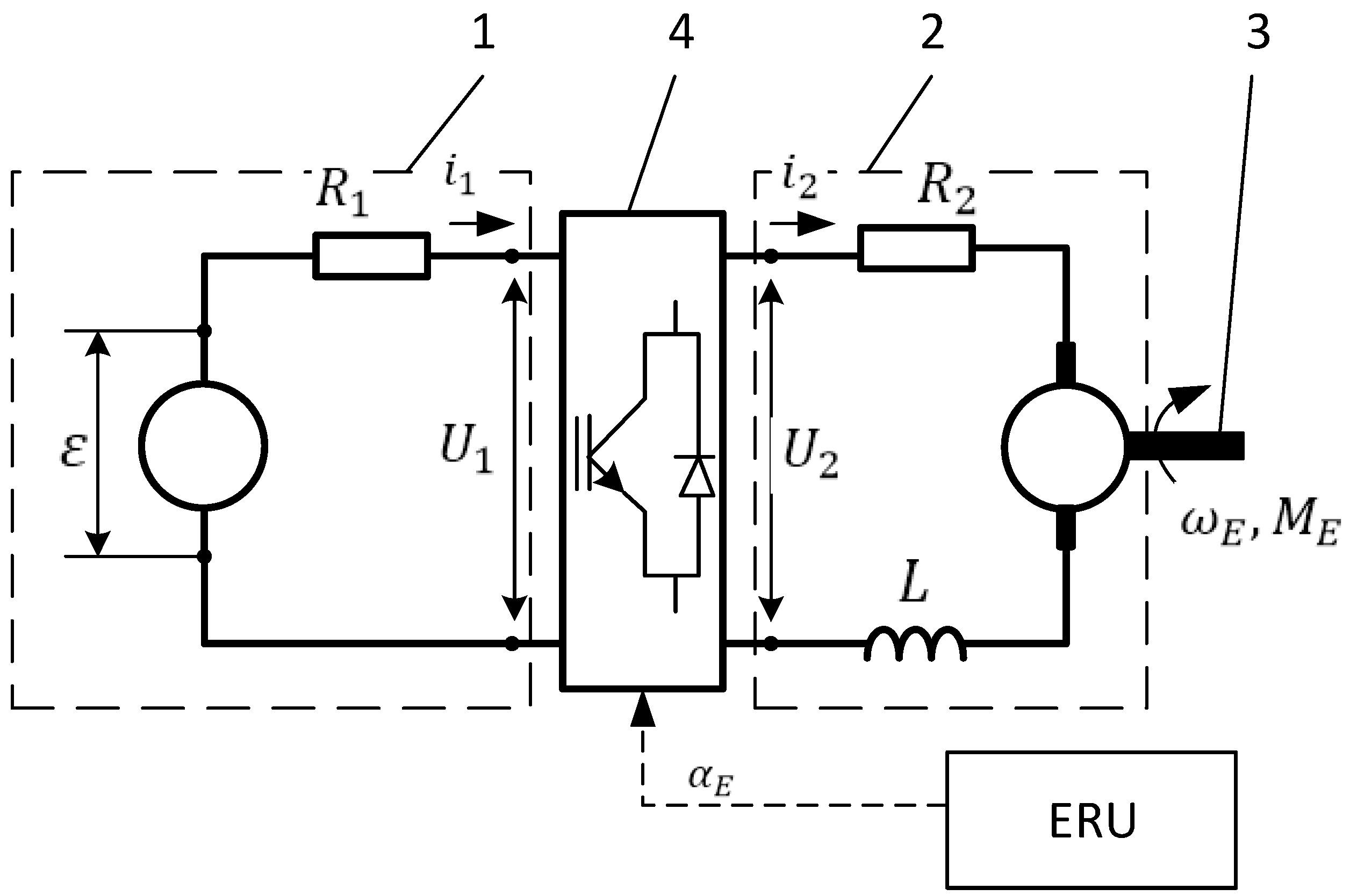
The scheme of the structure of the considered electric drive is shown in
Figure 3. The system consists of: 1—battery; 2—electric motor which can also operate in a generator mode; 3—drive shaft; and 4 —transistorized DC/DC voltage converter.
In this article, a model of a direct current commutator motor with Permanent Magnet Direct Current (PMDC) magnets is studied. Such a motor was chosen due to a relatively simple mathematical description of energy conversion process. In the scheme of the electric drive the names of variables are shown, by means of which the process of energy conversion was described. The symbols denote:
—current flowing through the battery,
—current flowing through the motor winding,
—voltage on the battery terminals and on converter terminals from the side of the battery,
—voltage on the motor terminals and on converter terminals from the side of the motor,
—inductance of motor winding,
—internal resistance of the battery,
—resistance of motor winding,
—signal controlling voltage converter,
—angular velocity of the drive shaft,
—moment of forces acting upon the drive shaft.
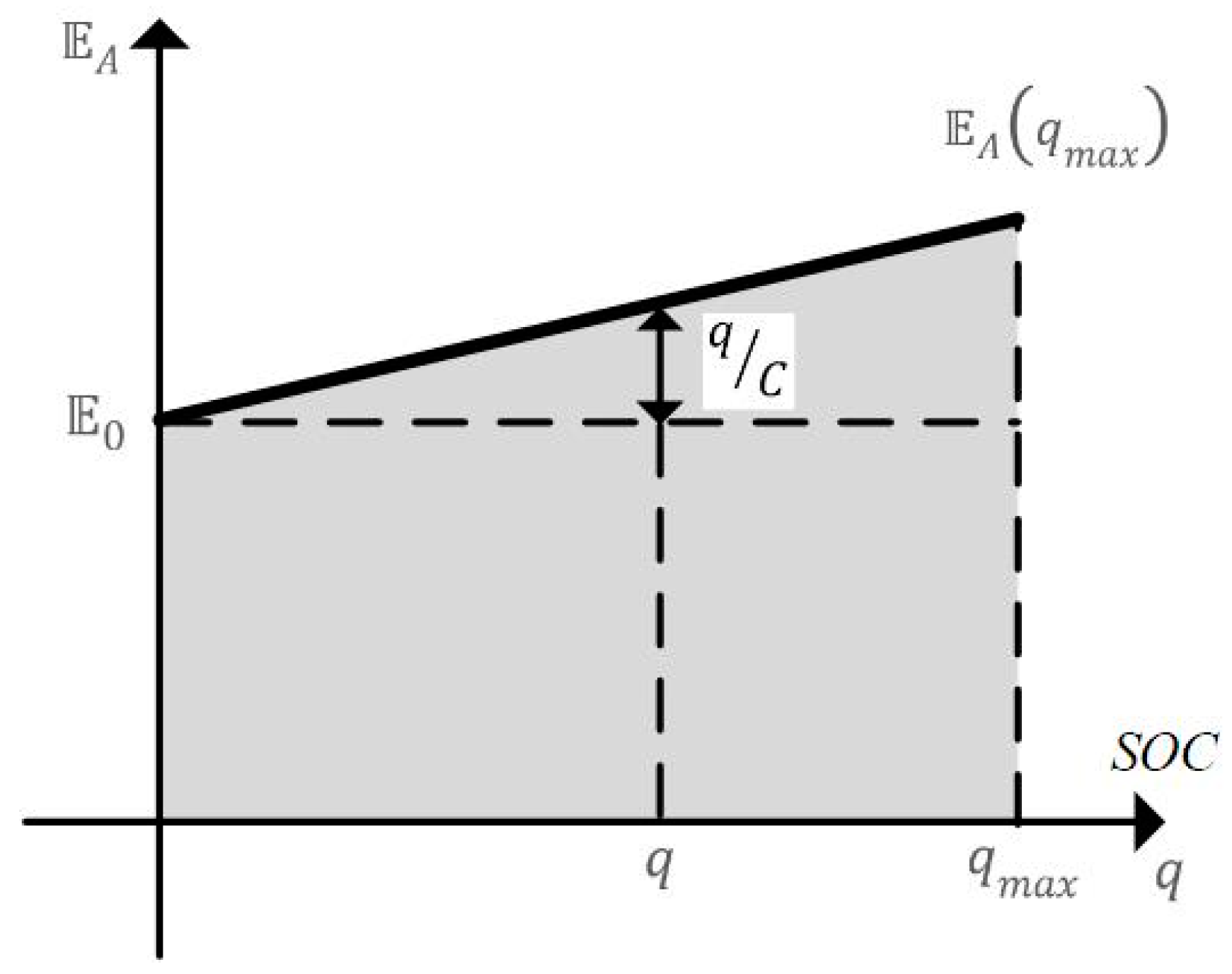
Based on the initial measurements, the form of characteristics of the electro-chemical battery was established, defining the dependencies of electromotive force
on the accumulated electric charge. Additionally, it was assumed that the internal resistance of the battery is represented by the resistor
(see
Figure 3). The scheme of the form of characteristics of the battery is shown in
Figure 4, and its description is defined by the formula:
where
—two parameters defining the form of characteristics.
Very often, instead of an electric charge the SOC (State of Charge) variable is used, and it defines the rate of battery charge in relation to the full charge state, i.e.,
The amount of energy accumulated in the battery characterized in such a way is:
and at the beginning of the simulation, at the moment
we adopt
(full charge), that is:
Thus, voltage
on the battery terminals is established by the formula:
whereas the relation occurs:
The considered electric motor is powered by voltage
, the value of which is adjusted in the converter 4 by means of the signal
. It is assumed that the converter is perfect, i.e., the balance of power is fulfilled:
and the operation of the converter is defined by the relations:
The description of current
flowing through the motor winding 2 is in the form of balance of power:
where the expression
determines electromotive force, which is induced in the motor winding rotating at the angular velocity
. In the above expression
denotes magnetic flux generated by stator permanent magnets, whereas
is the constant characterizing the motor.
It is assumed, that the perfect energy conversion occurs in the motor, determined by the following balance of power:
thus the formula for the moment of forces on the motor shaft is obtained (cf.
Figure 3):
The dependencies presented above define the process of energy conversion in the electric drive. The description of this process consists of the following formulae: (12)–(14), and (16).
2.4. Mathematical Description of the Vehicle
The considered model of the vehicle is used to analyze the process of energy conversion during vehicle accelerating and braking. For this reason the vehicle in which all wheels are connected to the power transmission system, as shown in
Figure 1, is considered. It is assumed that the vehicle performs a rectilinear motion and the vibrations of the vehicle body and the slip of wheels are omitted. Energetic features of such a vehicle are characterized by:
—mass,
—velocity,
—function describing the resistance of vehicle movement and resistances in the system of power transmission between the wheels of the vehicle and the shaft of the electric motor and the hydrostatic motor.
The equation describing the movement of such a vehicle is presented in the form of the equation:
where
—resultant moment of forces acting upon the wheels of the vehicle,
—radius of the vehicle wheels.
The value of the driving moment
is connected with moments of forces
(Formula (16)) and
(Formula (9)) acting upon the shafts of the electric motor and the pump-motor. The value is defined by the following relation:
where:
—kinematic transmission between the wheels of the vehicle and the shafts of the electric motor and the hydrostatic motor, and also that:
Formulae (18) define the energetic features of the energy transmission system from the motor shafts to the wheels of the vehicle, assuming that the balance of power is fulfilled:
Energetic losses occurring in the course of the above-mentioned energy transmission are included as an additional element of the function describing energetic losses connected with the movement of the vehicle.
Two pairs of magnitudes (), () enumerated in the Formulae (18) and (19) define energetic coupling of the vehicle with the drives described in points 3 and 4.
Thus, the description of the energy conversion process in the presented model of the vehicle with electro-hydrostatic drive also comprises the equations that were enumerated at the end of the two previous chapters (4)–(7), (9), (12)–(14), and (16), as well as the Equations (18) and (19).
It has to be stated that the above-mentioned overview of the formulae describing the process is not full, since it does not contain the method of designating the signals , controlling the drives. The method will be presented in the next section.
2.5. Description of the Electro-Hydrostatic Drive Control System
The description of the energy conversion process in the electro-hydrostatic drive was formulated in the Formulae (4)–(7), (12)–(14) and (16), as well as (17)–(19). The formulae constitute a set of ordinary differential equations with control:
if:
The presented initial issues will be referred to as a problem of hybrid drive dynamics. The form of the solution of this problem depends on two functions , describing control signals, the voltage of electric motor powering depends on, the issue described by Formulae (12)–(14), and the capacity of the hydrostatic pump-motor, described in the Formula (5).
The patterns of these signals are determined in the control system, where the conversion occurs of measuring signals defining physical quantities characterizing energetic state of both drive systems. Measuring signals are converted according to the established algorithm into control signals , , which control actuating modules of the voltage converter and the pump-motor. In this section, the designations of signals and physical quantities corresponding to them, will be the same.
Two signals external towards the power transmission system are the basis to establish the control signals , s. The first signal, described by the function determines the given speed of the vehicle within an established time frame , whereas the second signal determines the role of the hydrostatic drive in vehicle accelerating and braking.
The problem of adjusting the vehicle speed consists in designating signals
and
so that the vehicle moves at the speed
. The problem may be realized in approximation defined by the function of speed error:
where
—is the signal of speed established on the basis of solving the problem of dynamics. The obtained approximation is usually assessed by the value of integral:
The problem of speed adjustment described above does not have an unequivocal solution, since the resultant moment of forces
on the drive shaft of the electro-hydrostatic system, defined in the Formula (19) may be obtained by different moments
and
. The considered signal
determines the following relations between the enumerated moments:
Relations (23) enable establishing a clear solution to the considered problem of dynamics and control.
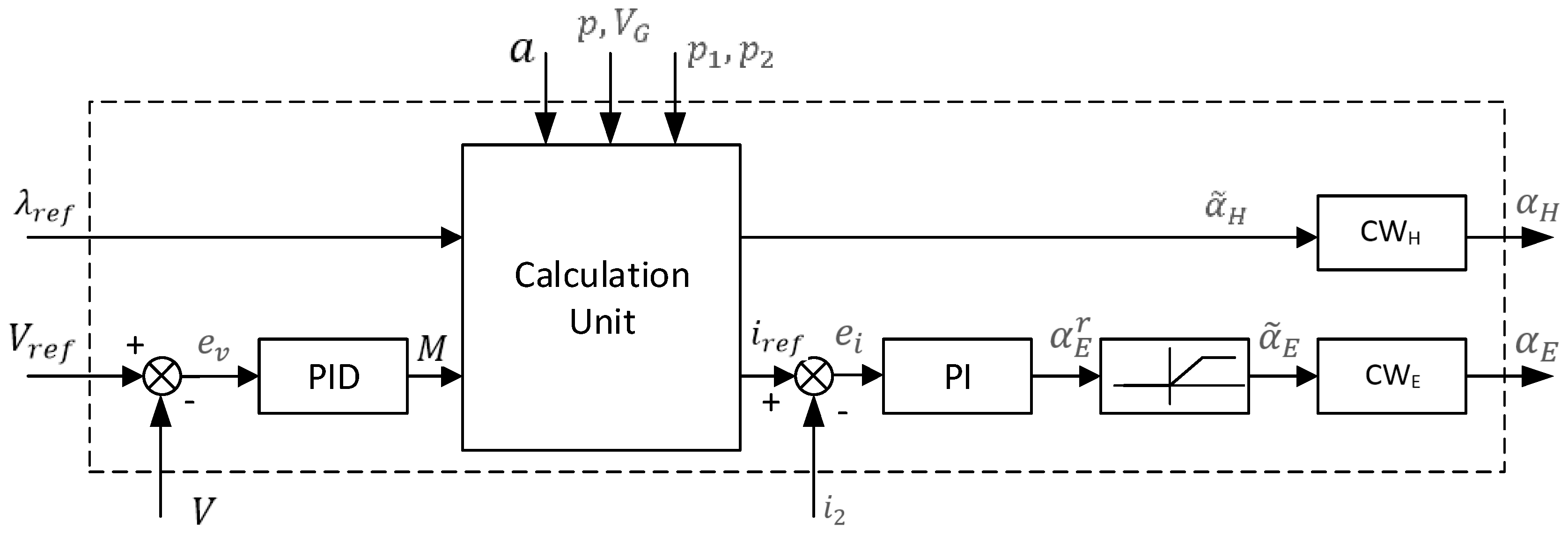
Figure 5 shows the scheme of the algorithm of signal conversion in the considered control system. The key element of the system is the PID speed controller, in which error signal
from the Formula (21) is converted into a signal of resultant driving moment
:
where
,
,
are the constants of the PID controller.
In the calculation segment, the signals and as well as a set of measurement signals are converted into the signal of the given current flowing through the motor and control signal , which flows to the executing unit in the hydraulic pump-motor .
Converting signals in the calculation segment also refers to adjusting control signals to limitations, which are imposed on physical quantities defining the state of the hydrostatic system. The moment the vehicle is being slowed down, and the pressure of gas is higher than allowable , the hydrostatic drive is disconnected. The drive is also disconnected when the vehicle is accelerated and the volume of gas is lower that the allowable, i.e., .
The next limitation concerns the efficiency of the pump. In this case, the value of the moment of the pump , calculated according to the Formula (23) may be realized only when the value of the signal determined by the Formula (9) fulfills the condition .
The limitations described above result in the reduction of load on the hydrostatic drive, which in turn causes the load of the electric drive, so that the balance of moments described in the Formula (19) is fulfilled. The procedure described above enables calculating the moment of the electric motor , and then establishing by means of the Formula (16) the value of current intensity , which is adjusted in such a way, so that it does not exceed the allowable value . As a result of this adjustment, the given value of the current is obtained so that .
Then, the signal of the current error is established:
where
is the measurement signal of the current flowing through the motor.
The signal of the current error is converted in the PI controller, i.e.,
As a result, a signal controlling the voltage converter is obtained. The constants , define the settings of the PI current controller. It was assumed, that in the considered converter, voltage powering the motor may not exceed the voltage of the battery , which was described in the Formulae (13).
Hence, the adjustment of signal occurs, so that its value is lower than 1. The signal adjusted in such a way, flows to the execution unit in the converter.
It was assumed that the operation of the execution units
i
is modelled using the 1st order inertial system, i.e., the sought control signals
(cf.
Figure 5) are defined by equations:
The algorithm of signal conversion in the drive control system described above and schematically shown in
Figure 5 enables establishing the solution to the problem of dynamics of the electro-hydrostatic drive (20).
It has to be stressed that the form of the solution depends upon two defining signals: vehicle speed and the role of the hydrostatic drive in the energy conversion process .
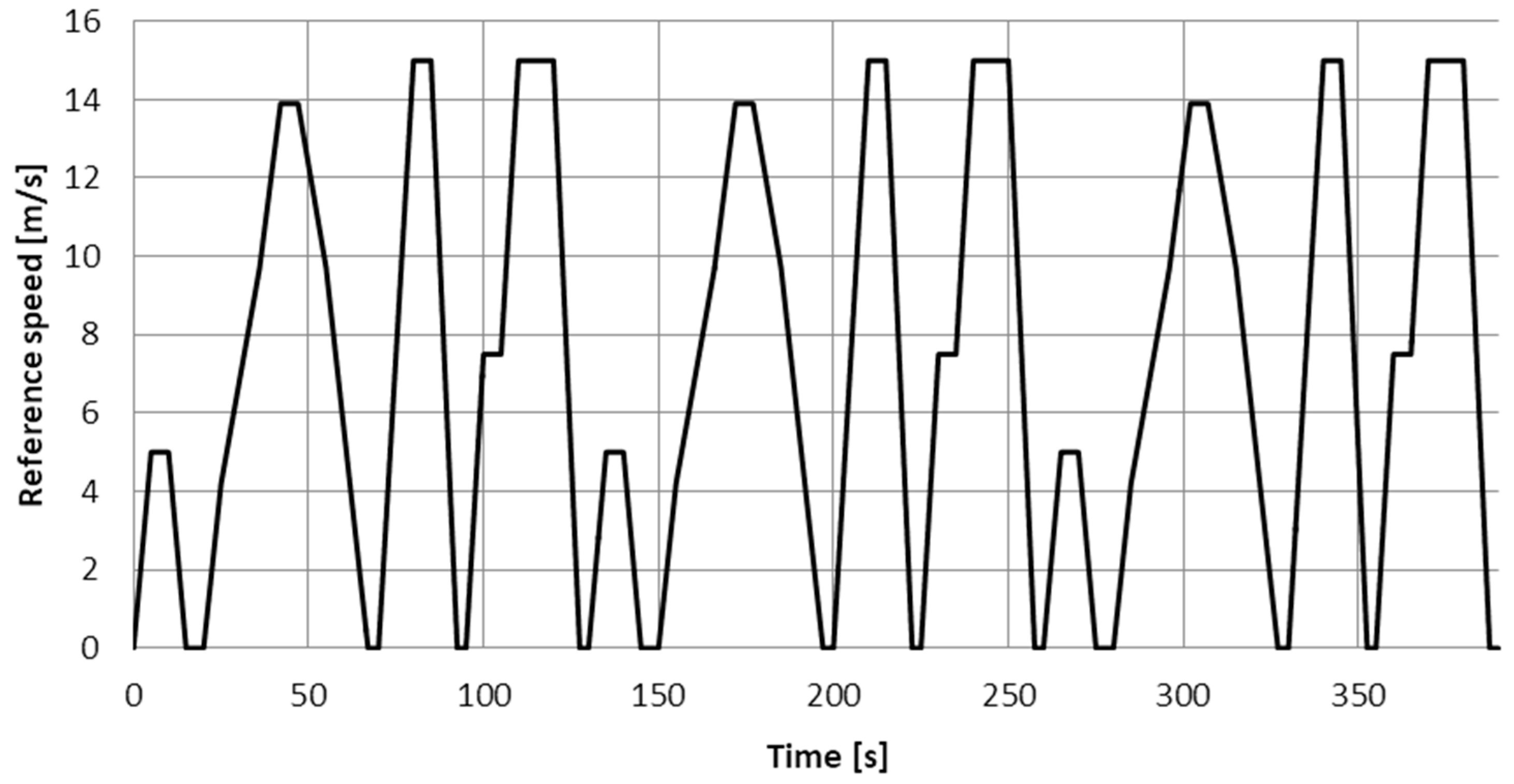
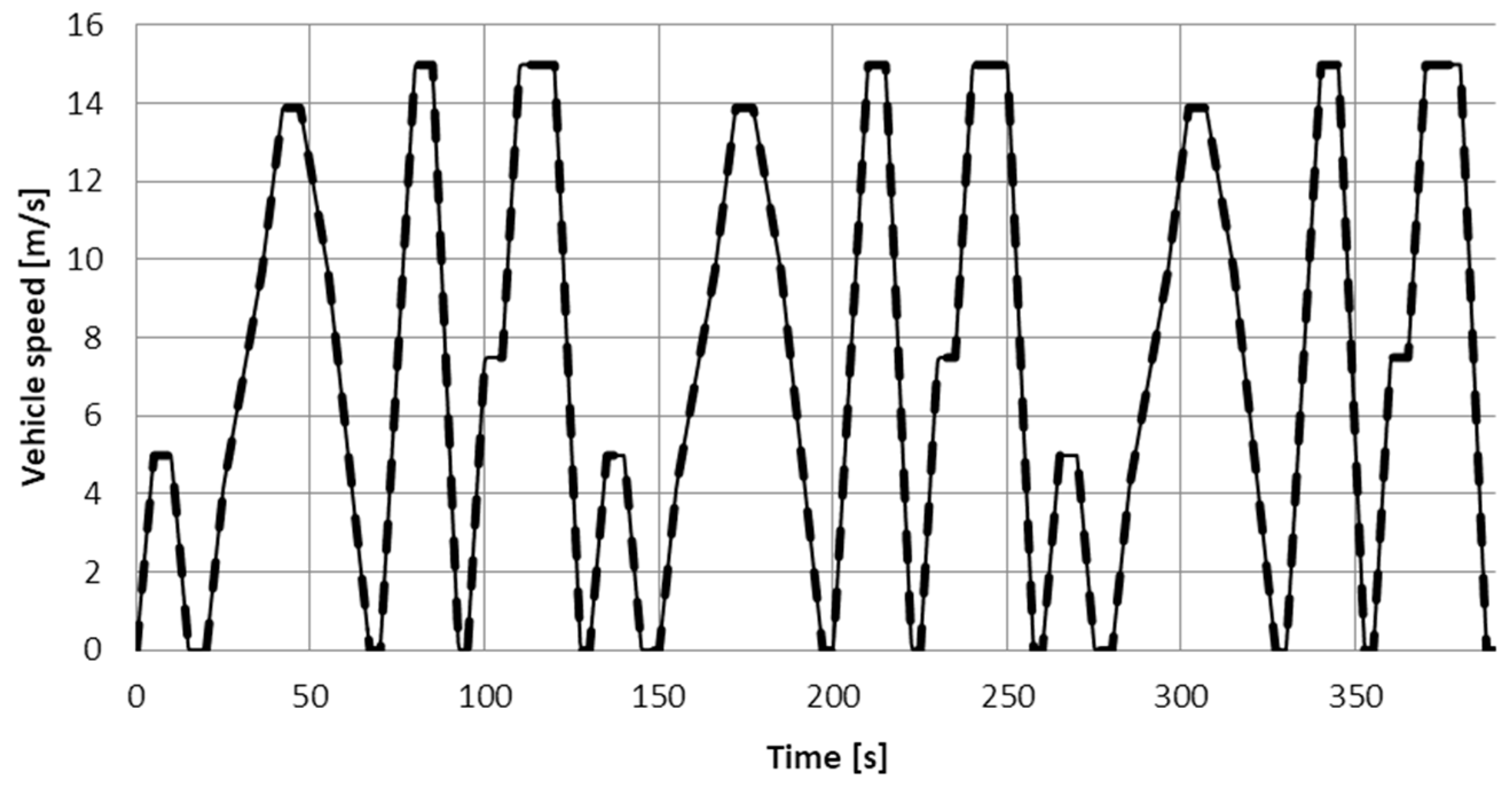
In this article, the signal
, rendering the speed of the vehicle in the city traffic is considered.
Figure 6 shows the graph of the assumed function
, which is similar to the New European Driving Cycle (NEDC) function developed for the traffic of a vehicle with a combustion engine in European cities [
10].
The essential property of the considered idea of the electro-hydrostatic drive is higher effectiveness of energy conversion in comparison with the electric drive, and the decreased load on the electric battery. The effectiveness will be evaluated based on the amount of energy necessary to cover an established route at the speed defined by the function , and the load of the electric system will be assessed by the effective value of the current.
In the electro-hydrostatic drive, the signal
defining the role of the hydrostatic drive in the energy conversion, has the greatest influence on the amount of energy collected from the batteries and on the value of current. The optimal signal
can be established using various methods. Similar issues are considered in traditional hybrid drives, in which the combustion engine is supported by an electric drive (HEV) [
11,
12,
13,
14] or in hydrostatic drives (HHV) [
9,
15] as well as in electric drives with hybrid energy storage system (HESS) [
16].
In the article, the signal
was established based on initial simulation studies of the modelled movement of the vehicle. Signal
was described using a function:
where
—vehicle acceleration,
—values that will be shown in the results of simulation studies in the next chapter.
The values of signals
presented above can be changed when the load of the drive reaches border values. Due to the comparative nature of the evaluation of the effectiveness of energy conversion in the electro-hydrostatic drive, a model of a vehicle with electric drive was also considered. In both these models the electric drives are the same, whereas the electric drive control system contains only the elements that are in the bottom part of the scheme shown in
Figure 5.
2.6. Description of the Model Parameters
Below are presented the values of parameters of the model of the vehicle with hybrid drive, the mathematical description of which was given in previous sections.
A commercial vehicle with an unladen mass kg and a load with a mass kg was considered. The following parameters of the vehicle were assumed: radius of the wheel m, leverage transmission connecting wheels with motor shafts , movement resistance was described using the formula where is the moment of forces defining the moment of resistances of the pump-motor movement. It was assumed that Nm.
Function
describing the electromotive force of the battery has the following form:
if
V,
kF (see
Figure 4), and the internal resistance of the battery is
Ω. It was assumed that in a fully charged state, the electric charge amounts to
Ah and the energy of the fully charged battery equals
kWh. The values of the motor parameters are as follows:
mH,
Ω,
Nm/A,
A.
The hydrostatic drive is characterized by the following values of parameters: in the bladder of the hydro-pneumatic battery there is nitrogen; in the initial state: bar, dm3 and K, J/kgK, mass of gas amounts to kg, and the amount of energy accumulated in one battery kWh. Additionally, it was assumed that the time constant defining the process of heat exchange equals s, and ambient temperature K. The hydrostatic system is powered by two hydro-pneumatic batteries described above. The values of parameters of the pump-motor and of the hydraulic installation, given in the Formulae (7) and (8) amount to: l/obr, bar, bar.
The settings of the PID speed controller are defined by the coefficients , s, s, and for the PI current controller the settings amount to , s.
Considered simulations referred to the passage on the route of 2860 m lasting 390 s at a given speed
, the course of which is illustrated by the graph in
Figure 6. The average speed of the trip is 26.3 km/h.
As mentioned before, signal , defining the role of particular drives in performing driving or braking moments of the vehicle, plays a crucial role in controlling the hybrid drive. Based on initial studies, the following values of constants from the Formula (28) were assumed: —when the vehicle is accelerated, —when the vehicle is slowed down, —when the vehicle moves at a constant speed.
Apart from the vehicle with a hybrid drive, a model of an electric vehicle was also considered. It was assumed that both vehicles had the same electric drives, and the mass of the electric vehicle was lower by 100 kg. The obtained simulation results were performed in terms of the influence of the hydrostatic support on the effectiveness of the energy conversion, and the amount of energy collected from the electric battery until the passage finished was assumed as the ratio of this effectiveness.
2.7. Results of Simulation of Energy Conversion Process
Simulation of the energy conversion process in the considered drive was performed using a software for computer calculations, which was devised based on the presented description of the problem of dynamics and control (20).
A passage on the described route of vehicles with the electro-hydrostatic drive and the electric drive with the load of about 500 kg was simulated. The results of the simulation constitute the solution to the problem of dynamics and control, in the form of variable courses defining the energy conversion process and the control signals.
Due to the relatively broad scope of simulation results, the chosen results, referring to the transport of the load of 500 kg, are given.
Initially, in
Figure 7, two graphs illustrating the vehicle speed error are shown (Equation (21)). The graphs refer to the hybrid drive. By comparing the graphs it may be concluded that a satisfactory approximation of two graphs was obtained (Equation (22)), which confirms the proper choice of control system parameters. It ought to be added that an analogous result was obtained for the vehicle equipped only with an electric drive.
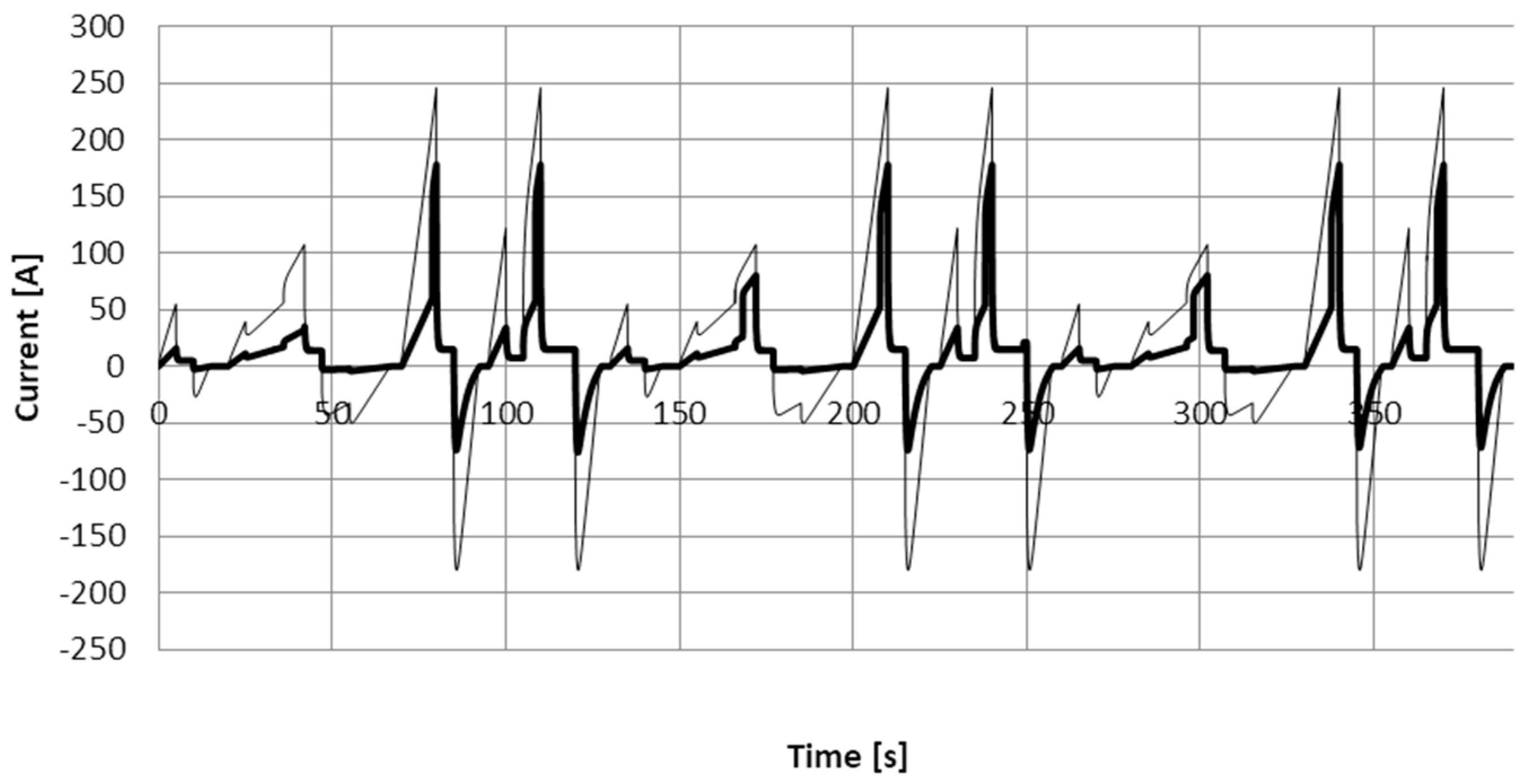
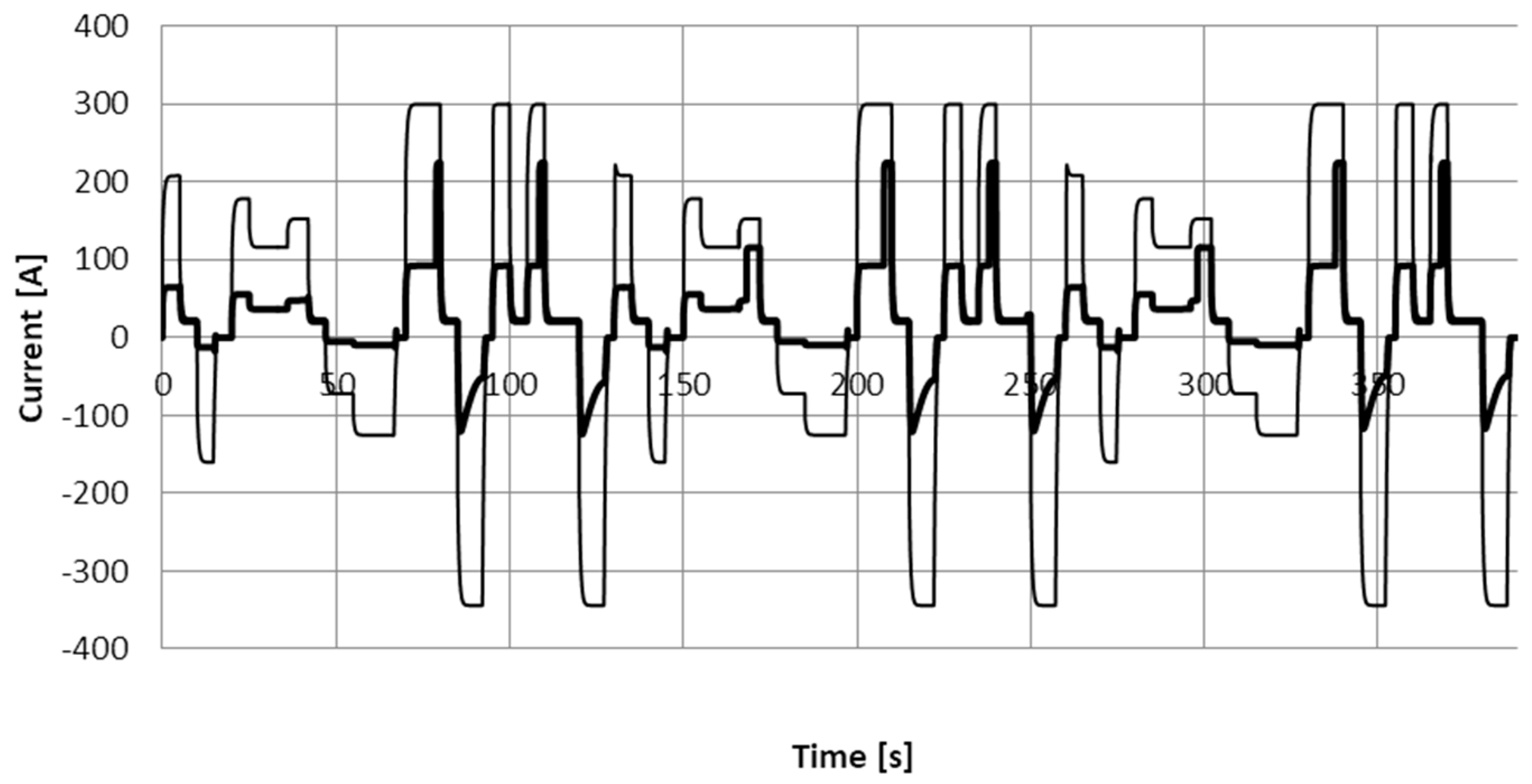
The load of the electric system in the electric drive and in hybrid drive will be illustrated by the graphs of currents flowing through the battery
and through the motor
.
Figure 8 shows an overview of the graphs of currents flowing through the batteries of both drives, i.e., the hybrid electro-hydrostatic and electric drives. Analogous graphs, shown in
Figure 9, refer to the current flowing through the electric motor.
Comparison of the presented graphs allows for the conclusion that the load of the electric system in the hybrid drive is considerably lower. In order to evaluate the load, two indices are assumed:
where
and
—defined according to the Formula (11),
—the amount of energy collected from the electric battery during the entire passage,
—effective value of intensity of current flowing through the electric motor during the entire passage.
The value of these indices in the considered passages amounted to:
kJ and A—for the vehicle with only electric drive,
kJ and A—for the vehicle with the hybrid electro-hydrostatic drive.
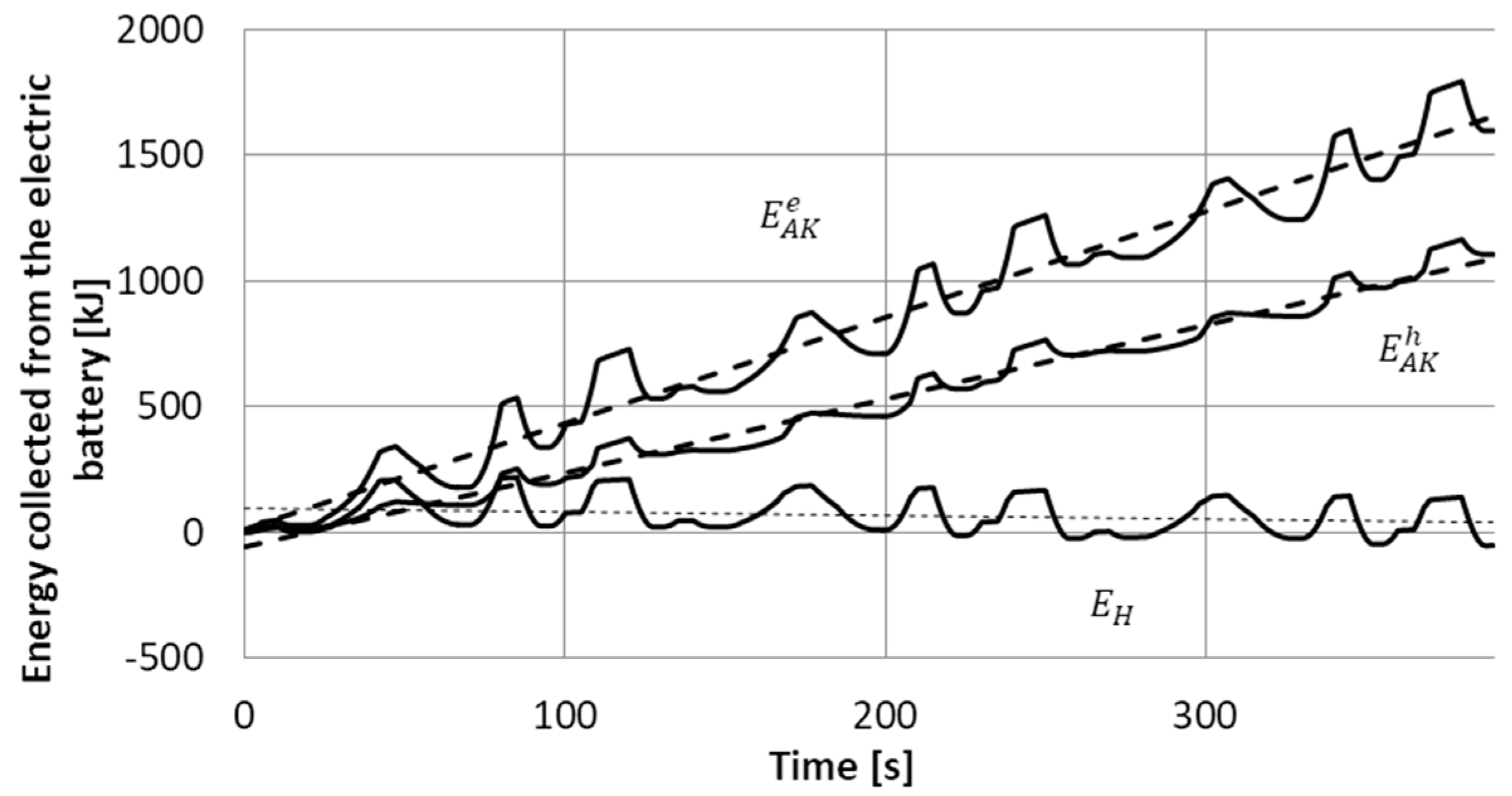
Graphs shown in
Figure 10 illustrate the curves of energy collection from the electric battery in the electric drive and in hybrid drive, as well as from the hydro-pneumatic battery.
Based on these graphs an average integral power of the electric battery may be established. In the electric drive, the power amounts to 4.31 kW, and in the hybrid drive 2.68 kW which constitutes 62% of the power of the electric drive. An oscillating course of energy collection from the hydro-pneumatic battery, with the amplitude of 100 kJ is worth noting. It means, that the average amount of energy in the battery does not change.
The simulation results presented above confirm the thesis on the possibility of increasing the effectiveness of energy conversion in the electric drive due to applying the hydrostatic support.
The values of indices given above show, that in the hybrid drive the amount of energy collected from the electric battery is lower by 30%, and the values of the effective current intensity decreased by 65%.
In the course of the passage, almost entire energy collected from the batteries is dispersed by movement resistances and hydraulic resistances, as well as by electric resistance. A detailed analysis of the performed simulations enables to develop a balance of energy conversion during the passage. For example, for the passage with the load of 500 kg, the balance had the following form:
Balance of energy for the electric drive:
kJ—energy collected from the electric battery,
kJ—energy dispersed by the resistances of movement of the vehicle,
kJ—energy dispersed due to the internal resistance of the battery
kJ—energy dispersed due to the resistance of motor winding;
Balance of energy for the hybrid drive:
kJ—energy collected from the electric battery,
kJ—energy collected from the hydro-pneumatic battery,
kJ—energy collected from the environment,
kJ—energy supplied to the oil tank,
kJ—energy dispersed due to the resistances of movement of the vehicle,
kJ—energy dispersed due to the resistance of the electric system,
kJ—energy dispersed in the hydraulic system.
The energy balance elements listed above indicate the difference between the amount of energy dispersed due to the resistance of the electric system in the electric drive, amounting to
kJ, and the analogous energy dispersion in the hybrid drive
kJ. It stems from a significant decrease in the value of current intensity in the hybrid drive, which is shown in
Figure 8 and
Figure 9.
A secondary effect of energy conversion process in the hybrid drive, resulting from the energy exchange between the hydro-pneumatic battery and the environment, described in Formula (6) is also worth mentioning. In the course of the considered passage, the battery collected the energy from the environment in the amount of kJ.
The presented analysis of the results of simulation of energy conversion process, confirms the assumed thesis on the possibility of increasing the effectiveness of energy conversion in the electric drive of a vehicle by means of the hydrostatic support. In the next chapter, the results of experimental studies on energy conversion in analogous drives will be given.