1. Introduction
In demand response (DR) programs, electricity consumers play a significant role in power system operations in terms of reducing their electricity usage during system peak load in response to a time-based rate or incentive payment [
1]. DR is implemented to avoid expensive electricity or peak demand prices and operated by a utility or an independent system operator (ISO). Recently, DR programs have emerged globally as an interesting approach for accommodating the high penetration of renewable energy sources. Although much effort has been made to increase renewable energy uptake to help solve environmental issues, their inherent uncertainties complicate balancing demand against supply. Therefore, there have been many attempts to utilize DR resources to ensure that they can respond faster than conventional resources, thereby facilitating stable power systems.
Of the various incentive-based DR programs, this paper focuses exclusively on peak-time rebate (PTR) programs. These programs are normally offered to residential consumers, and they provide financial incentives based on how much participants curtail their usage during specified times known as events—each event usually lasts 3 or 4 h for residential DR programs [
2]. The most important aspect of DR program operation is accurate estimation of the amount of demand reduction by individual DR participants during the event period in order to pay appropriate incentives to them. The demand reduction is calculated as the difference between the customer baseline load (CBL), i.e., their estimated demand if there was no event, and the actual load during the event [
3]. Thus, the CBL must be predicted precisely so that the utility can pay the correct incentives and ensure its financial/economic sustainability.
Many studies have presented statistical methods for estimating the CBL. Historical demand-averaging and day matching are conventionally used to this end by utility companies [
3,
4]. regression is also a typical method used for baseline estimation [
5,
6,
7,
8]. Optimized exponential smoothing was developed based on demand and weather [
5,
6]. Hatton [
9] performed baseline estimation of residential customers using available residential load curves from a control group that did not participate in the DR program. Additionally, machine learning has also been applied to CBL estimation to mitigate the numerous uncertainties particular to residential customers. Appling machine learning in baseline estimation can be categorized into two parts: (i) Clustering customers before the estimation and (ii) using the prediction model [
2,
10,
11,
12,
13]. Examples for the first category include using
k-means for estimation of clustered customers based on their load patterns [
9], and implementing
k-means with self-organizing map techniques [
10,
11] in an attempt to conduct baseline estimations using customer groups. Jazaeri et al. [
2] demonstrated that estimation model-based machine learning with an artificial neural network (ANN) and polynomial extrapolation outperforms historical demand-averaging, regression, ANNs, and polynomial interpolation. Problems with regard to DR program operation, such as erroneous system operation and miscalculated payment, have been solved using probabilistic estimation [
13]. However, despite the need to accurately predict the CBL to ensure economically viable DR programs, the customers must be able to understand how their CBL is being calculated, which limits practical application of machine learning methods [
4,
14].
Baseline estimation is similar to short-term load forecasting (STLF), which is a research area being actively investigated, because both baseline estimation and STLF provide demand forecasts for less than 24 h. STLF research has been conducted with multiple methodologies; among them, support vector regression (SVR) and support vector machines (SVMs) have been employed to predict electric load [
14,
15,
16,
17]. Hybrid parameter optimization [
14] and ant colony optimization [
15] have been utilized in STLF to find the best parameters for SVR. SVM with simulated annealing has been presented [
15], and a genetic algorithm-based SVM has been proposed [
17]. Hybrid models based on SVMs, such as hybrid autoregressive integrated moving average (ARIMA) and SVM and hybrid ANN and SVM, have also been studied [
18,
19,
20]. ANNs have been researched in the past, and they are again being actively discussed and studied as deep learning became feasible. Many papers have proposed ANN models for STLF [
21,
22,
23,
24]: e.g., a gray neural network model including wavelet decomposition [
23]. Statistical time series forecasting models, such as regression, exponential smoothing, and autoregressive moving average (ARMA), have traditionally been employed, but these models analyze their components linearly. To overcome this limitation, ARMA with a non-Gaussian process has been used to predict short-term load [
25], and double-seasonal exponential smoothing has been proposed and shown to have superior performance [
26,
27].
Unfortunately, even with such advanced estimation algorithms, accurate baseline estimation for residential customers on the distribution side is quite difficult because of the uncertainty and variability in demand due to the various factors that affect residential customers, such as home appliance usage patterns, the number of family members, life patterns, customer occupations (i.e., schedules), and income. Moreover, these factors cause residential demand to have far more variability than commercial and industrial demand [
7]. Accordingly, some utility companies that use DR programs for residential customers, such as Pacific Gas & Electric (PG&E) and San Diego Gas & Electric (SDG&E) [
3], have been concerned about low accuracy in CBL estimation. In particular, CBL overestimation causes inappropriate incentive payments, potentially resulting in free riders, i.e., those who receive incentive payments despite not reducing demand during an event. Existing research indicates that in order to reduce excessive incentive payments to free riders, utility companies would need to operate DR programs aimed at targeted participants who respond well to reduction notices [
3]. Barring this or other solutions that address customer participation in demand reduction, the free rider problem may occur with any CBL estimation method when used alone owing to the possibility of overestimation. Thus, CBL estimation techniques are intrinsically limited in their ability to address this problem, so the inclusion of a corrective step after CBL estimation may provide the best route to addressing the free rider problem in an algorithm.
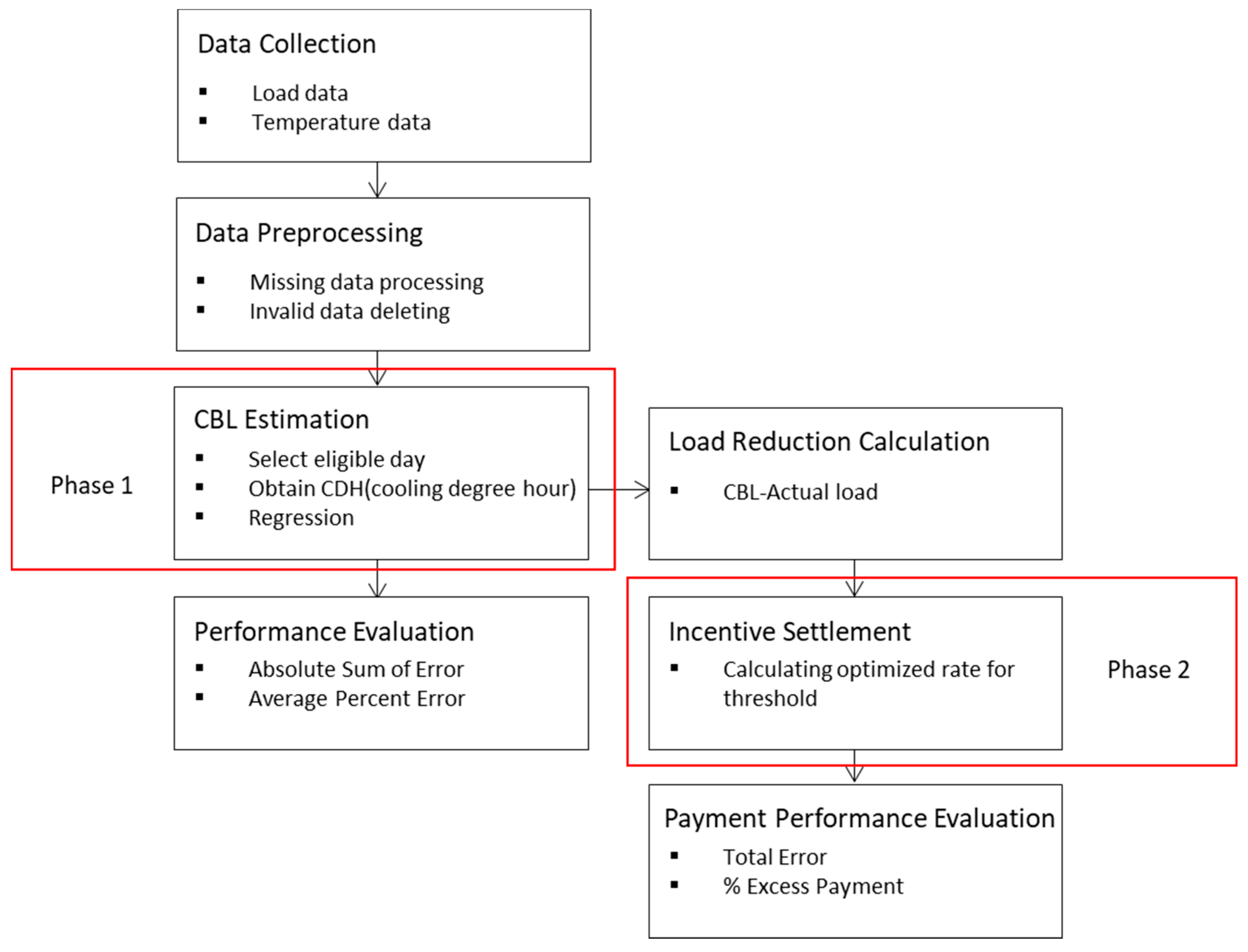
Therefore, in this study, we propose a two-step method to address the free rider problem. In the first step, the CBL is predicted using a regression-based CBL estimation method. In the second step, the incentives are settled using a new incentive payment rule, which calculates incentives depending on load reduction for a specific baseline rate in order to avoid excessive CBL prediction. The results of this study reveal an appropriate rate for residential customers. The remainder of this paper is organized as follows. In
Section 2, we present existing statistical CBL methods used for simulating baseline estimations for residential customers in DR programs. In
Section 3, we present the proposed 2-step model, which ensures effective incentive settlement to minimize the scale of free riders. In
Section 4, we show the amount of incentives offered by different CBL methods and present incentive payment rules for a DR program operated for residential customers in Korea.
Section 5 concludes the paper and outlines ideas for further research in this area.
4. Case Study: Incentive Scale Analysis in a Korean Residential DR Program
Although much attention has been devoted to demand-side management, DR operations in Korea have traditionally been limited to commercial and industrial customers. However, utility companies have recently opened up DR programs to residential customers as well. As a result, the Korea Electric Power Corporation (KEPCO) has been conducting a peak-time rebate (PTR) pilot program. As an alternative to time-of-use (TOU) and critical-peak-pricing (CPP), the PTR provides incentives matching the amount of electricity reduction achieved by participants after they receive the notification to reduce their demand. The DR program in Korea has adopted the high 4 of 5 method to determine CBL. Accordingly, the PTR pilot program for residential customers in Korea has also been applied in the same manner. In order to settle incentives, we analyzed residential customer demand data from the PTR pilot program and applied the proposed two-step methodology discussed in the previous section.
4.1. Input Data
This study was conducted by using residential demand data from the case study. We obtained residential hourly demand data and temperature data in the region where the residential customers live from KEPCO and the Korea Meteorological Administration, respectively. These data included 27,660 residential customers, of which 896 participated in the PTR pilot program. The data were from June through September in 2017, during which the PTR pilot program was operated from late July to mid-September. Events occurred on 10 days in total from 13:00 to 17:00. In this paper, we considered the data for all residential customers when we evaluated CBL estimation performance; in contrast, the payment rule analysis was conducted based on the demand data from the PTR program participants to recognize the influence of incentive payments for participants in the PTR program.
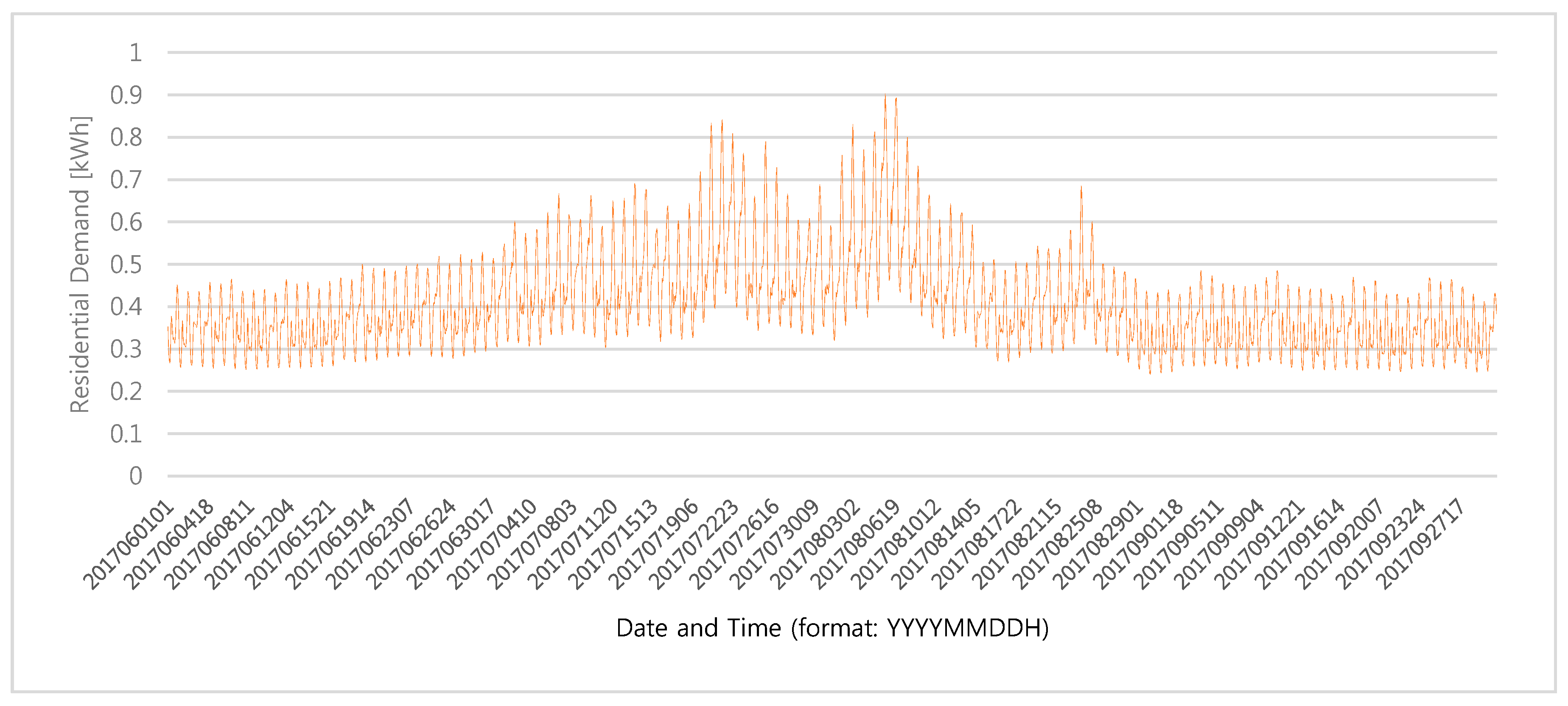
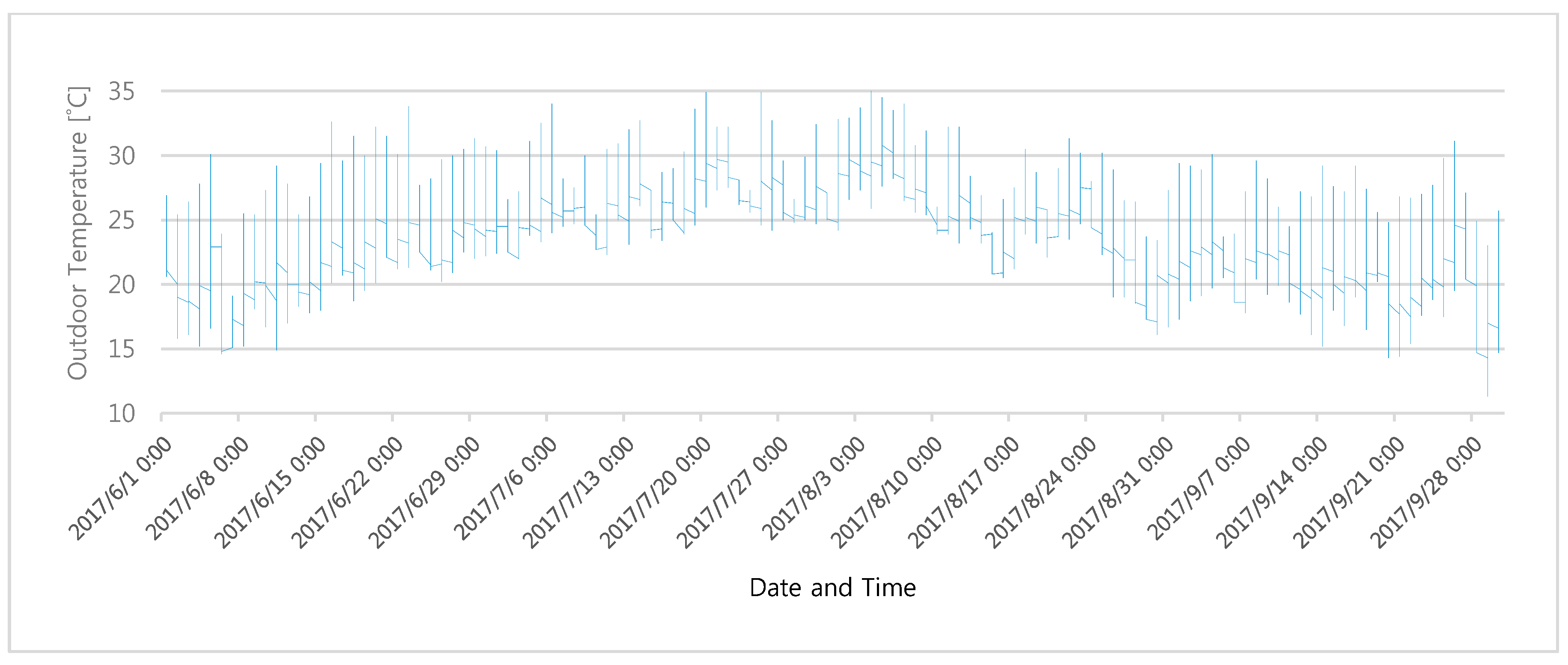
The hourly demand and temperature data are illustrated in
Figure 2 and
Figure 3, respectively.
Figure 2 reveals that the average hourly demand for residential PTR program customers in Seoul, Korea, was highest from late July to the middle of August. However, demand was relatively low on event days, despite occurring in periods of high demand occurrence.
Figure 3 confirms that the daily temperature in Seoul, Korea, has seasonal variation, with the highest temperatures occurring during daytime. The temperature was corresponding high during periods with high demand.
4.2. Proxy Day Selection
When we selected proxy event days, a similarity with event days in terms of peak demand and maximum temperature was considered. To find proxy event days, the trend line of actual event days was considered. The trend line is obtained by regression of peak demand as a dependent variable and maximum temperature as an independent variable. Then, we selected 10 proxy event days which are close to the trend line as shown in
Figure 4. As shown in
Figure 4, a trend line of proxy event days (blue line) is similar with the trend line of actual event days (red line). Among 10 proxy event days, five days were selected in order of similarity with the trend line of actual event days. They were used for evaluating CBL estimation accuracy and proposed payment rule. Then, suitable thresholds rate (
) was evaluated using the remaining five proxy event days. In the sensitivity analysis, the
obtained using the remaining five proxy event days and the root rate calculated using the first five proxy event days were analyzed to investigate and compare the results.
4.3. Free Rider Problem
This study examined the accuracy of the CBL calculated for 896 residential customers in Seoul, Korea, by selecting five proxy days similar to days with real PTR events from June through September in 2017. Proxy days were selected to have peak power and average temperature similar to those of the event days. If too many proxy days were selected, the characteristics commensurate with the weather and consumption of electricity on event days, which only include hot days with high consumption during short periods in Korea, would be obscured. Similarly, SDG&E considers only the five proxy days to perform PTR baseline evaluation and evaluate incentive payment rules [
3]. Therefore, the proxy days of 7 August, 14 August, 21 August, 1 September, and 5 September were selected.
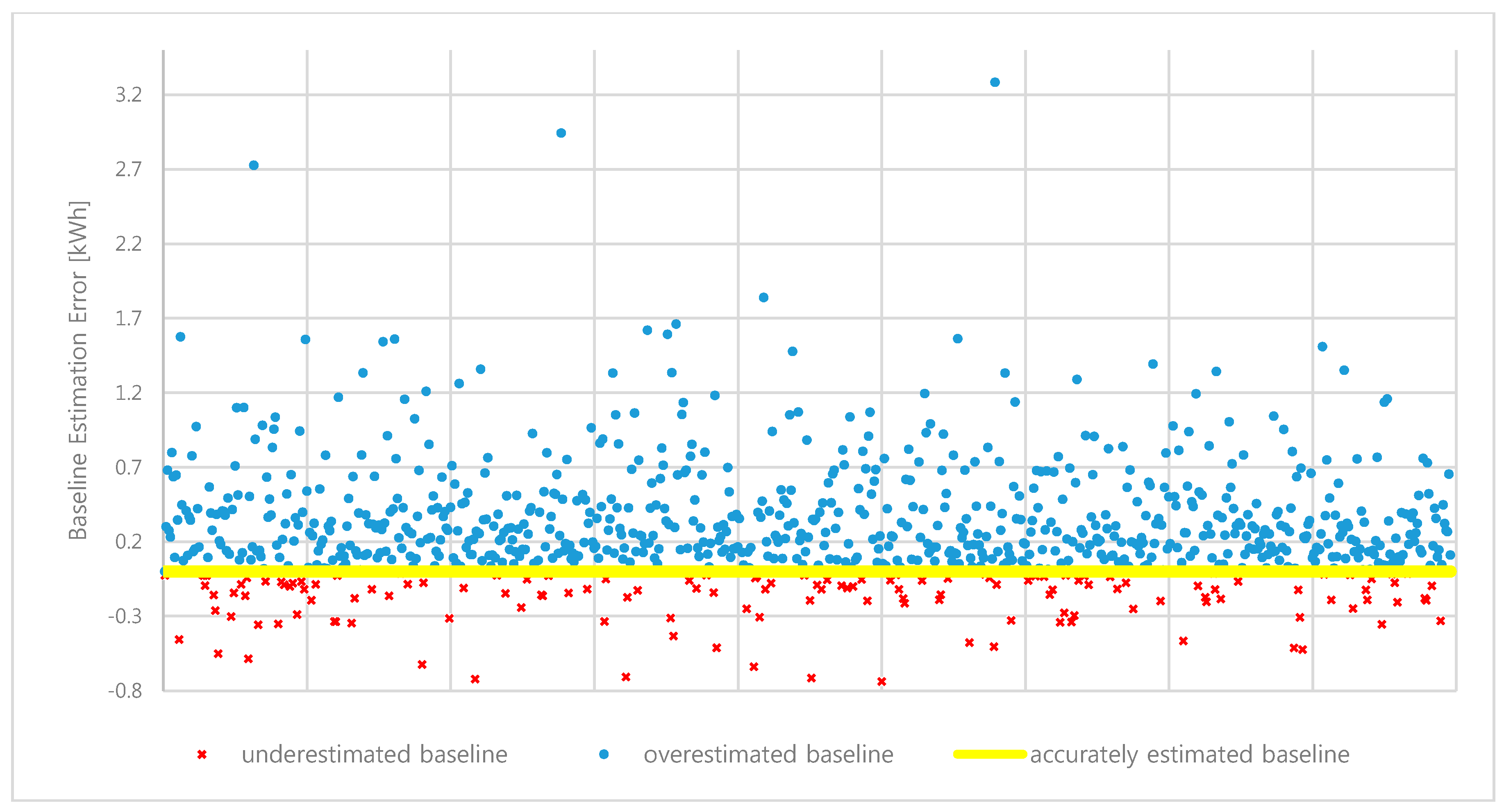
Utility companies generally use the high 4 of 5 method to determine how accurately incentives are paid to individual customers. However, the CBL is overestimated in most cases. The percentage of overestimated customers was approximately 83.04%, which indicates that 744 of 896 customers received higher than justified incentives. Customers with CBLs higher than their actual loads are free riders. This large number poses an obvious and severe financial risk. The distribution of error for these individual customers is illustrated in
Figure 5. The positive and negative values signify overestimated and underestimated CBLs, respectively. Utility companies face the problem of paying additional incentives for an average of 282 kWh per event owing to overestimation by the high 4 of 5 method. As an alternative to the high 4 of 5 approach, we applied regression as the first step in the proposed methodology to reduce the number of free riders.
4.4. Results of the Regression
Baseline accuracy analysis was conducted with various baseline estimation methods, including the high 4 of 5, for the residential DR program, which serves 27,660 residential customers in Korea. As described previously, five proxy days were selected for the analysis.
4.4.1. Regression Model Selection
Before baseline accuracy analysis was conducted with the various baseline estimation methods, we established a suitable regression model for residential customers. To construct the regression models, the CDH and historical data were utilized in various combinations as independent variables in five regression models, which are described in
Table 4.
According to the average relative error and sum of absolute error indicators, of these regression models, regression with CDH and historical data for two eligible days (regression w/ CDH (2 eligible days)) was the best model. These results are presented in
Table 5. The regression models that included CDH performed best in the aspect of bias (average relative error), but they were inferior in terms of average absolute error per customer/event (goodness of fit) to the regression models omitting CDH while using two or three days of historical data. Although inconsistent evaluation results were obtained, we concluded that regression with CDH and historical data from two eligible days was the best model because the total impact in absolute error per customer per event is small.
4.4.2. Performance Evaluation
The CBL accuracy analysis was conducted for various baseline methods. The results are displayed in
Figure 5,
Figure 6 and
Figure 7.
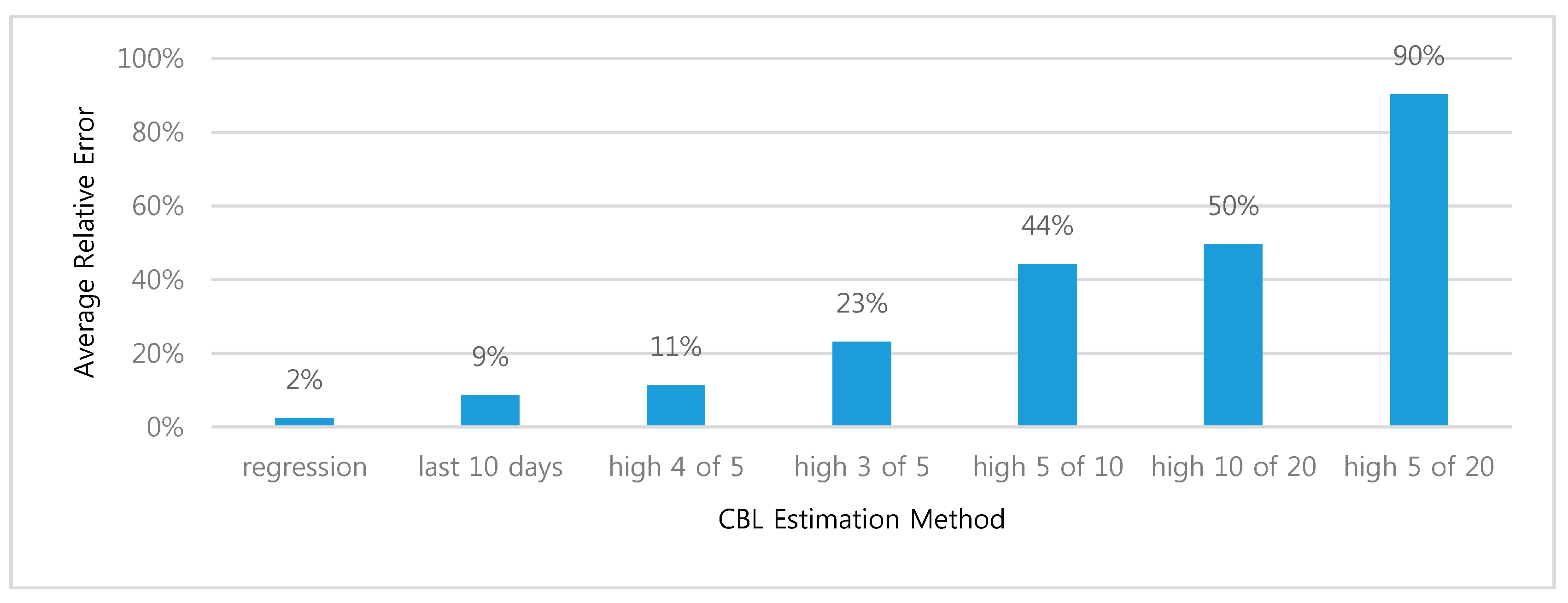
Figure 6 shows that the regression had the smallest average relative error.
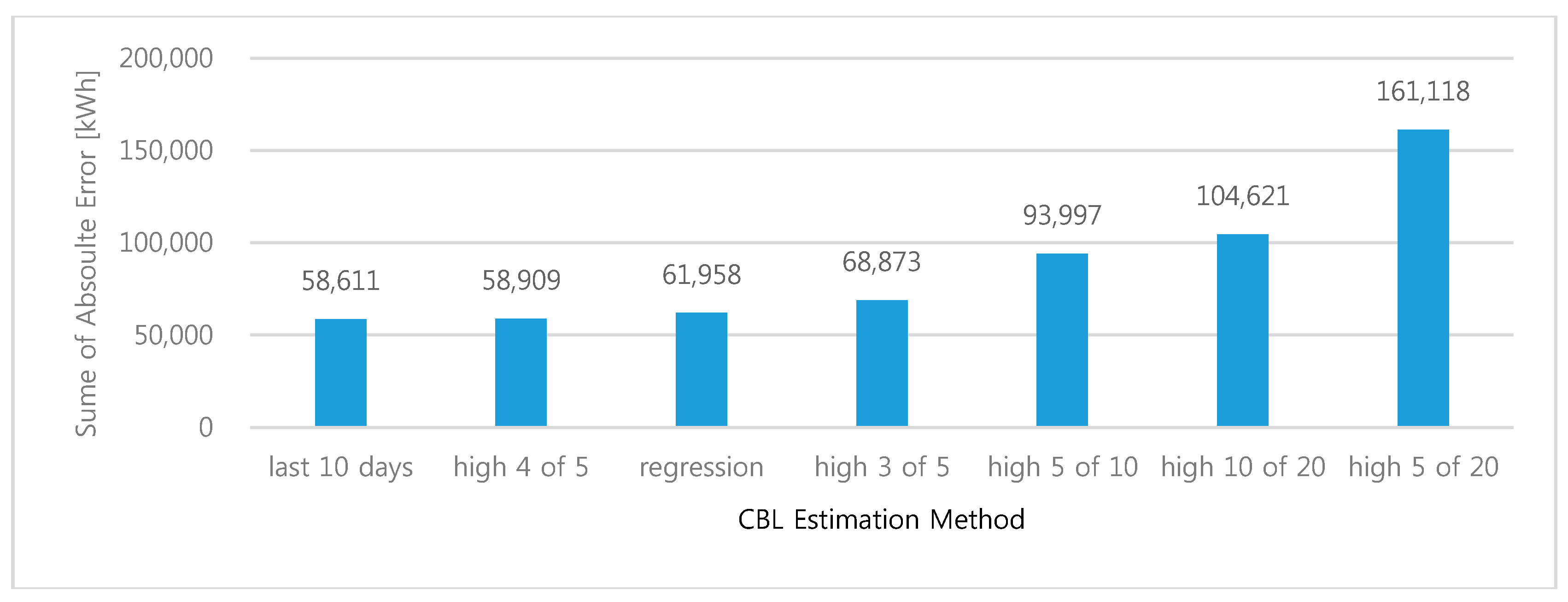
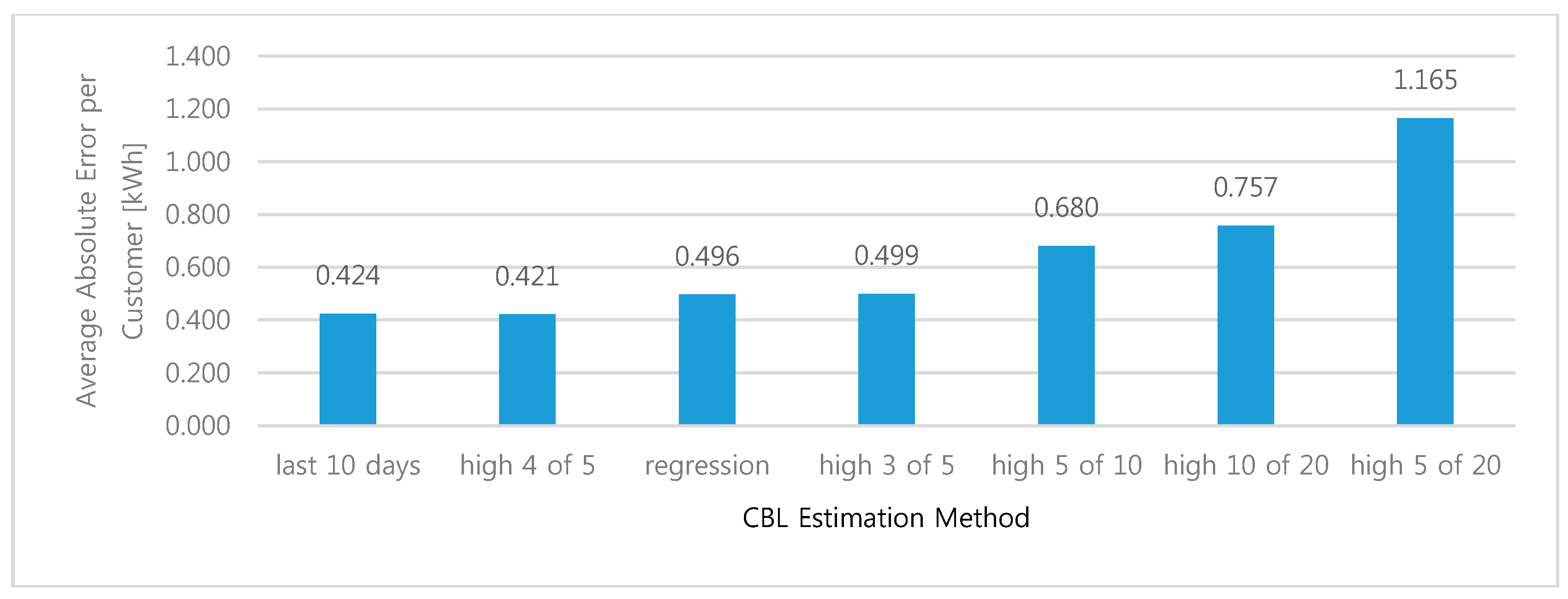
Figure 7 reveals that the last 10 days method yielded the lowest sum of absolute error per event (58,611 kWh), indicating that this method was the most suitable approach with regard to accuracy. Different methods indicated the best bias and goodness of fit. The average absolute sum of error for a customer was 0.424 kWh and 0.496 kWh for the last 10 days method and the regression in
Figure 8, respectively. The difference between these approaches was as low as 0.072 kWh, a very small value. Therefore, the results suggest that the regression method is the most suitable for decreasing the number of free riding residential customers.
Free riders comprised approximately 61.05% of the 547 customers as per the regression method when using the standard incentive settlement method, translating into a decrease of as many as 197 free riders. In other words, the rate of free riding declined by 21.99 percentage points for the regression method compared to the high 4 of 5 approach. The results of the baseline accuracy analysis show that while the regression method could reduce the number of free riders considerably, it could not do so entirely.
4.5. Payment Rule Analysis
The results of the CBL analysis confirmed that the regression method could improve baseline accuracy and thereby reduce payment to free riders. Nevertheless, changing the baseline method to regression still has limits; namely, the number of free riders cannot be nullified completely. Hence, we proposed a new payment rule. The proposed rule is designed to settle payment when the demand reduction is larger than a specific baseline rate. However, the suitable rate,
, for residential customers must be determined in order to use the proposed payment rule as intended. Using the methodology explained in
Section 3.3,
was determined to be 26.28%. When deriving this value, we considered other proxy days compared with the proxy days used in
Section 4.3. These proxy days for obtaining
were selected carefully because inappropriate (i.e., normal) days can result in a high rate for
. Normally, peak electricity consumption is assumed to occur on event days and proxy days; in contrast, customers use less electricity during normal days. By inappropriately including normal days as proxy days, the value of
can increase owing to larger differences between the estimated CBL and the actual load. Excluding the 10 event days and weekends limited the selection of proxy days such that random selection of viable proxy days would have a high probability of normal day selection. Furthermore, existing research on PTR baseline evaluation conducted by SDG&E included incentive payment rule evaluation based on five proxy days [
3]. For these reasons, the five proxy days selected in
Section 4.3 were used to calculate
.
This paper thus compared the results obtained by applying the existing method incentive payment rule to those obtained using the proposed rule. The residential load data of the PTR pilot program implemented in Korea during the summer of 2017 were used for this analysis. In order to assess the effect of the proposed incentive payment rule, the incentive accuracy analysis for the residential DR program was conducted using the proxy days selected in
Section 4.3. According to the operational results provided by the DR pilot program, the average load impact was 13.86% for the events. In other words, customers normally reduced their demand by approximately 13.86% during the events in 2017. Therefore, according to Equation (8), the ideal incentive was found to be 196,246KRW (
$163.51), which can be considered an affordable incentive because the extent of load reduction should equal the load impact.
Incentive Settlement Evaluation
Using the incentive evaluation metrics described in
Section 3.4.2, this study analyzed the outcomes of high 4 of 5, regression alone, and regression combined with the new payment rule. The results appear in
Table 6 and
Table 7. According to
Table 6, assuming that reduction is equal to load impact, the ideal total electricity reduction, by participating customers amounted to 197 kWh; thus, the amount of actual incentives provided to these customers by the utility was
$163.51. The high 4 of 5 method estimated a reduction approximately 332 kWh higher than the actual value. Therefore, the utility would have to pay its customers
$275.56 more (on average) to operate the residential DR program. Similar to the previous result, the regression method was more reasonable compared with the existing method, but it still overestimated load reduction. However, the new payment rule, which pays incentives for the extent of load reduction over the threshold, yielded the most accurate load reduction after estimating the baseline by the regression method. While it offered less incentive settlement to customers, it was considerably efficient. The new payout rule reduced load impact by approximately 53 kWh compared to the actual scenario, and the incentive payment was
$43.99 less than the ideal payment to the 896 customers. Additionally, the free rider problem was considerably alleviated by using the new payout method, as shown by the results in
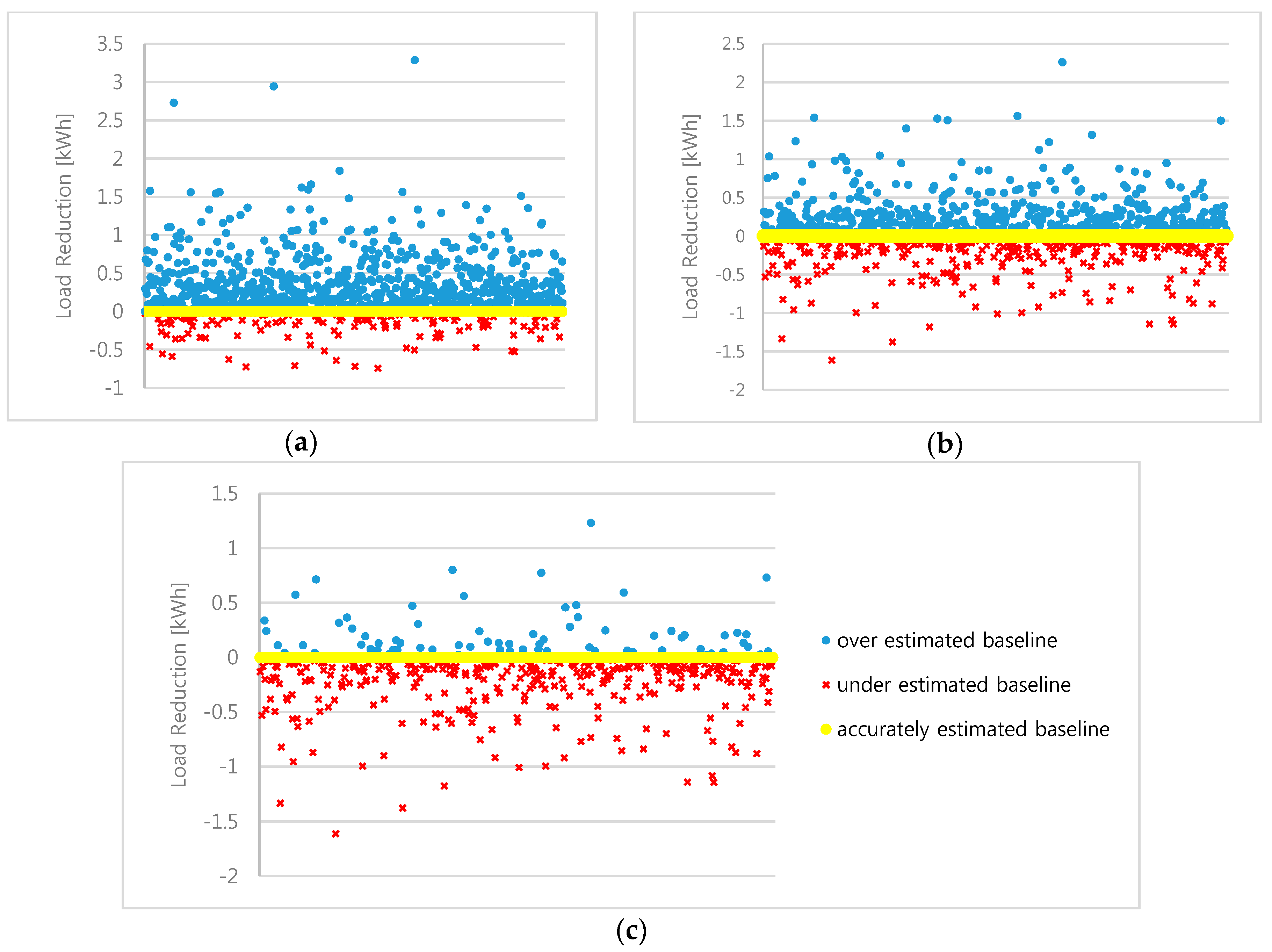
Table 7. Notably, 663 free-riding customers with overestimated CBLs were eliminated, so the free rider rate decreased to 9.04%. The distributions of customer load reduction for each method are shown in
Figure 9, where the positive values represent free riders. Both the quantity and scale of free riders decreased considerably with the new payment rule compared to the traditional incentive settlement rule.
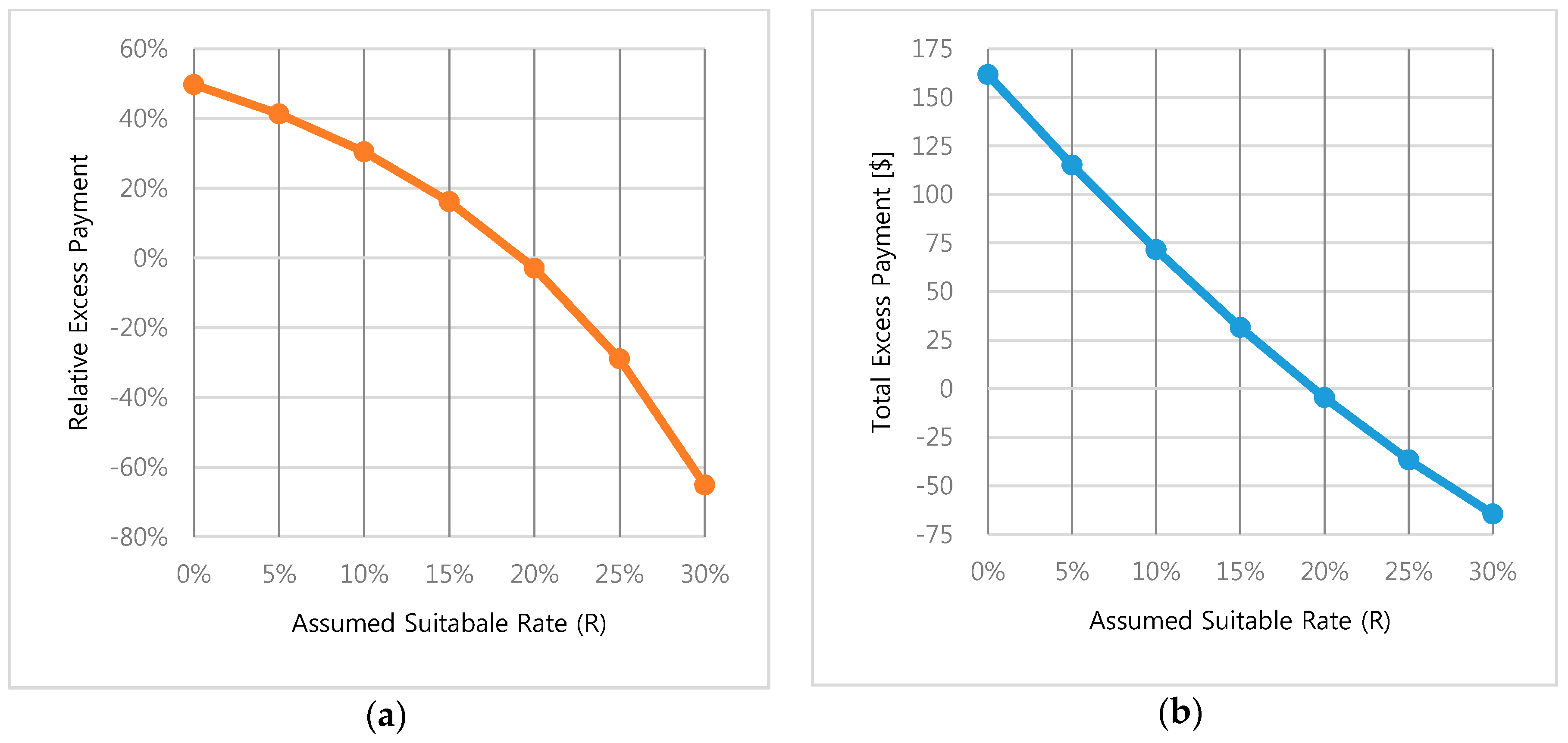
Although the proposed methodology curtailed the number of free riders, many negative values were also observed in the incentive evaluation, which means that the introduced rate may be too high. Therefore, we analyzed the payment error for a different set of proxy days according to the threshold rate. The change was confirmed by increasing the rate from 0% to 30% in increments of 5%. The results showing the relative and total excess payment values are displayed in
Figure 10a,b, respectively. The relative incentive payment error gradually decreased with increasing threshold rate and fell to 0% when the threshold rate reached 19.32%. This value differs from the optimal rate because different proxy days were used to obtain the optimal rates. The results of the incentive evaluation showed a negative value when 26.28% was used as the threshold rate for the alternate proxy days.
There is a 9.96 percentage point difference between (26.28%) and the root rate (19.32%; i.e., the rate at which 0% relative error occurs) for the alternate proxy days. This gap could be regarded as a big difference. However, each case indicates that there is an average of 0.43 kWh or 0.32 kWh for which incentives are settled, leaving only 0.11 kWh between them. This suggests that is somewhat sensitive to the proxy days being selected, but for the scope of the problem, this is acceptable.
5. Conclusions
We established an incentive settlement methodology for a Korean residential DR program as a solution to the free rider problem. The proposed method outperformed other methods, especially when considering the payment rule improvement. The proposed method consists of two steps, namely, predicting the CBL using regression and implementing a minimum threshold of load for customers to receive incentive settlement. The results of the various analyses led us to the following conclusions. The proposed methodology can reliably reduce the uncertainty about free riders if it is used to predict the CBL. Using residential customer load data for Korea, we also showed that it could curtail the number of free riders. The utility can thus offer fewer (and more economically sustainable) incentives to customers. In addition, it is possible to apply this method to other DR programs with different load characteristics, as the optimal rate calculation is independent of the CBL estimation method; thus, the level of free riders can be successfully reduced. Specifically, free riders comprised approximately 61.05% of the 896 customers as per the regression method, translating into a decrease of as many as 197 free riders. With regard to incentive settlement evaluation, compared to the ideal scenario, the settled payment was $119.52 when using the regression and new payment rule, which was $43.99 lower than the ideal payment to the 896 customers in the DR program.
Although the threshold rate applied in the payment rule differs depending on which proxy days are selected, the relative difference has an acceptably minor effect on the incentive payment. If the proposed incentive payment rule were applied in a DR program, free-riding customers and those that scarcely reduce their demand would leave in this program. Beneficially, customers who significantly reduce their consumption would remain and the DR program, making operation more efficient than before. However, further research about the effect of customers leaving in accordance with threshold rate () in DR program would then be necessary. Overall, this methodology model is effective for mitigating the free rider problem, and it can be easily applied by simply modifying the threshold rate () when operating any DR program.