1. Introduction
The energy system has become a fundamental pillar of our society and has to be changed dramatically. The Three Ds—Decarbonisation, Decentralisation and Digitalisation—headline the major requirements of Western society these days [
1]. The ongoing process of climate change speeds up under ominous conditions. New research results of the Intergovernmental Panel on Climate Change strengthen assumptions of the negative effects on human society [
2,
3].These effects were provoked by the humanity itself by emitting carbon dioxide in large amounts from burning fossil resources (i.e., oil, gas, and coal). On 4 November 2016 in Paris, the world community committed to an agreement that will be keeping global temperature well below two degrees Celsius above pre-industrial level [
4]. To achieve this goal, the entirety of human society will have to change their energy supply infrastructure to a renewable energy-based system.
The transition towards renewable energy and decentralised power supply leads to several challenges for the electrical grid operation, particularly on the distribution level [
5,
6]. Handling the large number of different characteristics of a fluctuating renewable generation and orchestrating the flexibility of decentralised loads and generation units in context of the distribution grids are complex challenges. To avoid potential problems in the distribution grid, such as voltage violations and line or power transformer overloading, Distribution System Operators (DSO) need to undertake smart operation and planning strategies, based on Information and Communication Technology (ICT) [
7].
Examples and background to these ideas are given in [
8,
9,
10,
11] which supposedly will result in more resilient infrastructure [
12,
13] and are the context of various research projects [
14,
15,
16,
17]. This resulting change from capital expenditure- to operational expenditure-dominated grid operation should supposedly result in lower overall costs. This was also suggested by ref [
18].
Digitalisation in a decentralised energy grid produces many data. This is what a complex ICT system is supposed to take care of. Taking into account that the energy grid is a sensitive system with massive consequences for society in case of a collapse, the ICT has to be tested in a save environment of a laboratory before deployment into the real world. Different test approaches have to be evaluated for specific use cases and boundaries [
19]. The “Three Ds” will headline not only the major requirements for the transformation of the energy system, but also the motivation to develop the approach of this paper. To summarise, the question where the answers were sought for was: How can one test and validate systems which are performing a smart grid control strategy?
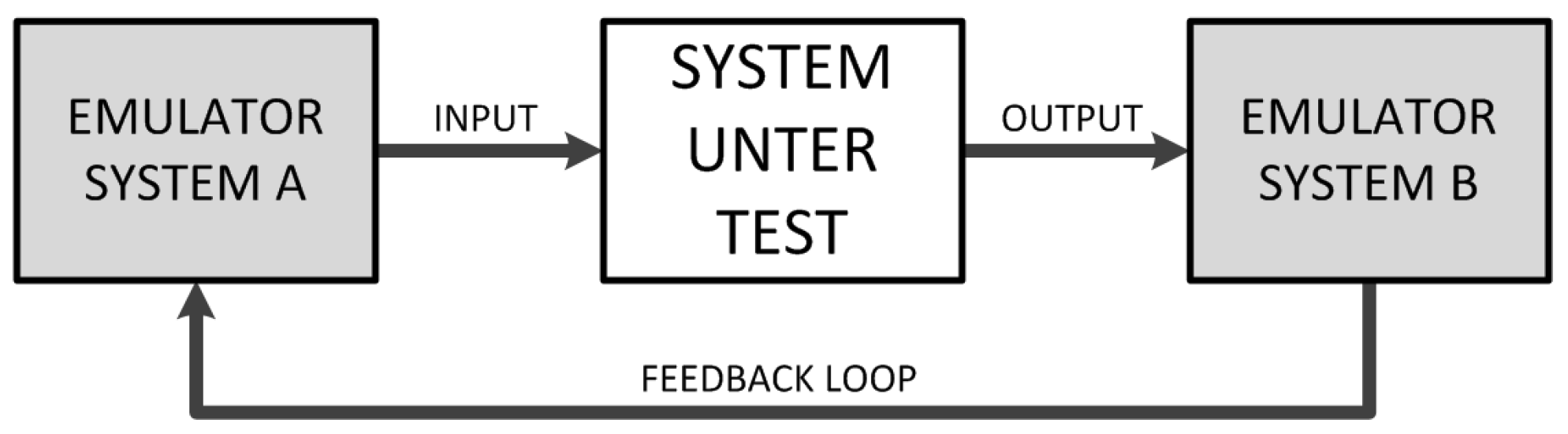
For the laboratory testing, one seeks for an environment with a variety of parameters to control. Such a setup can be described with the term of real-time Hardware-in-the-Loop (HIL) concepts [
20,
21,
22]. The basic idea behind it is to place a system in an environment in which all inputs and outputs can be controlled. In general terms, this means that a test candidate (system, component or algorithm) is placed in an environment, where the adjacent systems are simulated, and the behaviour at the points of interface is emulated.
Figure 1 depicts this approach in a generic way. Based on the reaction of the System-under-Test (SUT), the simulated environment adopts accordingly.
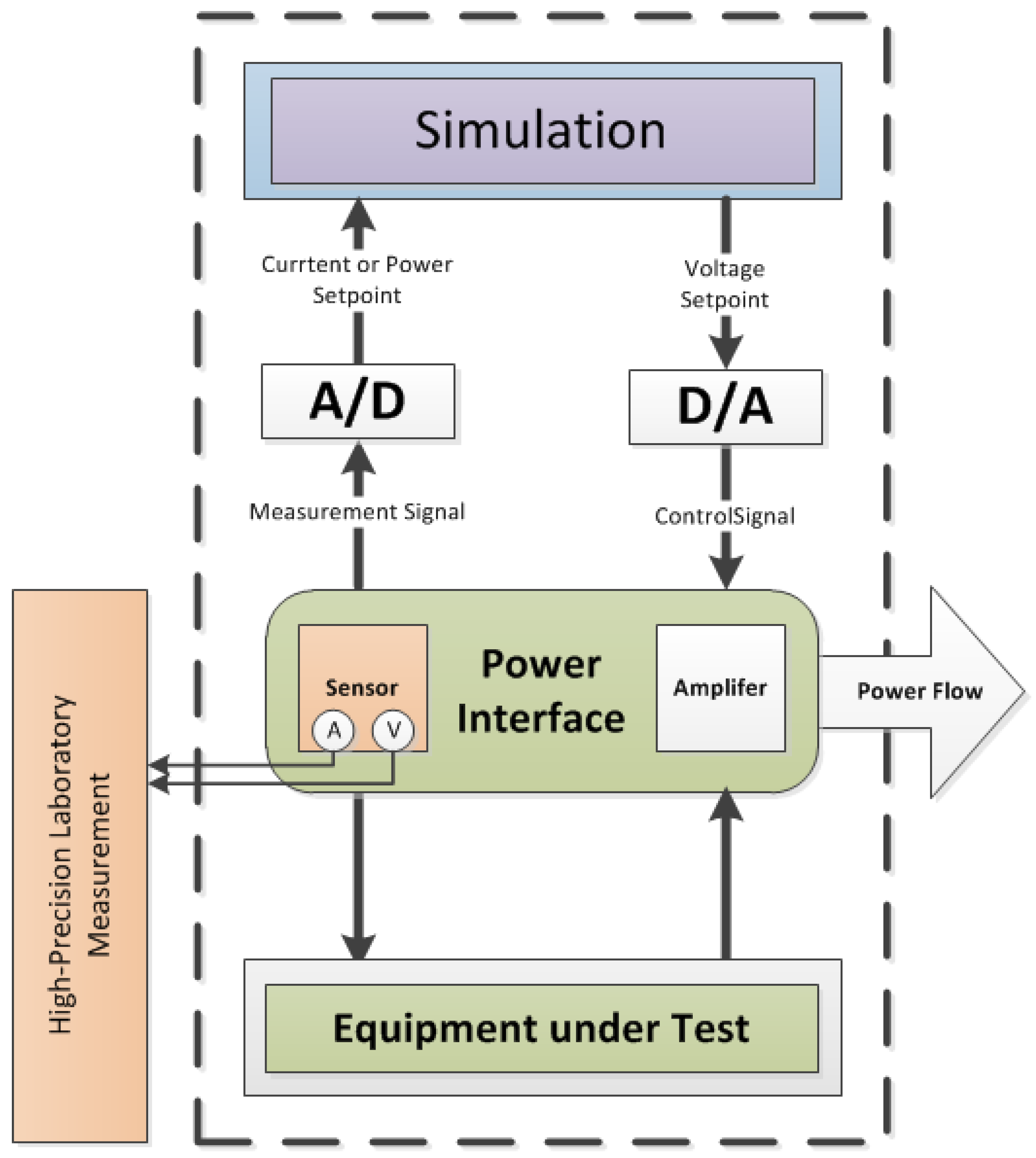
For the testing of power system components, an additional interface is necessary, i.e. the Power Interface (PI), as it can provide voltages (or currents) in the typical range of a power hardware device. Linear amplifier, switched-mode amplifier and coupled motor-generator assemblies are typically used [
23,
24]. In this article, two representatives from the switched-mode and linear amplifier category are utilised for the experiments. Beside the physical properties of the PI, the used Interface Algorithms (IA) are relevant for the success, as these algorithms deal with the occurring stability problems. This is discussed in detail in [
25,
26,
27]. Combined with the issues regarding the stability of a PHIL experiment, as discussed in [
26,
27], such an experiment cannot be considered as
plug’n’play. A simplification to enable a boarder range of research institutes to carry out PHIL experiments is the transition from PHIL to Quasi-Dynamic PHIL (QDPHIL). The main idea is to increase the time step which will enable the possibility to use steady state load flow simulation tools for the process. The typical temporal resolution of a PHIL experiment is in the range of 10–100
s [
24], where, as with the implemented QDPHIL setup, a time step below one second is intended and realised. Through this simplification, the accuracy is supposedly reduced and the system setup needs to be analysed and the functionality validated.
This analysis is the scope of this paper. Details on the actual PHIL and QDPHIL setup used in this paper are given in
Section 3. The transition from real-time calculation to steady state is discussed in more detail in
Section 3.4. The QDPHIL concept will presumably enable the testing of superimposed control regimes as well as local control regimes such as a energy management systems. On the other hand, examples for topics which are in the scope examined with PHIL but not with QDPHIL experiments are given in [
28,
29,
30]. All of the referenced experiments involve operation states which can be summarised as “disturbed operation”, whereas QDPHIL focuses on undisturbed operation. A detailed definition of requirements for the QDPHIL setup is given in
Section 3.1. In [
31], QDPHIL and quasi-static PHIL are mentioned as topics of current investigation.
The remaining part of this contribution is organised according to the following schema: In
Section 2, a more detailed introduction to PHIL setups and smart grid testing in general is given. This includes the discussion of multi-domain Smart Grid testing and the application of the HIL concept to other domains such as ICT. The used PHIL and QDPHIL setups are introduced in
Section 3.
Section 4 describes the chosen validation methodology for comparing them.
Section 5 presents the results of the carried out experiments and
Section 6 describes the application of the proposed test methodology at the example of a case study. The results of the comparison are discussed in
Section 7. Finally, this article is concluded by
Section 8 with an outlook for further steps. The results of this paper are based on the work of the “Smart beats Copper” project within the ERIGrid Trans-national Access funding framework [
32].
4. Validation Methodology
This article focuses on the comparison of the two system setups as introduced in
Section 3. It is proposed that both systems can be used to evaluate the performance of smart grid components, solutions, and technologies as well as new approaches with high renewable energy feed-in if the requirements in
Section 3.1 are met. For the validation of the QDPHIL setup, a two-stage process was chosen. In the first phase, the proposed system setup was tested and compared against the PHIL setup. Therefore, three test cases were used to characterise the differences in the response of the system to the test case scenarios. In the second phase, the QDPHIL system setup was used to conduct an experiment to gather results from a actual application of the QDPHIL concept. The results are presented in
Section 6. A complex scenario was chosen which involves SIL components as well.
4.1. Test Methodology
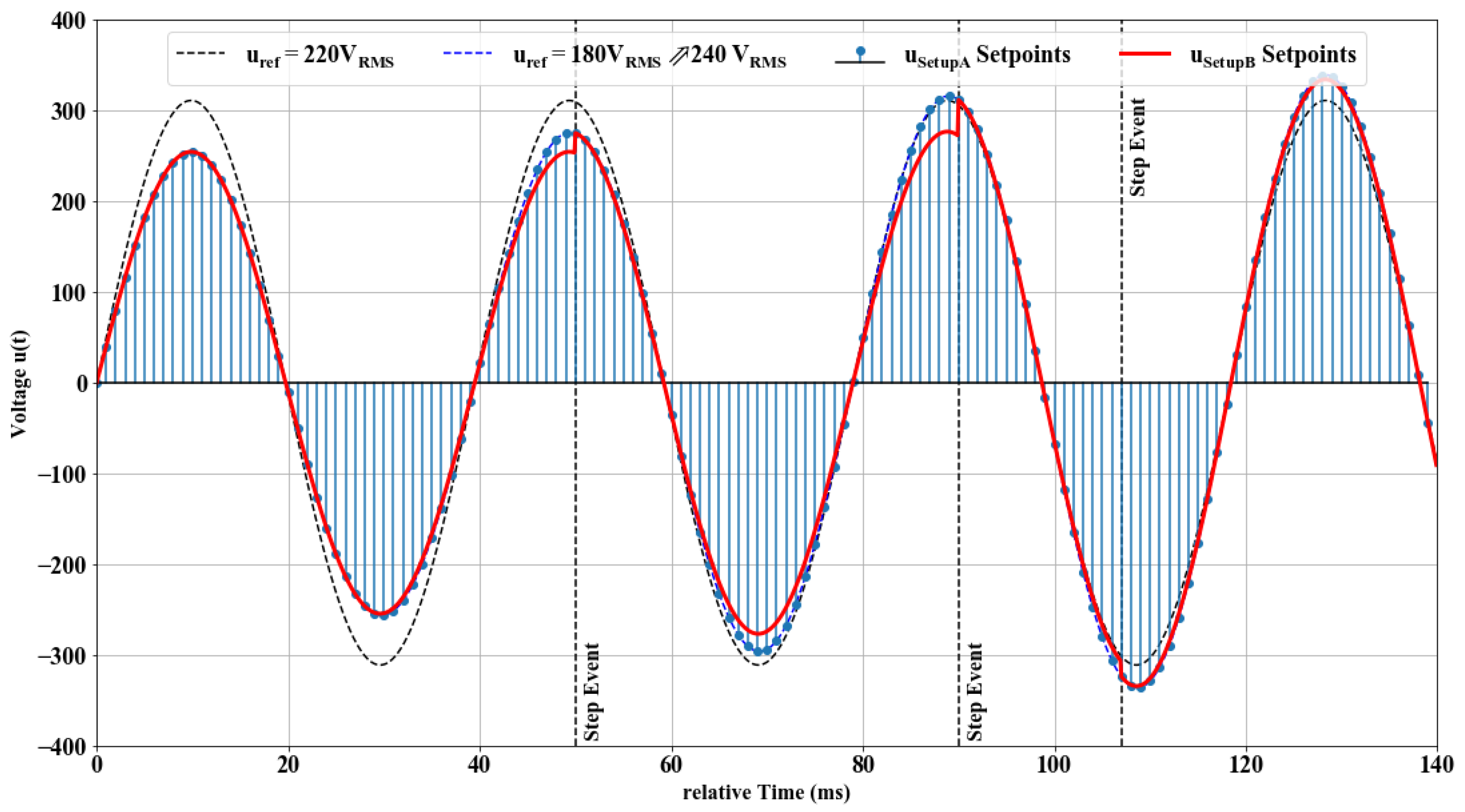
The examination of both used system setups was carried out by comparing the response of the systems within three different scenarios. The scenarios reflect the most extreme possible variation as well as variations typically observed in real world test cases of the QDPHIL setup. The test cases are:
Step Function: Voltage deviation at the slack bus bar from 1.04 p.u. to 1.08 p.u. in a step. This represents the most extreme change of a parameter in the modelled system. It was chosen to evaluate the difference in the dynamic behaviour of the systems in the time domain of seconds.
Transient Behaviour of the Step Function: The voltage change of the two setups was evaluated regarding the transient behaviour of the system.
Ramp Function: Voltage deviation at the slack bus bar from 1.04 p.u. to 1.08 p.u. as a voltage ramp over the course of 1–10 min. These are typical changes which were deployed to examine the stability of systems in varying conditions.
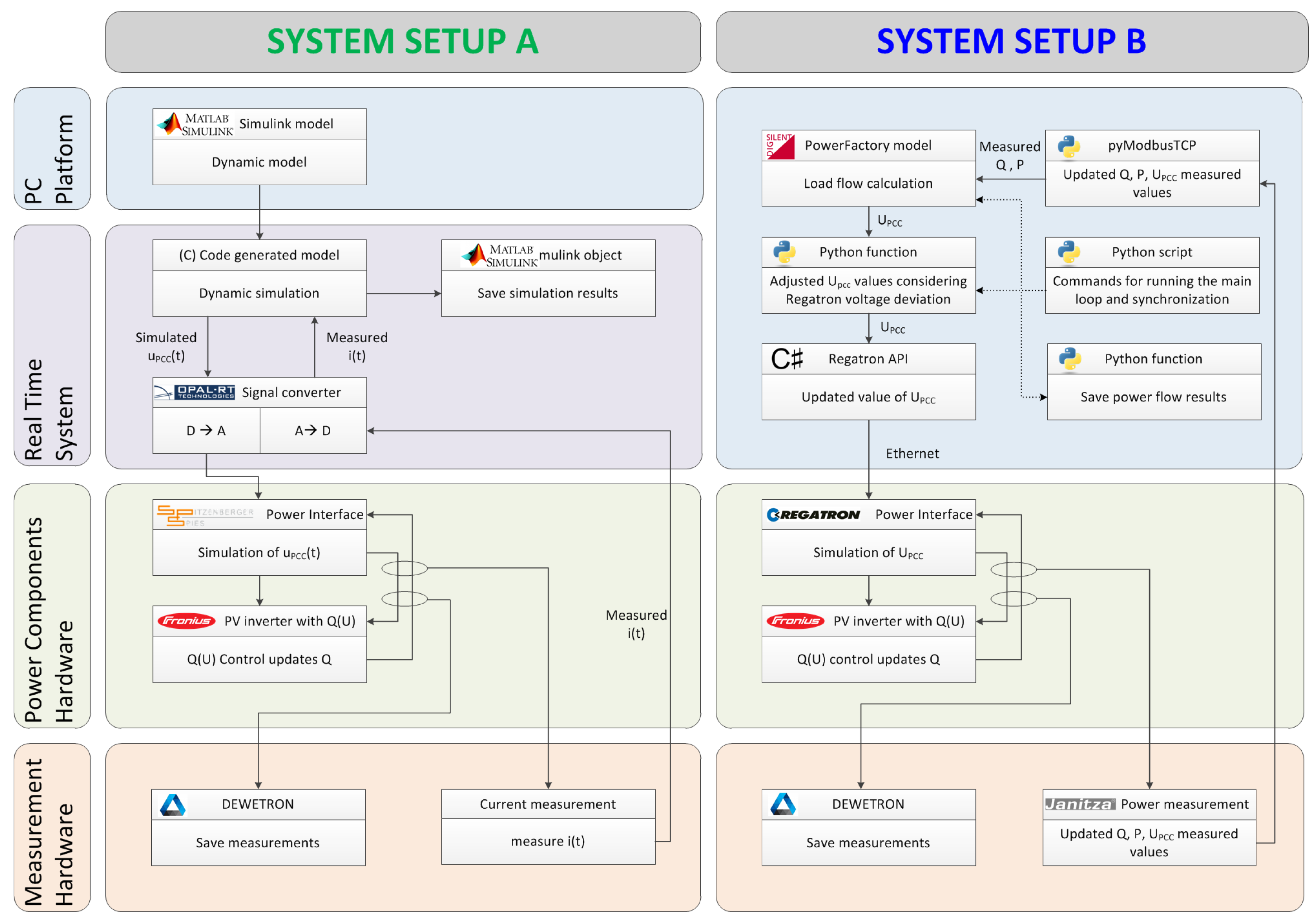
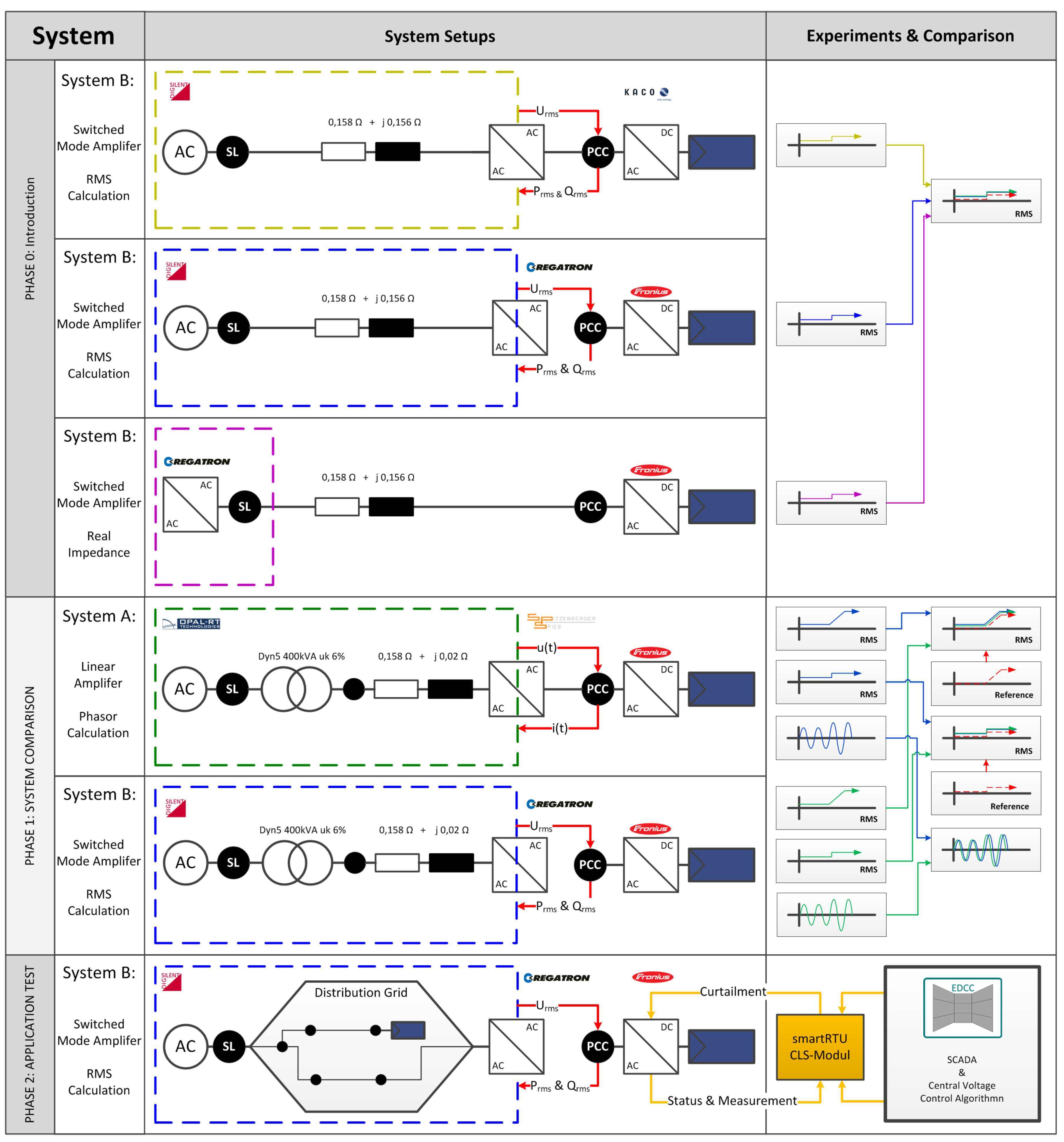
The individually used experiments are depicted in
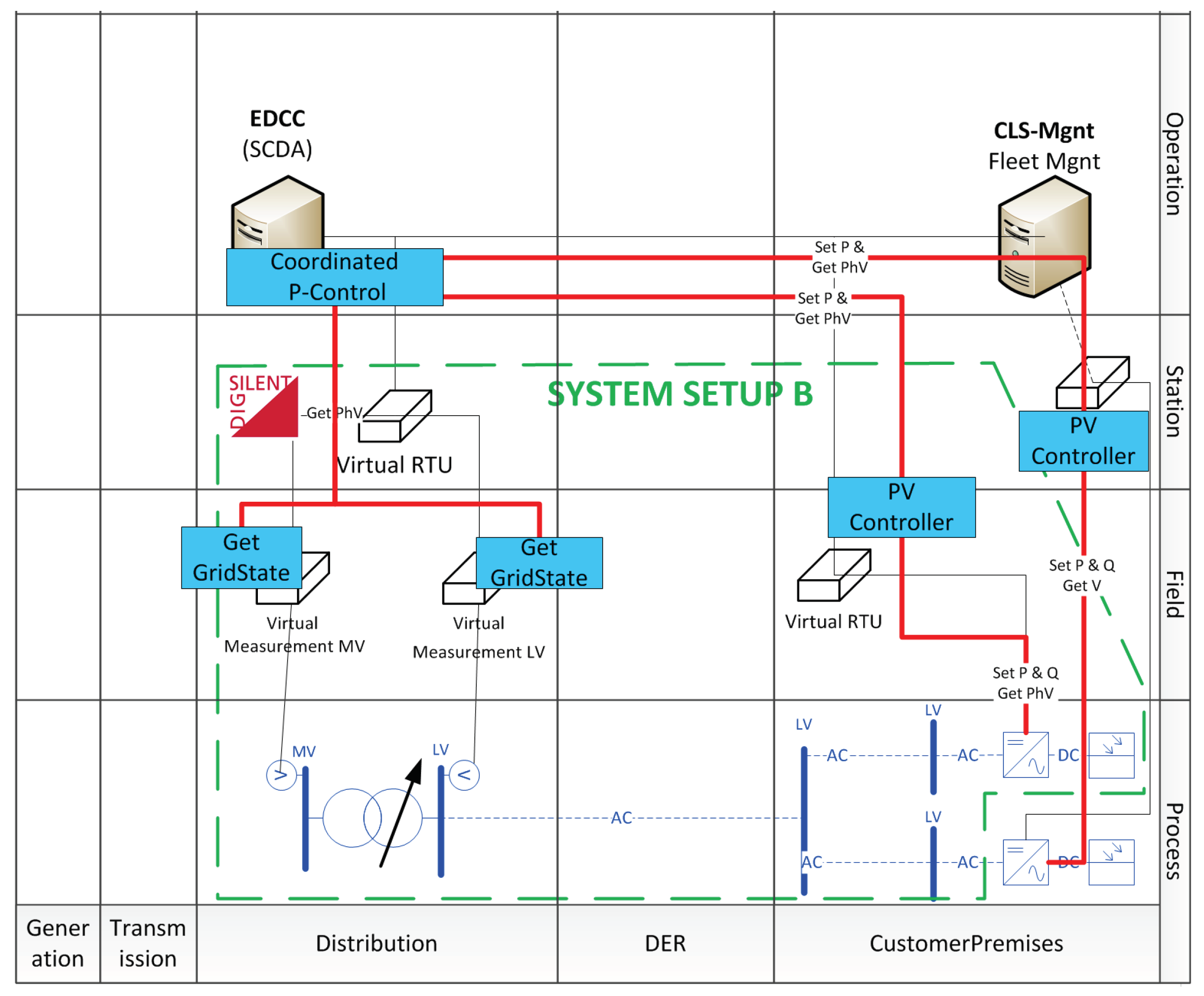
Figure 6 which also shows the system setups and the used grid model. The depicted experiments are grouped into three parts. These are the previous described tests for the comparison which are called Phase 1. Phase 1 is accompanied with a preliminary test to characterise the system setups, which is referred to as Phase 0. The subsequent tests are subject to a case study, which is called Phase 2 and is discussed in
Section 6. These tests were also executed within the ERIGrid TA project “Smart beats Copper” at the host facility AIT in Vienna, Austria. Additional tests with System Setup B were executed at the Smart Grid Lab of Ulm University of Applied Sciences, Ulm, Germany.
4.2. Used Grid Model
The proposed system setups were investigated in Phase 1 when simulating a simplified grid model which consists of a regional Low-Voltage (LV) transformer, a power line represented as an impedance and a connection point (i.e., grid node), where a PV inverter is connected as depicted in
Figure 6. It should be taken into consideration that the developed system can also be used for simulating large-scale grids, however, a simple grid was adopted for this study to avoid complexity in the simulation results.
4.3. Used EUT for the Test
The proposed system setups were tested considering a PV inverter as the EUT. Two inverters were used for the experiments, which was due to their availability at the different involved laboratories. The models Symo 20.0-3-M with nominal apparent power of 20 kVA and Symo 15.0-3-M with a nominal apparent power of 15 kVA from the manufacturer Fronius were used. Both systems originate from the same series and have the properties described in [
44]. In addition, the function Q(U) for voltage control was configured in adaption to the suggestions by Elbs and Pardatscher [
50] which again results in the parametrised Q(U) curve. Due to the reactive power priority of the implemented algorithm, the limit was lowered by 5% to prevent an oscillation of the controller. The selected set points are extreme scenarios as most of the relevant grid codes (e.g., [
49,
51]) or related documents rarely expect capabilities exceeding the limit of
which corresponds to a limit of ±0.42
. The Q(U) controller has the option to set a time constant
. Different time constants were chosen. All chosen time constants represent challenging scenarios as the value suggested by the manufacturer is 5 s. An overview of the chosen parameters for the different tests is provided in
Table 4.
4.4. Used Test Scenarios for Phase 1
To examine the performance of the developed systems, two simulation scenarios were applied. In the first scenario, a voltage increase in single steps was implemented by means of increasing the set voltage in the slack bus bar. Such a scenario of voltage increase can be observed in practice, if a regional transformer changes the position of its On-Load Tap Changer (OLTC). In the second scenario, a gradual voltage increase in a ramp was implemented by means of increasing the set voltage in the slack bus bar. Such a scenario can be observed in practice if voltages in the medium-voltage grid increase according to natural increase of PV feed-in during a clear sky day.
5. Phases 0 and 1: Results of the Comparison of the System Properties of System Setup A and B
The comparison of the two system setups is the subject of this section. The preliminary tests of Phase 0 introduced the system properties.
Section 5.2 and
Section 5.3 discuss the transient and dynamic behaviour of the different systems setups when handling the voltage step. The discussion of the system behaviour for the modelled voltage ramp is given in the following section. The analysis of the cycles, especially of System Setup B, is outlined in
Section 5.5.
Section 7 concludes the Phases 1 and 2 discussion.
5.1. Introduction to the Compared Systems
As a first step, a basic analysis of the behaviour of System Setup B is presented. The system was tested first with a non-PHIL configuration and a physical impedance between the PI and the EUT. In a next step, this was compared with the corresponding PHIL configuration. The impedance is typically used for flicker tests according to IEC 61000-3-3 [
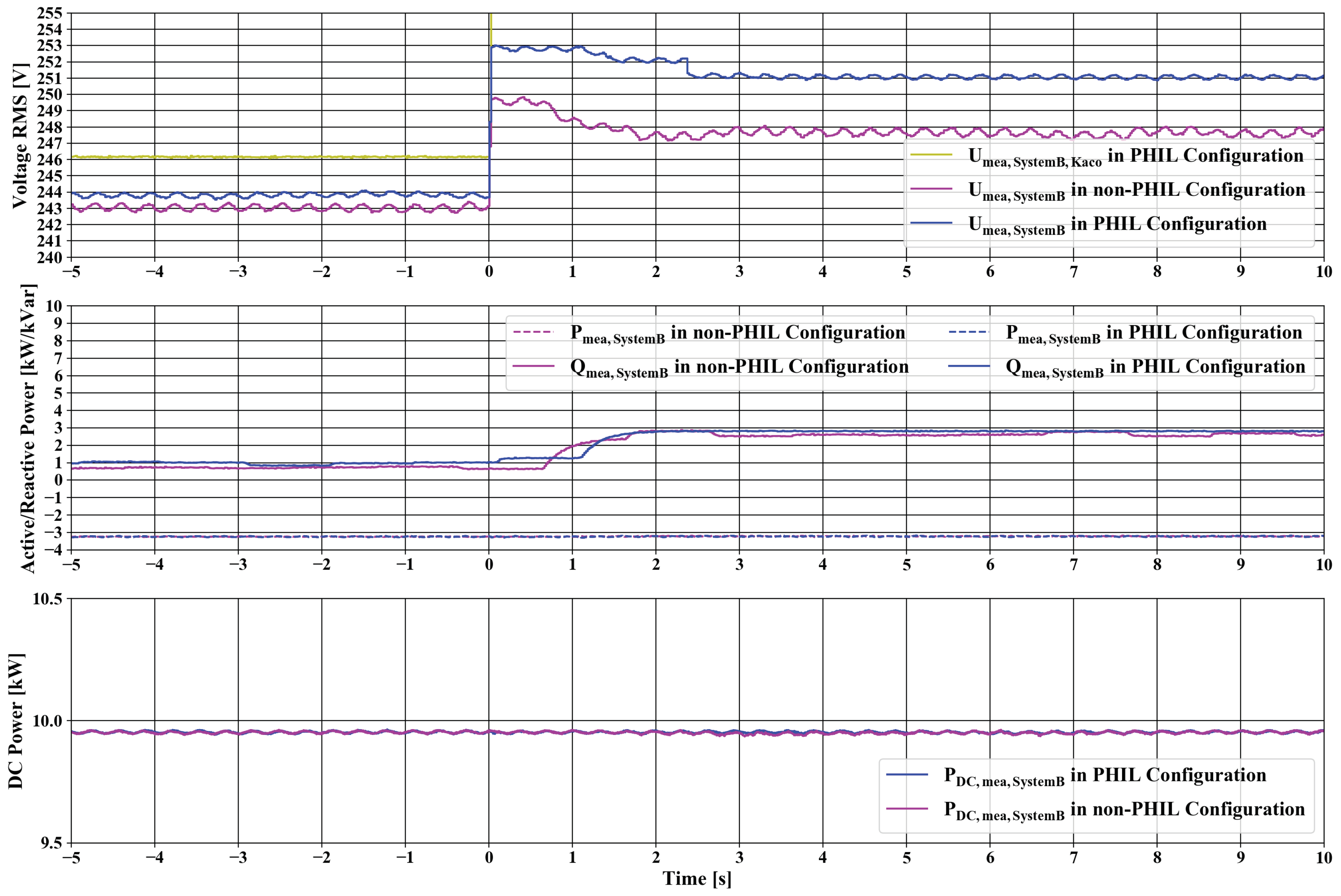
52], and is part of the SmartEST facility at AIT. As shown in
Figure 7, an oscillation behaviour was present for both configurations. It was assumed that the oscillation was caused by the searching algorithm of Maximum Power Point Tracking (MPPT) of the Fronius PV inverter. For additional comparison, the pre-step part of a comparable setup with another type of inverter [
53] is depicted. The voltage was more stable with this specific product in comparison to the results of the PV inverter. As this oscillation was caused by varying power in-feed, it was present in both configurations.
The difference between the two configurations could be seen most explicitly at the small voltage step of 2.5 s of the PHIL-configuration. Besides, a voltage deviation was present for both configurations. This offset ranged from approximately 1 to 3 . Active and reactive power were fairly constant before and after the step which caused a change in reactive power due to the implemented Q(U)-control.
5.2. Comparison of the Transient System Response for Voltage Step
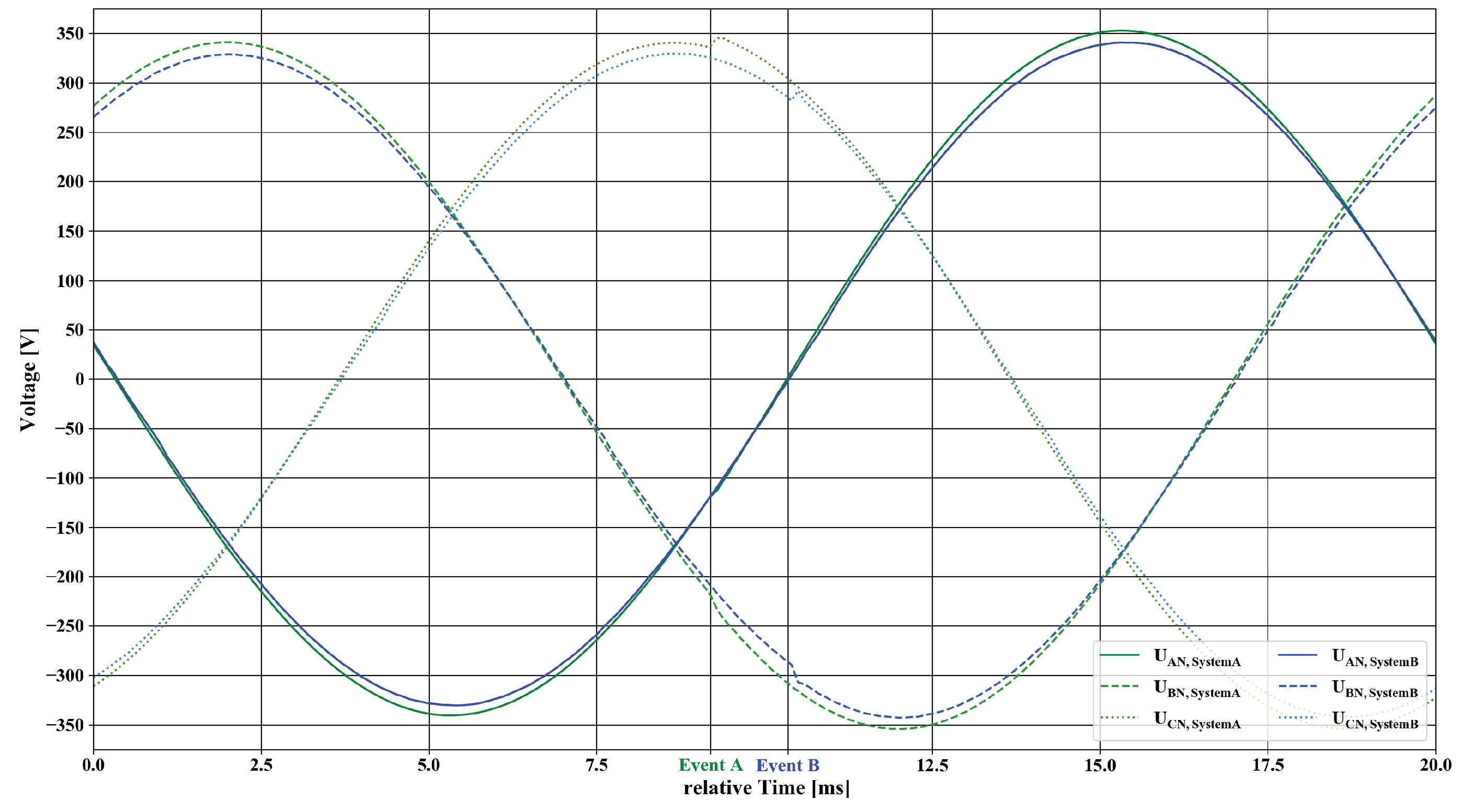
This section focuses on the comparison of the two setups described in
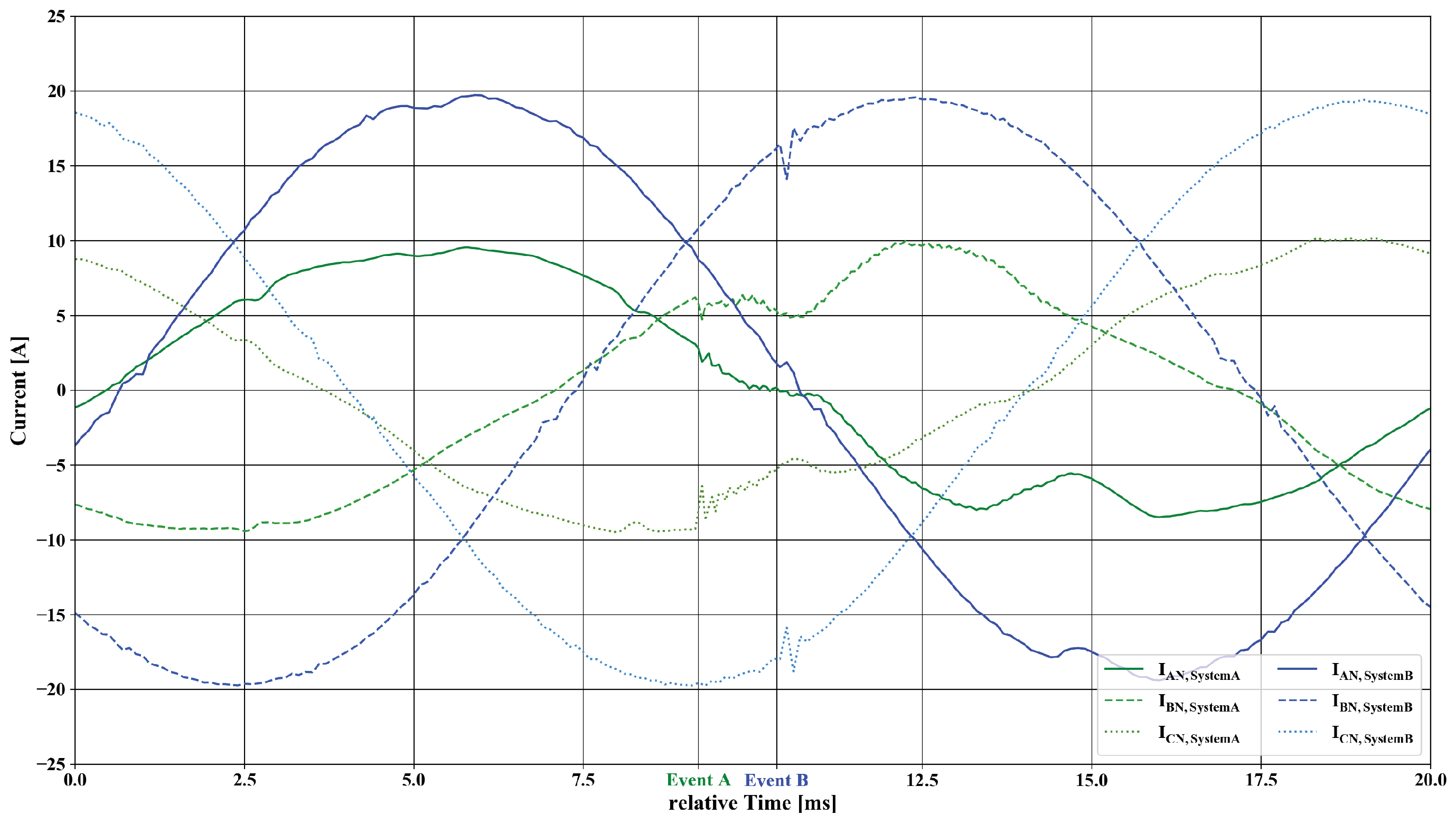
Section 3.4. At first, the comparison of the used systems was made by analysing their transient behaviour. The trend of the voltage and the current of the two three-phase systems are depicted in
Figure 8 and
Figure 9, respectively. Both systems changed from one given waveform, which corresponded to a value of 240.6
, to another waveform with a corresponding value of 249.7
and from 232.9
to 241.3
within roughly 100
s, respectively. For both systems, no lasting disturbance in waveform of the voltage could be observed. The given ideal sinusoidal waveform for the voltage was generated by both systems with neglectible fractions of no fundamental parts. The capabilities of both systems to generate a varying amount of non-fundamental disturbance have not been examined further in this contribution.
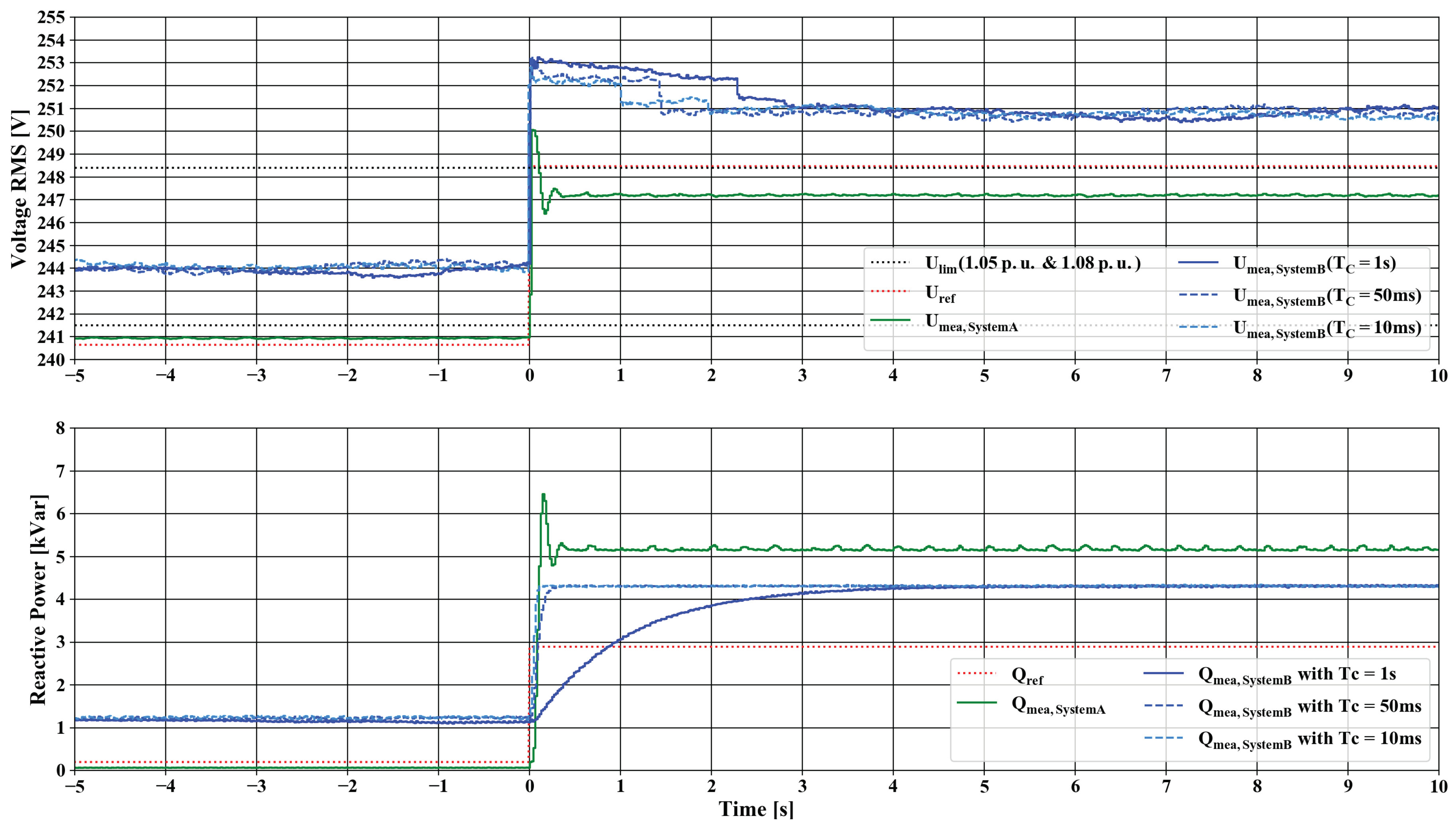
5.3. Comparison of the Dynamic System Response for Voltage Step
The evaluation depicted in
Figure 10 focuses on the dynamic behaviour of the systems for the test scenario. This change of perspective can also be understood as change from the evaluation of the individual power interface to the evaluation of the complete PHIL setup. Statistical key parameters are listed in
Table 5 to quantify the observations made in the figure. The one-period RMS values provided by the independent measurement device were used for this evaluation.
As a reference, the steady state values for the used grid model and implemented Q(U)-control are the parameters for the constructed curve which is plotted as a red dashed line. The experiments were carried out in individual runs. This means that the measured curves are aligned with the ideal step function. Therefore, an offset between the parameterised step and the actual step cannot be observed in the graphs. This offset was limited to a maximum of one simulation step. For System Setup B, this was limited to a maximum of 420 ms. Details regarding the simulation time are given in
Section 5.5.
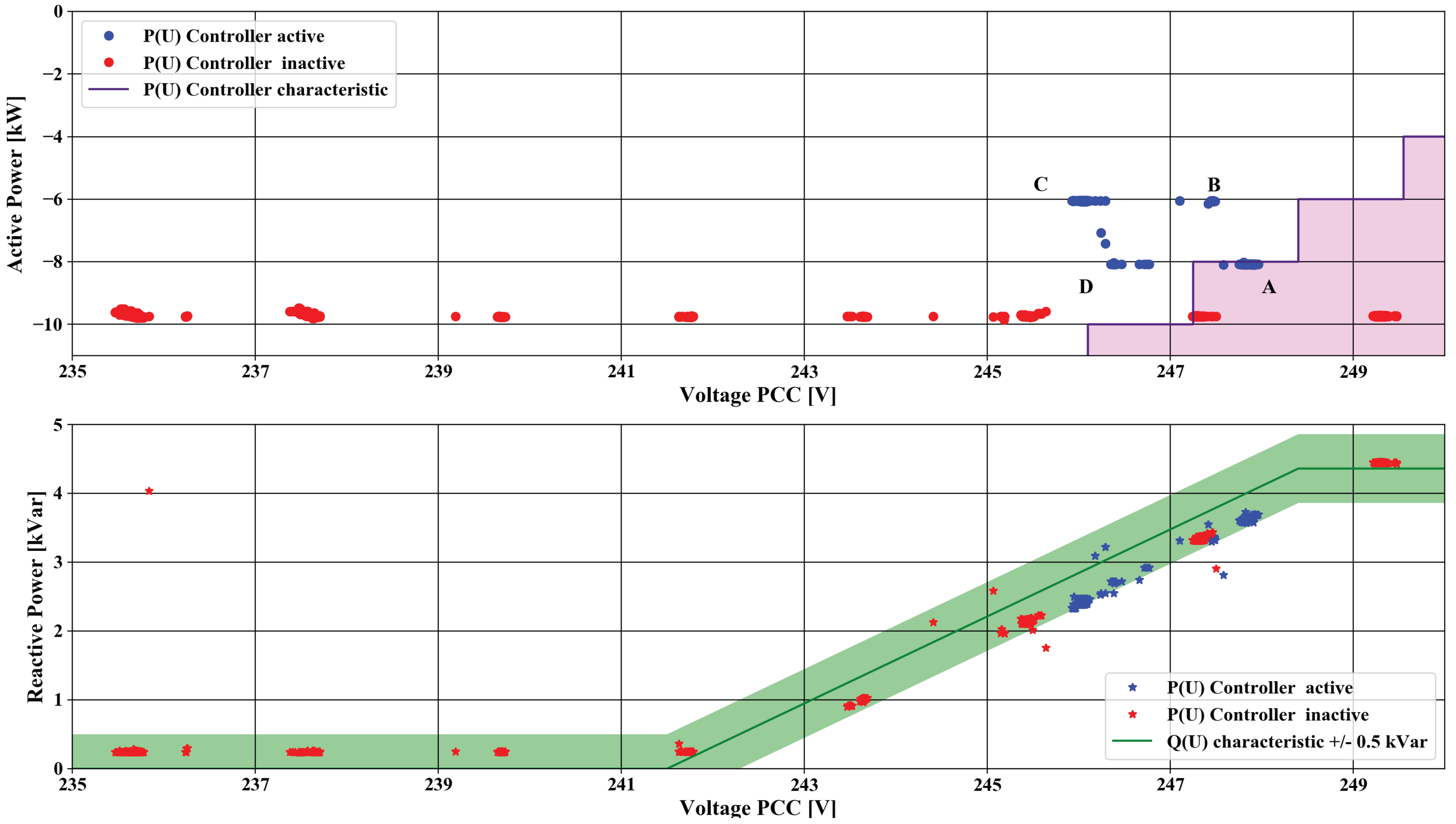
Three interesting aspects could be observed regarding the step functions: (i) the voltage deviation for the steady state situations before and after the step; (ii) the constancy of selected setpoints and the overall stabilisation time; and (iii) the stabilisation time, which is highly affected by the implemented control algorithm (e.g., Q(U) control) and the selected parameters.
The varying time constants of the Q(U) control could be observed when looking at the different responses of the PV inverter to the voltage step. For System Setups A and B, the inverter reacted immediately with a small time constant with a reactive power in-feed when the voltage changed. Smaller time constants resulted in faster reach of a steady state. For both setups, the reaction of the inverter was immediate when small time constants were used. In contrast to that was the calculated reaction to the changed reactive power in-feed by the system setups. For System Setup A, the reaction of the voltage happened immediately due to small time steps of the PHIL-setup, whereas, for System Setup B, the reaction was delayed in more discrete steps, which corresponded to the cycle time. As described in
Section 4.3, the time constant suggested by the manufacturer is
= 5 s, which will result in a highly damped system response. This seems to be a preferred strategy for DSO to prevent interference with multiple deployed systems.
Looking at the results of this test scenario, both systems showed a fairly linear offset to the reference value. This effect was reflected in the
Mean Error (ME). However, the overall result was quite pleasurable showing a high
Correlation Coefficient (CC) for both systems with a negligible difference between them. This occurrence could be expected as the calculated time for the time periods before and after the step function was included. The presented values were for Phase A to neutral of the three-phase system. Therefore, the readings were only a third of the in-feed of the three phase inverter. The oscillation already observed in
Section 5.1 was quantified by the maximum spread
(DELTA) and the resulting
Standard Deviation (STD) of the voltage readings. As presented in the previous section, this related to the MPPT algorithm of the used PV inverters. As a result of the comparison of these values, one could see that System Setup A was more constant than System Setup B. The further examination also showed that these oscillations have a relatively constant subfundamental peak of around 3.570 Hz. This behaviour was also present for System Setup A but with a significantly lower amplitude. This also diminished when changing the voltage setpoint, and the oscillation was overlayed with other effects. Together with further analyses of the PI, it seemed that the immanent impedance of System Setup B was significantly higher than of System Setup A.
The upper dashed line represents the 1.08 p.u. value and, as one can see, the voltage of System Setup B never dropped below this parameterised limit of the Q(U) control. According to the given droop curve of the Q(U) controller, this resulted in a constant reactive power.
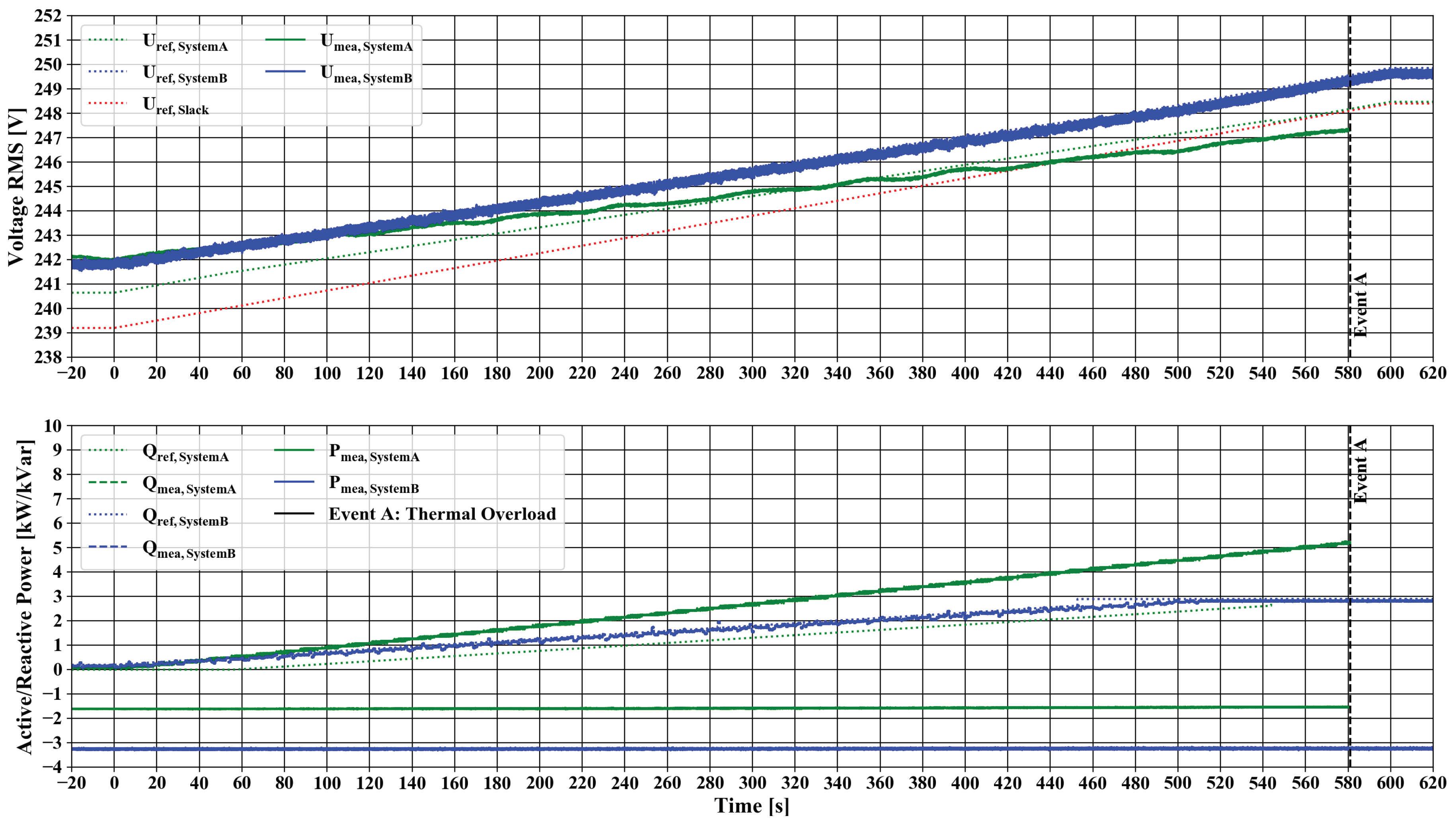
5.4. Comparison of the System Response for Voltage Ramp
In comparison to the previous section where the focus lay on the comparison of the two systems in regard to the transient and dynamic behaviour when changing the voltage in an extreme manner, this section presents the comparison of both systems in the context of a slowly but constantly rising voltage level and the interaction of the Q(U) control. The results are shown in
Figure 11. The corresponding statistical key figures are given in
Table 6 (Statistical Key Figures for the Evaluation are shown in
Appendix A). In contrast to the short term evaluation of the step function, this test scenario was executed with a variety of durations with up to 10 min of rise time. The scenario with a rise time of 10 min is outlined in the current section. To evaluate this rather long-term scenario, two different active power levels were chosen. This is due to the system properties of System Setup A, as the complete feed-in energy was dissipated by the PI. In the course of the experiment, issues regarding the overheating and thermal shutdown had to be tackled.
The reference curves for the ramp illustrate what is expected in theory. The red dashed line represents the constantly raising voltage level of the upstream grid with the inverter working against the voltage raise with feeding-in reactive power. When comparing the measured values, both systems showed a voltage deviation from the calculated value. For System Setup B, this deviation lay within the same order as it already could have been observed in the step experiment. With System Setup A, the voltage changed from over-voltage in respect to the reference curve to under-voltage due to a higher reactive power feed-in. The individual oscillation appeared in the same order of magnitude as in the previous scenario. The reactive power response of System Setup B became in the bigger time frame of this analysis quite pleasing. For System Setup A, the reactive in-feed was too high due to a different parameterisation.
The active in-feed power remained constant for both setups. The vertical line which is annotated with “Event A” represents the point where the power interface of System Setup A shuts down due to over-temperature.
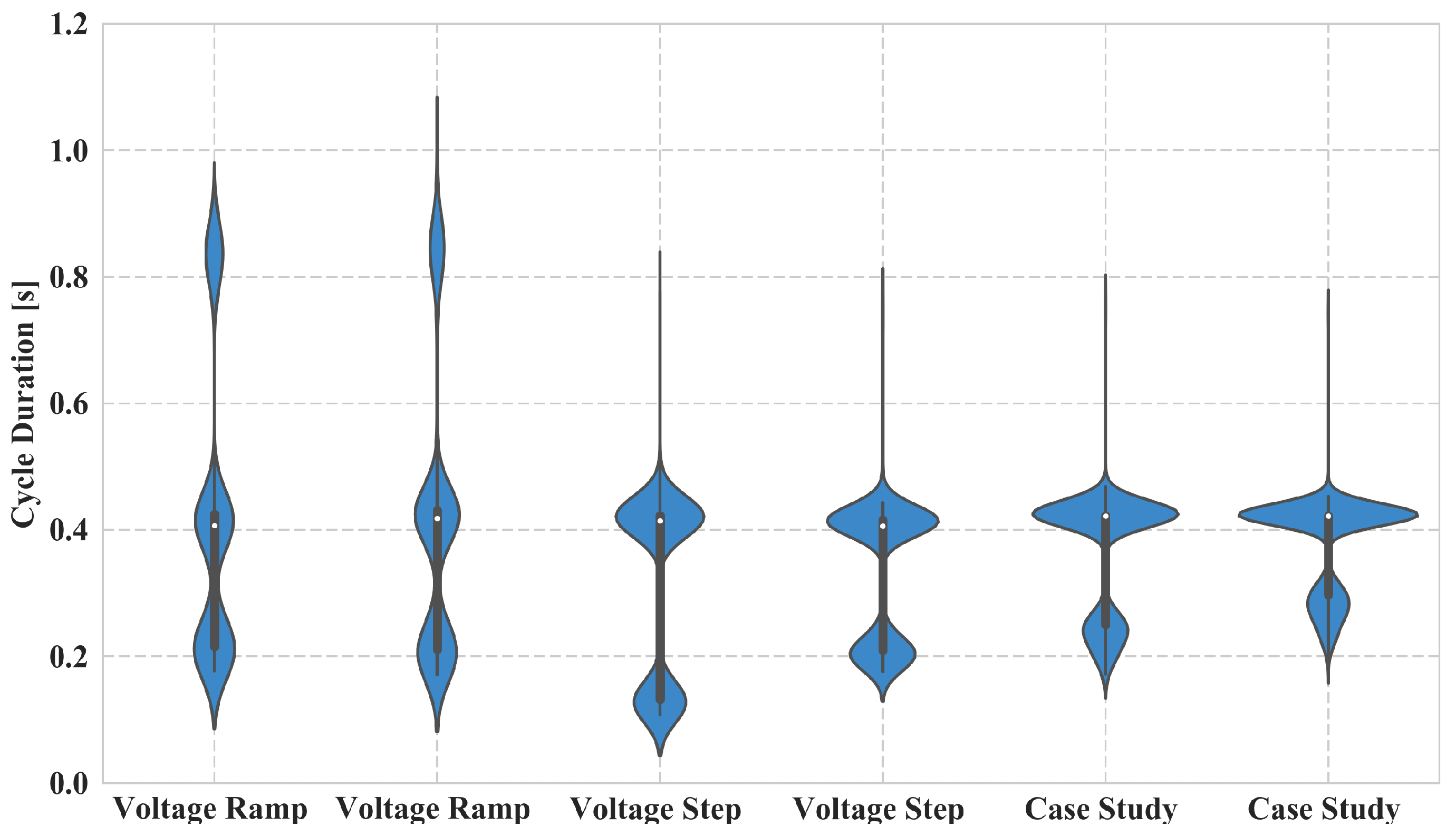
5.5. Analysis of the Cycle Time for the Examined Setups
System Setup A was able to meet the time requirements due to its real-time control loop with a cycle time well below 50
s. For the QDPHIL system setup, the cycle time was significantly higher and required a more detailed analysis. As shown in
Figure 12, the total cycle time remained under one second. The cycle time
for System Setup B consisted of the control loop in the main loop, the calculation of the new setpoints in PowerFactory, the control of the switched-mode amplifier
Section 3.3 and the feedback of the measured values. The main control algorithm was implemented as a python script, which took about 20–30 ms runtime. Although the underlying interpreter required a bit more time to execute than a compiled program, new power interfaces can be quickly and flexibly integrated into the process using Python. This also applies to PowerFactory, which is controlled by a dedicated Python interface. Besides the python interface, there are several other ways to solve this task. Other possibilities such as
OPC UA are discussed in detail in [
54]. The solution was chosen because the whole functionality of PowerFactory’s internal scripting language (DPL) can also be addressed using the Python interface. Since Python has established itself as the standard in the given research infrastructure, it offers the possibility to use this interface also for the investigation of other research questions. Due to the simple grid model (see
Section 4.2), the load flow calculation including feedback took 50 ms (±5), which can increase with larger modelled systems. The feedback contained the new set point for the switched mode amplifier. Its manufacturer provides a C# library, with which the new set point value can be communicated to the device via Ethernet. The time needed to execute the command could not be further optimised and lies at 250 ms (±50). One possibility to actually achieve faster response times is to use the option of analog control of the network simulator in “amplifier mode”. To access the C# interface, a helper application was used, which is coupled to the python main loop via a named pipe. Subsequently, a new actual value was queried by Modbus/TCP from the measuring device and thus the control loop started again. This last step required 100 ms (±20). Overall, a
with a median of 420 ms could be achieved with System Setup B. The cycle time shown for different experiments is depicted as violin plot in
Figure 12. The density representation shows two and three clusters for the cycle time with the highest density around the median. The second cluster is in range of 0.2–0.3 s. Due to the added IEC61850 simulator function used in the case study, this cluster is moved towards the median.
7. Discussion of the Results
The experiments of Phase 1 showed that the System Setups A and B have been able to provide three-phase voltage systems, which are suitable to synchronise the given PV inverters, and started to operate properly. The modelled grid was used for a load flow calculation, and the extracted voltage signal was forwarded to the power interface. The Q(U)-function of the inverter was also tested. The biggest draw back observed in the carried out experiments was the significant voltage deviation for System Setup B which ranged from 2.3 to 3.4 for the step function experiment. Based on further examinations, we assume that the offset was caused by an immanent impedance. In these examinations, a proportional offset from the idle state voltage setpoint to the idle state voltage present at the terminals of the power interface occurred. When changing the consumed or feeding power independent of voltage set point, the voltage offset changed as well. Therefore, it is expected that the offset could be compensated with simple correction equations, which do not even introduce another controller to the system. Alternatively, the PI of System Setup B could be replaced with the superior PI of System Setup A, which featured a lower impedance and would therefore have reduced the undesired effects. Nonetheless, the dynamic properties would stay the same. Both experiments showed the correlation coefficient is >0.99 for both of the system setups. Since all of experiments presented in this contribution have in common that they utilised voltage setpoints, and a current or power, as feedback loops, the results presumably are not applicable for current type experiments. Regarding the cycle time of the given QDPHIL setup, a median of 0.42 s could be achieved. The communication between the simulation and the PI has a big share of approximately 250 ms of this process and offers the possibility for further improvements.
The occurred automatic power shut-off to prevent overheating of the PI of System Setup A could be tackled by using an additional load to prevent the feed-in energy being dissipated within the PI. This would also alter the Thevenin-equivalent of the setup, which might be undesirable. Regarding the quality of the provided voltage signals, both systems generated negligible amounts of harmonics. To represent real grid situations, introducing a realistic amount of harmonics must be considered.
Regarding the soft facts, involving setup and training, System Setup B seemed less challenging as the options were more limited. In addition, the software PowerFactory is one of the standard tools used at Ulm University of Applied Science not only for real-time simulation but also for scenario and time series analysis of distribution grids. Using those models and calculation algorithms in pure simulation experiments and in PHIL testing is beneficial. The models had to be setup up only once and results from the simulation were helpful in the PHIL experiment design. In addition, the results from the PHIL experiment could improve the models implemented in the simulation environment.
Another difference between the PI of the two setups was the maximal frequency at which the systems could reproduce harmonics. For System Setup A, this was limited to 30 kHz, whereas, for System Setup B, this was limited to 5 kHz. This aspect was not a prominent requirement for the contemplated usage, however. The described aspects are given in a short overview in
Table 7.
8. Conclusions and Outlook
The conclusions of this work are manifold and can be divided into the following parts. The first part summarises the findings of the voltage step and ramp experiments carried out in Phase 1, while the second part discusses the findings of the case study (Phase 2). In the third part, the conclusions are provided and finally the planned improvements and the utilisation of the entire setup is summed up.
The contribution presents results for a comparison of two PHIL setups—these were called System Setup A for the combination of an Opal-RT system and Spitzenberger Spies PAS PI and System Setup B for the combination of a Digsilent PowerFactory instance and a Regatron TC.ACS PI. The use case—testing of coordinated smart grid control function in an undisturbed operation—which was examined with both setups is only a subset of the capabilities of classical PHIL setups. The expected outcome of the experiments was that both systems are capable of solving this task. The fundamental difference between both systems were the calculation principles which are phasor calculation for System Setup A and the use of steady-state simulation for System Setup B. For this comparison, two scenarios were considered: (i) change of voltage level with a step; and (ii) a ramp function in the modelled grid at slack element. As a result, different levels of accuracy and continuity of the output signal were observed. The difference of the systems are apparent for the reaction of the Q(U) controller of the PV inverter within the test environment. If the time constant of the Q(U) controller is significantly lower than the cycle time, System Setup B shows discrete steps of the voltage and the stabilisation time is prolonged. As an overall statement, System Setup B is suitable for the use case described in
Section 3.1. One issue which occurred during the test was an offset between the set-point sent to the PI and the actual voltage measured at the terminals. It is suspected that this problem is caused by the high immanent impedance of System Setup B. This problem needs to be tackled.
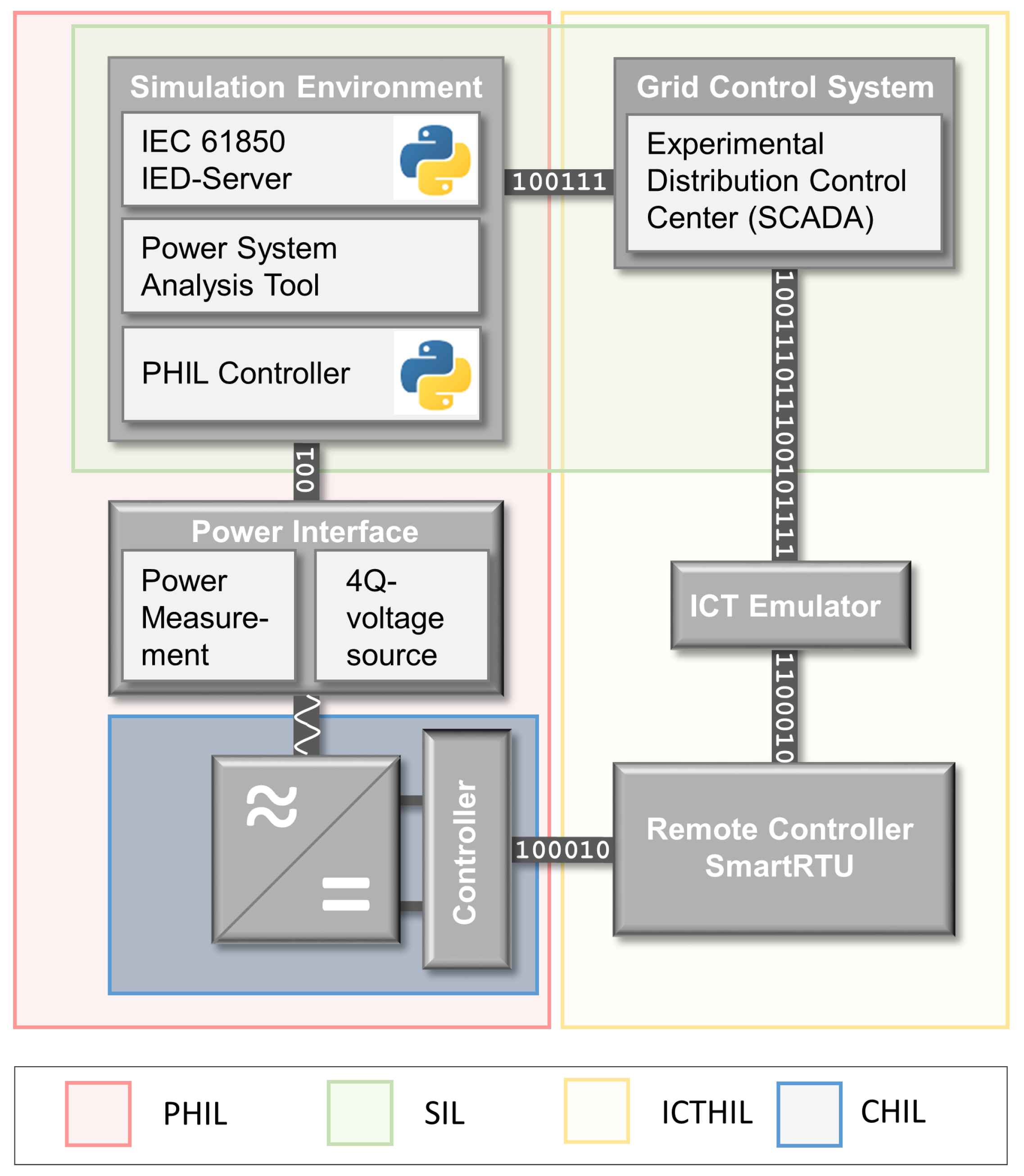
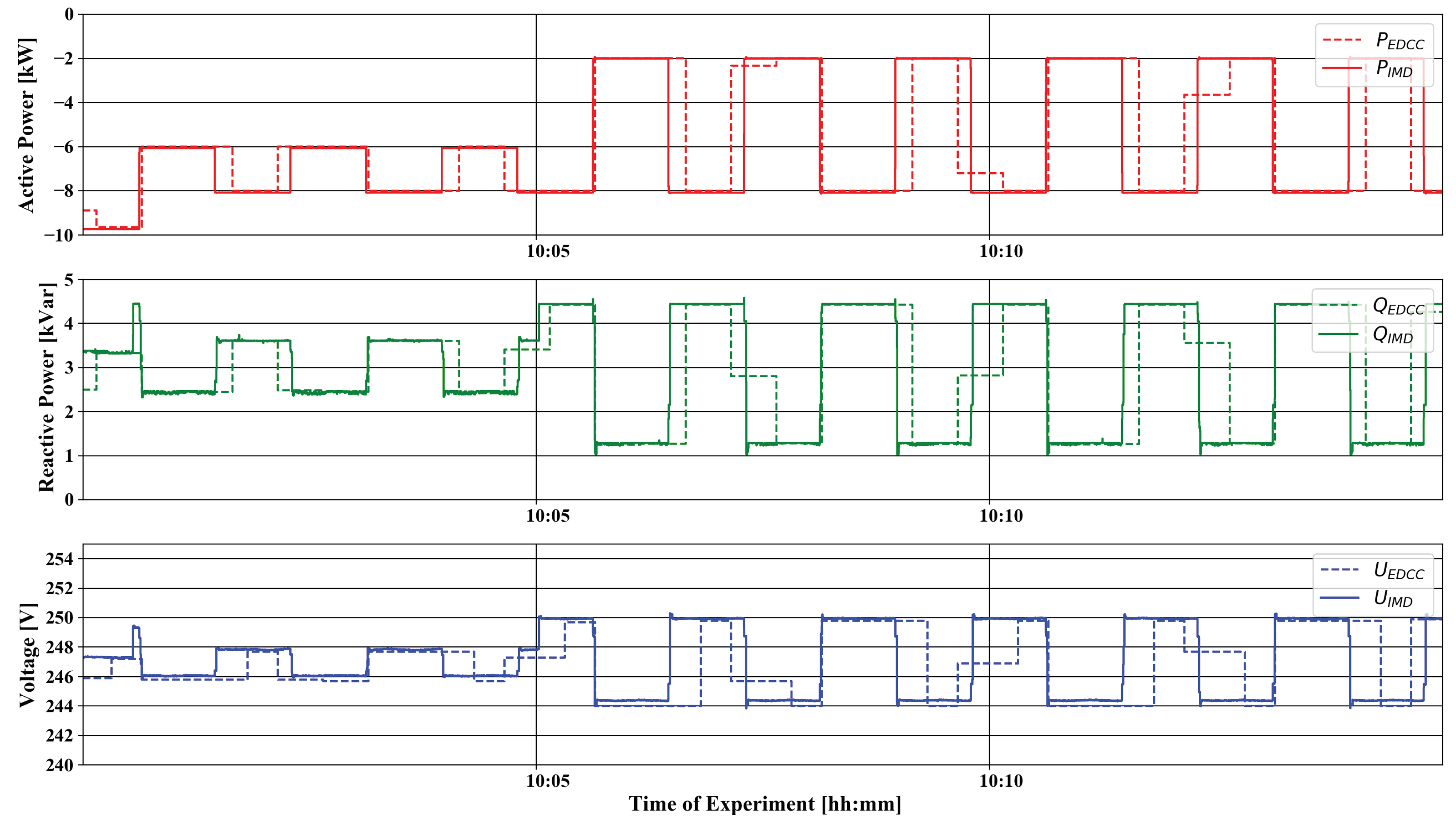
In the second part of this contribution, an actual utilisation of System Setup B is presented, which shows the intended use for a combined PHIL and SIL testing of complex smart grid control functions. The use of the SGAM presentation provided a basis for a common understanding of the presented test. This is in line with the holistic testing description introduced by the ERIgrid Consortium [
61]. Due to the description of the planned scenario, the different facilities were able to implement sub-functions in an efficient manner and were able to test the relevant sub-functions before the actual experiment. As the outcome of this case study, the tested central control algorithm is not useful for actual grid operation, as it was anticipated and deliberately chosen at the stage of test design. However, the gathered data provided a good basis for the validation of the process. In addition, the carried out experiment is a successful pilot test for the application of the RTU. It showed clearly that gathering of relevant measured values at the grid connection point and the generation unit is possible with the implemented SunSpec to the IEC 61850 converter. The other way round was tested as well and the curtailment of the PV inverter was successfully carried out.
As a conclusion, it can be stated that there was a significant difference in the working principle of the two system setups. Both systems could provide a function essential for the evaluation of EUT and SUT with respect to the requirements stated in
Section 3.1. The PHIL System Setup A was more accurate and showed more capabilities than the QDPHIL System Setup B but this came at the price of a more complex system regarding modelling, setup and operation than it was required in System Setup B. In addition, the expenditures for purchase and maintenance have been higher for System Setup A compared to System Setup B. Regarding the use of electric energy, the PI of System Setup B was able to feed back into the grid, whereas the linear PI of System Setup A dissipated the energy.
As further steps, System Setup B will be improved to solve the issues regarding the occurring offset without the use of an additional controller. As first evaluations suggest the effects are fairly linear and are likely caused by a high immanent impedance of the PI, further analyses and engineering will be necessary. These will also include considerations regarding the implementation of the immanent impedance in the grid model. The implemented System Setup B is and will be used at the Ulm University of Applied Science in the course of different research projects. The setup will be mainly used for pilot testing of applications involving small decentralised control units in combination with the German Smart Meter Infrastructure, which consists of the combination of Smart Meter, Smart Meter Gateway and CLS-Module to enable information gathering and control of small generation units such as PV inverters, as tested in the case study of
Section 6. These measurements are necessary in preparation of a broader deployment in the demonstration project C/sells [
62]. As specific suggestions for future work, the examination of effect of different interface algorithms and a detailed study of the influence communication interface between simulation and power interface for the quasi-static PHIL setups can be given. In this context, the implementation of the IA transmission line model is considered. This would enable the utilisation of a available and standardised line impedance network which is typically used for tests according to IEC 61000 series standard.