Impact of Holder Materials on the Heating and Explosive Breakup of Two-Component Droplets
Abstract
:1. Introduction
1.1. Motivation
1.2. Review of Time Ranges of Droplet Breakup through Microexplosion
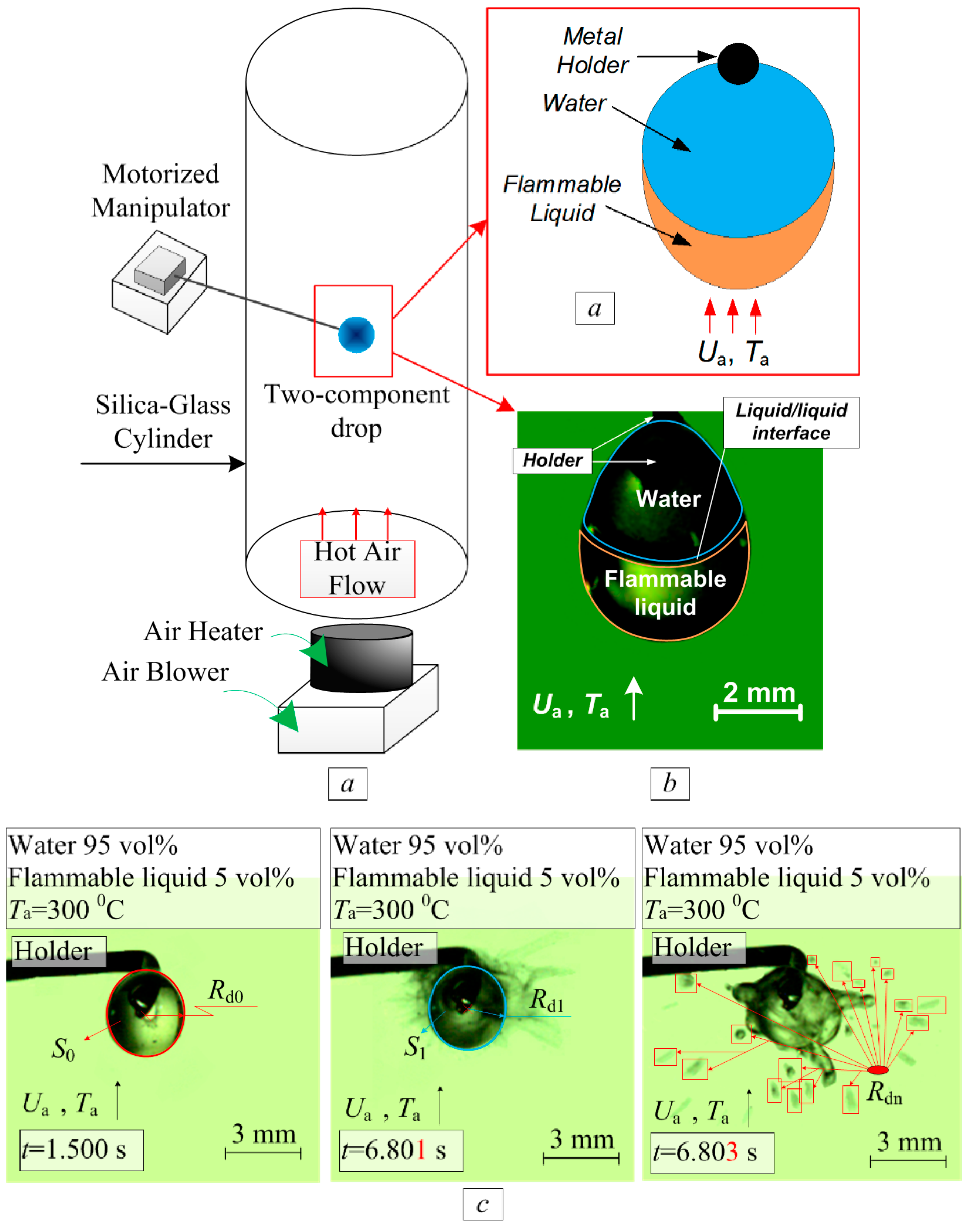
2. Experimental Setup and Procedure
2.1. Components of Two-Component Droplets and their Production Procedure
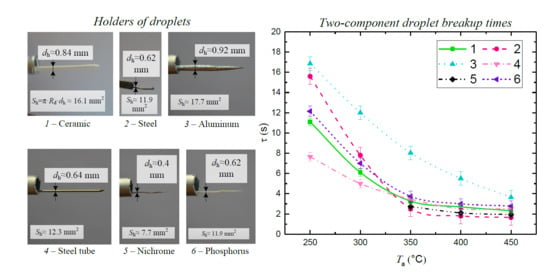
2.2. Holder Materials
2.3. Methods for Studying the Disintegration of Boiling Droplets
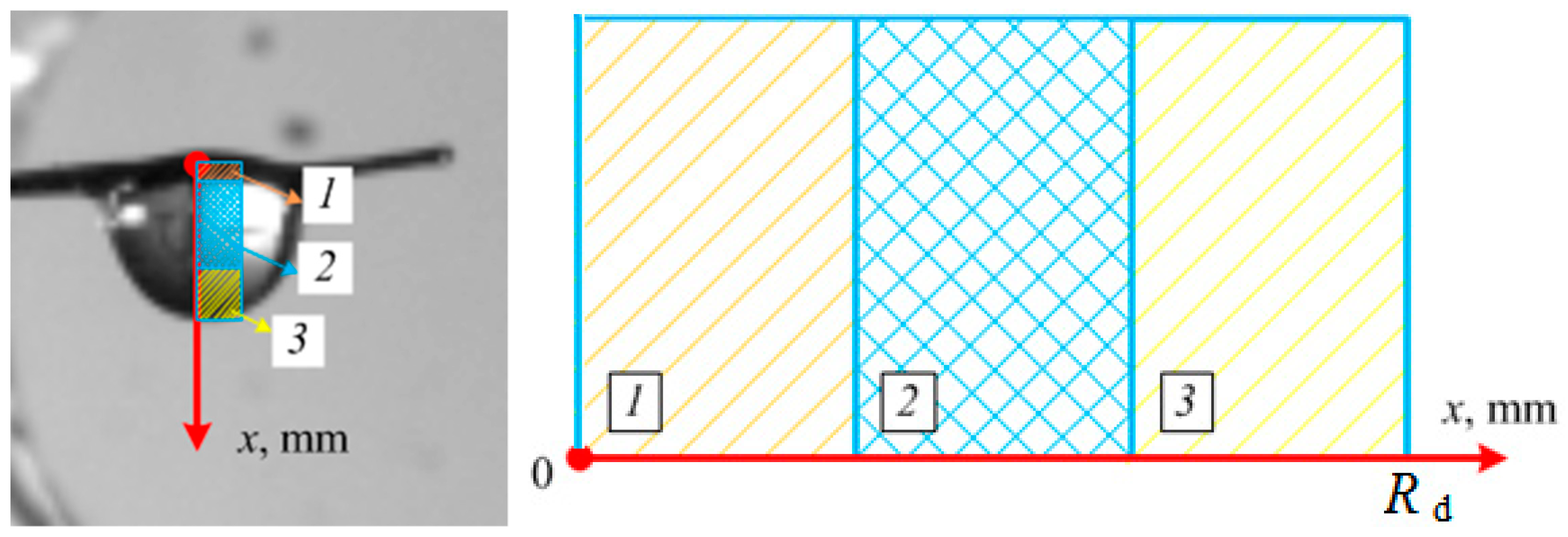
2.4. Main Registered Parameters and Tolerances
3. Results and Discussion
3.1. Droplet Disintegration Regimes
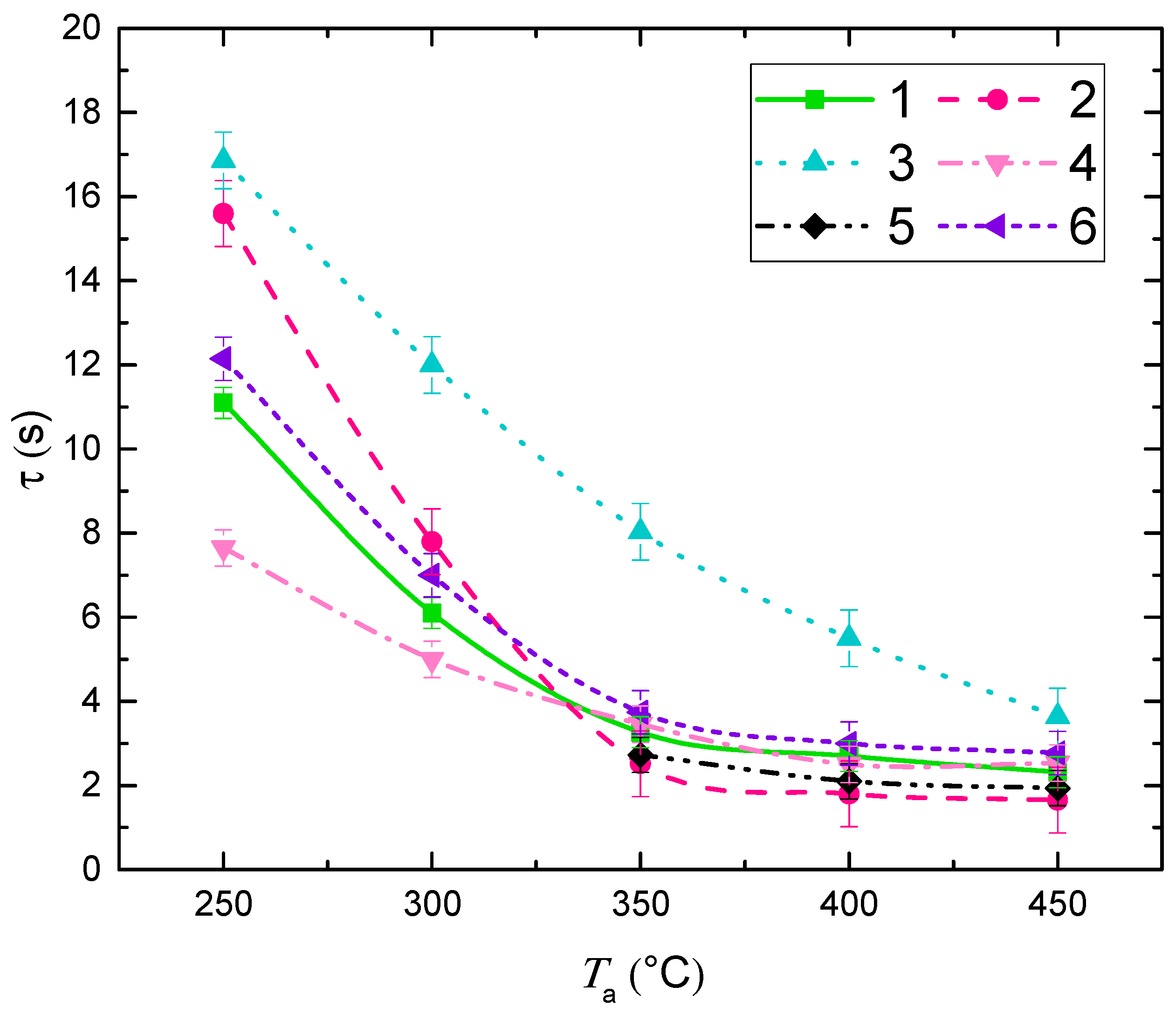
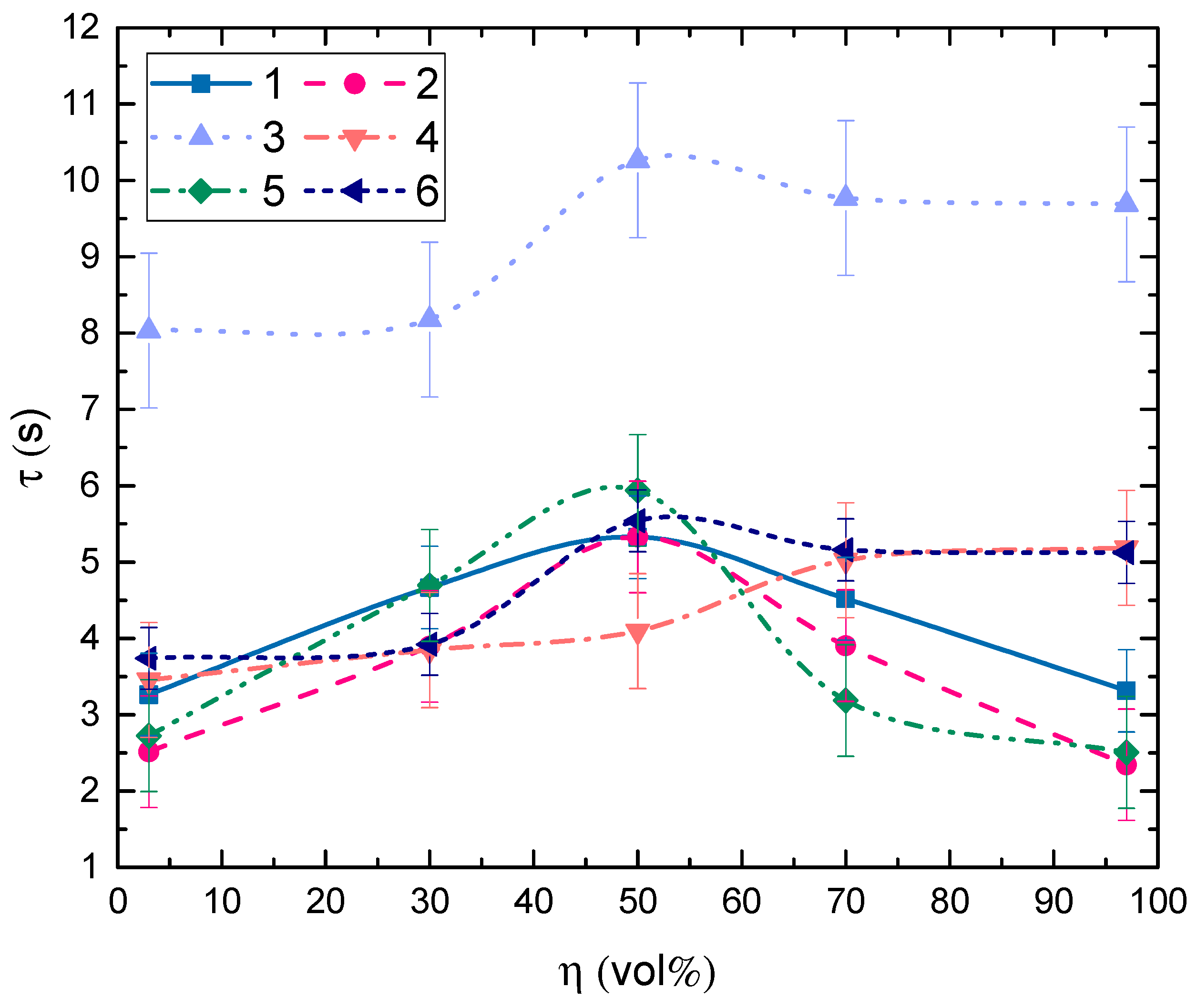
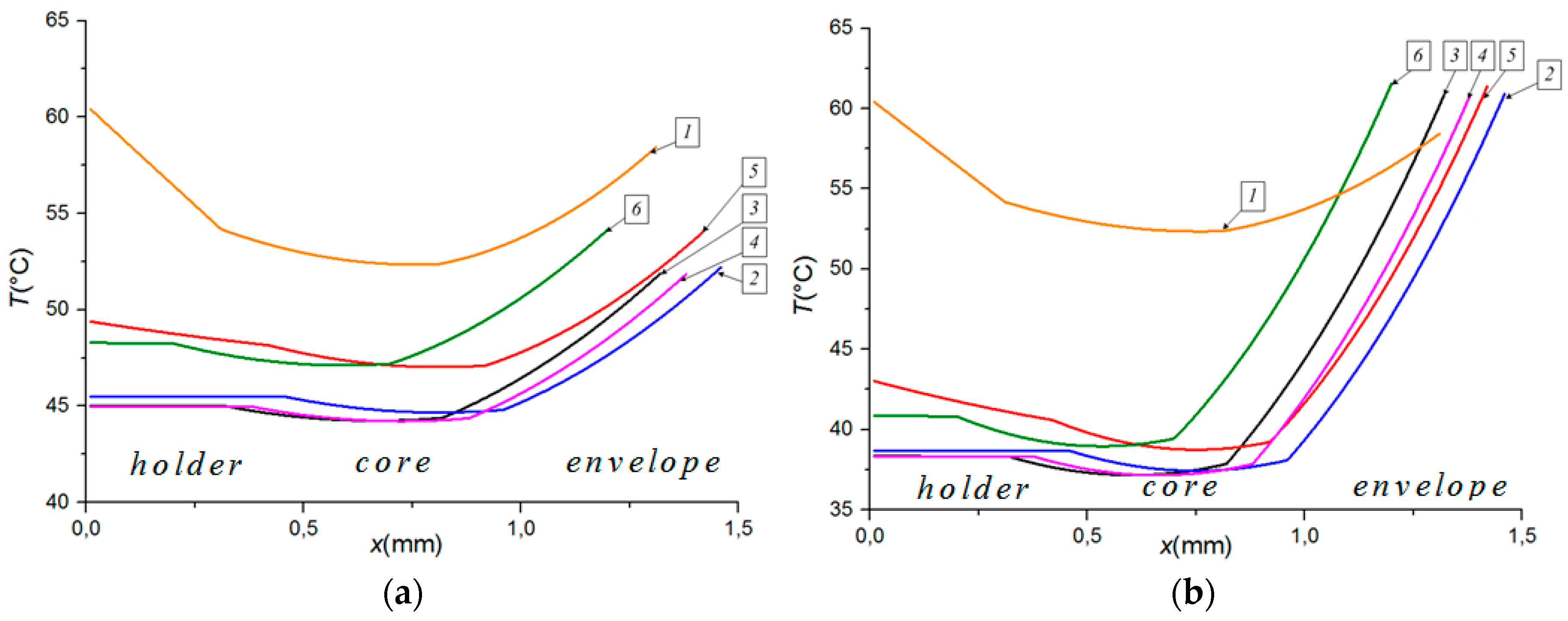
3.2. Impact of Key Factors
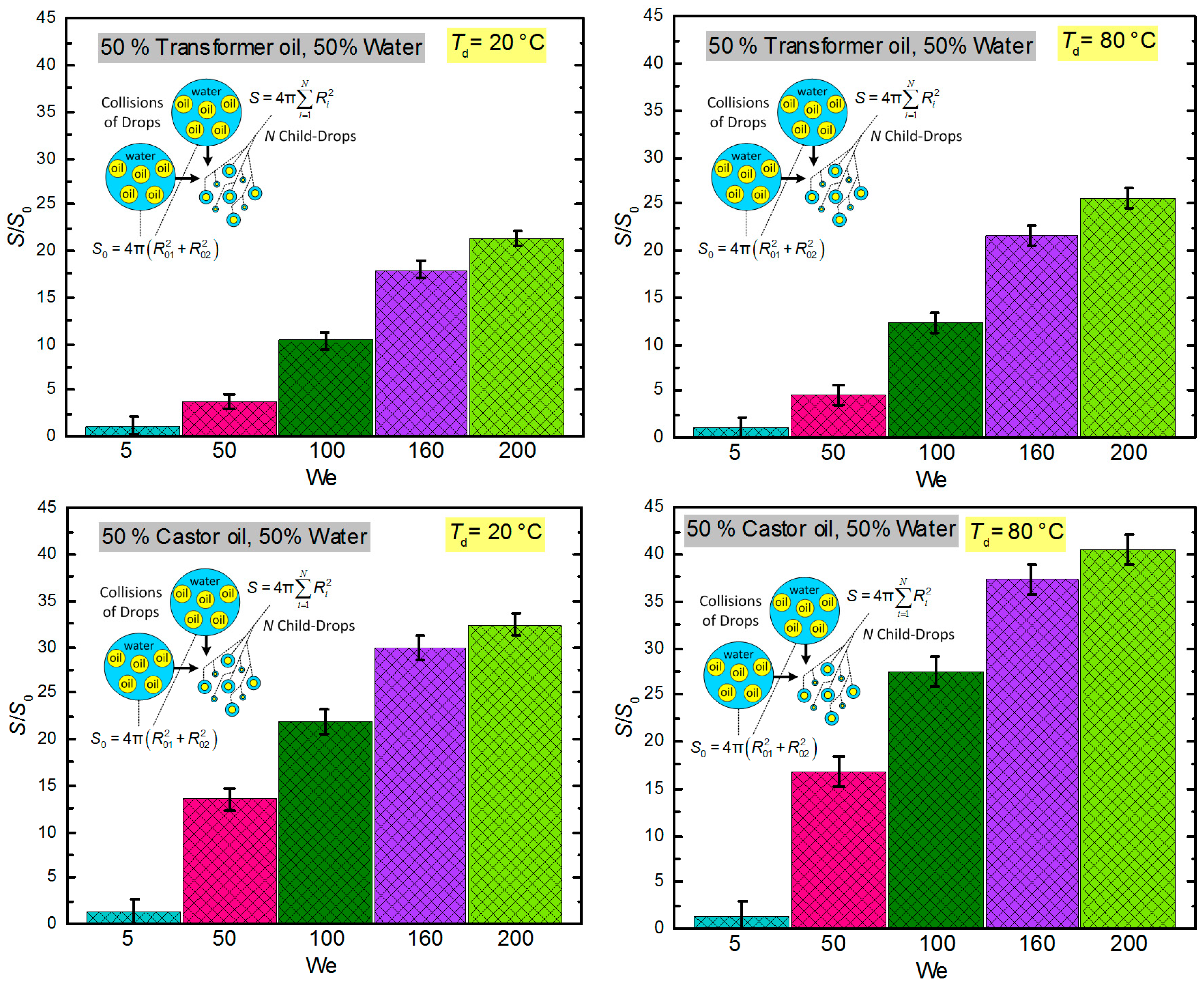
3.3. Droplet Disintegration Outcomes
3.4. Generalization of Research Findings
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature and Units
| a | thermal diffusivity, m2/s |
| C | specific heat capacity, J/(kg·°C) |
| dh | holder diameter, mm |
| m | number of groups |
| n | number of droplets in each group |
| Rd | droplet radius, mm |
| Rd0 | initial two-component droplet radius, mm |
| Rd1 | droplet radius before breakup, mm |
| Rdn | mean radius of droplets in a group, mm |
| S | total area of droplet evaporation surface after breakup, mm2 |
| S0 | initial droplet surface area, mm2 |
| S1 | droplet surface area before breakup, mm2 |
| Sh | contact surface area of a droplet and holder surface, m2 |
| Sm | frontal cross-sectional area of droplet, mm2 |
| Sn | evaporation surface area in each droplet group, mm2 |
| T | temperature, °C |
| Ta | gas flow temperature, °C |
| Td | temperature in a droplet, °C |
| t | time, s |
| Ua | high-temperature gas flow velocity, m/s |
| Vd | drop volume, µL |
| We | Weber number |
| x | coordinate in a one-dimension model, mm |
| η | flammable liquid concentration, vol% |
| λ | thermal conductivity, W/(m·°C) |
| ρ | density, kg/m3 |
| τ | two-component droplet breakup times, s |
| τh | two-component droplet lifetimes, s |
References
- Kuznetsov, G.V.; Strizhak, P.A.; Volkov, R.S. The influence of initial sizes and velocities of water droplets on transfer characteristics at high temperature gas flow. Int. J. Heat Mass Transf. 2014, 79, 838–845. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Strizhak, P.A.; Volkov, R.S. Experimental investigation of mixtures and foreign inclusions in water droplets influence on integral characteristics of their evaporation during motion through high-temperature gas area. Int. J. Therm. Sci. 2015, 88, 193–200. [Google Scholar] [CrossRef]
- Volkov, R.S.; Kuznetsov, G.V.; Legros, J.C.; Strizhak, P.A. Experimental investigation of consecutive water droplets falling down through high-temperature gas zone. Int. J. Heat Mass Transf. 2016, 95, 184–197. [Google Scholar] [CrossRef]
- Sazhin, S.S. Modelling of fuel droplet heating and evaporation: Recent results and unsolved problems. Fuel 2010, 196, 69–101. [Google Scholar] [CrossRef]
- Snegirev, A.Y. Transient temperature gradient in a single-component vaporizing droplet. Int. J. Heat Mass Transf. 2013, 65, 80–94. [Google Scholar] [CrossRef]
- Vysokomornaya, O.V.; Kuznetsov, G.V.; Strizhak, P.A. Evaporation of water droplets in a high-temperature gaseous medium. J. Eng. Phys. Thermophys. 2016, 89, 141–151. [Google Scholar] [CrossRef]
- Spalding, D.B. Some Fundamentals of Combustion; Butterworth’s: London, UK, 1955. [Google Scholar]
- Fuchs, N.A. Evaporation and Droplet Growth in Gaseous Media; Pergamon Press: London, UK, 1959. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops—I. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Vershinina, K.Y.; Egorov, R.I.; Strizhak, P.A. The ignition parameters of the coal-water slurry droplets at the different methods of injection into the hot oxidant flow. Appl. Therm. Eng. 2016, 107, 10–20. [Google Scholar] [CrossRef]
- Watanabe, H.; Harada, T.; Matsushita, Y.; Aoki, H.; Miura, T. The characteristics of puffing of the carbonated emulsified fuel. Int. J. Heat Mass Transf. 2009, 52, 3676–3684. [Google Scholar] [CrossRef]
- Suzuki, Y.; Harada, T.; Watanabe, H.; Shoji, M.; Matsushita, Y.; Aoki, H.; Miura, T. Visualization of aggregation process of dispersed water droplets and the effect of aggregation on secondary atomization of emulsified fuel droplets. Proc. Combust. Inst. 2011, 33, 2063–2070. [Google Scholar] [CrossRef]
- Tarlet, D.; Josset, C.; Bellettre, J. Comparison between unique and coalesced water drops in micro-explosions scanned by differential calorimetry. Int. J. Heat Mass Transf. 2016, 95, 689–692. [Google Scholar] [CrossRef]
- Strizhak, P.A.; Piskunov, M.V.; Volkov, R.S.; Legros, J.C. Evaporation, boiling and explosive breakup of oil-water emulsion drops under intense radiant heating. Chem. Eng. Res. Des. 2017, 127, 72–80. [Google Scholar] [CrossRef]
- Vysokomornaya, O.V.; Piskunov, M.V.; Strizhak, P.A. Breakup of heterogeneous water drop immersed in high-temperature air. Appl. Therm. Eng. 2017, 127, 1340–1345. [Google Scholar] [CrossRef]
- Piskunov, M.V.; Strizhak, P.A. Using Planar Laser Induced Fluorescence to explain the mechanism of heterogeneous water droplet boiling and explosive breakup. Exp. Therm. Fluid Sci. 2018, 91, 103–116. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Piskunov, M.V.; Volkov, R.S.; Strizhak, P.A. Unsteady temperature fields of evaporating water droplets exposed to conductive, convective and radiative heating. Appl. Therm. Eng. 2018, 131, 340–355. [Google Scholar] [CrossRef]
- Misyura, S.Y. Evaporation of a sessile water drop and a drop of aqueous salt solution. Nat. Sci. Rep. 2017, 7, 14759. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Misyura, S.Y. Evaporation and heat and mass transfer of a sessile drop of aqueous salt solution on heated wall. Int. J. Heat Mass Transf. 2018, 116, 667–674. [Google Scholar] [CrossRef]
- Misyura, S.Y. Non-isothermal evaporation in a sessile droplet of water-salt solution. Int. J. Therm. Sci. 2018, 124, 76–84. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Shmakov, A.G.; Shvartsberg, V.M.; Chernov, A.A.; Yakimov, S.A.; Koutsenogii, K.P.; Makarov, V.I. Fire suppression by low-volatile chemically active fire suppressants using aerosol technology. Fire Saf. J. 2012, 51, 102–109. [Google Scholar] [CrossRef]
- Varaksin, A.Y. Fluid dynamics and thermal physics of two-phase flows: Problems and achievements. High Temp. 2013, 51, 377–407. [Google Scholar] [CrossRef]
- Tarlet, D.; Allouis, C.; Bellettre, J. The balance between surface and kinetic energies within an optimal micro-explosion. Int. J. Therm. Sci. 2016, 107, 179–183. [Google Scholar] [CrossRef]
- Kichatov, B.; Korshunov, A.; Kiverin, A.; Son, E. Experimental study of foamed emulsion combustion: Influence of solid microparticles, glycerol and surfactant. Fuel Process. Technol. 2017, 166, 77–85. [Google Scholar] [CrossRef]
- Salgansky, E.A.; Zaichenko, A.Y.; Podlesniy, D.N.; Salganskaya, M.V.; Toledo, M. Coal dust gasification in the filtration combustion mode with syngas production. Int. J. Hydrogen Energy. 2017, 42, 11017–11022. [Google Scholar] [CrossRef]
- Zhukov, V.E.; Pavlenko, A.N.; Moiseev, M.I.; Kuznetsov, D.V. Dynamics of interphase surface of self-sustaining evaporation front in liquid with additives of nanosized particles. High Temp. 2017, 55, 79–86. [Google Scholar] [CrossRef]
- Sazhin, S.S.; Shchepakina, E.; Sobolev, V. Order reduction in models of spray ignition and combustion. Combust. Flame 2018, 187, 122–128. [Google Scholar] [CrossRef]
- Mura, E.; Calabria, R.; Califano, V.; Massoli, P.; Bellettre, J. Emulsion droplet micro-explosion: Analysis of two experimental approaches. Exp. Therm. Fluid Sci. 2014, 56, 69–74. [Google Scholar] [CrossRef]
- Strizhak, P.A.; Volkov, R.S.; Castanet, G.; Lemoine, F.; Rybdylova, O.; Sazhin, S.S. Heating and evaporation of suspended water droplets: Experimental studies and modelling. Int. J. Heat Mass Transf. 2018, 127, 92–106. [Google Scholar] [CrossRef]
- Tsue, M.; Yamasaki, H.; Kadota, T.; Segawa, D.; Kono, M. Effect of gravity on onset of microexplosion for an oil-in-water emulsion droplet. Symp. Comb. 1998, 27, 2587–2593. [Google Scholar] [CrossRef]
- Hou, S.-S.; Rizal, F.M.; Lin, T.-H.; Yang, T.-Y.; Wan, H.-P. Microexplosion and ignition of droplets of fuel oil/bio-oil (derived from lauan wood) blends. Fuel 2013, 113, 31–42. [Google Scholar] [CrossRef]
- Chaitanya KumarRao, D.; Syam, S.; Karmakar, S.; Joarder, R. Experimental investigations on nucleation, bubble growth, and micro-explosion characteristics during the combustion of ethanol/Jet A-1 fuel droplets. Exp. Therm. Fluid Sci. 2017, 89, 284–294. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.H.; Hung, W.G.; Fu, S.Y.; Huang, W.C.; Law, C.K. On the burning and microexplosion of collision-generated two-component droplets: Miscible fuels. Combust. Flame 2003, 134, 289–300. [Google Scholar] [CrossRef]
- Antonov, D.V.; Volkov, R.S.; Kuznetsov, G.V.; Strizhak, P.A. Experimental Study of the Effects of Collision of Water Droplets in a Flow of High-Temperature Gases. J. Eng. Phys. Thermophys. 2016, 89, 100–111. [Google Scholar] [CrossRef]
- Volkov, R.S.; Kuznetsov, G.V.; Strizhak, P.A. Statistical analysis of consequences of collisions between two water droplets upon their motion in a high-temperature gas flow. Tech. Phys. Lett. 2015, 41, 840–843. [Google Scholar] [CrossRef]
- Antonov, D.V.; Kuznetsov, G.V.; Strizhak, P.A. Determination of Temperature and Concentration of a Vapor–Gas Mixture in a Wake of Water Droplets Moving through Combustion Products. J. Eng. Therm. 2016, 25, 337–351. [Google Scholar] [CrossRef]
- Mura, E.; Massoli, P.; Josset, C.; Loubar, K.; Bellettre, J. Study of the micro-explosion temperature of water in oil emulsion droplets during the Leidenfrost effect. Exp. Therm. Fluid Sci. 2012, 43, 63–70. [Google Scholar] [CrossRef]
- Tarlet, D.; Mura, E.; Josset, C.; Bellettre, J.; Allouis, C.; Massoli, P. Distribution of thermal energy of child-droplets issued from an optimal micro-explosion. Int. J. Heat Mass Transf. 2014, 77, 1043–1054. [Google Scholar] [CrossRef]
- Moussa, O.; Tarlet, D.; Massoli, P.; Bellettre, J. Parametric study of the micro-explosion occurrence of W/O emulsions. Int. J. Therm. Sci. 2018, 133, 90–97. [Google Scholar] [CrossRef]




| Article | Components | Material of Holder | Range of Two-Component Droplet Breakup Times | Experimental Setup |
|---|---|---|---|---|
| [30] | Water + n-dodecane Water + n-tetradecane Droplet size Vd = 5–15 µm | Quartz fiber D = 0.25 mm | On the holder (0.22–0.85 s) During fall (0.25–0.95 s) | A droplet is placed on the holder inside the combustion chamber with a temperature of 30 °C. After that, the droplet ignites by an electrically heated wire. The temperature of the droplet is measured by the Pt–PtRh thermocouple. A video camera records the microexplosion process. The fall process lies in the simultaneous motion of the chamber and the droplet during ~ 1 s. |
| [31] | Pure bio-oils D0 = 1.12 mm Pure bio-oils D0 = 1.08 mm | A droplet is fixed on a thermocouple junction (K-type) | t~7s (Ta = 300 °C) t~4s (Ta = 500 °C) | A droplet is fixed on a thermocouple. By using a linear module, it is introduced into the space between two plates heated by electricity. |
| [32] | Ethanol + Jet A-1; D0 = 2 mcl | Quartz holder D = 0.2 mm | (1.5–2.3 s) | By using a dispenser, a droplet is placed on a holder. The droplet ignites by using a nichrome wire. The process under study is recorded by a high-speed video camera. |
| [33] | Heptane C7H16 + Hexadecane C16H34 | Without holder | (170–205 ms) | A device is applied to collide two droplets of the required size, and to form a two-component droplet. The droplet moves through the combustion chamber heated up to 1050 °C. High-speed video recording allows the determination of droplet lifetimes and their breakup times. In addition, as a comparison, the experiments are performed with the preliminary formed two-component droplets. |
| [28,29] | Sunflower oil, distilled water, non-ionic surfactant SPAN 83 | K-type thermocouple (Nickel–Chromium, Nickel–Alumel) | (0.9–1.3 s) | A bare K-type thermocouple (wire diameter 76.2 µm) is heated from below by the means of a highly resistive coil with its asymptotic temperature of 350 °C. The emulsion drop is maintained on the thermocouple junction by interfacial tension. The thermocouple signal is acquired by an oscilloscope, and the shadowgraph frames are visualized using a high speed camera (10,000 fps). |
| Component | Thermal Physical Properties | Kinematic Viscosity, m2/s | Surface Tension, N/m | Boiling Temperature, °C | Heat of Vaporization, MJ/kg |
|---|---|---|---|---|---|
| Transformer Oil | ρ = 877 kg/m3, λ = 0.12 W/(m·°C), C = 1670 J/(kg·°C), a = 8∙10−8 m2/s | 22∙10−6 m2/s at 20 °C, 0.295∙10−6 m2/s at 100 °C | 26.15∙10−3 | 320 | 0.209 |
| Water | ρ = 1000 kg/m3, λ = 0.6 W/(m·°C), C = 4200 J/(kg·°C), a = 14∙10−8 m2/s | 1.006∙10−6 m2/s at 20 °C, 2.56∙10−6 m2/s at 100 °C | 72.86∙10−3 | 100 | 2.258 |
| Sunflower Oil | ρ = 865 kg/m3, λ = 0.165 W/(m·°C), C = 2500 J/(kg·°C) | 6.03∙10−5 m2/s at 25 °C | 33.7∙10−3 | 225 | 0.21 |
| Material | λ, W/(m·°C) | C, J/(kg·°C) | ρ, kg/m3 | a·106, m2/s |
|---|---|---|---|---|
| Copper | 376.86 | 416.12 | 8770.31 | 103.4 |
| Aluminum | 229.56 | 1044.76 | 2642.526 | 83.62 |
| Ceramic | 1.4 | 770 | 2355 | 0.772 |
| Steel | 42.8 | 561.8 | 7723 | 9.912 |
| Nichrome | 22.5 | 460 | 8660 | 5.648 |
| Phosphorus | 0.236 | 23.82 | 1820 | 5.444 |
| Physical Magnitude | Droplet Volume (Vd) | Droplet Radius (Rd) | Temperature Inside the Droplet (Td) | Two-Component Droplet Breakup Times (τ) and Lifetimes (τh) | Air Temperature (Тa) | Air flow Velocity (Ua) |
|---|---|---|---|---|---|---|
| Measurement Tool/Technique | Finnpipette Novus dispensers | High-speed cameras Phantom Miro M310 and Photron Fastcam SA1, Tema Automotive software | Planar Laser Induced Fluorescence (PLIF) | High-speed cameras Phantom Miro M310, Photron Fastcam SA1, and Phantom V 411, Tema Automotive software | Temperature meter (IT-8) | Particle Image Velocimetry (PIV) |
| Systematic Errors | ±0.05 µL | ≤ 4% | ±1.5–2 °C | ≤ 4% | ±(0.2+0.001T) °C | ± 2% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonov, D.; Bellettre, J.; Tarlet, D.; Massoli, P.; Vysokomornaya, O.; Piskunov, M. Impact of Holder Materials on the Heating and Explosive Breakup of Two-Component Droplets. Energies 2018, 11, 3307. https://doi.org/10.3390/en11123307
Antonov D, Bellettre J, Tarlet D, Massoli P, Vysokomornaya O, Piskunov M. Impact of Holder Materials on the Heating and Explosive Breakup of Two-Component Droplets. Energies. 2018; 11(12):3307. https://doi.org/10.3390/en11123307
Chicago/Turabian StyleAntonov, Dmitry, Jérôme Bellettre, Dominique Tarlet, Patrizio Massoli, Olga Vysokomornaya, and Maxim Piskunov. 2018. "Impact of Holder Materials on the Heating and Explosive Breakup of Two-Component Droplets" Energies 11, no. 12: 3307. https://doi.org/10.3390/en11123307
APA StyleAntonov, D., Bellettre, J., Tarlet, D., Massoli, P., Vysokomornaya, O., & Piskunov, M. (2018). Impact of Holder Materials on the Heating and Explosive Breakup of Two-Component Droplets. Energies, 11(12), 3307. https://doi.org/10.3390/en11123307