Thermal Residual Stress Analysis of Soldering and Lamination Processes for Fabrication of Crystalline Silicon Photovoltaic Modules

Abstract

In this study, we developed a finite element model to assess the residual stress in the soldering and lamination processes during the fabrication of crystalline silicon (Si) photovoltaic (PV) modules. We found that Si wafers experience maximum thermo-mechanical stress during the soldering process. Then, the Si solar cells experience pressure during the process of lamination of each layer of the PV module. Thus, it is important to decrease the residual stress during soldering of thin Si wafers. The residual stress is affected by the number of busbars, Si wafer thickness, and solder type. Firstly, as the number of busbars increases from two to twelve, the maximum principal stress increases by almost a factor of three (~100 MPa). Such a high first principal stress can cause mechanical failure in some Si wafers. Secondly, thermal warpage increases immediately after the soldering process when the thickness of the Si wafers decreases. Therefore, the number and width of the busbars should be considered in order to avoid mechanical failure. Finally, the residual stress can be reduced by using low melting point solder. The results obtained in this study can be applied to avoid mechanical failure in PV modules employing thin Si wafers.

1. Introduction

Crystalline silicon (c-Si) solar cells are the predominant type of solar cells used in the manufacture of photovoltaic (PV) modules. With the global PV module production capacity at the end of 2016 estimated to be over 90 GWp, the market share of c-Si cells was above 90% [1]. Cost reduction and efficiency improvement have enhanced the competitiveness of c-Si PV modules. To ensure steady growth in the use of c-Si PV modules, it is important to reduce the cost of its materials. These include poly-Si wafers, cells, and modules. The wafers account for more than 15% of the PV module cost. The cost of the wafers can be further reduced by using thin wafers [1]. The wafer thickness is expected to be reduced to 140 µm for mono-Si wafers by 2027 [1]. In addition, wafer thickness can be further decreased to 120 µm through future innovative technological advances in solar cells and PV modules. However, it is acknowledged that thin wafers may increase mechanical failures during the manufacturing process [2,3,4,5,6,7,8,9]. Mechanical failures arise from the difference in the coefficients of thermal expansion (CTE) of materials. Si wafers experience thermal history during the soldering process, which connects individual solar cells in series using flattened copper wires dipped in molten soldering material. The wires are soldered to the silver electrode on the surface of the wafers. In addition, the series connected cells are laminated under high pressure and temperature to fabricate the PV modules. The lamination process creates residual stress in the Si wafers. To decrease the wafer thickness, it is important to understand the mechanical stress of the Si wafers during the soldering and lamination processes.

A systematic approach based on finite element simulations for the Si PV module would be helpful to effectively understand the thermal residual stress of the Si wafers during soldering and lamination. Similarly, numerical investigation on optical power splitter using waveguides has been successfully demonstrated when understanding its impact on newly designed devices before being applied [10,11,12]. Several numerical studies have been conducted on the mechanical failures of Si solar cells and PV modules [13,14,15]. Lai et al. [13] conducted finite element simulations to analyze the thermal warpage of Si solar cells. They found that the thermal warpage and thermal residual stress during the soldering process were well matched with the experimental data. Further, they concluded that the thermal residual stress of Si wafers increases with increases in the Si cell thickness and decreases in soldering rod thickness and soldering rod width.

PV modules with three and four busbars occupy more than 90% of the current market. By 2027, Si cells with more busbars and busbar-less cells are expected to occupy more than 80% of the market, and those with three and four busbars are expected to occupy less than 20% of the market. Therefore, it is necessary to investigate the influence of number of busbars on the thermal residual stress. Geipel et al. [16] investigated the thermal residual stress at the soldered interconnections. To apply the brittle material failure criteria, the first and third principal stresses of the busbars were computed. The simulation results showed that the first principal stress is more clearly sensitive to the number of busbars than the third principal stress. However, the mechanical failure of Si wafers requires more consideration because Si wafers are more likely to experience mechanical failure than the other components owing to their brittleness. Thermo-mechanical failures of the PV modules have been reported during the lamination process [17]. Tippabhotla et al. [3] presented a systematic approach to investigating the thermal residual stress during the lamination process, based on synchrotron X-ray submicron diffraction coupled with physics-based finite element modeling. They found that the highly localized thermal residual stress is induced by local bending near the interconnection.

The study was conducted with the following objectives: (1) Investigate the thermal residual stress during the soldering and lamination processes in the fabrication of PV modules, (2) examine the effect of number of busbars on the thermal-induced stress, (3) study the effects of Si wafer thickness on thermal warpage and residual stress, and (4) consider the influence of solder types on the mechanical stress of Si wafers. Consequently, we developed a finite element model to investigate residual stress and wafer warpage. The details of the finite element model and simulation are presented in Section 2. The results obtained are presented and discussed in Section 3.

2. Finite Element Simulations

In this study, ANSYS v14 (Canonsburg, PA, USA) was used for finite element modeling and simulation. Each finite element model was composed of approximately 100,000 shell elements. The system details and boundary conditions are given in the following subsections.

2.1. System Details

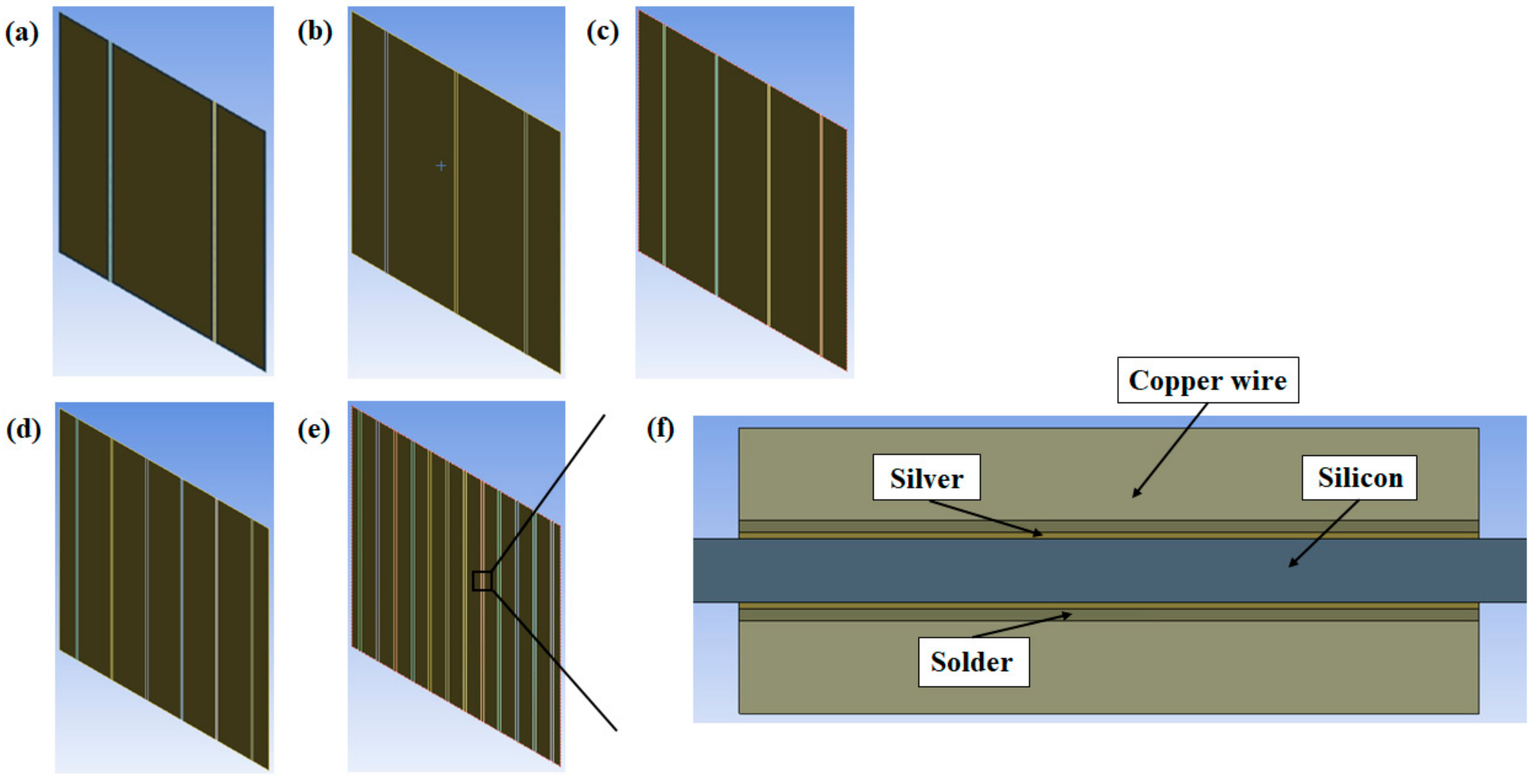
The PV modules consisted of a Si wafer, silver electrode, and copper wire coated with solder, as shown in Figure 1. We investigated the effect of the geometric dimensions (thickness of the wafer and the number and width of the busbars) on the residual stress of the Si wafers during the soldering and lamination processes. The detailed geometric dimensions for the numerical simulations are listed in

Table 1. Geometric dimensions of PV modules in the finite element models.

Geometric Parameters	Silicon Wafer	Silver Electrode	Solder	Copper Wire
Lx (mm)	156
Ly (mm)	156	1.2, 1.6, 2.0
Lz (mm)	0.01, 0.05, 0.10, 0.20	0.01	0.02	0.15

. It was assumed that the busbar is perfectly bonded to the Si wafer. The thermo-mechanical properties of each constituent are listed in

Table 2. Thermo-mechanical properties of PV module components [13,18,19].

Material	Young’s Modulus (GPa)	Thermal Expansion Coefficient (ppm/K)	Poisson’s Ratio	Melting Point (°C)
Silicon	130	2.6	0.28	1411
Silver	27.3	19.7	0.30	961
Copper	128	16.5	0.34	1084
Solder I (63Sn37Pb)	32.0	24.7	0.38	183
Solder II	51.0	23.5	0.38	217
(96.5Sn3.0Ag0.5Cu)
Solder III	39.4	15.0	0.35	138
(42Sn58Bi)

.

2.2. Simulation Conditions

Structural boundary conditions were imposed on the four vertices of the Si wafers for the soldering process, as shown in Figure 2. The displacements in the out-of-plane direction (z-axis) of the four vertices were defined as zero. This was imposed to describe the symmetric deflections in the out-of-plane direction. Among the four vertices, three vertices were allowed for the free deformations in the in-plane (x- and y-axes) directions. To avoid the rigid body motion across the in-plane directions, a vertex was imposed on the fixed displacement boundary conditions for the in-plane directions.

We used the enforced nodal displacement-based approach to explain the lamination process of the PV modules. Specifically, the curved Si wafers in which curvature is induced by the soldering process are flattened during the lamination process. A pressure of 150 kPa is applied perpendicularly on the Si wafer. Although this pressure is sufficient to flatten the Si wafer, it cannot induce in-plane directional displacements [3]. Therefore, the details regarding pressure were not considered in the finite element simulations; instead, out-of-plane direction nodal displacement fields were enforced to flatten the surface of the Si wafer.

Figure 3 shows the thermal boundary conditions of the hot air-based soldering and lamination processes. The temperature profiles of the soldering process were determined based on previous research [13]. We considered 183 °C, 217 °C, and 138 °C as the soldering temperatures for solder I, II, and III, respectively. These values were simply determined by the melting points of each solder. The temperature boundary conditions of the soldering and lamination processes are shown in Figure 3a,b, respectively.

2.3. Failure Criteria of Brittle Materials

The maximum stress criterion that is based on the principal stress is generally used to predict the failure of brittle solid materials as follows [20]:

σ_c < σ₃ < σ₁ < σ_t,

(1)

where σ_t and σ_c denote the tensile and compressive ultimate strengths of the materials, respectively, and σ₁ and σ₃ denote the first and third principal stresses, respectively. Therefore, we used the first and third principal stresses of the Si wafers.

3. Results and Discussions

3.1. Thermal Residual Stress during Soldering and Lamination

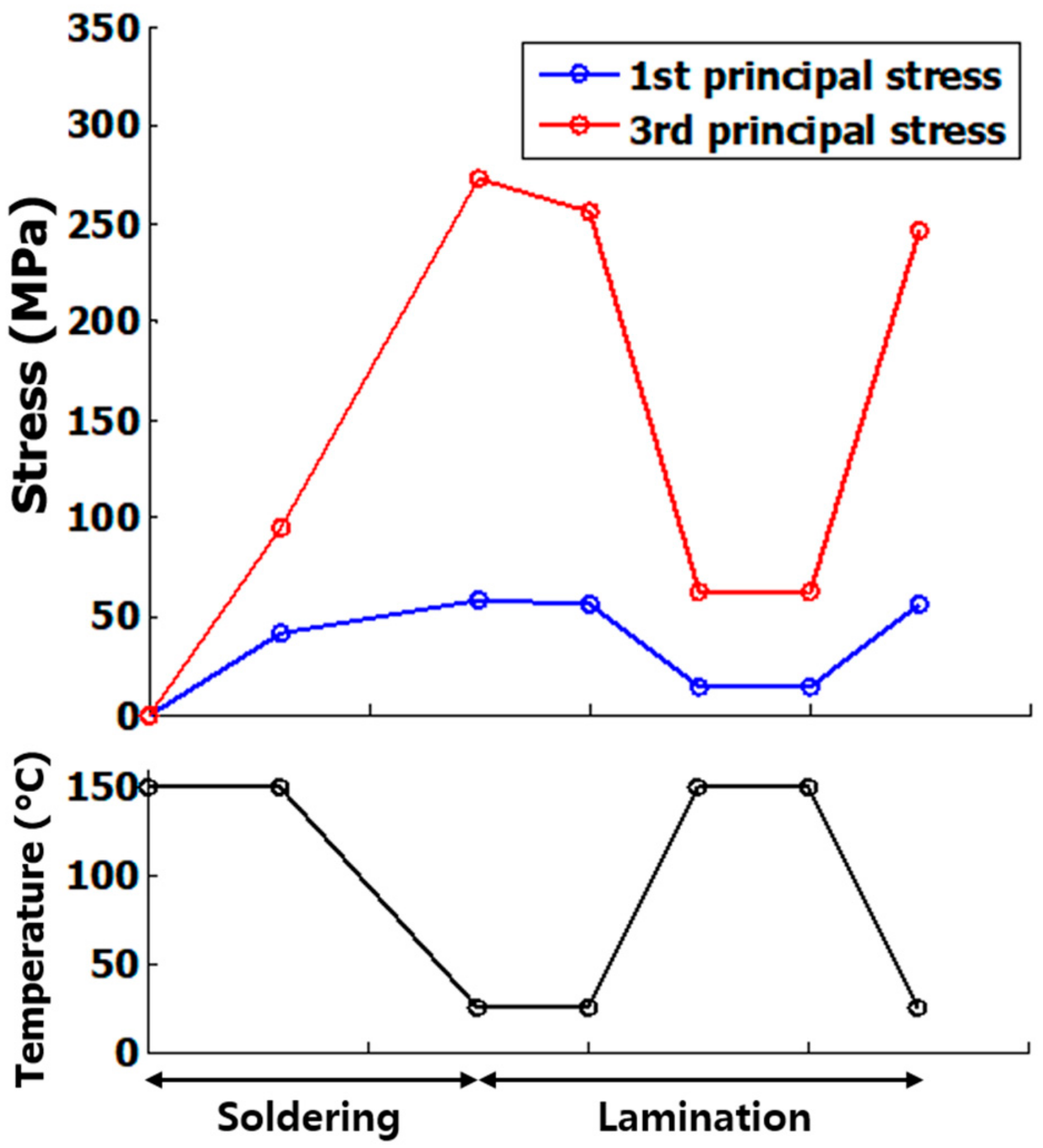
PV modules experience thermal history during soldering and lamination, as shown in Figure 4. The soldering and lamination temperatures are dependent on the type of solder and the encapsulant material, respectively. Figure 4 illustrates that Si wafers experience the maximum absolute values of the first principal stress and the third principal stress at the end of the soldering process. The residual stress was calculated as approximately 260 MPa when the PV modules cooled from 150 °C to 25 °C. Then, the components of the PV modules were arranged in the order of glass, EVA (Ethylene Vinyl Acetate), soldered solar cells, EVA, and backsheet for lamination. The PV modules are subject to a pressure of sub-MPa during lamination. Interestingly, the thermal residual stress of the Si wafers slightly decreased when the temperature increased from 25 °C to 150 °C to laminate each layer of the PV modules. This is attributed to the elastic strain recovery of the Si wafer. The thermal residual stress of the Si wafers is the main contributing factor for mechanical failure during the soldering and lamination processes. Therefore, it is important to consider the residual stress during the soldering process when the solar cells employ thin Si wafers. The residual stress depends on the dimension of the busbars, the thickness of the Si wafers, and the type of soldering material. Firstly, we will explain the effect of the dimension of bus bars on the residual stress, and then discuss the influence of the Si wafers and the soldering materials.

3.2. Effect of Busbars on Thermal Residual Stress

Figure 5 illustrates the maximum values of the first principal stress (Figure 5a) and the third principal stress (Figure 5b) of the Si wafers. The results show that the absolute values of the third principal stress significantly exceed those of the first principal stress. This is attributable to the thermal shrinkage of the bus bars, which occurs during the cooling process. However, it should be noted that the tensile strength (100–200 MPa) of Si is approximately 20–30 times less than its compressive strength (3000–4000 MPa). Therefore, with regard to the failure criteria, the first principal stress is more important than the third principal stress. In Figure 5a, the first principal stress has a positive relation with the number of bus bars. The first principal stress is sufficiently lower than the uniaxial tensile strength when we use three or four bus bars. However, in the case of twelve bus bars, the first principal stress can be up to 80 MPa. Based on previous research [21], the ultimate strength of the thin Si wafers is less than 117 MPa. Considering the Weibull theory [22], we can deduce that the failure probability of Si wafers increases with the number of bus bars. Meanwhile, the third principal stress exhibits a convex tendency with increases in the number of busbars, as shown in Figure 5b. The compressive stress of the Si wafers is the maximum value when the number of busbars is 4 or 6.

3.3. Effect of Thickness of Si Wafers

The thickness of Si wafers is one of the main factors contributing to thermal warpage and residual stress. In Figure 6a, the variation in the warpage of Si wafers is plotted as a function of the wafer thickness. A clear tendency is observed wherein the thermal warpage of Si wafers decreases with increasing wafer thickness. According to a previous study [13], the thickness of the Si wafers for manufacturing solar cells is limited to 4 mm to avoid thermo-mechanical failure.

However, the finite element simulation results indicate that the thermal warpage exceeds 5 mm when the thickness of the Si wafer decreases to 100 μm.

The high thermal warpage influences the critical thermal residual stress of the Si wafer. As shown in Figure 6b, the thermal residual stress does not approach the critical value of 40 MPa if the thickness of the Si wafer is near 200 μm. Meanwhile, the thermal residual stress increases to ~70 MPa even if the width of the busbars is uniformly 1.2 mm. When we consider the Weibull distribution, this is not a negligible range of stress because the ultimate tensile strength of Si wafers is approximately 117 MPa, as mentioned in the previous subsection. Specifically, the finite element simulation results in Figure 5a show that the thermal residual stress can be attained near 80 MPa when the PV modules are designed with 12 busbars of 1.2-mm width and 63Sn37Pb solder. Therefore, the thickness of the Si wafers is a key factor in minimizing the probability of thermo-mechanical failure induced by thermal warpage. Based on a previous study [13], thermal warpage should be less than 4 mm.

3.4. Influence of Solder Type

There are various types of solders for Si wafers. These solders require different temperature conditions for the soldering and lamination processes according to the ratios of the constituent material components. Accordingly, solder type influences the residual stress of Si wafers. Three types of solders (63Sn37Pb, 96.5Sn3.0Ag0.5Cu, and 42Sn58Bi) were considered when designing the PV modules. Their detailed thermo-mechanical properties and melting points are listed in Table 2. The finite element simulation employed different thermal boundary conditions for each solder, as presented in Figure 3.

Figure 7 shows the first and third maximum principal stresses for two solders, 96.5Sn3.0Ag0.5Cu and 42Sn58Bi. The effects of the number and width of the busbars were also considered in the analysis of the tendencies. The thermal residual stress of the Si wafers maintains its tendency to increase with the number and width of the busbars regardless of the type of solder. Despite this, the absolute values of the first principal stress and the third principal stress clearly decrease when the Si wafers are designed with low melting point solders. The first principal stress of the Si wafers with the low-temperature solder (42Sn58Bi) remarkably decreases by up to nearly two times the decrease observed with the high-temperature solder (96.5Sn3.0Ag0.5Cu), as shown in Figure 7. This phenomenon is due to the thermal strains of materials, which are linearly proportional to the temperature drop.

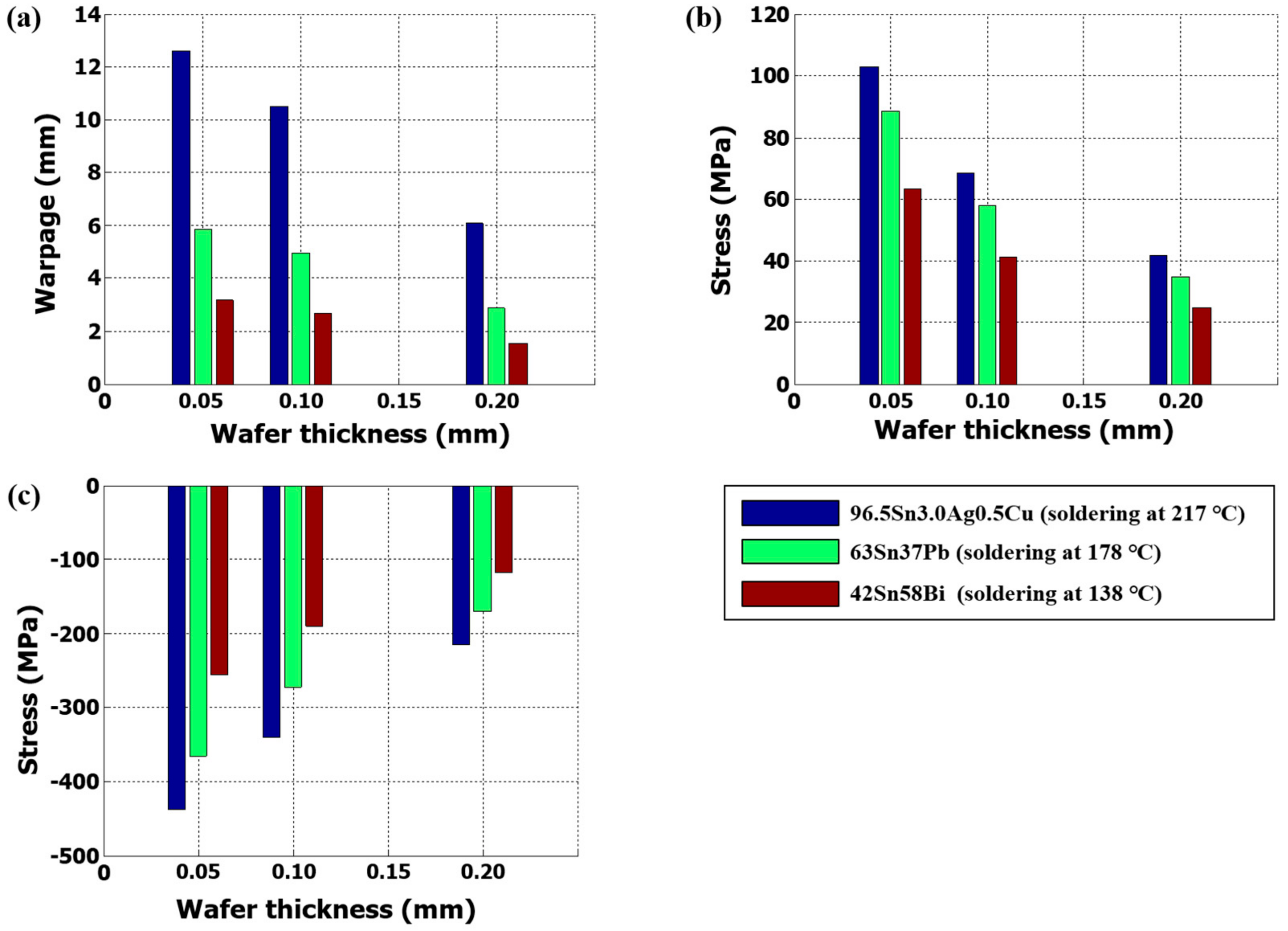
The influence of the Si wafer thickness on the thermal warpage and residual stress for the lamination process are compared for different types of solders in Figure 8. The results have a noticeable tendency of Si wafers undergoing higher thermal warpage with increasing soldering temperature. For 0.2-mm wafer thickness, Si wafers with 96.5Sn3.0Ag0.5Cu solder experienced nearly three times the warpage and two times the thermal residual stress of 42Sn58Bi solder, as shown in Figure 8a,b, respectively.

In the final step of this study, we examined whether we could fabricate PV modules with different types of solders without the Si wafers sustaining cracks. The 96.5Sn3.0Ag0.5Cu and 42Sn58Bi solders were used to fabricate a PV module comprising four cells. The solder was heated to melting point. A standard PV module containing 63Sn37Pb solder was also manufactured for comparison. The solar cells were then laminated with 3.2-mm thick low-iron glass, with an EVA sheet and with back-sheets. The PV module was laminated at 150 °C for 12 min. After the manufacturing process, we examined the PV module via an electroluminescence image to ensure that there were no cracks. We discovered that cracking of the Si wafers decreased with solder melting point. However, the fact that this effect may be caused by the tabbing process or the solar cells themselves cannot be fully excluded. This is currently under investigation.

Figure 9 shows that cracks occurred in many places when high melting point solder was used. This indicates that low-temperature solders can reduce the probability of mechanical failure. Therefore, thermo-mechanical simulation could be a useful tool for PV module fabrication when different types of materials are used.

4. Conclusions

In this study, we developed a finite element model for crystalline silicon PV modules with various Si wafer thicknesses, busbar thicknesses, number of busbars, and solders. The results obtained facilitate estimation of the warpage and thermal residual stress during soldering and lamination. In addition, recommendations are provided for decreasing the mechanical failure in PV modules employing thin Si wafers. PV modules experience thermal stress during soldering and lamination. Interestingly, the residual stress of Si wafers decreases during the lamination process. This is attributable to the strain recovery of Si wafers, which experience the maximum values of thermo-mechanical stress during the soldering process. The results also indicate that the thermal residual stress should be controlled during the soldering process to enable the use of thin Si wafers without the risk of mechanical failure. This thermal residual stress of Si wafers can be reduced by using thin busbars. When using thick busbars, a low melting point soldering material should be considered in order to protect the Si wafers from mechanical failure. We expect that these approaches will be important for the mechanical design of PV modules that include weak mechanical strength Si wafers.