Magnetization-Dependent Core-Loss Model in a Three-Phase Self-Excited Induction Generator
Abstract
:1. Introduction
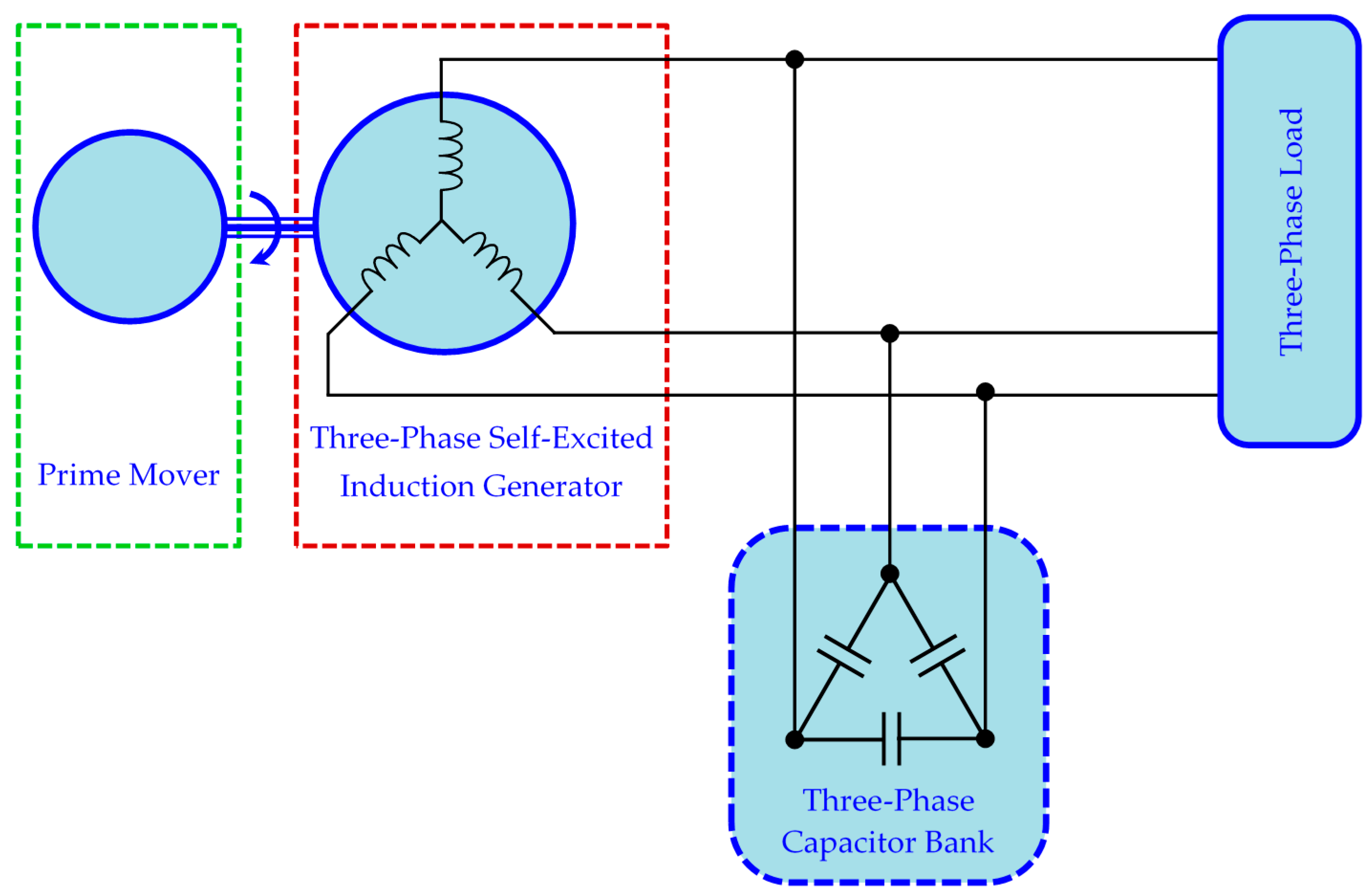
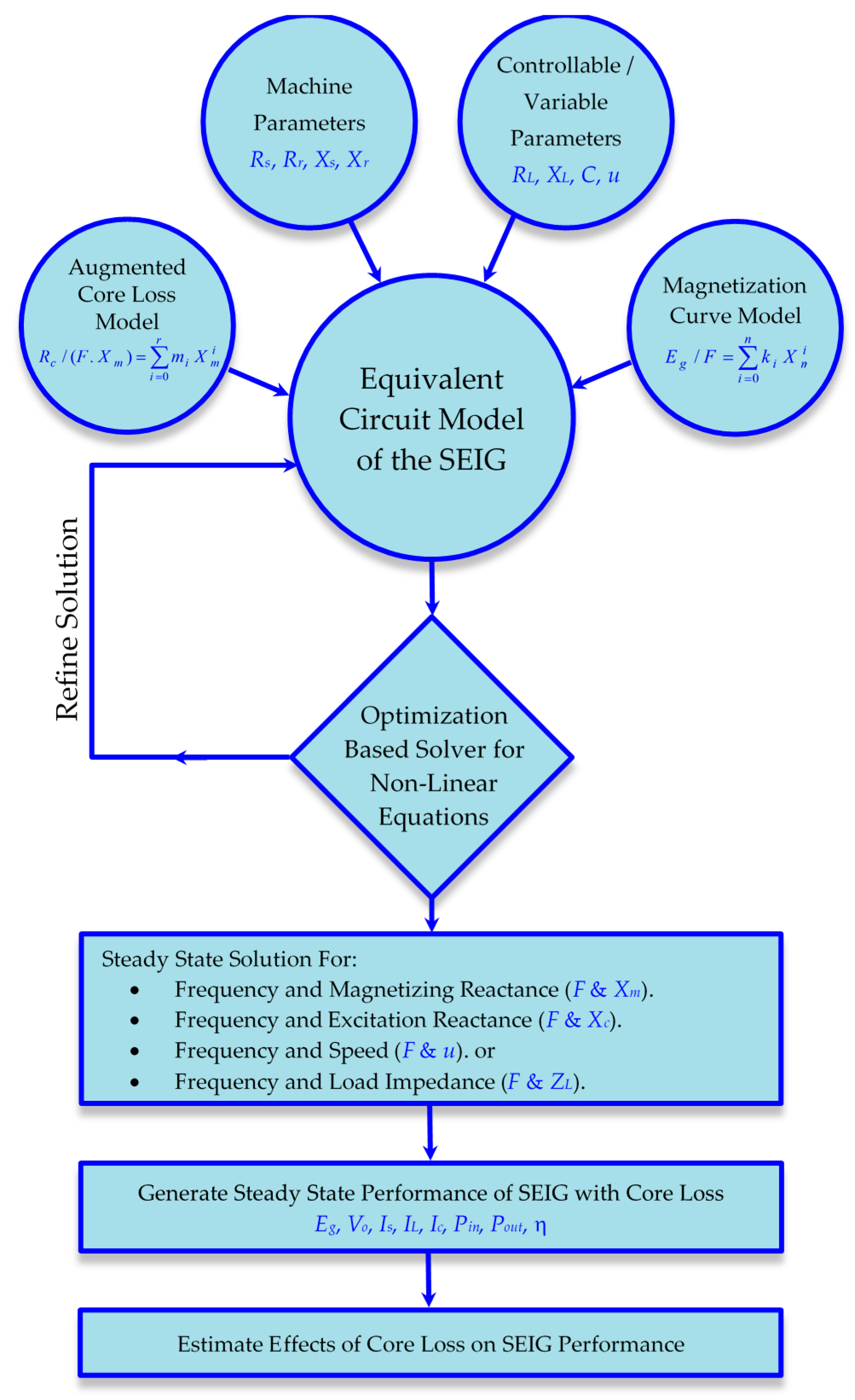
2. Analysis
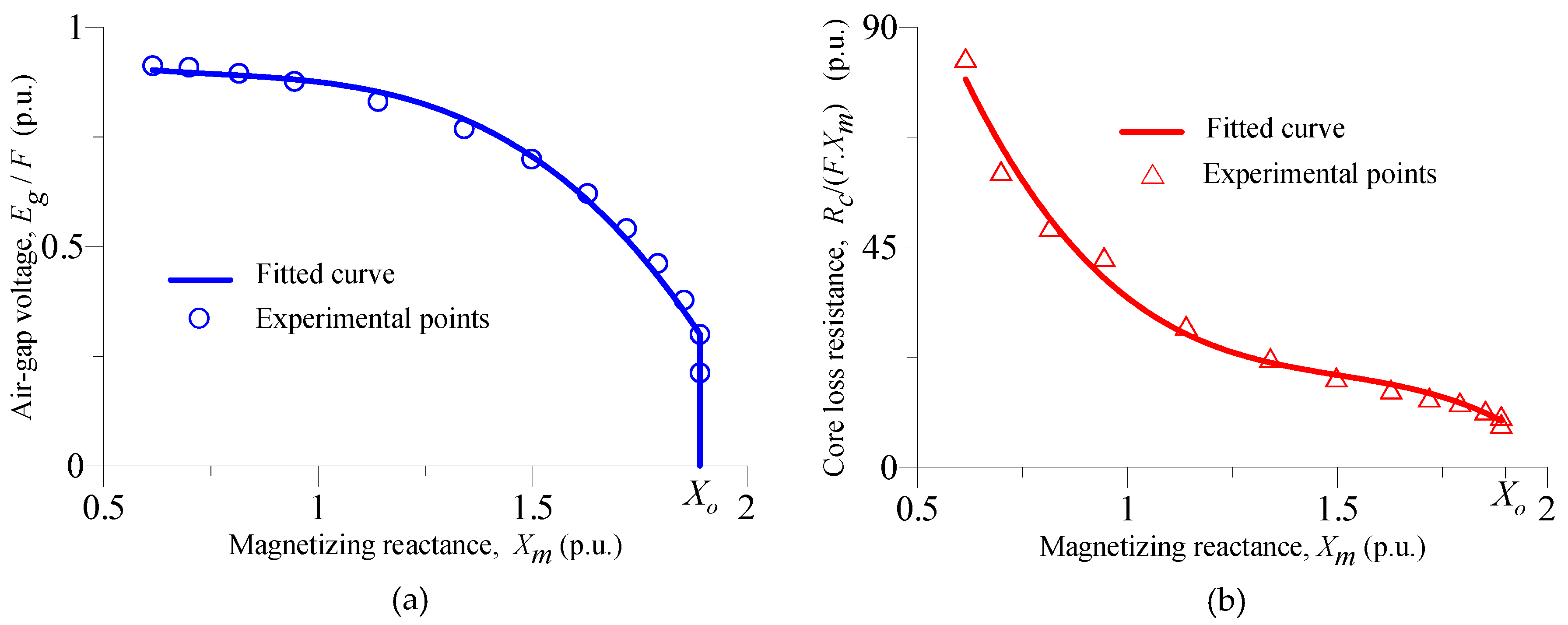
2.1. Core-Loss Modeling
2.2. Loop-Impedance Solution
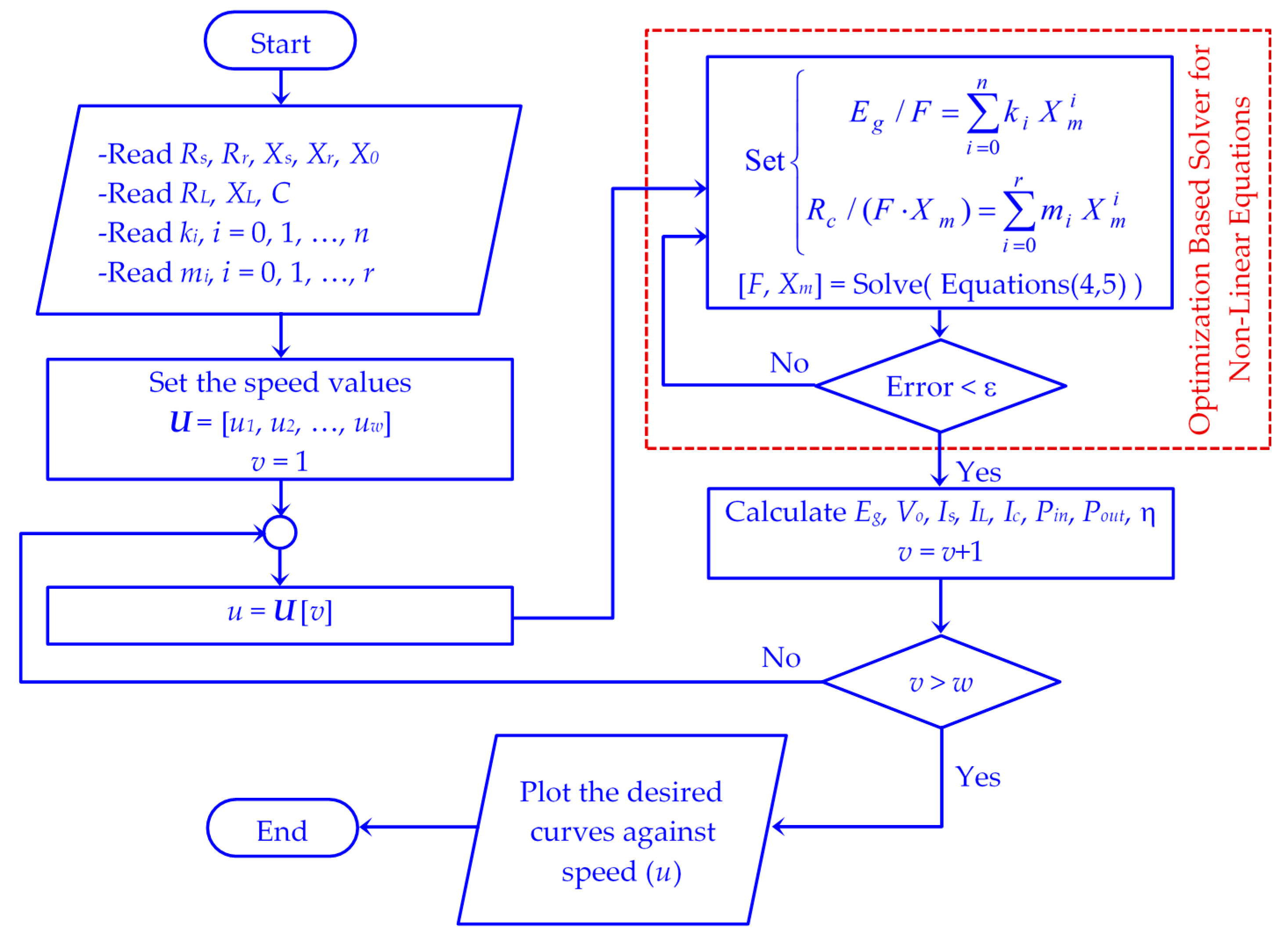
2.3. Method of Solution
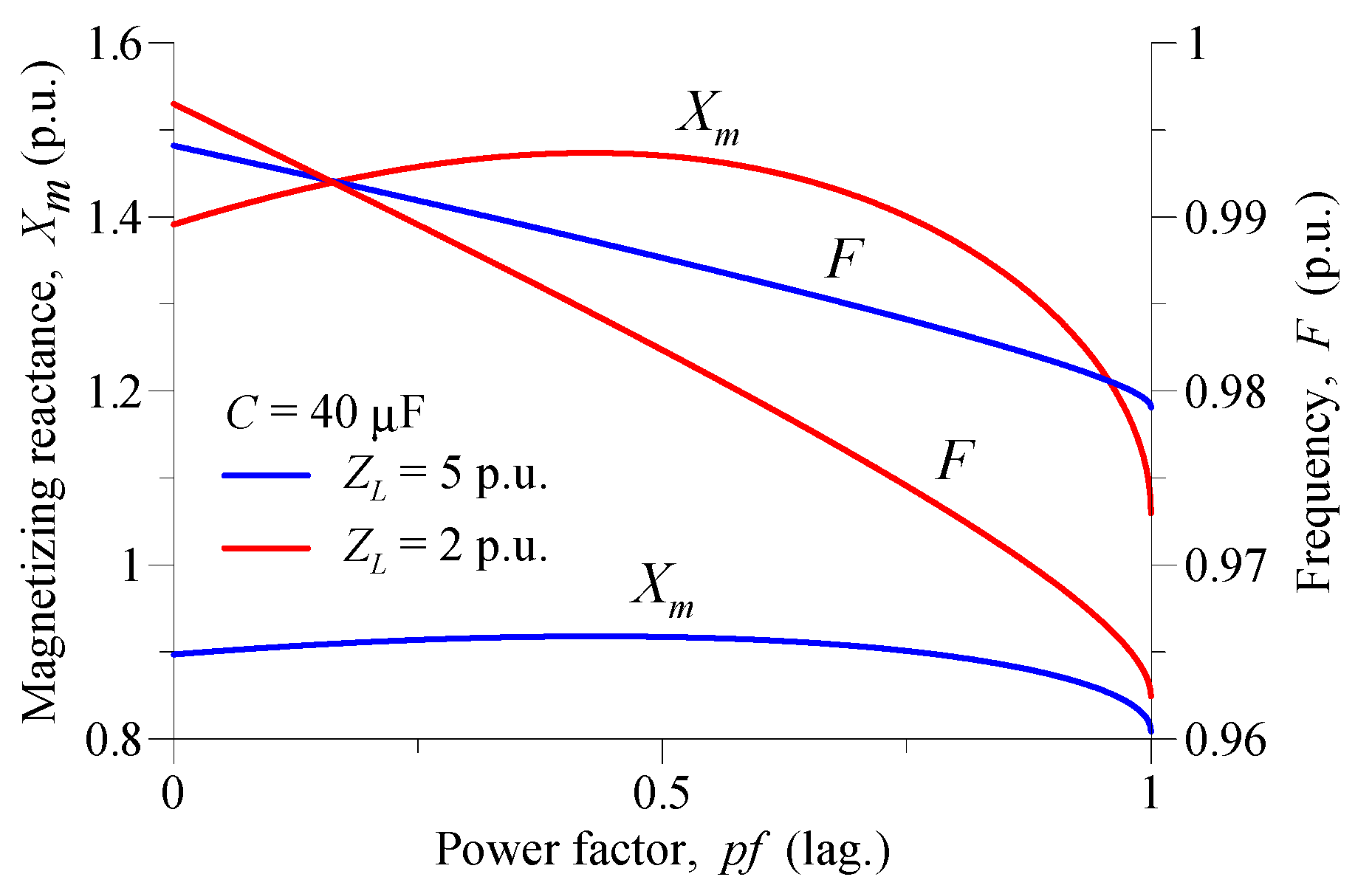
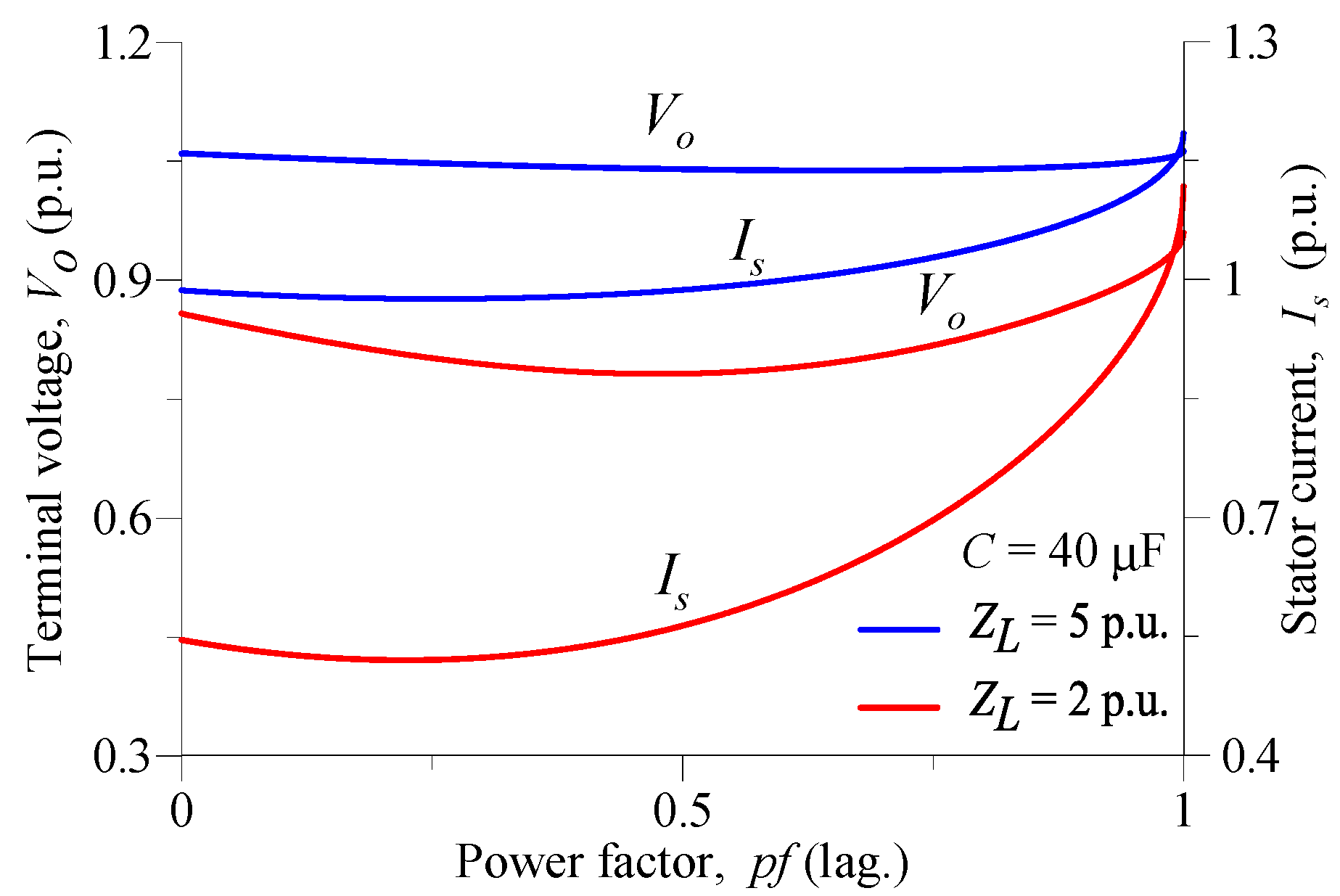
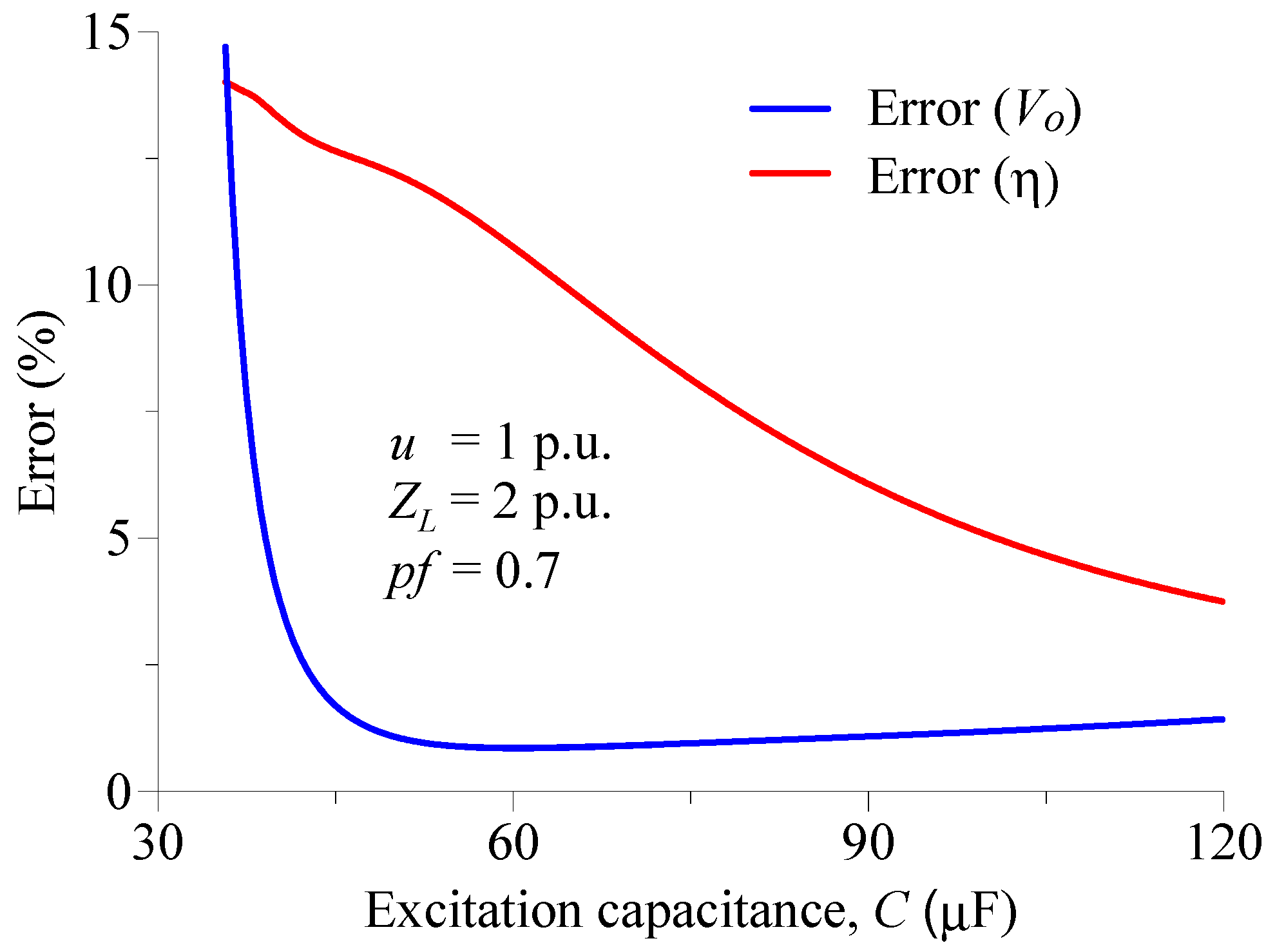
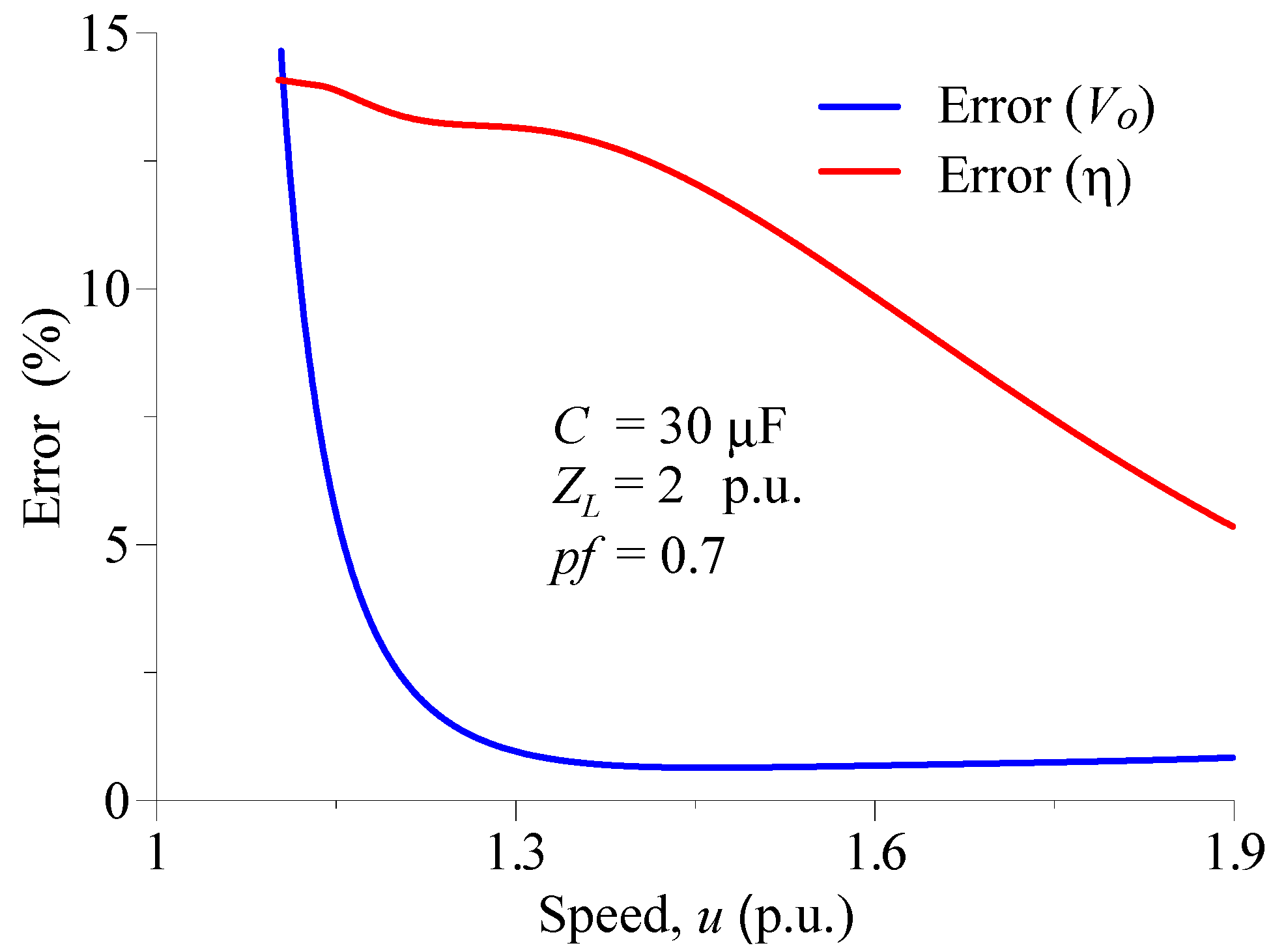
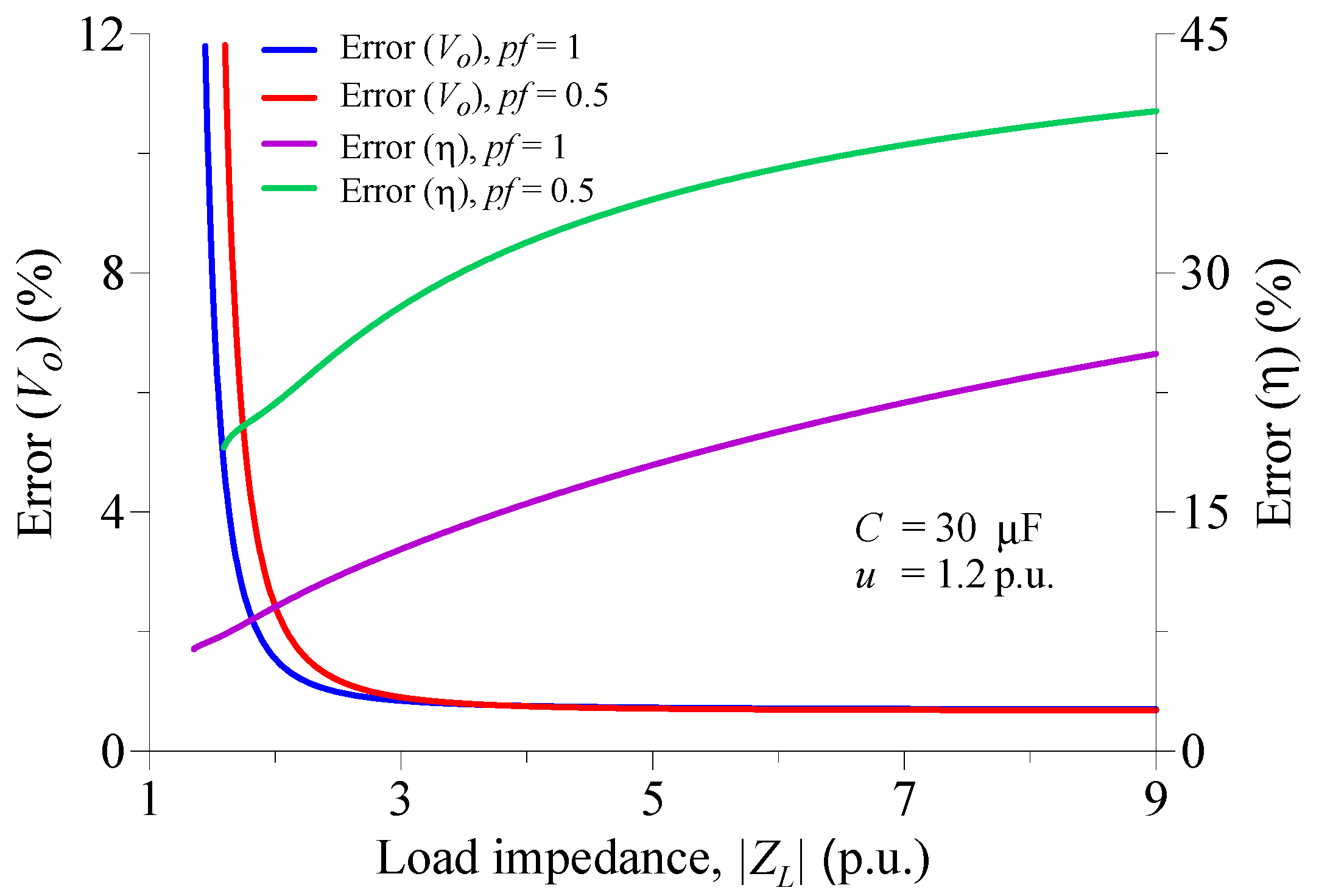
3. Results and Discussion
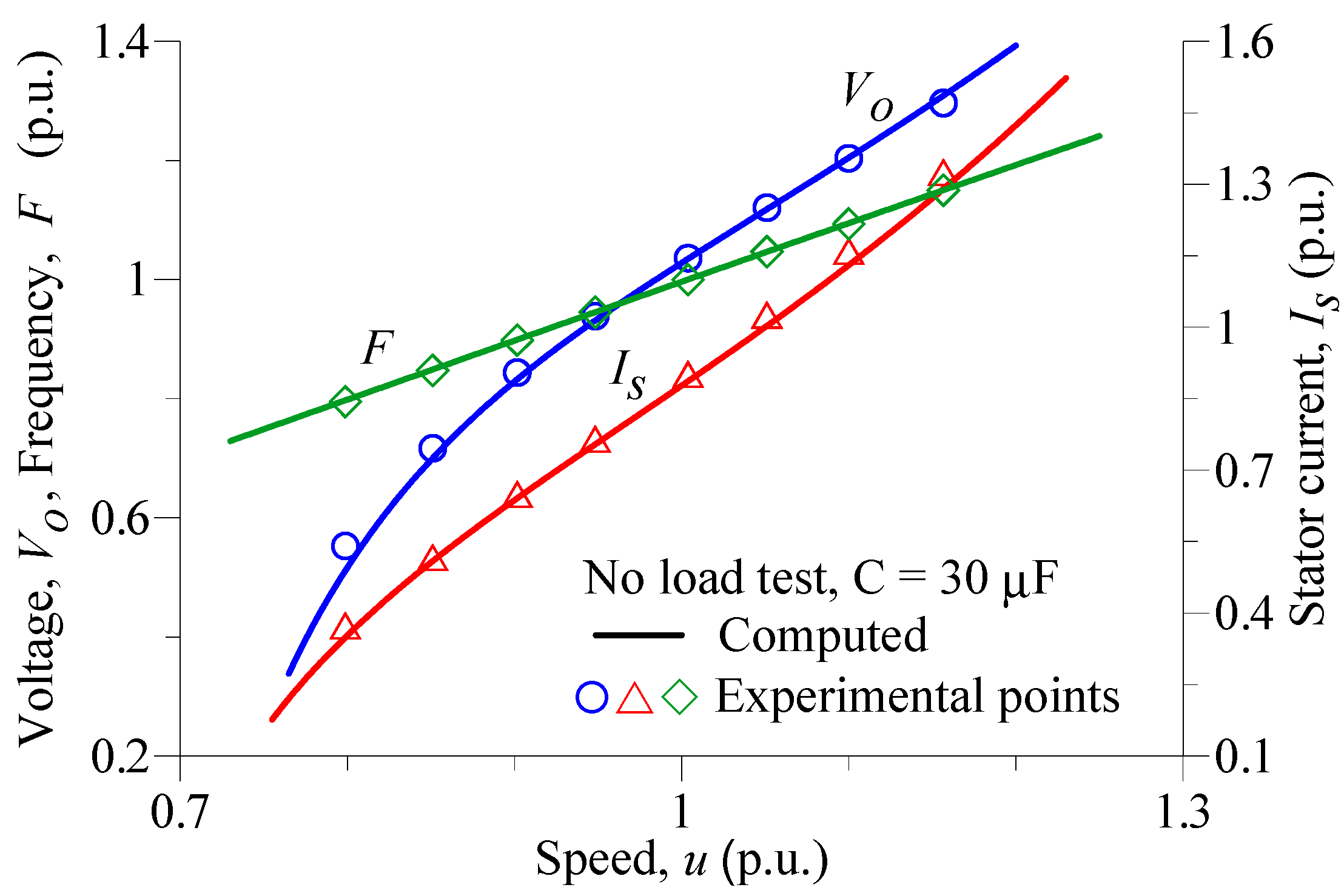
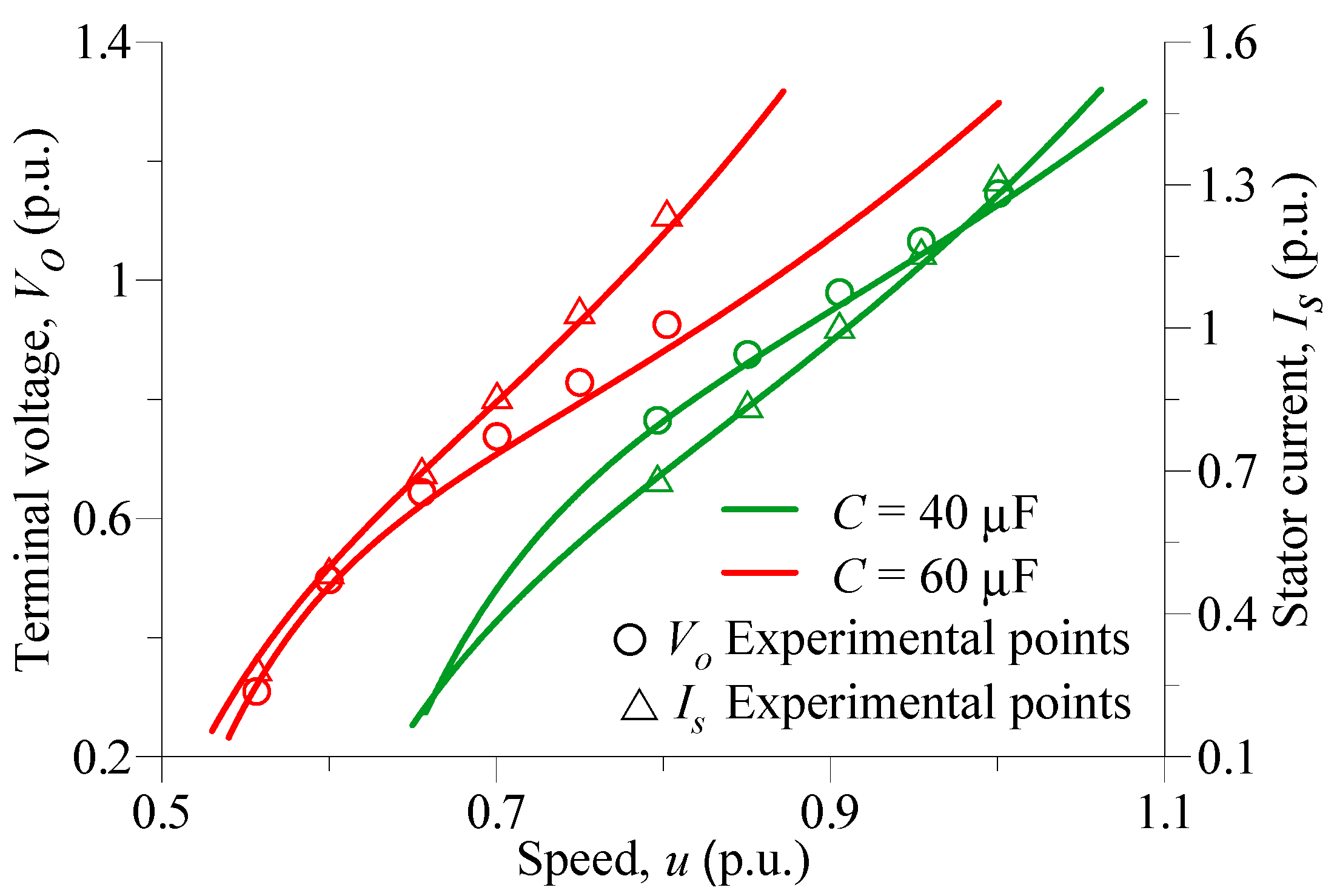
4. Experimental Verification
4.1. Setup
4.2. Performance Measurements
5. Influence of Core Loss
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| F, u | p.u frequency and speed, respectively |
| C, Xc | value of excitation capacitance (µF) and its p.u reactance (at base frequency), respectively |
| Cmin | minimum excitation capacitance (µF) |
| Rs, Rr, RL | p.u stator, rotor, and load resistances, respectively |
| Xs, Xr, XL | p.u stator, rotor leakage, and load reactances (at base frequency), respectively |
| Xm, Xo | p.u saturated and unsaturated magnetizing reactances at base frequency, respectively |
| Ic, IL, Is | p.u. excitation capacitance, load, and stator currents, respectively |
| Eg, Vo | air-gap and terminal voltages, respectively |
| Vb, Ib, Zb | base voltage, current, and impedance, respectively |
| fb, Nb | base frequency and speed in Hz and rpm, respectively |
Appendix A
Appendix A.1. Machine Parameters
| Vb (V) | Ib (A) | Zb = Vb/Ib (Ω) | Nb (rpm) | fb (Hz) | Rs (p.u.) | Rr (p.u.) | Xs = Xr (p.u.) | Xo (p.u.) |
|---|---|---|---|---|---|---|---|---|
| 220 | 2.9 | 75.862 | 1800 | 60 | 0.086 | 0.044 | 0.19 | 1.89 |
Appendix A.2. Fitted Curves
Appendix A.3. Total Impedance
References
- Boldea, I. Variable Speed Generators, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015; ISBN 1498723578. [Google Scholar]
- International Renewable Energy Agency (IRENA). Renewable Capacity Statistics 2017. Available online: http://www.irena.org/publications/2017/Mar/Renewable-Capacity-Statistics-2017 (accessed on 26 February 2018).
- Musgrove, P. Wind Power, 1st ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 0521762383. [Google Scholar]
- Singh, G.K. Self-excited induction generator research—a survey. Electr. Power Syst. Res. 2014, 69, 107–114. [Google Scholar] [CrossRef]
- Al Jabri, A.K.; Alolah, A.I. Limits on the performance of the three-phase self-excited induction generators. IEEE Trans. Energy Convers. 1990, EC-5, 350–356. [Google Scholar] [CrossRef]
- Al Jabri, A.K.; Alolah, A.I. Capacitance requirement for isolated self-excited induction generator. IEEE Proc. B-Electr. Power Appl. 1990, 137, 154–159. [Google Scholar] [CrossRef]
- Alolah, A.I.; Alkanhal, M.A. Optimization-based steady state analysis of three phase self-excited induction generator. IEEE Trans. Energy Convers. 2000, EC-15, 61–65. [Google Scholar] [CrossRef]
- Alnasir, Z.; Kazerani, M. An analytical literature review of stand-alone wind energy conversion systems from generator viewpoint. Renew. Sustain. Energy Rev. 2013, 28, 597–615. [Google Scholar] [CrossRef]
- Sam, K.N.; Kumaresan, N.; Gounden, N.A.; Katyal, R. Analysis and Control of Wind-Driven Stand-Alone Doubly-Fed Induction Generator with Reactive Power Support from Stator and Rotor Side. Wind Eng. 2015, 39, 97–112. [Google Scholar] [CrossRef]
- Kheldoun, A.; Refoufi, L.; Khodja, D.E. Analysis of the self-excited induction generator steady state performance using a new efficient algorithm. Electr. Power Syst. Res. 2012, 86, 61–67. [Google Scholar] [CrossRef]
- Nigim, K.; Salama, M.; Kazerani, M. Identifying machine parameters influencing the operation of the self-excited induction generator. Electr. Power Syst. Res. 2004, 69, 123–128. [Google Scholar] [CrossRef]
- Wang, L.; Lee, C.H. A novel analysis on the performance of an isolated self-excited induction generator. IEEE Trans. Energy Convers. 1997, EC-12, 109–117. [Google Scholar] [CrossRef]
- Kersting, W.H.; Phillips, W.H. Phase Frame Analysis of the Effects of Voltage Unbalance on Induction Machines. IEEE Trans. Ind. Appl. 1997, IA-33, 415–420. [Google Scholar] [CrossRef]
- Malik, N.H.; Haque, S.E. Steady State Analysis and Performance of an Isolated Self-Excited Induction Generator. IEEE Trans. Energy Convers. 1986, EC-1, 134–140. [Google Scholar] [CrossRef]
- Sharma, A.; Kaur, G. Assessment of Capacitance for Self-Excited Induction Generator in Sustaining Constant Air-Gap Voltage under Variable Speed and Load. Energies 2018, 11, 2509. [Google Scholar] [CrossRef]
- Hashemnia, M.; Kashiha, A. A Novel Method for Steady State Analysis of the Three Phase SEIG Taking Core Loss into Account. In Proceedings of the 4th Iranian Conference on Electrical and Electronics Engineering (ICEEE2012), Gonabad, Iran, 28–30 August 2012. [Google Scholar]
- Farrag, M.E.; Putrus, G.A. Analysis of the Dynamic Performance of Self-Excited Induction Generators Employed in Renewable Energy Generation. Energies 2014, 7, 278–294. [Google Scholar] [CrossRef] [Green Version]
- Arjun, M.; Rao, K.U.; Raju, A.B. A Novel Simplified Approach for Evaluation of Performance Characteristics of SEIG. In Proceedings of the 2014 International Conference on Advances in Energy Conversion Technologies (ICAECT), Manipal, India, 23–25 January 2014. [Google Scholar]
- Selmi, M.; Rehaoulia, H. Effect of the Core Loss Resistance on the Steady State Performances of SEIG. In Proceedings of the International Conference on Control, Engineering & Information Technology (CEIT’2014), Sousse, Tunisia, 22–25 March 2014. [Google Scholar]
- Haque, M.H. A Novel Method of Evaluating Performance Characteristics of a Self-Excited Induction Generator. IEEE Trans. Energy Convers. 2009, EC-24, 358–365. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Senaidi, S.H.; Alolah, A.I.; Alkanhal, M.A. Magnetization-Dependent Core-Loss Model in a Three-Phase Self-Excited Induction Generator. Energies 2018, 11, 3228. https://doi.org/10.3390/en11113228
Al-Senaidi SH, Alolah AI, Alkanhal MA. Magnetization-Dependent Core-Loss Model in a Three-Phase Self-Excited Induction Generator. Energies. 2018; 11(11):3228. https://doi.org/10.3390/en11113228
Chicago/Turabian StyleAl-Senaidi, Saleh H., Abdulrahman I. Alolah, and Majeed A. Alkanhal. 2018. "Magnetization-Dependent Core-Loss Model in a Three-Phase Self-Excited Induction Generator" Energies 11, no. 11: 3228. https://doi.org/10.3390/en11113228
APA StyleAl-Senaidi, S. H., Alolah, A. I., & Alkanhal, M. A. (2018). Magnetization-Dependent Core-Loss Model in a Three-Phase Self-Excited Induction Generator. Energies, 11(11), 3228. https://doi.org/10.3390/en11113228





