Hourly Day-Ahead Wind Power Prediction Using the Hybrid Model of Variational Model Decomposition and Long Short-Term Memory
Abstract
1. Introduction
2. Materials and Methods
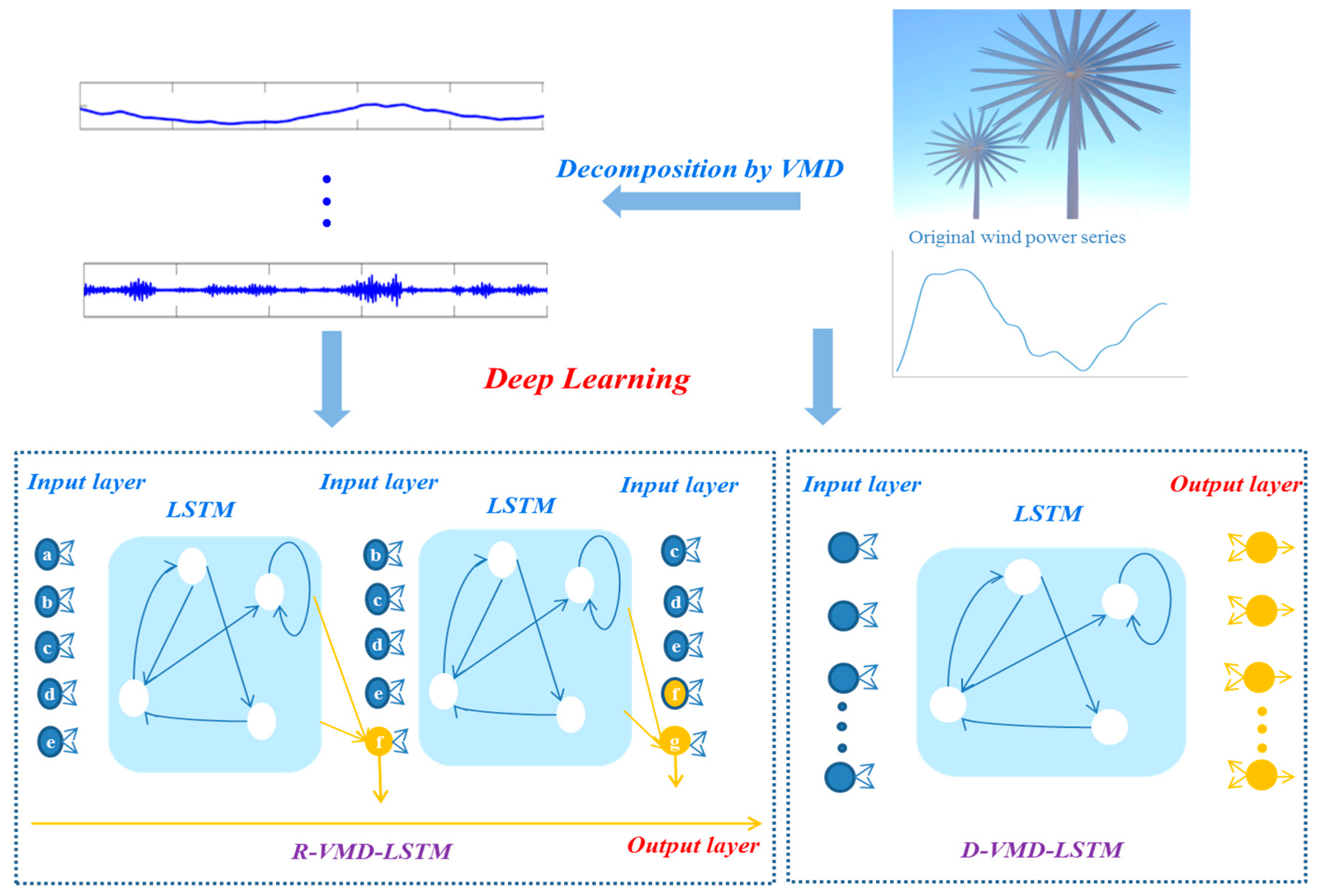
2.1. The Whole Process of the VMD-LSTM Method
- (1)
- The LSTM neural network, with three hidden layers serving as efficient and fast learning machine tools, is adopted to complete the forecasting for each decomposed mode obtained by VMD. LSTM is utilized as the prediction core of the proposed forecasting engine to extract the complicated input–output mapping between historical and forecasting data. Thus, the number of required LSTMs is equal to the number of decomposed modes. The output of each LSTM denotes the forecasted wind power of the same mode order. The LSTM neural network is described in Section 2.2.
- (2)
- VMD is adopted to decompose the original wind power series into m modes with different frequencies. The analysis of the time series of wind power can be helpful for the precise modeling of its intermittent characteristics. These modes are then used to construct training patterns and forecasted outputs. The details of VMD are presented in Section 2.3.
- (3)
- The prediction results of the mode values are summed as the ultimate prediction of wind power by the wind farm.
2.2. LSTM Network
2.3. VMD
- (1)
- According to the Hilbert transform, the corresponding analytic signal of each sub-modal uk(t) is calculated, so that the single-side spectrum can be obtained.
- (2)
- By mixing the index of each modal analytical signal corresponding center frequency ωk, the sub-modal signal uk(t) spectrum is changed to the base frequency band.
- (3)
- The norm of the square of the demodulation signal gradient L2 is calculated to estimate the width of the sub-modal signal uk(t). The variational problem with constraint is:where {uk} and {ωk} represent the set of sub-signals and its corresponding central frequency, k is the total number of sub-signals, δ(t) is the Dirac distribution, and represents the convolution operation.
- (1)
- Initialize , , and , set the number of iterations to 1.
- (2)
- For each sub-signal, according to Equations (10) and (11), update operations to obtain and .
- (3)
- Update the Lagrange multiplier according to Equation (12):where τ is the update parameter.
- (4)
- The decomposition process ends when the convergence condition is satisfied; otherwise, the iteration number is updated, and the process returns to Step 2.
2.4. Performance Evaluation Index
3. R-VMD-LSTM and D-VMD-LSTM Models
3.1. R-VMD-LSTM
3.2. D-VMD-LSTM
4. Results
4.1. Experimental Date Description
4.2. Parameter Selection
4.3. Analysis of Proposed Models
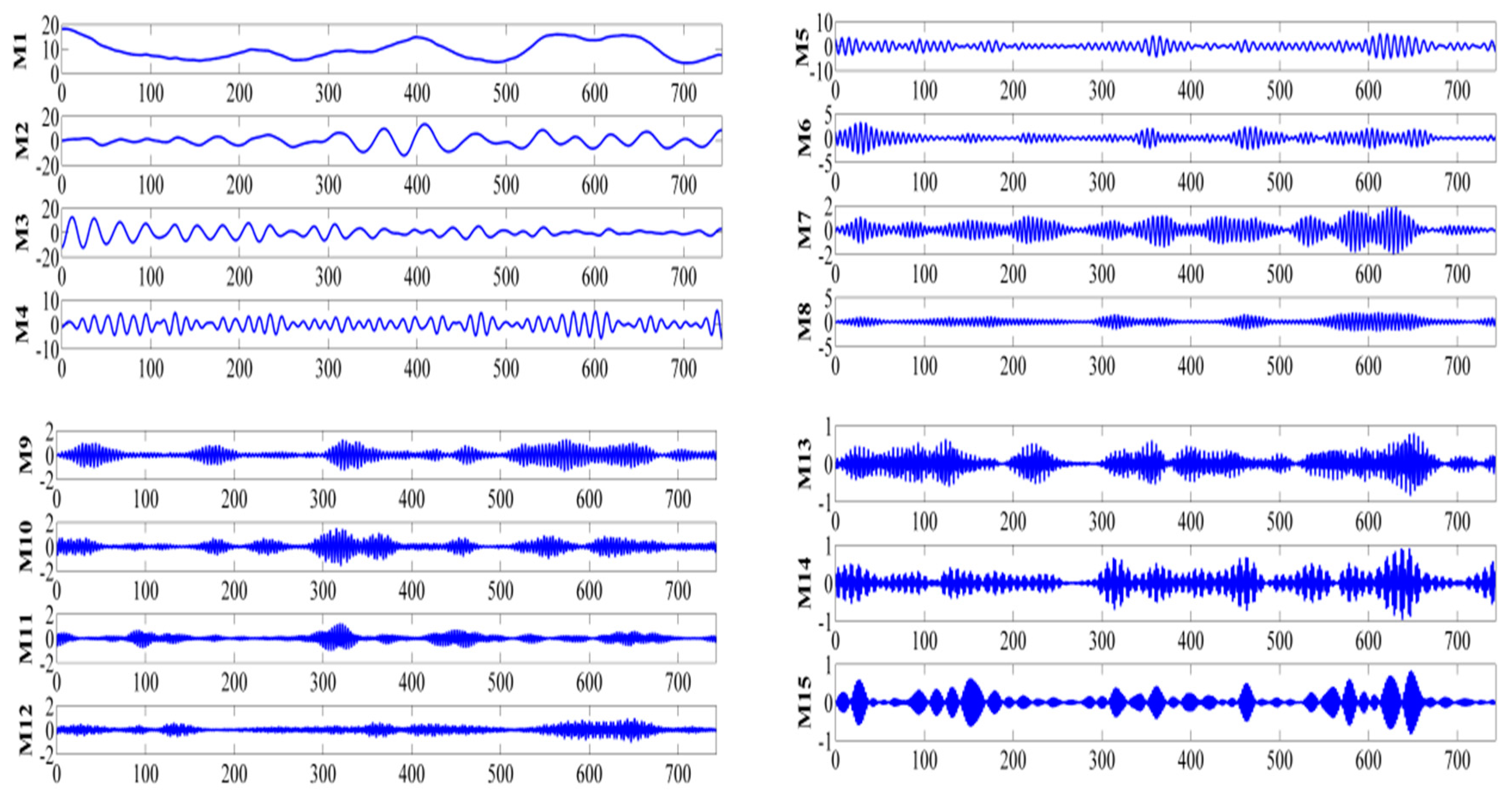
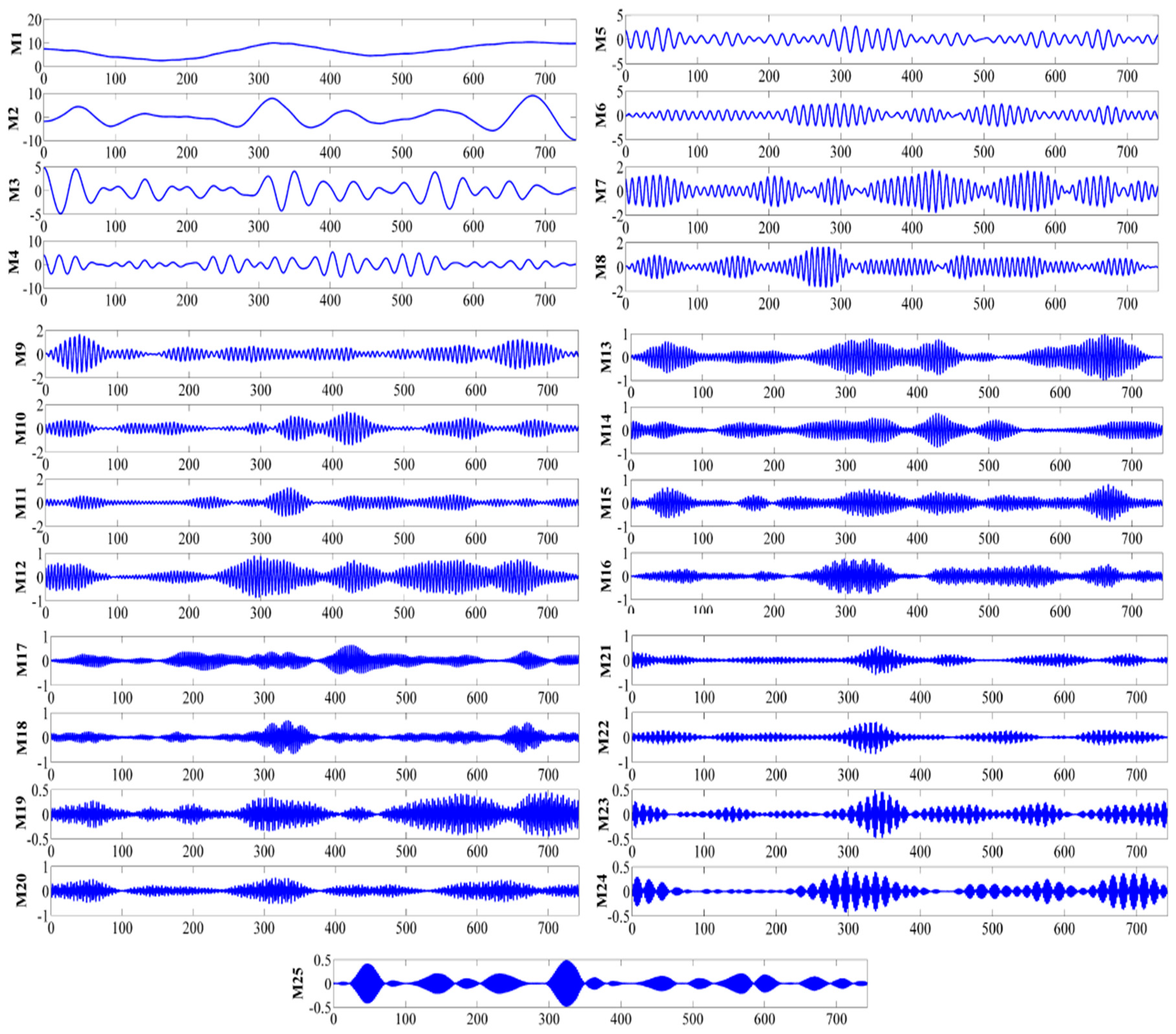
4.3.1. Decomposed Results by VMD
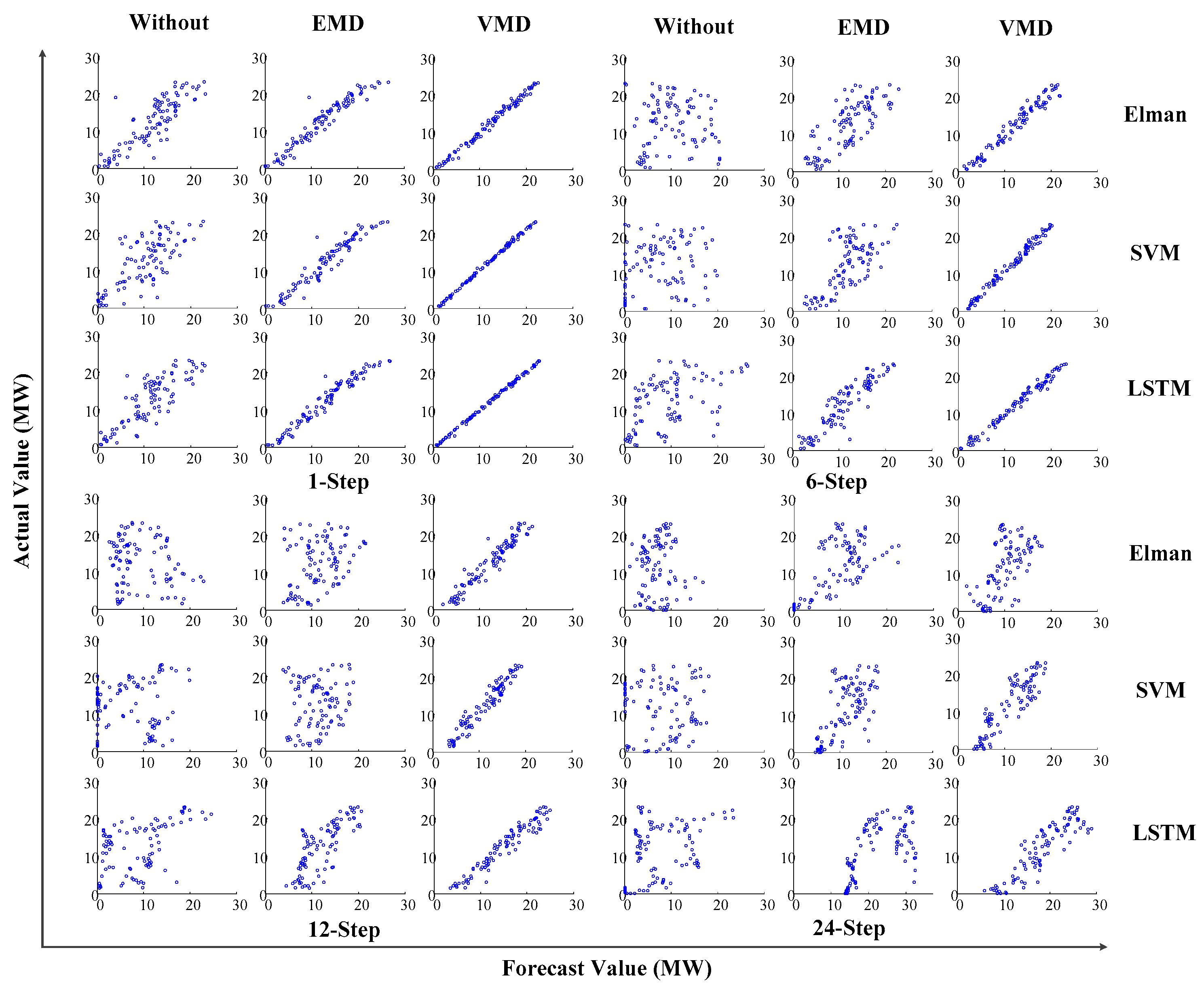
4.3.2. Recursive Hourly Day-Ahead Forecasting
4.3.3. Direct Hourly Day-Ahead Forecasting
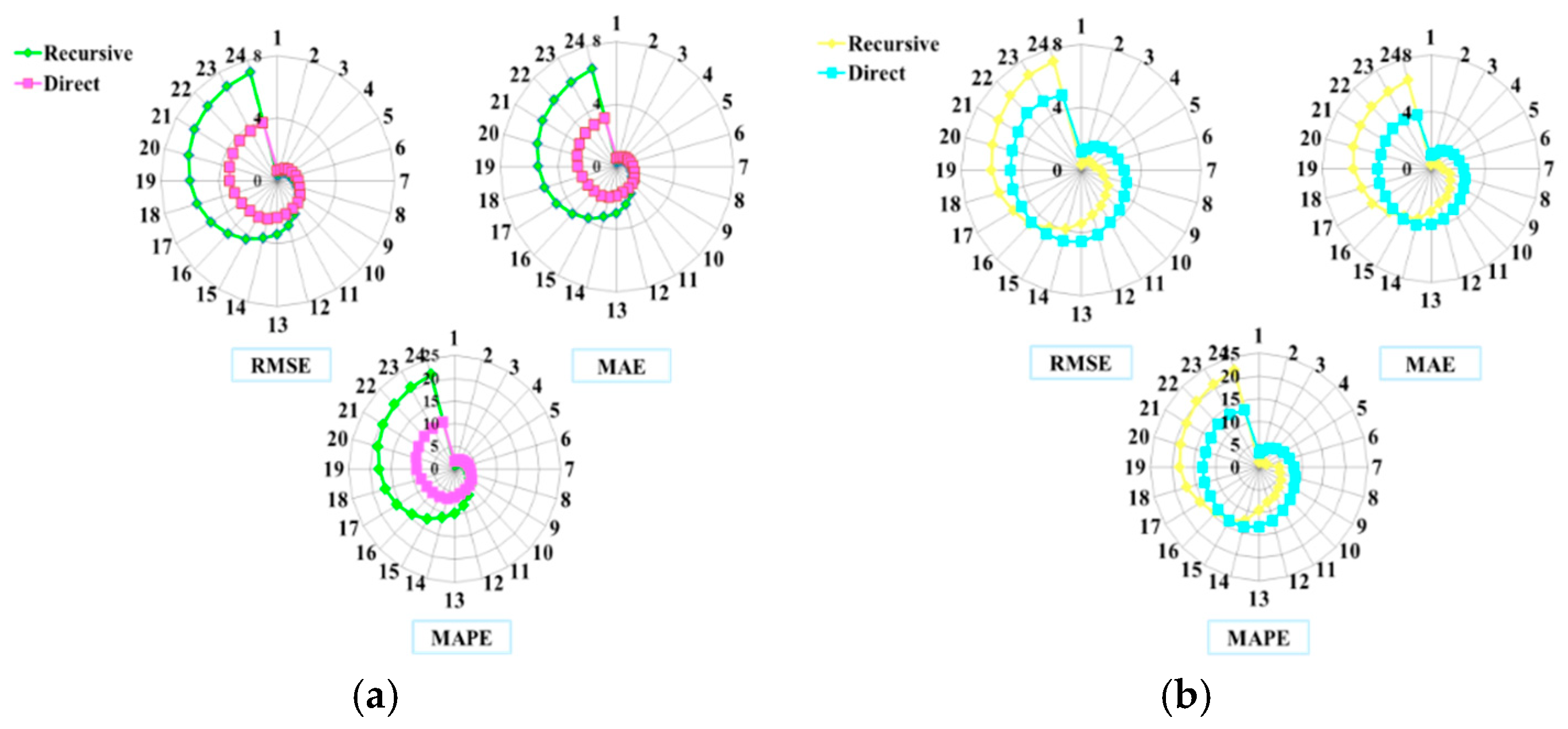
4.4. Contrast Analysis between R-VMD-LSTM and D-VMD-LSTM Models
5. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| VMD | Variational Model Decomposition Method |
| EMD | Empirical Mode Decomposition Method |
| LSTM | Long Short Term Memory Network |
| ELM | Extreme Learning Machines |
| WPF | Wind Power Forecast |
| FFNN | Feed Forward Neural Network |
| SNN | Shallow Neural Network |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| R- | Recursive Multi-Step Forecast |
| D- | Direct Multi-Step Forecast |
| BP | Back Propagation Network |
| SVM | Support Vector Machine |
| ANN | Artificial Neural Network |
| DNN | Deep Neural Network |
| DBN | Deep Belief Network |
| PCA | Principal Component Analysis |
References
- Gallego-Castillo, C.; Cuerva-Tejero, A.; Lopez-Garcia, O. A review on the recent history of wind power ramp forecasting. Renew. Sustain. Energy Rev. 2015, 52, 1148–1157. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.Z.; Huang, G.H.; Huang, Q.; Wang, H.; Wang, L.; Zhang, Y.; Li, P.; Man, L. Copulas-based risk analysis for inter-seasonal combinations of wet and dry conditions under a changing climate. Int. J. Clim. 2018. [Google Scholar] [CrossRef]
- Liu, S.Y.; Huang, S.Z.; Xie, Y.Y.; Wang, H.; Leng, G.Y.; Huang, Q.; Wei, X.T.; Wang, L. Identification of the non-stationary of floods: Changing patterns, causes, and implications. Water Res. Manag. 2018. [Google Scholar] [CrossRef]
- Sarshar, J.; Moosapour, S.S.; Joorabian, M. Multi-objective energy management of a micro-grid considering uncertainty in wind power forecasting. Energy 2017, 139, 680–693. [Google Scholar] [CrossRef]
- De Queiroz, A.R. Stochastic hydro-thermal scheduling optimization: An overview. Renew. Sustain. Energy Rev. 2016, 62, 382–395. [Google Scholar] [CrossRef]
- China Energy Storage Network News Center. Available online: www.escn.com.cn (accessed on 9 October 2018). (In Chinese).
- Wang, C.; Li, X.; Wang, Z.; Dong, X.; Liang, Z.; Liu, X.; Liang, J.; Han, X. Day-ahead unit commitment method considering time sequence feature of wind power forecast error. Int. J. Electr. Power Energy Syst. 2018, 98, 156–166. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Yu, D.; Chang, J. One-day-ahead probabilistic wind speed forecast based on optimized numerical weather prediction data. Energy Convers. Manag. 2018, 164, 560–569. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Liu, F.; Hou, R. Analysis and application of forecasting models in wind power integration: A review of multi-step-ahead wind speed forecasting models. Renew. Sustain. Energy Rev. 2016, 60, 960–981. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, Z.; Su, Z.; Zhao, Z.; Xiao, X.; Liu, F. An improved multi-step forecasting model based on WRF ensembles and creative fuzzy systems for wind speed. Appl. Energy 2016, 162, 808–826. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Uzunoglu, M. A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 2014, 34, 243–254. [Google Scholar] [CrossRef]
- Ahmed, A.; Khalid, M. Multi-step Ahead Wind Forecasting Using Nonlinear Autoregressive Neural Networks. Energy Procedia 2017, 134, 192–204. [Google Scholar] [CrossRef]
- Niu, T.; Wang, J.; Zhang, K.; Du, P. Multi-step-ahead wind speed forecasting based on optimal feature selection and a modified bat algorithm with the cognition strategy. Renew. Energy 2018, 118, 213–229. [Google Scholar] [CrossRef]
- Yuan, X.; Tan, Q.; Lei, X.; Yuan, Y.; Wu, X. Wind power prediction using hybrid autoregressive fractionally integrated moving average and least square support vector machine. Energy 2017, 129, 122–137. [Google Scholar] [CrossRef]
- Aydin, O.; Guldamlasioglu, S. Using LSTM networks to predict engine condition on large scale data processing framework. In Proceedings of the 2017 4th International Conference on Electrical and Electronic Engineering (ICEEE), Ankara, Turkey, 8–10 April 2017; pp. 281–285. [Google Scholar]
- Srivastava, S.; Lessmann, S. A comparative study of LSTM neural networks in forecasting day-ahead global horizontal irradiance with satellite data. Sol. Energy 2018, 162, 232–247. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Wind speed forecasting method based on deep learning strategy using empirical wavelet transform, long short term memory neural network and Elman neural network. Energy Convers. Manag. 2018, 156, 498–514. [Google Scholar] [CrossRef]
- Qu, X.; Kang, X.; Zhang, C.; Jiang, S.; Ma, X. Short-Term Prediction of Wind Power Based on Deep Long Short-Term Memory. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016. [Google Scholar]
- Liu, H.; Mi, X.; Li, Y. Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, LSTM network and ELM. Energy Convers. Manag. 2018, 159, 54–64. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Lu, H.; Guo, Z. Research and application of a combined model based on variable weight for short term wind speed forecasting. Renew. Energy 2018, 116, 669–684. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, Y.; Xiao, X.; Wang, J.; Chi, D.; Guo, Z. Multi-step wind speed and power forecasts based on a WRF simulation and an optimized association method. Appl. Energy 2017, 197, 183–202. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Ren, K.; Huang, Q. Examining the applicability of different sampling techniques in the development of decomposition-based streamflow forecasting models. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Erhao, M.; Shengzhi, H.; Huang, Q.; Fang, W. A robust method for non-stationary streamflow prediction based on improved EMD-SVM model. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Abdoos, A.A. A new intelligent method based on combination of VMD and ELM for short term wind power forecasting. Neucomputing 2016, 203, 111–120. [Google Scholar] [CrossRef]
- Wu, W.; Chen, K.; Qiao, Y.; Lu, Z. Probabilistic short-term wind power forecasting based on deep neural networks. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016; pp. 1–8. [Google Scholar]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 2858–2865. [Google Scholar]
- Rosebrock, A. Available online: http://www.tensorflow.org/version/r0.10/get_started/os_setup (accessed on 4 July 2016).
- Zhang, Y.; Liu, K.; Qin, L.; An, X. Deterministic and probabilistic interval prediction for short-term wind power generation based on variational mode decomposition and machine learning methods. Energy Convers. Manag. 2016, 112, 208–219. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, H.; Xu, Y.; Jiang, W. A Hybrid Framework for Short Term Multi-Step Wind Speed Forecasting Based on Variational Model Decomposition and Convolutional Neural Network. Energies 2018, 11, 2292. [Google Scholar] [CrossRef]










| Algorithm | Parameters | Value |
|---|---|---|
| BP/ELM | Maximum iterations | 200 |
| Learning rate | 0.1 | |
| Momentum operator | 0.9 | |
| Hidden layer neurons | 30 | |
| SVM | Penalty factor | 48.8 |
| Gamma | 0.06 | |
| Loss function | 0.01 | |
| LSTM | Batch size | 10 |
| Maximum iterations | 200 | |
| LSTM layer neurons | 48 | |
| Dropout layer neurons | 48 | |
| Hidden layer neurons | 60 |
| Input Lengths | 24 Points (One-Day Ahead) | 48 Points (Two-Days Ahead) | 72 Points (Three-Days Ahead) |
|---|---|---|---|
| RMSE (MW) | 8.8 | 7.6 | 8.2 |
| MAE (MW) | 7.0 | 6.4 | 6.9 |
| MAPE (%) | 23 | 21 | 23 |
| Mode Number | 3 | 5 | 7 | 9 | 11 | 15 | 20 | 25 | 30 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|
| Series 1 (MAPE, %) | 4.5 | 3.7 | 2.6 | 2.2 | 1.62 | 1 | 0.7 | 0.6 | 0.6 | 0.5 |
| Series 2 (MAPE, %) | 6.4 | 4.9 | 4.1 | 2.7 | 2.3 | 2.1 | 1.2 | 1 | 0.9 | 0.6 |
| Models | Indexed | 1-Step | 6-Step | 12-Step | 24-Step |
|---|---|---|---|---|---|
| ELM | RMSE (MW) | 3.39 | 8.61 | 9.46 | 9.01 |
| MAE (MW) | 2.48 | 6.92 | 8.19 | 7.94 | |
| MAPE (%) | 8 | 23 | 27 | 26 | |
| SVM | RMSE (MW) | 4.98 | 9.11 | 9.96 | 9.64 |
| MAE (MW) | 3.87 | 7.71 | 8.94 | 8.18 | |
| MAPE (%) | 13 | 26 | 30 | 27 | |
| LSTM | RMSE (MW) | 3.67 | 7.24 | 7.27 | 8.39 |
| MAE (MW) | 2.81 | 6.02 | 5.88 | 6.72 | |
| MAPE (%) | 9 | 20 | 20 | 22 | |
| EMD-ELM | RMSE (MW) | 1.74 | 4.14 | 6.41 | 5.87 |
| MAE (MW) | 1.26 | 3.48 | 5.12 | 4.44 | |
| MAPE (%) | 4 | 12 | 17 | 15 | |
| EMD-SVM | RMSE (MW) | 1.89 | 4.83 | 7.07 | 5.37 |
| MAE (MW) | 1.38 | 3.74 | 5.8 | 4.34 | |
| MAPE (%) | 5 | 12 | 19 | 14 | |
| EMD-LSTM | RMSE (MW) | 1.54 | 2.9 | 4.08 | 11.92 |
| MAE (MW) | 1.19 | 2.27 | 3.37 | 10.33 | |
| MAPE (%) | 4 | 8 | 11 | 34 | |
| VMD-ELM | RMSE (MW) | 0.85 | 1.56 | 2.09 | 5.77 |
| MAE (MW) | 0.66 | 1.3 | 1.65 | 4.6 | |
| MAPE (%) | 2 | 4 | 5.5 | 15.2 | |
| VMD-SVM | RMSE (MW) | 0.79 | 1.75 | 2.72 | 3.61 |
| MAE (MW) | 0.65 | 1.41 | 2.29 | 3.19 | |
| MAPE (%) | 2.2 | 4.7 | 7.6 | 10.6 | |
| R-VMD-LSTM | RMSE (MW) | 0.35 | 0.92 | 2.97 | 7.16 |
| MAE (MW) | 0.28 | 0.72 | 2.51 | 6.44 | |
| MAPE (%) | 1 | 2 | 8 | 22 |
| Models | Indexed | 1-Step | 6-Step | 12-Step | 24-Step |
|---|---|---|---|---|---|
| BP | RMSE (MW) | 5.32 | 6.01 | 7.76 | 8.75 |
| MAE (MW) | 4.35 | 5.00 | 6.57 | 7.93 | |
| MAPE (%) | 15 | 17 | 22 | 26 | |
| LSTM | RMSE (MW) | 6.06 | 9.51 | 10.34 | 12.08 |
| MAE (MW) | 5.04 | 8.19 | 9.32 | 10.83 | |
| MAPE (%) | 17 | 27 | 31 | 36 | |
| EMD-BP | RMSE (MW) | 3.16 | 4.78 | 5.29 | 6.9 |
| MAE (MW) | 2.54 | 3.9 | 4.4 | 5.61 | |
| MAPE (%) | 8 | 13 | 15 | 19 | |
| EMD-LSTM | RMSE (MW) | 2.91 | 4.55 | 5.61 | 6.57 |
| MAE (MW) | 2.1 | 3.49 | 4.71 | 5.78 | |
| MAPE (%) | 7 | 12 | 16 | 19 | |
| VMD-BP | RMSE (MW) | 1.69 | 2.98 | 3.36 | 4.46 |
| MAE (MW) | 2.1 | 3.49 | 4.71 | 5.78 | |
| MAPE (%) | 4 | 8 | 9 | 12 | |
| D-VMD-LSTM | RMSE (MW) | 0.67 | 1.30 | 2.17 | 3.86 |
| MAE (MW) | 0.54 | 1.00 | 1.70 | 3.21 | |
| MAPE (%) | 2 | 3 | 6 | 10 |
| Step Number | Series 1 | Series 2 | ||||
|---|---|---|---|---|---|---|
| RMSE (MW) | MAE (MW) | MAPE (%) | RMSE (MW) | MAE (MW) | MAPE (%) | |
| 1-step | 0.67 | 0.54 | 1.80 | 1.15 | 0.92 | 3.10 |
| 2-step | 0.75 | 0.61 | 2.00 | 1.4 | 1.12 | 3.70 |
| 3-step | 0.91 | 0.72 | 2.40 | 1.73 | 1.45 | 4.80 |
| 4-step | 1.04 | 0.82 | 2.70 | 2.04 | 1.71 | 5.70 |
| 5-step | 1.16 | 0.9 | 3.00 | 2.31 | 1.96 | 6.50 |
| 6-step | 1.3 | 1 | 3.30 | 2.56 | 2.16 | 7.20 |
| 7-step | 1.42 | 1.12 | 3.70 | 2.86 | 2.42 | 8.10 |
| 8-step | 1.55 | 1.24 | 4.10 | 3.14 | 2.61 | 8.70 |
| 9-step | 1.77 | 1.42 | 4.70 | 3.31 | 2.78 | 9.30 |
| 10-step | 1.92 | 1.5 | 5.00 | 3.57 | 3.04 | 10.10 |
| 11-step | 2.03 | 1.59 | 5.30 | 3.86 | 3.29 | 11.00 |
| 12-step | 2.17 | 1.7 | 5.70 | 4.26 | 3.65 | 12.20 |
| 13-step | 2.34 | 1.85 | 6.20 | 4.55 | 3.95 | 13.20 |
| 14-step | 2.52 | 2.02 | 6.70 | 4.66 | 4.09 | 13.60 |
| 15-step | 2.63 | 2.13 | 7.10 | 4.68 | 4.09 | 13.60 |
| 16-step | 2.69 | 2.18 | 7.30 | 4.69 | 3.98 | 13.30 |
| 17-step | 2.83 | 2.28 | 7.60 | 4.63 | 3.86 | 12.90 |
| 18-step | 3.05 | 2.47 | 8.20 | 4.71 | 3.91 | 13.00 |
| 19-step | 3.27 | 2.69 | 9.00 | 4.74 | 3.9 | 13.00 |
| 20-step | 3.4 | 2.82 | 9.40 | 4.75 | 3.82 | 12.70 |
| 21-step | 3.52 | 2.95 | 9.80 | 4.87 | 3.85 | 12.80 |
| 22-step | 3.63 | 3.03 | 10.10 | 5.12 | 4 | 13.30 |
| 23-step | 3.69 | 3.08 | 10.30 | 5.07 | 3.99 | 13.30 |
| 24-step | 3.86 | 3.21 | 10.70 | 4.94 | 3.89 | 13.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.; Lei, X.; Huang, Q.; Huang, S.; Ren, K.; Hu, Y. Hourly Day-Ahead Wind Power Prediction Using the Hybrid Model of Variational Model Decomposition and Long Short-Term Memory. Energies 2018, 11, 3227. https://doi.org/10.3390/en11113227
Shi X, Lei X, Huang Q, Huang S, Ren K, Hu Y. Hourly Day-Ahead Wind Power Prediction Using the Hybrid Model of Variational Model Decomposition and Long Short-Term Memory. Energies. 2018; 11(11):3227. https://doi.org/10.3390/en11113227
Chicago/Turabian StyleShi, Xiaoyu, Xuewen Lei, Qiang Huang, Shengzhi Huang, Kun Ren, and Yuanyuan Hu. 2018. "Hourly Day-Ahead Wind Power Prediction Using the Hybrid Model of Variational Model Decomposition and Long Short-Term Memory" Energies 11, no. 11: 3227. https://doi.org/10.3390/en11113227
APA StyleShi, X., Lei, X., Huang, Q., Huang, S., Ren, K., & Hu, Y. (2018). Hourly Day-Ahead Wind Power Prediction Using the Hybrid Model of Variational Model Decomposition and Long Short-Term Memory. Energies, 11(11), 3227. https://doi.org/10.3390/en11113227





