Computer Simulation of Temperature Distribution during Cooling of the Thermally Insulated Room
Abstract
:1. Introduction
2. Model Description
- Specified temperature () on a surface:
- Heat flow density on a surface:
- Convective boundary condition:
2.1. Simulation Conditions
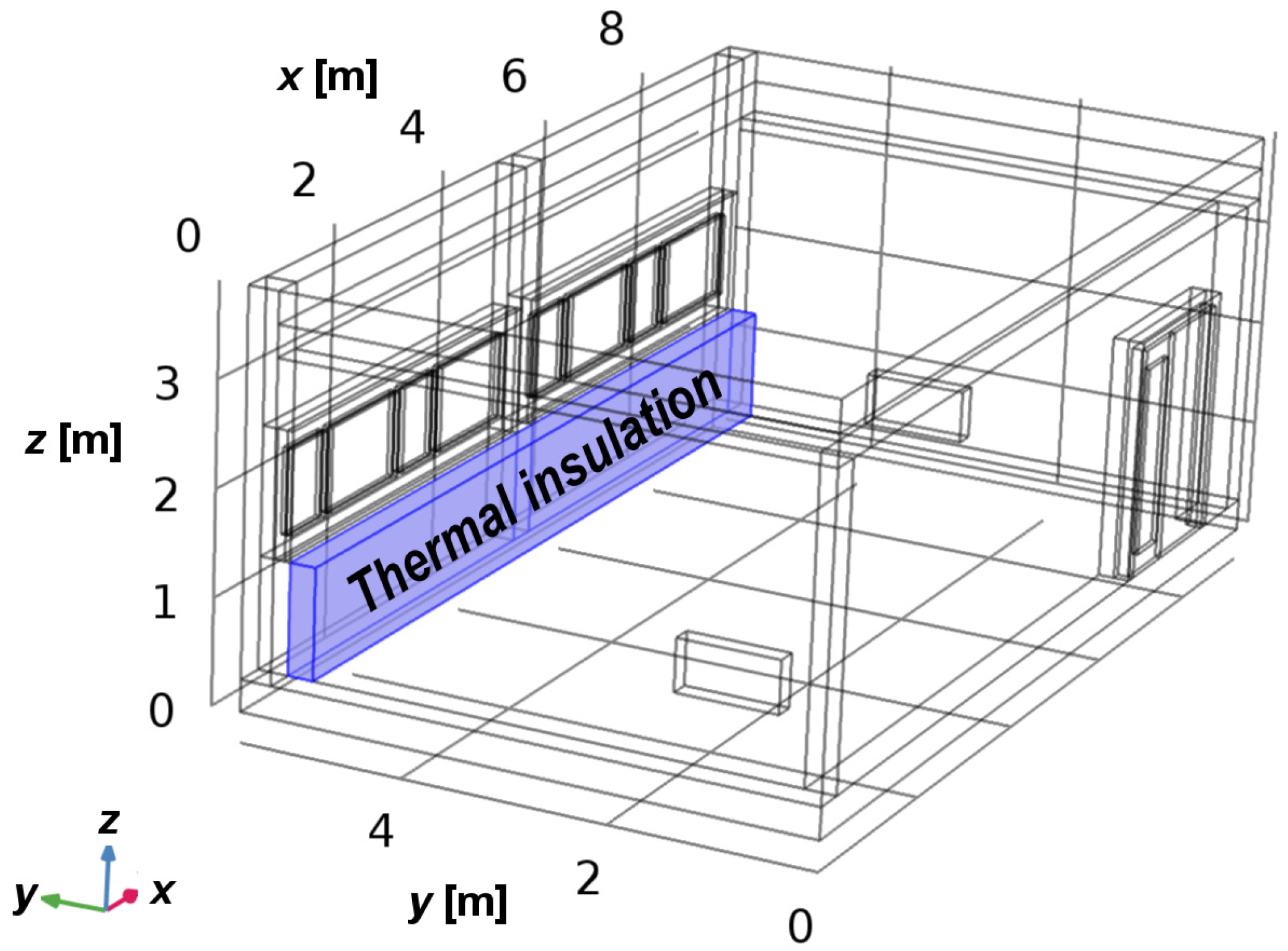
- Room dimensions: length 8.7 m, width 5 m, height 3 m.
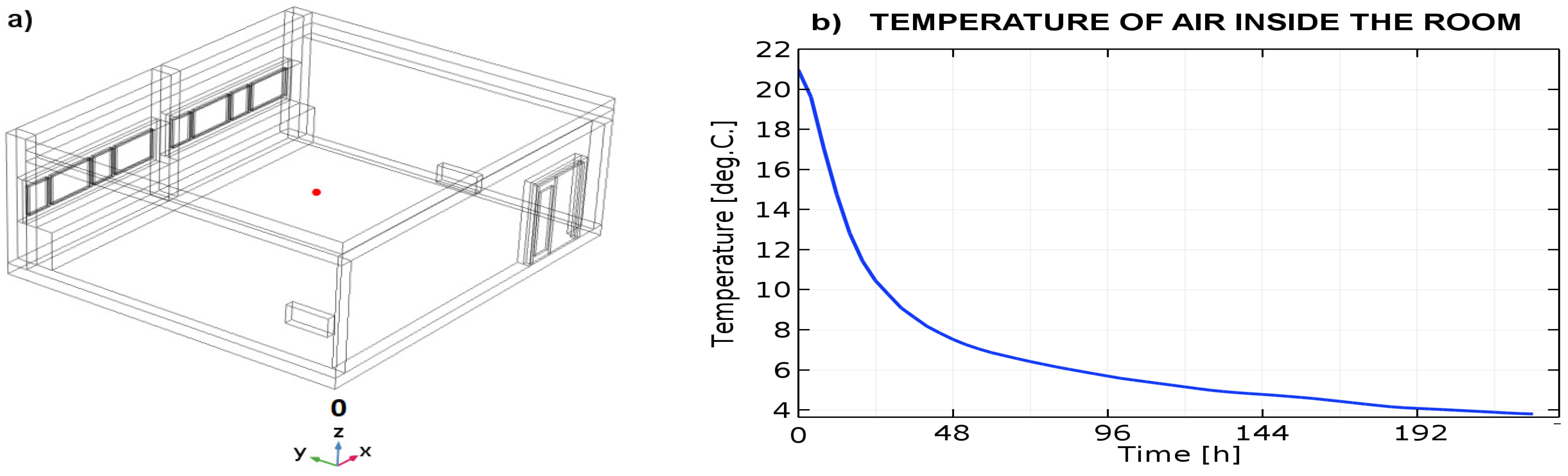
- The initial temperature of the air inside the tested room .
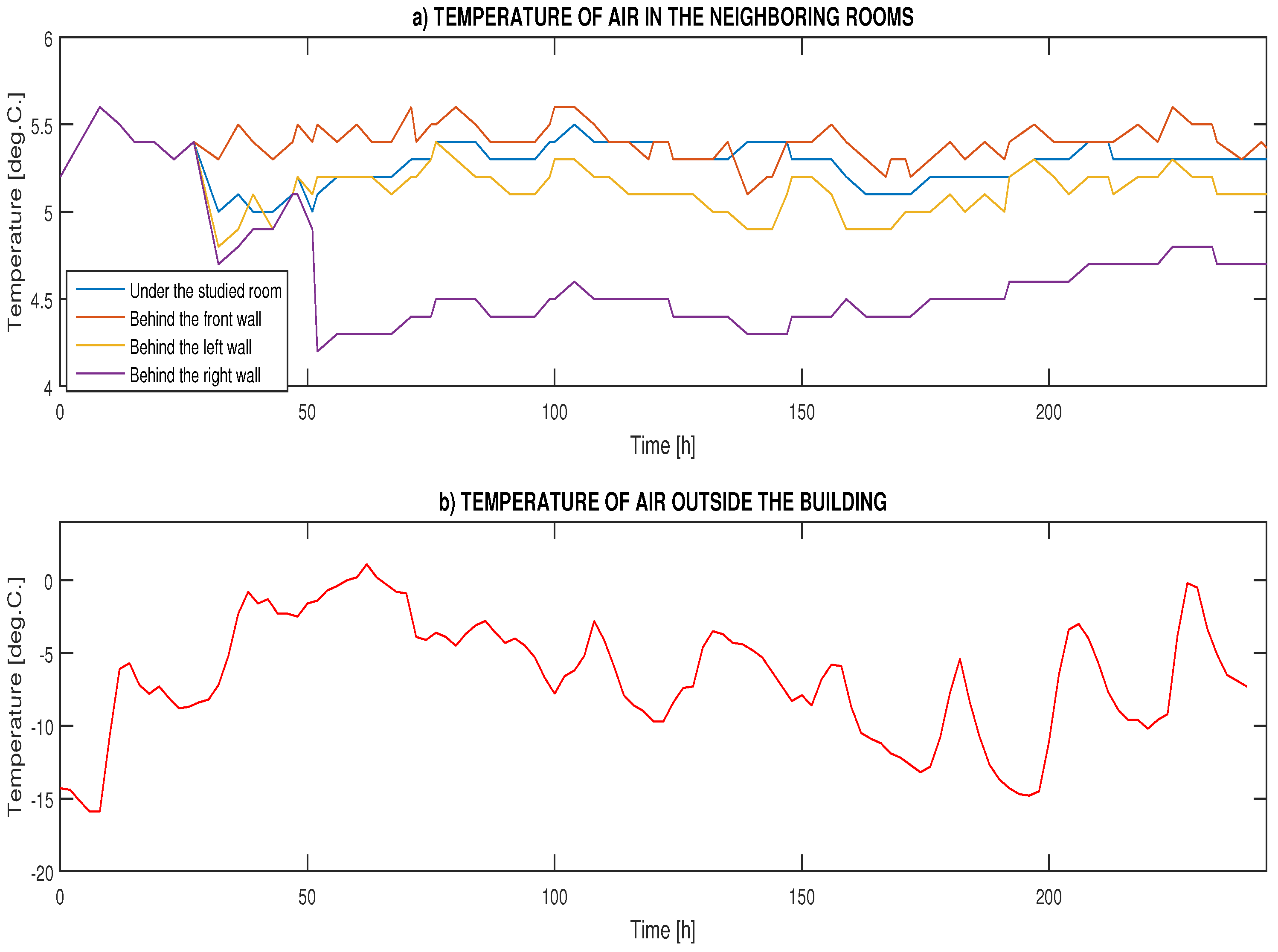
- Temperature of air in the adjoining rooms of the building .
- Velocity of the airflow inside the tested room .
- Heat transfer coefficient inside the building .
- Heat transfer coefficient outside the building .
2.1.1. Domain Setting
2.1.2. Boundary Setting
2.2. Computer Model Construction
- Defining the dimensions and location of all model elements.
- Defining the physical properties (specific heat capacity, thermal conductivity, density) of all model elements.
- Defining the initial and boundary conditions.
- Solving the model under modified conditions.
- Displaying the results as both 3D and 2D plots and export the output data into the TXT files.
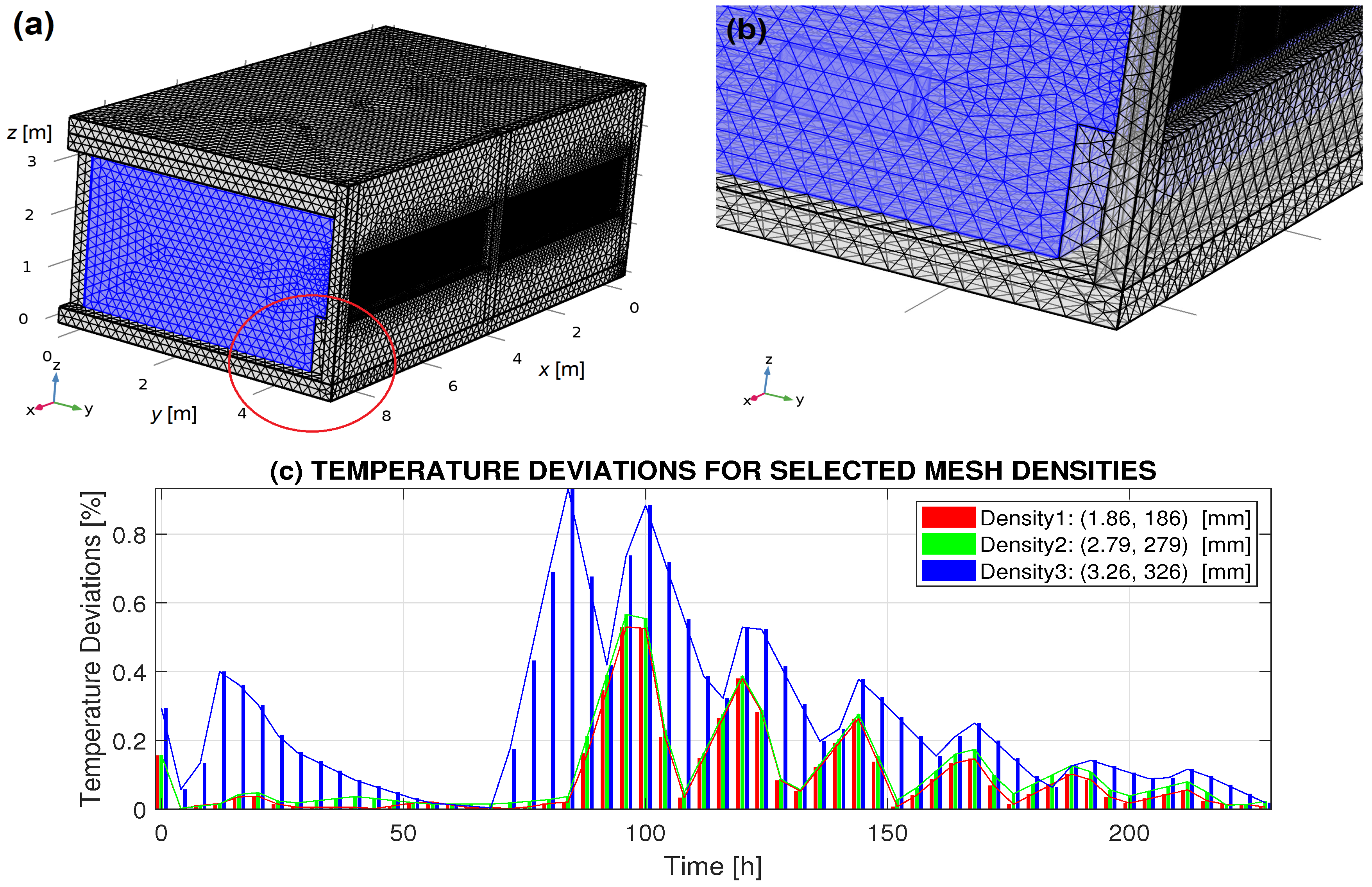
2.3. Simulation Setup
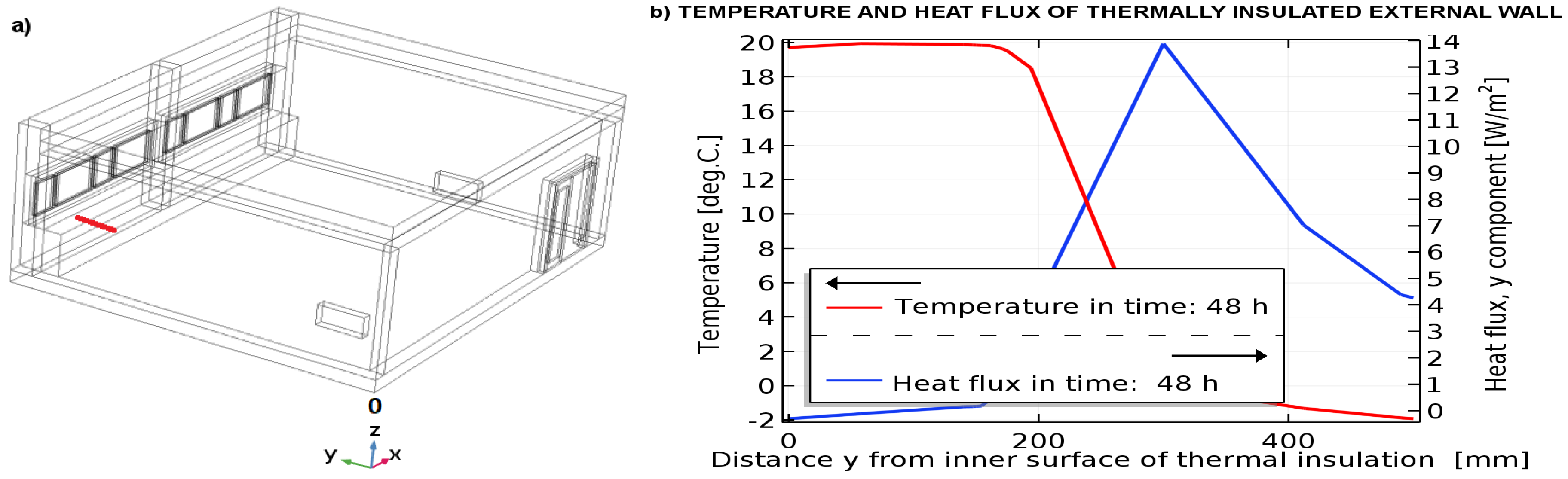
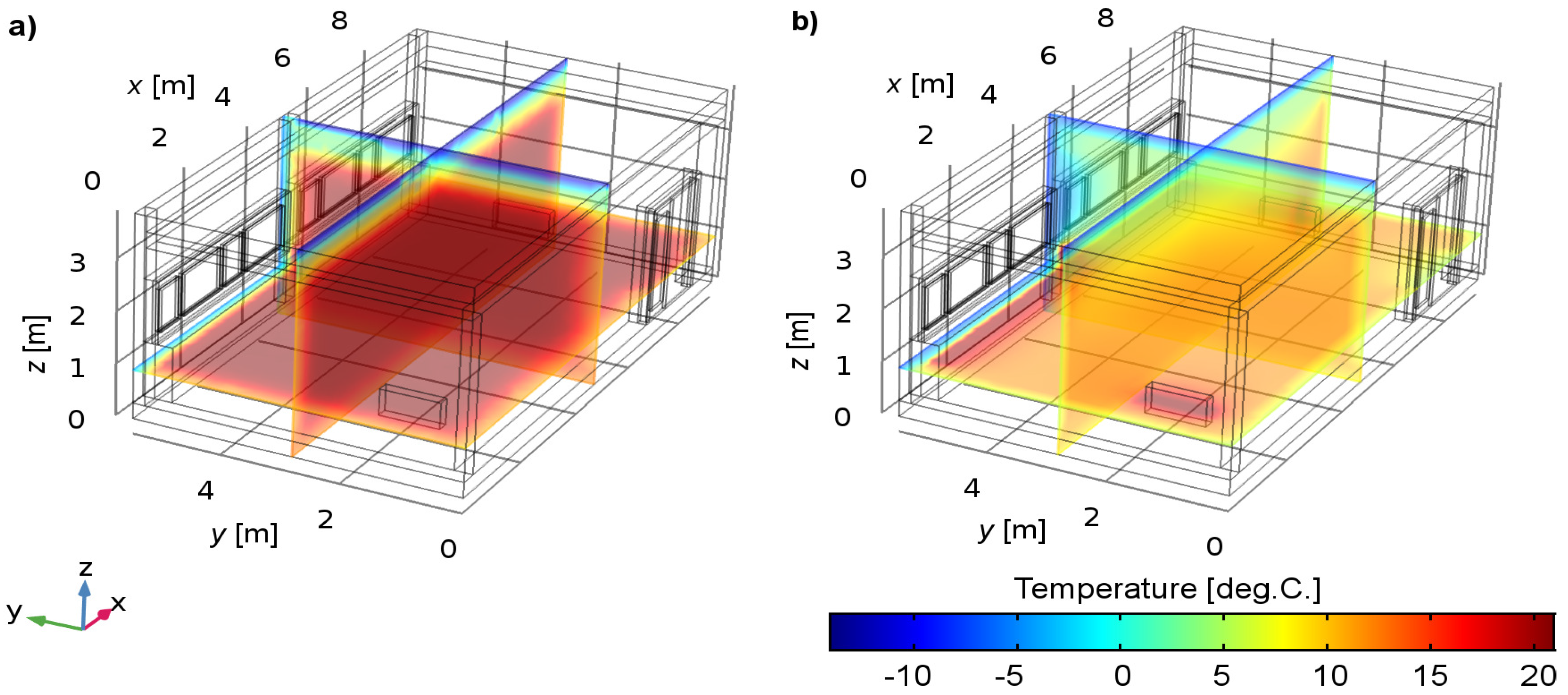
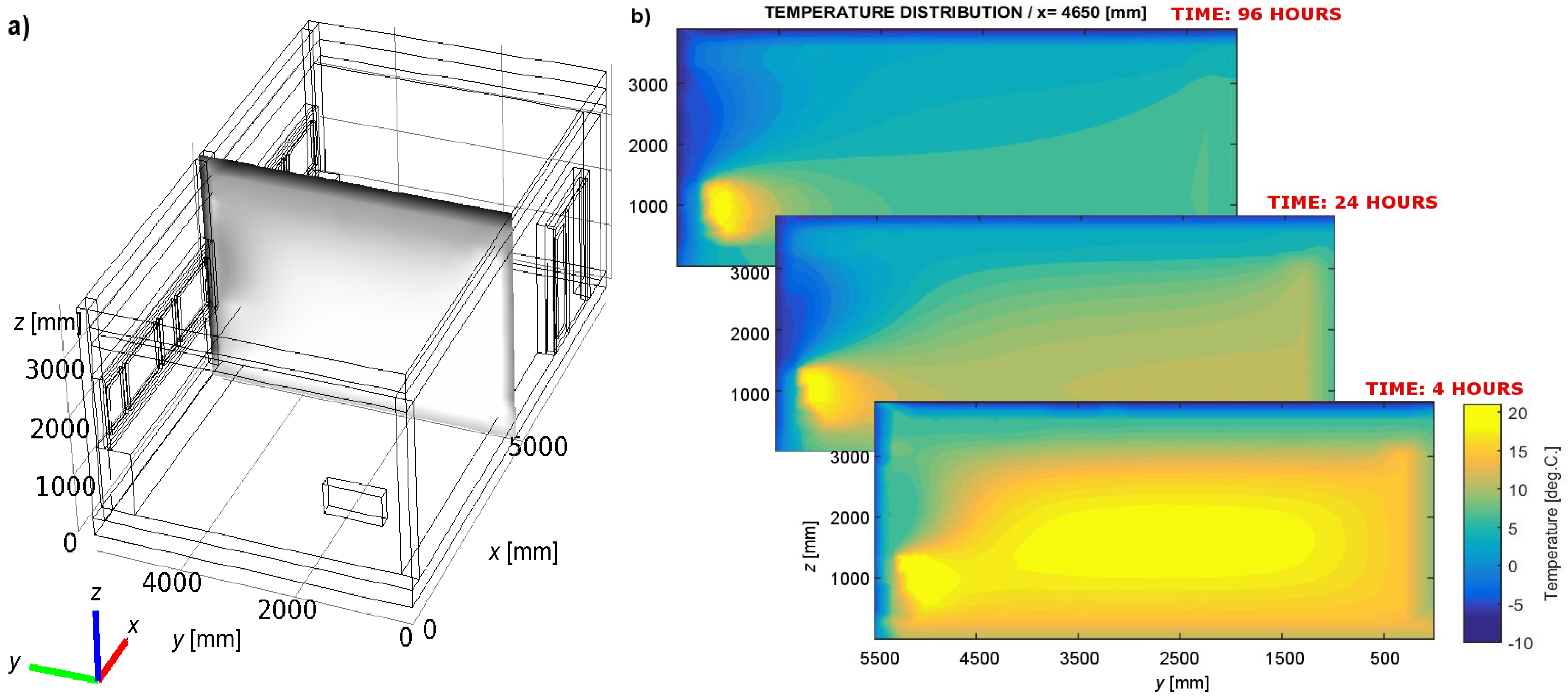
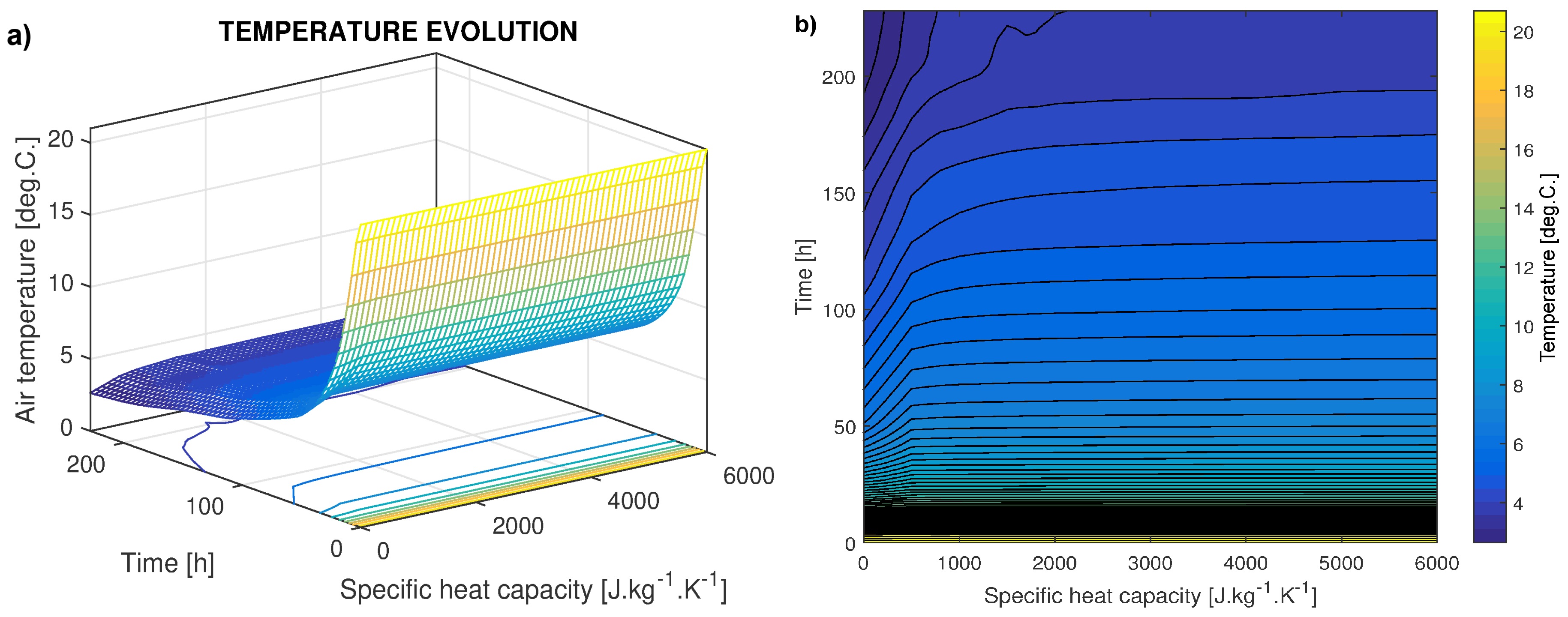
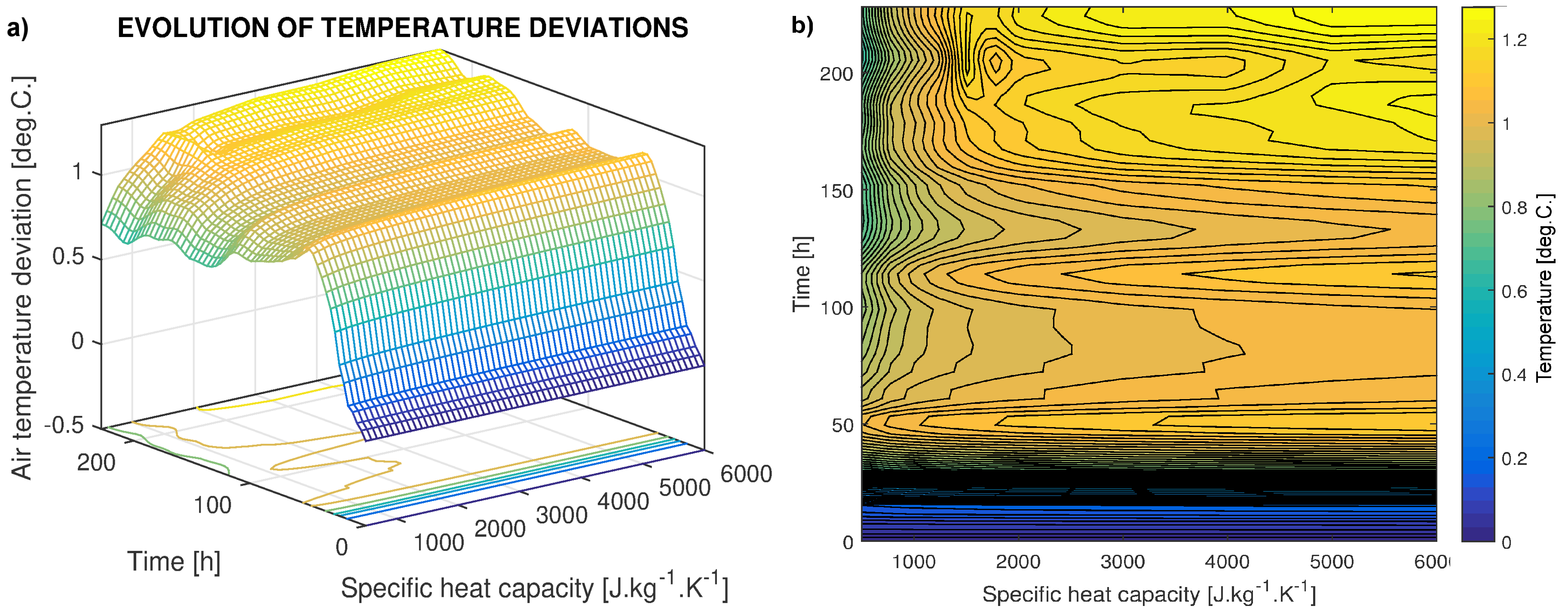
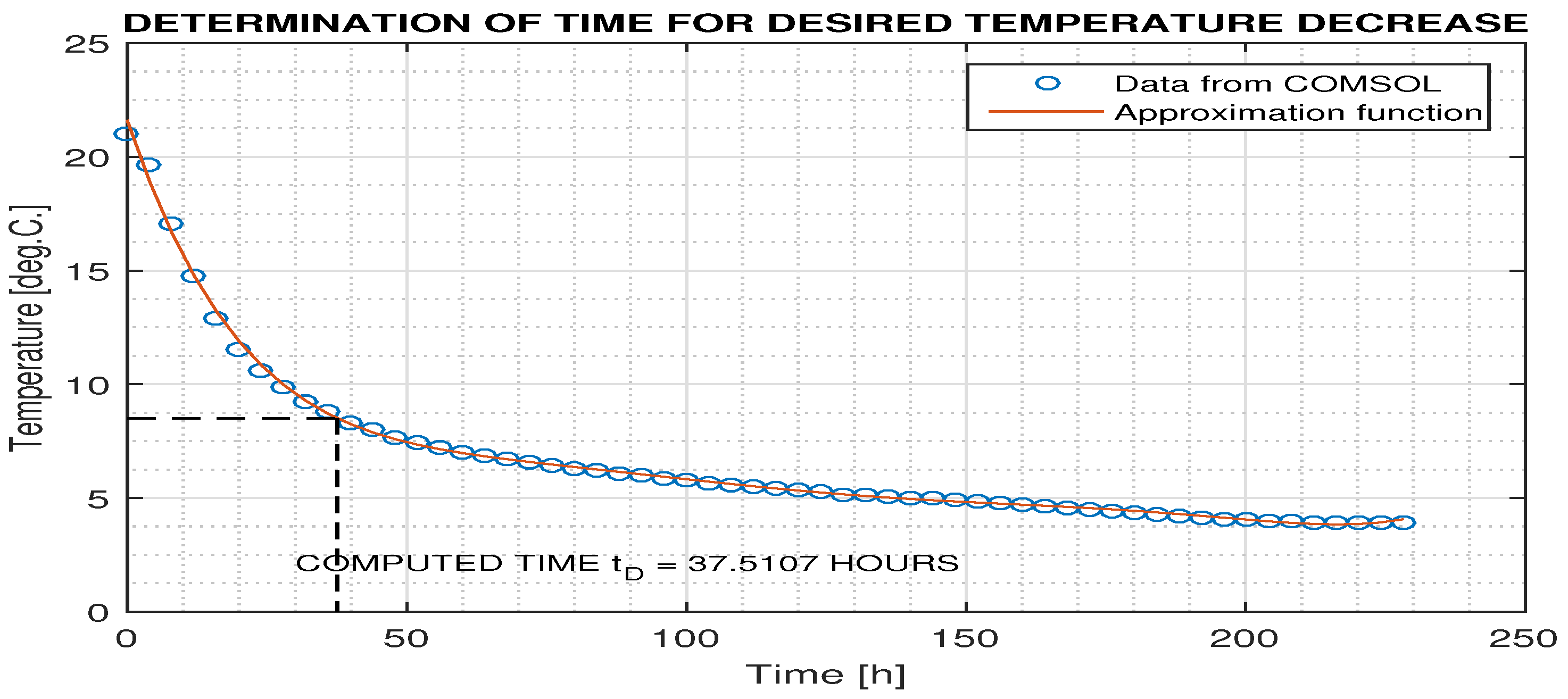
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| Heat capacity, ; | |
| Specific heat capacity, ; | |
| h | Heat transfer coefficient, ; |
| n | Normal vector, ; |
| q | Heat flow density, ; |
| Incident radiant heat flow per unit surface area, ; | |
| Heat flow density on the surface, ; | |
| t | Time, ; |
| Time to achieve desired temperature decrease, ; | |
| T | Temperature, ; |
| Ambient temperature, ; | |
| External temperature, ; | |
| Convective exchange temperature, ; | |
| Surface temperature, ; | |
| Initial temperature of a body, ; | |
| v | Fluid velocity, ; |
| x, y, z | Space coordinates, ; |
| Thermal conductivity, ; | |
| Inner heat-generation rate per unit volume, ; | |
| Emissivity, | |
| Stephan–Boltzmann constant, |
References
- Zawieska, J.; Pieriegud, J. Smart city as a tool for sustainable mobility and transport decarbonisation. Transp. Policy 2018, 63, 39–50. [Google Scholar] [CrossRef]
- Lazaroiu, G.C.; Mariacristina, R. Definition methodology for the smart cities model. Energy 2012, 47, 326–332. [Google Scholar] [CrossRef]
- De Groote, M.; Fabbri, M. Smart Buildings in a Decarbonised Energy System; Buildings Performance Institute Europe (BPIE): Brussels, Belgium, 2016. [Google Scholar]
- Kejriwal, S.; Mahajan, S. Smart Buildings. How IoT Technology Aims to Add Value for Commercial Real Estate Companies. Available online: https://www2.deloitte.com/insights/us/en/focus/internet-of-things/iot-commercial-real-estate-intelligent-building-systems.html (accessed on 16 November 2018).
- Weng, T.; Agarval, Y. From buildings to smart buildings—Sensing and actuation to improve energy efficiency. IEEE Des. Test Comput. 2012, 29, 36–44. [Google Scholar] [CrossRef]
- Battista, G.; Evangelisti, L.; Guattari, C.; Basilicata, C.; de Lieto Vollaro, R. Buildings energy efficiency: Interventions analysis under a smart cities approach. Sustainability 2014, 6, 4694–4705. [Google Scholar] [CrossRef]
- Heim, D.; Wieprzkowicz, A. Attenuation of temperature fluctuations on an external surface of the wall by a phase change material-activated layer. Appl. Sci. 2018, 8. [Google Scholar] [CrossRef]
- Shen, C.; Li, X. Potential of Utilizing Different Natural Cooling Sources to Reduce the Building Cooling Load and Cooling Energy Consumption: A Case Study in Urumqi. Energies 2017, 10, 366. [Google Scholar] [CrossRef]
- Bisegna, F.; Mattoni, B.; Gori, P.; Asdrubali, F.; Gyatarri, C.; Evangelisti, L.; Sambuco, S.; Bianchi, F. Influence of insulating materials on green building rating system results. Energies 2016, 9, 712. [Google Scholar] [CrossRef]
- Li, M.; Gui, G.; Lin, Z.; Jiang, L.; Pan, H.; Wang, X. Numerical thermal characterization and performance metrics of building envelopes containing phase change materials for energy-efficient buildings results. Sustainability 2018, 10, 2657. [Google Scholar] [CrossRef]
- Ferroukhi, M.; Belarbi, R.; Limam, K.; Bosschaerts, W. Impact of coupled heat and moisture transfer effects on buildings energy consumption. Therm. Sci. 2017, 21, 1359–1368. [Google Scholar] [CrossRef]
- Badea, N. Design for Micro-Combined Cooling, Heating and Power Systems: Stirling Engines and Renewable Power Systems; Springer-Verlag: London, UK, 2015. [Google Scholar]
- Zmrhal, V.; Hensen, J.L.M.; Drkal, F. Modeling and simulation of a room with a radiant cooling ceiling. In Proceedings of the 8th International IBPSA Building Simulation Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 1491–1496. [Google Scholar]
- Tam, W.; Yuen, W.; Chow, W. Numerical study on the importance of radiative heat transfer in building energy simulation. Numer. Heat Transf. Part A Appl. 2016, 69, 694–709. [Google Scholar] [CrossRef]
- Rodriguez-Munoz, N.A.; Najera-Trejo, M.; Alarcon-Herrera, O.; Martin-Dominguez, I.R. A building’s thermal assessment using dynamic simulation. Indoor Built Environ. 2018, 27, 173–183. [Google Scholar] [CrossRef]
- Perera, D.W.U.; Skeie, N.-O. Estimation of the Heating Time of Small-Scale Buildings Using Dynamic Models. Buildings 2016, 6, 10. [Google Scholar] [CrossRef]
- Bahar, Y.N.; Pere, Ch.; Landrieu, J.; Nicolle, C. A Thermal Simulation Tool for Building and Its Interoperability through the Building Information Modeling (BIM) Platform. Buildings 2013, 3, 380–398. [Google Scholar] [CrossRef] [Green Version]
- Taoum, S.; Lefrançois, E. Dual analysis for heat exchange: Application to thermal bridges. Comput. Math. Appl. 2018, 75, 3471–3487. [Google Scholar] [CrossRef]
- Sehnalek, S.; Zalesak, M.; Vincenec, J.; Oplustil, M.; Chrobak, P. Evaluation of SolidWorks Flow Simulation by Ground-Coupled Heat Transfer Test Cases. In Proceedings of the International Conferences: Latest Trends on Systems, Latest Trends on Systems, Santorini, Greece, 17–21 July 2014; Volume II, pp. 492–498. [Google Scholar]
- Maliki, M.; Laredj, N.; Bendani, K.; Missoum, H. Two-dimensional transient modeling of energy and mass transfer in porous building components using COMSOL Multiphysics. J. Appl. Fluid Mech. 2017, 10, 319–328. [Google Scholar] [CrossRef]
- Promis, G.; Douzane, O.; Tran Le, A.D.; Langlet, T. Moisture hysteresis influence on mass transfer through bio-based building materials in dynamic state. Energy Build. 2018, 166, 450–459. [Google Scholar] [CrossRef]
- Kupczak, A.; Sadłowska-Sałęga, A.; Krzemień, L.; Sobczyk, J.; Radoń, J.; Kozłowski, R. Impact of paper and wooden collections on humidity stability and energy consumption in museums and libraries. Energy Build. 2018, 158, 77–85. [Google Scholar] [CrossRef]
- Portal, N.; van Schijndel, A.; Kalagasidis, A. The multiphysics modeling of heat and moisture induced stress and strain of historic building materials and artefacts. Build. Simul. 2014, 7, 217–227. [Google Scholar] [CrossRef]
- Bida, S.M.; Aziz, F.N.A.A.; Jaafar, M.S.; Hejazi, F.; Nabilah, A.B. Thermal performance of super-insulated precast concrete structural sandwich panels. Energy Build. 2018, 176, 418–430. [Google Scholar] [CrossRef]
- Tsvetkov, N.; Khutornoi, A.; Kozlobrodov, A.; Romanenko, S.; Shefer, Y.; Golovko, A. Influence of metal frame on heat protection properties of a polystyrene concrete wall. MATEC Web Conf. 2018, 143, 1–7. [Google Scholar] [CrossRef]
- Bianchi Janetti, M.; Colombo, L.P.M.; Ochs, F.; Feist, W. Effect of evaporation cooling on drying capillary active building materials. Energy Build. 2018, in press. [Google Scholar] [CrossRef]
- Putra, J. A Study of Thermal Comfort and Occupant Satisfaction in Office Room. Procedia Eng. 2017, 170, 240–247. [Google Scholar] [CrossRef]
- Missoum, A.; Elmir, M.; Bouanini, M.; Draoui, B. Numerical simulation of heat transfer through the building facades of buildings located in the city of Bechar. Int. J. Multiphys. 2016, 10, 441–450. [Google Scholar]
- Biswas, K. Development and Validation of Numerical Models for Evaluation of Foam-Vacuum Insulation Panel Composite Boards, Including Edge Effects. Energies 2018, 11, 2228. [Google Scholar] [CrossRef]
- Gerlich, V.; Sulovská, K.; Zálešák, M. COMSOL Multiphysics validation as simulation software for heat transfer calculation in buildings: Building simulation software validation. Meas. J. Int. Meas. Confed. 2013, 46, 2003–2012. [Google Scholar] [CrossRef] [Green Version]
- Neymark, J.; Judkoff, R. International Energy Agency Building Energy Simulation TEST and Diagnostic Method (IEA BESTEST). In Depth Diagnostic Cases for Ground Coupled Heat Transfer Related to Slab-on-Grade Construction; National Renewable Energy Lab.: Golden, CO, USA, 2008. [Google Scholar]
- Charvátová, H.; Zálešák, M. Calculation of heat losses of the room with regard to variable outside air temperature. In Proceedings of the 19th International Conference on Systems, Recent Advances in Systems, Zakynthos Island, Greece, 16–20 July 2015; pp. 627–631. [Google Scholar]
- Eppes, T.; Milanovic, I. Application building in engineering courses. In Proceedings of the Global Engineering Education Conference (EDUCON), Athens, Greece, 25–28 April 2017; pp. 78–85. [Google Scholar]
- Charvátová, H.; Zálešák, M. Testing of Method for Assessing of Room Thermal Stability. MATEC Web Conf. 2017, 125. [Google Scholar] [CrossRef]
- CSN EN ISO 13790: Energy Performance of Buildings—Calculation of Energy Consumption for Heating and Cooling, (Czech Edition) ed; Czech Office for Standards, Metrology and Testing: Prague, Czech Republic, 2009.
- COMSOL Multiphysics 5.3; COMSOL, Inc.: Stockholm, Sweden, 2017.
- Nikishkov, G.P. Introduction to the Finite Element Method. Lecture Notes; University of Aizu: Aizu-Wakamatsu, Japan, 2004. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Procházka, A.; Charvátová, H.; Vyšata, O.; Kopal, J.; Chambers, J. Breathing Analysis Using Thermal and Depth Imaging Camera Video Records. Sensors 2017, 17, 1408. [Google Scholar] [CrossRef] [PubMed]
- Spilak, M.P.; Sigsgaard, T.; Takai, H.; Zhang, G. A comparison between temperature-controlled laminar airflow device and a room air-cleaner in reducing exposure to particles while asleep. PLoS ONE 2016, 11, e0166882. [Google Scholar] [CrossRef] [PubMed]
| Geometrical Element | Size | Thermal Conductivity | Density | Specific Heat Capacity | Emissivity |
|---|---|---|---|---|---|
| Rear wall | 0.27 | 900 | 960 | 0.85 | |
| Left side wall | 0.27 | 900 | 960 | 0.85 | |
| Right side wall | 0.27 | 900 | 960 | o.85 | |
| Wall under the windows | 0.80 | 1700 | 900 | 0.80 | |
| Wall above the windows | 0.80 | 1700 | 900 | 0.80 | |
| Columns in the outside wall | 0.32 | 2192 | 1018 | 0.85 | |
| Floor | 1.43 | 2300 | 1020 | 0.85 | |
| Ceiling | 0.82 | 1251 | 1021 | 0.8 | |
| Insulation above the ceiling | 0.04 | 30 | 1270 | 0.90 | |
| Insulation of the outside wall | 0.05 | 3000 | 1500 | 0.85 | |
| Window frames | 0.18 | 400 | 2510 | 0.89 | |
| Glass in larger windows | 0.76 | 2600 | 840 | 0.99 | |
| Glass in smaller windows | 0.76 | 2600 | 840 | 0.99 | |
| Door leaf | 0.11 | 800 | 1150 | 0.89 | |
| Panel next to the door | 0.20 | 1380 | 1100 | 0.94 | |
| Door frame | 58 | 7850 | 440 | 0.89 | |
| Door trim | 0.76 | 2600 | 840 | 0.9 | |
| Left heater | 58 | 7850 | 440 | 0.88 | |
| Right heater | 58 | 7850 | 440 | 0.88 |
| Geometrical Element | Convection Inside the Building | Convection Outside the Building | Radiation Inside the Studied Room |
|---|---|---|---|
| Rear wall | yes | - | yes |
| Left side wall | yes | - | yes |
| Right side wall | yes | - | yes |
| Wall under the windows | - | yes | yes |
| Columns in the outside wall | - | yes | yes |
| Floor | yes | - | yes |
| Ceiling | yes | - | yes |
| Thermal insulation above the ceiling | - | - | yes |
| Wall above the windows | - | yes | yes |
| Window frames | - | yes | yes |
| Glass in windows | - | yes | yes |
| Door leaf | yes | - | yes |
| Panel next to the door | yes | - | yes |
| Door frame | yes | - | yes |
| Door trim | yes | - | yes |
| Left heater | - | - | yes |
| Right heater | - | - | yes |
| Room with Windows | Room without Windows | |||||
|---|---|---|---|---|---|---|
| 500 | 12.6074 | 13.3499 | 14.2084 | 18.1518 | 22.0157 | 24.5785 |
| 750 | 12.9352 | 13.7329 | 14.4724 | 19.5924 | 23.7279 | 25.8499 |
| 1000 | 13.1871 | 13.9521 | 14.6941 | 20.6716 | 24.7484 | 26.4313 |
| 1250 | 13.3796 | 14.1097 | 14.7164 | 21.4888 | 25.3784 | 26.7341 |
| 1500 | 13.5251 | 14.3165 | 14.8331 | 22.1175 | 25.7770 | 26.9165 |
| 1750 | 13.5287 | 14.2861 | 14.9097 | 22.6085 | 26.0335 | 27.0439 |
| 2000 | 13.7390 | 14.3729 | 14.9442 | 22.9967 | 26.2005 | 27.1444 |
| 3000 | 13.9666 | 14.4867 | 15.2986 | 23.9202 | 26.4593 | 27.4503 |
| 4000 | 13.9131 | 14.4992 | 15.3654 | 24.3236 | 26.5035 | 27.6890 |
| 5000 | 13.9715 | 14.5845 | 15.4119 | 24.5015 | 26.5105 | 27.8799 |
| 6000 | 14.0064 | 14.5970 | 15.4464 | 24.5761 | 26.5175 | 28.0317 |
| Room with Windows | Room without Windows | |||||
|---|---|---|---|---|---|---|
| 500 | 32.1153 | 33.8433 | 35.9988 | 55.1043 | 80.0684 | 91.1732 |
| 750 | 32.8130 | 34.6268 | 36.7179 | 63.5432 | 92.1786 | 102.1550 |
| 1000 | 33.3046 | 35.0553 | 37.2446 | 70.5980 | 99.1117 | 107.5477 |
| 1250 | 33.6671 | 35.3828 | 37.3249 | 76.1967 | 103.1024 | 110.2212 |
| 1500 | 33.9439 | 35.7448 | 37.5107 | 80.5065 | 105.3731 | 111.5354 |
| 1750 | 34.1608 | 35.7814 | 37.6306 | 83.7865 | 106.6239 | 112.1786 |
| 2000 | 34.3339 | 35.9529 | 37.9464 | 86.2689 | 107.2701 | 112.5012 |
| 3000 | 34.7661 | 36.7179 | 38.8484 | 91.3301 | 107.5326 | 113.0086 |
| 4000 | 34.6406 | 36.7179 | 39.0384 | 91.3301 | 107.5326 | 113.0086 |
| 5000 | 34.7647 | 36.5074 | 39.1732 | 92.6092 | 106.7862 | 114.1834 |
| 6000 | 34.8449 | 36.5793 | 39.2757 | 92.1753 | 106.7278 | 114.8614 |
| Description | Room with Windows | Room without Windows | ||||
|---|---|---|---|---|---|---|
| Minimum element quality | 0.01214 | 0.01214 | 0.01214 | 0.09427 | 0.09427 | 0.09427 |
| Average element quality | 0.7235 | 0.7239 | 0.7237 | 0.7716 | 0.7738 | 0.7710 |
| Tetrahedral elements | 3,062,131 | 3,058,890 | 3,062,773 | 519,500 | 512,976 | 519,485 |
| Triangular elements | 378,689 | 378,706 | 378,558 | 45,982 | 46,160 | 46,048 |
| Edge elements | 12,220 | 12,203 | 12,184 | 2611 | 2615 | 2611 |
| Vertex elements | 276 | 276 | 276 | 112 | 112 | 112 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charvátová, H.; Procházka, A.; Zálešák, M. Computer Simulation of Temperature Distribution during Cooling of the Thermally Insulated Room. Energies 2018, 11, 3205. https://doi.org/10.3390/en11113205
Charvátová H, Procházka A, Zálešák M. Computer Simulation of Temperature Distribution during Cooling of the Thermally Insulated Room. Energies. 2018; 11(11):3205. https://doi.org/10.3390/en11113205
Chicago/Turabian StyleCharvátová, Hana, Aleš Procházka, and Martin Zálešák. 2018. "Computer Simulation of Temperature Distribution during Cooling of the Thermally Insulated Room" Energies 11, no. 11: 3205. https://doi.org/10.3390/en11113205
APA StyleCharvátová, H., Procházka, A., & Zálešák, M. (2018). Computer Simulation of Temperature Distribution during Cooling of the Thermally Insulated Room. Energies, 11(11), 3205. https://doi.org/10.3390/en11113205







