On Field Weakening Performance of a Brushless Direct Current Motor with Higher Winding Inductance: Why Does Design Matter?
Abstract
:1. Introduction
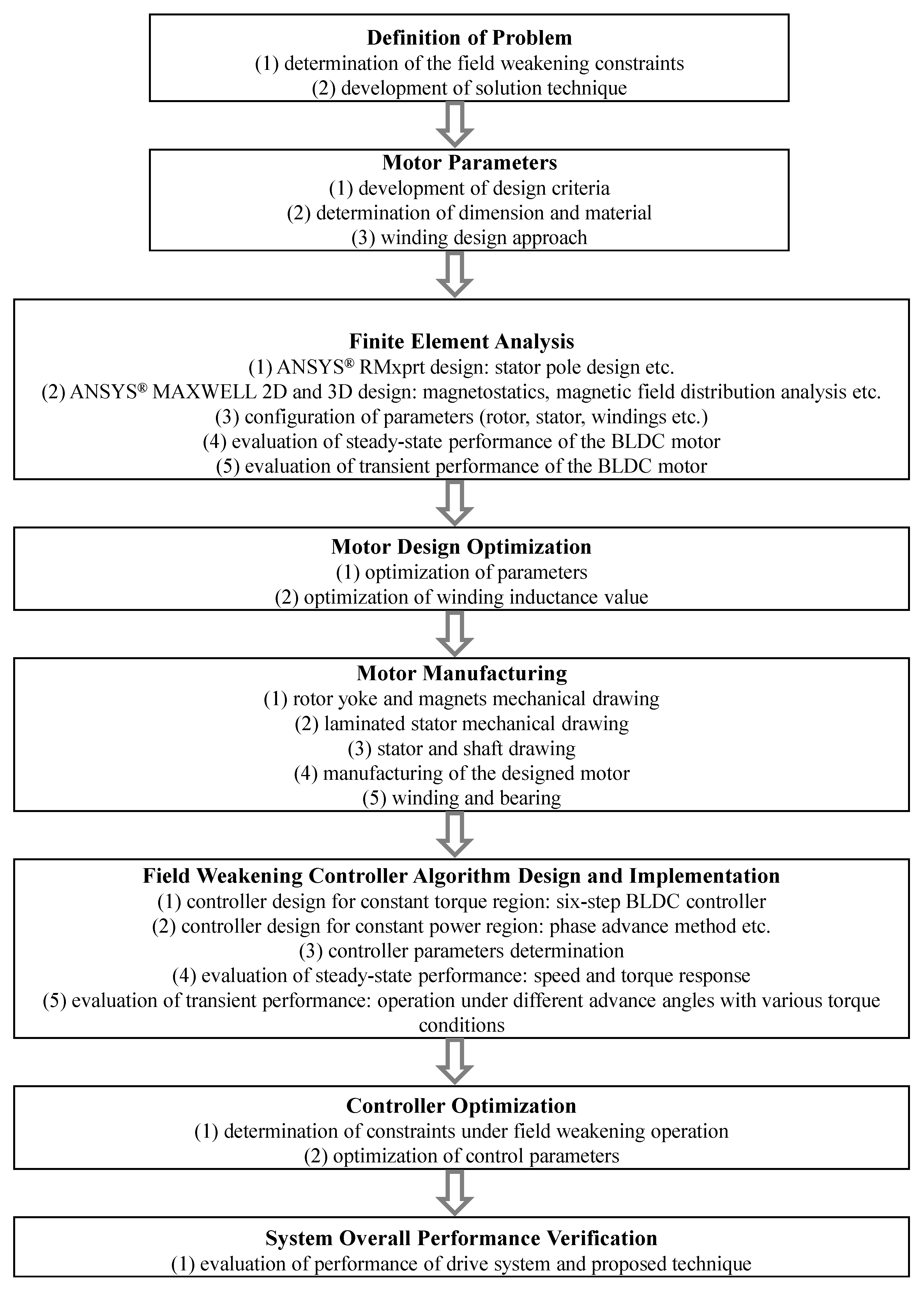
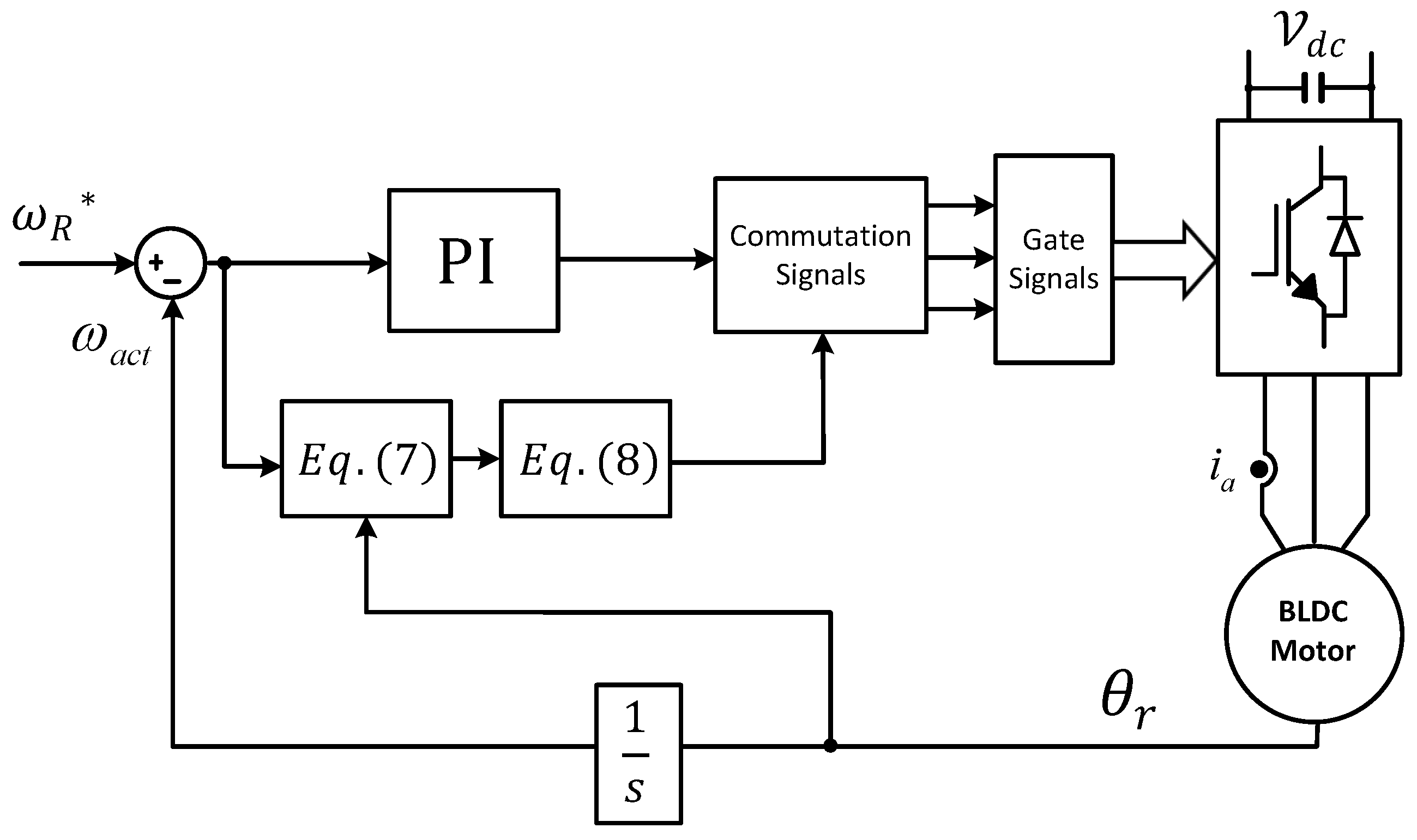
2. Materials and Methods
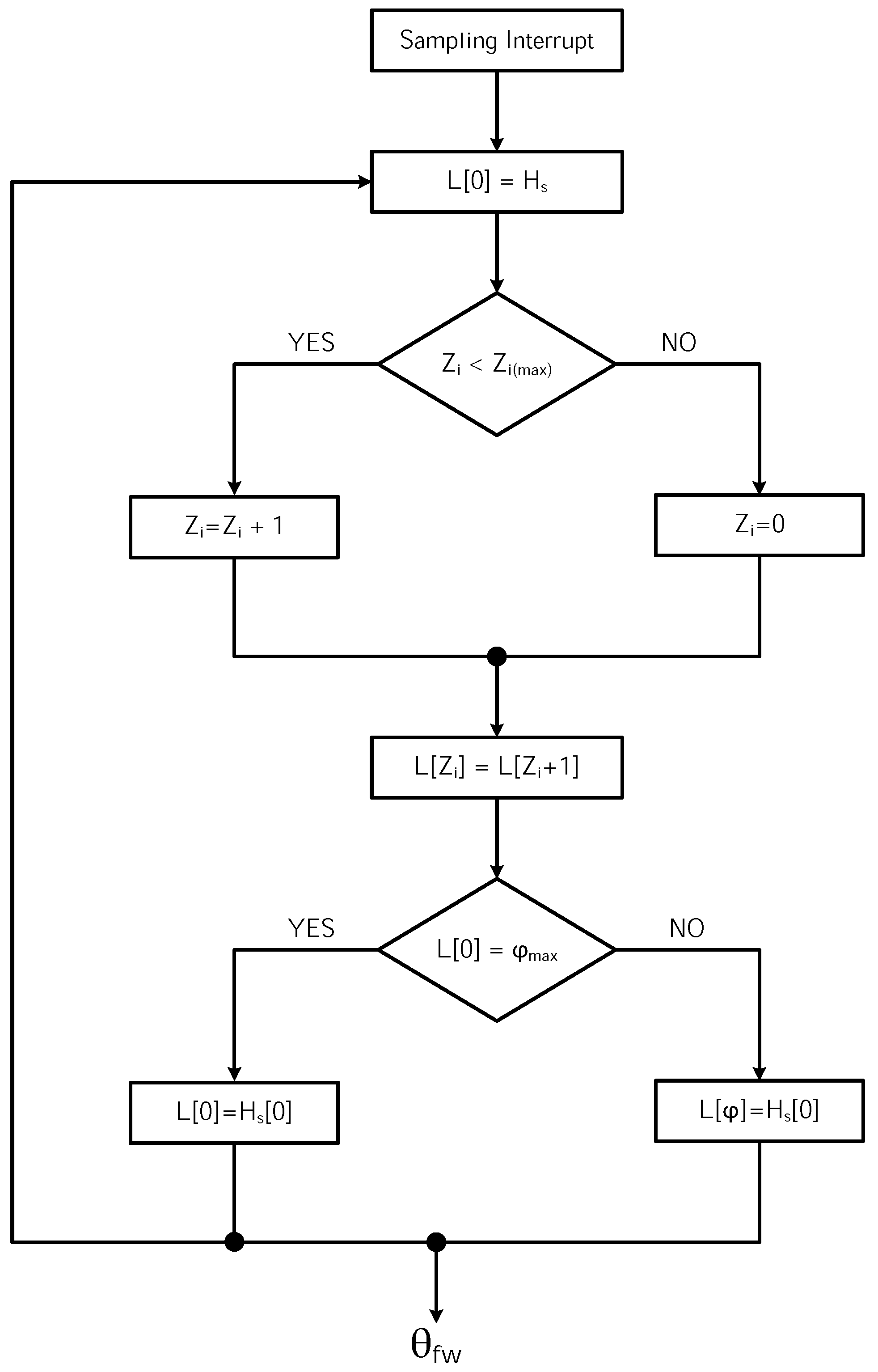
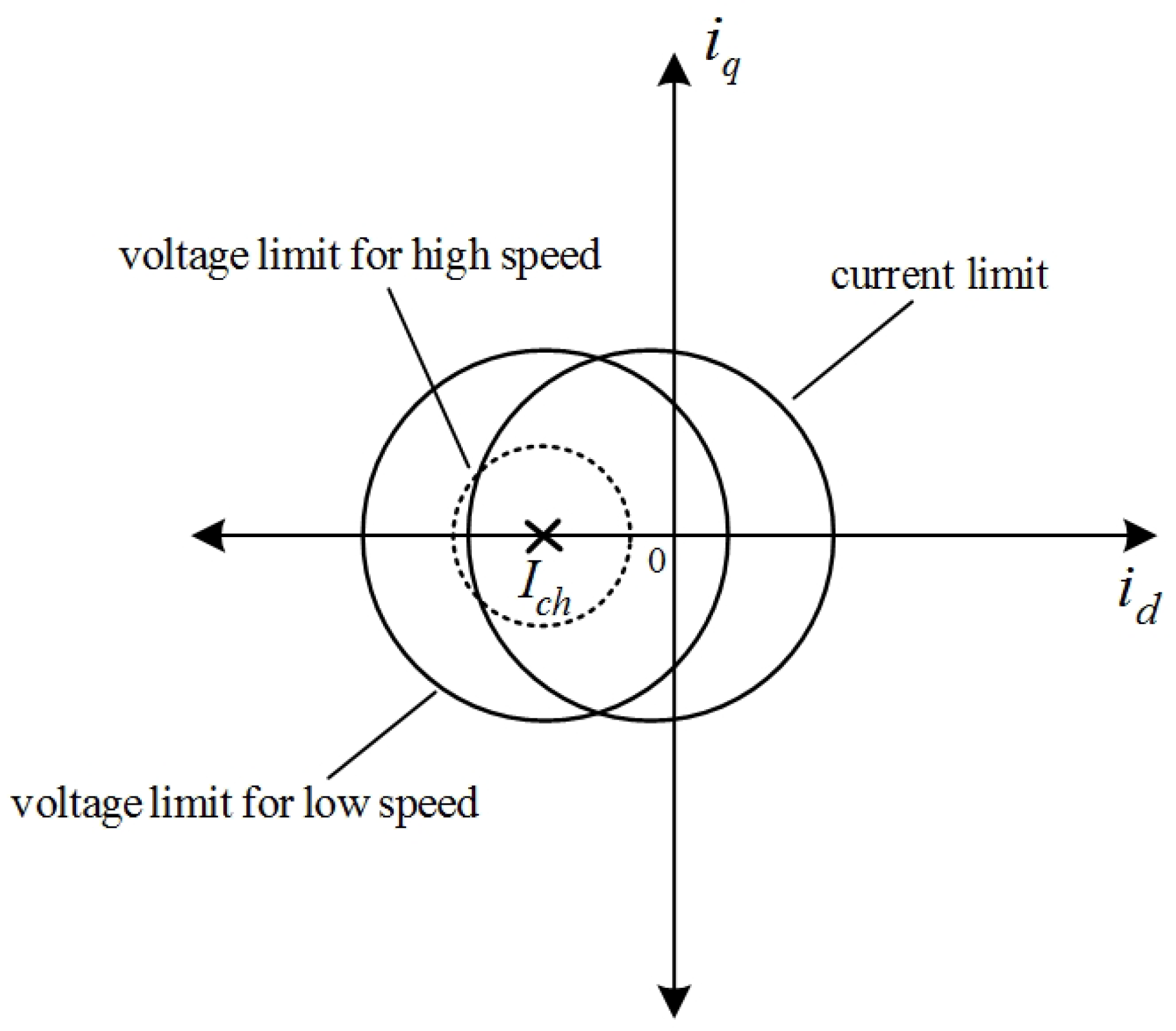
2.1. Principle of the Field Weakening Operation of SMPM Motors
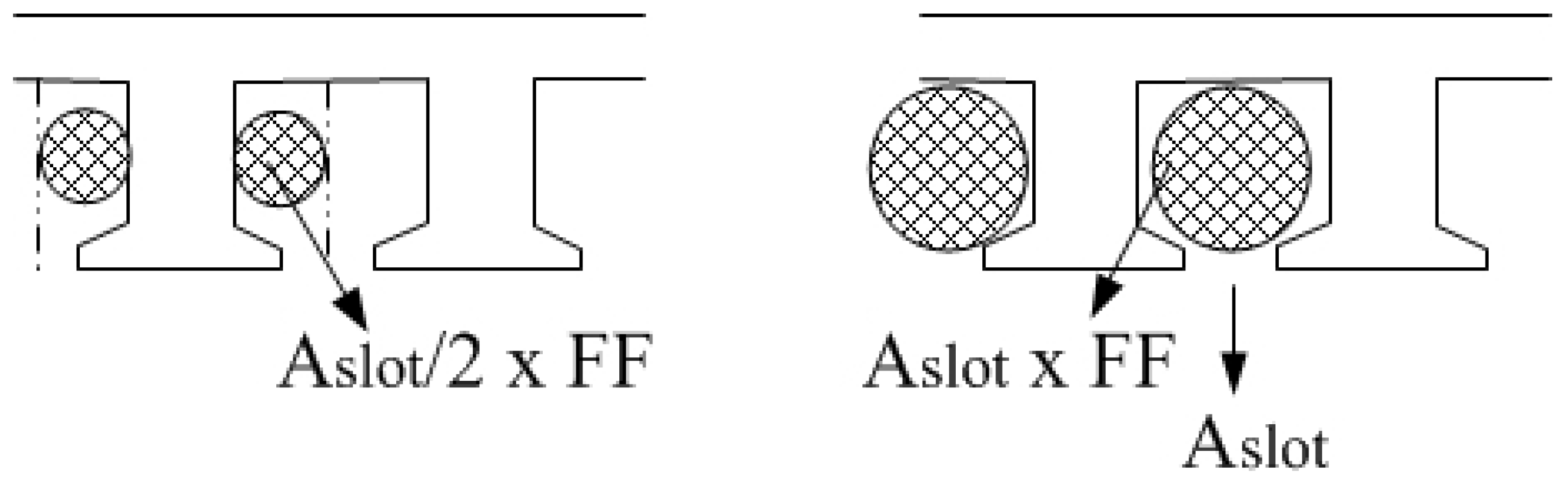
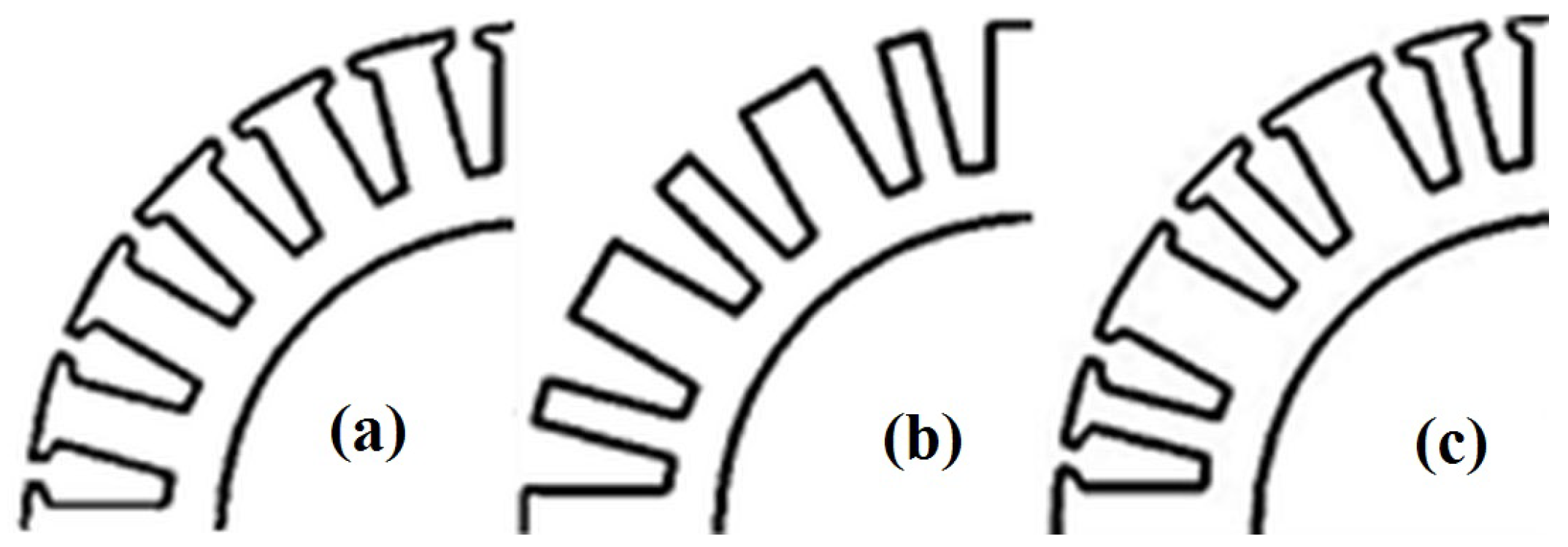
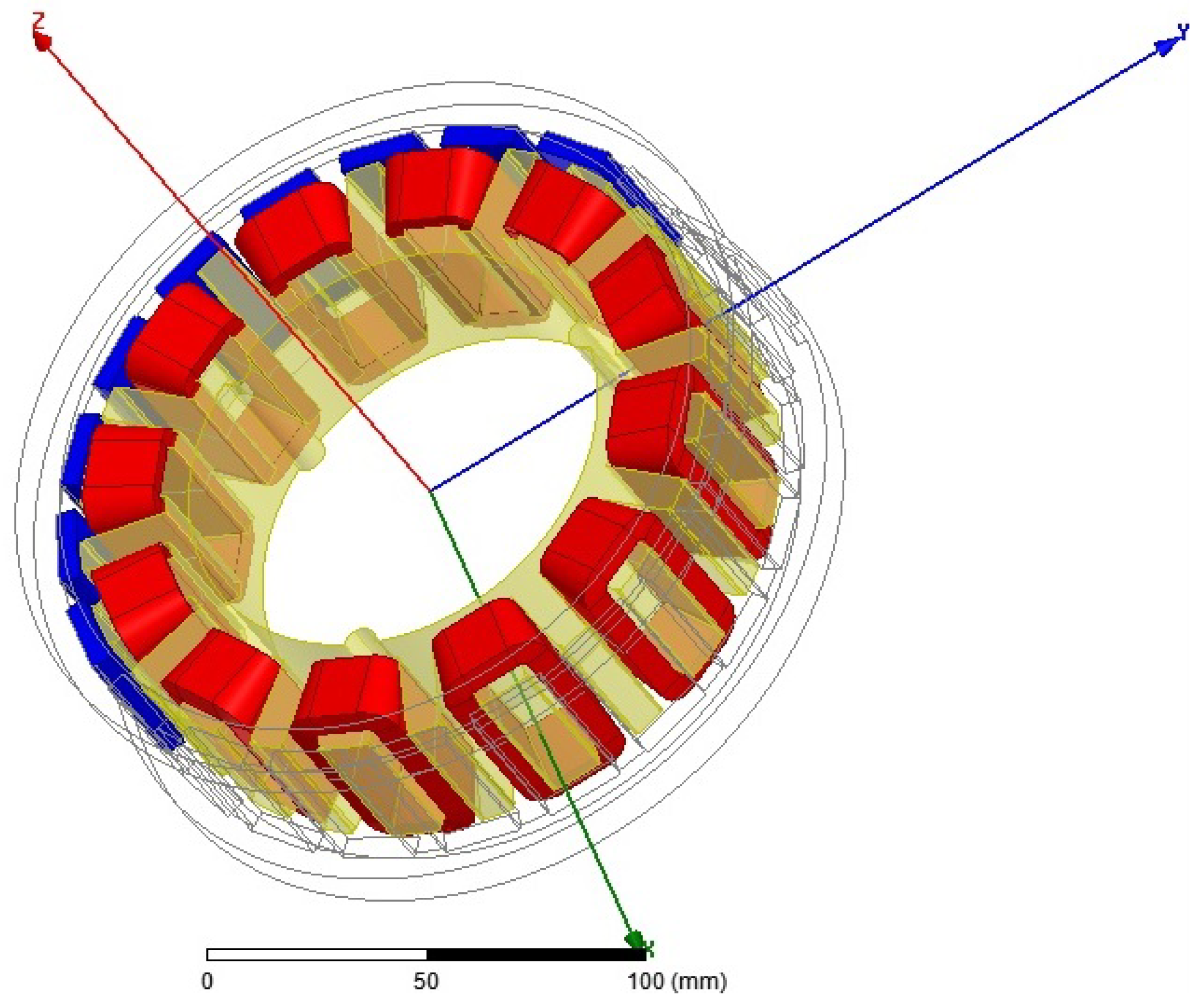
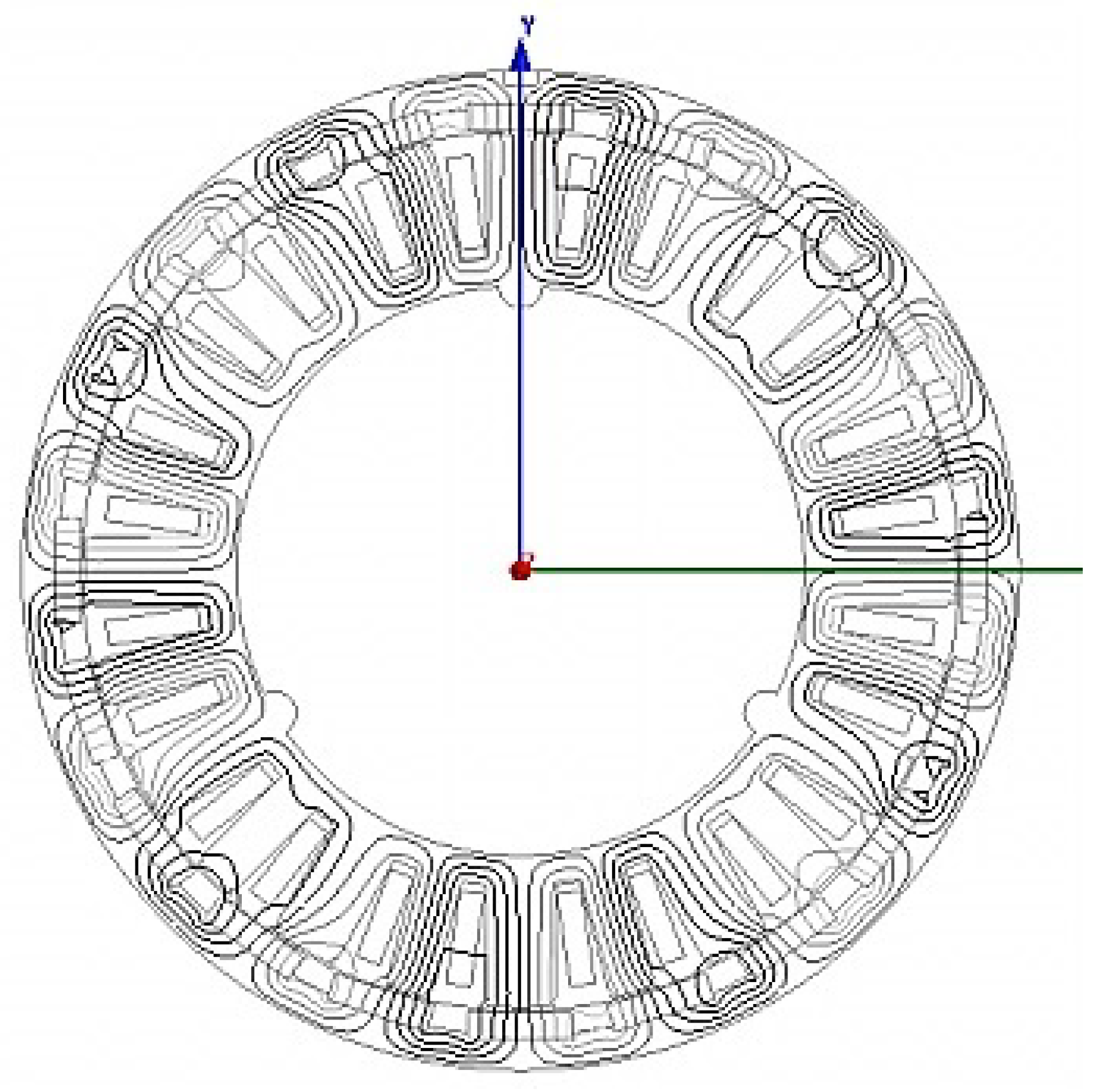
2.2. The Proposed Sub-Fractional Slot-Concentrated Windings Structure
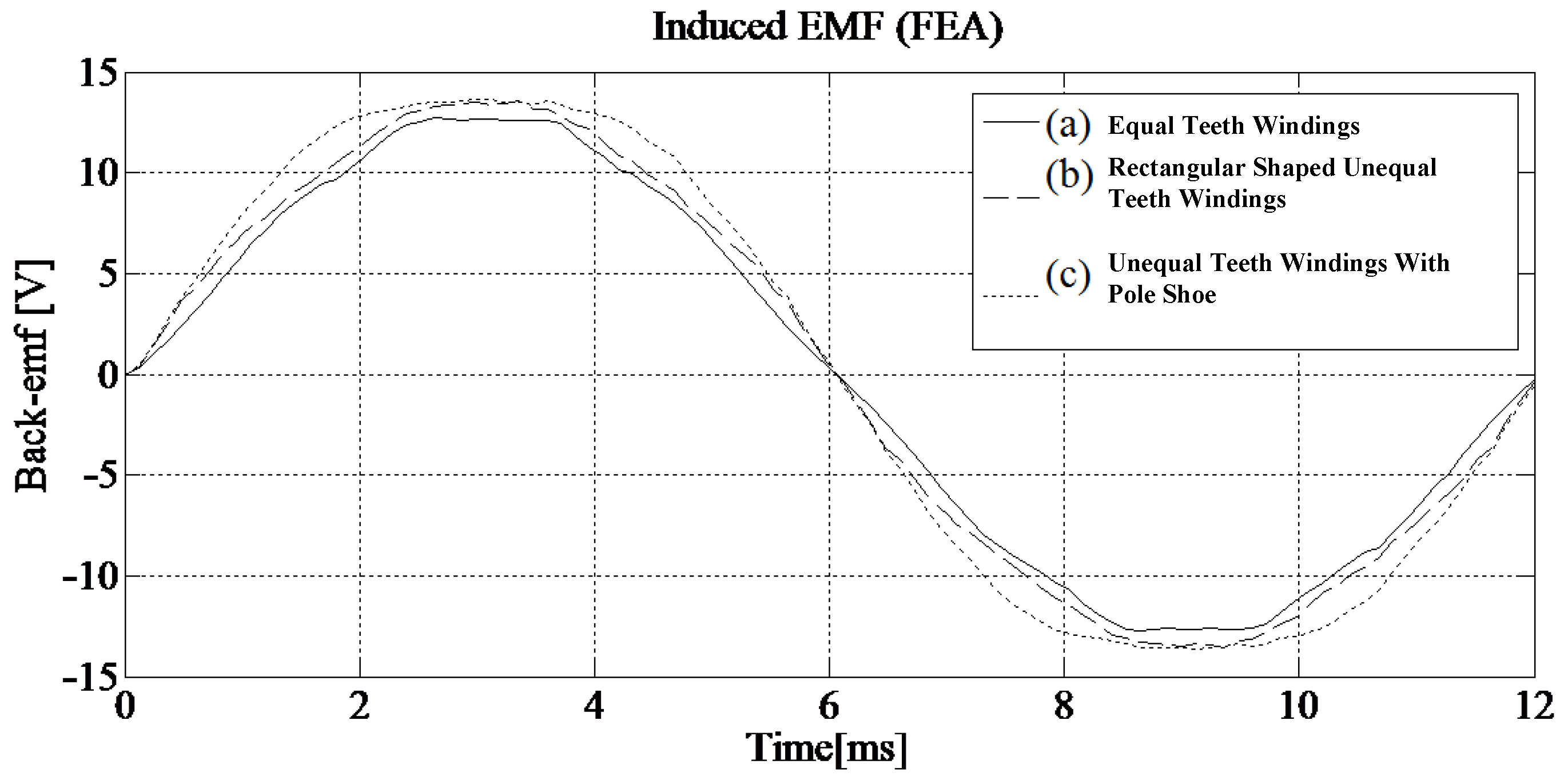
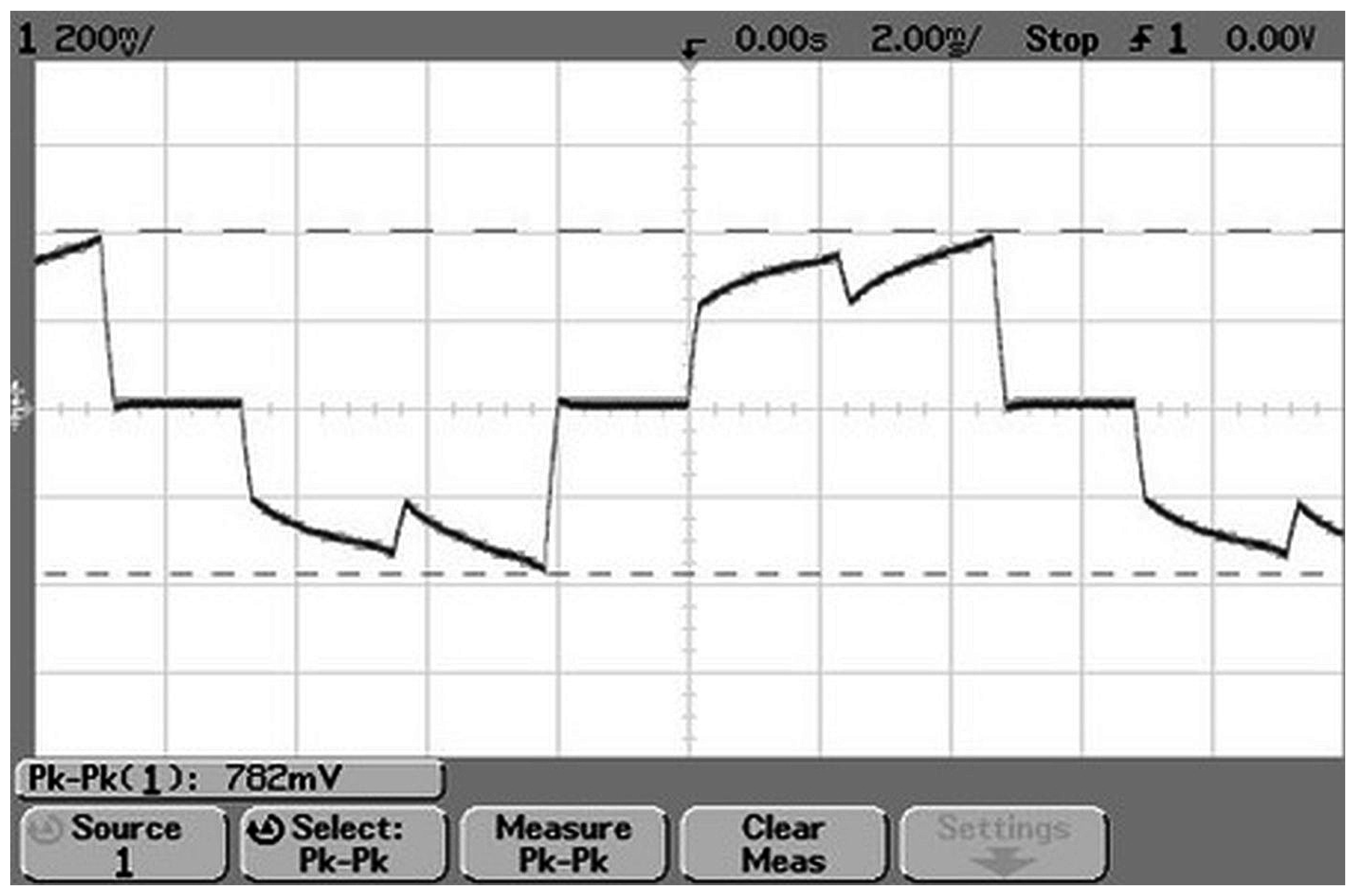
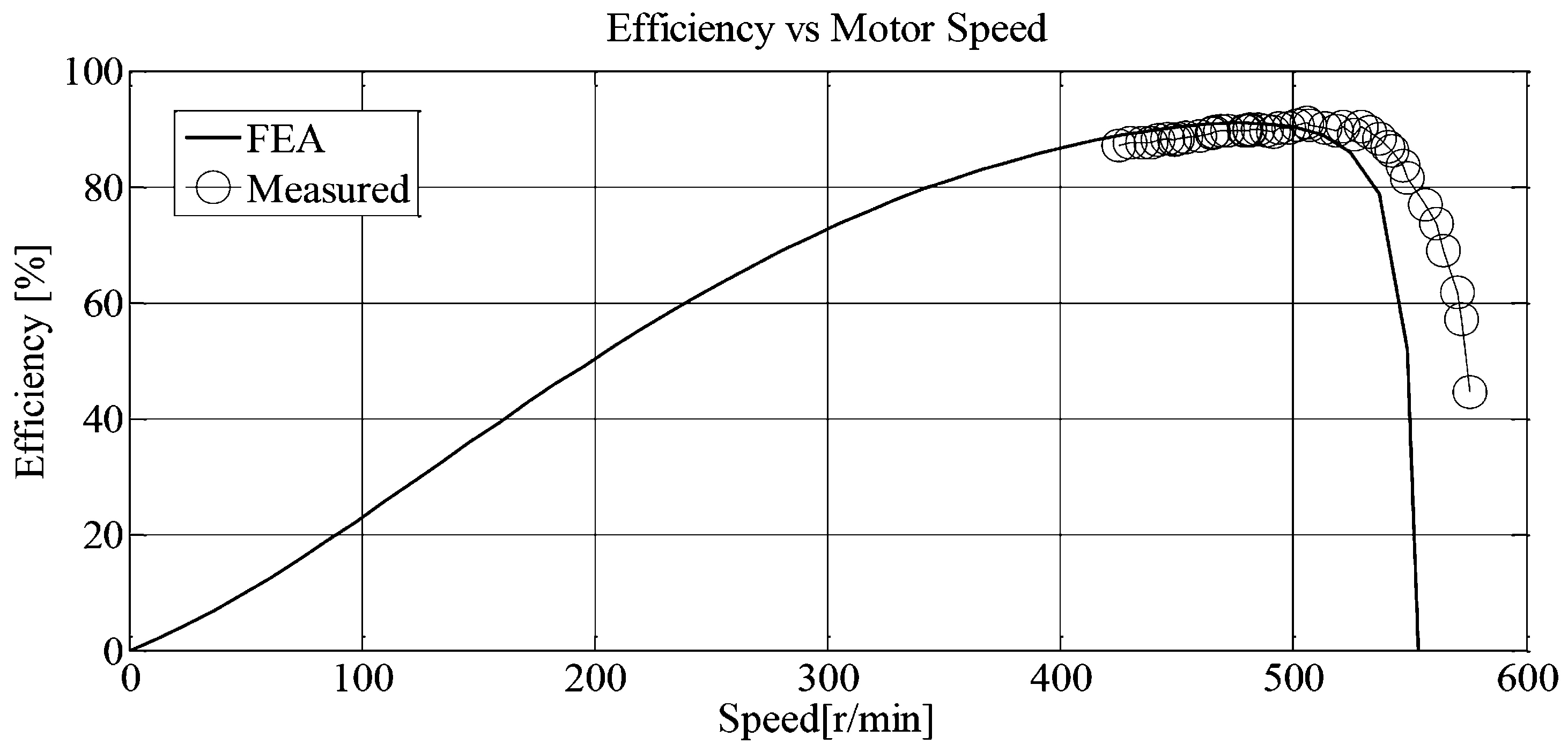
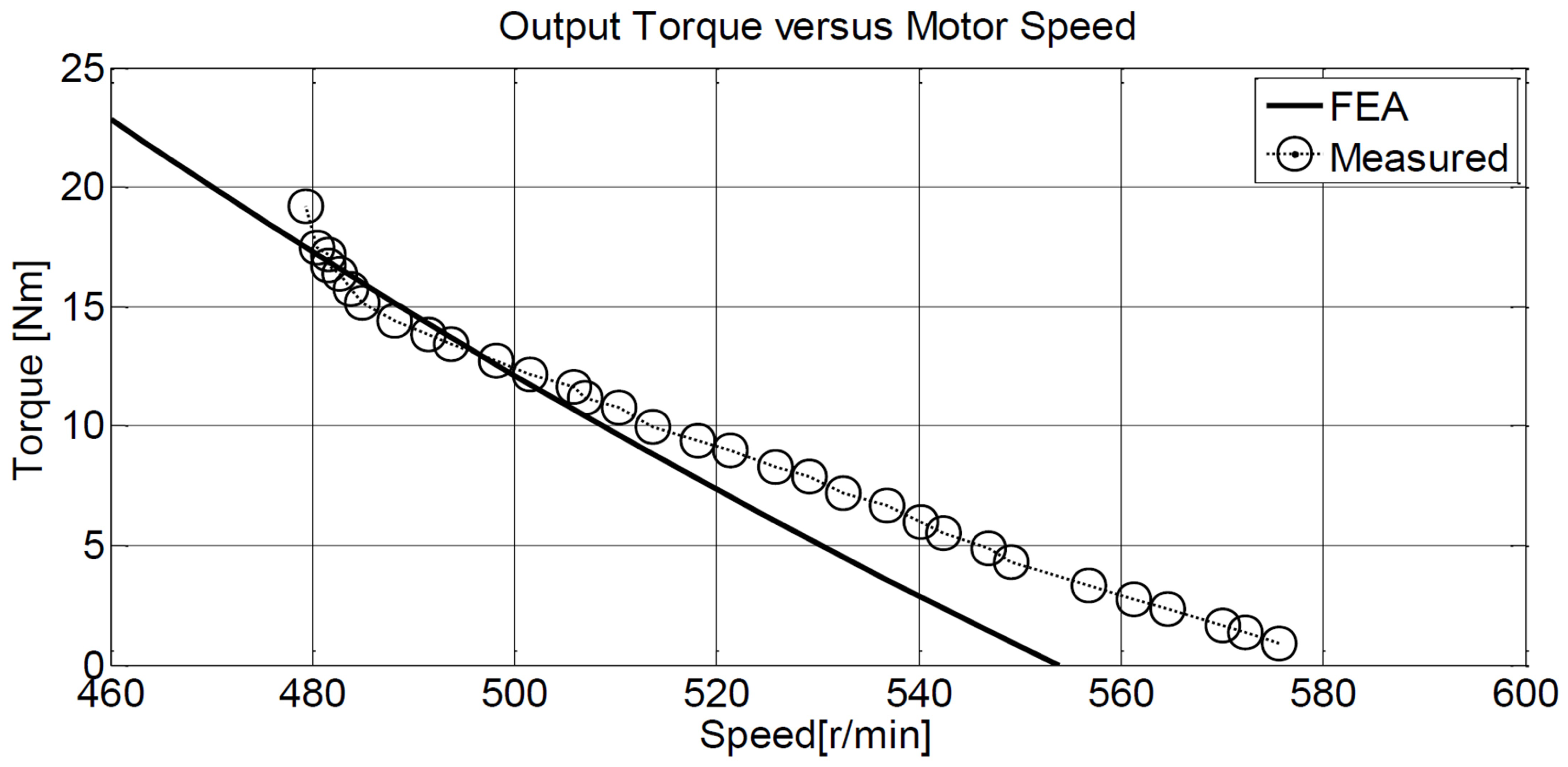
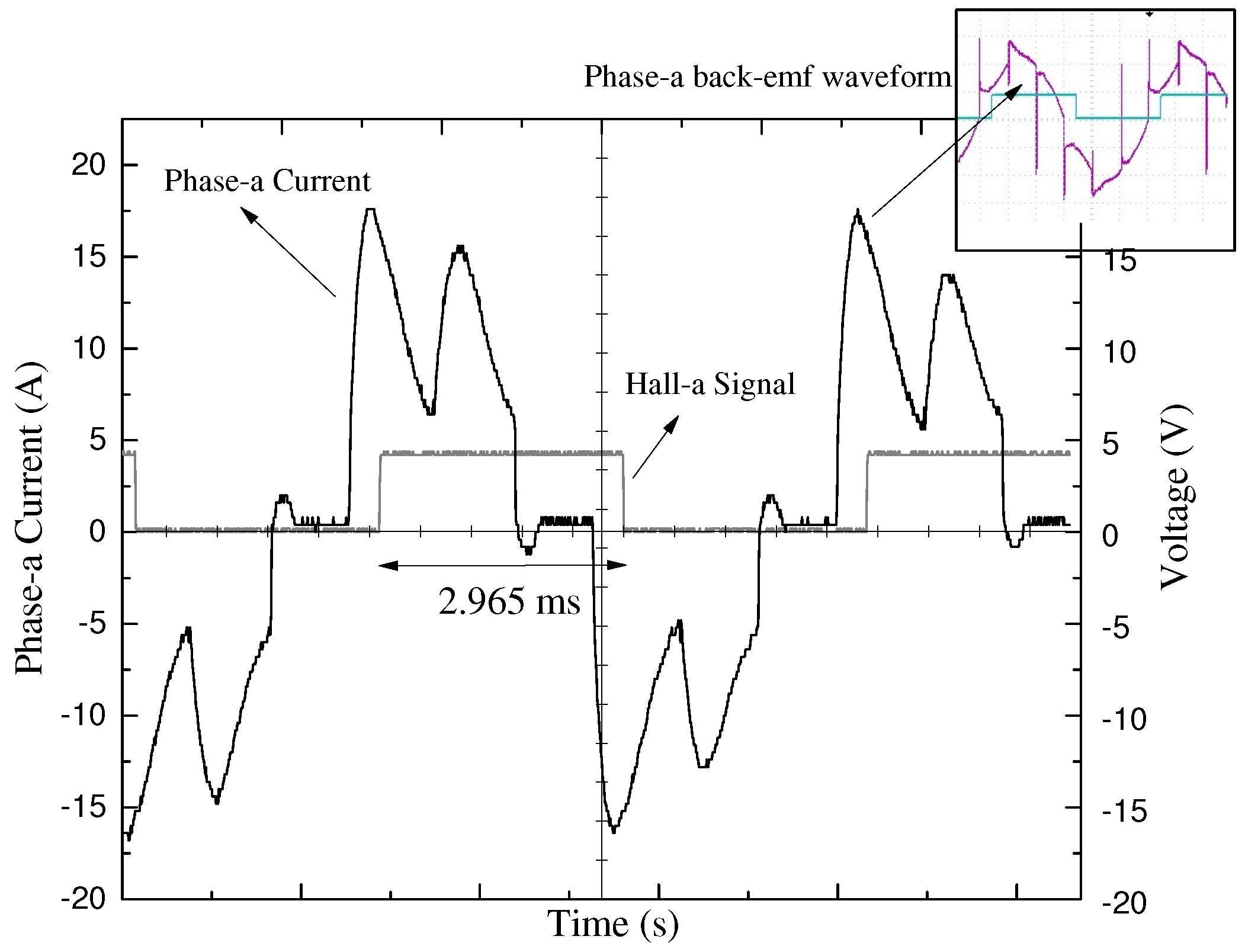
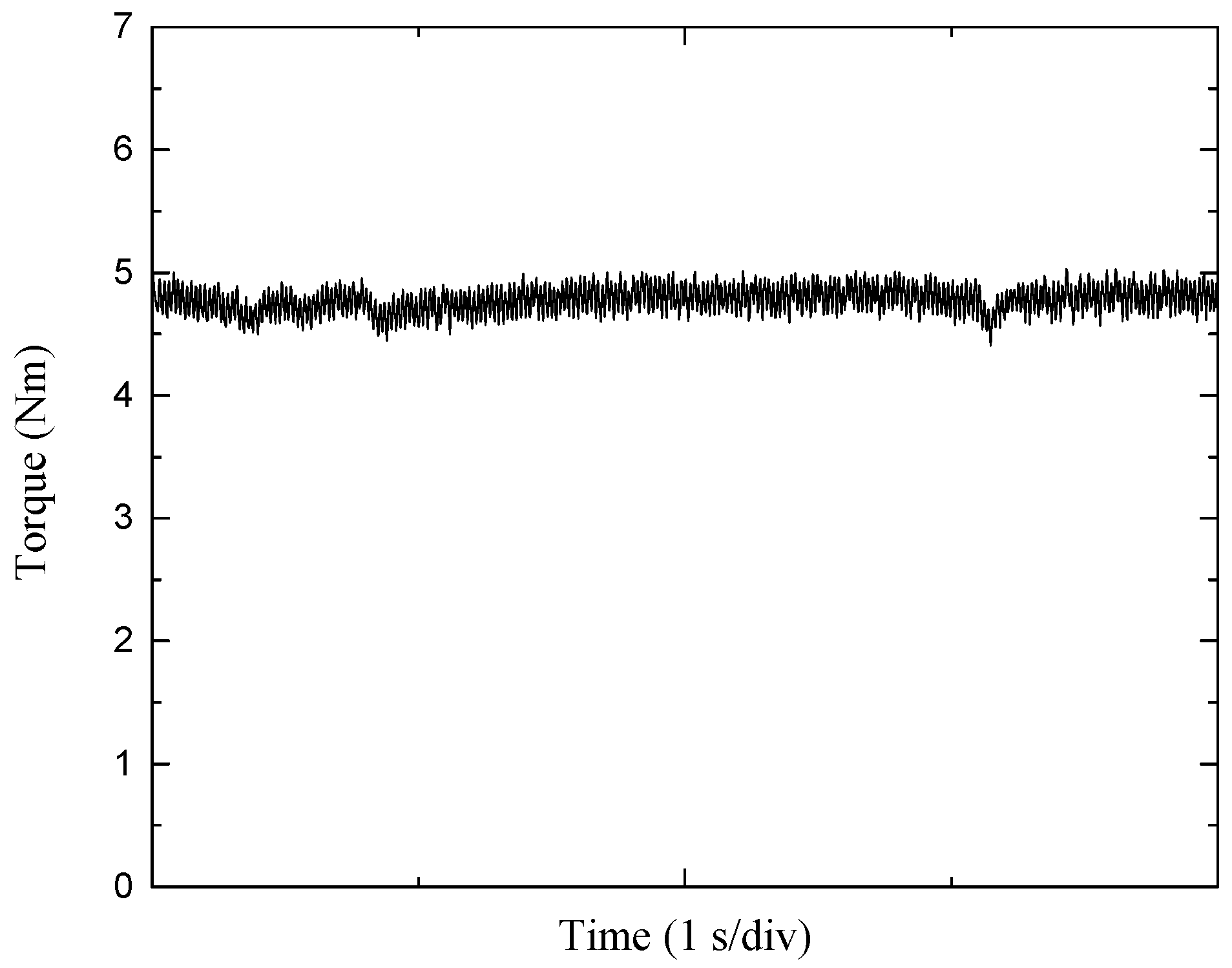
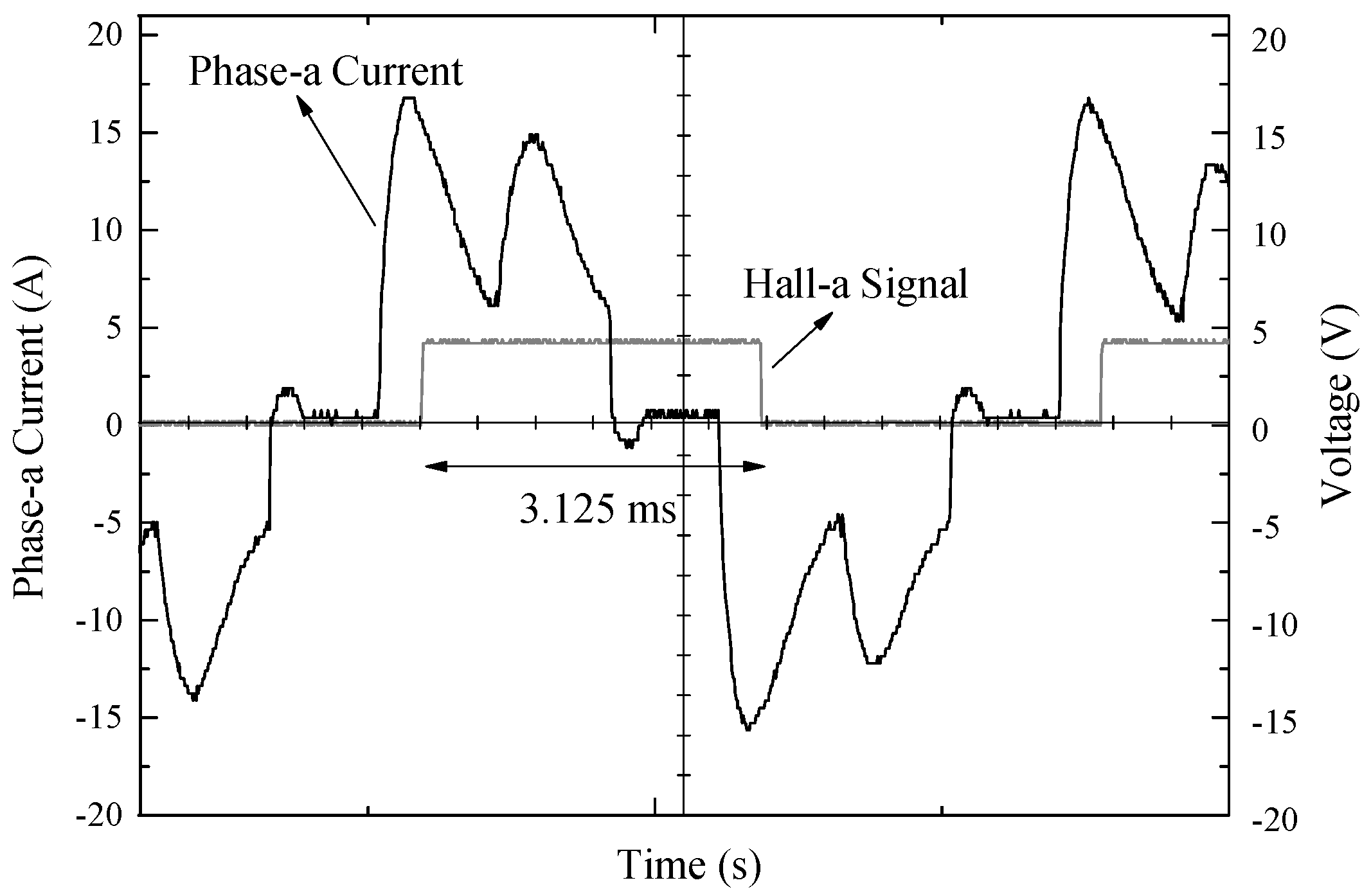
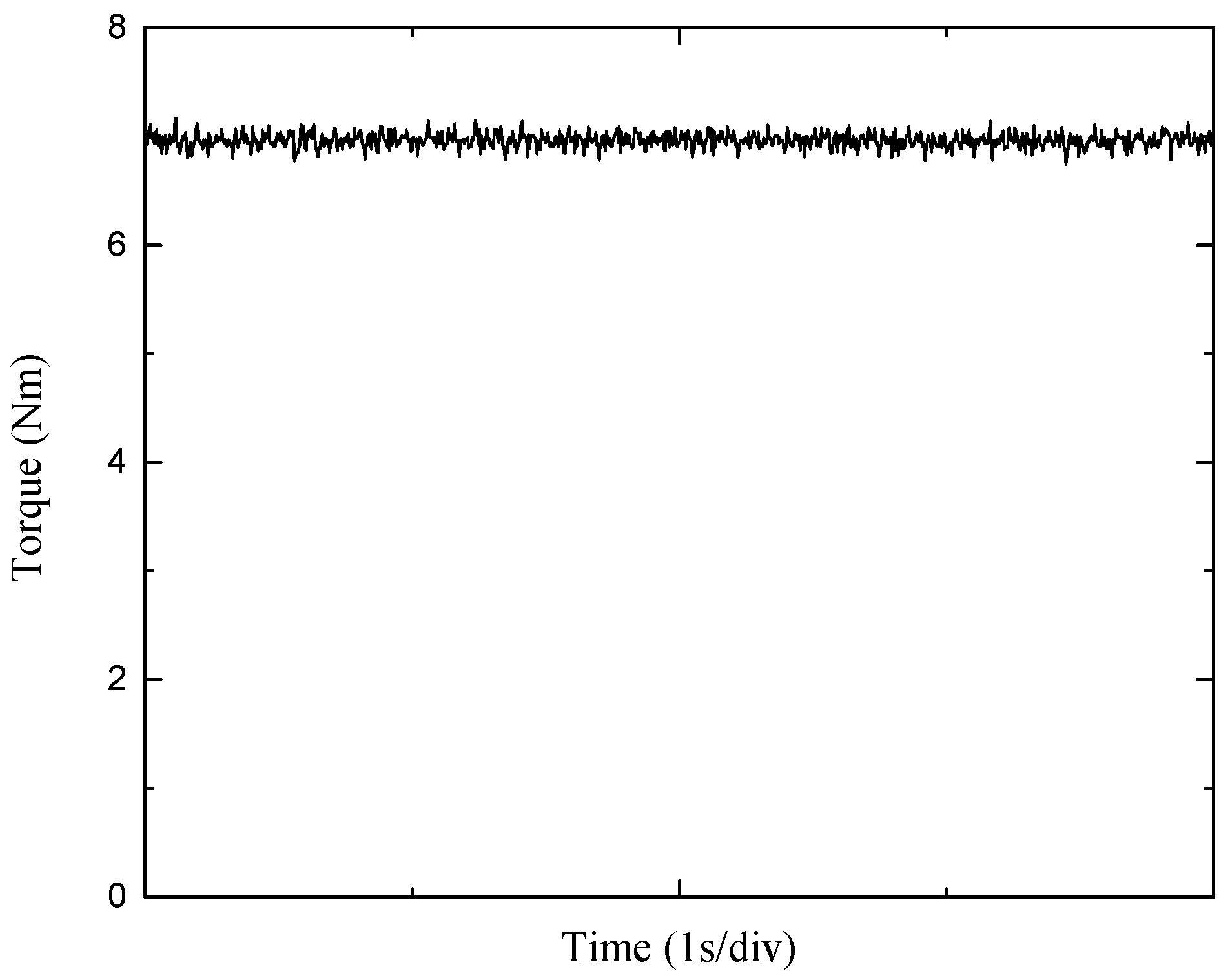
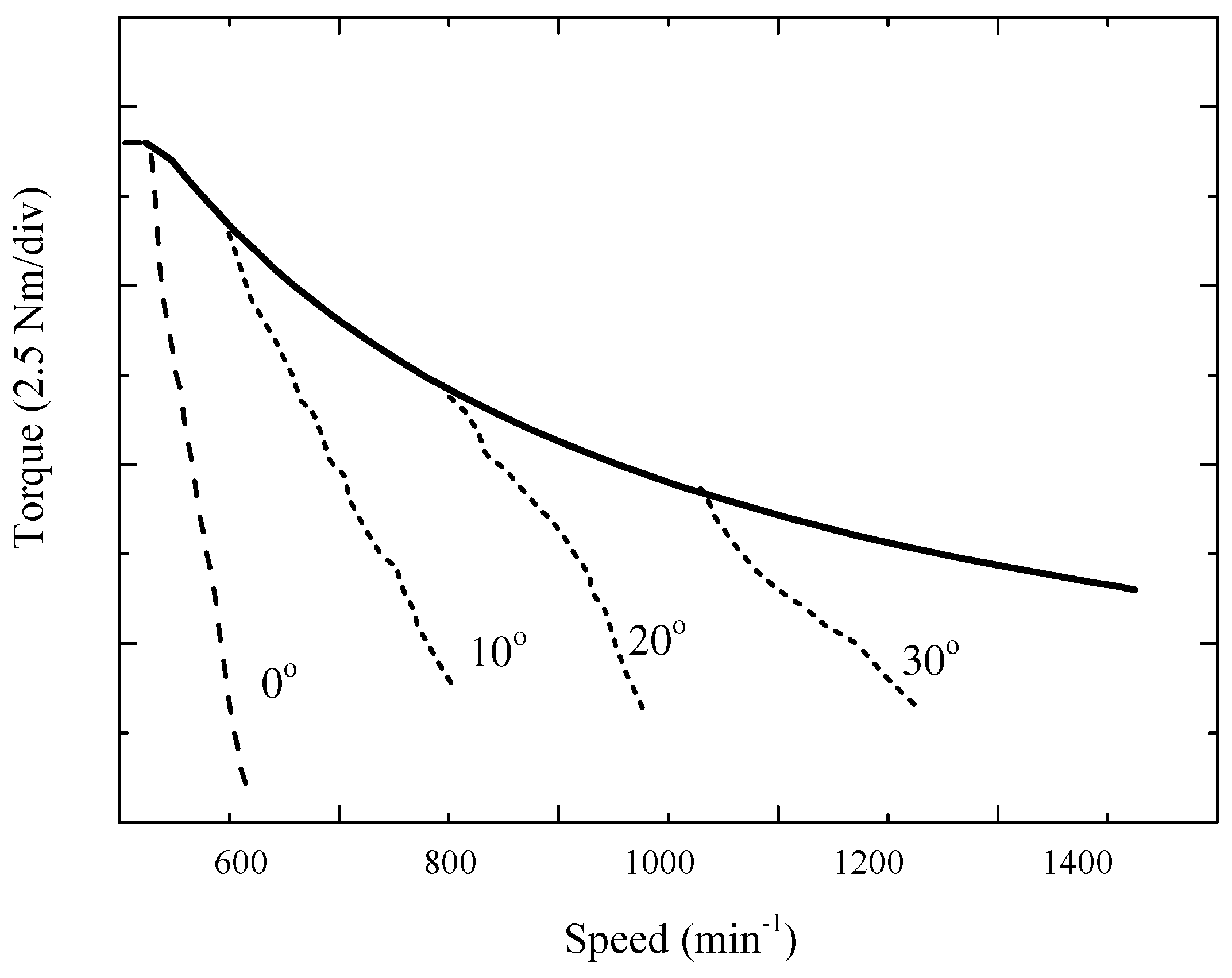
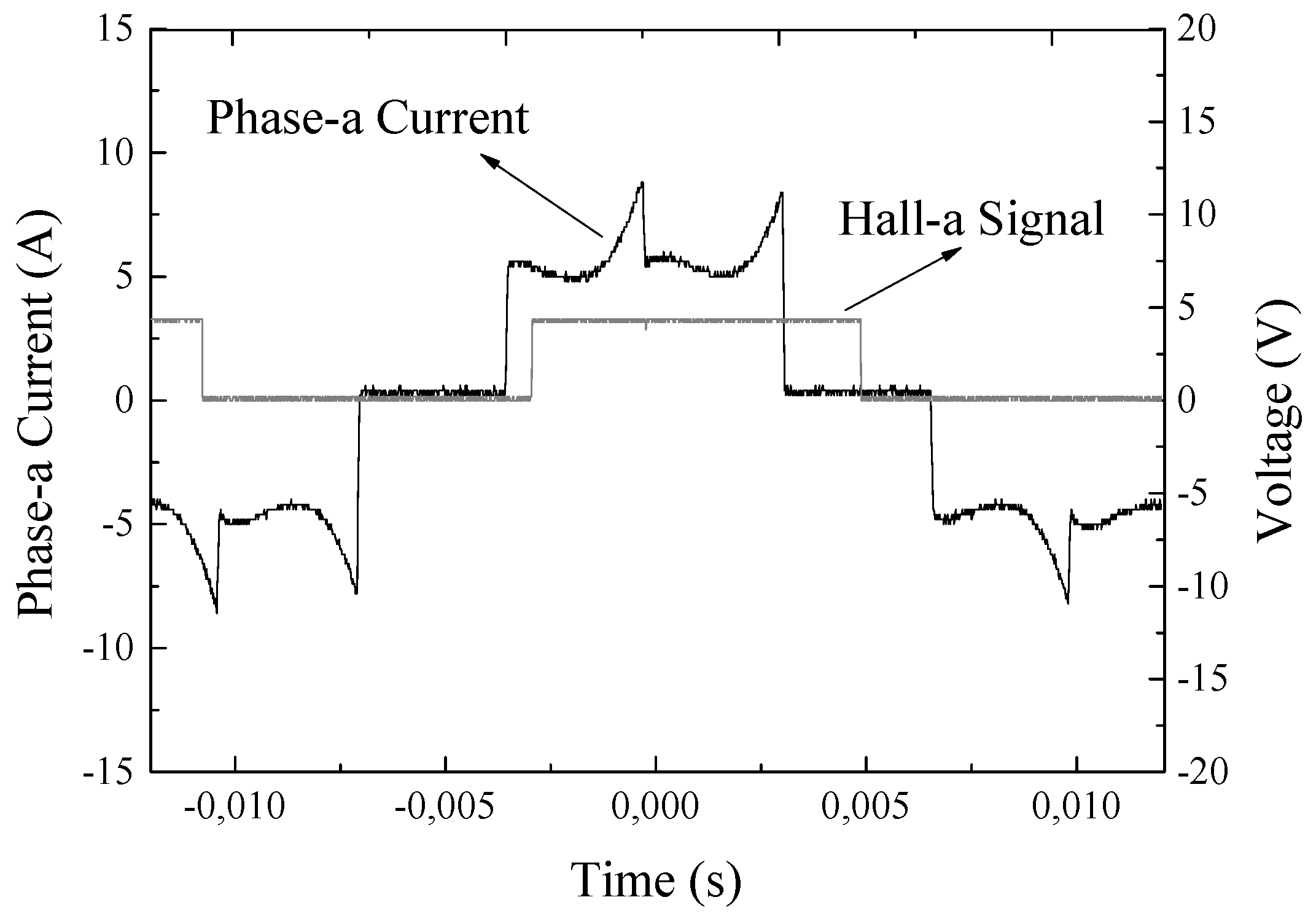
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Parameters | Value |
|---|---|
| Rated Power | 1 (kW) |
| Rotor Length | 40 (mm) |
| Rated Voltage | 24 (V) |
| Outer Diameter | 180.5 (mm) |
| Rated Speed | 500 (min) |
| Winding Factor of the Stator | 0.965 |
| Fill Factor of the Stator | 65.94 (%) |
| d-axis Inductance | 98.41 ( + ) (H) |
| Part of BLDC Motor | Material |
|---|---|
| Rotor Yoke | Stell 1010 |
| Magnets | NdFe35 |
| Stator | M36-29G |
| Coils | Copper |
| Inner and Outer Regions | Vacuum |
References
- He, C.; Wu, T. Permanent magnet brushless DC motor and mechanical structure design for the electric impact wrench system. Energies 2018, 11, 1360. [Google Scholar] [CrossRef]
- Jahns, T.M. Flux-weakening regime operation of an interior permanent-magnet synchronous motor drive. IEEE Trans. Ind. App. 1987, IA-23, 681–689. [Google Scholar] [CrossRef]
- Schiferl, R.; Lipo, T.A. Power Capability of Salient Pole Permanent Magnet Synchronous Motors in Variable Speed Drive Applications. In Proceedings of the Industry Applications Society Annual Meeting, Pittsburgh, PA, USA, 2–7 October 1988. [Google Scholar]
- Patil, N.A.; Lawler, J.S.; McKeever, J.W. Determining Constant Power Speed Ratio of the Induction Motor from Equivalent Circuit Parameters. In Proceedings of the IEEE SoutheastCon, Huntsville, AL, USA, 3–6 April 2008. [Google Scholar]
- Senol, S.; Ustun, O. Study on a BLDC Motor Having Higher Winding Inductance: A Key to Field Weakening. In Proceedings of the XXth International Conference on Electrical Machines (ICEM), Marseille, France, 2–5 September 2012. [Google Scholar]
- Chaithongsuk, S. Optimal design of permanent magnet motors to improve field-weakening performances in variable speed drives. IEEE Trans. Ind. Electron. 2012, 59, 2484–2494. [Google Scholar] [CrossRef]
- Kong, H.; Cui, G.; Zheng, A. Field-Weakening Speed Extension of BLDCM Based on Instantaneous Theory. In Proceedings of the International Conference on Electrical and Control Engineering, Wuhan, China, 25–27 June 2010. [Google Scholar]
- Jung, S.; Mi, C.C.; Nam, K. Torque control of IPMSM in the field-weakening region with improved DC-link voltage utilization. IEEE Trans. Ind. Electron. 2015, 62, 3380–3387. [Google Scholar] [CrossRef]
- Junlong, L.; Yongxiang, X.; Jibin, Z.; Baochao, W.; Qian, W.; Weiyan, L. Analysis and design of SPM machines with fractional slot concentrated windings for a given constant power region. IEEE Trans. Magn. 2015, 51, 1118–1125. [Google Scholar] [CrossRef]
- Hanselman, D.C. Brushless Permanent Magnet Motor Design, 2nd ed.; The Writers’ Collective: Columbus, OH, USA, 2003; ISBN 978-1932133639. [Google Scholar]
- El-Refaie, A.M.; Jahns, T.M.; Novotny, D. Analysis of surface permanent magnet machines with fractional-slot concentrated windings. IEEE Trans. Energy Convers. 2006, 21, 34–43. [Google Scholar] [CrossRef]
- Cros, J.; Viarouge, P. Synthesis of high performance PM motors with concentrated windings. IEEE Trans. Energy Convers. 2002, 17, 248–253. [Google Scholar] [CrossRef]
- Soong, W.L.; Miller, T. Field-weakening performance of brushless synchronous AC motor drives. IEE Proc. Electr. Power Appl. 1994, 141, 331–340. [Google Scholar] [CrossRef]
- Dorrell, D.G. A Review of the design issues and techniques for radial-flux brushless surface and internal rare-earth permanent-magnet motors. IEEE Trans. Ind. Electron. 2011, 58, 3741–3757. [Google Scholar] [CrossRef]
- Chan, C.C.; Jiang, J.Z.; Xia, W.; Chan, K.T. Novel wide range speed control of permanent magnet brushless motor drives. IEEE Trans. Pow. Electron. 1995, 10, 539–546. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, N.; Bolognani, S.; Chalmers, B.J. Salient-rotor PM synchronous motors for an extended flux-weakening operation range. IEEE Trans. Ind. Electron. 2000, 36, 1118–1125. [Google Scholar] [CrossRef]
- Miti, G.K.; Renfrew, A.C.; Chalmers, B.J. Field-weakening regime for brushless DC motors based on instantaneous power theory. IEE Proc. Electr. Power Appl. 2001, 148, 265–271. [Google Scholar] [CrossRef]
- Yang, Y.; Ting, Y. Improved angular displacement estimation based on hall-effect sensors for driving a brushless permanent-magnet motor. IEEE Trans. Ind. 2014, 61, 504–511. [Google Scholar] [CrossRef]
- Hemmati, S.; Lipo, T.A. Field Weakening of a Surface-Mounted Permanent Magnet Motor by Winding Switching. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012. [Google Scholar]
- El-Refaie, A.M.; Zhu, Z.Q.; Jahns, T.M.; Howe, D. Winding Inductances of Fractional Slot Surface-Mounted Permanent Magnet Brushless Machines. In Proceedings of the Industry Applications Society Annual Meeting IAS’08, Edmonton, AB, Canada, 5–9 October 2008. [Google Scholar]
- Soong, W.; Ertugrul, N. Field-weakening performance of interior permanent-magnet motors. IEEE Trans. Ind. Appl. 2002, 38, 1251–1258. [Google Scholar] [CrossRef] [Green Version]
- Li, G.J.; Zhu, Z.Q. Analytical modeling of modular and unequal tooth width surface-mounted permanent magnet machines. IEEE Trans. Magn. 2015, 51, 8107709. [Google Scholar] [CrossRef]
- Ishak, D.; Zhu, Z.; Howe, D. Permanent Magnet Brushless Machines With Unequal Tooth Widths and Similar Slot and Pole Numbers. In Proceedings of the 39th IAS Annual Meeting Industry Applications Conference, Seattle, WA, USA, 3–7 October 2004. [Google Scholar]
- Ishak, D.; Zhu, Z.; Howe, D. Comparison of PM brushless motors, having either all teeth or alternate teeth wound. IEEE Trans. Energy Convers. 2006, 21, 95–103. [Google Scholar] [CrossRef]
- Lawler, J.; Bailey, J.M.; McKeever, J.W.; Pinto, J. Extending the constant power speed range of the brushless DC motor through dual-mode inverter control. IEEE Trans. Power Electron. 2004, 19, 783–793. [Google Scholar] [CrossRef]
- Rong, L.; Weiguo, L. A Novel PM BLDC Motors Inverter Topology for Extending Constant Power Region. In Proceedings of the 33rd Annual Conference of the IEEE Industrial Electronics Society, Taipei, Taiwan, 5–8 November 2007. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ustun, O.; Kivanc, O.C.; Senol, S.; Fincan, B. On Field Weakening Performance of a Brushless Direct Current Motor with Higher Winding Inductance: Why Does Design Matter? Energies 2018, 11, 3119. https://doi.org/10.3390/en11113119
Ustun O, Kivanc OC, Senol S, Fincan B. On Field Weakening Performance of a Brushless Direct Current Motor with Higher Winding Inductance: Why Does Design Matter? Energies. 2018; 11(11):3119. https://doi.org/10.3390/en11113119
Chicago/Turabian StyleUstun, Ozgur, Omer Cihan Kivanc, Seray Senol, and Bekir Fincan. 2018. "On Field Weakening Performance of a Brushless Direct Current Motor with Higher Winding Inductance: Why Does Design Matter?" Energies 11, no. 11: 3119. https://doi.org/10.3390/en11113119






