Battery Storage-Based Frequency Containment Reserves in Large Wind Penetrated Scenarios: A Practical Approach to Sizing
Abstract
:1. Introduction
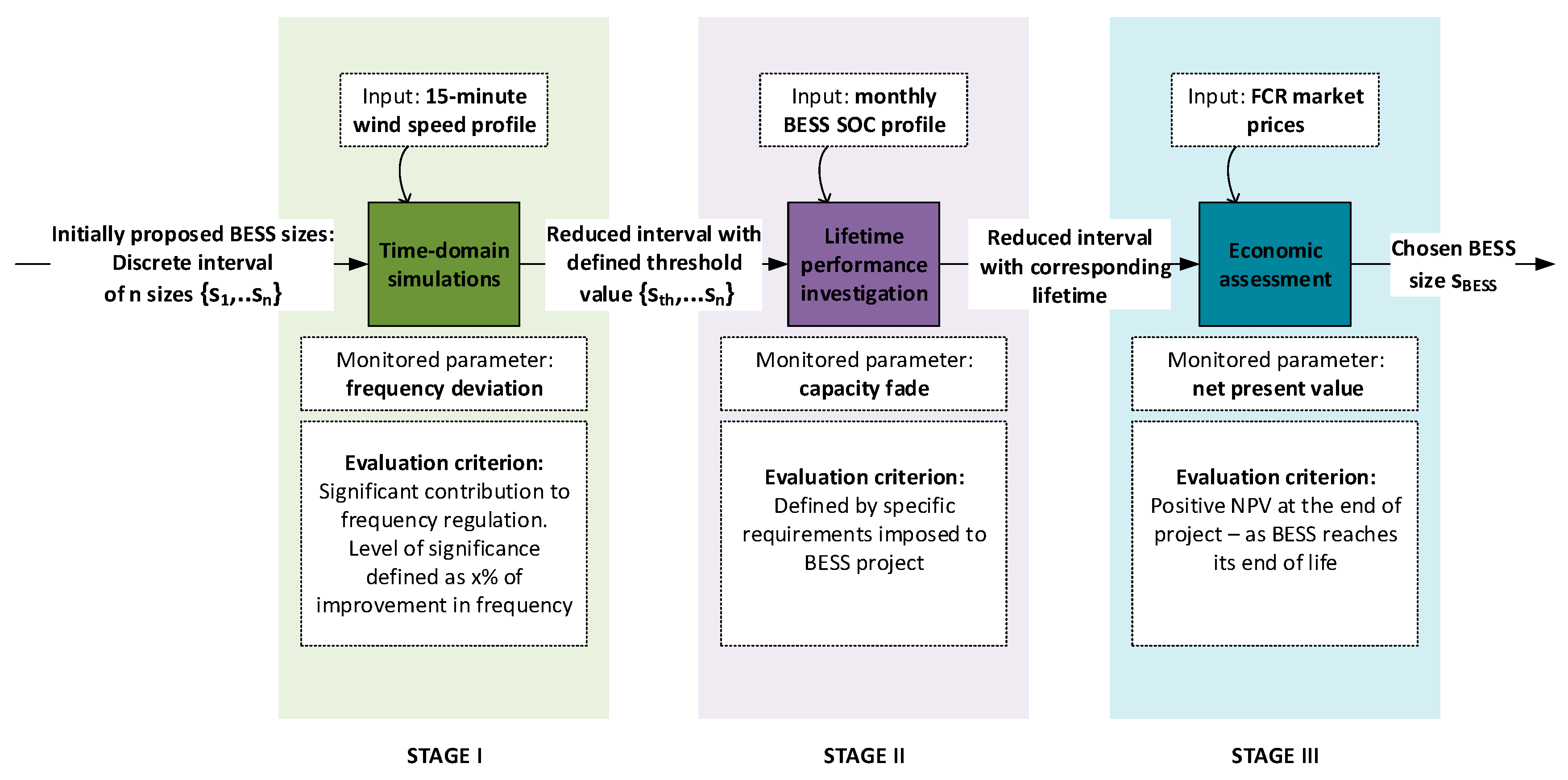
2. Sizing Methodology
3. System Modelling
3.1. Battery Energy Storage System
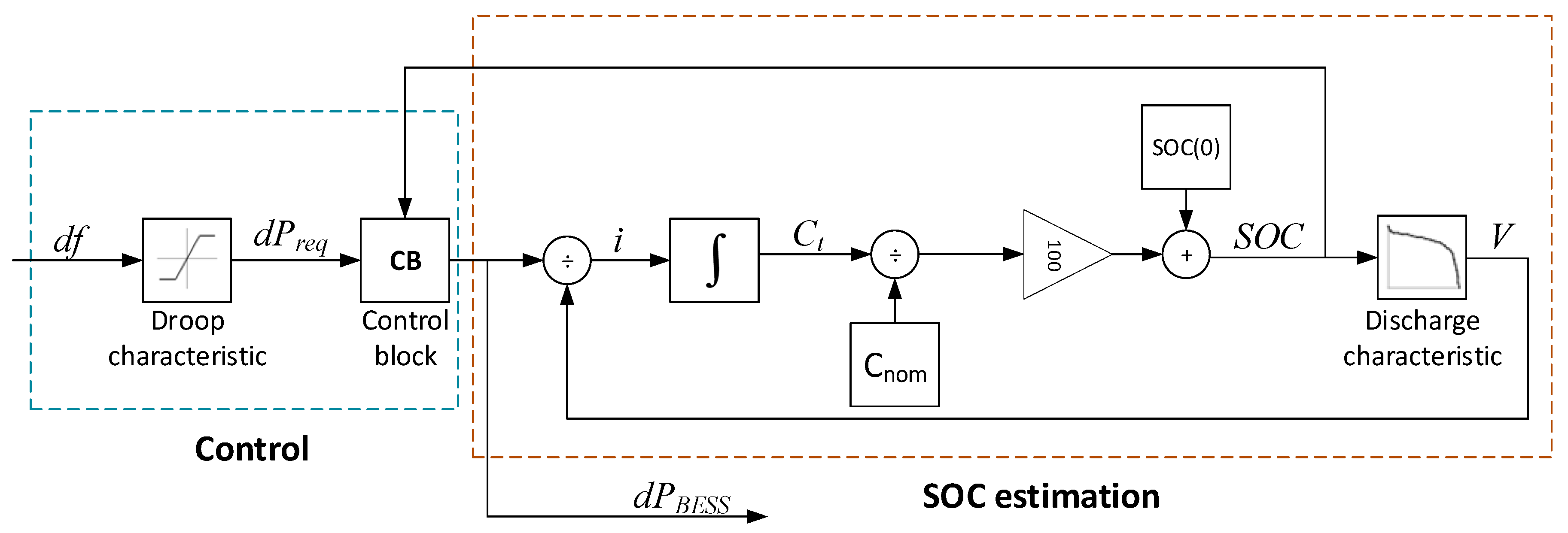
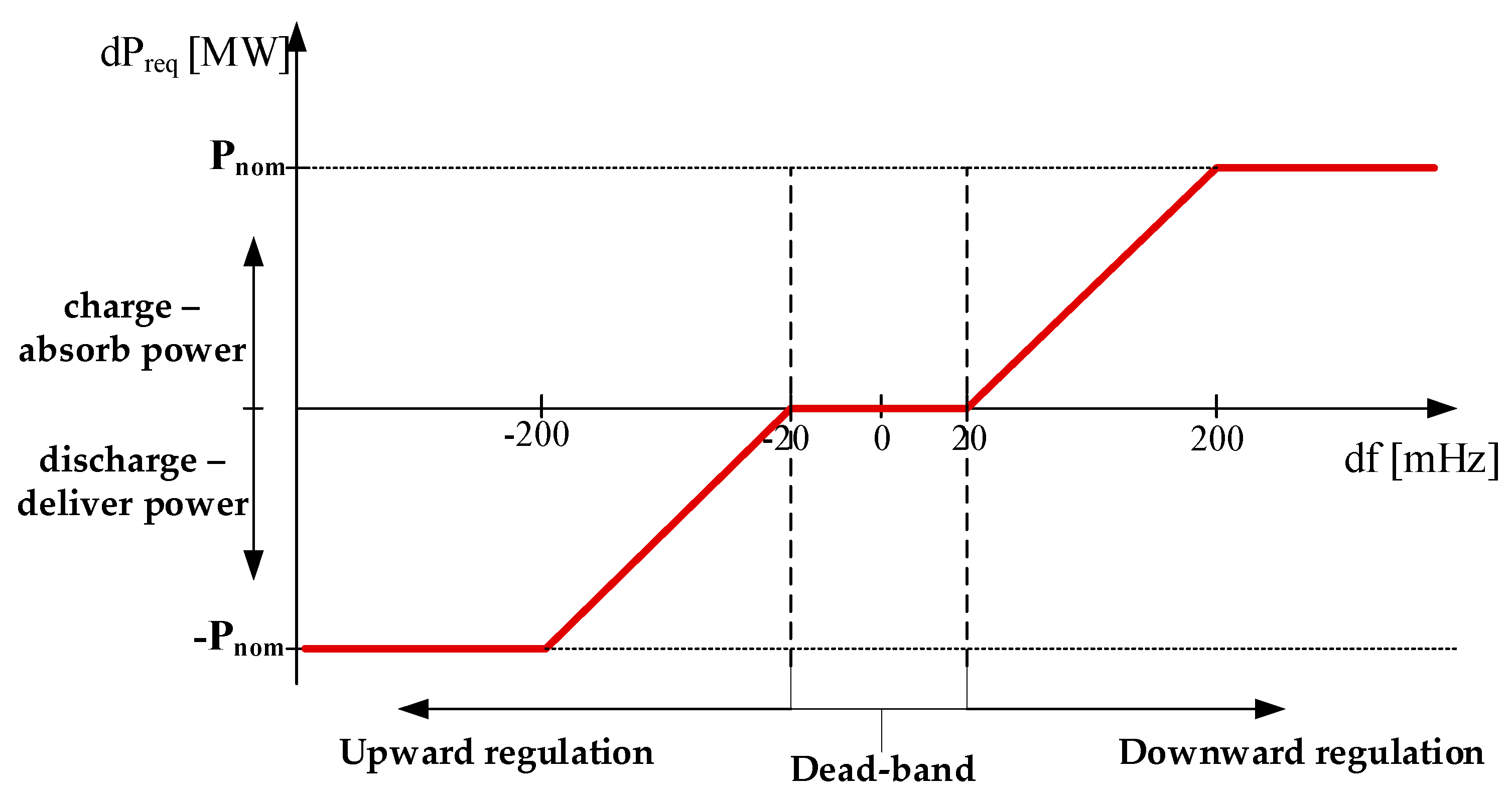
3.1.1. Performance Model
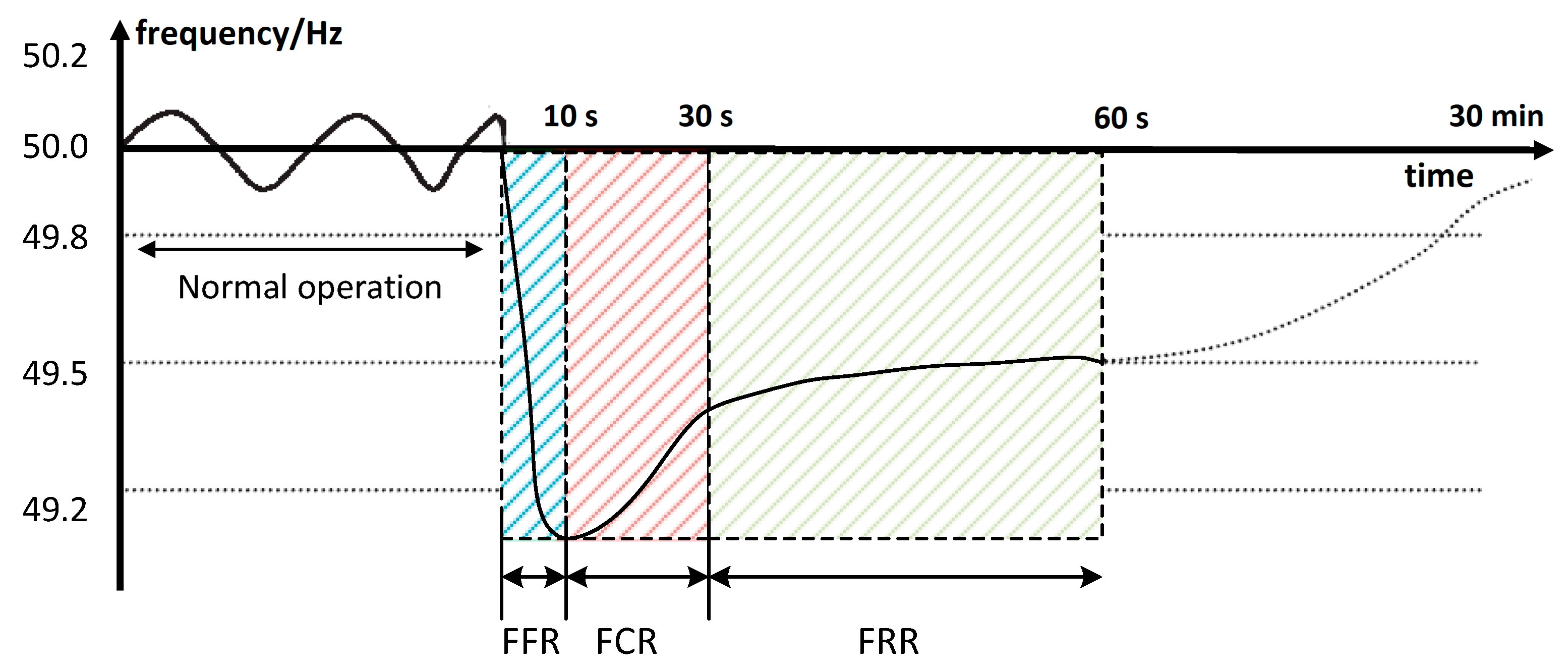
- half of the reserves need to be provided in the first 15 s after the disturbance and full activation is expected within 30 s
- participating units need to have the ability to provide the reserves for 15 min at nominal power
- participating units are entitled to 15 min re-establishing period after 15 min of reserve provision
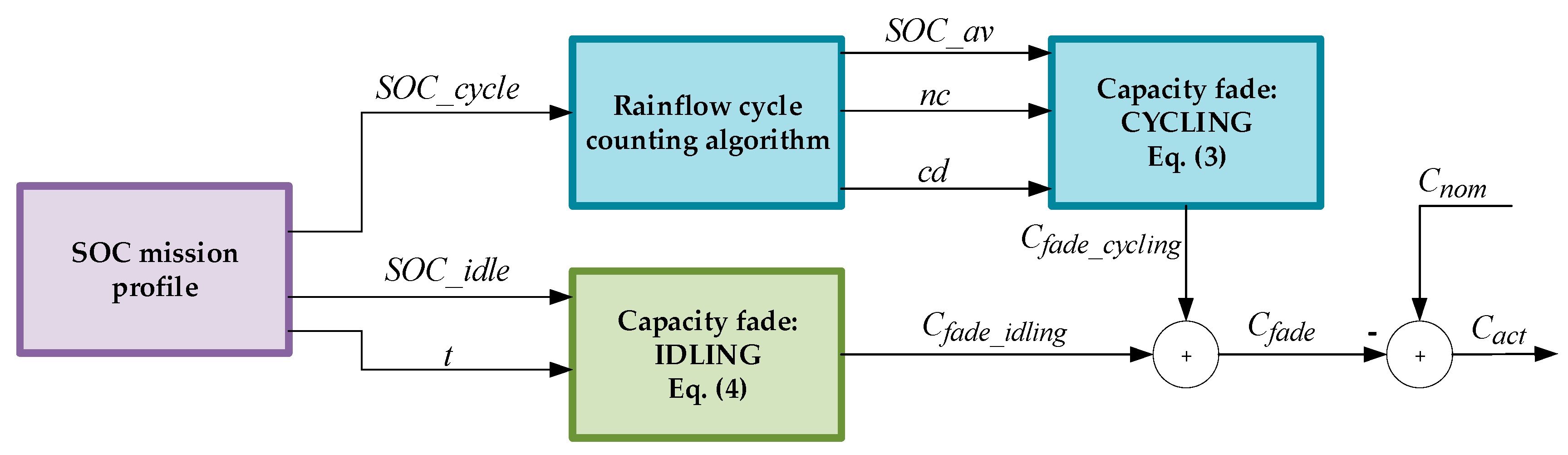
3.1.2. Lifetime Model
3.1.3. Economic Model
3.2. Benchmark Power System Model
4. Assessment Study
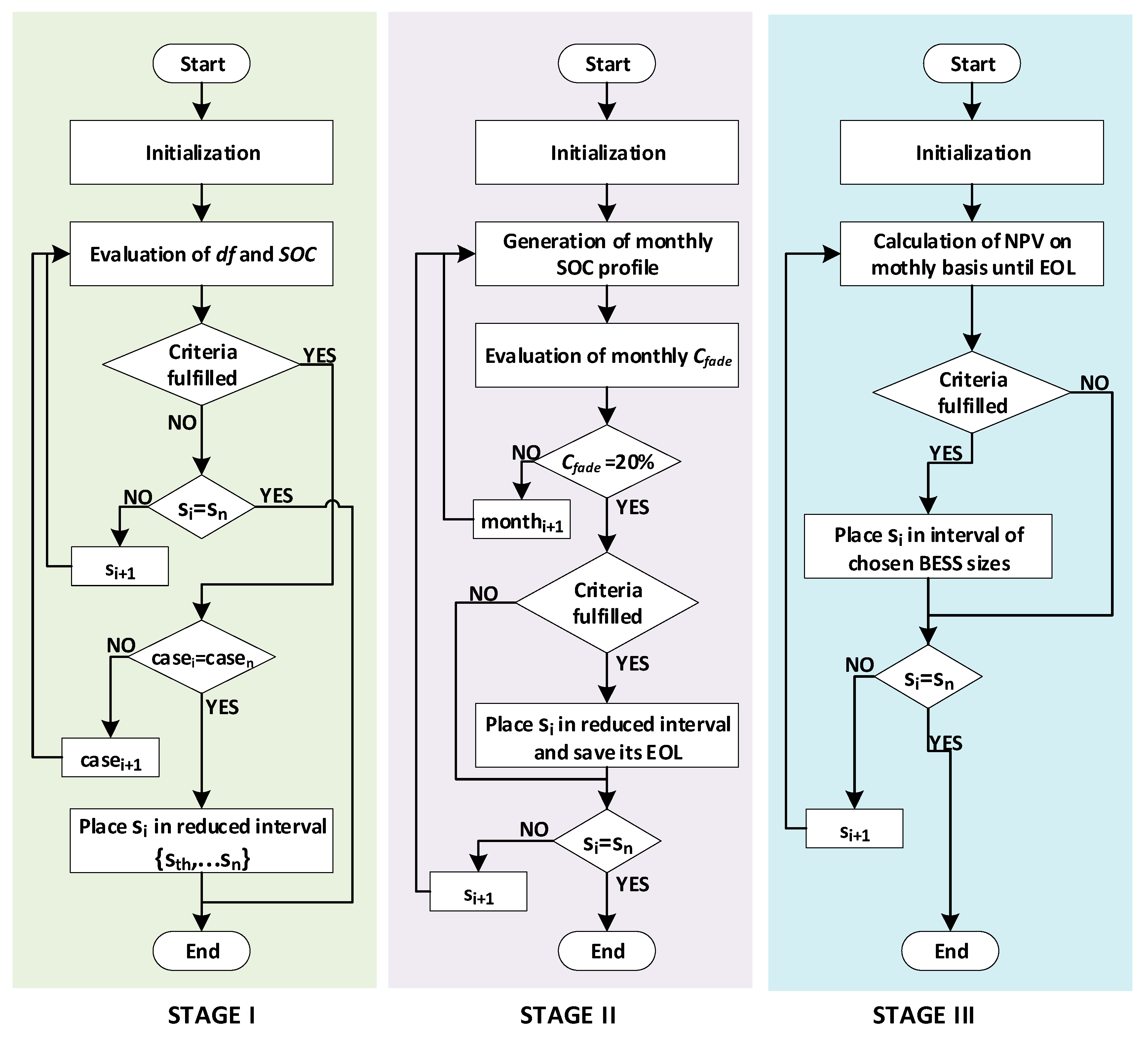
4.1. Stage I—Time-Domain Assesment
4.1.1. Initialization
4.1.2. Results
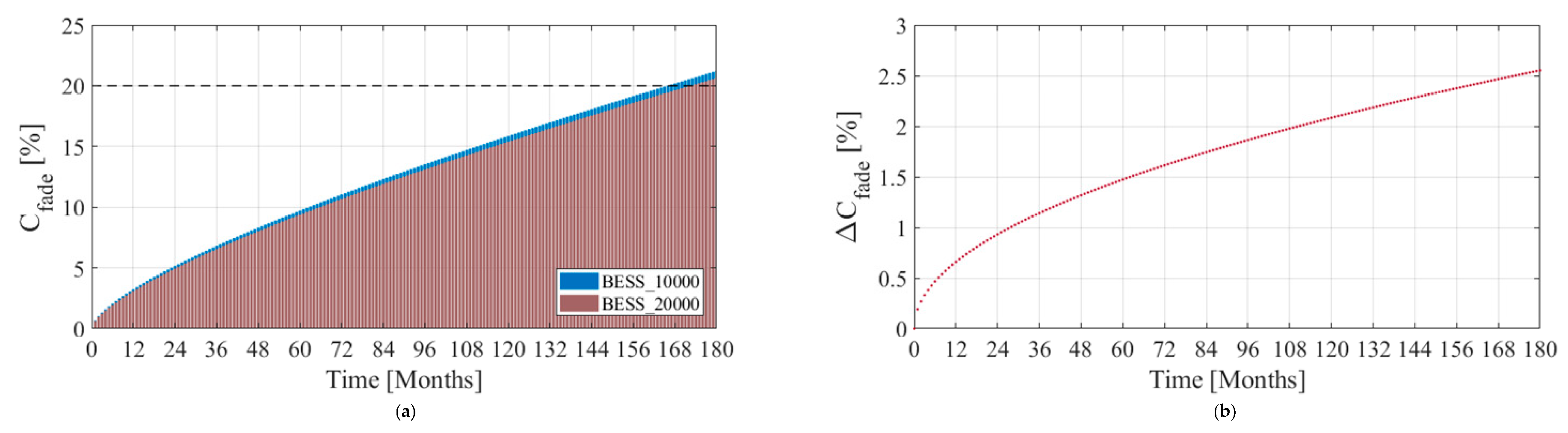
4.2. Stage II—Lifetime Performance Assessment
4.2.1. Initialization
4.2.2. Results
4.3. Stage III—Economic Assessment
4.3.1. Initialization
4.3.2. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Component | Parameter | Value |
|---|---|---|
| Gen 01: generator—steam turbine set | Nominal active power output | 200.8 MW |
| Droop value | 4% | |
| Gen 02: generator—gas turbine set | Nominal active power output | 40 MW |
| Droop value | 4% | |
| WT | Installed capacity | 96 MW |
| Load | Overall active power demand | 320 MW |
| Load damping constant of each load | 1% |
References
- REN21 Renewables. Global Status Report. 2018. Available online: http://www.ren21.net/wp-content/uploads/2018/06/17-8652_GSR2018_FullReport_web_final_.pdf (accessed on 7 August 2018).
- European Commission COMMISSION REGULATION (EU) 2017/1485—of 2 August 2017—Establishing a Guideline on Electricity Transmission System Operation. Available online: http://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32017R1485&from=EN (accessed on 7 August 2018).
- Swierczynski, M.; Stroe, D.; Teodorescu, R.; Stan, A.I. Primary Frequency Regulation with Li-ion Battery Energy Storage System: A Case Study for Denmark. In Proceedings of the IEEE ECCE Asia Downunder, Melbourne, Australia, 3–6 June 2013; pp. 487–492. [Google Scholar]
- Kjar, P.C.; Larke, R. Experience with primary reserve supplied from energy storage system. In Proceedings of the 17th European Conference on Power Electronics and Applications, EPE-ECCE Europe, Geneva, Switzerland, 8–10 September 2015; pp. 1–6. [Google Scholar]
- World Energy Council World Energy Resources E-Storage 2016. Available online: https://www.worldenergy.org/wp-content/uploads/2017/03/WEResources_E-storage_2016.pdf (accessed on 20 May 2018).
- Stroe, D.; Swierczynski, M.; Stan, A.; Teodorescu, R. Accelerated Lifetime Testing Methodology for Lifetime Estimation of Lithium-ion Batteries used in Augmented Wind Power Plants. IEEE Trans. Ind. Appl. 2014, 50, 690–698. [Google Scholar] [CrossRef]
- Liu, X.; Wang, P.; Loh, P.C. A hybrid AC/DC microgrid and its coordination control. IEEE Trans. Smart Grid 2011, 2, 278–286. [Google Scholar]
- Xu, L.; Chen, D. Control and operation of a DC microgrid with variable generation and energy storage. IEEE Trans. Power Deliv. 2011, 26, 2513–2522. [Google Scholar] [CrossRef]
- Shi, W.; Xie, X.; Chu, C.C.; Gadh, R. Distributed Optimal Energy Management in Microgrids. IEEE Trans. Smart Grid 2015, 6, 1137–1146. [Google Scholar] [CrossRef]
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of energy storage for microgrids. IEEE Trans. Smart Grid 2012, 3, 142–151. [Google Scholar] [CrossRef]
- Chaouachi, A.; Kamel, R.M.; Andoulsi, R.; Nagasaka, K. Multiobjective Intelligent Energy Management for a Microgrid—Aymen Chaouachi—Academia. IEEE Trans. Ind. Electron. 2013, 60, 1688–1699. [Google Scholar] [CrossRef]
- Liu, H.; Hu, Z.; Song, Y.; Wang, J.; Xie, X. Vehicle-to-Grid Control for Supplementary Frequency Regulation Considering Charging Demands. IEEE Trans. Power Syst. 2015, 30, 3110–3119. [Google Scholar] [CrossRef]
- Han, S.; Soo, H.H.; Sezaki, K. Design of an optimal aggregator for vehicle-to-grid regulation service. In Proceedings of the 2010 Innovative Smart Grid Technologies (ISGT), Gothenburg, Sweden, 19–21 January 2010. [Google Scholar]
- He, Y.; Venkatesh, B.; Guan, L. Optimal scheduling for charging and discharging of electric vehicles. IEEE Trans. Smart Grid 2012, 3, 1095–1105. [Google Scholar] [CrossRef]
- Yilmaz, M.; Krein, P.T. Review of the impact of vehicle-to-grid technologies on distribution systems and utility interfaces. IEEE Trans. Power Electron. 2013, 28, 5673–5689. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.; Huang, J.; Tan, S.; Wang, M.; Xu, T.; Cheng, X. Modeling and control strategy of battery energy storage system for primary frequency regulation. In Proceedings of the International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 543–549. [Google Scholar]
- Knap, V.; Chaudhary, S.K.; Stroe, D.; Swierczynski, M.; Craciun, B.; Teodorescu, R. Sizing of an Energy Storage System for Grid Inertial Response and Primary Frequency Reserve. Trans. Power Syst. 2016, 31, 3447–3456. [Google Scholar] [CrossRef]
- Benato, R.; Dambone Sessa, S.; Musio, M.; Palone, F.; Polito, R. Italian Experience on Electrical Storage Ageing for Primary Frequency Regulation. Energies 2018, 11, 2087. [Google Scholar] [CrossRef]
- Stroe, D.; Swierczynski, M.; Stroe, A.; Member, S.; Laerke, R.; Kjaer, P.C.; Member, S.; Teodorescu, R. Degradation Behavior of Lithium-Ion Batteries Based on Lifetime Models and Field Measured Frequency Regulation Mission Profile. IEEE Trans. Ind. Appl. 2016, 52, 5009–5018. [Google Scholar] [CrossRef]
- Stroe, D.I.; Knap, V.; Swierczynski, M.; Stroe, A.I.; Teodorescu, R. Operation of a grid-connected lithium-ion battery energy storage system for primary frequency regulation: A battery lifetime perspective. IEEE Trans. Ind. Appl. 2017, 53, 430–438. [Google Scholar] [CrossRef]
- Gatta, F.; Geri, A.; Lamedica, R.; Lauria, S.; Maccioni, M.; Palone, F.; Rebolini, M.; Ruvio, A. Application of a LiFePO4 Battery Energy Storage System to Primary Frequency Control: Simulations and Experimental Results. Energies 2016, 9, 887. [Google Scholar] [CrossRef]
- Jozef, M.; Thorbergsson, E.; Knap, V.; Swierczynski, M.; Stroe, D.; Teodorescu, R. Primary Frequency Regulation with Li-Ion Battery Based Energy Storage System—Evaluation and Comparison of Different Control Strategies. In Proceedings of the Intelec 2013, 35th International Telecommunications Energy Conference, Hamburg, Germany, 13–17 October 2013; pp. 1–6. [Google Scholar]
- Mercier, P.; Cherkaoui, R.; Member, S.; Oudalov, A. Optimizing a Battery Energy Storage System for Frequency Control Application in an Isolated Power System. IEEE Trans. Power Syst. 2009, 24, 1469–1477. [Google Scholar] [CrossRef]
- Brekken, T.K.A.; Yokochi, A.; Von Jouanne, A.; Yen, Z.Z.; Hapke, H.M.; Halamay, D.A.; Member, S. Optimal Energy Storage Sizing and Control for Wind Power Applications. Trans. Power Syst. 2011, 2, 69–77. [Google Scholar] [CrossRef]
- Oudalov, A.; Chartouni, D.; Ohler, C. Optimizing a Battery Energy Storage System for Primary Frequency Control. IEEE Trans. Power Syst. 2007, 22, 1259–1266. [Google Scholar] [CrossRef]
- Bignucolo, F.; Caldon, R.; Coppo, M.; Pasut, F.; Pettinà, M. Integration of lithium-ion battery storage systems in hydroelectric plants for supplying primary control reserve. Energies 2017, 10, 98. [Google Scholar] [CrossRef]
- Bignucolo, F.; Caldon, R.; Pettinà, M.; Pasut, F. Renewables contributing to Primary Control Reserve: The role of Battery Energy Storage Systems. In Proceedings of the 17th IEEE International Conference on Environment and Electrical Engineering and 2017 1st IEEE Industrial and Commercial Power Systems Europe, EEEIC/I and CPS Europe, Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Pillai, J.R.; Bak-Jensen, B. Integration of vehicle-to-grid in the Western Danish power system. IEEE Trans. Sustain. Energy 2011, 2, 12–19. [Google Scholar] [CrossRef]
- Technical Regulation 3.3.1 for Battery Plants. Available online: https://en.energinet.dk/Electricity/Rules-and-Regulations/Regulations-for-grid-connection (accessed on 20 April 2018).
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- KEMA Inc. Battery Energy Storage Study for the 2017. Available online: http://www.pacificorp.com/content/dam/pacificorp/doc/Energy_Sources/Integrated_Resource_Plan/2017_IRP/10018304_R-01-D_PacifiCorp_Battery_Energy_Storage_Study.pdf (accessed on 20 May 2018).
- Illinois Center for a Smarter Electric Grid (ICSEG) IEEE 14-bus System. Available online: http://icseg.iti.illinois.edu/ieee-14-bus-system/ (accessed on 20 April 2018).
- Altin, M.; Teodorescu, R.; Jensen, B.B.; Annakkage, U.D.; Iov, F.; Kjaer, P.C. Methodology for assessment of inertial response from wind power plants. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Energinet Data Service. Available online: https://www.energidataservice.dk/en/ (accessed on 1 October 2018).
- Danish Technological Institute BESS project—Smart Grid Ready Battery Energy Storage System for Future Grid. Available online: https://energiforskning.dk/sites/energiteknologi.dk/files/slutrapporter/bess_final_report_forskel_10731.pdf (accessed on 16 May 2018).
- NordPool Historical Market Data. Available online: https://www.nordpoolgroup.com/historical-market-data/ (accessed on 20 May 2018).

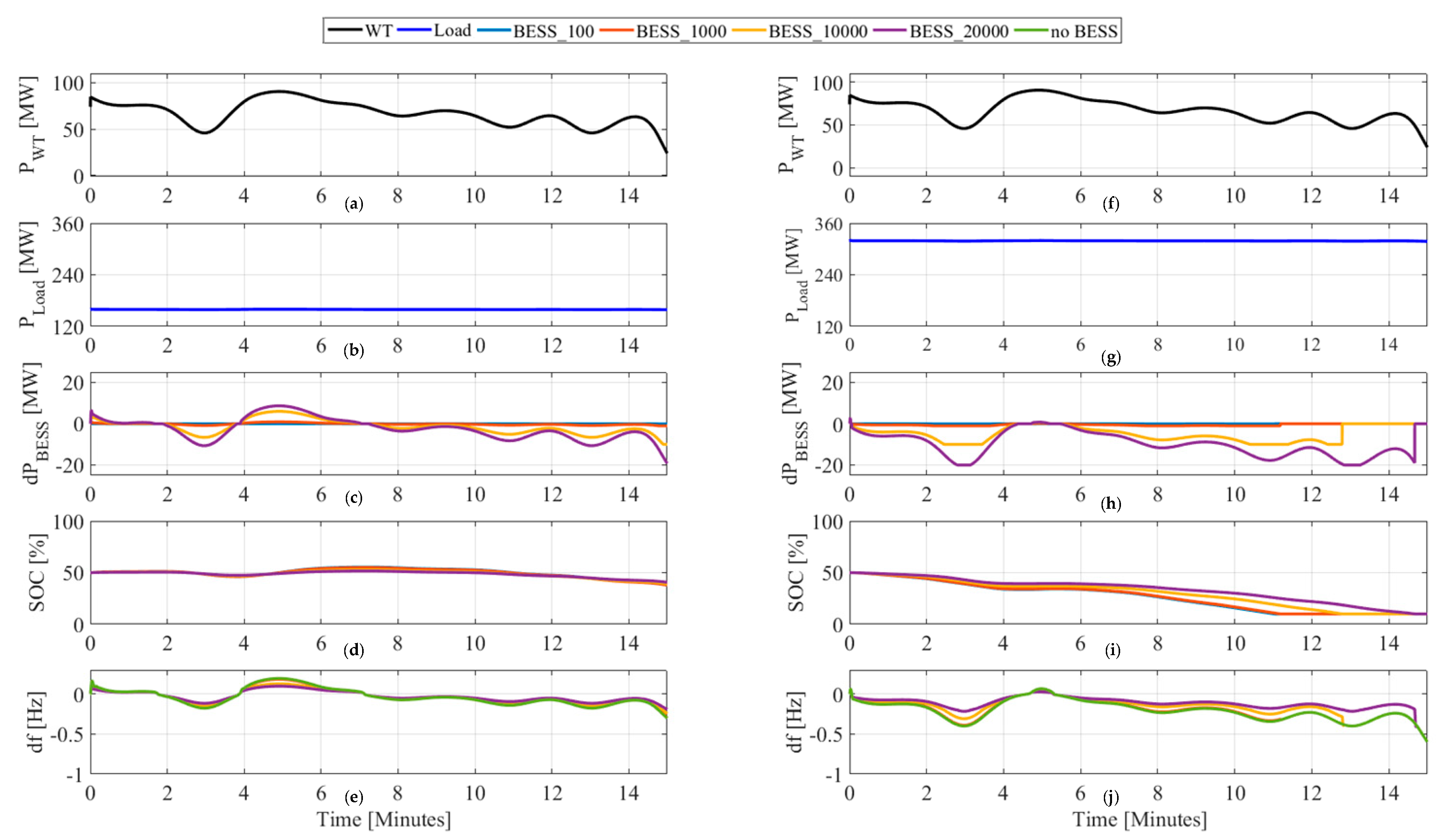
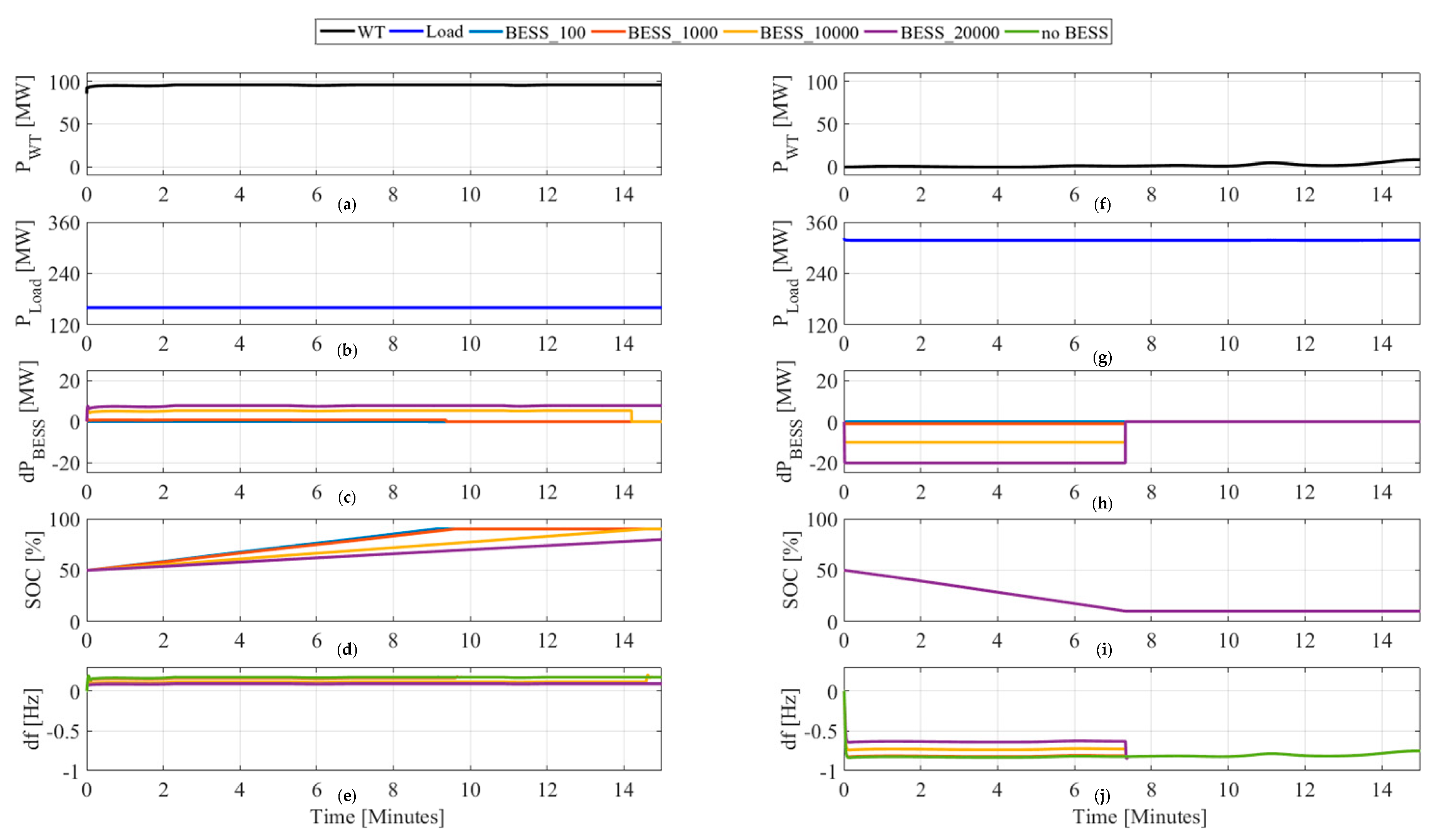


| Scenario | Wind Power Generation as Percentage of 96 MW Installed Capacity | Active Power Required by the Load | |
|---|---|---|---|
| First | Case I | Fluctuating Maximum: 95% Minimum: 25% | Low 160 MW or 50% of daily peak |
| Case II | High 320 MW daily peak | ||
| Second | High Maximum: 100% Minimum: 95% | Low 160 MW or 50% of daily peak | |
| Third | Low Maximum: 10% Minimum: 0% | High 320 MW daily peak | |
| BESS Name for Given Size | Power/Energy Rating |
|---|---|
| BESS_100 | 0.1 MW/0.025 MWh |
| BESS_1000 | 1 MW/0.25 MWh |
| BESS_10000 | 10 MW/2.5 MWh |
| BESS_20000 | 20 MW/5 MWh |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandelic, M.; Stroe, D.-I.; Iov, F. Battery Storage-Based Frequency Containment Reserves in Large Wind Penetrated Scenarios: A Practical Approach to Sizing. Energies 2018, 11, 3065. https://doi.org/10.3390/en11113065
Sandelic M, Stroe D-I, Iov F. Battery Storage-Based Frequency Containment Reserves in Large Wind Penetrated Scenarios: A Practical Approach to Sizing. Energies. 2018; 11(11):3065. https://doi.org/10.3390/en11113065
Chicago/Turabian StyleSandelic, Monika, Daniel-Ioan Stroe, and Florin Iov. 2018. "Battery Storage-Based Frequency Containment Reserves in Large Wind Penetrated Scenarios: A Practical Approach to Sizing" Energies 11, no. 11: 3065. https://doi.org/10.3390/en11113065
APA StyleSandelic, M., Stroe, D.-I., & Iov, F. (2018). Battery Storage-Based Frequency Containment Reserves in Large Wind Penetrated Scenarios: A Practical Approach to Sizing. Energies, 11(11), 3065. https://doi.org/10.3390/en11113065







