Distributed Thermal Response Tests Using a Heating Cable and Fiber Optic Temperature Sensing
Abstract
1. Introduction
2. Field Test Methodology
3. Test Analysis
3.1. Thermal Conductivity Assessment
3.2. Uncertainty Analysis
3.3. Free Convection Assessment Inside GHE Pipe
4. Results
4.1. Thermal Conductivity Estimation
4.2. Uncertainty Analysis
4.3. Free Convection Assessment
5. Discussion
5.1. Thermal Conductivity Estimation
5.2. Uncertainty Analysis
5.3. Comparison of TRT Methods
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Fo | Fourier’s number (-) |
| G | gravitational acceleration (L t-2) |
| g | finite heat source function (-) |
| h | length of heat source (L) |
| H | height of the water column (L) |
| I | electric current intensity (I) |
| m | slope (-) |
| n | number of observations (-) |
| q | heat injection rate per unit length (M L t−3) |
| R | electric resistance (M L2 t-3 I−2) |
| r | radius (L) |
| Ra | Rayleigh number (-) |
| S | error of the estimate |
| t | time (t) |
| T | temperature (T) |
| U | electric potential difference (M L2 t-3 I−1) |
| Greek symbols | |
| α | thermal diffusivity (L2 t−1) |
| λ | thermal conductivity (M L T−1 t−3) |
| δ | uncertainty |
| σ | standard deviation |
| ν | cinematic viscosity (L2 t−1) |
| subscripts | |
| a | aspect-ratio (-) |
| c | calculated |
| cr | critical |
| h | heating |
| nh | non-heating |
| m | measured |
| off | end of heat injection |
| s | subsurface |
| t | critical height |
| tot | total |
| 0 | initial condition |
References
- Marcotte, D.; Pasquier, P. On the estimation of thermal resistance in borehole thermal conductivity test. Renew. Energy 2008, 33, 2407–2415. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, Z.; Liu, Y.; Cong, X.; Peng, D. A review on thermal response test of ground-coupled heat pump systems. Renew. Sustain. Energy Rev. 2014, 40, 851–867. [Google Scholar] [CrossRef]
- Mogensen, P. Fluid to duct wall heat transfer in duct system heat storages. In Proceedings of the International Conference on Subsurface Heat Storage in Theory and Practice, Stockholm, Sweden, 6–8 June 1983. [Google Scholar]
- Eklöf, C.; Gehlin, S. TED-a Mobile Equipment for Thermal Response Test: Testing and Evaluation. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 1996. [Google Scholar]
- Austin, W.A., III. Development of an In Situ System for Measuring Ground Thermal Properties. Master’s Thesis, Oklahoma State University, Stillwater, OK, USA, 1998. [Google Scholar]
- Gehlin, S. Thermal Response Test Method Development and Evaluation. Ph.D. Thesis, Luleå University of Techonology, Luleå, Sweden, 2002. [Google Scholar]
- Sanner, B.; Hellström, G.; Spitler, J.; Gehlin, S. More Than 15 years of Mobile Thermal Response Test—A Summary of Experiences and Prospects. Available online: https://hvac.okstate.edu/sites/default/files/pubs/papers/2013/03-Sanner_et_al_2013_EGC_TRT-overview.pdf (accessed on 3 May 2017).
- Spitler, J.D.; Gehlin, S. Thermal response testing for ground source heat pump systems—An historical review. Renew. Sustain. Energy Rev. 2015, 50, 1125–1137. [Google Scholar] [CrossRef]
- Gehlin, S. Thermal Response Test: In Situ Measurements of Thermal Properties in Hard Rock. Licentiate Dissertation, Luleå University of Technology, Luleå, Sweden, 1998. [Google Scholar]
- Raymond, J.; Therrien, R.; Gosselin, L. Borehole temperature evolution during thermal response tests. Geothermics 2011, 40, 69–78. [Google Scholar] [CrossRef]
- Carslaw, H.S. Introduction to the Mathematical Theory of the Conduction of Heat in Solids; Macmillan: London, UK, 1921. [Google Scholar]
- Ingersoll, L.R.; Plass, H.J. Theory of the ground heat pipe heat source for the heat pump. Trans. Am. Soc. Heat. Vent. Eng. 1948, 20, 119–122. [Google Scholar]
- Kavanaugh, S.P. Investigation of Methods for Determining Soil Formation Thermal Characteristics from Short Term Field Tests; ASHRAE: Atlanta, GA, USA, 2001. [Google Scholar]
- Sanner, B.; Hellström, G.; Spitler, J.; Gehlin, S. Thermal response test—Current status and world-wide application. In Proceedings of the World Geothermal Congress, Antalya, Turkey, 24–29 April 2005. [Google Scholar]
- Fujii, H.; Okubo, H.; Itoi, R. Thermal response tests using optical fiber thermometers. GRC Trans. 2006, 30, 545–551. [Google Scholar]
- Gehlin, S.; Hellström, G. Influence on thermal response test by groundwater flow in vertical fractures in hard rock. Renew. Energy 2003, 28, 2221–2238. [Google Scholar] [CrossRef]
- Gustafsson, A.M.; Westerlund, L. Heat extraction thermal response test in groundwater-filled borehole heat exchanger—Investigation of the borehole thermal resistance. Renew. Energy 2011, 36, 2388–2394. [Google Scholar] [CrossRef]
- Bense, V.F.; Read, T.; Bour, O.; Le Borgne, T.; Coleman, T.; Krause, S.; Chalari, A.; Mondanos, M.; Ciocca, F.; Selker, J.S. Distributed Temperature Sensing as a downhole tool in hydrogeology. Water Resour. Res. 2016, 52, 9259–9273. [Google Scholar] [CrossRef]
- Fujii, H.; Okubo, H.; Nishi, K.; Itoi, R.; Ohyama, K.; Shibata, K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers. Geothermics 2009, 38, 399–406. [Google Scholar] [CrossRef]
- Beier, R.A.; Acuña, J.; Mogensen, P.; Palm, B. Vertical temperature profiles and borehole resistance in a U-tube borehole heat exchanger. Geothermics 2012, 44, 23–32. [Google Scholar] [CrossRef]
- Acuña, J.; Palm, B. Distributed thermal response tests on pipe-in-pipe borehole heat exchangers. Appl. Energy 2013, 109, 312–320. [Google Scholar] [CrossRef]
- Freifeld, B.M.; Finsterle, S.; Onstott, T.C.; Toole, P.; Pratt, L.M. Ground surface temperature reconstructions: Using in situ estimates for thermal conductivity acquired with a fiber-optic distributed thermal perturbation sensor. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Raymond, J.; Lamarche, L. Development and numerical validation of a novel thermal response test with a low power source. Geothermics 2014, 51, 434–444. [Google Scholar] [CrossRef]
- Raymond, J.; Lamarche, L.; Malo, M. Field demonstration of a first thermal response test with a low power source. Appl. Energy 2015, 147, 30–39. [Google Scholar] [CrossRef]
- Raymond, J.; Robert, G.; Therrien, R.; Gosselin, L. A novel thermal response test using heating cables. In Proceedings of the World Geothermal Congress, Bali, Indonesia, 25–29 April 2010. [Google Scholar]
- Raymond, J. Colloquium 2016: Assessment of the subsurface thermal conductivity for geothermal applications. Can. Geotech. J. 2018, 55, 1209–1229. [Google Scholar] [CrossRef]
- Simon, F. Développement D’une Approche Nouvelle Pour Les Tests de Réponse Thermique en Géothermie. Master’s Thesis, École de technologie supérieure, Montréal, QC, Canada, 2016. [Google Scholar]
- Love, A.J.; Simmons, C.T.; Nield, D.A. Double-diffusive convection in groundwater wells. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Raymond, J.; Ballard, J.-M.; Koubikana Pambou, C.H. Field assessment of a ground heat exchanger performance with a reduced borehole diameter. In Proceedings of the 70th Canadian Geotechnical Conference and the 12th Joint CGS/IAH-CNC Groundwater Conference, Ottawa, ON, Canada, 1–4 October 2017. [Google Scholar]
- Philippe, M. Development and Experimental Validation of Vertical and Horizontal Ground Heat Exchangers for residential buildings heating. Ph.D. Thesis, École Nationale Supérieure des Mines de Paris, Paris, France, 2010. [Google Scholar]
- van de Giesen, N.; Steele-Dunne, S.C.; Jansen, J.; Hoes, O.; Hausner, M.B.; Tyler, S.; Selker, J. Double-ended calibration of fiber-optic raman spectra distributed temperature sensing data. Sensors 2012, 12, 5471–5485. [Google Scholar] [CrossRef] [PubMed]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and testing of a generalized reduced gradient code for nonlinear programming. ACM Trans. Math. Softw. 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Beck, A.E.; Anglin, F.M.; Sass, J.H. Analysis of heat flow data—In situ thermal conductivity measurements. Can. J. Earth Sci. 1971, 8, 1–19. [Google Scholar] [CrossRef]
- Pehme, P.E.; Greenhouse, J.P.; Parker, B.L. The active line source temperature logging technique and its application in fractured rock hydrogeology. J. Environ. Eng. Geophys. 2007, 12, 307–322. [Google Scholar] [CrossRef]
- Witte, H.J.L. Error analysis of thermal response tests. Appl. Energy 2013, 109, 302–311. [Google Scholar] [CrossRef]
- Evaluation of Measurement Data—Supplement 1 to the Guide to the Expression of Uncertainty in Measurement. Available online: https://www.bipm.org/utils/common/documents/jcgm/JCGM_101_2008_E.pdf (accessed on 9 September 2018).
- Ellison, S.; Williams, A. Eurachem/CITAC guide: Quantifying Uncertainty in Analytical Measurement. Available online: https://www.eurachem.org/images/stories/Guides/pdf/QUAM2012_P1.pdf (accessed on 12 July 2017).
- Ballard, J.M.; Koubikana, C.; Raymond, J. Développement des Tests de Réponse Thermique Automatisés et Vérification de la Performance des Forages Géothermiques d’un Diamètre de 4,5 Po. Internal Report R1601; Institut National de la Recherche Scientifique: Qubec City, QC, Canada, 2016. [Google Scholar]
- Maragna, C. Analyse D’un Test de Réponse Thermique; Internal Report; Division Géothermie, Bureau de Recherche Géologique et Minières de France: Orléans, France, 2014. [Google Scholar]
- Asselin, S. Manuel D’utilisation: Appareil de Lecture de Conductivité Thermique; Internal Report; Institut National de la Recherche Scientifique: Quebec City, QC, Canada, 2014. [Google Scholar]
- Klepikova, M.; Roques, C.; Loew, S.; Selker, J. Improved Characterization of Groundwater Flow in Heterogeneous Aquifers Using Granular Polyacrylamide (PAM) Gel as Temporary Grout. Water Resour. Res. 2018, 54, 1410–1419. [Google Scholar] [CrossRef]
- Berthold, S.; Resagk, C. Investigation of thermal convection in water columns using particle image velocimetry. Exp. Fluids 2012, 52, 1465–1474. [Google Scholar] [CrossRef]
- Witte, H.J.L.; van Gelder, G.; Spitler, J.D. In-situ thermal conductivity testing: A dutch perspective. ASHRAE Trans. 2002, 108, 263–272. [Google Scholar]
- Raymond, J.; Therrien, R.; Gosselin, L.; Lefebvre, R. A review of thermal response test analysis using pumping test concepts. Ground Water 2011, 49, 932–945. [Google Scholar] [CrossRef] [PubMed]
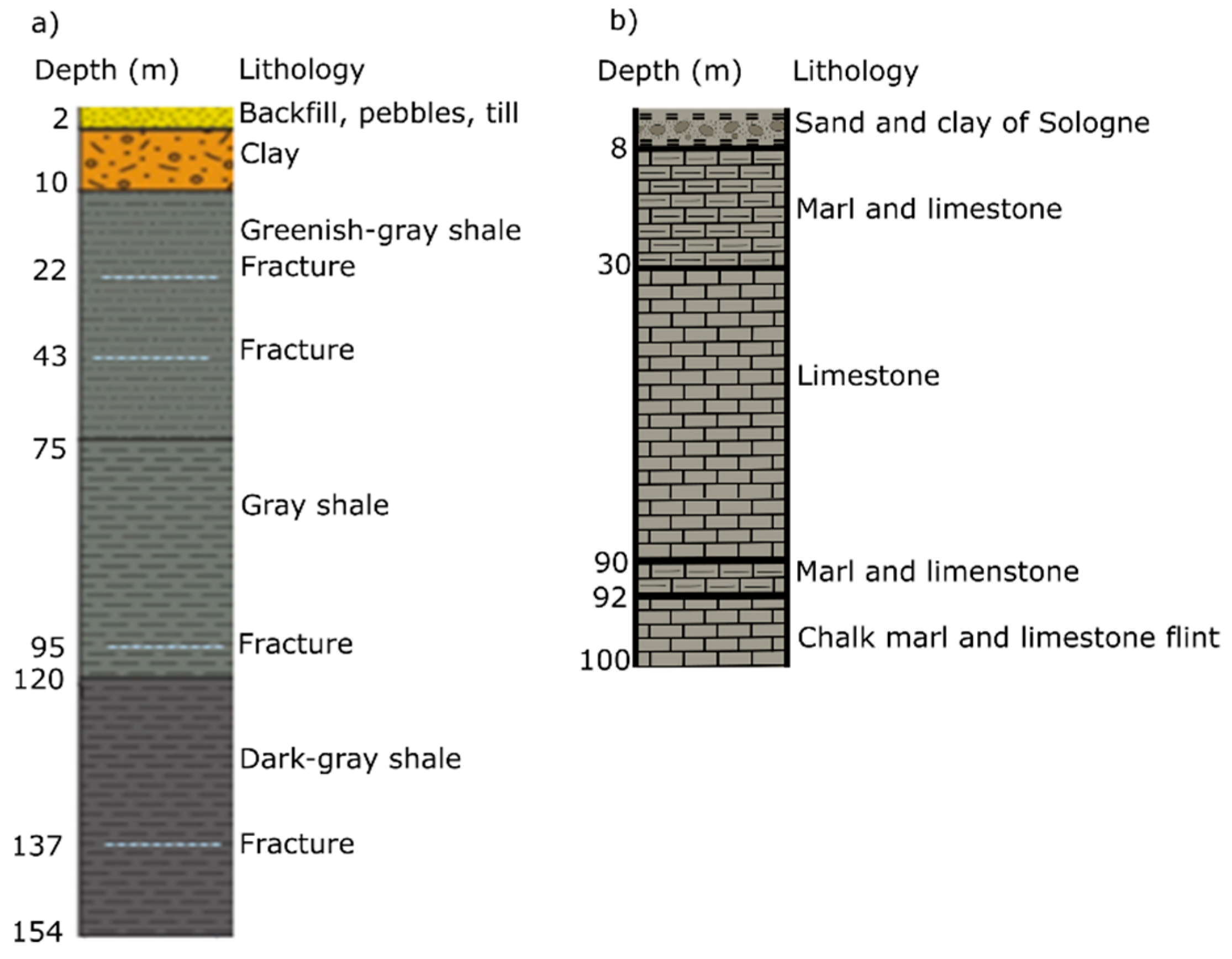
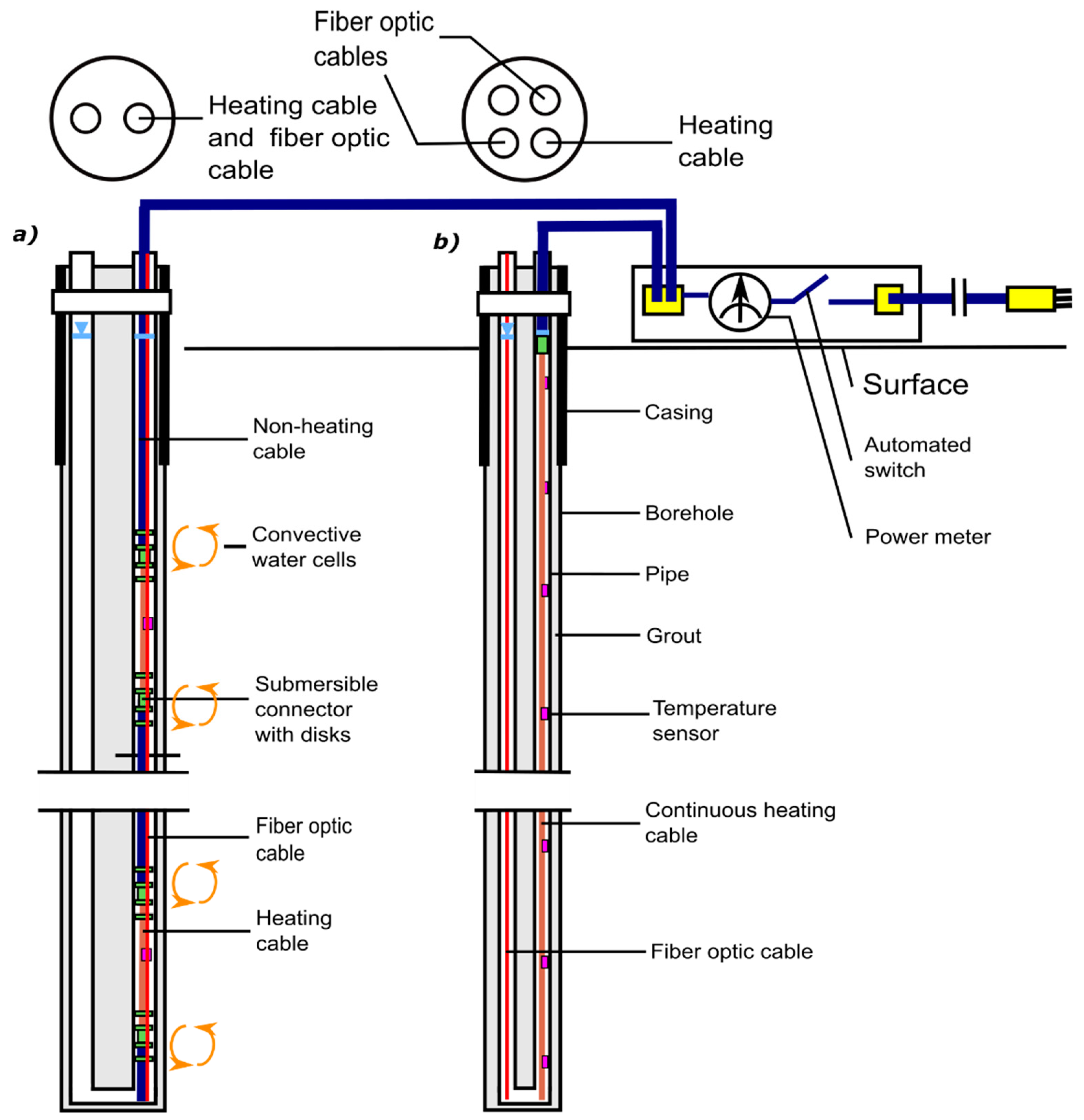

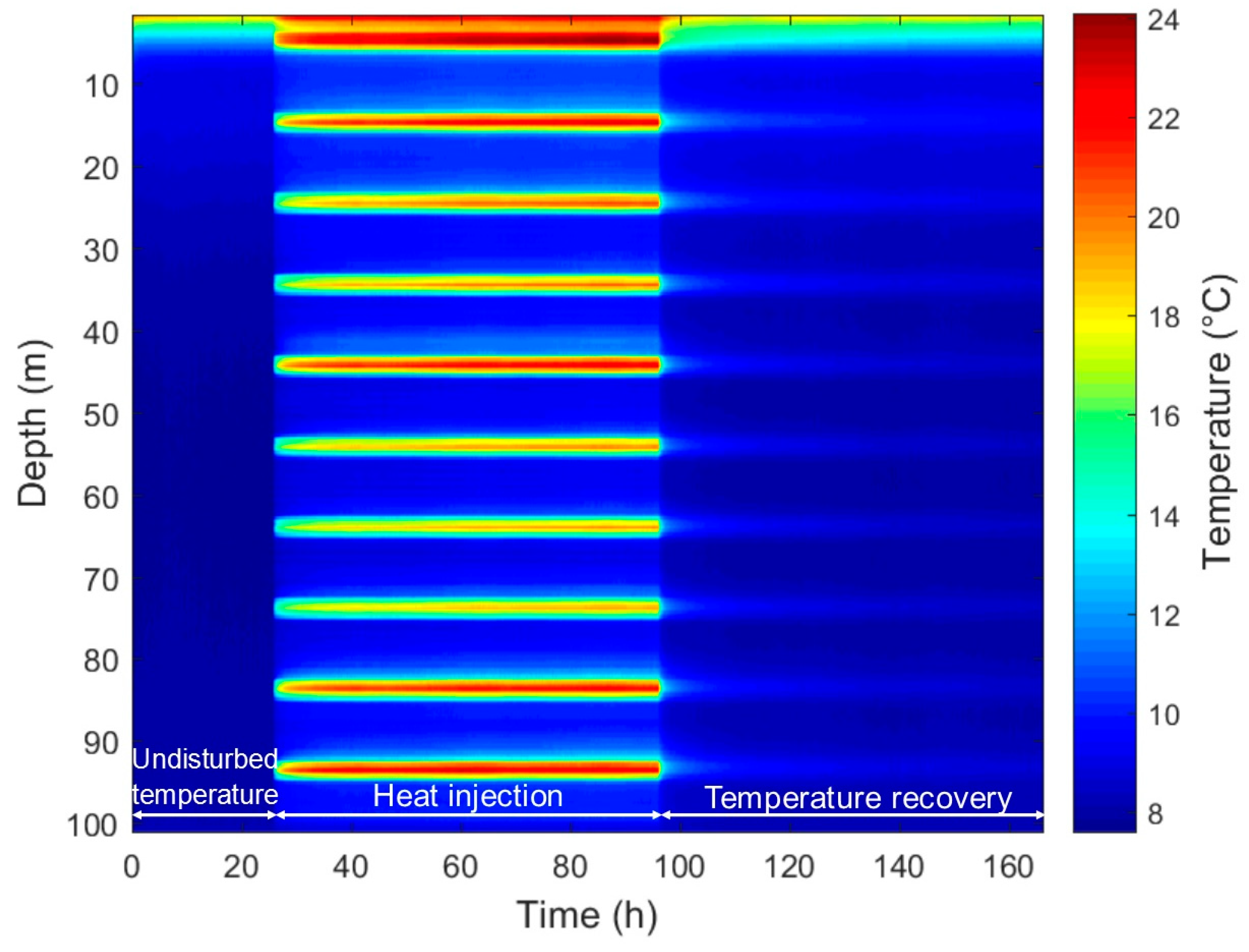
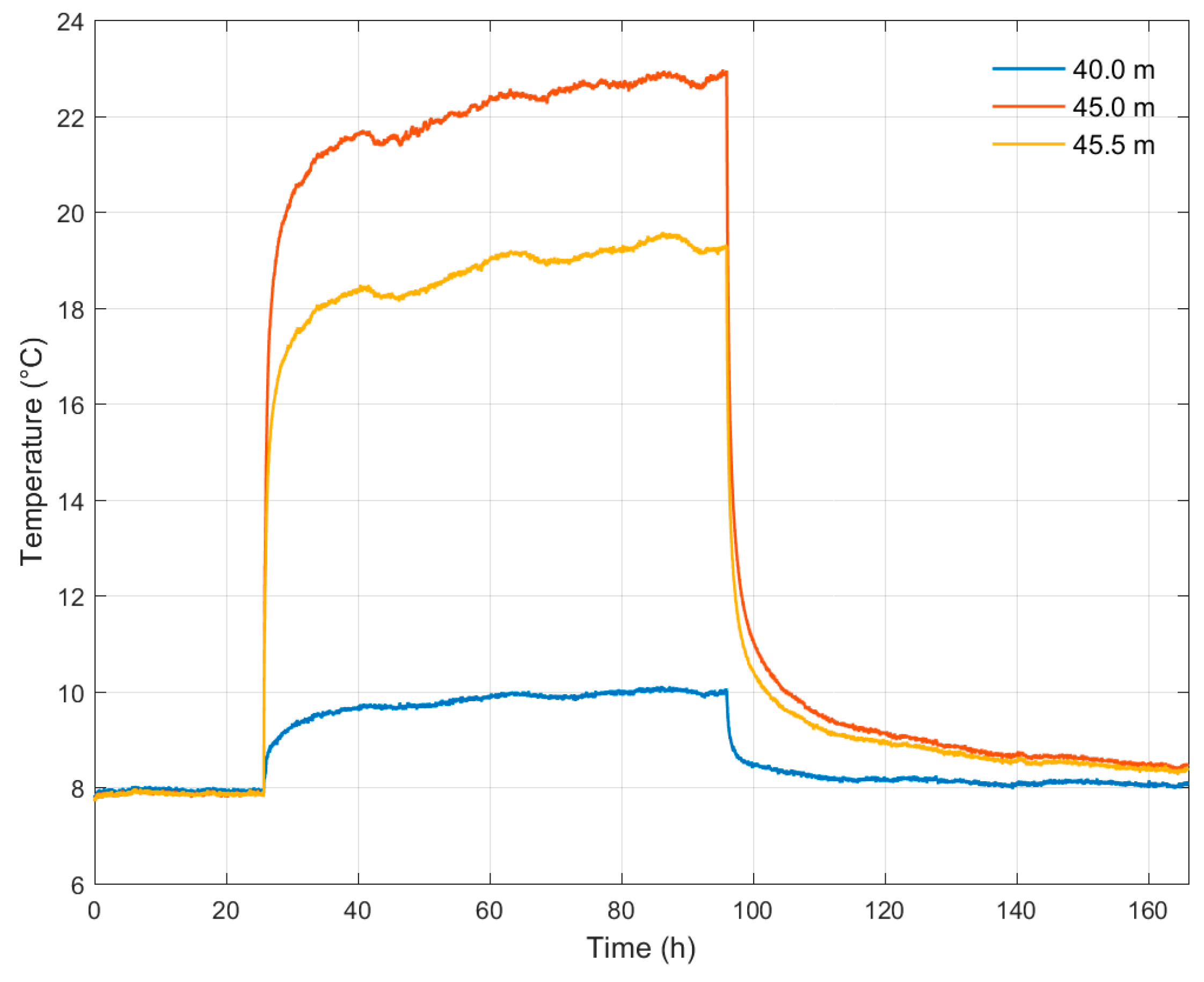
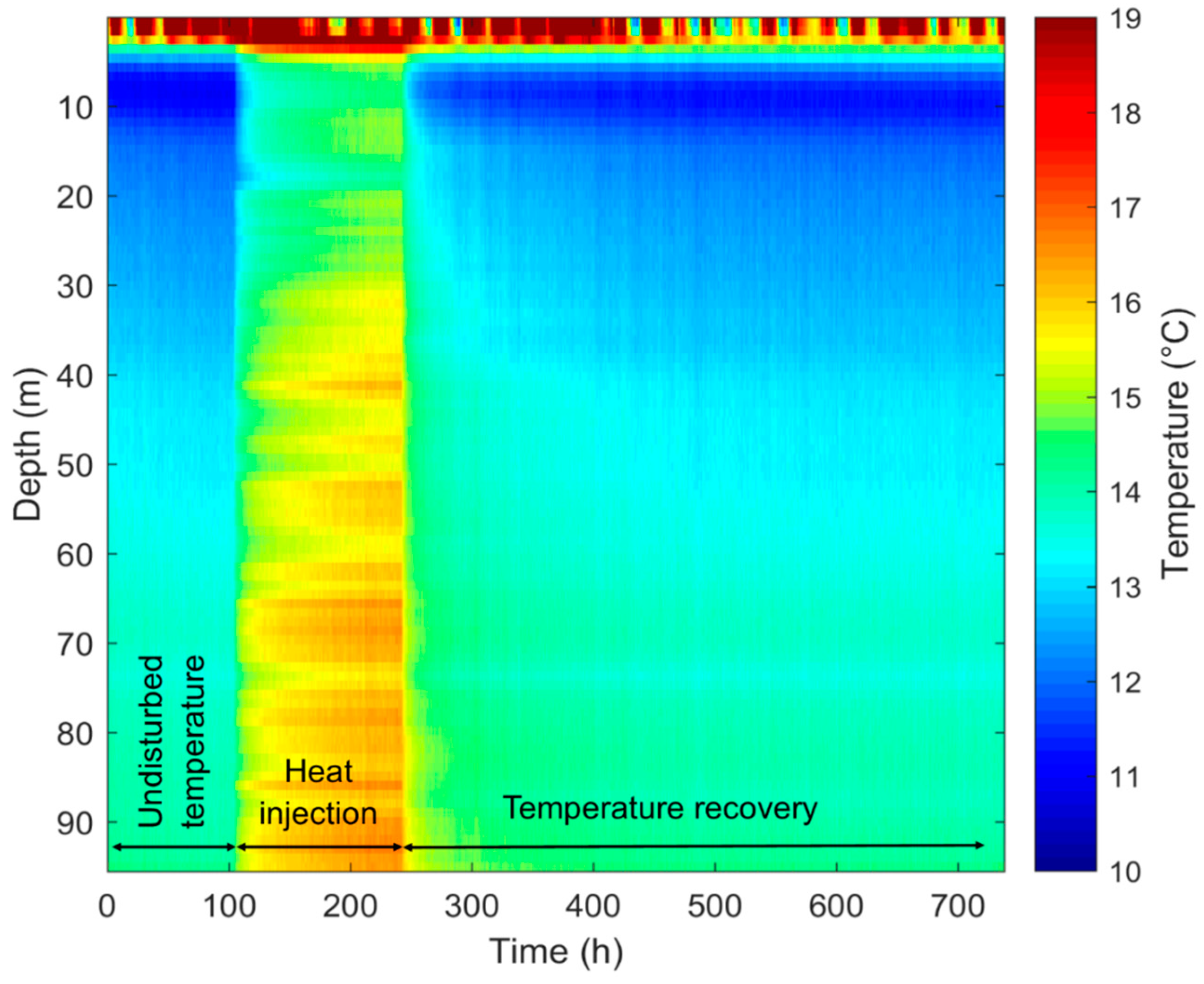
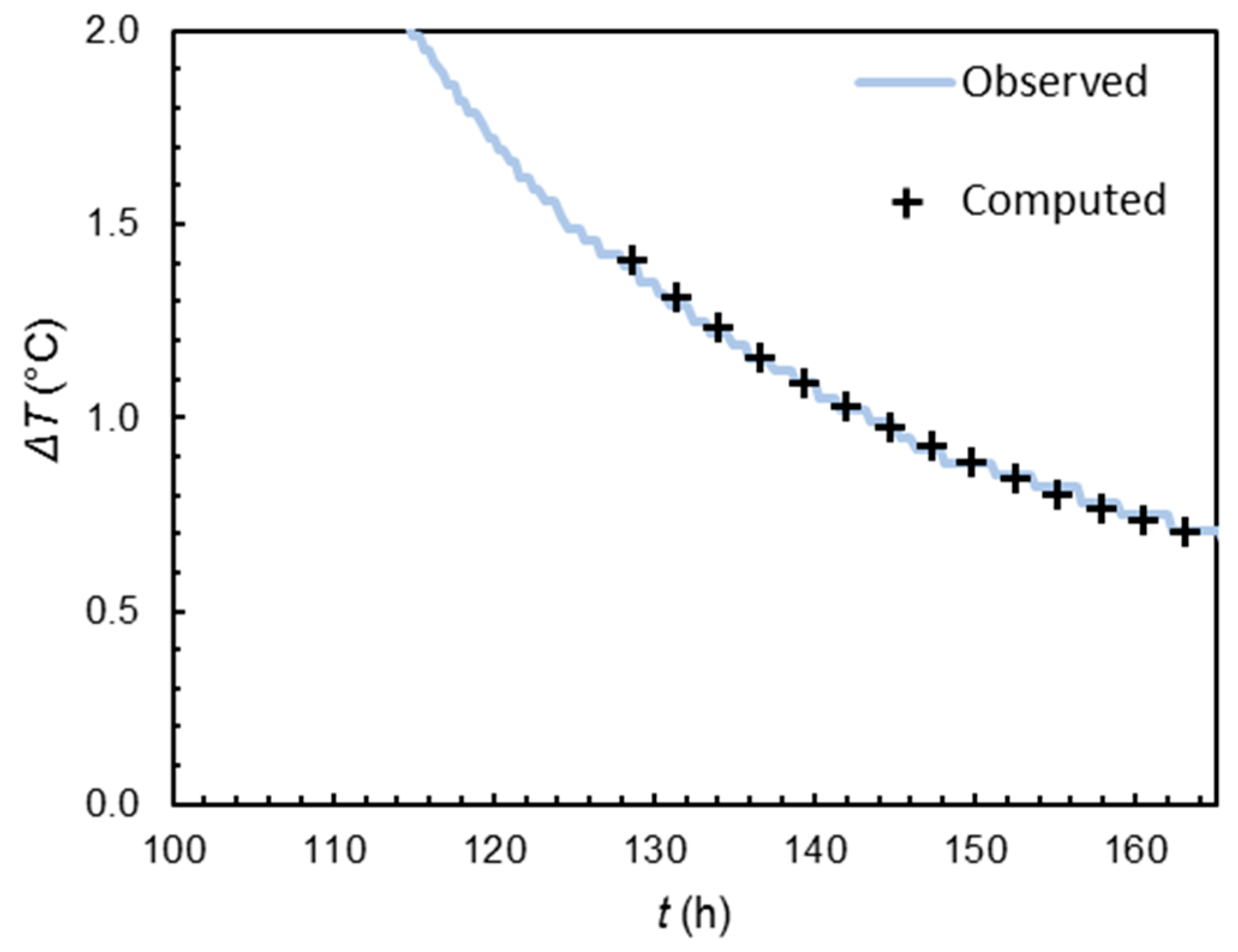
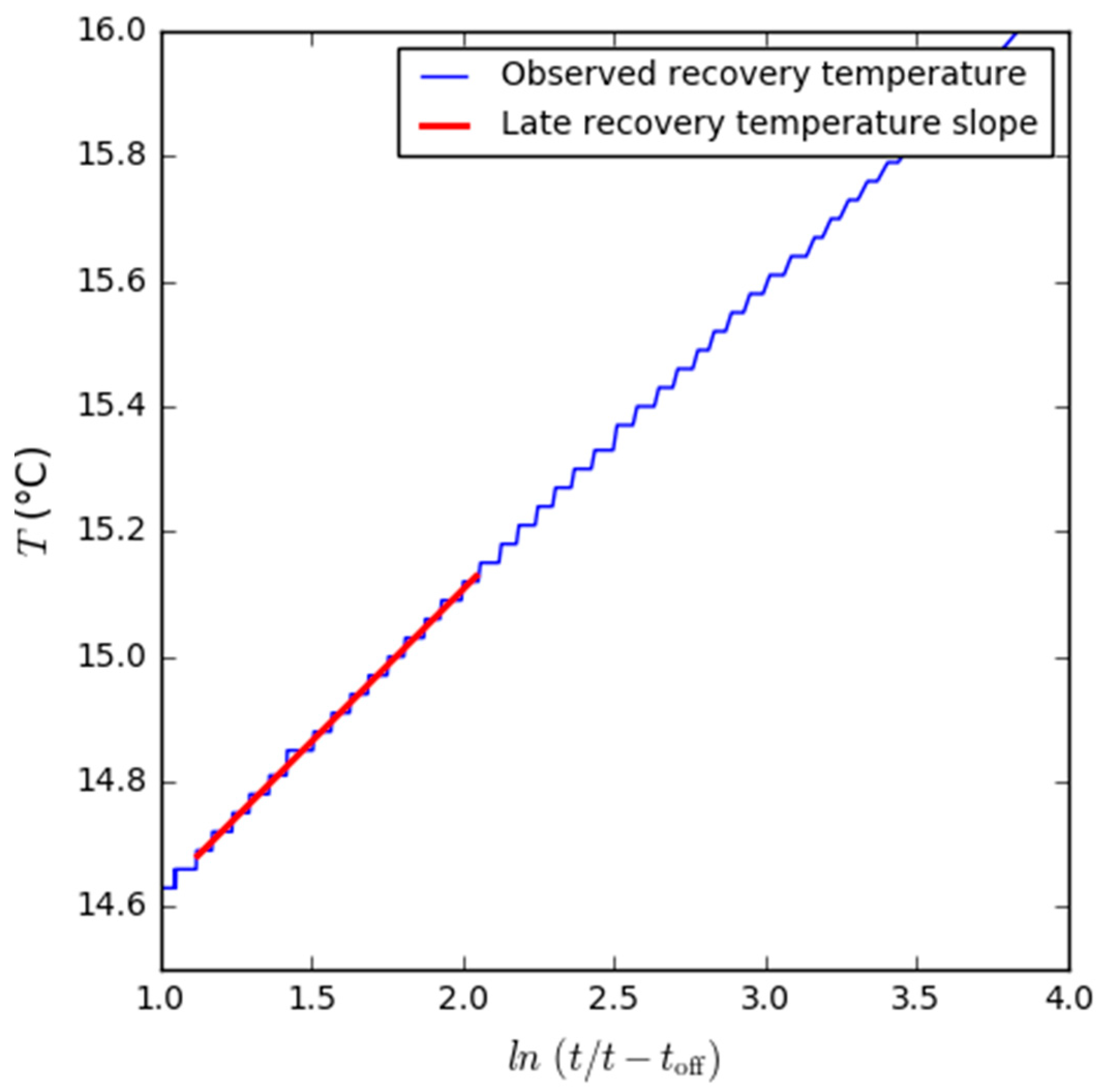
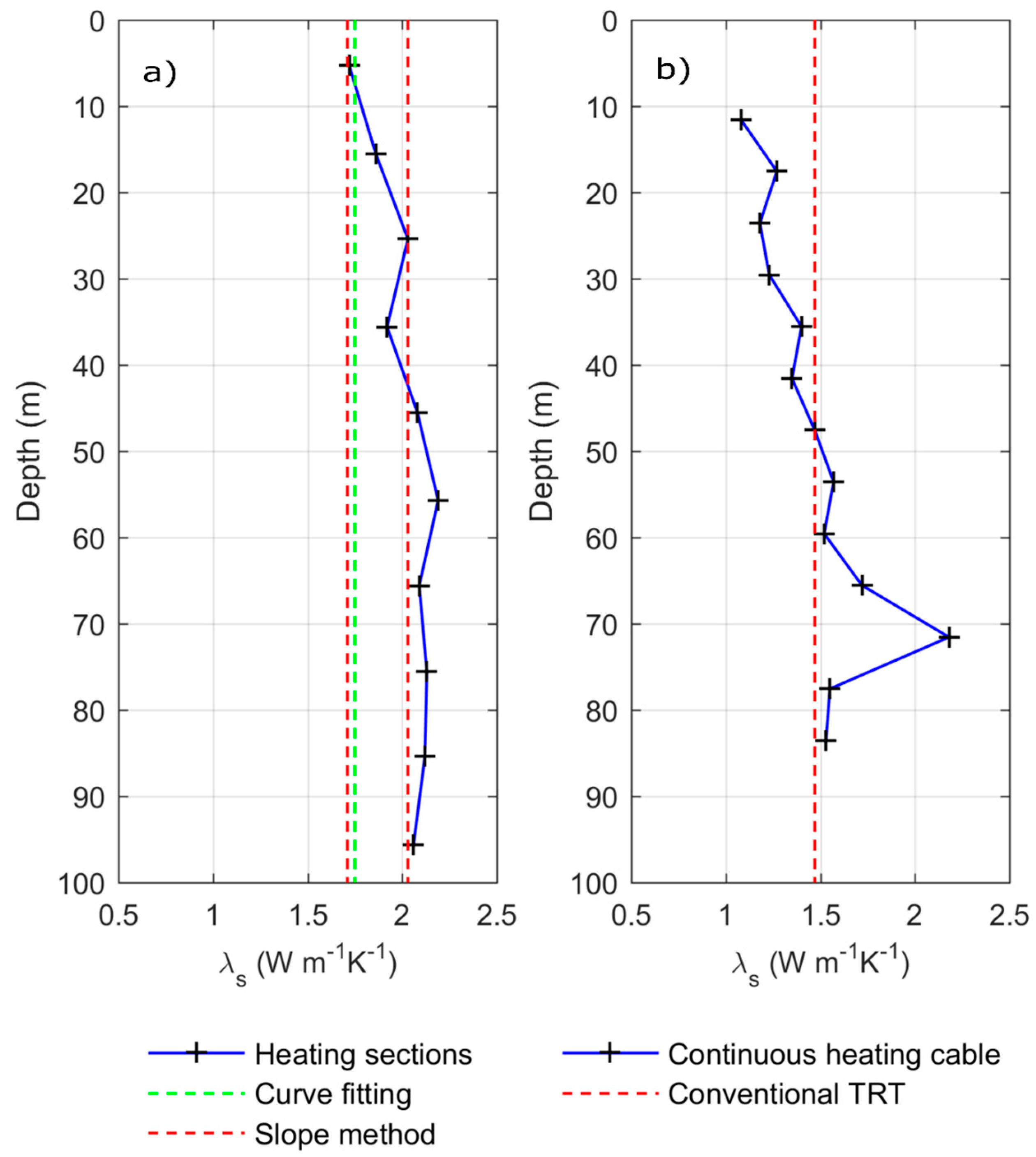
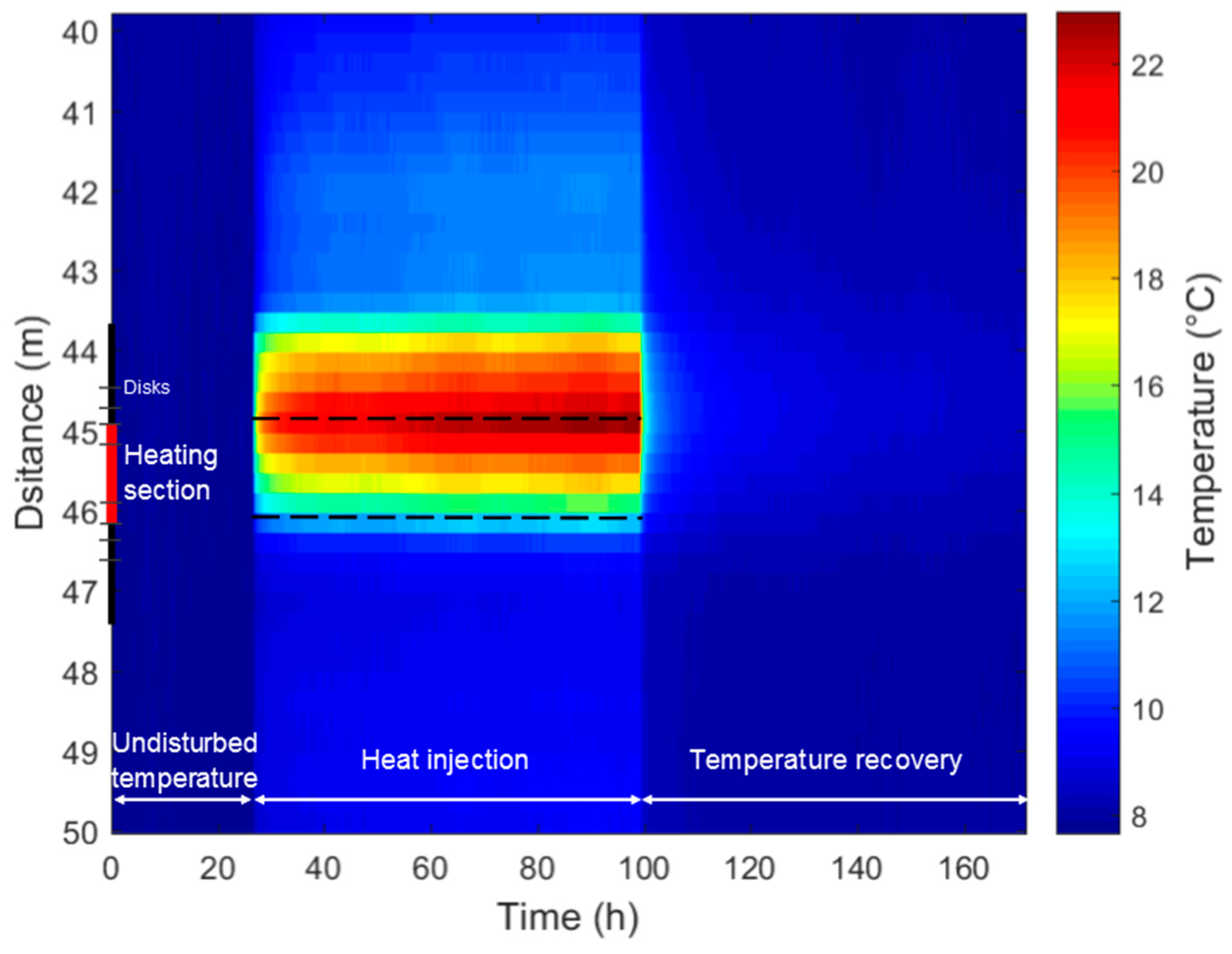
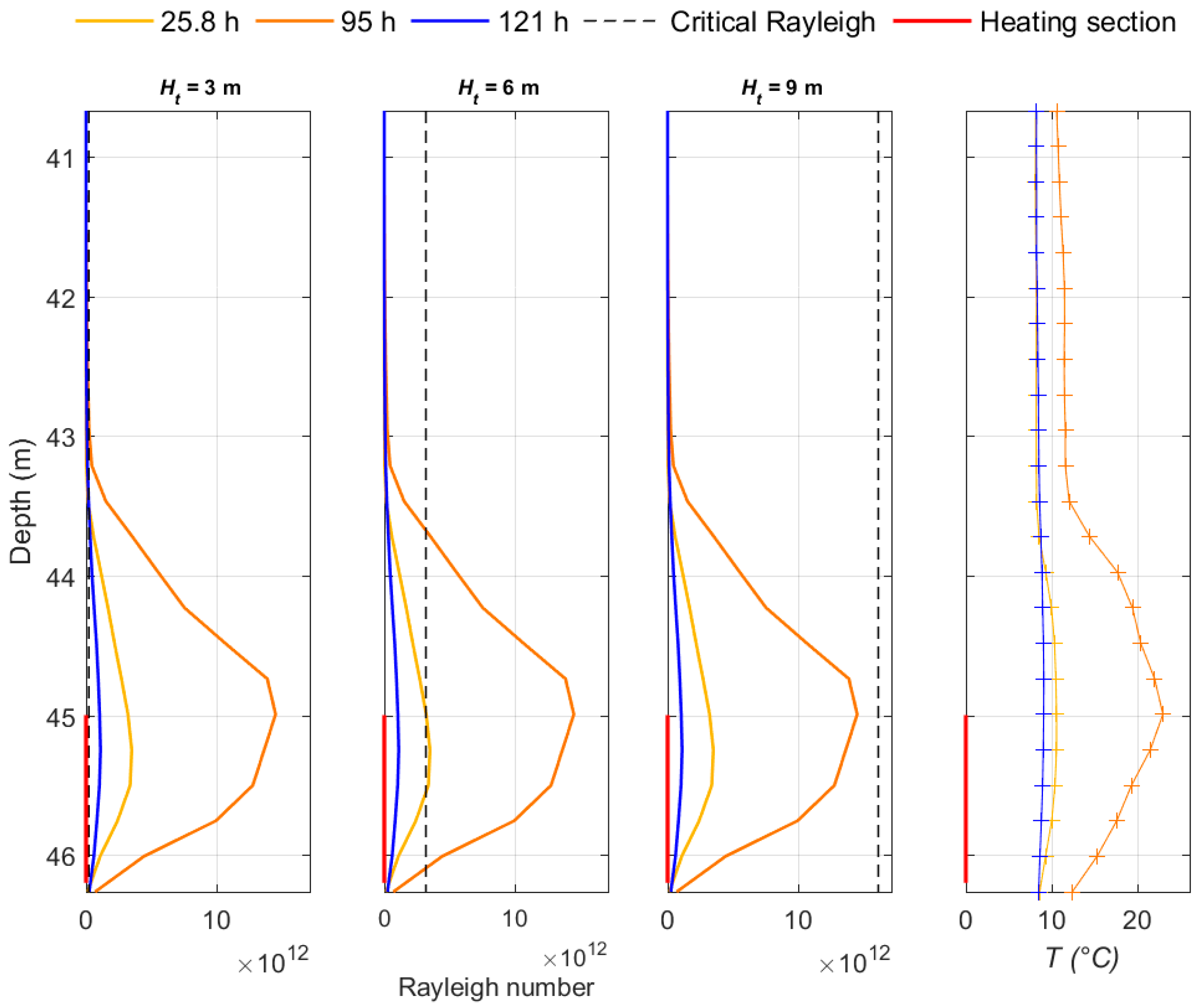
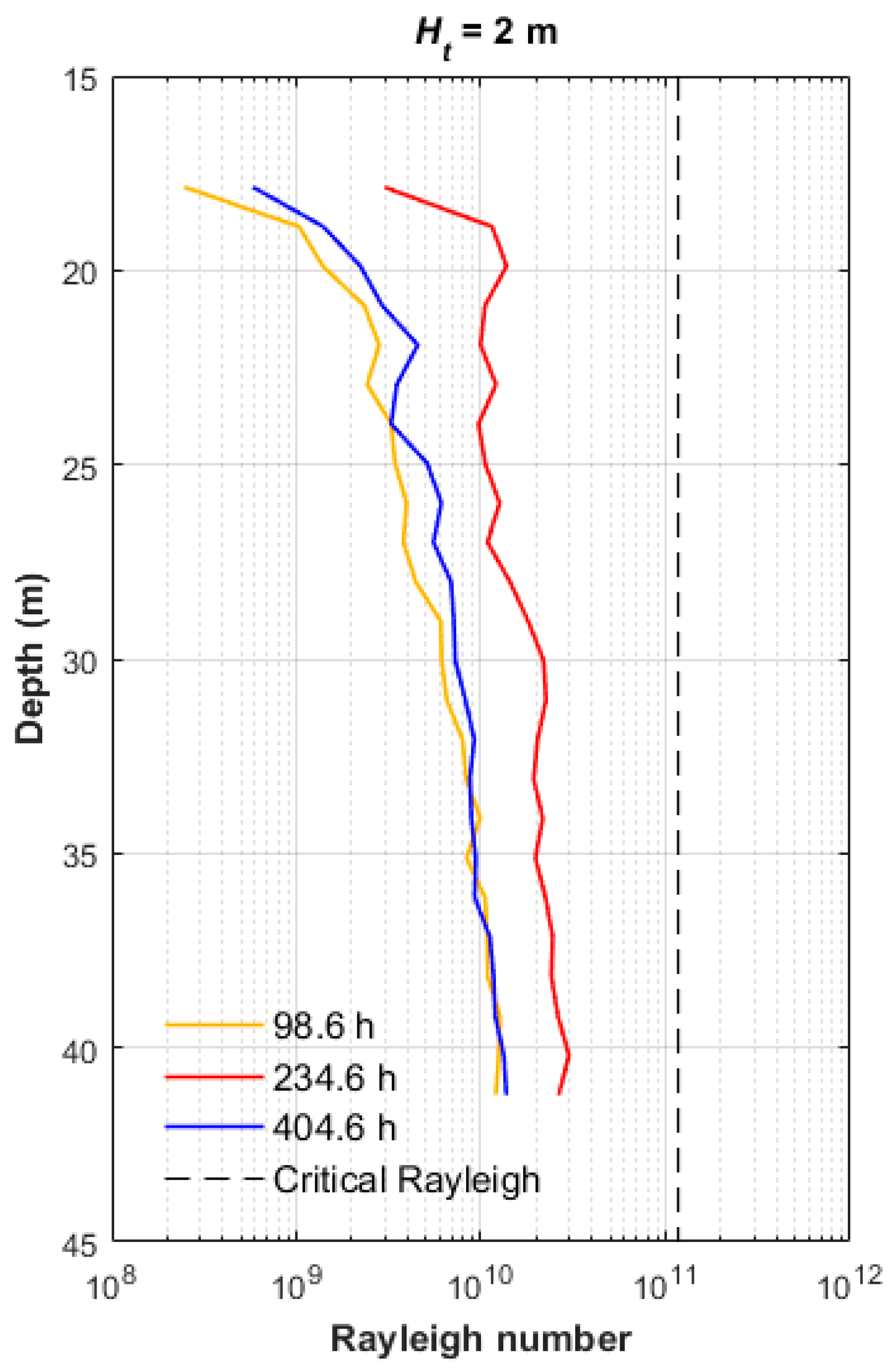
| Parameter | Quebec City | Orléans |
|---|---|---|
| Heating cable type | Heating section | Continuous heating cable |
| Test analysis method | Finite line source | Infinite line source |
| Borehole configuration | Single U-pipe | Double U-pipe |
| TRT start date | 31 August 2016 | 3 July 2017 |
| TRT start time | 11:20:00 | 13:00:00 |
| TRT end date | 7 September 2016 | 2 August 2017 |
| TRT end time | 12:11:00 | 10:00:00 |
| Borehole depth (m) | 150 | 100 |
| Heating cable length (m) | 100 | 95 |
| Borehole diameter (mm) | 114 | 180 |
| Pipe diameter (mm) | 32.00 | 26.20 |
| Duration of undisturbed temperature monitoring (h) | 26.00 | 100.00 |
| Heat injection period (h) | 73.00 | 135.70 |
| Thermal recovery period (h) | 70.00 | 481.30 |
| Total test duration (h) | 169.00 | 717.00 |
| Initial temperature (°C) | 8.20 | 13.10 |
| Heat injection rate (W·m−1) | 42.50 | 9.90 |
| Temperature sensors vertical distance (m) | 10 | 6 |
| Parameter Measured Repeatedly during the Test | Absolute Error | Relative Error (%) | Reference Value-Quebec City | Reference Value-Orléans |
|---|---|---|---|---|
| Temperature T (°C) | 0.10 | |||
| Electric power P (W) | 0.02 | 0.002 | 985.13 | 940.45 |
| Electric current intensity I (A) | 0.02 | 0.17 | 8.71 | 8.99 |
| Electric potential difference U (V) | 0.02 | 0.01 | 113.12 | 104.70 |
| Parameter measured once and separately | ||||
| Length of the heating cable H (m) | 0.01 | 0.01 | - | 95.00 |
| Length of the heating section Lh (m) | 0.01 | 0.81 | 1.24 | - |
| Electrical resistance per unit length of the non-heating section Rnh (Ω·m−1) | 0.0002 | 0.50 | 0.04 | - |
| Continuous Heating Cable | Absolute Error | Relative Error (%) | Reference Value |
| Heat injection rate q (W·m−1) | 0.21 | 2.12 | 9.91 |
| Slope m′ (-) | 0.001 | 0.23 | 0.55 |
| Heating Cable Section | Absolute Error | Relative Error (%) | Reference Value |
| Total electrical resistance of the cable assembly Rtot (Ω) | 0.12 | 0.94 | 12.99 |
| Electrical resistance of the heating cable sections Rh (Ω) | 0.13 | 14.26 | 0.90 |
| Heat injection rate q (W·m−1) | 6.07 | 14.29 | 42.50 |
| Analytical model Z (-) | 1.06 | 5.00 | 21.14 |
| Depth (m) | Thermal Conductivity (W·m−1·K−1) | Absolute Error δk (W·m−1·K−1) | Relative error (%) |
|---|---|---|---|
| 5.3 | 1.72 | 0.27 | 15.61 |
| 15.5 | 1.86 | 0.31 | 16.38 |
| 25.4 | 2.03 | 0.30 | 14.85 |
| 35.6 | 1.91 | 0.29 | 15.02 |
| 45.5 | 2.07 | 0.30 | 14.62 |
| 55.7 | 2.19 | 0.33 | 14.95 |
| 65.6 | 2.08 | 0.32 | 15.44 |
| 75.5 | 2.12 | 0.33 | 15.31 |
| 85.4 | 2.12 | 0.32 | 14.88 |
| 95.6 | 2.06 | 0.30 | 14.73 |
| Average | 2.02 | 0.31 | 15.18 |
| Depth (m) | Thermal Conductivity (W·m−1·K−1) | Absolute Error δk (W·m−1·K−1) | Relative Error (%) |
|---|---|---|---|
| 11.6 | 1.08 | 0.02 | 2.13 |
| 17.6 | 1.27 | 0.03 | 2.13 |
| 23.6 | 1.18 | 0.03 | 2.13 |
| 29.6 | 1.23 | 0.03 | 2.13 |
| 35.6 | 1.4 | 0.03 | 2.13 |
| 41.6 | 1.35 | 0.03 | 2.13 |
| 47.6 | 1.47 | 0.03 | 2.14 |
| 53.6 | 1.57 | 0.03 | 2.14 |
| 59.6 | 1.52 | 0.03 | 2.13 |
| 65.6 | 1.72 | 0.04 | 2.14 |
| 71.6 | 2.18 | 0.05 | 2.15 |
| 77.6 | 1.55 | 0.03 | 2.13 |
| 83.6 | 1.53 | 0.03 | 2.14 |
| Average | 1.47 | 0.03 | 2.14 |
| Parameter | Continuous Heating Cable | Heating Cable Sections | Conventional with FO-DTS |
|---|---|---|---|
| Power requirement | Low | Low | High |
| Test time | +++ | ++ | ++ |
| Equipment complexity | + | ++ | +++ |
| Cost | $ | $$ | $$$ |
| Measured parameters | T0, λs | T0, λs | T0, λs, Rb |
| Surface disturbances | No | No | Yes |
| Analysis method | Infinite line source solution | Finite line source solution | Infinite line source solution |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vélez Márquez, M.I.; Raymond, J.; Blessent, D.; Philippe, M.; Simon, N.; Bour, O.; Lamarche, L. Distributed Thermal Response Tests Using a Heating Cable and Fiber Optic Temperature Sensing. Energies 2018, 11, 3059. https://doi.org/10.3390/en11113059
Vélez Márquez MI, Raymond J, Blessent D, Philippe M, Simon N, Bour O, Lamarche L. Distributed Thermal Response Tests Using a Heating Cable and Fiber Optic Temperature Sensing. Energies. 2018; 11(11):3059. https://doi.org/10.3390/en11113059
Chicago/Turabian StyleVélez Márquez, Maria Isabel, Jasmin Raymond, Daniela Blessent, Mikael Philippe, Nataline Simon, Olivier Bour, and Louis Lamarche. 2018. "Distributed Thermal Response Tests Using a Heating Cable and Fiber Optic Temperature Sensing" Energies 11, no. 11: 3059. https://doi.org/10.3390/en11113059
APA StyleVélez Márquez, M. I., Raymond, J., Blessent, D., Philippe, M., Simon, N., Bour, O., & Lamarche, L. (2018). Distributed Thermal Response Tests Using a Heating Cable and Fiber Optic Temperature Sensing. Energies, 11(11), 3059. https://doi.org/10.3390/en11113059







