Short-Term Wind Speed Forecasting Based on Signal Decomposing Algorithm and Hybrid Linear/Nonlinear Models
Abstract
:1. Introduction
- ■
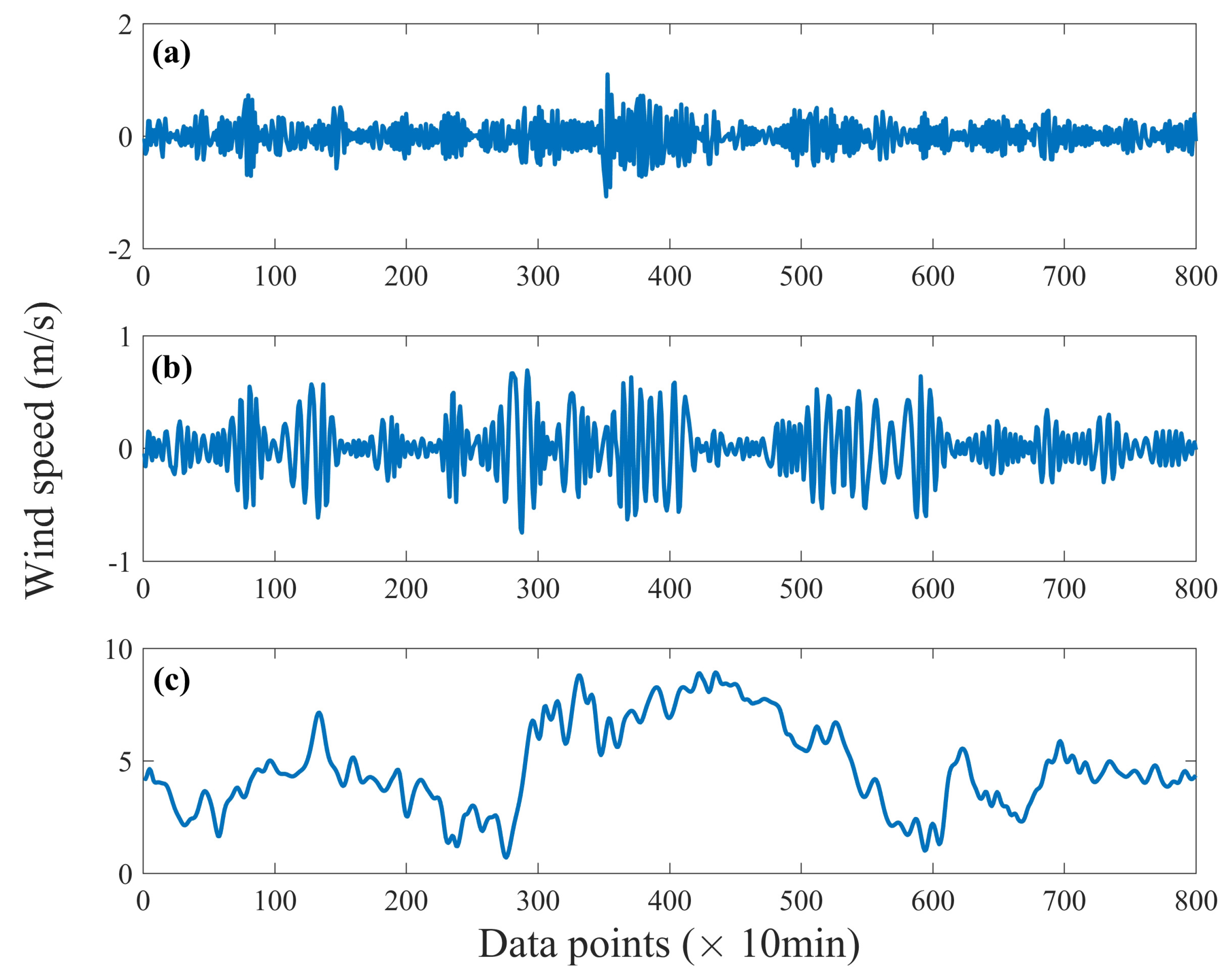
- A framework for short-term wind speed forecasting is introduced based on EMD and hybrid linear/nonlinear models. The EMD is adopted to decompose the original wind speed series into a finite number of IMFs and residuals, i.e., low-frequency residuals (LFR), medium-frequency IMF (MIMF) and high-frequency IMF (HIMF).
- ■
- Several popular linear models (ARIMA) and nonlinear models (SVM, random forest (RF), BP, ELM and convolutional neural network (CNN)) are, respectively, utilized to study each IMFs and residuals. An ensemble forecast for the original wind speed series is then obtained.
- ■
- Various experiments are conducted on the real wind speed data at four wind sites in China. The performance and robustness of various hybrid linear/nonlinear models at two time intervals (10 min and 1 h) are compared comprehensively. The forecasting model with the best performance is then recommended for real applications.
2. Methods
2.1. EMD
- (1)
- For wind speed series , all of the local maximal and minimal data points are found and located;.
- (2)
- Two cubic spline lines are used to connect all of the local maximal and minimal points, respectively. Then, upper and lower envelopes and are gained accordingly.
- (3)
- Mean values are calculated.
- (4)
- New time series is defined. If satisfies condition (a) and (b), then the could be considered as a IMF; otherwise, replace by , and repeat step (1)–(4) until the condition (a) and (b) are simultaneously obeyed.
- (5)
- Residuals are then calculated. Replace by , and repeat step (1)–(5) until all the IMFs and residuals are found.
2.2. Single Linear Models (ARIMA)
2.3. Single Nonlinear Models
- (1)
- The SVM model has recently been used in a range of applications such as regression and time series forecasting. The basic idea of SVM for regression is to use a nonlinear mapping model to transform the data into a high-dimensional feature space, and then perform a linear regression in the feature space. Optimal weight and bias values are obtained by solving the quadratic optimization problem [43].
- (2)
- The RF model, which was suggested by Breiman [44], is an ensemble learning method for classification and regression. It is operated by constructing a multitude of decision tress at the training stage and outputting the mean prediction of individual trees. Classification and regression trees (CARTs) [45] in the RF model use the binary rules to divide data samples. CARTs could correct decision trees’ habit of overfitting to their original dataset.
- (3)
- Among many available learning algorithms, BP has been the most popular implemented learning algorithm for all ANN models [46]. The time series data is introduced by the input layer, and the forecast value is produced by the output layer. The layer between the input and output layers is called the hidden layer, where data are processed. The procedure of BP is repeated by adjusting the weights of the connection in the network using the gradient descent. Ref. [47] presented the detailed algorithm.
- (4)
- The ELM’s structure is similar to the single hidden layer feed-forward neural network [48]. The main idea of the ELM model is to randomly set the network weights and then obtain the inverse output matrix of the hidden layer. This concept makes the ELM model operate extremely fast and maintain better accuracy compared with other learning models. The number of hidden nodes, which is the key parameter of ELM model, should be carefully estimated in order to obtain good results [16].
- (5)
- CNN is a class of deep, feed-forward ANNs, most commonly applied to image classification and then generalized for time series prediction. In order to simply the preprocessing, CNN utilizes a variation of multilayer perceptrons. Except that the filter weights need to be shared, there are no other connections between the neurons. Thus, CNN could be trained more efficiently and have reliable abilities to extract the hidden features [49].
2.4. Hybrid Linear/Nonlinear Models
2.5. Forecasting Performance Metrics
3. Data Descriptions
4. Results and Discussions
4.1. Single Models without EMD
4.1.1. ARIMA
4.1.2. SVM, RF, BP, ELM and CNN
4.2. Single Models with EMD
4.2.1. EMD-ARIMA
4.2.2. EMD-SVM, EMD-RF, EMD-BP, EMD-ELM, EMD-CNN
4.3. Hybrid Models with EMD
4.4. Forecasting Performance Comparisons
- (1)
- Single ARIMA models have better prediction accuracy than the single SVM, RF, BP, ELM and CNN models, except for the 1 h data of the GD and HLJ sites. For 1 h data of the GD site (see Figure 11), the RMSE value of RF (1.095) is slightly lower than the ARIMA model (1.128). At the HLJ site (see Figure 13), from the MAPE metric, the RF model (0.2306) is better than the ARIMA model (0.2542).
- (2)
- The introduction of EMD is beneficial to most single models’ prediction accuracy, but there are exceptions. For instance, both RMSE and MAE values of EMD-CNN model on the 10 min data of the AH site (see Figure 6) seem to show little difference from that of the single CNN model. A similar phenomenon could also be found in the EMD-BP model on the 10 min data of the GD site (see Figure 7).
- (3)
- EMD based hybrid linear/nonlinear models (EMD-ARIMA-SVM, EMD-ARIMA-RF, EMD-ARIMA-BP, EMD-ARIMA-ELM and EMD-ARIMA-CNN) always have the top ranked metric (see the minimum value in these figures), which means that the EMD based hybrid linear/nonlinear models generally have better accuracy and more robust performance than the single models with/without EMD. Quantitative comparisons between hybrid models and single ARIMA models are taken as an example. Maximum accuracy increase of RMSE is found at the 10 min data of the GD site (see Figure 7), from 0.2569 of the ARIMA model to 0.121 of the EMD-ARIMA-RF model. The relative accuracy increase is about 52.9%; the maximum accuracy increase of MAE is found at the 10 min data of the GD site (see Figure 7), from 0.2012 of the ARIMA model to 0.088 of the EMD-ARIMA-RF model. The relative accuracy increase is about 56.26%; the maximum accuracy increase of MAPE is found at the 1 h data of the HLJ site (see Figure 13), from 0.2542 of the ARIMA model to 0.1021 of the EMD-ARIMA-RF model. The relative accuracy increase is about 59.83%. Thus, EMD based hybrid models could greatly improve the forecast accuracy (higher than 50%).
- (4)
- Among the five hybrid models, EMD-ARIMA-RF has the best accuracy on the whole for 10 min data. However, for the 1 h data, no model can always perform well on the whole dataset. EMD-ARIMA-CNN seems to be better as it outperforms other hybrid models on the 1 h data of the AH site (see Figure 10) and GD site (see Figure 11). EMD-ARIMA-SVM and EMD-ARIMA-RF have better precision on the 1 h data of the GS site (see Figure 12) and HLJ site (see Figure 13), respectively.
4.5. Discussions
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| EMD | empirical mode decomposition |
| IMF | intrinsic mode functions |
| ARIMA | autoregressive integrated moving average |
| SVM | support vector machine |
| RF | random forest |
| ANN-BP | artificial neural network with back propagation |
| ELM | extreme learning machines |
| CNN | convolutional neural network |
| MAPE | mean absolute percentage error |
| GARCH | generalized autoregressive conditional heteroscedastic |
| RBF | radial basis function |
| DLN | deep learning networks |
| FEEMD | fast ensemble EMD |
| MLP | Multilayer perceptron |
| ANFIS | Adaptive neuro fuzzy inference system |
| WPD | wavelet packet decomposition |
| WNN | wavelet neural network |
| ENN | Elman neutral network |
| GRNN | generalized regression neural network |
| LFR | low-frequency residuals |
| MIMF | medium-frequency IMF |
| HIMF | high-frequency IMF |
| ADF | Augmented Dickey-Fuller |
| ACF | autocorrelation function |
| PACF | partial autocorrelation function |
References
- Preliminary Statistics Published by WWEA. Available online: https://wwindea.org/blog/2018/02/12/2017-statistics/ (accessed on 12 February 2018).
- Ding, Y.; Shao, C.; Yan, J.; Song, Y.; Zhang, C.; Guo, C. Economical flexibility options for integrating fluctuating wind energy in power systems: The case of China. Appl. Energy 2018, 228, 426–436. [Google Scholar] [CrossRef]
- Jurasz, J.; Mikulik, J.; Krzywda, M.; Ciapala, B.; Janowski, M. Integrating a wind- and solar-powered hybrid to the power system by coupling it with a hydroelectric power station with pumping installation. Energy 2018, 144, 549–563. [Google Scholar] [CrossRef]
- Huang, Y.; Keatley, P.; Chen, H.; Zhang, X.; Rolfe, A.; Hewitt, N. Techno-economic study of compressed air energy storage systems for the grid integration of wind power. Int. J. Energy Res. 2018, 42, 559–569. [Google Scholar] [CrossRef]
- Lee, D. Very short-Term wind power ensemble forecasting without numerical weather prediction through the predictor design. J. Electr. Eng. Technol. 2017, 12, 2177–2186. [Google Scholar]
- Zhang, C.; Zhou, J.; Li, C.; Fu, W.; Peng, T. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 143, 360–376. [Google Scholar] [CrossRef]
- Liu, H.; Duan, Z.; Han, F.; Li, Y. Big multi-step wind speed forecasting model based on secondary decomposition, ensemble method and error correction algorithm. Energy Convers. Manag. 2018, 156, 525–541. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, LSTM network and ELM. Energy Convers. Manag. 2018, 159, 54–64. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, N.; Jia, B.; Peng, T. A novel decomposition-optimization model for short-term wind speed forecasting. Energies 2018, 11, 1752. [Google Scholar] [CrossRef]
- Torres, J.; Garcia, A.; De Blas, M. Forecast of hourly average wind speed with ARMA models in Navarre (Spain). Sol. Energy 2005, 79, 65–77. [Google Scholar] [CrossRef]
- Liu, H.; Erdem, E.; Shi, J. Comprehensive evaluation of ARMA-GARCH(-M) approaches for modeling the mean and volatility of wind speed. Appl. Energy 2011, 88, 724–732. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.; Selvakumar, A.; Kumar, G. Linear and non-linear autoregressive models for short-term wind speed forecasting. Energy Convers. Manag. 2016, 112, 115–124. [Google Scholar] [CrossRef]
- Li, G.; Shi, J. On comparing three artificial neural networks for wind speed forecasting. Appl. Energy 2010, 87, 2313–2320. [Google Scholar] [CrossRef]
- Noorollahi, Y.; Jokar, M.; Kalhor, A. Using artificial neural networks for temporal and spatial wind speed forecasting in Iran. Energy Convers. Manag. 2016, 115, 17–25. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, J.; Li, G. Fine tuning support vector machines for short-term wind speed forecasting. Energy Convers. Manag. 2011, 52, 1990–1998. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Pastor-Sánchez, A.; Prieto, L.; Blanco-Aguilera, A.; Garcia-Herrera, R. Feature selection in wind speed prediction systems based on a hybrid coral reefs optimization–Extreme learning machine approach. Energy Convers. Manag. 2014, 87, 10–18. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, R.; Zhou, Y. Transfer learning for short-term wind speed prediction with deep neural networks. Renew. Energy 2016, 85, 83–95. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, G.; Zhou, W.; Du, W.; Lu, K. Wind speed forecasting using nonlinear-learning ensemble of deep learning time series prediction and extremal optimization. Energy Convers. Manag. 2018, 165, 681–695. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Uzunoglu, M. A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 2014, 34, 243–254. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Boudraa, A.; Cexus, J. EMD-Based Signal Filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Liang, X.; Li, Y. New wind speed forecasting approaches using fast ensemble empirical model decomposition, genetic algorithm, Mind Evolutionary Algorithm and Artificial Neural Networks. Renew. Energy 2015, 83, 1066–1075. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Li, Y. Comparison of new hybrid FEEMD-MLP, FEEMD-ANFIS, wavelet packet-MLP and wavelet packet-ANFIS for wind speed predictions. Energy Convers. Manag. 2015, 89, 1–11. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Liang, X.; Li, Y. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks. Appl. Energy 2015, 157, 183–194. [Google Scholar] [CrossRef]
- Xiao, L.; Qian, F.; Shao, W. Multi-step wind speed forecasting based on a hybrid forecasting architecture and an improved bat algorithm. Energy Convers. Manag. 2017, 143, 410–430. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y. Short-term wind speed forecasting based on fast ensemble empirical mode decomposition, phase space reconstruction, sample entropy and improved back-propagation neural network. Energy Convers. Manag. 2018, 157, 1–12. [Google Scholar] [CrossRef]
- Santhosh, M.; Venkaiah, C.; Vinod Kumar, D. Ensemble empirical mode decomposition based adaptive wavelet neural network method for wind speed prediction. Energy Convers. Manag. 2018, 168, 482–493. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.; Guo, Z.; Yang, W. Research and application of a novel hybrid forecasting system based on multi-objective optimization for wind speed forecasting. Energy Convers. Manag. 2017, 150, 90–107. [Google Scholar] [CrossRef]
- He, Q.; Wang, J.; Lu, H. A hybrid system for short-term wind speed forecasting. Appl. Energy 2018, 226, 756–771. [Google Scholar] [CrossRef]
- Song, J.; Wang, J.; Lu, H. A novel combined model based on advanced optimization algorithm for short-term wind speed forecasting. Appl. Energy 2018, 215, 643–658. [Google Scholar] [CrossRef]
- Wang, J.; Yang, W.; Du, P.; Niu, T. A novel hybrid forecasting system of wind speed based on a newly developed multi-objective sine cosine algorithm. Energy Convers. Manag. 2018, 163, 134–150. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Li, Y. Four wind speed multi-step forecasting models using extreme learning machines and signal decomposing algorithms. Energy Convers. Manag. 2015, 100, 16–22. [Google Scholar] [CrossRef]
- Mi, X.; Liu, H.; Li, Y. Wind speed forecasting method using wavelet, extreme learning machine and outlier correction algorithm. Energy Convers. Manag. 2017, 151, 709–722. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. An experimental investigation of three new hybrid wind speed forecasting models using multi-decomposing strategy and ELM algorithm. Renew. Energy 2018, 123, 694–705. [Google Scholar] [CrossRef]
- Sun, W.; Liu, M. Wind speed forecasting using FEEMD echo state networks with RELM in Hebei, China. Energy Convers. Manag. 2016, 114, 197–208. [Google Scholar] [CrossRef]
- Zheng, W.; Peng, X.; Lu, D.; Zhang, D.; Liu, Y.; Lin, Z.; Lin, L. Composite quantile regression extreme learning machine with feature selection for short-term wind speed forecasting: A new approach. Energy Convers. Manag. 2017, 151, 737–752. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J.; Zeng, G. A hybrid forecasting approach applied to wind speed time series. Renew. Energy 2013, 60, 185–194. [Google Scholar] [CrossRef]
- Zhang, C.; Wei, H.; Zhao, J.; Liu, T.; Zhu, T.; Zhang, K. Short-term wind speed forecasting using empirical mode decomposition and feature selection. Renew. Energy 2016, 96, 727–737. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, Z.; Zhang, K.; Mao, W.; Ma, Y.; Fan, X. A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 136, 439–451. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Lu, H.; Guo, Z. Research and application of a combined model based on variable weight for short term wind speed forecasting. Renew. Energy 2018, 116, 669–684. [Google Scholar] [CrossRef]
- Woodward, W.; Gray, H.; Elliott, A. Applied Time Series Analysis; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Shi, J.; Guo, J.; Zheng, S. Evaluation of hybrid forecasting approaches for wind speed and power generation time series. Renew. Sustain. Energy Rev. 2012, 16, 3471–3480. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Charles, J.; Breiman, L.; Friedman, J.; Olshen, R.A. Classification and Regression Trees; Chapman&Hall: New York, NY, USA, 1984. [Google Scholar]
- Khashei, M.; Bijari, M. An artificial neural network (p,d,q) model for time series forecasting. Expert Syst. Appl. 2010, 37, 479–489. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design; PWS Publishing: Boston, MA, USA, 1996. [Google Scholar]
- Huang, G.; Zhu, Q.; Siew, C. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef] [Green Version]
- Oehmcke, S.; Zielinski, O.; Kramer, O. Input quality aware convolutional LSTM networks for virtual marine sensors. Neurocomputing 2018, 275, 2603–2615. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. Smart deep learning based wind speed prediction model using wavelet packet decomposition, convolutional neural network and convolutional long short term memory network. Energy Convers. Manag. 2018, 166, 120–131. [Google Scholar] [CrossRef]












| Observation Station | Longitude | Latitude | Altitude (m) |
|---|---|---|---|
| AnHui (AH) | E | N | 20 |
| GuangDong (GD) | E | N | 11 |
| GanSu (GS) | E | N | 1500 |
| HeiLongJiang (HLJ) | E | N | 128 |
| Max-Min Values (m/s) | Mean (m/s) | Standard Deviation (m/s) | Skewness | Kurtosis | |
|---|---|---|---|---|---|
| AH-10 min | 9.42-0 | 4.8756 | 1.8278 | 0.1328 | 2.5460 |
| AH-1 h | 10.41-0 | 4.6009 | 1.6494 | 0.1648 | 2.9031 |
| GD-10 min | 11.9-3.0 | 7.4867 | 1.7079 | 0.1357 | 2.6211 |
| GD-1 h | 13.05-0 | 6.7162 | 2.3287 | −0.0621 | 2.5962 |
| GS-10 min | 19.15-0 | 7.2653 | 4.1582 | 0.6476 | 2.9146 |
| GS-1 h | 18.54-0 | 5.8787 | 3.3801 | 0.9460 | 3.8657 |
| HLJ-10 min | 15.97-0 | 9.4065 | 2.7275 | −0.9519 | 4.8296 |
| HLJ-1 h | 16.56-0 | 8.5214 | 2.8915 | −0.3391 | 3.0986 |
| Order | Intercept | ar1 | ma1 | ma2 | ma3 | |
|---|---|---|---|---|---|---|
| AH-10 min | (1,1,1) | 0 | 0.5383 | −0.6908 | - | - |
| AH-1 h | (1,0,1) | 4.6518 | 0.8923 | 0.1126 | - | - |
| GD-10 min | (1,1,1) | 0 | 0.8936 | −0.9664 | - | - |
| GD-1 h | (1,1,3) | 0 | 0.7755 | −0.7402 | −0.0913 | −0.0837 |
| GS-10 min | (0,1,1) | 0 | - | 0.2025 | - | - |
| GS-1 h | (1,1,1) | 0 | −0.1772 | 0.4780 | - | - |
| HLJ-10 min | (0,1,1) | 0 | - | 0.0767 | - | - |
| HLJ-1 h | (1,1,2) | 0 | 0.7807 | −0.8125 | −0.1378 |
| 10 min Data | |||||||
| 0.1 | 0.25 | 1 | 4 | 16 | 100 | 1000 | |
| 0.25 | 0.444 | 0.445 | 0.512 | 1.378 | 1.384 | 1.384 | 1.384 |
| 1 | 0.542 | 0.540 | 0.651 | 1.383 | 1.384 | 1.384 | 1.384 |
| 4 | 0.744 | 0.739 | 0.926 | 1.384 | 1.384 | 1.384 | 1.384 |
| 16 | 1.074 | 1.088 | 1.226 | 1.385 | 1.384 | 1.384 | 1.384 |
| 256 | 1.473 | 1.466 | 1.415 | 1.386 | 1.384 | 1.384 | 1.384 |
| 1 h Data | |||||||
| 0.1 | 0.25 | 1 | 4 | 16 | 100 | 1000 | |
| 0.25 | 0.758 | 0.754 | 0.780 | 1.596 | 1.816 | 1.816 | 1.816 |
| 1 | 0.995 | 0.996 | 1.050 | 1.769 | 1.816 | 1.816 | 1.816 |
| 4 | 1.400 | 1.407 | 1.530 | 1.863 | 1.816 | 1.816 | 1.816 |
| 16 | 1.848 | 1.849 | 1.879 | 1.877 | 1.816 | 1.816 | 1.816 |
| 256 | 1.964 | 1.961 | 1.957 | 1.879 | 1.816 | 1.816 | 1.816 |
| Parameters | AH-10 min | AH-1 h | GD-10 min | GD-1 h | GS-10 min | GS-1 h | HLJ-10 min | HLJ-1 h | |
|---|---|---|---|---|---|---|---|---|---|
| SVM | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 | |
| 0.1 | 0.1 | 0.1 | 0.25 | 0.1 | 0.25 | 0.25 | 0.25 | ||
| RF | Tree number | 50 | 200 | 300 | 700 | 200 | 200 | 100 | 300 |
| Feature number | 3 | 4 | 4 | 3 | 3 | 2 | 2 | 3 | |
| BP | Structures | s4 | s4 | s3 | s1 | s4 | s2 | s3 | s1 |
| ELM | 200 | 60 | 200 | 1000 | 40 | 200 | 40 | 100 | |
| CNN | Channels of convolutional layers are 4, 16 and 32 | ||||||||
| 10 min Data | ||||||||
| Feature Number | Tree Number | |||||||
| 50 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | |
| 1 | 0.9346 | 0.9226 | 0.9188 | 0.927 | 0.9154 | 0.9268 | 0.9266 | 0.926 |
| 2 | 0.9018 | 0.8992 | 0.902 | 0.9122 | 0.9024 | 0.9144 | 0.907 | 0.9044 |
| 3 | 0.912 | 0.9302 | 0.9192 | 0.9244 | 0.9186 | 0.9316 | 0.9236 | 0.9242 |
| 4 | 0.9774 | 0.9564 | 0.9702 | 0.9664 | 0.969 | 0.963 | 0.9752 | 0.962 |
| 1 h Data | ||||||||
| Feature number | Tree Number | |||||||
| 50 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | |
| 1 | 1.0764 | 1.0744 | 1.0598 | 1.062 | 1.0632 | 1.0598 | 1.0598 | 1.0568 |
| 2 | 1.034 | 1.0264 | 1.024 | 1.0244 | 1.022 | 1.0236 | 1.0226 | 1.026 |
| 3 | 1.022 | 1.023 | 1.0268 | 1.0194 | 1.0206 | 1.0204 | 1.0206 | 1.0226 |
| 4 | 1.0278 | 1.0212 | 1.0258 | 1.0288 | 1.026 | 1.0302 | 1.025 | 1.0258 |
| 10 min Data | ||||
| Structures | s1 | s2 | s3 | s4 |
| 0.457 | 0.4544 | 0.483 | 0.4084 | |
| 1 h Data | ||||
| Structures | s1 | s2 | s3 | s4 |
| 1.3316 | 0.6874 | 0.6496 | 0.5652 | |
| 10 min Data | ||||||||
| 20 | 40 | 60 | 80 | 100 | 200 | 500 | 1000 | |
| 0.3790 | 0.1133 | 0.4325 | 0.1629 | 0.0915 | 0.1169 | 0.2867 | 0.2203 | |
| 1 h Data | ||||||||
| 20 | 40 | 60 | 80 | 100 | 200 | 500 | 1000 | |
| 0.3287 | 0.7767 | 0.5471 | 0.5139 | 0.8574 | 0.2672 | 0.7078 | 0.7046 | |
| Order | Intercept | ar1 | ar2 | ar3 | ar4 | ar5 | ma1 | ma2 | ma3 | ma4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AH-10 min HIMF | (2,0,2) | −0.0072 | 0.2677 | −0.3288 | - | - | - | −0.6236 | 0.1867 | - | - |
| AH-10 min MIMF | (2,0,4) | 0.0061 | 1.0409 | −0.5285 | - | - | - | 0.7289 | −0.436 | −0.5381 | −0.1572 |
| AH-10 min LFR | (5,1,3) | 0 | 1.0418 | 0.4034 | −1.0128 | 0.3023 | 0.0501 | 1.6185 | 0.7437 | 0.0824 | - |
| AH-1 h HIMF | (2,0,2) | 0 | 0.4791 | −0.3692 | - | - | - | −0.8025 | 0.2692 | - | - |
| AH-1 h MIMF | (5,0,4) | 0 | 1.954 | −1.711 | 0.6172 | −0.0029 | −0.0971 | −0.3561 | −0.7501 | 0.0919 | 0.3172 |
| AH-1 h LFR | (3,0,4) | 4.6149 | 2.2188 | −1.7555 | 0.515 | - | - | 1.2482 | 0.9488 | 0.6001 | 0.2004 |
| GD-10 min HIMF | (1,0,2) | 0 | 0.1935 | - | - | - | - | −0.3955 | −0.2374 | - | - |
| GD-10 min MIMF | (4,0,4) | 0 | 2.2572 | −2.2493 | 1.1458 | −0.2854 | - | −0.5511 | −0.8215 | 0.2857 | 0.3155 |
| GD-10 min LFR | (4,1,1) | 0 | 2.2822 | −2.1974 | 1.0208 | −0.2126 | - | 0.2556 | - | - | - |
| GD-1 h HIMF | (2,0,2) | 0 | 0.9411 | −0.5456 | - | - | - | −1.1692 | 0.4633 | - | - |
| GD-1 h MIMF | (5,0,4) | 0 | −0.0154 | −0.0193 | −0.4017 | −0.0127 | −0.2514 | 1.9025 | 1.4405 | 0.55 | 0.0407 |
| GD-1 h LFR | (4,1,2) | 0 | 2.9386 | −3.5466 | 2.0825 | −0.5146 | - | −0.3667 | −0.3251 | - | - |
| GS-10 min HIMF | (2,0,1) | 0 | 0.3224 | −0.3344 | - | - | - | −0.4286 | - | - | - |
| GS-10 min MIMF | (2,0,4) | 0 | 1.4583 | −0.7165 | - | - | - | 0.7456 | −0.3988 | −0.7145 | −0.28 |
| GS-10 min LFR | (3,1,2) | 0 | 2.2461 | −1.7913 | 0.494 | - | - | 0.6726 | 0.0931 | - | - |
| GS-1 h HIMF | (3,0,3) | 0 | 1.1227 | −0.2833 | 0.0774 | - | - | −1.1755 | −0.0924 | 0.3303 | - |
| GS-1 h MIMF | (3,0,4) | 0 | 0.6329 | 0.0703 | −0.4106 | - | - | 0.9912 | −0.1967 | −0.6348 | −0.2965 |
| GS-1 h LFR | (4,0,1) | 6.0967 | 3.0507 | −3.6816 | 2.0904 | −0.4697 | - | 0.4522 | - | - | - |
| HLJ-10 min HIMF | (2,0,1) | 0 | 0.1808 | −0.2572 | - | - | - | −0.4975 | - | - | - |
| HLJ-10 min MIMF | (3,0,3) | −0.0176 | 1.6717 | −1.1566 | 0.2937 | - | - | 0.2927 | −0.5431 | −0.3069 | - |
| HLJ-10 min LFR | (3,1,1) | 0 | 2.2675 | −1.8836 | 0.5543 | - | - | 0.57 | - | - | - |
| HLJ-1 h HIMF | (2,0,1) | 0.0101 | 0.3971 | −0.3318 | - | - | - | −0.7131 | - | - | - |
| HLJ-1 h MIMF | (2,0,3) | 0 | 1.2475 | −0.7229 | - | - | - | 0.4612 | −0.4266 | −0.3792 | - |
| HLJ-1 h LFR | (5,1,2) | 0 | 3.0145 | −3.533 | 1.8385 | −0.2716 | −0.0681 | −0.2828 | −0.5816 | - | - |
| EMD-SVM | EMD-RF | EMD-BP | EMD-ELM | EMD-CNN | |||
|---|---|---|---|---|---|---|---|
| Tree Number | Feature Number | Structures | Structures | ||||
| AH-10 min HIMF | 16 | 0.1 | 400 | 4 | s4 | 40 | Same with single CNN |
| AH-10 min MIMF | 4 | 0.1 | 600 | 4 | s1 | 80 | |
| AH-10 min LFR | 0.25 | 0.1 | 500 | 4 | s1 | 200 | |
| AH-1 h HIMF | 4 | 0.1 | 200 | 4 | s2 | 1000 | |
| AH-1 h MIMF | 1 | 0.1 | 700 | 4 | s3 | 60 | |
| AH-1 h LFR | 0.25 | 0.1 | 400 | 4 | s3 | 40 | |
| GD-10 min HIMF | 16 | 0.1 | 200 | 3 | s1 | 60 | |
| GD-10 min MIMF | 1 | 0.1 | 500 | 4 | s3 | 80 | |
| GD-10 min LFR | 0.25 | 0.1 | 100 | 4 | s1 | 40 | |
| GD-1 h HIMF | 4 | 0.1 | 200 | 4 | s3 | 80 | |
| GD-1 h MIMF | 0.25 | 0.1 | 100 | 4 | s2 | 40 | |
| GD-1 h LFR | 0.25 | 0.1 | 200 | 4 | s4 | 80 | |
| GS-10 min HIMF | 1 | 0.1 | 400 | 3 | s3 | 200 | |
| GS-10 min MIMF | 0.25 | 0.1 | 500 | 4 | s3 | 1000 | |
| GS-10 min LFR | 0.25 | 0.1 | 300 | 4 | s2 | 60 | |
| GS-1 h HIMF | 1 | 0.1 | 700 | 3 | s1 | 40 | |
| GS-1 h MIMF | 0.25 | 0.1 | 100 | 4 | s1 | 60 | |
| GS-1 h LFR | 0.25 | 0.1 | 400 | 4 | s1 | 80 | |
| HLJ-10 min HIMF | 4 | 0.1 | 100 | 4 | s1 | 40 | |
| HLJ-10 min MIMF | 1 | 0.1 | 700 | 4 | s2 | 80 | |
| HLJ-10 min LFR | 0.25 | 0.1 | 100 | 4 | s1 | 80 | |
| HLJ-1 h HIMF | 0.25 | 0.1 | 50 | 3 | s2 | 500 | |
| HLJ-1 h MIMF | 0.25 | 0.1 | 300 | 4 | s3 | 100 | |
| HLJ-1 h LFR | 0.25 | 0.1 | 500 | 4 | s4 | 100 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Q.; Wu, H.; Hu, T.; Chu, F. Short-Term Wind Speed Forecasting Based on Signal Decomposing Algorithm and Hybrid Linear/Nonlinear Models. Energies 2018, 11, 2976. https://doi.org/10.3390/en11112976
Han Q, Wu H, Hu T, Chu F. Short-Term Wind Speed Forecasting Based on Signal Decomposing Algorithm and Hybrid Linear/Nonlinear Models. Energies. 2018; 11(11):2976. https://doi.org/10.3390/en11112976
Chicago/Turabian StyleHan, Qinkai, Hao Wu, Tao Hu, and Fulei Chu. 2018. "Short-Term Wind Speed Forecasting Based on Signal Decomposing Algorithm and Hybrid Linear/Nonlinear Models" Energies 11, no. 11: 2976. https://doi.org/10.3390/en11112976
APA StyleHan, Q., Wu, H., Hu, T., & Chu, F. (2018). Short-Term Wind Speed Forecasting Based on Signal Decomposing Algorithm and Hybrid Linear/Nonlinear Models. Energies, 11(11), 2976. https://doi.org/10.3390/en11112976





