Simulation and Comparison of Mathematical Models of PV Cells with Growing Levels of Complexity
Abstract
:1. Introduction
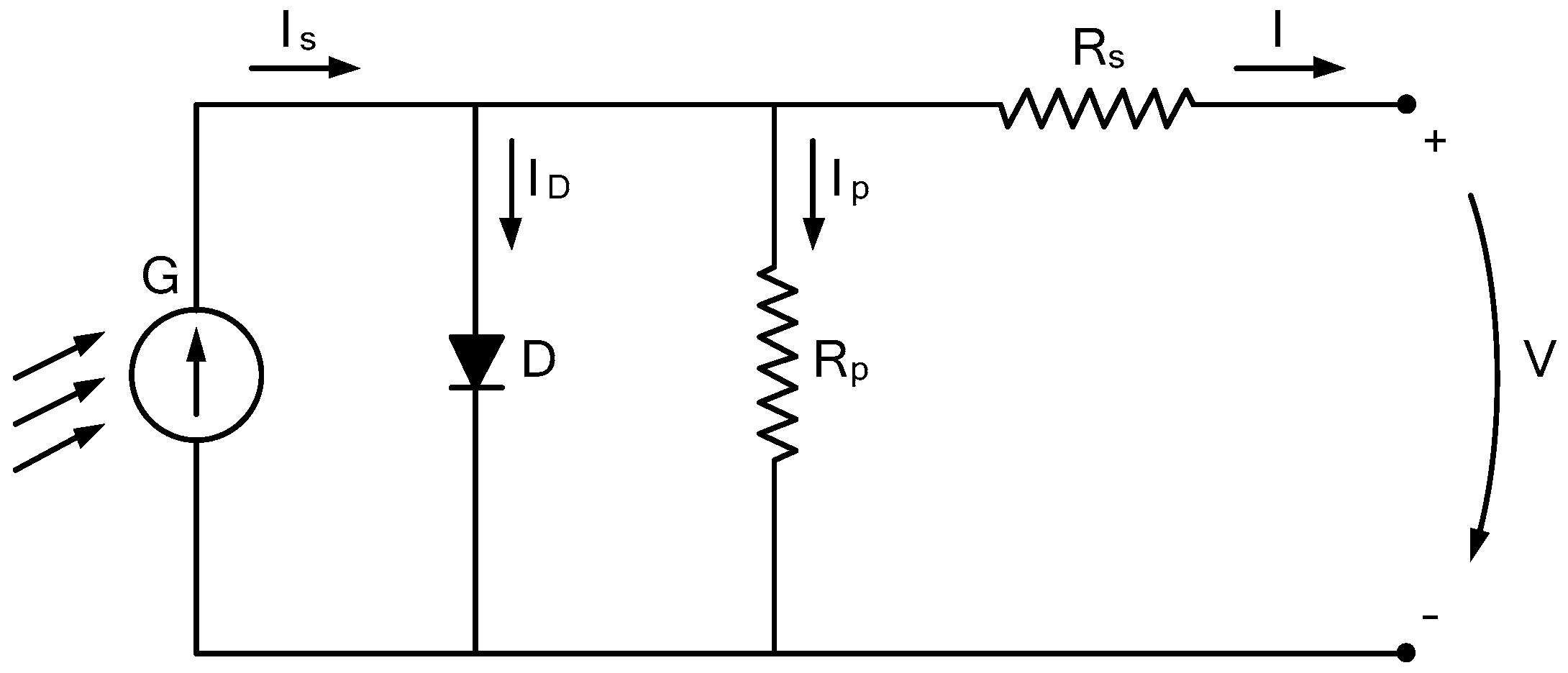
2. Equivalent Circuit with Five Parameters
2.1. Representative Equations
2.2. Analytical Extraction of Parameters
2.3. Simulation
2.3.1. Assessing Equations
2.3.2. Comparison between Constant Rs and Variable Rp
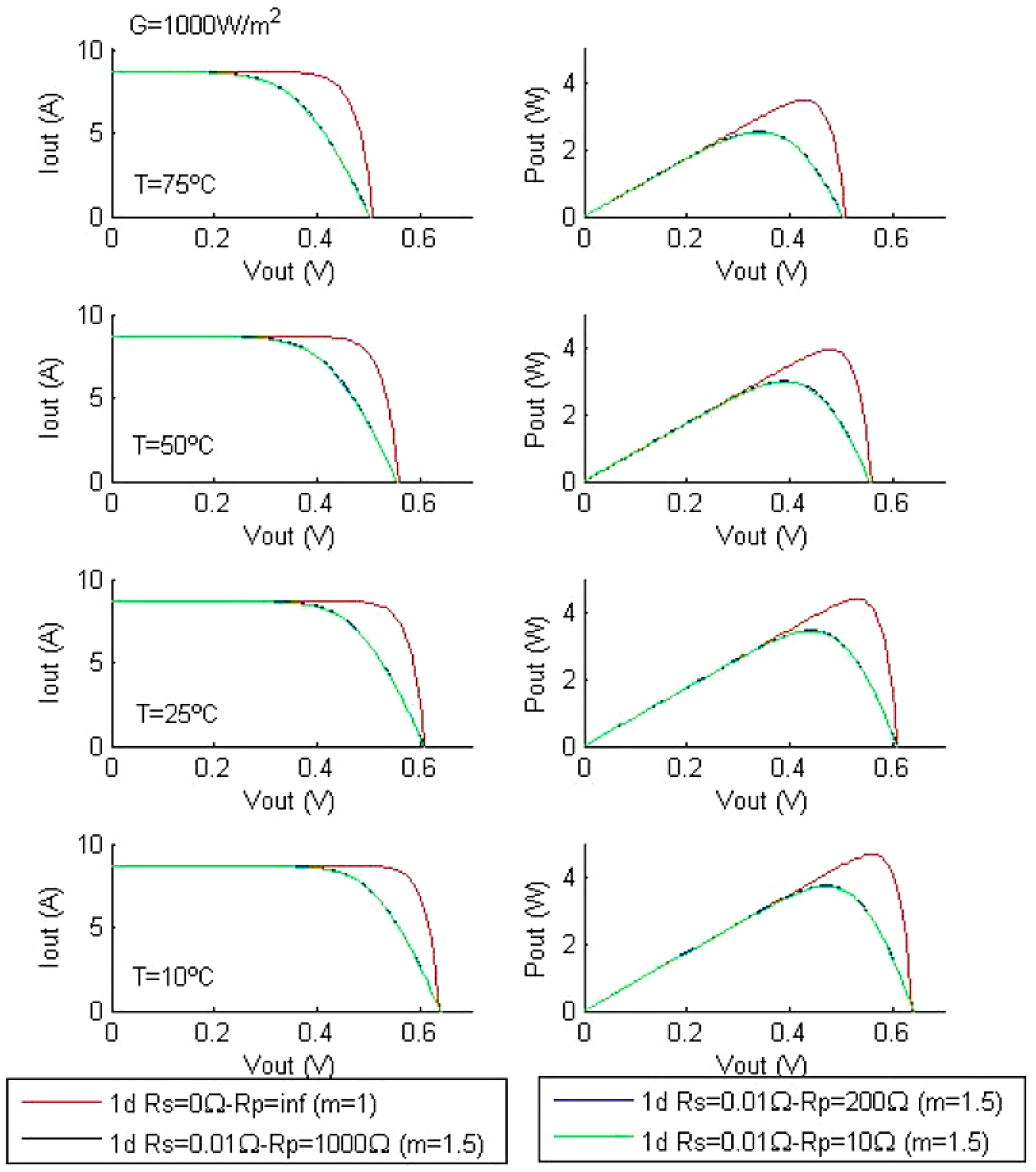
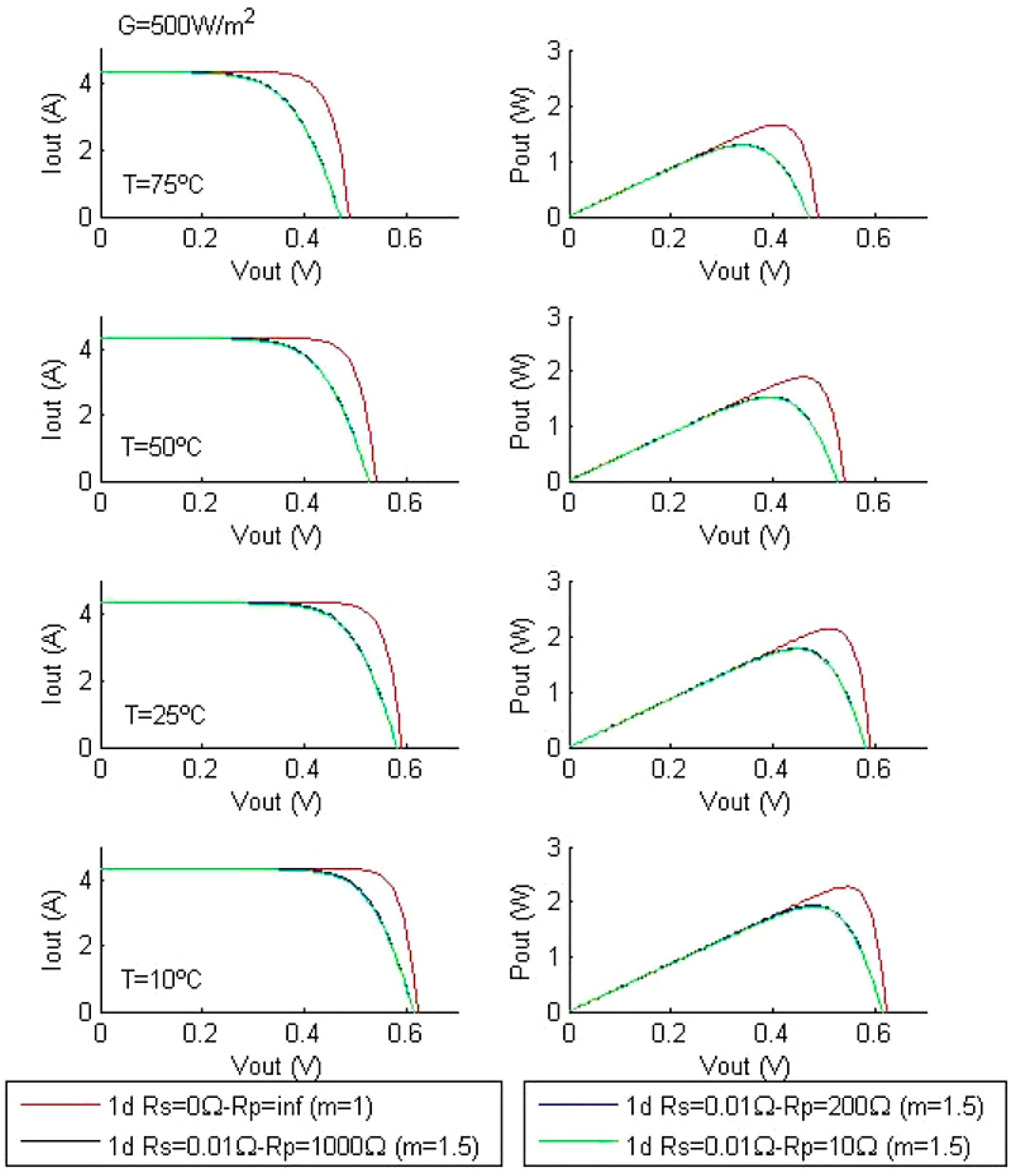
2.3.3. Characteristic Curves in Function of Temperature and Radiation
3. Equivalent Circuit with Seven Parameters
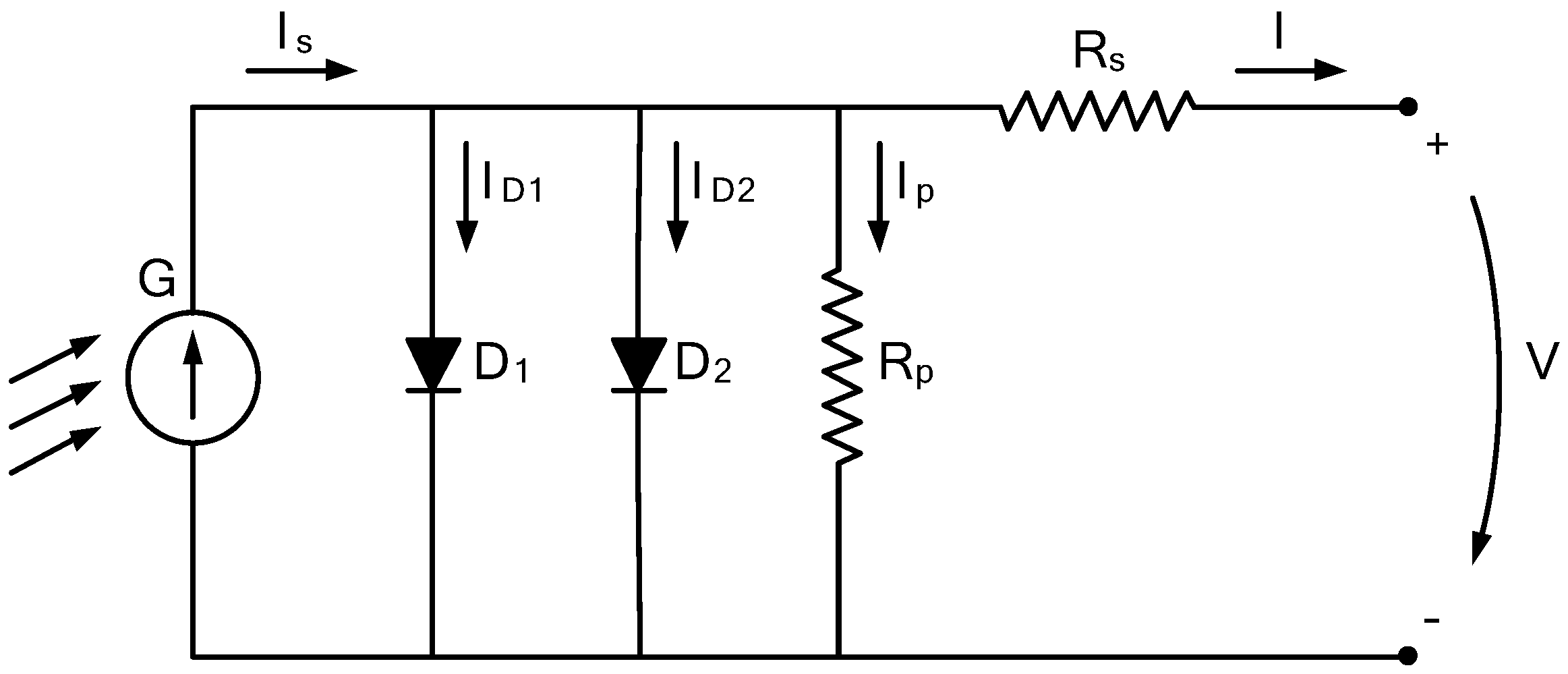
3.1. Representative Equations
3.2. Analytical Extraction of Parameters
3.3. Assessing the Simulation Equations
4. Comparison between the One-Diode Model and the Two-Diode Model
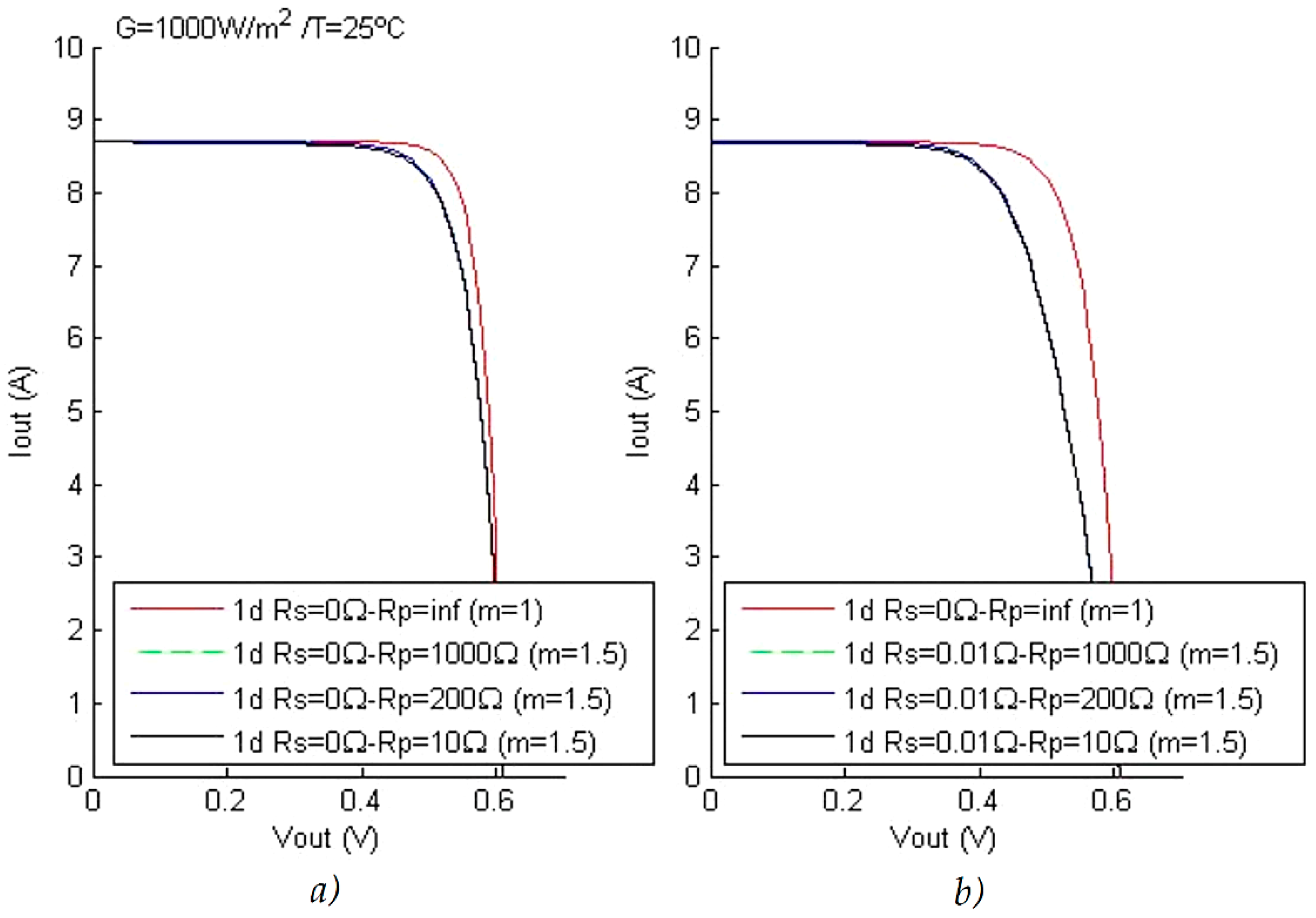
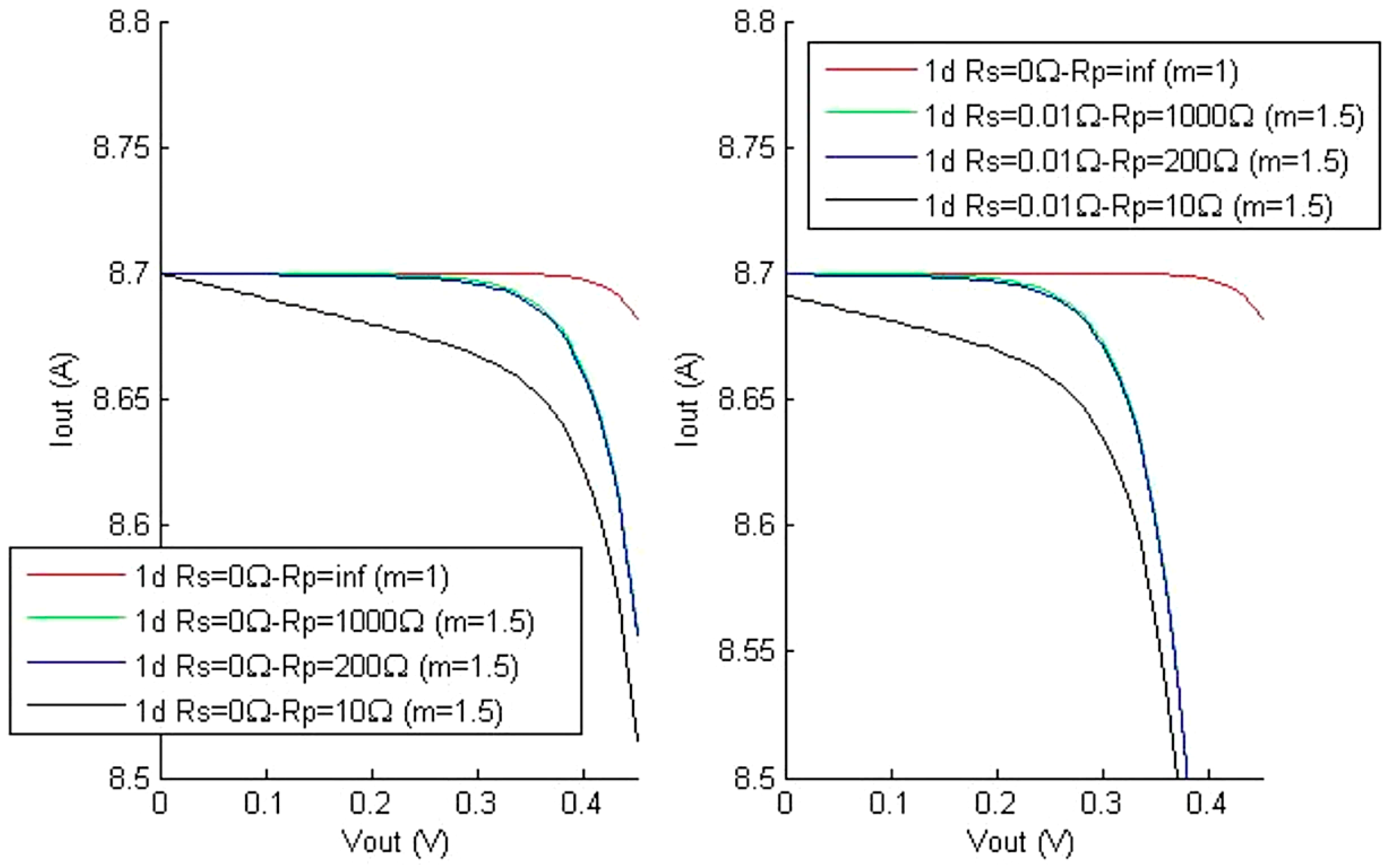
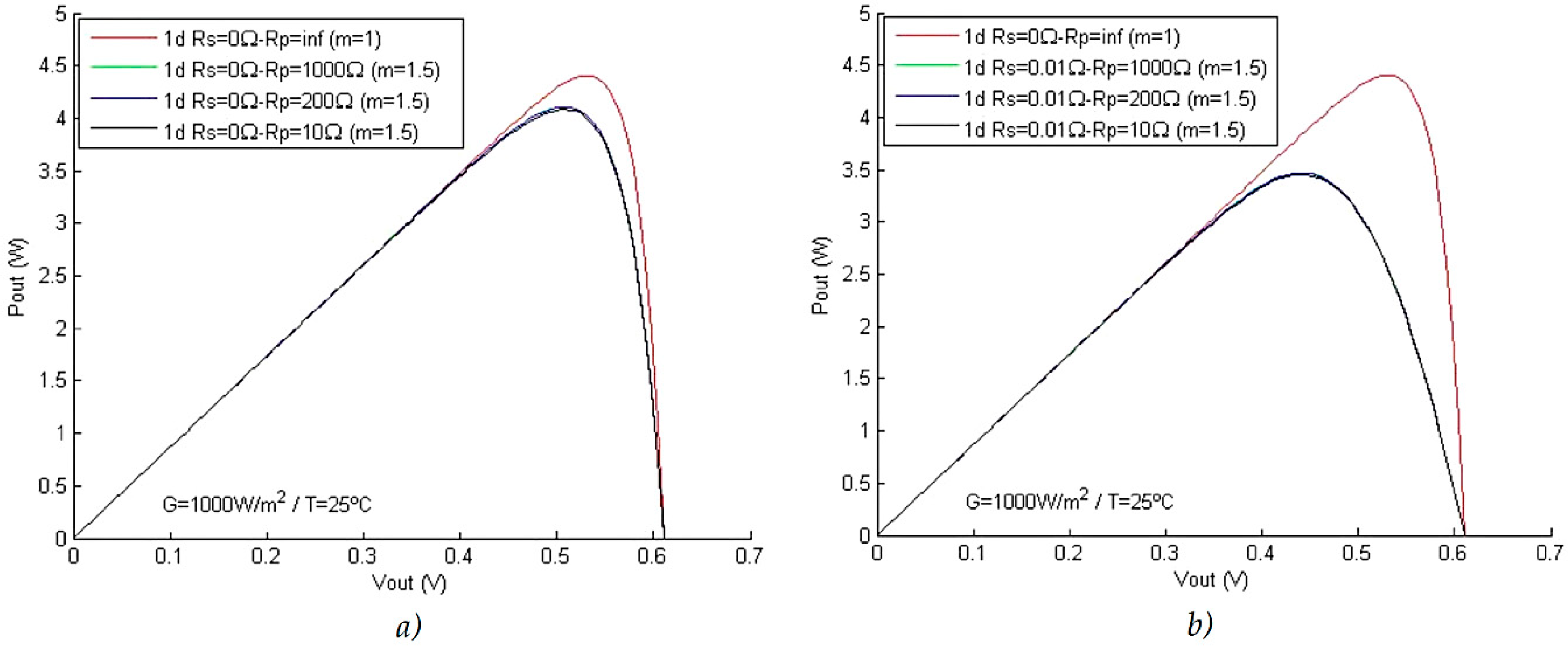
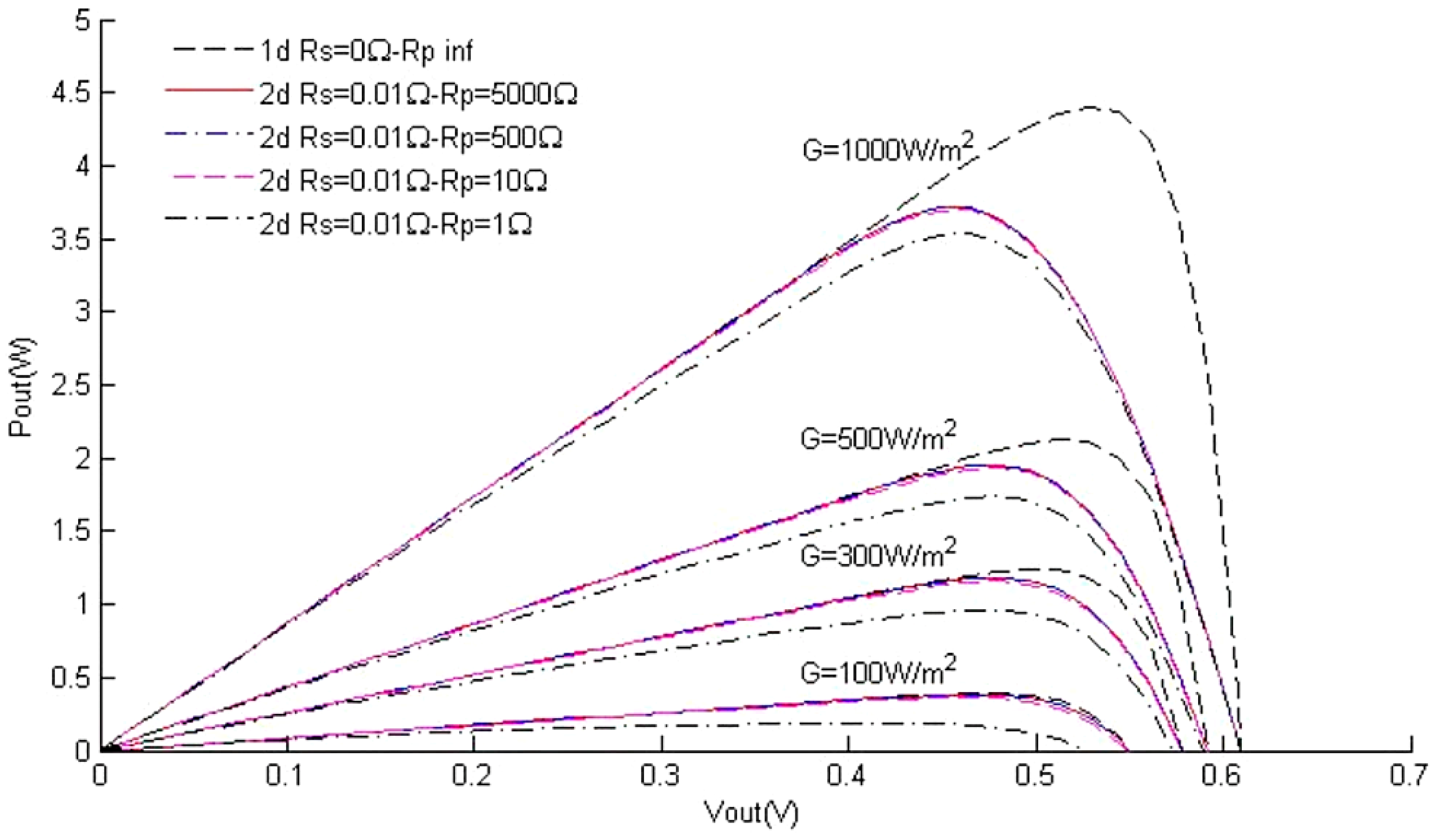
4.1. Characteristic Curves in Function of the Solar Radiation and the Parallel Resistance Rp
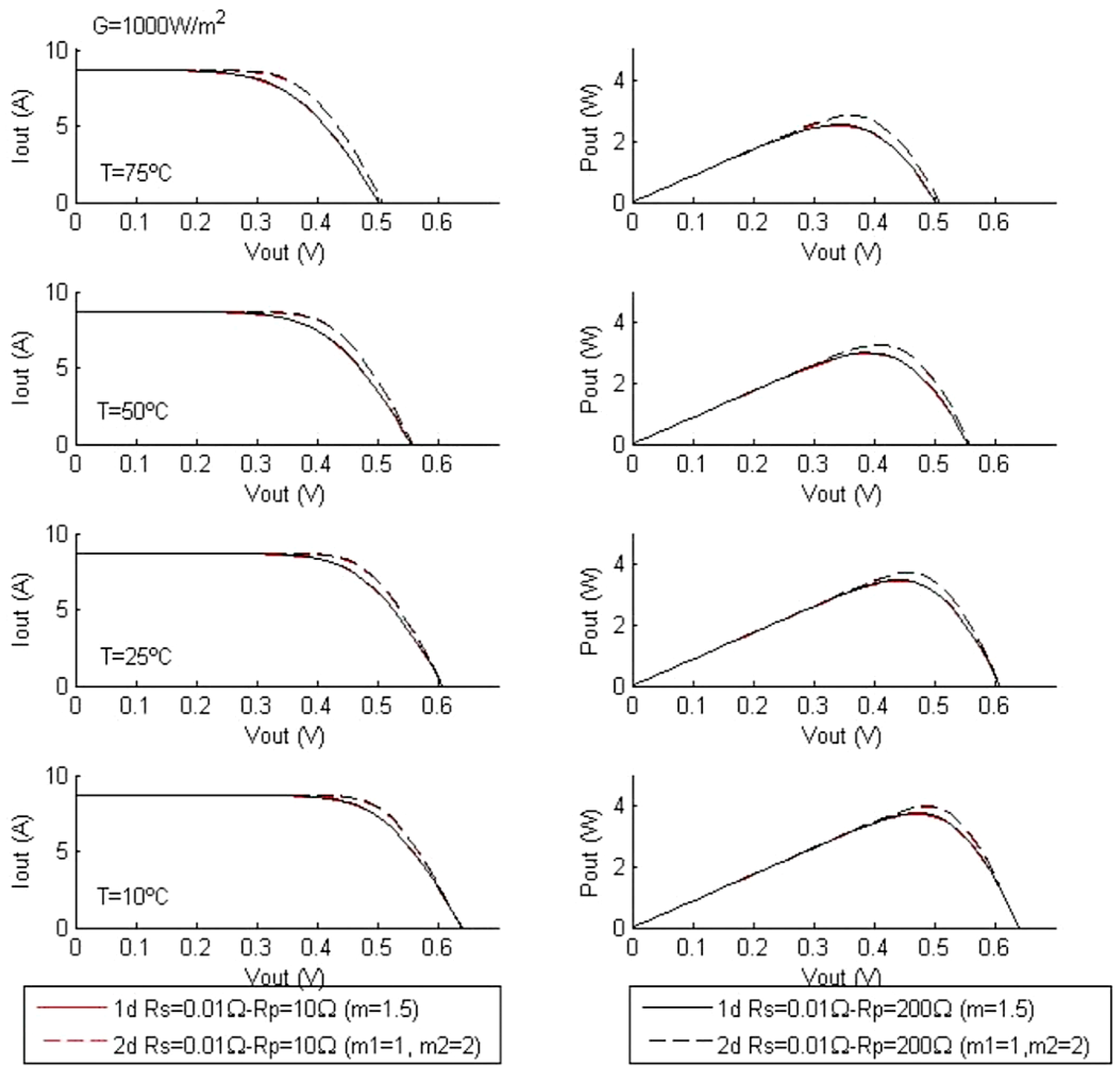
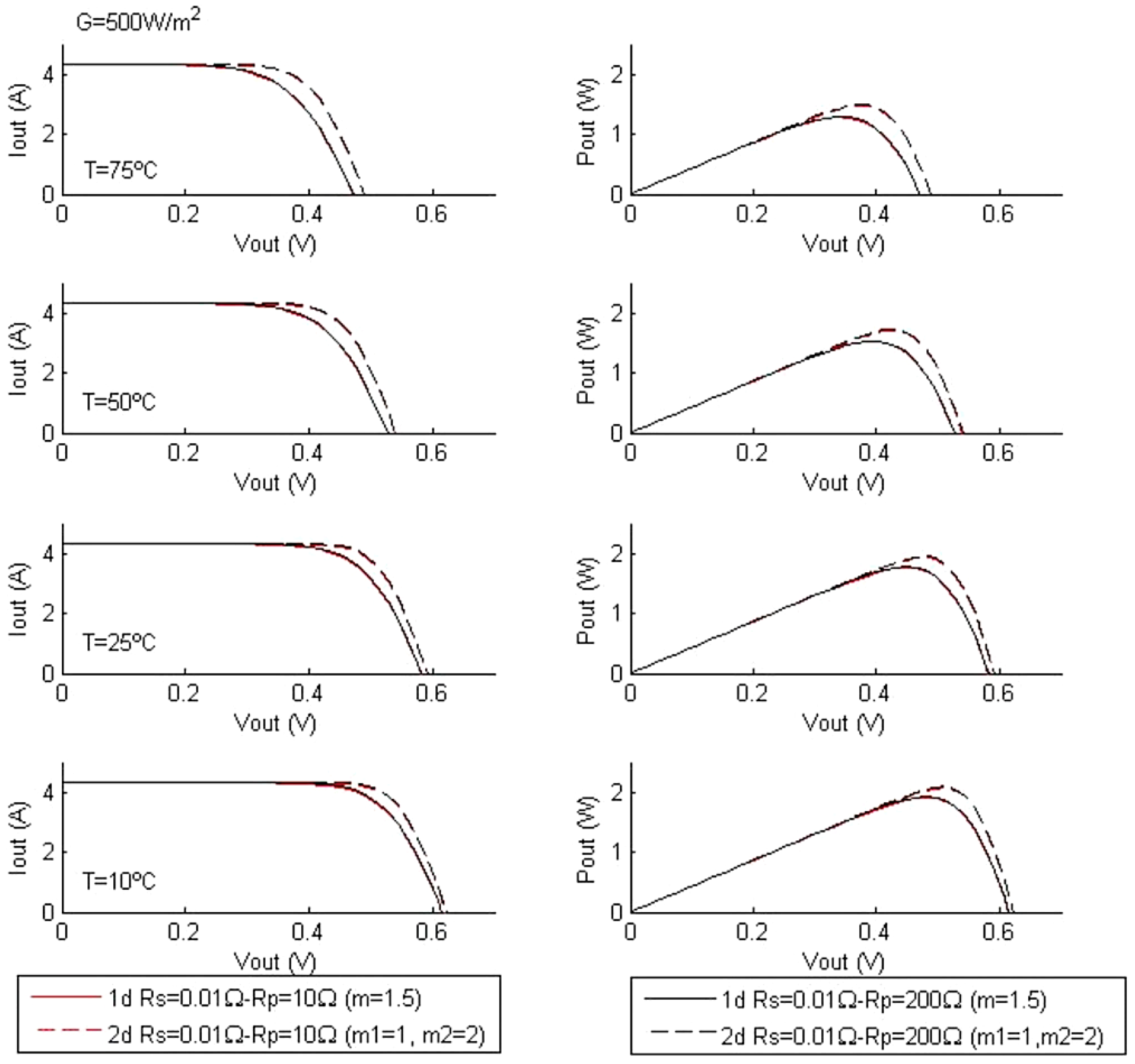
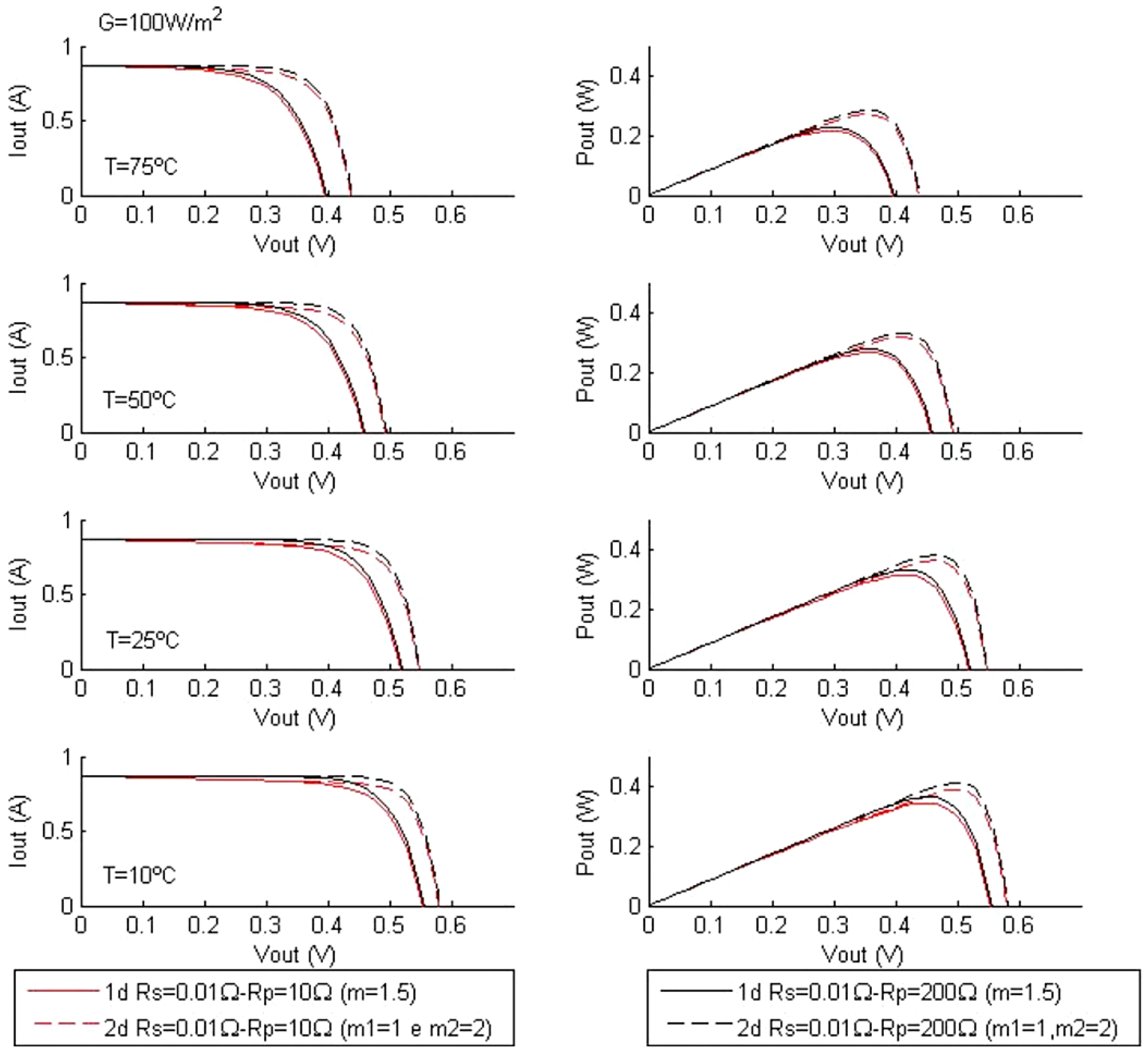
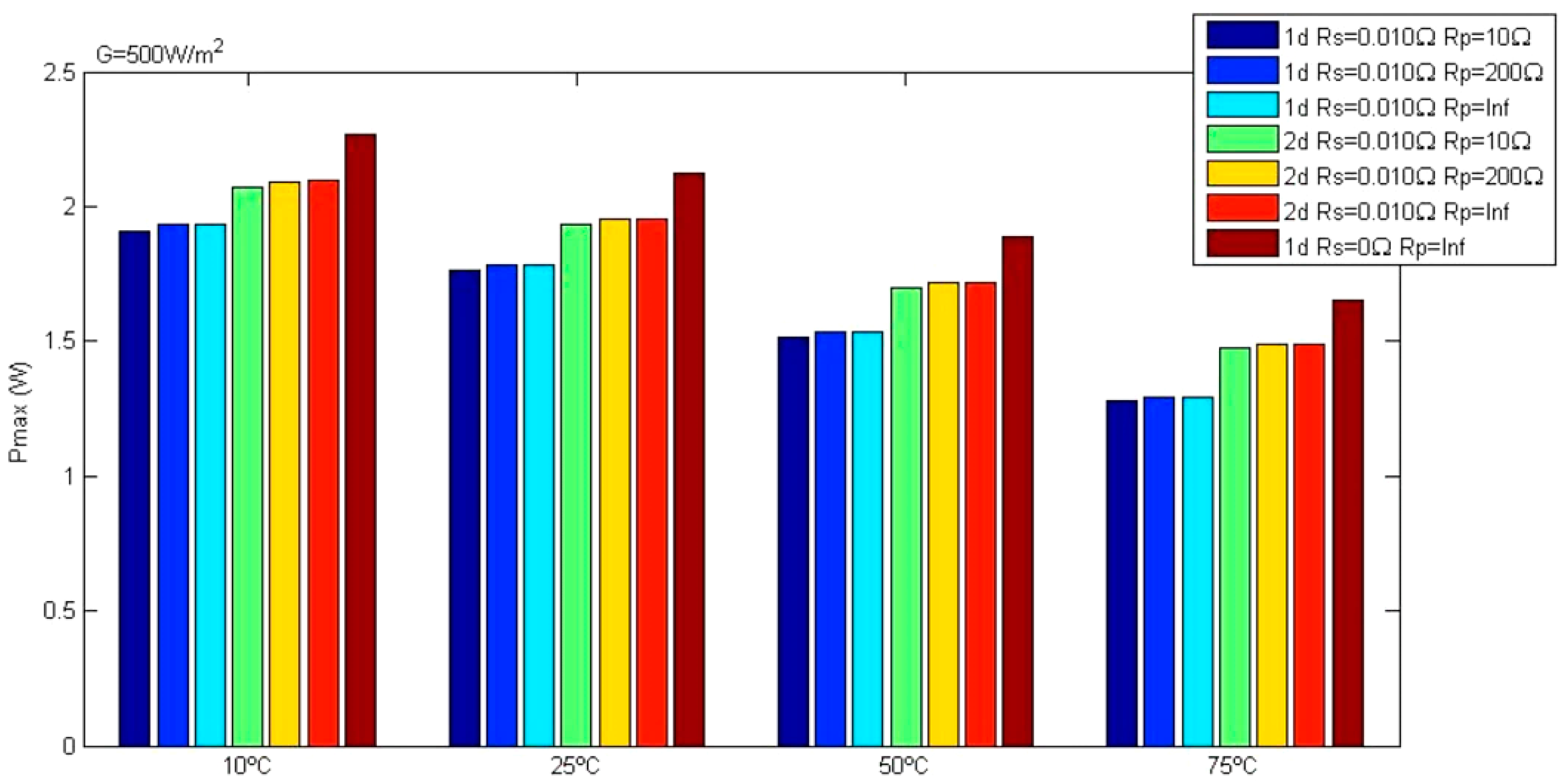
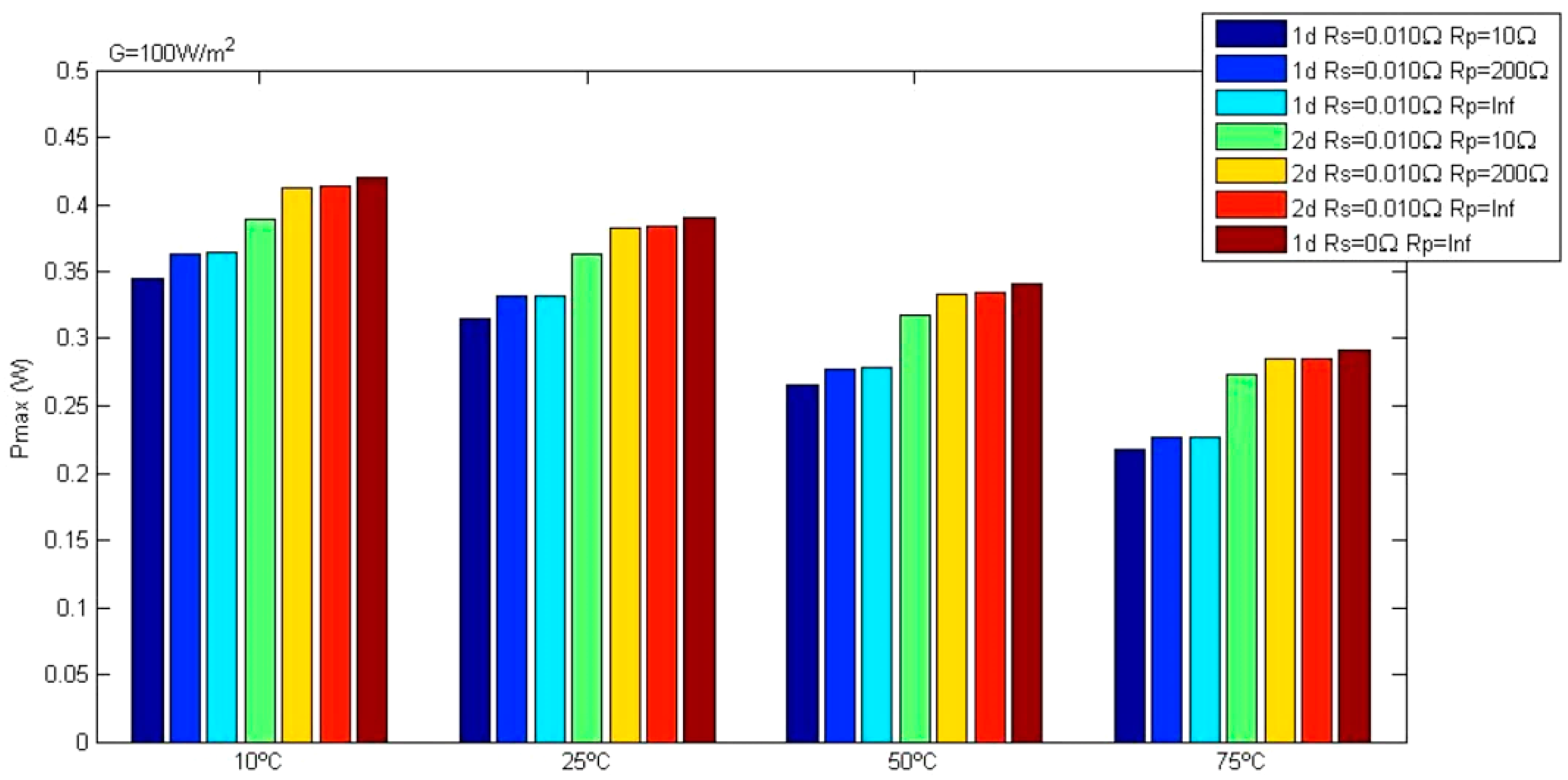
4.2. Characteristic Curves as a Function of Temperature and Parallel Resistance Rp
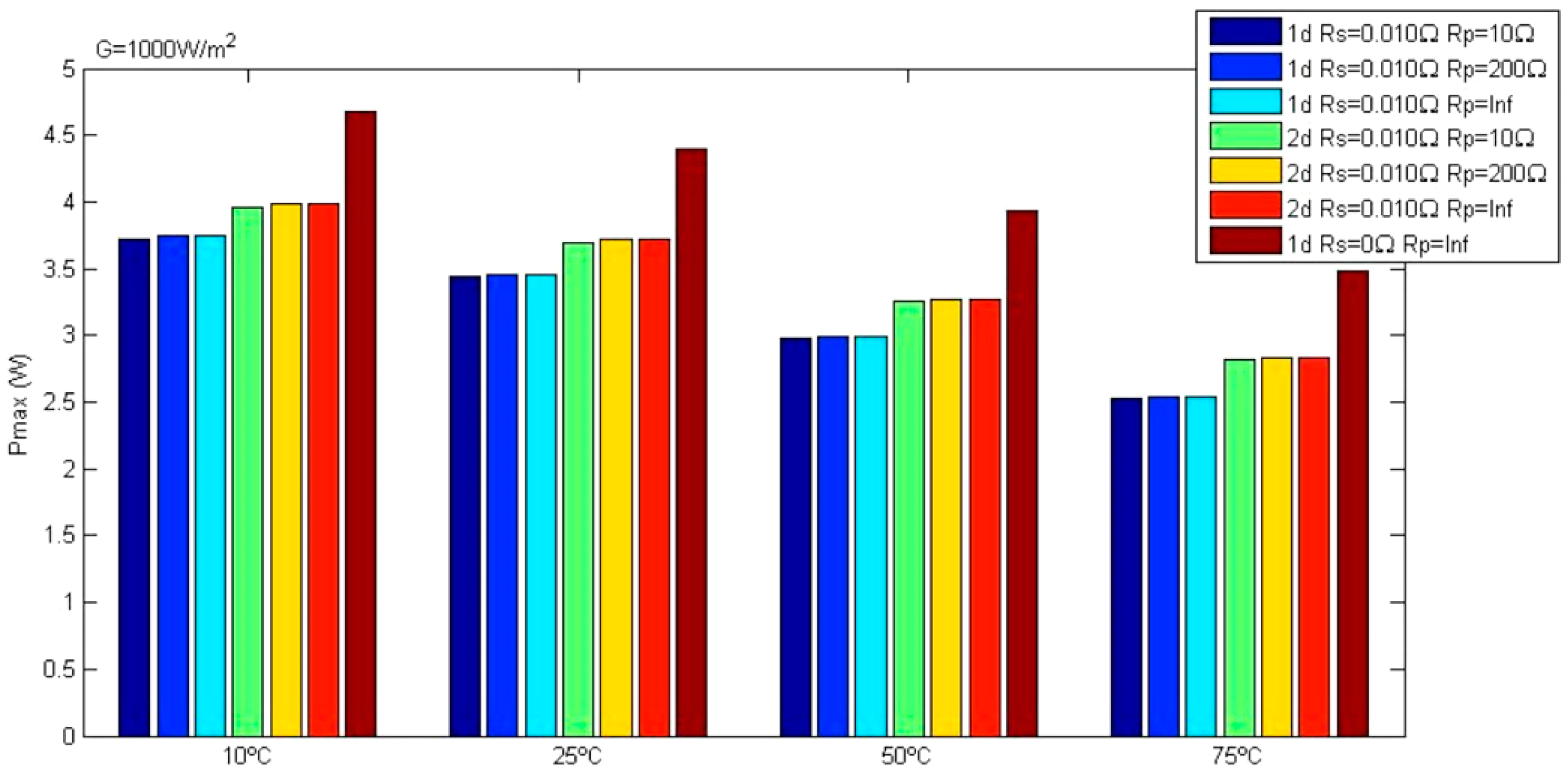
4.3. Comparative Table of Peak Power in the Set of Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M. Economic Analysis of a Photovoltaic System: A Resource for Residential Households. Energies 2017, 10, 814. [Google Scholar] [CrossRef]
- Sansaniwal, S.K.; Sharma, V.; Mathur, J. Energy and exergy analyses of various typical solar energy applications: A comprehensive review. Renew. Sustain. Energy Rev. 2018, 82, 1576–1601. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y.; Guo, S.; Zhou, H. Solar energy storage in the rechargeable batteries. Nano Today 2017, 16, 46–60. [Google Scholar] [CrossRef]
- Teo, J.C.; Tan, R.H.G.; Mok, V.H.; Ramachandaramurthy, V.K.; Tan, C. Impact of Partial Shading on the P-V Characteristics and the Maximum Power of a Photovoltaic String. Energies 2018, 11, 1860. [Google Scholar] [CrossRef]
- Jacobi, N.; Haas, W.; Wiedenhofer, D.; Mayer, A. Providing an economy-wide monitoring framework for the circular economy in Austria: Status quo and challenges. Resour. Conserv. Recycl. 2018, 137, 156–166. [Google Scholar] [CrossRef]
- Yousif, J.; Kazem, H.; Boland, J. Predictive Models for Photovoltaic Electricity Production in Hot Weather Conditions. Energies 2017, 10, 971. [Google Scholar] [CrossRef]
- Chang, B.; Starcher, K. Evaluation of Wind and Solar Energy Investments in Texas. Renew. Energy 2018. [Google Scholar] [CrossRef]
- Gimeno, J.Á.; Llera, E.; Scarpellini, S. Investment Determinants in Self-Consumption Facilities: Characterization and Qualitative Analysis in Spain. Energies 2018, 11, 2178. [Google Scholar] [CrossRef]
- Beránek, V.; Olšan, T.; Libra, M.; Poulek, V.; Sedláček, J.; Dang, M.-Q.; Tyukhov, I. New Monitoring System for Photovoltaic Power Plants’ Management. Energies 2018, 11, 2495. [Google Scholar] [CrossRef]
- Gelsor, N.; Gelsor, N.; Wangmo, T.; Chen, Y.-C.; Frette, Ø.; Stamnes, J.J.; Hamre, B. Solar energy on the Tibetan Plateau: Atmospheric influences. Sol. Energy 2018, 173, 984–992. [Google Scholar] [CrossRef]
- Todde, G.; Murgia, L.; Carrelo, I.; Hogan, R.; Pazzona, A.; Ledda, L.; Narvarte, L. Embodied Energy and Environmental Impact of Large-Power Stand-Alone Photovoltaic Irrigation Systems. Energies 2018, 11, 2110. [Google Scholar] [CrossRef]
- Huang, Y.-P.; Ye, C.-E.; Chen, X. A Modified Firefly Algorithm with Rapid Response Maximum Power Point Tracking for Photovoltaic Systems under Partial Shading Conditions. Energies 2018, 11, 2284. [Google Scholar] [CrossRef]
- Merzifonluoglu, Y.; Uzgoren, E. Photovoltaic power plant design considering multiple uncertainties and risk. Ann. Oper. Res. 2018, 262, 153–184. [Google Scholar] [CrossRef]
- Shah, S.W.A.; Mahmood, M.N.; Das, N. Strategic asset management framework for the improvement of large scale PV power plants in Australia. In Proceedings of the 2016 Australasian Universities Power Engineering Conference (AUPEC), Brisbane, QLD, Australia, 25–28 September 2016; pp. 1–5. [Google Scholar]
- Arefifar, S.A.; Paz, F.; Ordonez, M. Improving Solar Power PV Plants Using Multivariate Design Optimization. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 638–650. [Google Scholar] [CrossRef]
- Peng, Z.; Herfatmanesh, M.R.; Liu, Y. Cooled solar PV panels for output energy efficiency optimisation. Energy Convers. Manag. 2017, 150, 949–955. [Google Scholar] [CrossRef]
- Elibol, E.; Özmen, Ö.T.; Tutkun, N.; Köysal, O. Outdoor performance analysis of different PV panel types. Renew. Sustain. Energy Rev. 2017, 67, 651–661. [Google Scholar] [CrossRef]
- Zhou, Z.; Macaulay, J. An Emulated PV Source Based on an Unilluminated Solar Panel and DC Power Supply. Energies 2017, 10, 2075. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Horan, B.; Rahmani, R.; Maung Than Oo, A.; Stojcevski, A. Efficient Photovoltaic System Maximum Power Point Tracking Using a New Technique. Energies 2016, 9, 147. [Google Scholar] [CrossRef]
- Wang, F.; Wu, X.; Lee, F.C.; Wang, Z.; Kong, P.; Zhuo, F. Analysis of Unified Output MPPT Control in Subpanel PV Converter System. IEEE Trans. Power Electron. 2014, 29, 1275–1284. [Google Scholar] [CrossRef]
- Wang, Z.; Das, N.; Helwig, A.; Ahfock, T. Modeling of multi-junction solar cells for maximum power point tracking to improve the conversion efficiency. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, VIC, Australia, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Das, N.; Wongsodihardjo, H.; Islam, S. A Preliminary Study on Conversion Efficiency Improvement of a Multi-junction PV Cell with MPPT. In Smart Power Systems and Renewable Energy System Integration; Jayaweera, D., Ed.; Studies in Systems, Decision and Control; Springer International Publishing: Cham, Switzerland, 2016; pp. 49–73. ISBN 978-3-319-30427-4. [Google Scholar]
- Das, N.; Wongsodihardjo, H.; Islam, S. Modeling of multi-junction photovoltaic cell using MATLAB/Simulink to improve the conversion efficiency. Renew. Energy 2015, 74, 917–924. [Google Scholar] [CrossRef]
- Das, N.; Ghadeer, A.A.; Islam, S. Modelling and analysis of multi-junction solar cells to improve the conversion efficiency of photovoltaic systems. In Proceedings of the 2014 Australasian Universities Power Engineering Conference (AUPEC), Perth, WA, Australia, 28 September–1 October 2014; pp. 1–5. [Google Scholar]
- Jin, Y.; Hou, W.; Li, G.; Chen, X. A Glowworm Swarm Optimization-Based Maximum Power Point Tracking for Photovoltaic/Thermal Systems under Non-Uniform Solar Irradiation and Temperature Distribution. Energies 2017, 10, 541. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, X.; Ma, Y.; Liu, Y. Analysis of Dynamic Characteristic for Solar Arrays in Series and Global Maximum Power Point Tracking Based on Optimal Initial Value Incremental Conductance Strategy under Partially Shaded Conditions. Energies 2017, 10, 120. [Google Scholar] [CrossRef]
- Tobón, A.; Peláez-Restrepo, J.; Villegas-Ceballos, J.P.; Serna-Garcés, S.I.; Herrera, J.; Ibeas, A. Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods. Energies 2017, 10, 1316. [Google Scholar] [CrossRef]
- Hadji, S.; Gaubert, J.-P.; Krim, F. Real-Time Genetic Algorithms-Based MPPT: Study and Comparison (Theoretical an Experimental) with Conventional Methods. Energies 2018, 11, 459. [Google Scholar] [CrossRef]
- Cubas, J.; Pindado, S.; de Manuel, C. Explicit Expressions for Solar Panel Equivalent Circuit Parameters Based on Analytical Formulation and the Lambert W-Function. Energies 2014, 7, 4098–4115. [Google Scholar] [CrossRef] [Green Version]
- Bahrami, M.; Gavagsaz-Ghoachani, R.; Zandi, M.; Phattanasak, M.; Maranzanaa, G.; Nahid-Mobarakeh, B.; Pierfederici, S.; Meibody-Tabar, F. Hybrid maximum power point tracking algorithm with improved dynamic performance. Renew. Energy 2019, 130, 982–991. [Google Scholar] [CrossRef]
- Rodrigues, E.M.G.; Melício, R.; Mendes, V.M.F.; Catalão, J.P.S. Simulation of a Solar Cell Considering Single-diode Equivalent Circuit Model. Renew. Energy Power Qual. J. 2011, 1, 369–373. [Google Scholar] [CrossRef]
- Rodrigues, E.M.G.; Godina, R.; Pouresmaeil, E.; Catalão, J.P.S. Simulation study of a photovoltaic cell with increasing levels of model complexity. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–5. [Google Scholar]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Carrero, C.; Amador, J.; Arnaltes, S. A single procedure for helping PV designers to select silicon PV modules and evaluate the loss resistances. Renew. Energy 2007, 32, 2579–2589. [Google Scholar] [CrossRef]
- Rodriguez, C.; Amaratunga, G.A.J. Analytic Solution to the Photovoltaic Maximum Power Point Problem. IEEE Trans. Circuits Syst. Regul. Pap. 2007, 54, 2054–2060. [Google Scholar] [CrossRef]
- Patel, H.; Agarwal, V. MATLAB-Based Modeling to Study the Effects of Partial Shading on PV Array Characteristics. IEEE Trans. Energy Convers. 2008, 23, 302–310. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Mohsin, M. Analytical Determination of the Control Parameters for a Large Photovoltaic Generator Embedded in a Grid System. IEEE Trans. Sustain. Energy 2011, 2, 122–130. [Google Scholar] [CrossRef]
- Kim, I.; Kim, M.; Youn, M. New Maximum Power Point Tracker Using Sliding-Mode Observer for Estimation of Solar Array Current in the Grid-Connected Photovoltaic System. IEEE Trans. Ind. Electron. 2006, 53, 1027–1035. [Google Scholar] [CrossRef]
- Xiao, W.; Dunford, W.G.; Capel, A. A novel modeling method for photovoltaic cells. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551), Aachen, Germany, 20–25 June 2004; Volume 3, pp. 1950–1956. [Google Scholar]
- Yusof, Y.; Sayuti, S.H.; Latif, M.A.; Wanik, M.Z.C. Modeling and simulation of maximum power point tracker for photovoltaic system. In Proceedings of the PECon 2004 National Power and Energy Conference, Kuala Lumpur, Malaysia, 29–30 November 2004; pp. 88–93. [Google Scholar]
- Khouzam, K.; Ly, C.; Koh, C.K.; Ng, P.Y. Simulation and real-time modelling of space photovoltaic systems. In Proceedings of the 1994 IEEE 1st World Conference on Photovoltaic Energy Conversion—WCPEC (A Joint Conference of PVSC, PVSEC and PSEC), Waikoloa, HI, USA, 5–9 December 1994; Volume 2, pp. 2038–2041. [Google Scholar]
- Glass, M.C. Improved solar array power point model with SPICE realization. In Proceedings of the 31st Intersociety Energy Conversion Engineering Conference, Washington, DC, USA, 11–16 August 1996; Volume 1, pp. 286–291. [Google Scholar]
- Altas, I.H.; Sharaf, A.M. A Photovoltaic Array Simulation Model for Matlab-Simulink GUI Environment. In Proceedings of the 2007 International Conference on Clean Electrical Power, Capri, Itlay, 21–23 May 2007; pp. 341–345. [Google Scholar]
- Matagne, E.; Chenni, R.; Bachtiri, R.E. A photovoltaic cell model based on nominal data only. In Proceedings of the 2007 International Conference on Power Engineering, Energy and Electrical Drives, Setubal, Portugal, 12–14 April 2007; pp. 562–565. [Google Scholar]
- Tan, Y.T.; Kirschen, D.S.; Jenkins, N. A model of PV generation suitable for stability analysis. IEEE Trans. Energy Convers. 2004, 19, 748–755. [Google Scholar] [CrossRef]
- Kajihara, A.; Harakawa, A.T. Model of photovoltaic cell circuits under partial shading. In Proceedings of the 2005 IEEE International Conference on Industrial Technology, Hong Kong, China, 14–17 December 2005; pp. 866–870. [Google Scholar]
- Benavides, N.D.; Chapman, P.L. Modeling the effect of voltage ripple on the power output of photovoltaic modules. IEEE Trans. Ind. Electron. 2008, 55, 2638–2643. [Google Scholar] [CrossRef]
- Sera, D. Real-Time Modelling, Diagnostics and Optimised MPPT for Residential PV Systems; Institut for Energiteknik, Aalborg Universitet: Aalborg, Denmark, 2009; ISBN 978-87-89179-76-6. [Google Scholar]
- Bashirov, A. Transcendental Functions. In Mathematical Analysis Fundamentals; Bashirov, A., Ed.; Elsevier: Boston, MA, USA, 2014; Chapter 11; pp. 253–305. ISBN 978-0-12-801001-3. [Google Scholar]
- Danandeh, M.A.; Mousavi, G.S.M. Comparative and comprehensive review of maximum power point tracking methods for PV cells. Renew. Sustain. Energy Rev. 2018, 82, 2743–2767. [Google Scholar] [CrossRef]
- Batarseh, M.G.; Za’ter, M.E. Hybrid maximum power point tracking techniques: A comparative survey, suggested classification and uninvestigated combinations. Sol. Energy 2018, 169, 535–555. [Google Scholar] [CrossRef]
- Uoya, M.; Koizumi, H. A Calculation Method of Photovoltaic Array’s Operating Point for MPPT Evaluation Based on One-Dimensional Newton–Raphson Method. IEEE Trans. Ind. Appl. 2015, 51, 567–575. [Google Scholar] [CrossRef]
- Gow, J.A.; Manning, C.D. Development of a photovoltaic array model for use in power-electronics simulation studies. IEE Proc.—Electr. Power Appl. 1999, 146, 193–200. [Google Scholar] [CrossRef]
- Walker, G.R. Evaluating MPPT converter topologies using a Matlab PV model. Aust. J. Electr. Electron. Eng. 2001, 21, 49–55. [Google Scholar]
- Ishaque, K.; Salam, Z.; Taheri, H. Simple, fast and accurate two-diode model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2011, 95, 586–594. [Google Scholar] [CrossRef]
- Nishioka, K.; Sakitani, N.; Uraoka, Y.; Fuyuki, T. Analysis of multicrystalline silicon solar cells by modified 3-diode equivalent circuit model taking leakage current through periphery into consideration. Sol. Energy Mater. Sol. Cells 2007, 91, 1222–1227. [Google Scholar] [CrossRef]
- Enrique, J.M.; Durán, E.; Sidrach-de-Cardona, M.; Andújar, J.M. Theoretical assessment of the maximum power point tracking efficiency of photovoltaic facilities with different converter topologies. Sol. Energy 2007, 81, 31–38. [Google Scholar] [CrossRef]
- Chowdhury, S.; Chowdhury, S.P.; Taylor, G.A.; Song, Y.H. Mathematical modelling and performance evaluation of a stand-alone polycrystalline PV plant with MPPT facility. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar]
- Salam, Z.; Ishaque, K.; Taheri, H. An improved two-diode photovoltaic (PV) model for PV system. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems 2010 Power, New Delhi, India, 20–23 December 2010; pp. 1–5. [Google Scholar]
- Gow, J.A.; Manning, C.D. Development of a model for photovoltaic arrays suitable for use in simulation studies of solar energy conversion systems. In Proceedings of the 1996 Sixth International Conference on Power Electronics and Variable Speed Drives, Nottingham, UK, 23–25 September 1996; pp. 69–74. [Google Scholar]
- Hyvarinen, J.; Karila, J. New analysis method for crystalline silicon cells. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 1–18 May 2003; Volume 2, pp. 1521–1524. [Google Scholar]
- Bowden, S.; Rohatgi, A. Rapid and Accurate Determination of Series Resistance and Fill Factor Losses in Industrial Silicon Solar Cells. In Proceedings of the 17th European Photovoltaic Solar Energy Conference, Munich, Germany, 22–26 October 2001. [Google Scholar]
- Sandrolini, L.; Artioli, M.; Reggiani, U. Numerical method for the extraction of photovoltaic module double-diode model parameters through cluster analysis. Appl. Energy 2010, 87, 442–451. [Google Scholar] [CrossRef]
- Dolan, J.A.; Lee, R.; Yeh, Y.; Yeh, C.; Nguyen, D.Y.; Ben-Menahem, S.; Ishihara, A.K. Neural network estimation of photovoltaic I–V curves under partially shaded conditions. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 1358–1365. [Google Scholar]
- Ishaque, K.; Salam, Z.; Taheri, H.; Shamsudin, A. A critical evaluation of EA computational methods for Photovoltaic cell parameter extraction based on two diode model. Sol. Energy 2011, 85, 1768–1779. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manuel Godinho Rodrigues, E.; Godina, R.; Marzband, M.; Pouresmaeil, E. Simulation and Comparison of Mathematical Models of PV Cells with Growing Levels of Complexity. Energies 2018, 11, 2902. https://doi.org/10.3390/en11112902
Manuel Godinho Rodrigues E, Godina R, Marzband M, Pouresmaeil E. Simulation and Comparison of Mathematical Models of PV Cells with Growing Levels of Complexity. Energies. 2018; 11(11):2902. https://doi.org/10.3390/en11112902
Chicago/Turabian StyleManuel Godinho Rodrigues, Eduardo, Radu Godina, Mousa Marzband, and Edris Pouresmaeil. 2018. "Simulation and Comparison of Mathematical Models of PV Cells with Growing Levels of Complexity" Energies 11, no. 11: 2902. https://doi.org/10.3390/en11112902
APA StyleManuel Godinho Rodrigues, E., Godina, R., Marzband, M., & Pouresmaeil, E. (2018). Simulation and Comparison of Mathematical Models of PV Cells with Growing Levels of Complexity. Energies, 11(11), 2902. https://doi.org/10.3390/en11112902






