1. Introduction
The vehicle steering system has experienced several stages, such as manual steering, hydraulic steering, electro-hydraulic steering, electric power steering and by-wire steering. However, in order to achieve the latter two, the structure becomes more complicated because one or two extra motors are required [
1]. The appearance of four-wheel independent-drive (4WID) electric vehicles (EVs) opens up the possibility of differential steering system (DSS) by coupled control of left and right in-wheel motors (IWM), which eliminates the restrictions of a traditional steering system completely [
2]. With the emergence of intelligent vehicle systems (IVS), the 4WID system can also be used to solve the path tracking problem [
3,
4]. However, there are three functions of the DSS: (1) Steering the vehicle without the lateral turning of the wheel, i.e., skid steering [
5,
6]; (2) Assisting the driver to steer the vehicle, that is, differential drive assisted steering (DDAS) [
1,
2,
7,
8]; (3) Steering the vehicle instead of the regular steering system [
9,
10,
11,
12,
13]. Skid steering was realized by giving a tire speed differential between the left and right tires [
5,
6]. And the wheel torque difference between the left and right tires, which controlled the tire velocity difference, was defined as a function of the steering wheel angle. In addition, a stability compensator for the adhesion limit of tire/load and the yaw rate and yaw acceleration are used as control variables. However, the needed differential driving torque is not given in the paper [
5].
A closed loop control method of differential drive assisted steering (DDAS) was proposed, which includes a reference steering wheel torque (RSWT) design module and an integral anti-windup variable PI control module. The former was to design a three-dimensional characteristic curve of torque and steering wheel angle at different vehicle speeds, and the latter was aiming to address the saturation of motor’s output torque. The simulation results showed that the RSWT can be tracked perfectly by the DDAS, drivers’ handling efforts were reduced and the vehicle steering performance was improved [
1]. A multidiscipline collaborative optimization model of the differential steering system was built with the steering economy as the main system, and the steering flexibility, the steering road feel and the mechanic character of the steering sensors as the subsystems. And the main system and the subsystems were optimized by the multi-island algorithm and the sequential quadratic programming algorithm. The simulation results show that the differential steering system can have good economy, good steering road feel, good steering flexibility and good mechanic character of the steering sensors [
2]. The DDAS control system, the drive torque distribution and the compensation control system were designed. The proportional–integral (PI) feedback control loop was employed to track the reference steering effort. In addition, the traction control subsystem and the direct yaw moment control subsystem were both employed to make the DDAS work as well as wished [
7]. The structure and basic theory of the DSS were discussed and its dynamic model was built. A H
∞ mixed sensitivity controller is designed to suppress the model uncertainties and road disturbance. The simulation results verified the efficacy of the DSS with the designed controller [
8]. However, they are aimed at mitigating the driver’s steering efforts.
By regulating the four wheels to the desired differential speed base on the reference vehicle velocity, kinematic model of the distributed wheels, combined with Ackermann–Jeant and steering model, was introduced to achieve electrical differential steering for 4WID EVs. The effectiveness of the proposed control strategy was demonstrated by the simulation and experimental study [
9]. A continuous steering stability controller based on energy-saving torque distribution algorithm was proposed for four-wheeled built-in motor independent driving electric vehicle. The simulation results showed that, compared with the traditional servo controller and the ordinary continuous controller, the proposed controller can significantly reduce the energy consumption and improve the steering stability of the vehicle [
10]. The literature [
11,
12,
13] investigates the DSS in the case of the complete failure of the regular steering system. To achieve the yaw stabilization, a robust H
∞ output-feedback controller of the DSS was designed and parametric uncertainties for the cornering stiffness and the external disturbances were considered to guarantee the vehicle robustness [
11]. A multiple-disturbances observer-based composite nonlinear feedback (CNF) approach was proposed to improve the transient performance of the fault-tolerant control with the DDAS, and the disturbance observer was designed to estimate the external disturbances with unknown bounds. CarSim-Simulink joint simulation results verified the efficacy of the proposed controller [
12]. To realize the yaw control when the active front steering entirely breaks down and guarantee the transient control performance, a disturbance observer based integral sliding mode control (ISMC) strategy was designed to deal with the unknown mismatched disturbances, which was addressed by an adaptive super-twisting control approach. And the composite nonlinear feedback technique was applied to design the controller’s nominal part to depress overshoots and avoid steady-state errors considering the tire force saturations. The simulation results verified the effectiveness of the proposed control approach in the case of the steering failure [
13].
The innovation points are as follows: (1) Based on the reference model, the steering function of SSV and DSV are realized by the differential driving torque between the two sides of the front wheels instead of the normal desired differential speed; (2) An simple and practicable observer is constructed to estimate the actual sideslip angle; (3) The vehicle has parametric uncertainties, such as tire stiffness perturbation and external disturbances, and there is no direct relationship between handling wheel angle and differential driving torque of the left and right side wheels, thus two kinds of SMC controller are designed; (4) Contrast and analysis of the SSV and the DSV with controllers is carried out, such as the response curves, the needed differential torque and robustness.
The article structure is as follows: The SSV and DSV models, and reference model are described in
Section 2. Sideslip angle observer and two kinds of SMC controller based on the reference model are designed in
Section 3.
Section 4 is the joint simulation based on CarSim (MATLAB, R2012a, mathworks, Natick, MA, USA) and Simulink. (CarSim, 8.02, MSC software, Los Angeles, CA, USA)
Section 5 is the conclusion.
2. Vehicle Models and Problem Formulation
In this section, we will first present three kinds of vehicle models, including an SSV model, a DSV model and a reference model. Here vehicle models are based on the following assumptions: (1) The lateral acceleration is small and the roll motion can be ignored; (2) The left and right tire slip angles are equal; (3) The front and rear tire lateral forces are proportional to the tire slip angles. Then the problem formulation will be proposed.
The difference between SSV and DSV is that the former has no mechanical steering mechanism. However, both of them depend on the differential driving torque between the two sides of front wheels, but for the latter, the torque will also contribute to the generation of the front wheel angles. The SSV obtains steering yaw moment by increasing the speed of outer wheels and decreasing the speed of inner wheels, other than swinging the steered wheels.
2.1. Skid Steering Vehicle Model
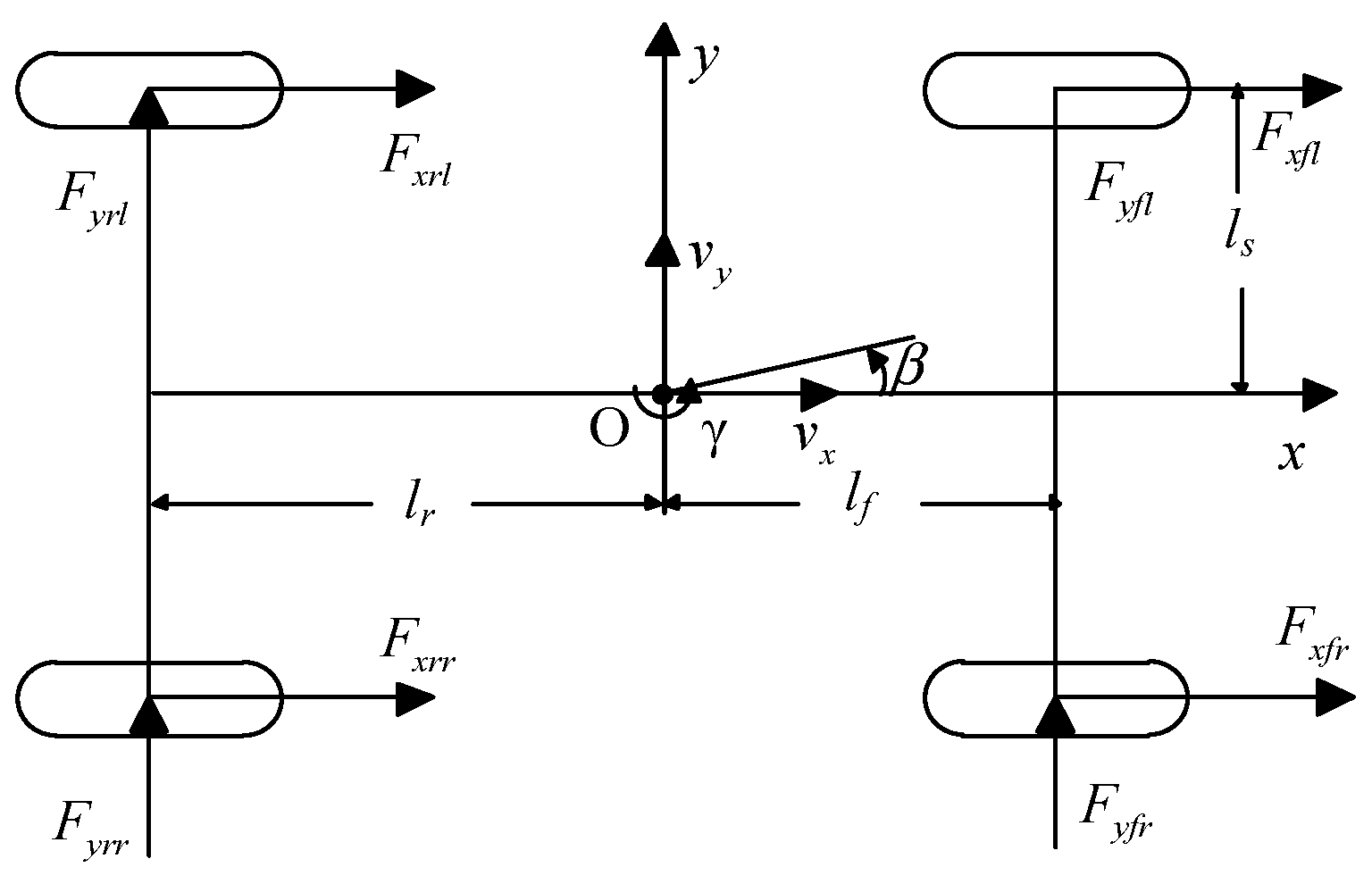
The forces acting on the vehicle body are shown in
Figure 1, where
Fxij (
i =
f,
r, j =
l,
r) is the tire longitudinal force of the left/right front/rear wheel,
Fyij (
i =
f,
r, j =
l,r) is the tire lateral force of the left/right front/rear wheel.
The lateral and yaw motion of the EV are modeled as:
where
m is the total vehicle mass,
ux is the longitudinal velocity at the CG point,
β is the sideslip angle,
γ is the yaw rate
, Iz is the yaw moment of inertia,
ls is the half of wheel track,
R is the radius of front wheel,
lf and
lr are the distances from the center of gravity (CG) to the front and rear axles, Δ
M is the differential driving torque between the two sides of the front wheels,
Tfr and
Tfl are the right and left driving torques of the front wheel.
Here a static wheel model is adopted and wheel rotational dynamics are not considered. Define the state variable and system input as
x(
t) = [
β, γ]
T,
u(
t) = Δ
M, the state equation of the two degree-of-freedom (2-DOF) model can be given as:
where
Considering that the tire cornering stiffness always fluctuates due to the change of the road conditions, they can be expressed as:
where
kf0 and
kr0 are the nominal values of the front and rear tire cornering stiffness, Δ
kf and Δ
kr are the corresponding perturbation values.
Then Equation (3) can be written as:
where
2.2. Differential Steering Vehicle Model
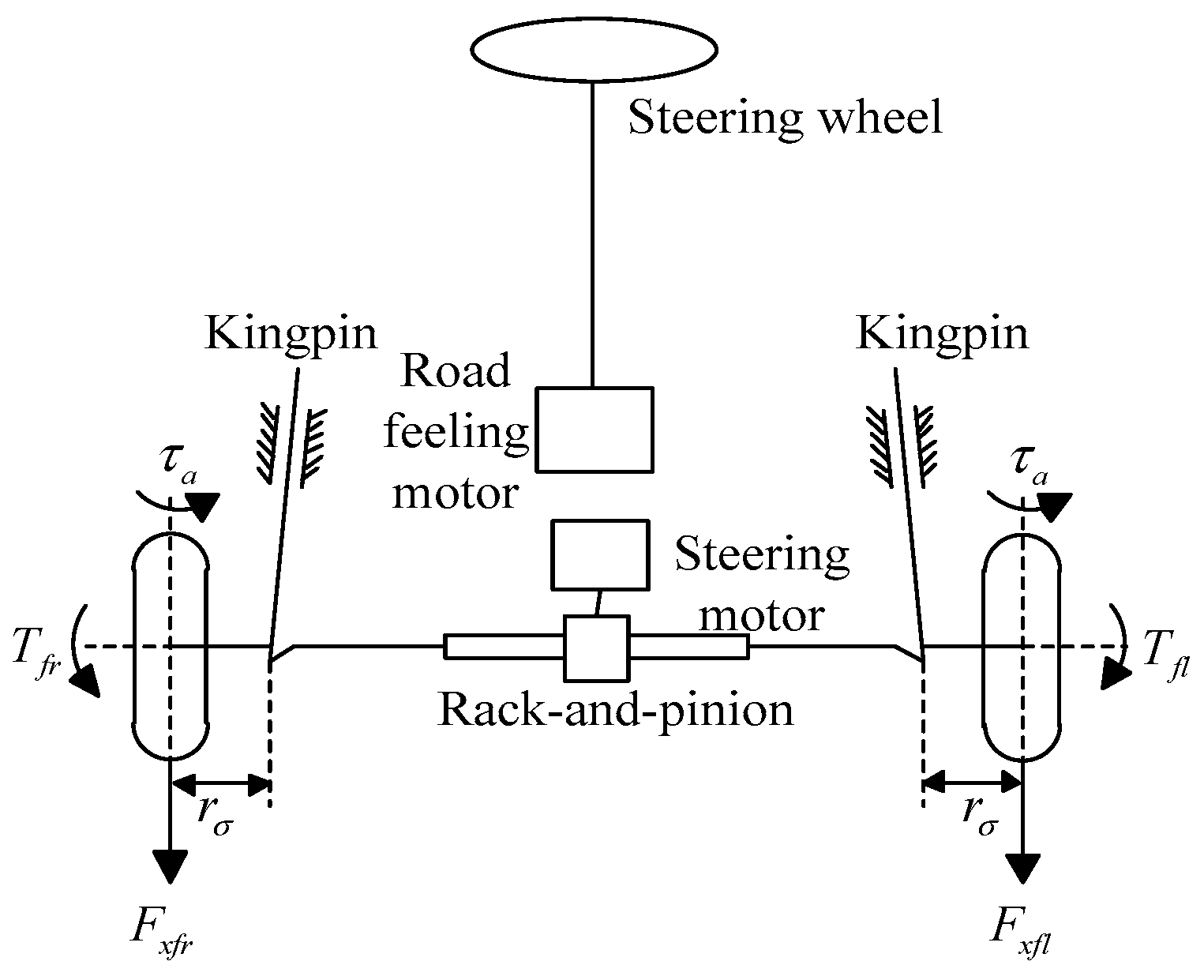
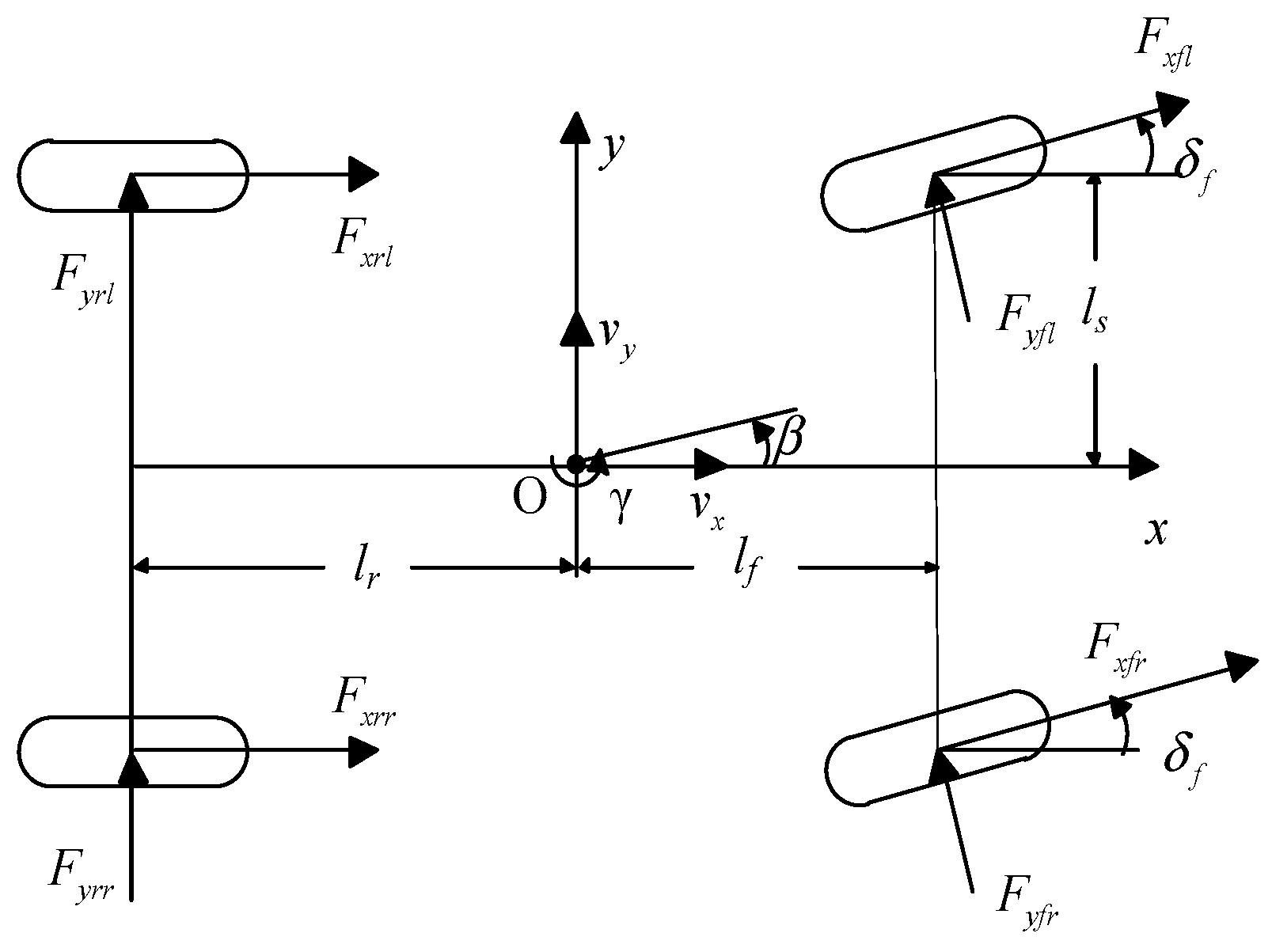
As we all know, when the braking force between the left and right sides is different, the vehicle will turn to the side with larger braking force. Similarly, the different driving force between the left and right sides will drive the steering wheel to generate the steering motion and the vehicle will turn to the side with smaller driving force. Differential steering system of the 4WID EV equipped with an SBW system and the force acting on the vehicle body are shown in
Figure 2 and
Figure 3, respectively.
The driver’s intention is provided to the electronic control unit (ECU), which gives instructions to the steering mechanism and achieves the steering according to the collected signals and internal control procedures. However, when the SBW system fails suddenly, the steering can only be realized by the differential driving torque, which can also generate the front wheel angles simultaneously.
The dynamic equation of the steering system (shown in
Figure 2) can be written as [
11]:
where
and
are the effective moment of inertia and damping of the SBW system,
is the front wheel steering angle,
is the tire self-aligning moment,
is the scrub radius,
is the friction torque,
is the tire slip angle of the front wheel,
l is the half of the tire contact length. In addition,
and
can be assumed as bounded disturbances.
The lateral and yaw motion (shown in
Figure 3) of the EV can be expressed as:
where
Define
,
, the state equation can be obtained as
where
Note: From Equations (1) and (11), it is not difficult to see that they are similar to each other and there are so many emerged in Equation (11). However, here is not the external input of the system, but the steering angle of front wheels produced by the differential driving torque between the two sides of the front wheels.
2.3. Reference Model
Here the 2DOF vehicle model with neutral steering characteristics, which can be easily obtained by adjusting the position of the CG, is employed to calculate the reference side-slip angle and yaw rate, and to estimate the actual side-slip angle.
Define
xd(
t) = [
βd,
γd]
T and
ud =
, the corresponding state equation is expressed as:
where
βd and
γd are the sideslip angle and the yaw rate of the reference model,
lfd and
lrd are the distances from the CG to the front and rear axles, respectively.
2.4. Problem Formulation
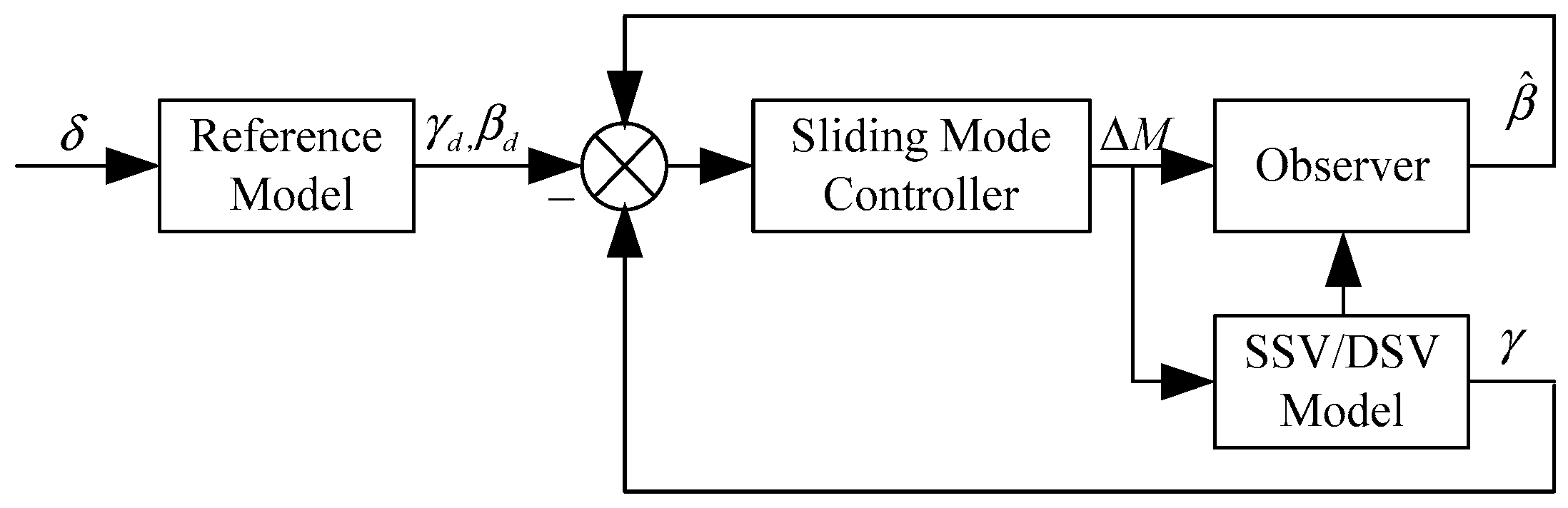
For the reference model, the normal input is the front wheel steering angle, which is proportional to the steering angle commanded by the driver. But for the SSV and DSV in the case of the steering failure, both of their inputs are the differential drive torque between the left and right front wheels, which should be controlled to drive the sideslip angle and yaw rate of the vehicles to their desired ones calculated by Equation (15). The sensors to measure the sideslip angle are usually very expensive. Consequently, the state observer should be firstly designed to estimate the actual sideslip angle. In addition, there is no direct relationship between the steering wheel angle and differential drive torque. To obtain the desired vehicle performance, sliding mode variable structure control strategy is applied. The diagram of control design is depicted in
Figure 4.
4. Simulation and Analysis
In this section, Simulink and CarSim are used to confirm the effectiveness of the control systems designed in this paper. The parameters used in the simulation are as follows: m = 1111 kg, Iz = 2031.4 kg m2, lf = 1.04 m, lr = 1.56 m, lfd = 1.04 m, lrd = 1.56 m, ls = 0.7405 m, R = 0.304 m, kf0 = −98,202.8 N/rad, kr0 = −63,947.18 N/rad. The simulation results are explained in the following subsections.
4.1. Simulation in J-Turn Manoeuvre
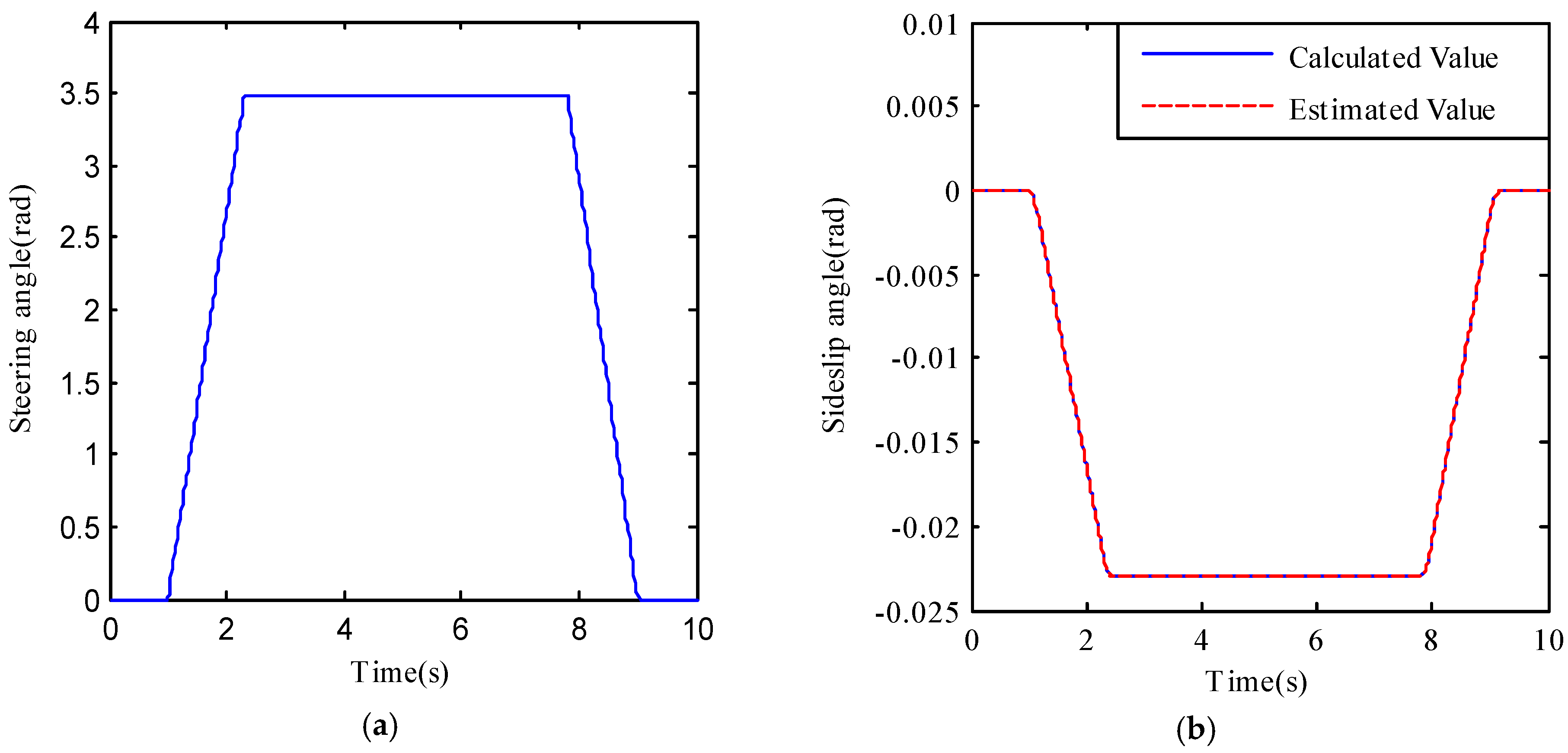
In this simulation,
ux = 10 m/s and the steering wheel steering angle with a maximum steering angle of 3.5 rad as shown in
Figure 5a is used as the input of the reference model.
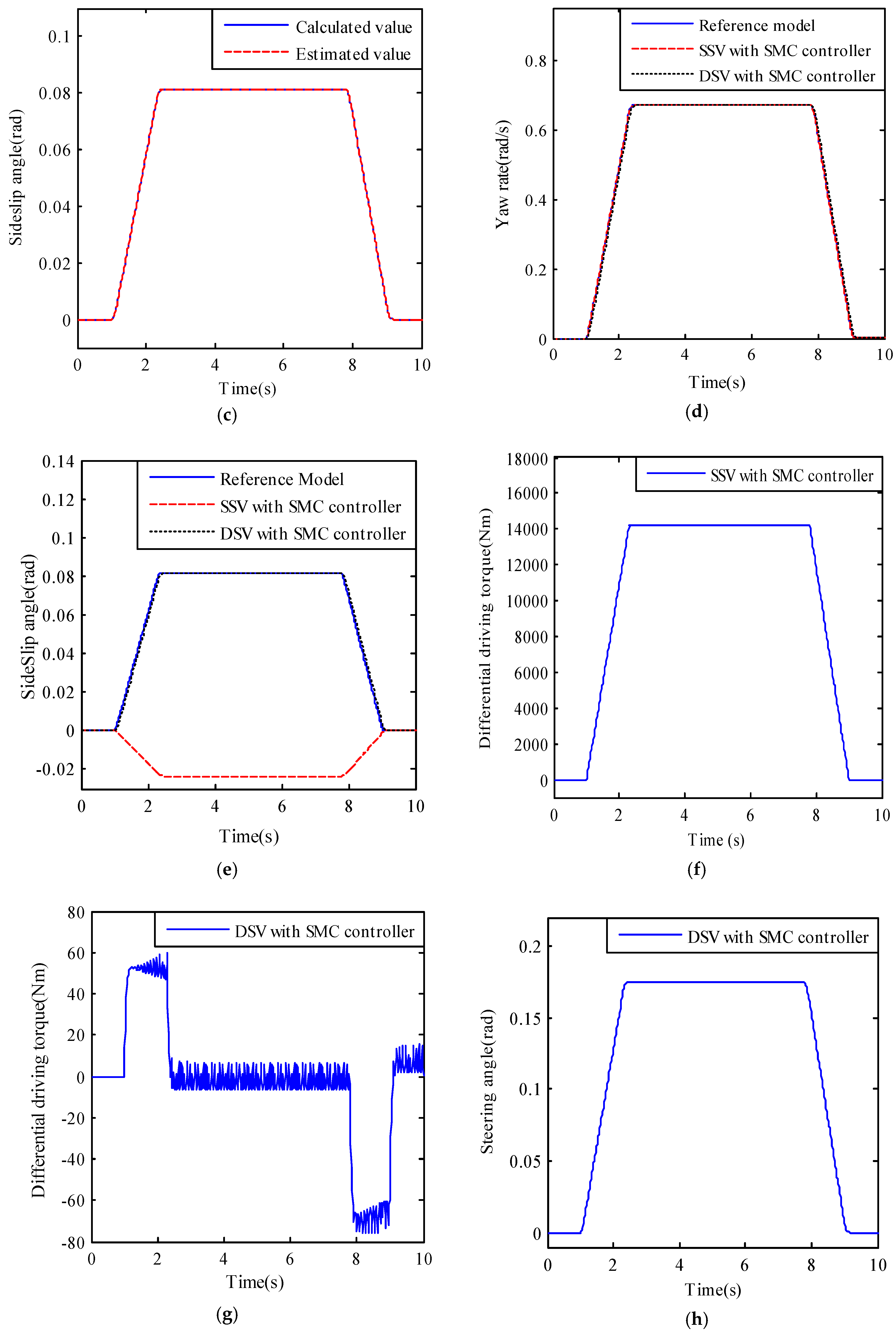
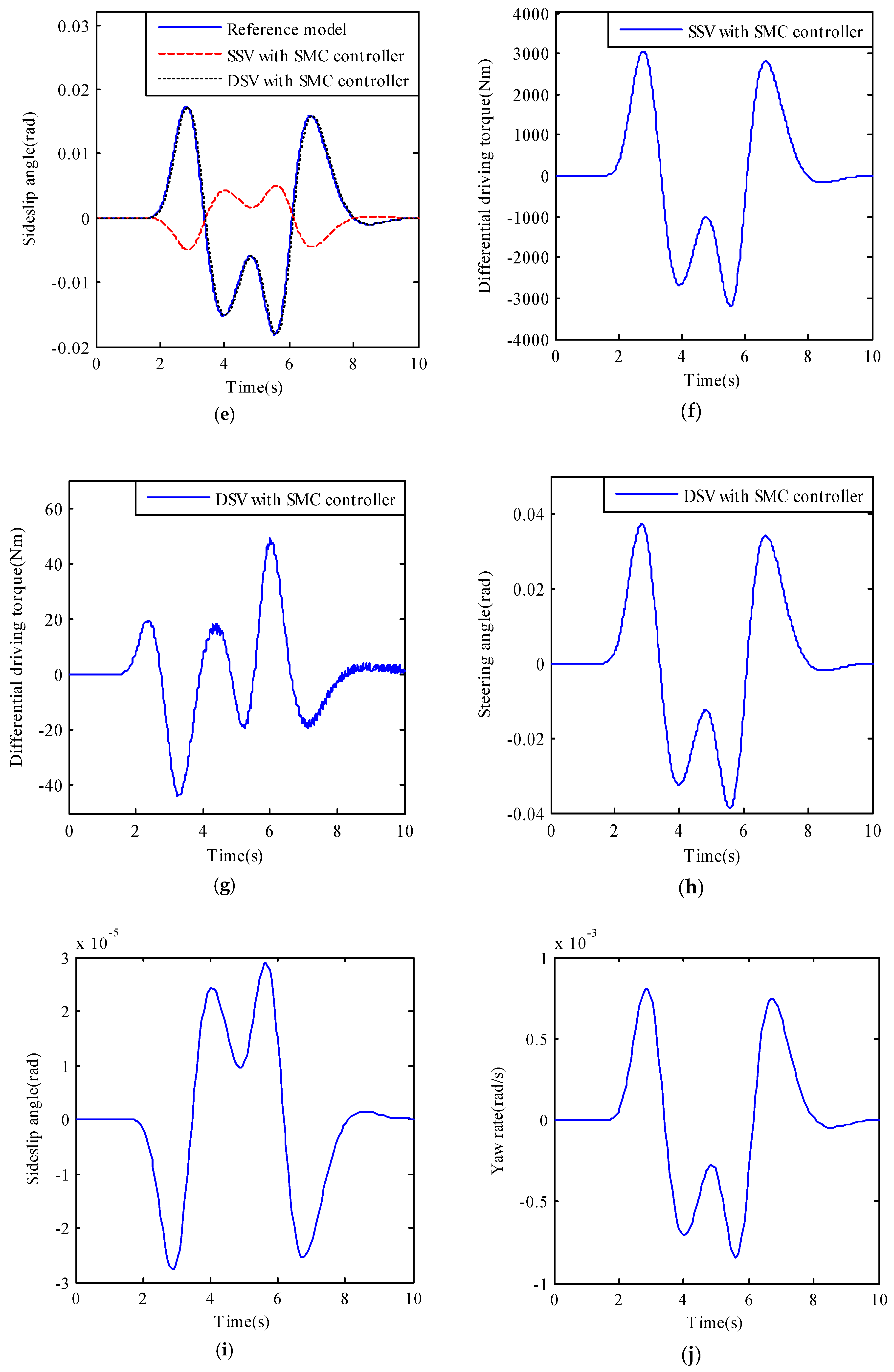
Figure 5b–l illustrate the simulation results of reference model, SSV and DSV with different SMC controllers.
Figure 5b,c are the calculated and the estimated sideslip angles of the SSV and the DSV with SMC controller. It can be drawn that the designed sideslip angle observer is effective to track the calculated sideslip angle.
Figure 5d,e are the yaw rate and sideslip angle curves of the three models. It can be seen that both of the yaw rate and sideslip angle of DSV with SMC controller can follow the desired ones, while only the yaw rate of SSV with SMC controller can follow the desired one. Generally speaking, the side slip angle and the yaw rate are coupled. It is often difficult to track two state variables simultaneously by a single control variable—differential torque. Here the desired yaw rate is tracked very well.
Figure 5f,g show that the differential driving torques for the controllers of SSV and DSV respectively, and their absolute maximum are 142,210 Nm and 75.86 Nm. Obviously, there is too large a difference between the two needed differential driving torques. The reason is for the DSV the differential torque also produces a front wheel steering angle at the same time, which decreases the needed differential torque in turn. And the maximum front wheel angle produced by the differential driving torque for the controller of DSV are 0.1745 rad as shown in
Figure 5h.
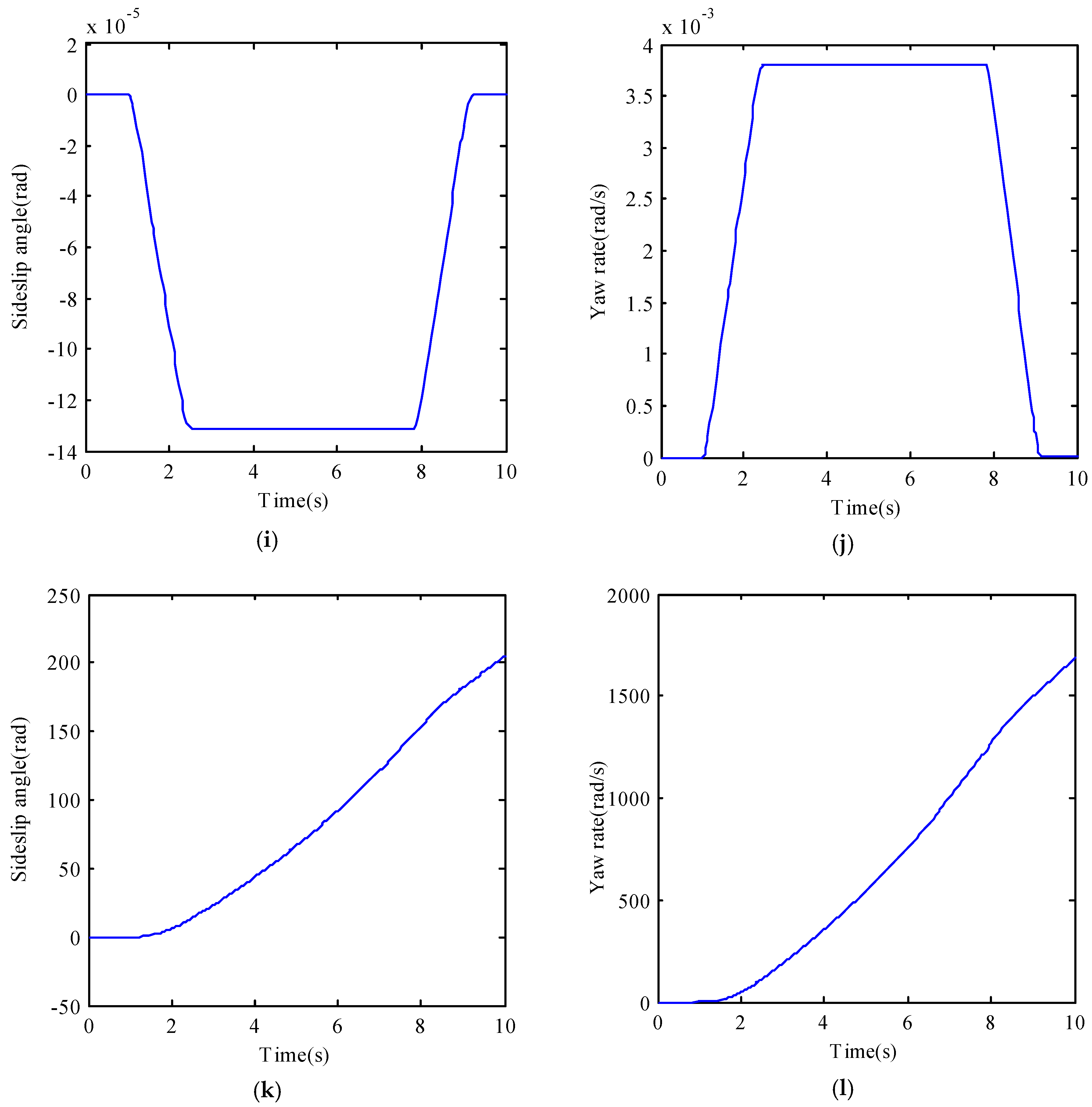
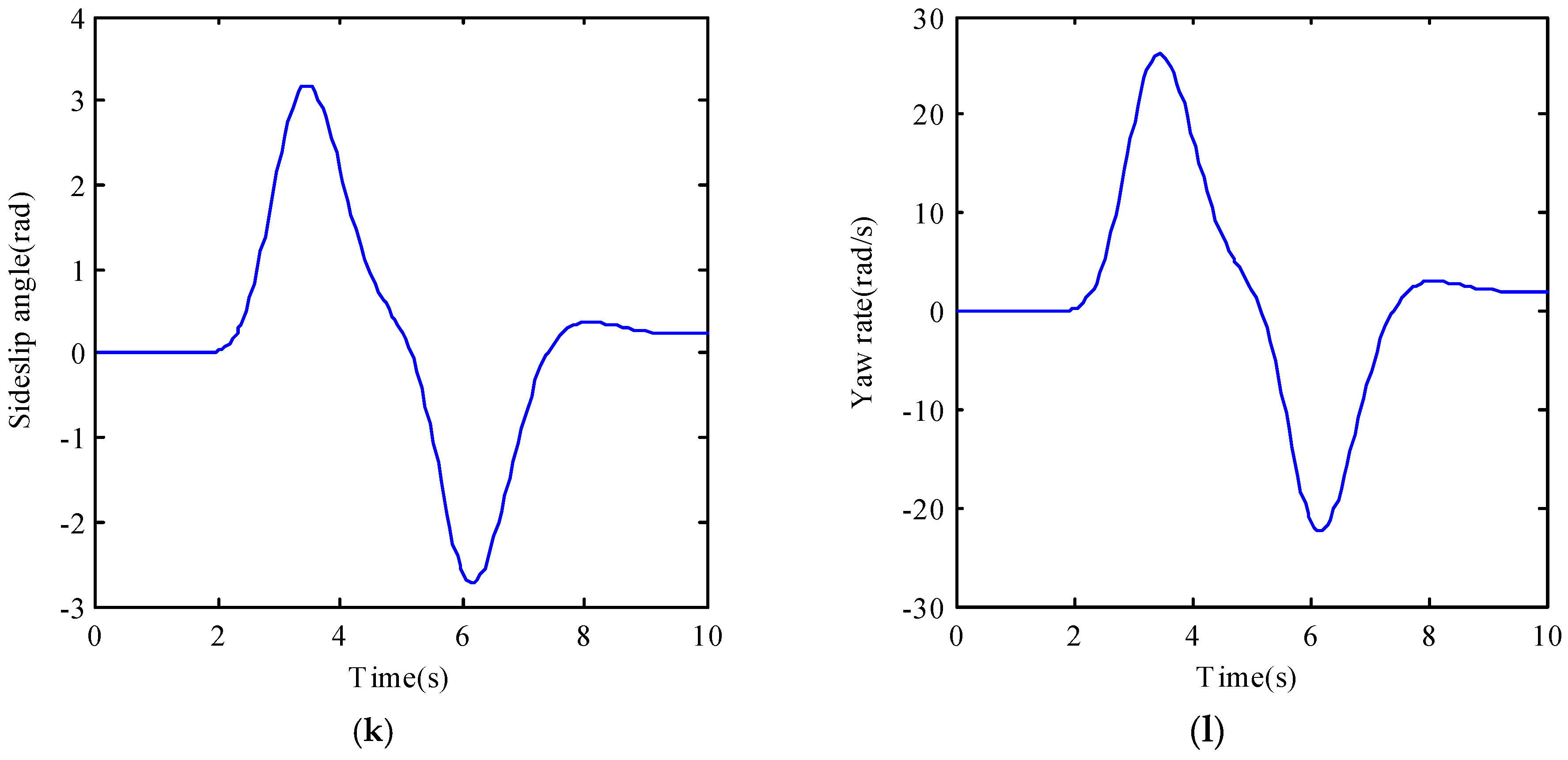
Figure 5i–l are the response curves of SSV and DSV without SMC controller. It can be seen that they are so different from the desired ones.
In conclusion, the simulation results show that the designed observer is effective and the responses of DSV with SMC controller can exactly track the ideal ones. Although the yaw rate of SSV with SMC controller can also exactly track that of the reference model, the differential driving torque needed for SSV is too much larger than that needed for DSV, which obviously exceeds the maximum torque provided by the in-wheel motor.
4.2. Simulation in Double Lane Change Maneuver
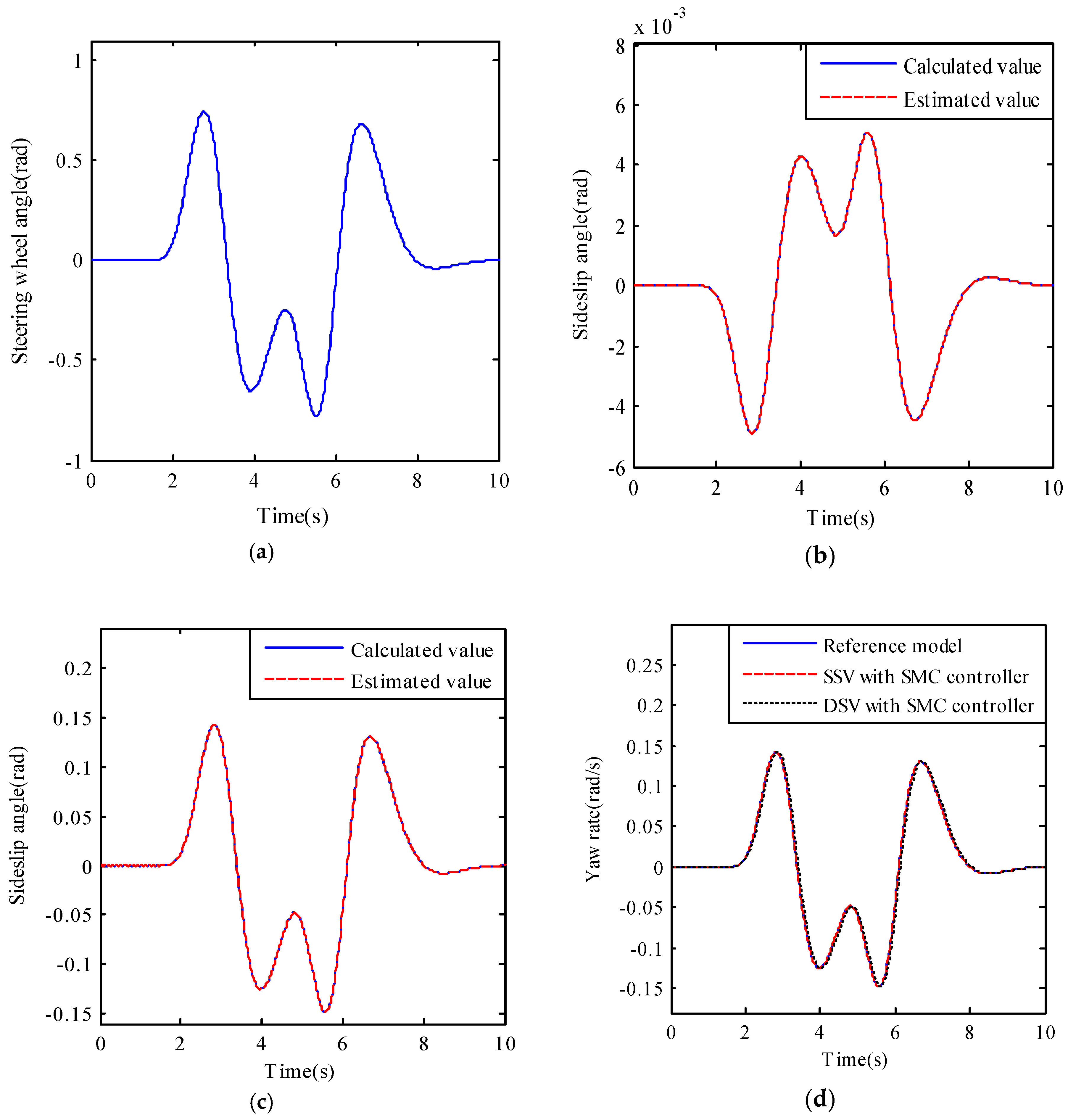
Double lane change maneuver is another important method to examine the maneuvering stability of the vehicle. In this simulation,
ux = 20 m/s and
Figure 6a shows the input of the reference model, which can guarantee the vehicle to achieve the double lane change maneuver.
Figure 6b–l illustrate the simulation results of reference model, SSV and DSV with different SMC controllers.
Figure 6b,c are the calculated and the estimated sideslip angles of the SSV and the DSV with SMC controller, which show that the designed observer can track the calculated sideslip angle very well.
Figure 6d is the yaw rate curves of the three models and their responses are almost the same.
Figure 6e is the sideslip angles of the three models, which illustrates that only the sideslip angle of the SSV with controller can follow the desired one. The differential drive torques between the left and right front wheels required for the SSV and the DSV with SMC controller are shown in
Figure 6f,g and their absolute maximums are 3150 Nm and 46.4 Nm. In addition, the external steering angle of the front wheel is as shown in
Figure 6h.
Figure 6i–l are the response curves of the SSV and the DSV without SMC controller. It can be seen that they are so different from the desired ones.
In conclusion, both of the differential driving torque and the external steering angle of the front wheel produced by the torque contribute to the steering of DSV with SMC controllers, which leads to a substantial reduction in the required differential driving torque. Therefore, the differential driving torque needed for the DSV is much smaller than that needed for the SSV.
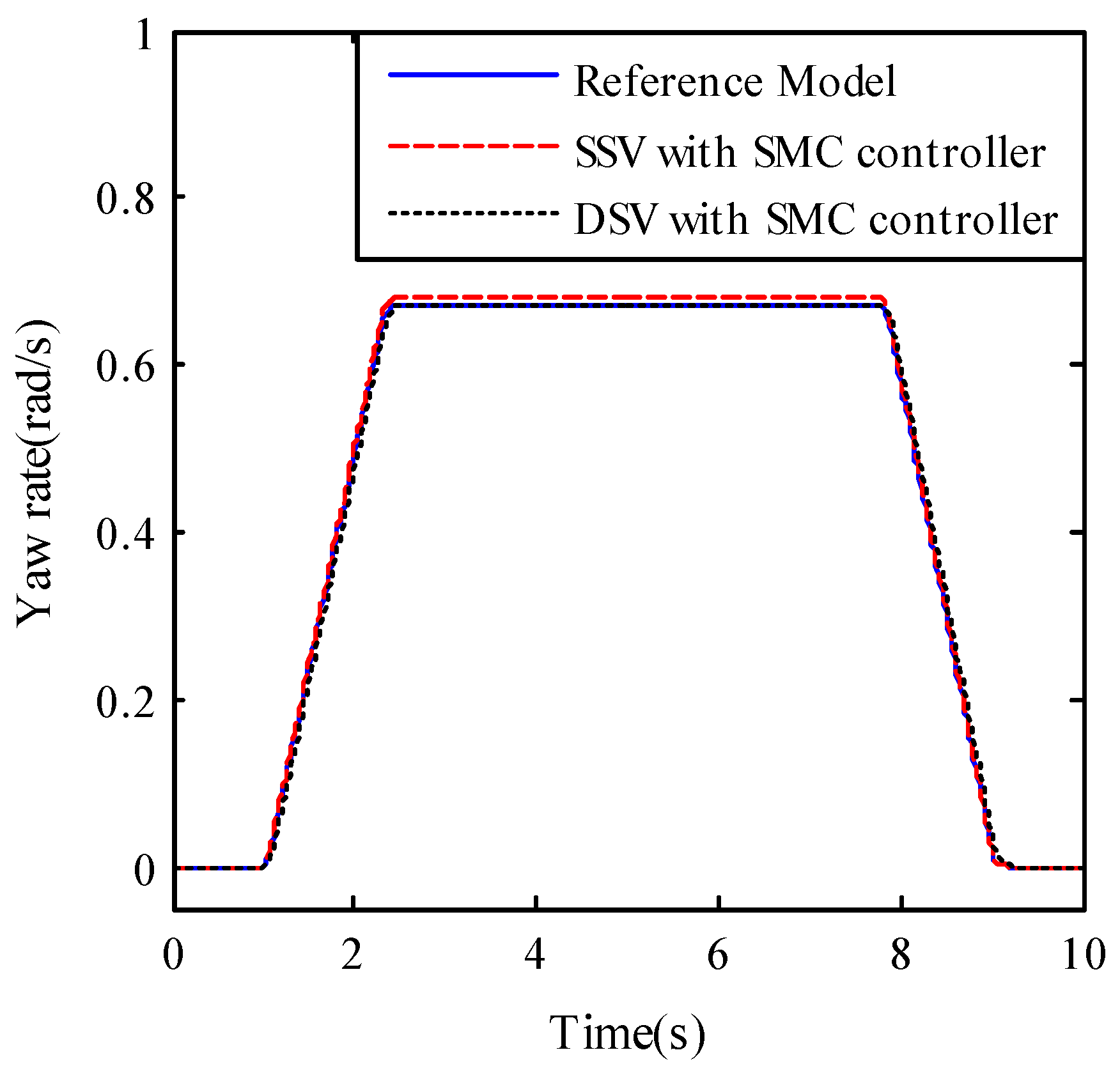
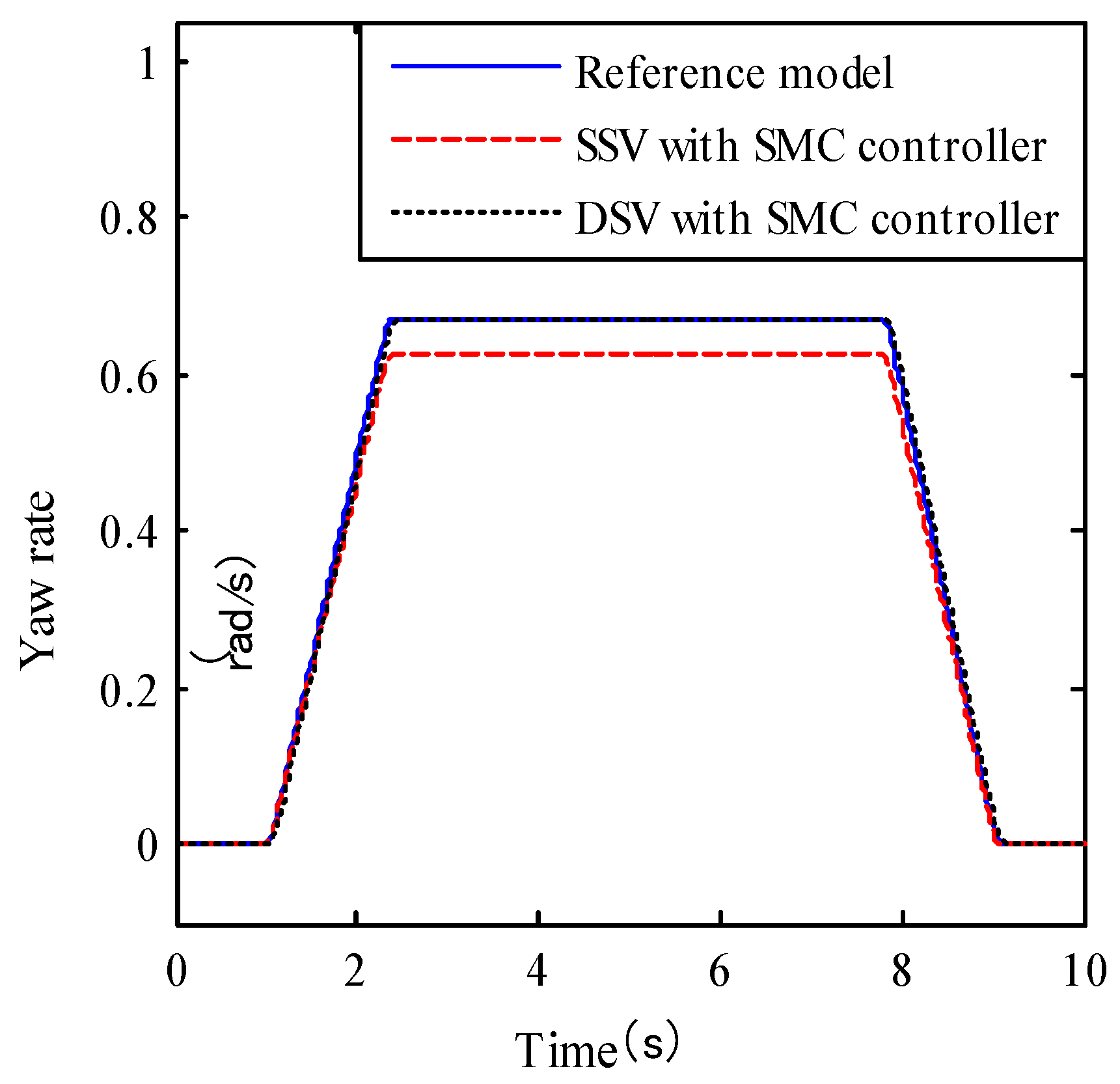
4.3. Robustness Analysis
When the cornering stiffness of the front and rear tires are decreased and increased by 5% respectively as other parameters remain unchanged, yaw rate curves of reference model, SSV and DSV with different SMC controllers are shown in
Figure 7 and
Figure 8, respectively.
From
Figure 7 and
Figure 8, it can be seen that the yaw rate curve of DSV with SMC controller can completely track that of the reference model when front or rear tire cornering stiffness is changed. However, there are always a little difference between the yaw rates of SSV with SMC controller and the reference model. It can be drawn that the robustness of DSV with SMC controller is better than that of SSV with SMC controller.