Efficiency Reduction in Stirling Engines Resulting from Sinusoidal Motion
Abstract
:1. Introduction
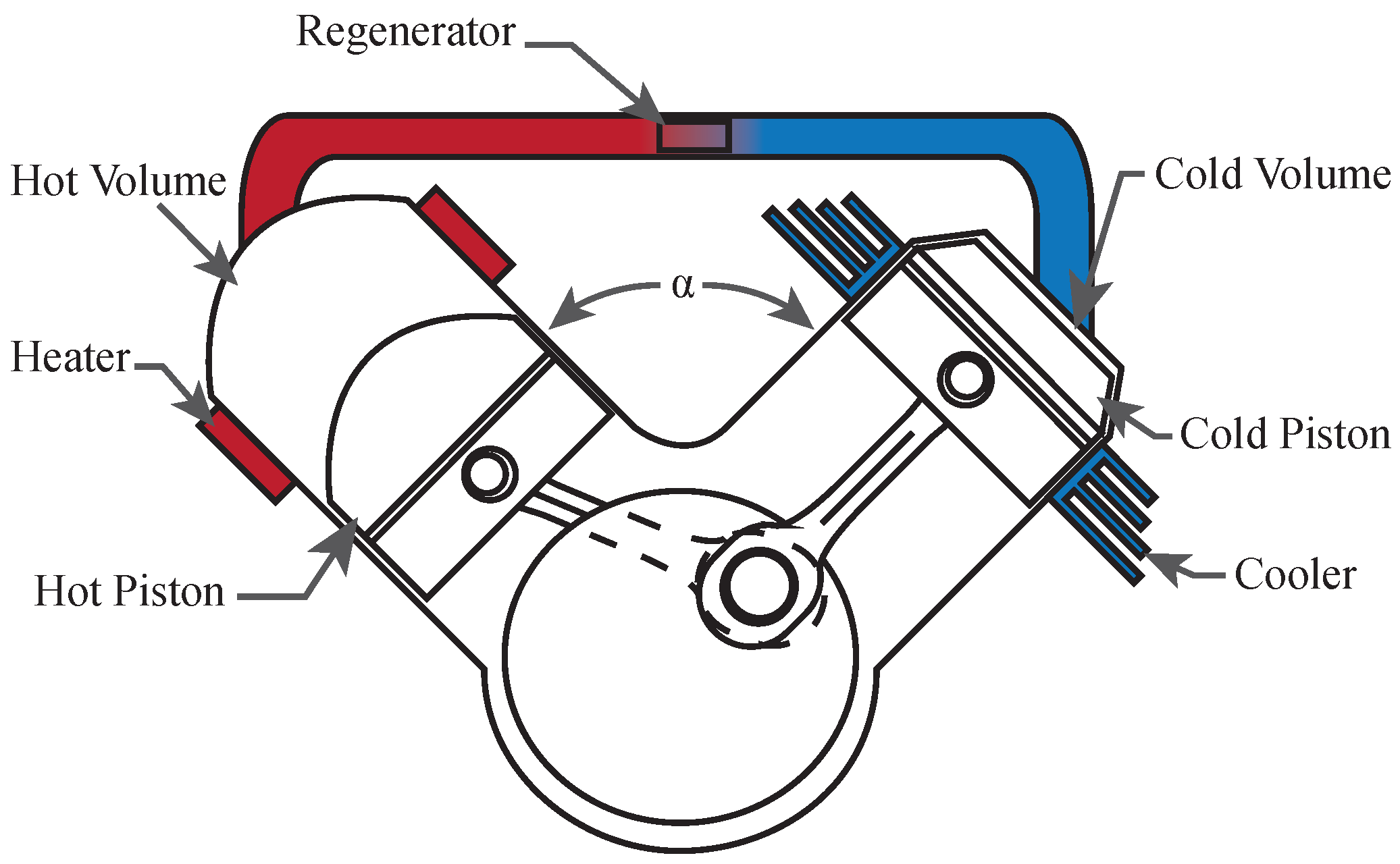
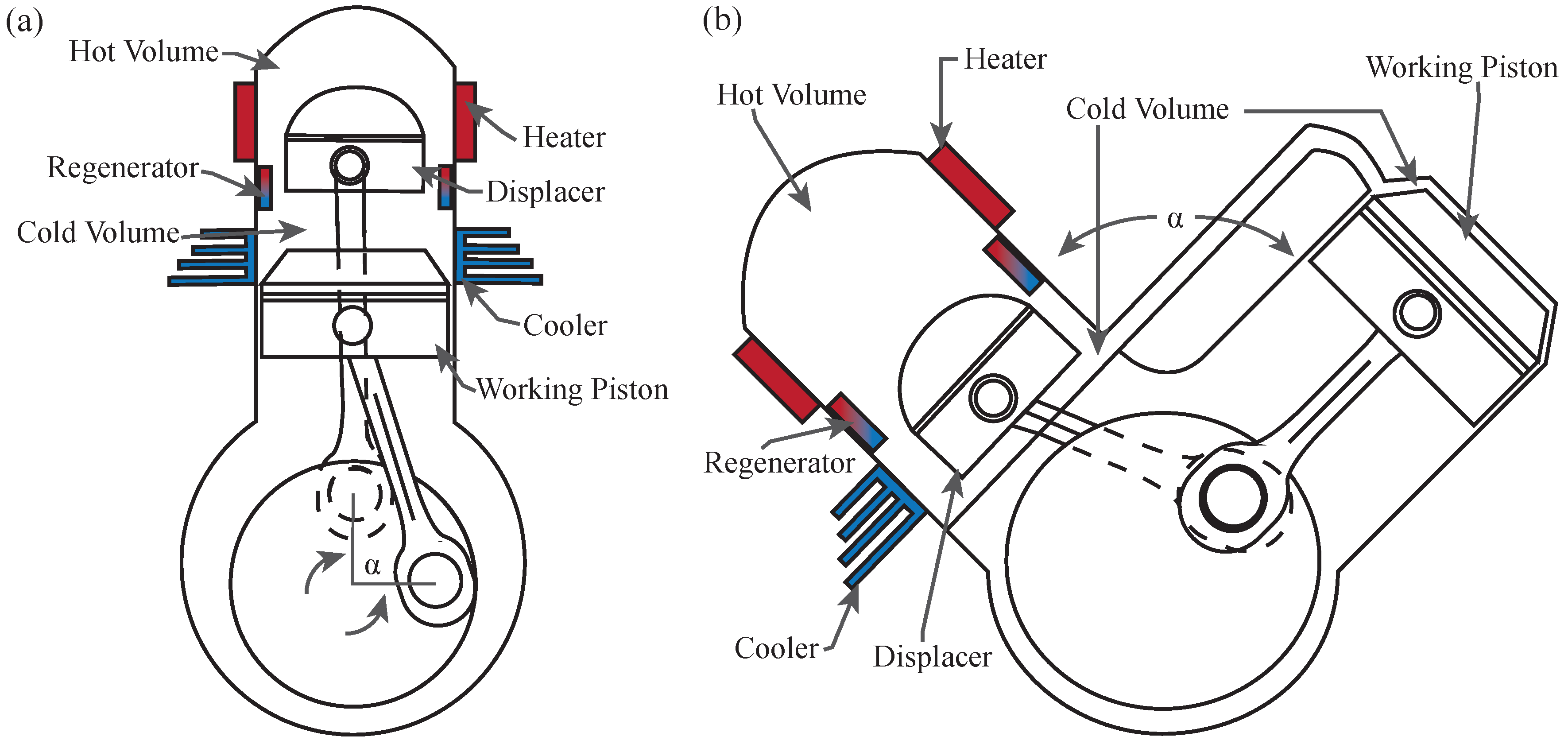
2. Engine Description
3. Thermodynamic Model
3.1. Discretization Approach
3.2. Calculating the System Variables
3.3. Calculating the Energy Transfer
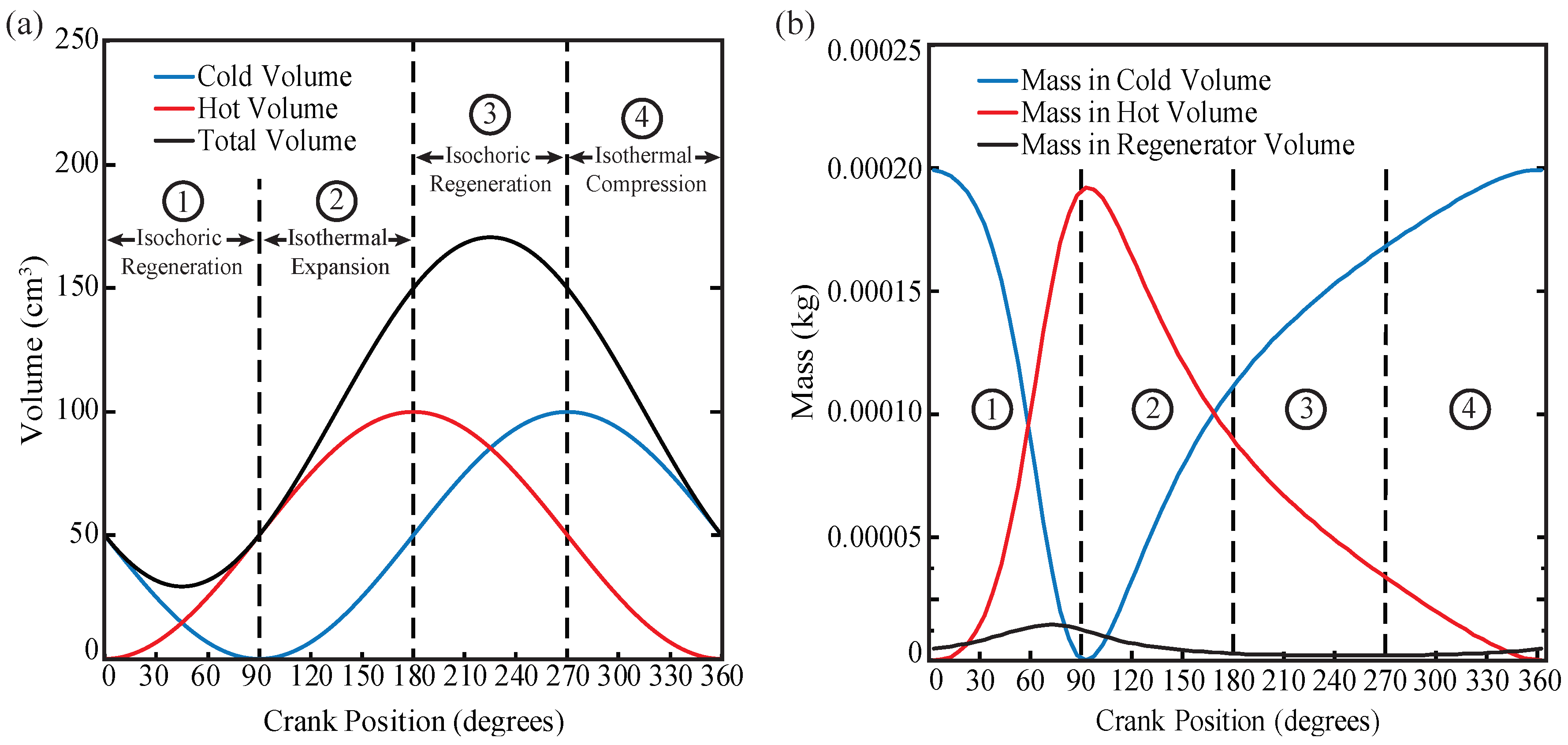
3.4. Mass Calculation
3.5. Efficiency Calculation
4. Results and Discussion
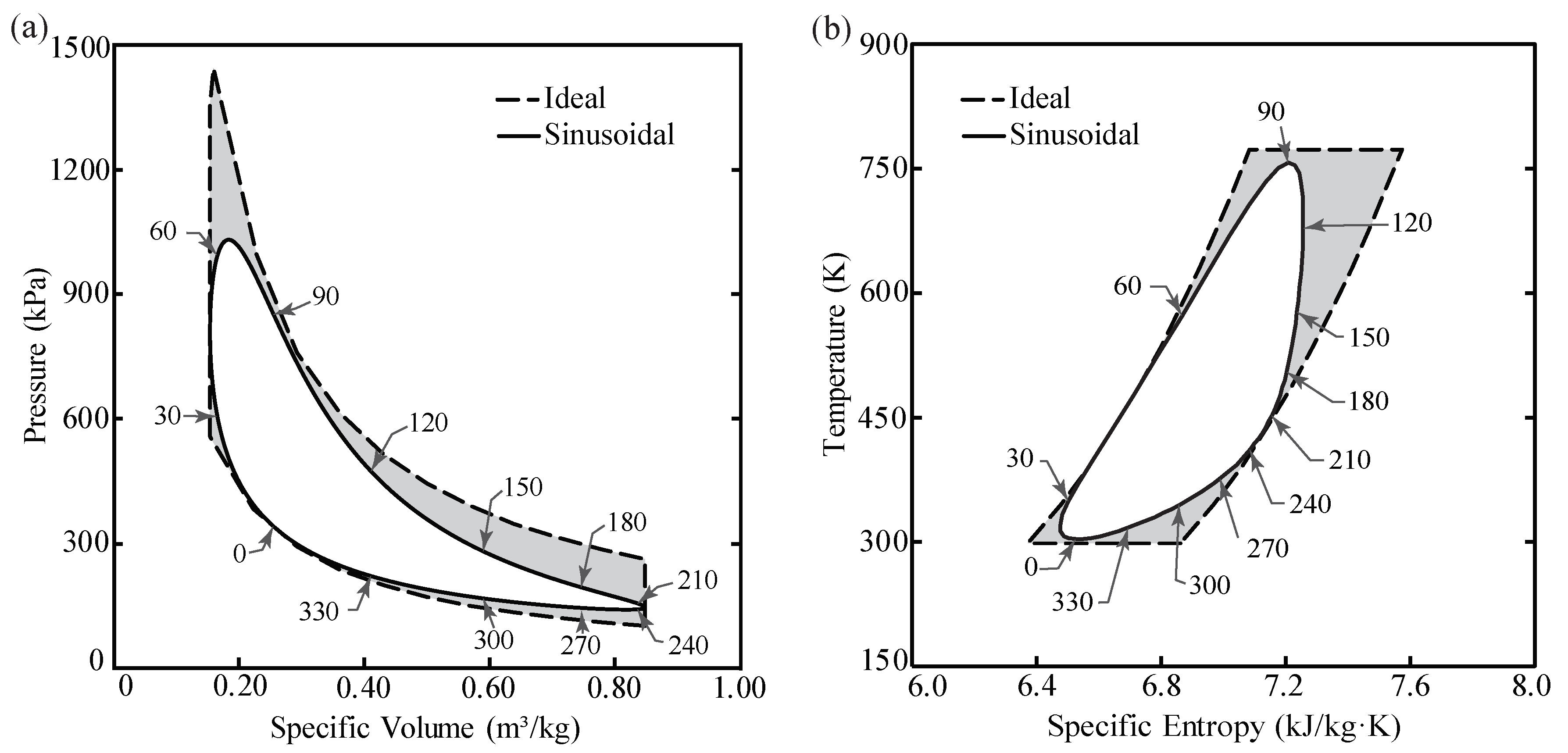
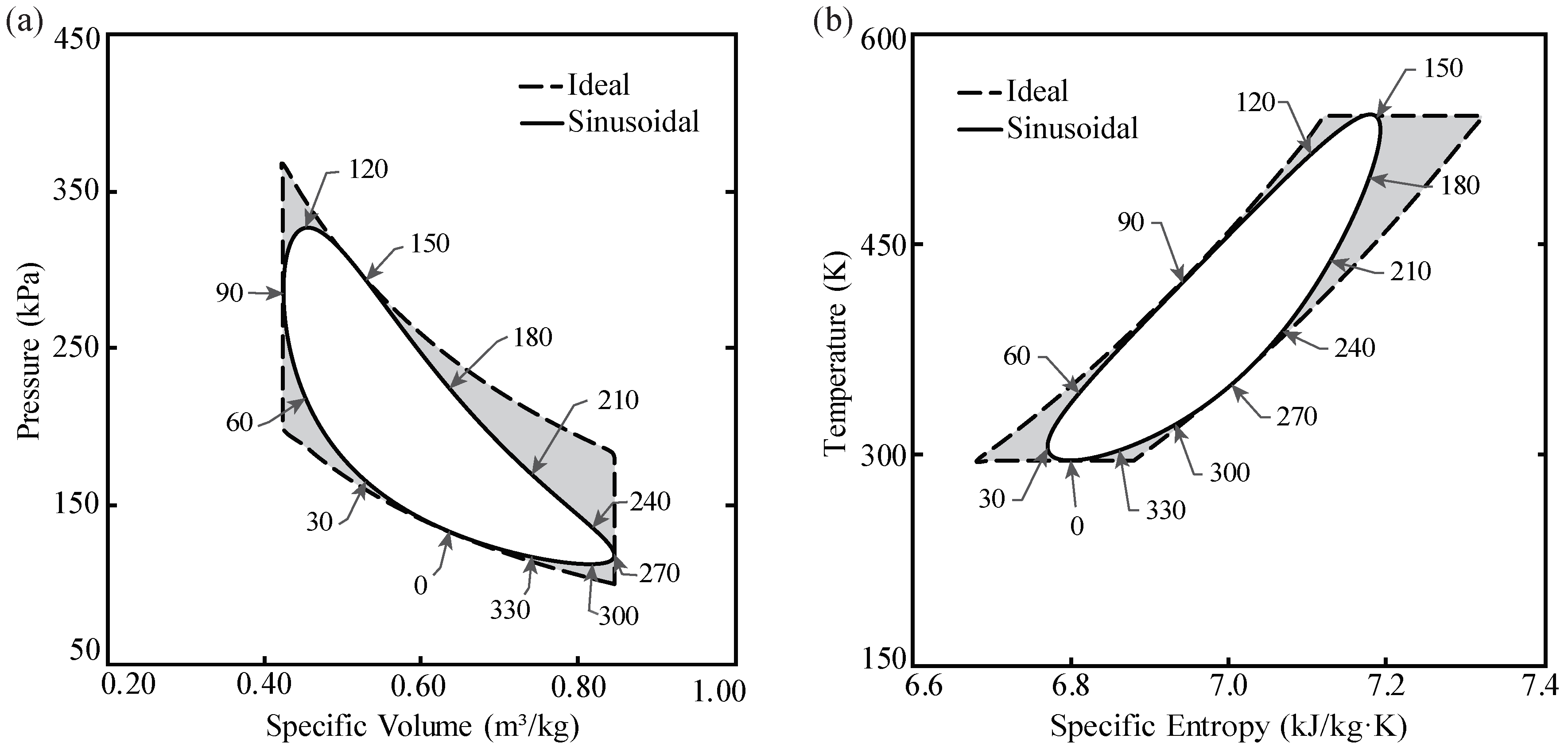
4.1. P-v and T-s Diagrams
4.1.1. Isochoric Regeneration –
4.1.2. Isothermal Expansion –
4.1.3. Isochoric Regeneration –
4.1.4. Isothermal Compression –
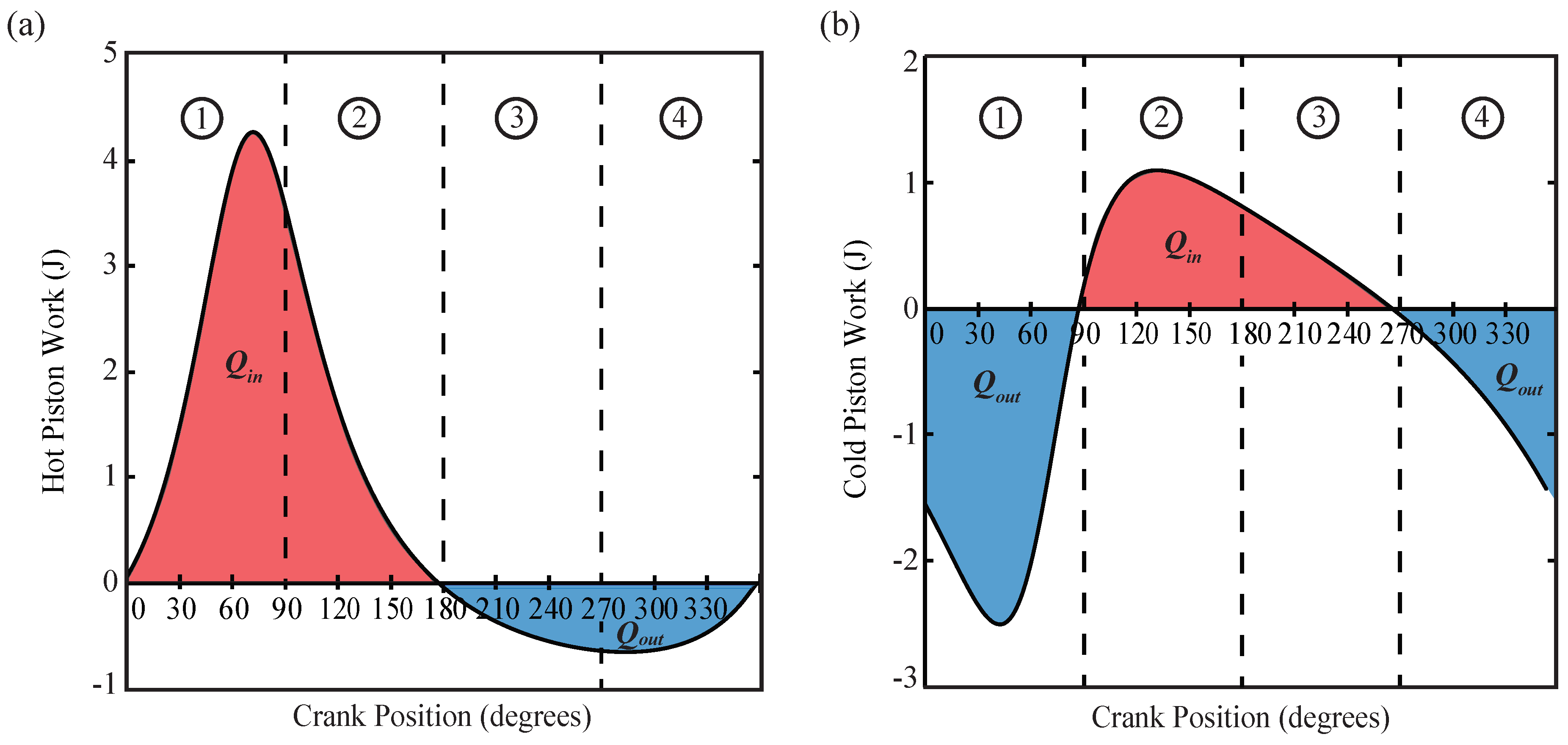
4.2. Work and Heat Transfer
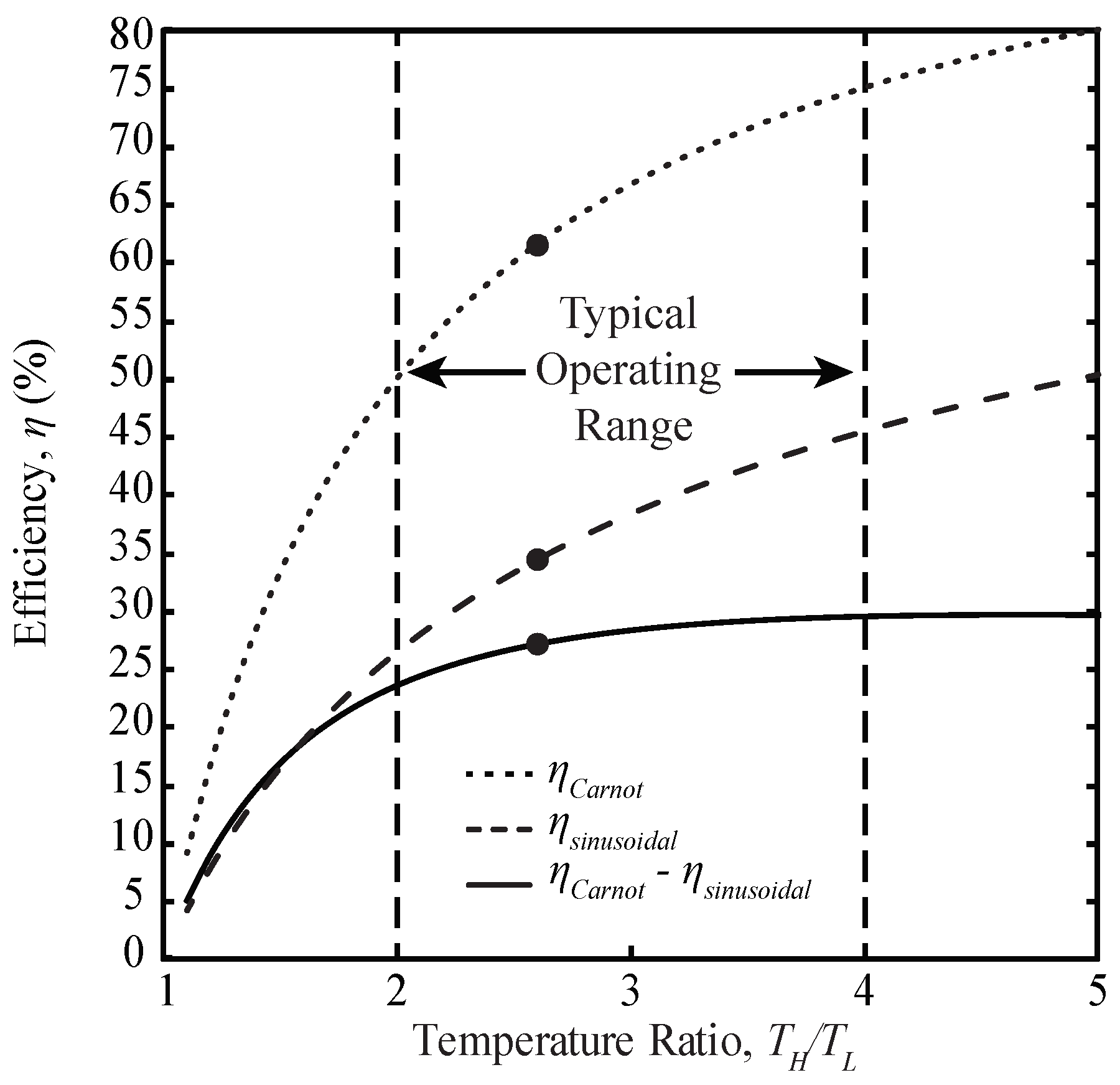
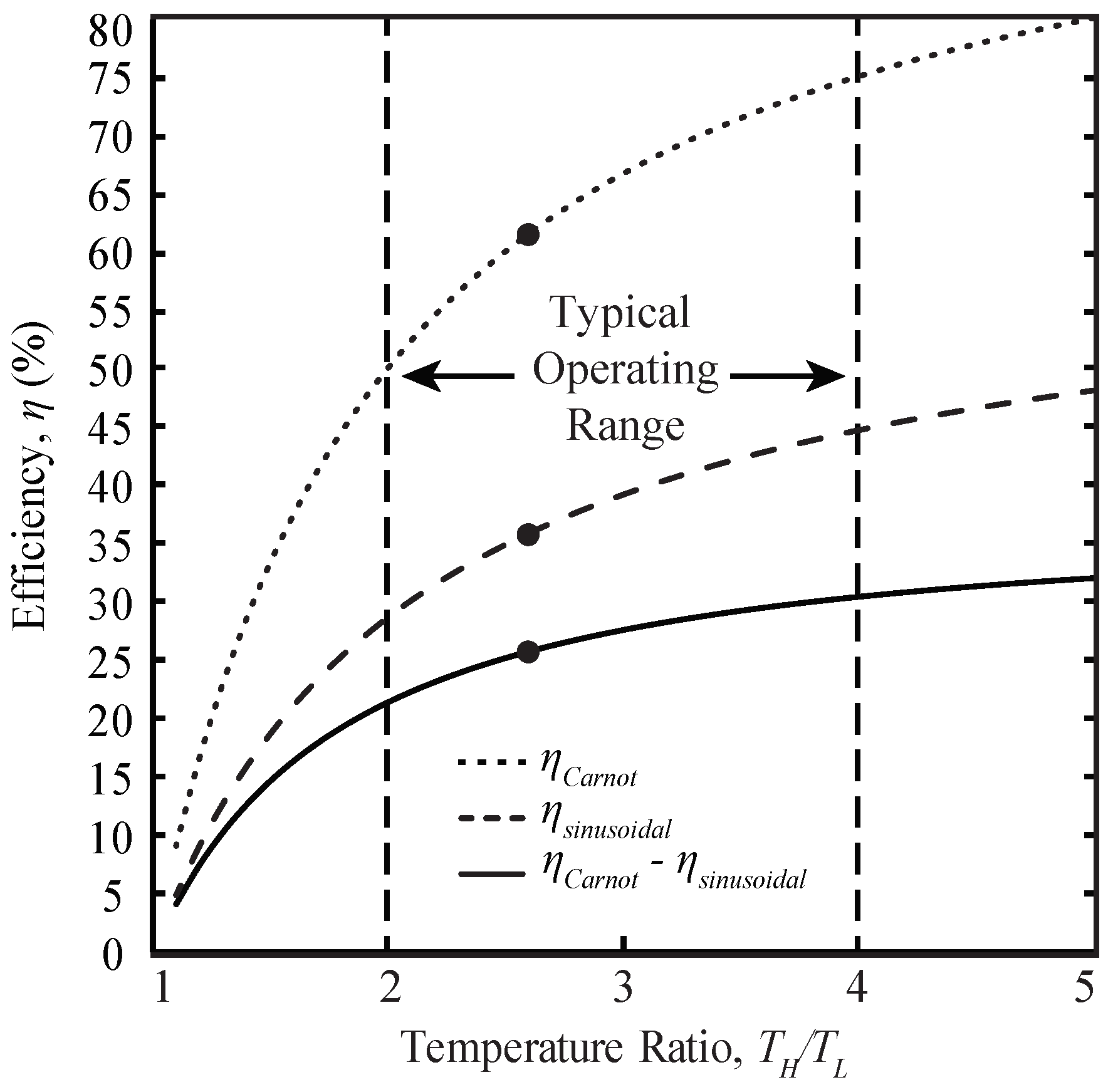
4.3. Deviation from Carnot Efficiency
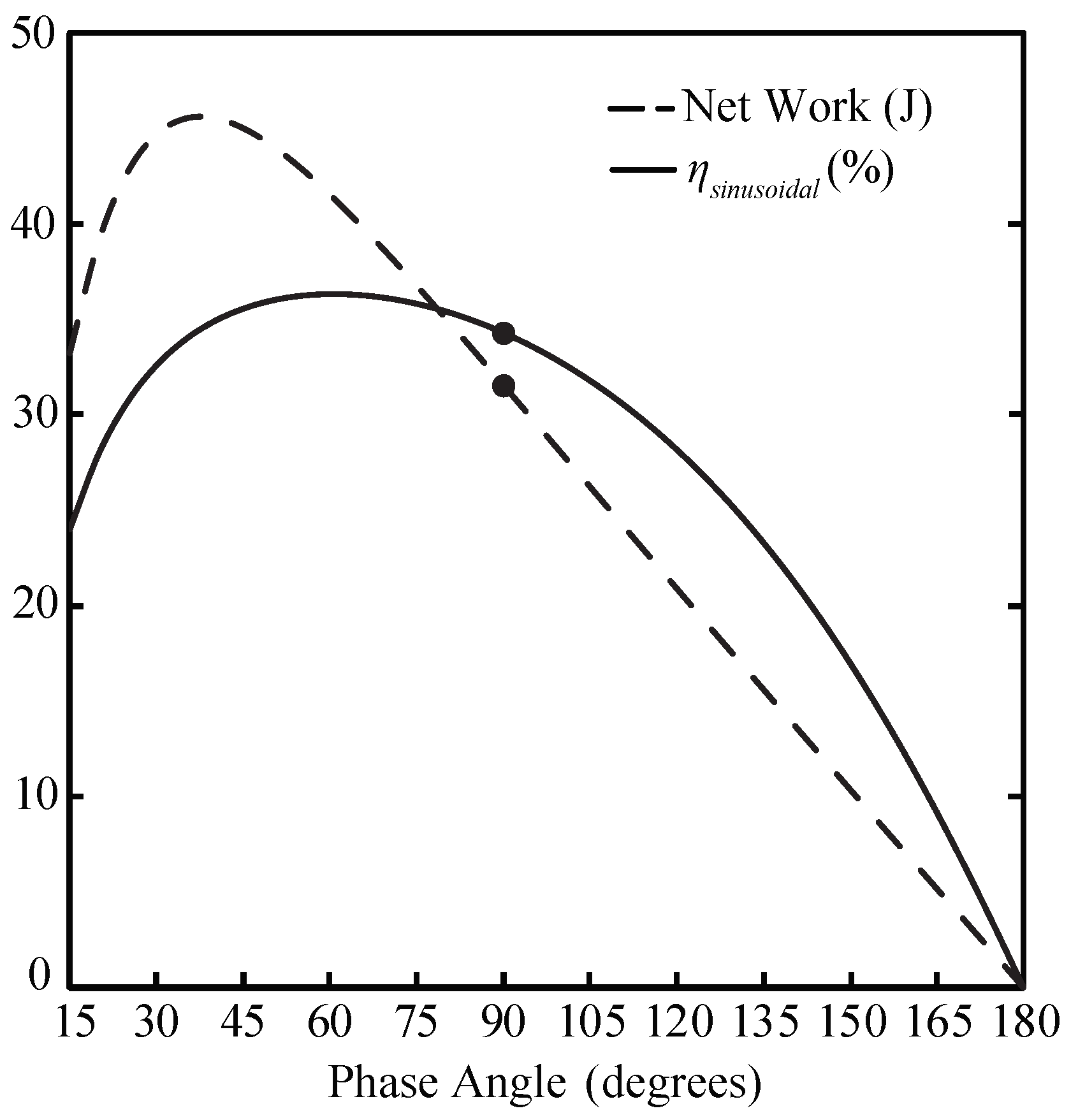
4.4. Phase Angle Dependency for a Sinusoidal Alpha-Type Stirling Engine
4.5. Effects of Sinusoidal Operation on Beta-Type and Gamma-Type Stirling Engines
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| hot volume (cm) | |
| cold volume (cm) | |
| regenerator volume (cm) | |
| total volume of working fluid (cm) | |
| hot space dead volume (cm) | |
| cold space dead volume (cm) | |
| total mass of working fluid (kg) | |
| mass of working fluid within hot volume (kg) | |
| mass of working fluid within cold volume (kg) | |
| mass of working fluid within regenerator (kg) | |
| v | specific volume (m/kg) |
| P | engine pressure (kPa) |
| R | gas constant (J/kg K) |
| hot temperature (K) | |
| cold temperature (K) | |
| regenerator temperature (K) | |
| total average temperature (K) | |
| s | specific entropy (J/kg K) |
| work from hot piston (J) | |
| work from cold piston (J) | |
| total work produced (J) | |
| heat addition (J) | |
| heat rejection (J) | |
| phase angle () | |
| thermal efficiency | |
| crank angle () |
References
- Cengel, Y.; Boles, M. Thermodynamics: An Engineering Approach, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Kim, Y.; Chun, W.; Chen, K. Thermal-Flow Analysis of a Simple LTD (Low-Temperature-Differential) Heat Engine. Energies 2017, 10, 567. [Google Scholar] [CrossRef]
- Martini, W.R. Stirling Engine Design Manual; US Department of Energy, Office of Conservation and Solar Applications, Division of Transportation Energy Conservation: Washington, DC, USA, 1978.
- Wu, F.; Chen, L.; Wu, C.; Sun, F. Optimum performance of irreversible Stirling engine with imperfect regeneration. Energy Convers. Manag. 1998, 39, 727–732. [Google Scholar] [CrossRef]
- Isshiki, S.; Sakano, A.; Ushiyama, I.; Isshiki, N. Studies on flow resistance and heat transfer of regenerator wire meshes of Stirling engine in oscillatory flow. JSME Int J. Ser. B 1997, 40, 281–289. [Google Scholar] [CrossRef]
- Muralidhar, K.; Suzuki, K. Analysis of flow and heat transfer in a regenerator mesh using a non-Darcy thermally non-equilibrium model. Int. J. Heat Mass Transf. 2001, 44, 2493–2504. [Google Scholar] [CrossRef]
- Kongtragool, B.; Wongwises, S. Thermodynamic analysis of a Stirling engine including dead volumes of hot space, cold space and regenerator. Renew. Energy 2006, 31, 345–359. [Google Scholar] [CrossRef]
- Wang, K.; Sanders, S.R.; Dubey, S.; Choo, F.H.; Duan, F. Stirling cycle engines for recovering low and moderate temperature heat: A review. Renew. Sustain. Energy Rev. 2016, 62, 89–108. [Google Scholar] [CrossRef]
- Briggs, M. Improving Free-Piston Stirling Engine Power Density. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, 2015. [Google Scholar]
- Sowale, A.; Kolios, A.J. Thermodynamic Performance of Heat Exchangers in a Free Piston Stirling Engine. Energies 2018, 11, 505. [Google Scholar] [CrossRef]
- Schmidt, G. The theory of Lehmann’s calorimetric machine. Z. Ver. Dtsch. Ing. 1871, 15 Pt I. [Google Scholar]
- Thombare, D.; Verma, S. Technological development in the Stirling cycle engines. Renew. Sustain. Energy Rev. 2008, 12, 1–38. [Google Scholar] [CrossRef]
- Finkelstein, T. Generalized Thermodynamic Analysis of Stirling Engines; SAE Technical Paper: Warrendale, PA, USA, January 1960. [Google Scholar] [CrossRef]
- Walker, G. An optimization of the principal design parameters of Stirling cycle machines. J. Mech. Eng. Sci. 1962, 4, 226–240. [Google Scholar] [CrossRef]
- Kirkley, D. Determination of the optimum configuration for a Stirling engine. J. Mech. Eng. Sci. 1962, 4, 204–212. [Google Scholar] [CrossRef]
- Urieli, I.; Berchowitz, D.M. Stirling Cycle Engine Analysis; Taylor & Francis: Milton Park, UK, 1984. [Google Scholar]
- Senft, J.R. Optimum Stirling engine geometry. Int. J. Energ. Res. 2002, 26, 1087–1101. [Google Scholar] [CrossRef]
- Cheng, C.H.; Yu, Y.J. Dynamic simulation of a beta-type Stirling engine with cam-drive mechanism via the combination of the thermodynamic and dynamic models. Renew. Energy 2011, 36, 714–725. [Google Scholar] [CrossRef]
- Cinar, C. Thermodynamic analysis of an α-type Stirling engine with variable phase angle. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2007, 221, 949–954. [Google Scholar] [CrossRef]
- Tlili, I.; Timoumi, Y.; Nasrallah, S.B. Analysis and design consideration of mean temperature differential Stirling engine for solar application. Renew. Energy 2008, 33, 1911–1921. [Google Scholar] [CrossRef]
- Formosa, F.; Despesse, G. Analytical model for Stirling cycle machine design. Energy Convers. Manag. 2010, 51, 1855–1863. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.H.; Yang, H.S. Optimization of geometrical parameters for Stirling engines based on theoretical analysis. Appl. Energy 2012, 92, 395–405. [Google Scholar] [CrossRef]
- Alfarawi, S.; Al-Dadah, R.; Mahmoud, S. Influence of phase angle and dead volume on gamma-type Stirling engine power using CFD simulation. Energy Convers. Manag. 2016, 124, 130–140. [Google Scholar] [CrossRef]
- Egas, J.; Clucas, D.M. Stirling Engine Configuration Selection. Energies 2018, 11, 584. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Working Fluid | Air |
| Cold Swept Volume (cm) | 100 |
| Hot Swept Volume (cm) | 100 |
| Charge Pressure (kPa) | 101.325 |
| Regenerator/passage volume (cm) | 2 |
| Total dead volume (cm) | 2 |
| Hot Volume temperature (K) | 773.15 |
| Cold Volume temperature (K) | 298.15 |
| Crank Angle Range () | Process | Work Summation Value (J) | |
|---|---|---|---|
| Cold Piston Work | Hot Piston Work | ||
| – | Isochoric regeneration | −32.6 | 43.0 |
| – | Isothermal expansion | 16.3 | 24.9 |
| – | Isochoric regeneration | 8.0 | −7.4 |
| – | Isothermal compression | −11.5 | −9.1 |
| Total | −19.9 | 51.5 | |
| Net Work | 31.6 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ranieri, S.; Prado, G.A.O.; MacDonald, B.D. Efficiency Reduction in Stirling Engines Resulting from Sinusoidal Motion. Energies 2018, 11, 2887. https://doi.org/10.3390/en11112887
Ranieri S, Prado GAO, MacDonald BD. Efficiency Reduction in Stirling Engines Resulting from Sinusoidal Motion. Energies. 2018; 11(11):2887. https://doi.org/10.3390/en11112887
Chicago/Turabian StyleRanieri, Salvatore, Gilberto A. O. Prado, and Brendan D. MacDonald. 2018. "Efficiency Reduction in Stirling Engines Resulting from Sinusoidal Motion" Energies 11, no. 11: 2887. https://doi.org/10.3390/en11112887
APA StyleRanieri, S., Prado, G. A. O., & MacDonald, B. D. (2018). Efficiency Reduction in Stirling Engines Resulting from Sinusoidal Motion. Energies, 11(11), 2887. https://doi.org/10.3390/en11112887





