Analysis of LC-LC2 Compensated Inductive Power Transfer for High Efficiency and Load Independent Voltage Gain
Abstract
:1. Introduction
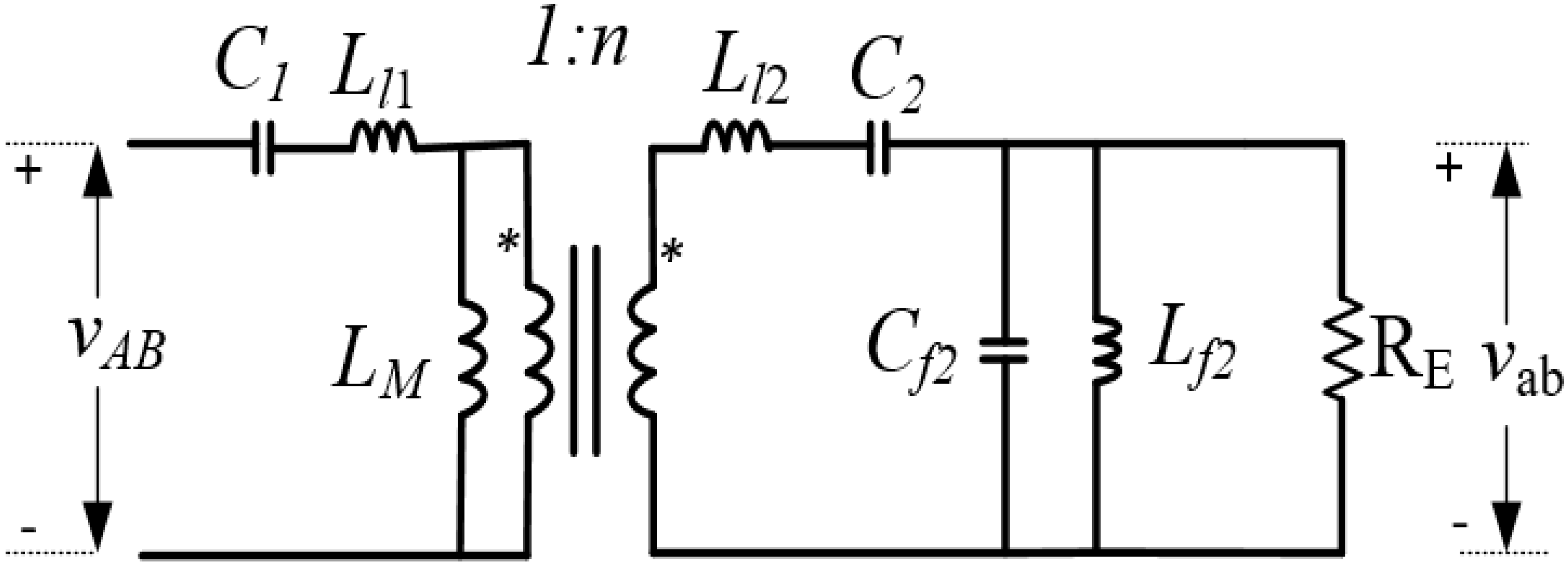
2. Proposed LC-LC2 Compensation
3. LC-LC2 Compensated Resonant Converter Using Frequency Domain Analysis
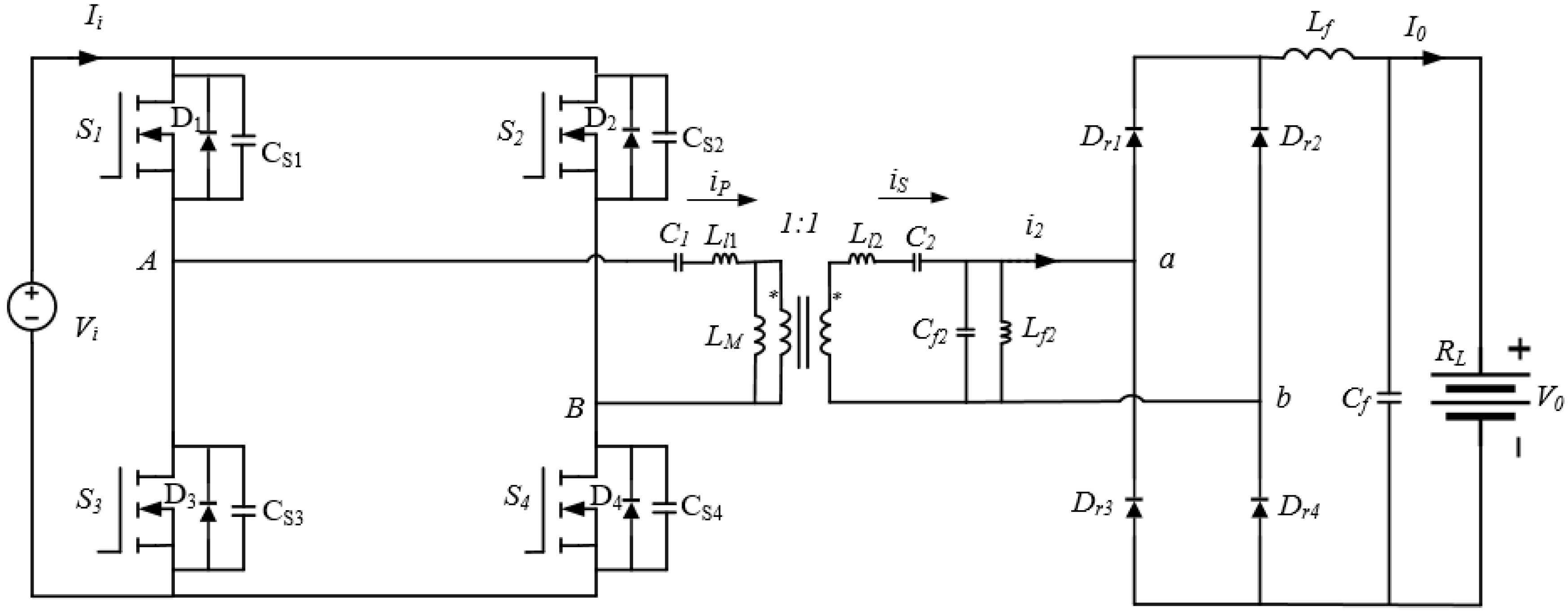
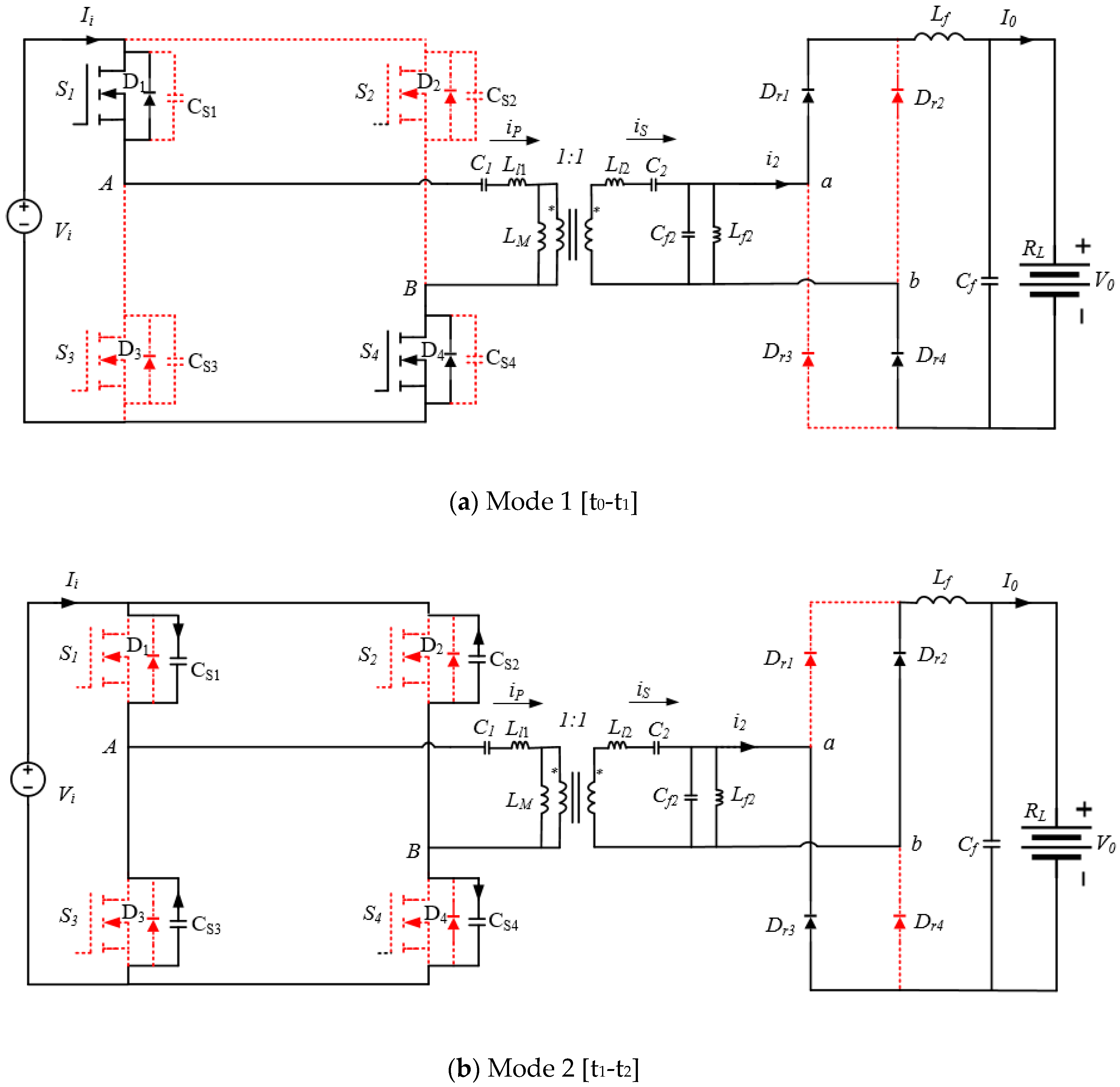
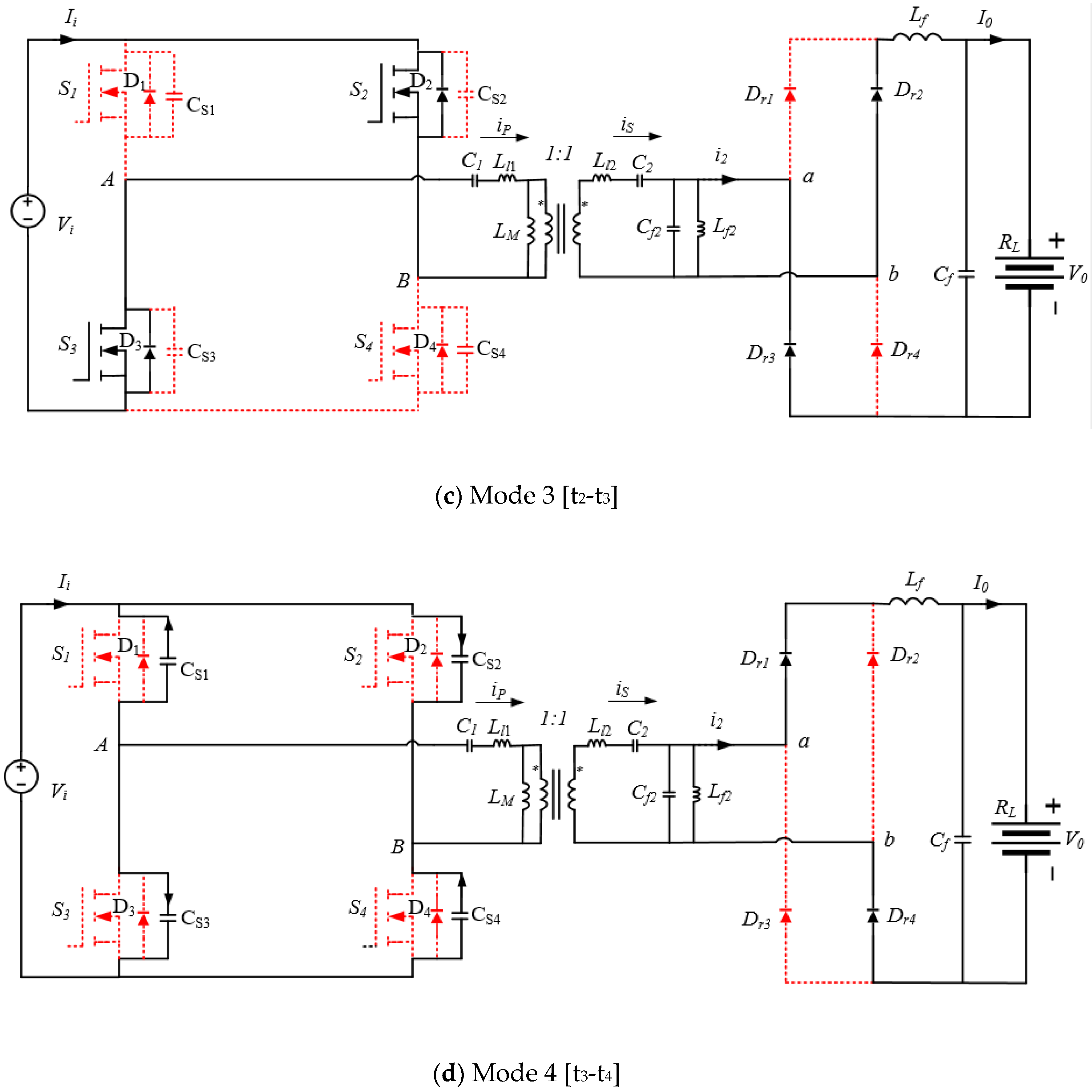
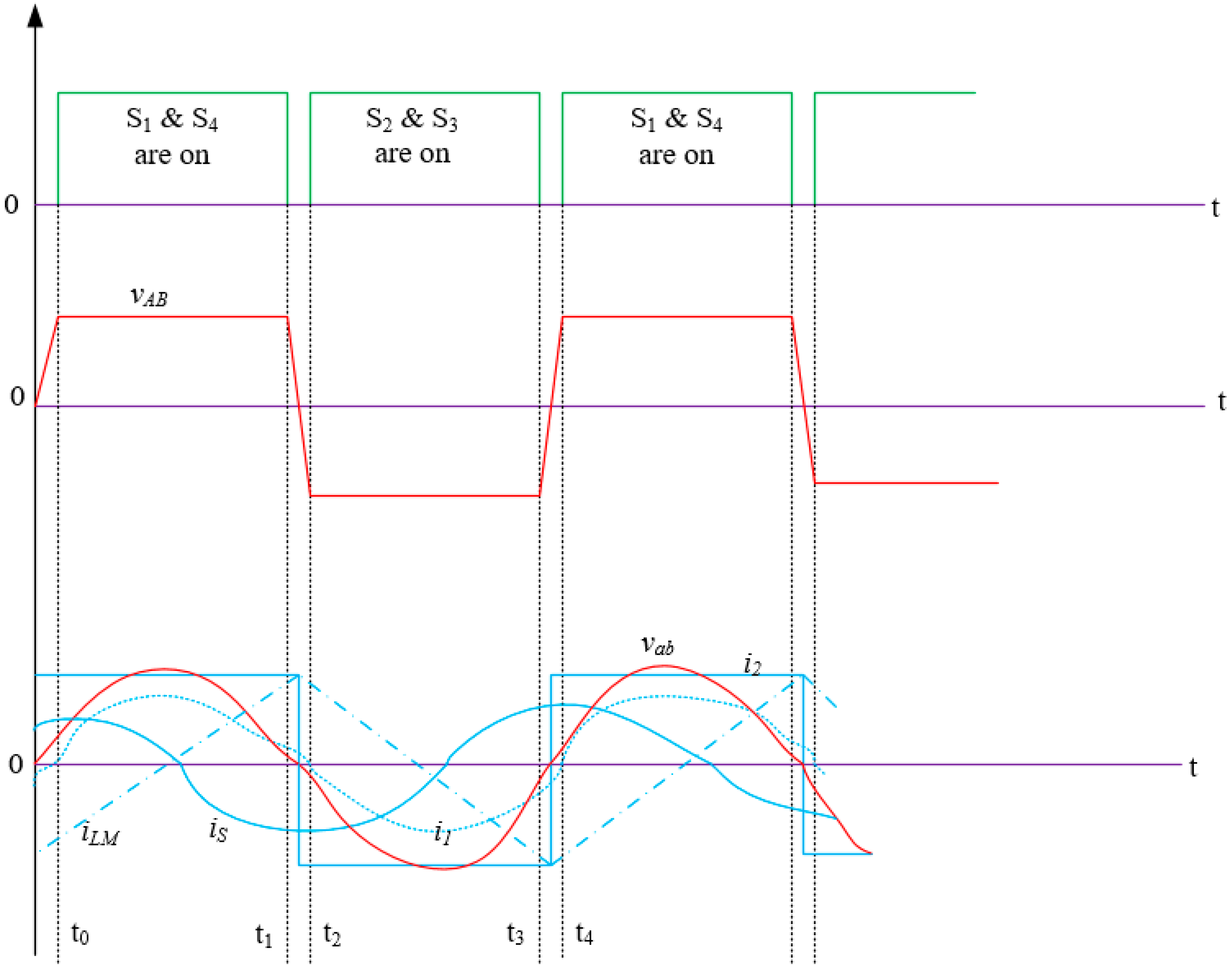
4. LC-LC2 Compensated Resonant Converter Using Time Domain Analysis
- (a)
- All semiconductor switches and diodes are ideal.
- (b)
- Receiver current, iS is almost sinusoidal since proposed converter operates near the resonant frequency.
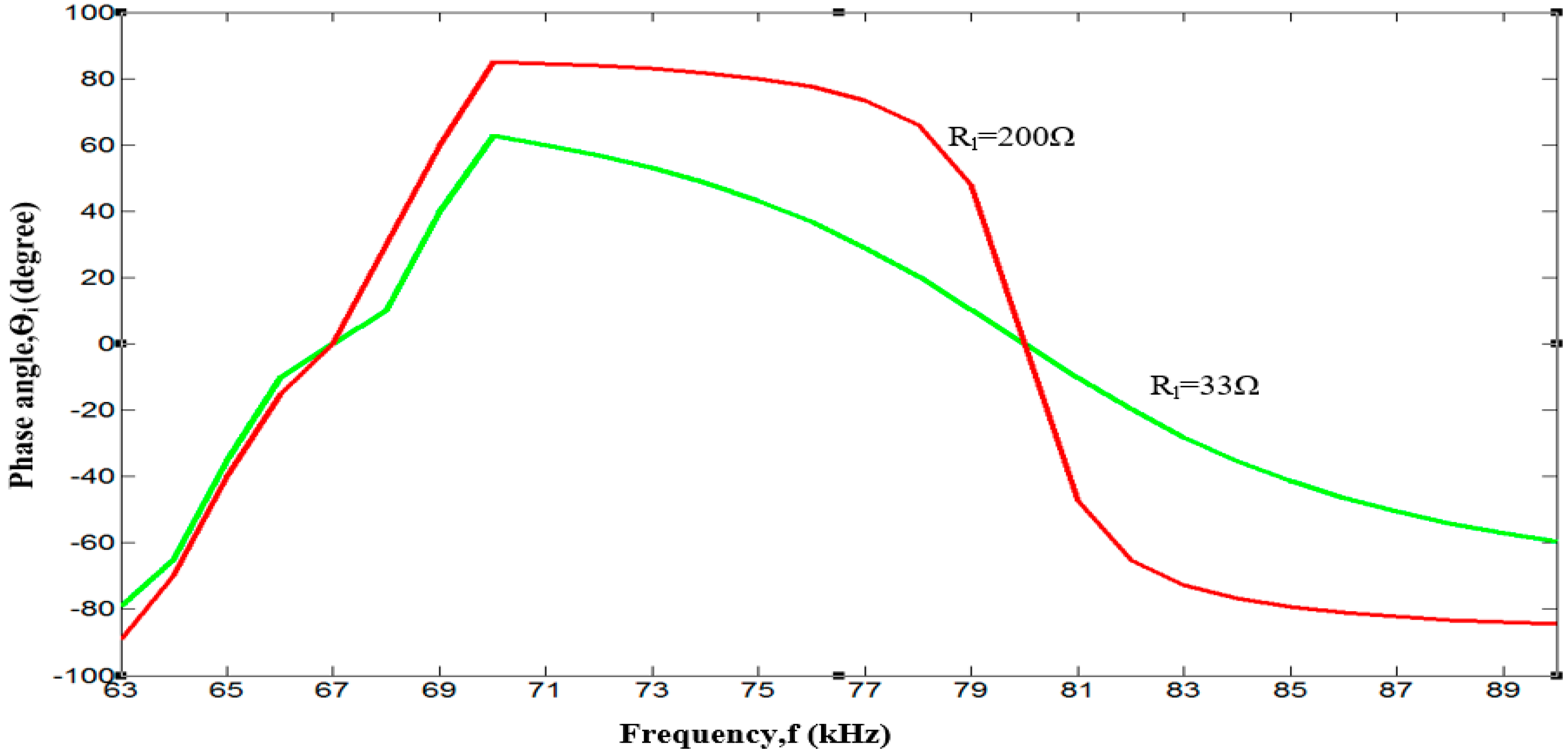
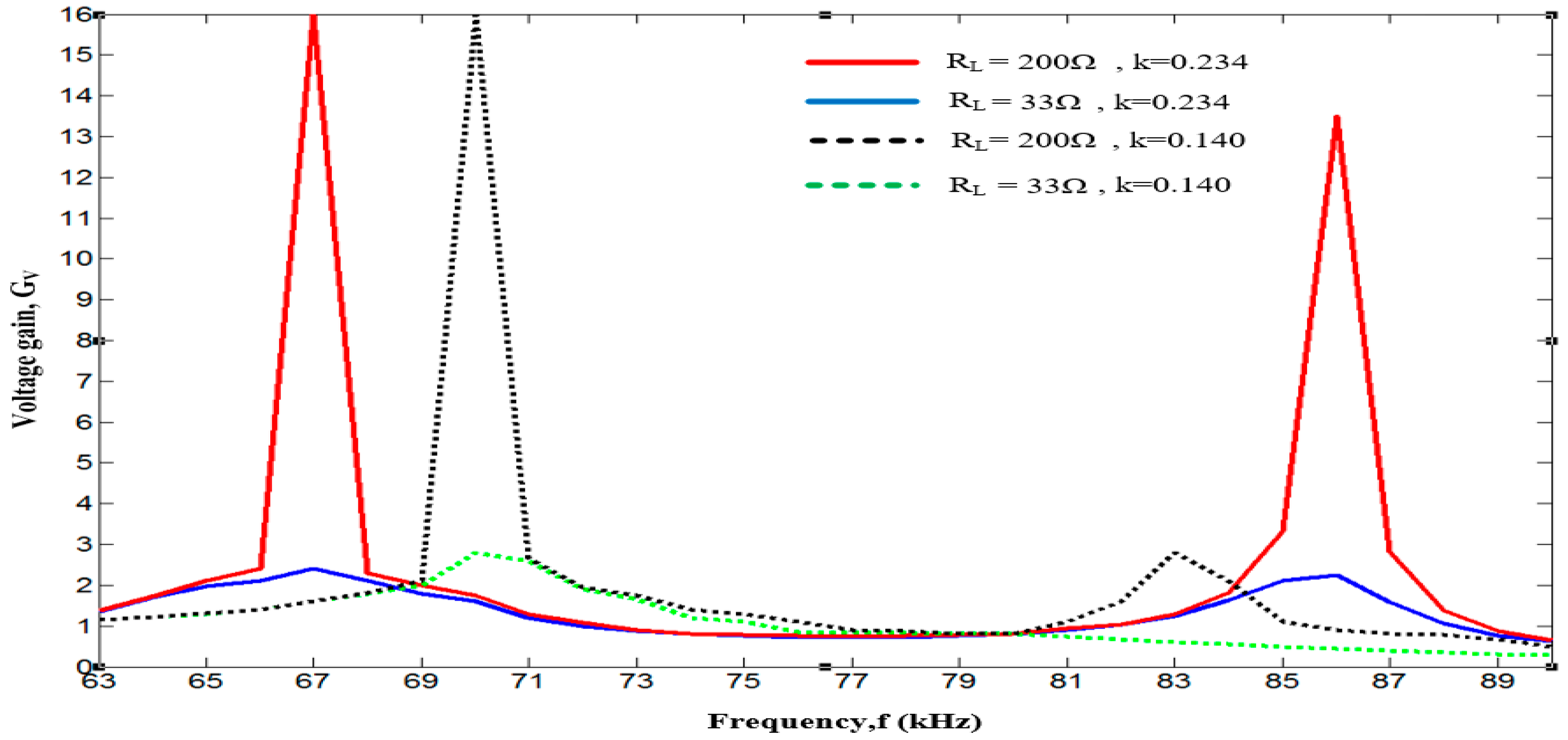
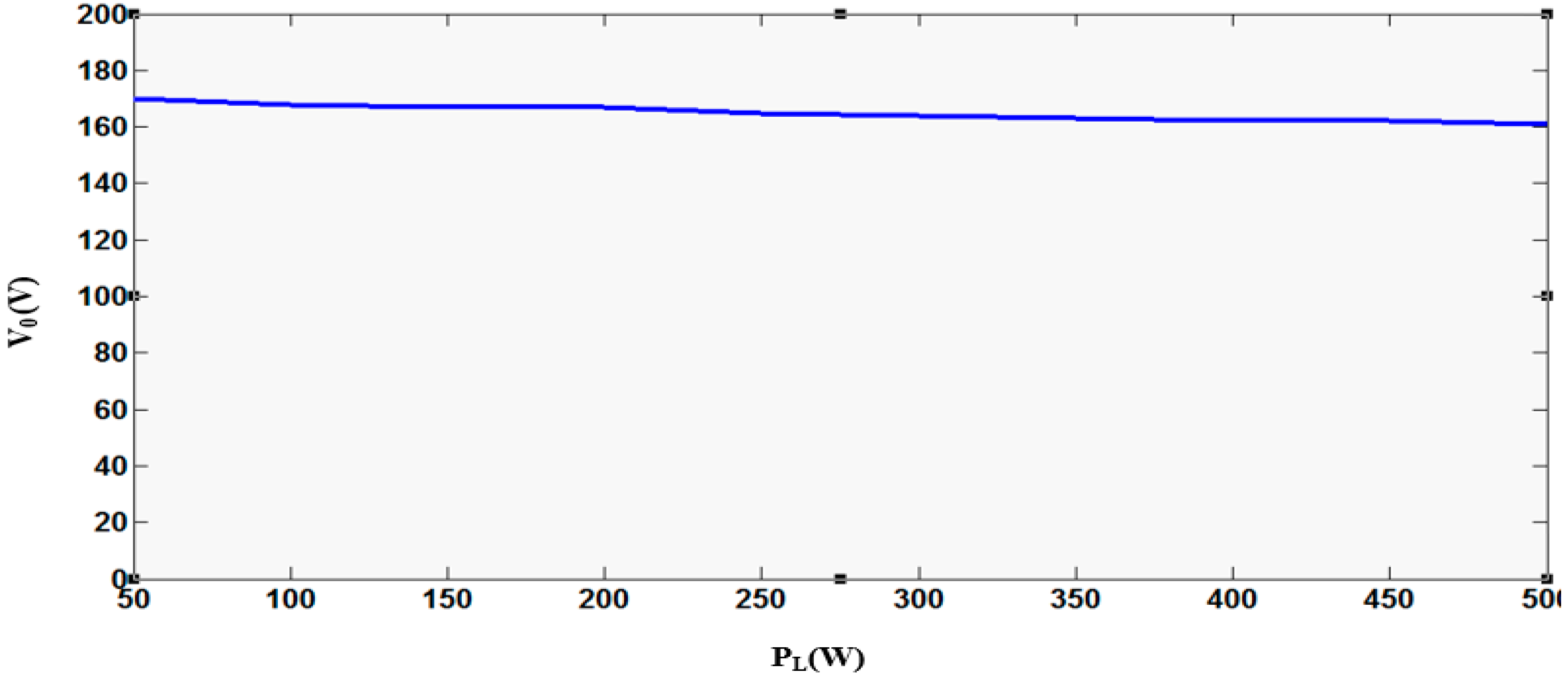
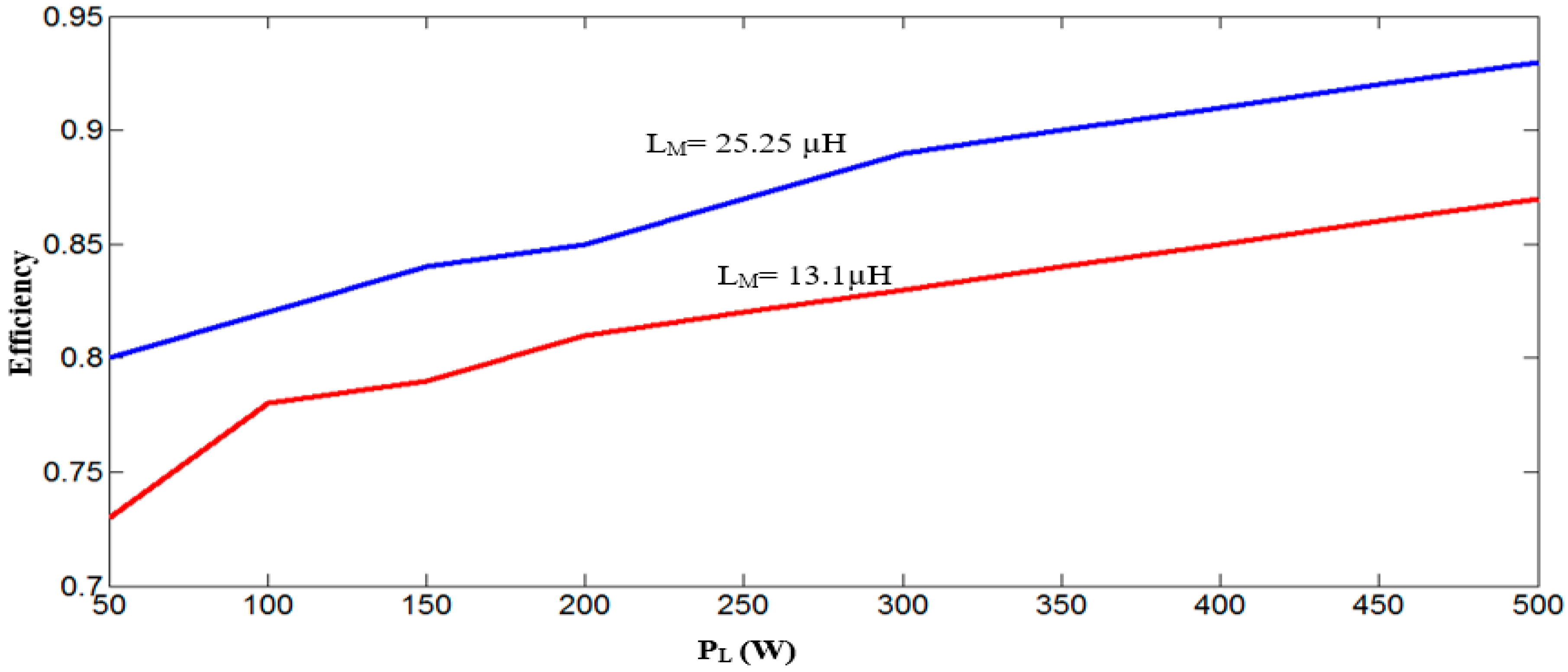
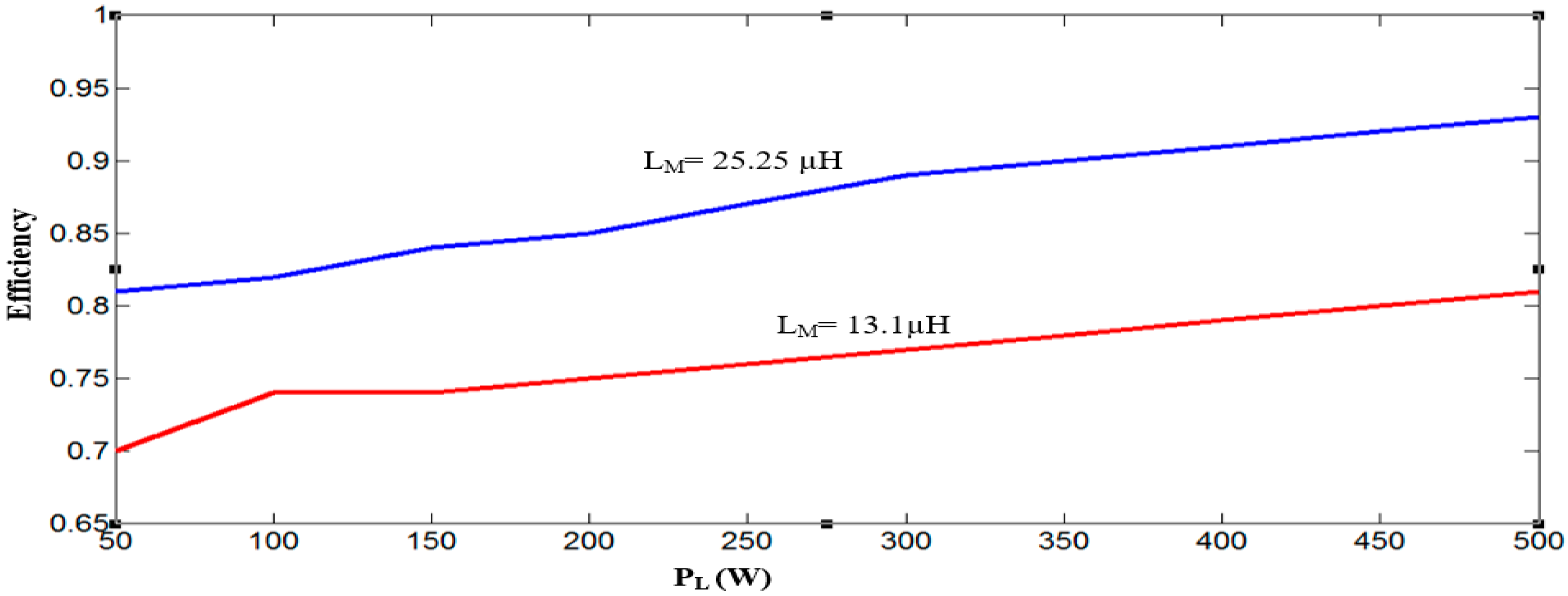
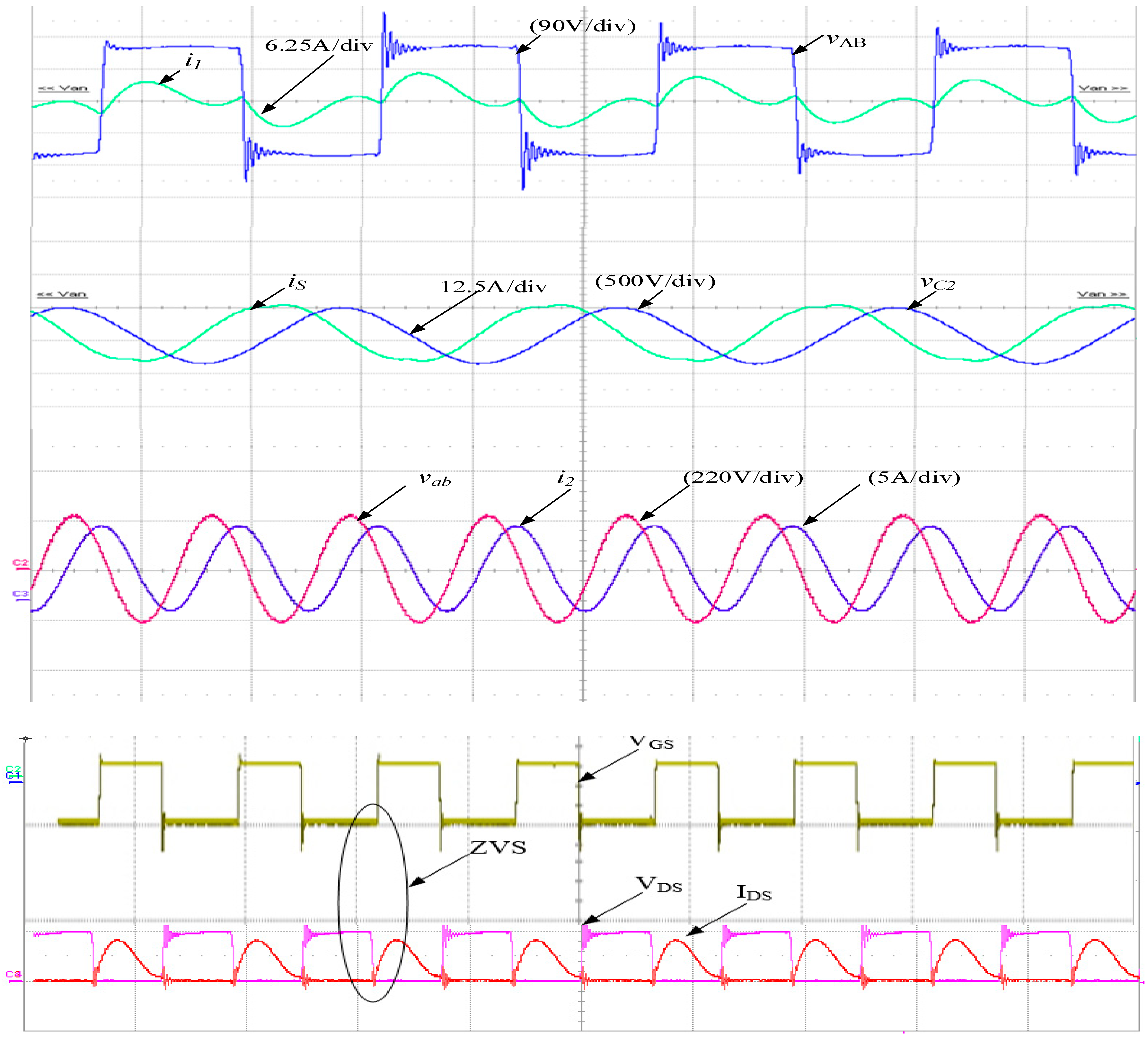
5. Analysis and Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cong, Z.; Jih-Sheng, L.; Rui, C.; Faraci, W.E.; Zahid, Z.U.; Bin, G.; Anderson, D. High-Efficiency Contactless Power Transfer System for Electric Vehicle Battery Charging Application. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 65–74. [Google Scholar] [CrossRef]
- Zhong, C.; Wuwei, J.; Xueliang, H.; Linlin, T.; Chen, C.; Wang, W. A Promoted Design for Primary Coil in Roadway-Powered System. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Sallan, J.; Villa, J.L.; Llombart, A.; Sanz, J.F. Optimal Design of ICPT Systems Applied to Electric Vehicle Battery Charge. IEEE Trans. Ind. Electron. 2009, 56, 2140–2149. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, H.; Hofmann, H.; Mi, C. A Dynamic Charging System with Reduced Output Power Pulsation for Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 6580–6589. [Google Scholar] [CrossRef]
- Kainan, C.; Zhengming, Z. Analysis of the Double-Layer Printed Spiral Coil for Wireless Power Transfer. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 114–121. [Google Scholar]
- Raju, S.; Rongxiang, W.; Mansun, C.; Yue, C.P. Modeling of Mutual Coupling Between Planar Inductors in Wireless Power Applications. IEEE Trans. Power Electron. 2014, 29, 481–490. [Google Scholar] [CrossRef]
- Chen, Q.; Wong, S.C.; Tse, C.K.; Ruan, X. Analysis, Design, and Control of a Transcutaneous Power Regulator for Artificial Hearts. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Klontz, K.W.; Divan, D.M.; Novotny, D.W.; Lorenz, R.D. Contactless power delivery system for mining applications. In Proceedings of the Conference Record of the 1991 IEEE Industry Applications Society Annual Meeting, Dearborn, MI, USA, 28 September–4 October 1991; pp. 1263–1269. [Google Scholar]
- Budhia, M.; Boys, J.T.; Covic, G.A.; Chang-Yu, H. Development of a Single-Sided Flux Magnetic Coupler for Electric Vehicle IPT Charging Systems. IEEE Trans. Ind. Electron. 2013, 60, 318–328. [Google Scholar] [CrossRef]
- Wei, Z.; Siu-Chung, W.; Tse, C.K.; Qianhong, C. Design for Efficiency Optimization and Voltage Controllability of Series-Series Compensated Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2014, 29, 191–200. [Google Scholar]
- Huh, J.; Lee, S.W.; Lee, W.Y.; Cho, G.H.; Rim, C.T. Narrow-Width Inductive Power Transfer System for Online Electrical Vehicles. IEEE Trans. Power Electron. 2011, 26, 3666–3679. [Google Scholar] [CrossRef]
- Chwei-Sen, W.; Covic, G.A.; Stielau, O.H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems. IEEE Trans. Ind. Electron. 2004, 51, 148–157. [Google Scholar]
- Raabe, S.; Covic, G.A. Practical Design Considerations for Contactless Power Transfer Quadrature Pick-Ups. IEEE Trans. Ind. Electron. 2013, 60, 400–409. [Google Scholar] [CrossRef]
- Keeling, N.A.; Covic, G.A.; Boys, J.T. A Unity-Power-Factor IPT Pickup for High-Power Applications. IEEE Trans. Ind. Electron. 2010, 57, 744–751. [Google Scholar] [CrossRef]
- Wu, H.H.; Gilchrist, A.; Sealy, K.D.; Bronson, D. A High Efficiency 5 kW Inductive Charger for EVs Using Dual Side Control. IEEE Trans. Ind. Inform. 2012, 8, 585–595. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Siu-Chung, W.; Tse, C.K.; Qianhong, C. Analysis and Comparison of Secondary Series- and Parallel-Compensated Inductive Power Transfer Systems Operating for Optimal Efficiency and Load-Independent Voltage-Transfer Ratio. IEEE Trans. Power Electron. 2014, 29, 2979–2990. [Google Scholar]
- Villa, J.L.; Sallan, J.; Sanz, J.F.; Llombart, A. High-Misalignment Tolerant Compensation Topology For ICPT Systems. IEEE Trans. Ind. Electron. 2012, 59, 945–951. [Google Scholar] [CrossRef]
- Hou, J.; Chen, Q.; Yan, K.; Ren, X.; Wong, S.C.; Tse, C.K. Analysis and control of S/SP compensation contactless resonant converter with constant voltage gain. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 2552–2558. [Google Scholar]
- Budhia, M.; Covic, G.A.; Boys, J.T.; Chang-Yu, H. Development and evaluation of single sided flux couplers for contactless electric vehicle charging. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Phoenix, AZ, USA, 17–22 September 2011; pp. 614–621. [Google Scholar]
- Ahmed, K.; Aamir, M.; Uddin, M.K.; Mekhilef, S. A new coil design for enhancement in misalignment tolerance of Wireless Charging System. In Proceedings of the IEEE Student Conference on Research and Development (SCOReD), Kuala Lumpur, Malaysia, 13–14 December 2015; pp. 215–219. [Google Scholar]
- Boys, J.T.; Covic, G.A.; Green, A.W. Stability and control of inductively coupled power transfer systems. IEEE Proc.-Electr. Power Appl. 2000, 147, 37–43. [Google Scholar] [CrossRef]
- Chwei-Sen, W.; Stielau, O.H.; Covic, G.A. Design considerations for a contactless electric vehicle battery charger. IEEE Trans. Ind. Electron. 2005, 52, 1308–1314. [Google Scholar]
- Zhu, Q.; Wang, L.; Guo, Y.; Liao, C.; Li, F. Applying LCC Compensation Network to Dynamic Wireless EV Charging System. IEEE Trans. Ind. Electron. 2016, 63, 6557–6567. [Google Scholar] [CrossRef]
- Weihan, L.; Han, Z.; Tianze, K.; Mi, C. Inter-operability considerations of the double-sided LCC compensated wireless charger for electric vehicle and plug-in hybrid electric vehicle applications. In Proceedings of the IEEE PELS Workshop on Emerging Technologies: Wireless Power (2015 WoW), Daejeon, Korea, 5–6 June 2015; pp. 1–6. [Google Scholar]
- Xiaoyong, R.; Qianhong, C.; Lingling, C.; Xinbo, R.; Siu-Chung, W.; Tse, C.K. Characterization and control of self-oscillating contactless resonant converter with fixed voltage gain. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; pp. 1822–1827. [Google Scholar]
- Hasanzadeh, S.; Vaez-Zadeh, S. Enhancement of overall coupling coefficient and efficiency of contactless energy transmission systems. In Proceedings of the 2nd Power Electronics, Drive Systems and Technologies Conference, Tehran, Iran, 16–17 February 2011; pp. 638–643. [Google Scholar]
- Li, W.; Zhao, H.; Li, S.; Deng, J.; Kan, T.; Mi, C.C. Integrated LCC Compensation Topology for Wireless Charger in Electric and Plug-in Electric Vehicles. IEEE Trans. Ind. Electron. 2015, 62, 4215–4225. [Google Scholar] [CrossRef]
- Huang, C.Y.; Boys, J.T.; Covic, G.A. LCL Pickup Circulating Current Controller for Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2013, 28, 2081–2093. [Google Scholar] [CrossRef]
- Amjad, M.; Salam, Z.; Facta, M.; Mekhilef, S. Analysis and Implementation of Transformerless LCL Resonant Power Supply for Ozone Generation. IEEE Trans. Power Electron. 2013, 28, 650–660. [Google Scholar] [CrossRef] [Green Version]

| Design Specifications | Value |
|---|---|
| Resonant frequency | f = 80 kHz |
| Parameters of IPT transformer | n = 1, Ll1 = 82.95 µH, Ll2 = 82.05 µH, LM = 25.25 µH–13.1 µH, k = 0.234–0.140 |
| Compensating inductor | Lf2 = 20 µH |
| Resonant capacitors | C1 = 47.71 nF, C2 = 48.24 nF, Cf2 = 354.65 nF |
| Load resistance | RL = 33–200 Ω |
| Filter parameters | Lf = 1000 µH and Cf = 500 nF |
| Load power | PL = 500 W |
| Air gap | H = 140–180 mm |
| Compensation Networks | Evaluation Criteria | ||||
|---|---|---|---|---|---|
| Maximum Efficiency | Power Rating | Air Gap | Efficiency Variation | Higher-Order Harmonics | |
| S–SP [18] | 93% | 1500 W | 200 mm | Affected by the mutual inductance changes | Injected to the rectifier side |
| LC-LC2 | 93% | 500 W | 140 mm | Less affected by the mutual inductance changes | Not injected to the rectifier side |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.M.; Mekhilef, S.; Bassi, H.; Rawa, M.J.H. Analysis of LC-LC2 Compensated Inductive Power Transfer for High Efficiency and Load Independent Voltage Gain. Energies 2018, 11, 2883. https://doi.org/10.3390/en11112883
Alam MM, Mekhilef S, Bassi H, Rawa MJH. Analysis of LC-LC2 Compensated Inductive Power Transfer for High Efficiency and Load Independent Voltage Gain. Energies. 2018; 11(11):2883. https://doi.org/10.3390/en11112883
Chicago/Turabian StyleAlam, Md Morshed, Saad Mekhilef, Hussain Bassi, and Muhyaddin Jamal Hosin Rawa. 2018. "Analysis of LC-LC2 Compensated Inductive Power Transfer for High Efficiency and Load Independent Voltage Gain" Energies 11, no. 11: 2883. https://doi.org/10.3390/en11112883
APA StyleAlam, M. M., Mekhilef, S., Bassi, H., & Rawa, M. J. H. (2018). Analysis of LC-LC2 Compensated Inductive Power Transfer for High Efficiency and Load Independent Voltage Gain. Energies, 11(11), 2883. https://doi.org/10.3390/en11112883






