1. Introduction
Smart gird, integrated power network with communication network, incorporates the latest innovative technologies to bring a revolutionary change and innovation of traditional power for future green energy [
1,
2,
3,
4,
5]. Although smart grid has lots of promising features, such as intelligent de-centralized control, resilience, flexibility, sustainability, digitalization, intelligence, consumer empowerment, renewable energy, smart infrastructure and so on, a number of critical challenges and open issues like need to be further discussed [
6,
7,
8,
9]. One of these critical challenges is risk of smart grid communication which is always the critical constraint in ultra high voltage (UHV) Grid [
7], Smart Home [
8], Microgrids [
9] and other smart grid applications.
Due to the complexity of smart grid communication environment, different communication technologies are used for the realization of smart grid, such as Optical fiber technology, power line communication (PLC), 4G/5G, wireless mesh network and so on [
10,
11,
12]. Among these communication technologies, optical fiber technology and the corresponding synchronous digital hierarchy (SDH) technology is widely used in the smart grid communication transmission network for the high bandwidth, high anti-interference, small signal attenuation and long transmission distance. However, there still exists communication violation risk.
With SDH technology, one optical fiber can carry multiple service channels. Each single service channel may have a great transmission capacity, such as STM-16 (10 Gbit/s). In this case, even a short interruption of the fiber can still cause a large amount of data loss. Therefore, the occurrence of interrupted service channel must be limited. To achieve this purpose, the statistical path availability
model is normally adopted to model the service channel and the basic rules to guarantee the availability of service channels are also specified [
12]. According to the rules, in the process of service channel planning, different levels of electric power communication services should be allocated to the different channels. For example, to guarantee the service quality, a service with statistical availability greater than 99.9% should be allocated to a channel with the predetermined statistical availability higher than 99.9%. In addition, to ensure the requirements of high availability and high real-time, services are planned with the primary channel and backup channel. Thus, when some electric power communication failure events occur and some channels are interrupted, the services can be safeguarded.
However, in practice, the faults of transmission equipment and optical cables carrying the service channels occur randomly. Therefore, during a period of time, the actual path availability of service channels may be significantly higher than 99.9%, or may be less than 99.9% due to a sudden failure. The backup channel strategy cannot ensure that the actual channel availability will not violate the rules. Thus, in practice, there exists a risk that service channel may violate the availability requirements, namely there exists a service channel violation risk (SCVR). In this case, the challenge that electric power communication network channel planning faces is how to effectively control the availability decline because of the channel random failures, thus to reduce the probability of SCVR.
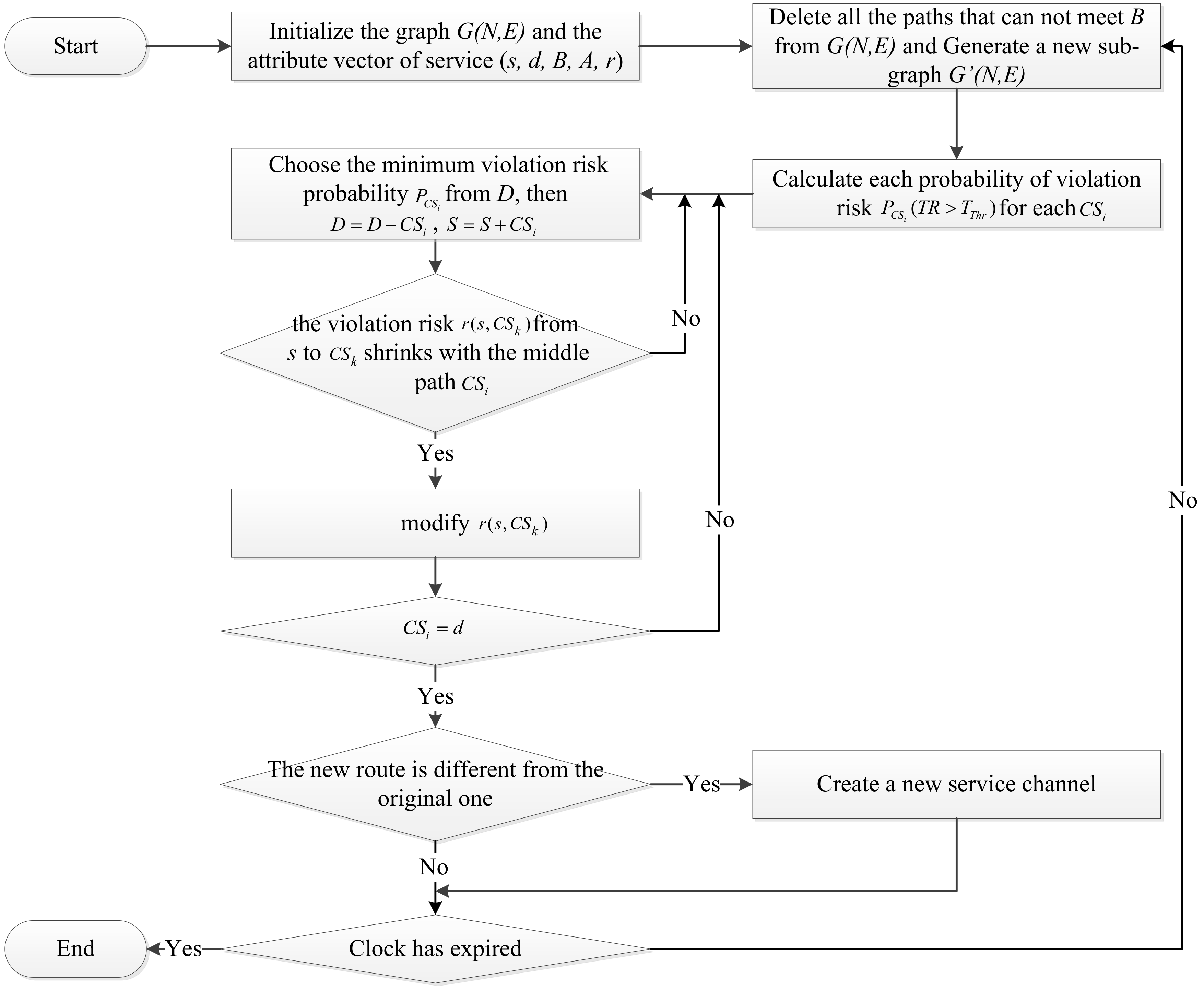
To solve this problem, the availability-aware routing mechanism should be considered. Through scientific and rational route planning, when a channel fails, the service carried by the channel can be conveyed by another channel and will not be affected, thus the violation risk caused by channel random failure can be avoided. To achieve the above goal, firstly, a probability distribution model of SCVR should be studied and designed. Then, a SCVR based routing mechanism should be proposed to reduce the failure number (FN) and failure duration of the electric power communication service. The goal is to minimize the violation risk caused by the random failures of transmission equipment and optical cable and thus to improve the availability of electric power communication service.
In this paper, the main contributions include: (1) A probability distribution model of SCVR, named service channel violation risk degree (SCVRD) model, is proposed, which is denoted by the probability of service channel cumulative failure duration exceeding the prescribed duration. (2) Based on SCVRD, a service channel violation risk degree routing (SCVRD-R) algorithm is proposed to improve the availability of electric power communication service.
The remainder of the paper is organized as follows.
Section 2 reviews the related work and analyzes the limitation of the current works. In
Section 3, the differences between
and
are analyzed and the
SCVRD model is proposed.
Section 4 gives the approximate transformation of violation risk distribution and proposes the
SCVRD-R algorithm.
Section 5 discusses the simulation results. Finally,
Section 6 concludes the paper.
2. Related Work
Currently, the body of work related to smart grid communication robustness is rapidly increasing. For the realization of smart grid, many studies have looked at the communication challenges in smart grid.
Papers [
6,
7,
8,
9] pointed the critical communication challenge of smart grid communications and also gave the feasible solutions and future directions from the overall perspective. One way is to improve the communication reliability by eliminating the defects of the technology itself. Paper [
10] proposed an orthogonal poly-phase-based multicarrier code division multiple access (OPP-MC-CDMA) system and implemented with a minimum mean square error equalizer and nonlinear preprocessing to overcome the effects of noise and multipath frequency-selective fading commonly experienced in PLC channels. This way is the most effective but it depends on the update of corresponding communication technology and it is difficult to make great progress.
The other way is to optimize the communication routing of communication service. Some studies adopt the method of optimizing the routing protocol of the corresponding communication network technology. Paper [
11] presented a QoS-aware wireless mesh network (WMN) routing technique that employed multiple metrics in optimized link state routing (OLSR) for AMI applications in a smart grid neighbor area network based wireless mesh network. They indicate to guarantee the optimized communication routing. Other studies turn to solve the service channel failure risk problem to guarantee the effective communication routing. The main way is to control the
SCVR by routing method. There are two kinds of routing methods: availability-aware routing based on statistics (AAR-OS) and availability-aware routing based on uncertainty (AAR-OU).
In respect of AAR-OS, the difference between
and
and how availability changes over time and geographical locations are pointed out in Reference [
13]. Based on the new availability calculation method, the 3W-availability aware routing (3WAR) algorithm was proposed in that paper which effectively narrowed the gap between the actual availability and target availability. In paper [
14], the definitions of min cross layer cut (MCLC) and min cross layer spanning tree (MCLST) were given and the availability routing algorithm under different failure probability conditions was proposed to maximize the MCLC and minimize the MCLST. Paper [
15] adopted the log information of path state as the basis for routing and considered the path with highest statistics availability as the service channel. Papers [
16,
17,
18] proposed
based multipath routing mechanism by increasing the redundancy of resources to enhance the
of the channel. Paper [
19] proposed a primary-backup sharing routing mechanism in optical networks to improve the resource utilization in premise of ensuring the statistical availability. In paper [
20], the cost of routing was taken into account in routing algorithm to minimize the cost in premise of ensuring the statistics availability.
The methods mentioned above are all using the as the decision indicator in routing mechanism. The advantages of those methods are simple, easy to reflect the availability in the overall trend and clear in physical meaning. But only has statistical meaning, which can reflect the availability variation trend on the whole but cannot reflect the actual availability fluctuations of channel. Thus, the threat to the grid due to network random failures cannot be effectively reduced by those methods.
In the aspect of AAR-OU, papers [
21,
22,
23,
24,
25] all studied the uncertainty of the path availability during a short time period. Paper [
21] proposed a dynamic availability-aware survivable routing architecture to provide the service path protection based on the partial restorability. Papers [
22,
23] defined the concept of availability border and proposed the path availability evaluation method and the routing algorithm on the assumption that failure arrival rate was dynamic and corresponding repair time was fixed. Paper [
24] replaced the statistical availability with service continuity and proposed the probability Equation of service uninterrupted, which effectively promoted the actual availability of the service. By statistical methods, paper [
25] obtained the accurate probability of service channel failure time exceeding the specified time according to a lot of simulation based a given network environment. But when the network environment changed, the simulation needed to be restarted which reduced the universality of this method.
The above methods mentioned are considering the actual availability which is more accurate than in routing. However, because the time to repair (TTR) of channel is changing with the environment and the geographical location, thus the assumption of a fixed TTR will limit the application scope of the above methods. On the other aspect, if the correlation among TTRs of different channels is not considered when selecting the primary and backup routing, the risk of primary and backup channels simultaneously being in failure will be increasing. Therefore, random TTR and its impact should be further considered for universal service channel failure risk routing mechanism.
Further studies showed that the occurrence of an electric power communication failure event and the fluctuations of service channel
are interrelated and the fluctuations of
is one of the root cause of electric power communication failure events [
26]. Because the fluctuations of
has the random nature according to the interaction of many factors, the occurrence of the electric power communication failure event is a complex random process. Moreover, the fluctuations of
makes the occurrence of the events that violate the availability rules (i.e., service channel failure events (SFE)) inevitable and hard to be precisely tracked. Therefore, it is necessary to precisely quantify the occurrence rule of SFE and
SCVR. The preliminary work in paper [
27] adopted the influence factors of service channel availability (
FN and
TTR) instead of
to equivalently quantify
SCVR. It just simply mentioned the idea without mathematical proof. However, it is proved to be an effective way to start with analysis of the influence factors of service channel availability and their relationship.
Thus, the study of distribution models of FN, failure arrival rate and TTR of transmission equipment and fiber cable and their internal relationship is the fundamental way to precisely quantify SCVR and control the influence degree of electric power communication failure events. According to the analysis above, the innovativeness of this paper are as follows.
(1) To precisely track the violation risk change of service channel under the condition that all of the FN, failure arrival rate and TTR are random, we deduce SCVRD model from the service channel violation risk model which is denoted by and denote SCVRD model by the probability of service channel cumulative failure duration exceeding the prescribed duration. We prove the deduction and simplify the SCVRD model with mathematical method.
(2) Based on SCVRD model, the SCVRD-R mechanism is proposed to reduce the FN and failure duration of the electric power communication service. The goal is to minimize the violation risk caused by the random failures and TTR of transmission equipment and optical cable and thus to improve the availability of electric power communication service.
3. SCVRD Model
In this section, the differences between and are compared firstly and the existing problem of AAR-OS algorithm is analyzed. Subsequently, the SCVRD model is established according to the joint distribution of failure arrival rate and repair time of the transmission equipment and optical cable.
3.1. Differences Between and
Before establishing the SCVRD model, the varying rule of should be analyzed to identify the influence factors which cause the differences between and .
is defined as the ratio of service un-interrupted duration in a statistical period of time [
22]. Let the graph
G(
V,
E) represent the network topology,
V denotes the node set and
E denotes the edge set.
can be calculated by Equations (1)–(3) based on the statistical data at the end of each time period.
denotes the
ith node in network topology
G(
V,
E) and
denotes the edge between node
i and node
j in
G(
V,
E).
denotes the statistical availability of the
ith node.
and
respectively denote the mean time between failures (
MTBF) and mean
TTR (
MTTR) of the
i-th node.
denotes the statistical availability of the edge
.
and
respectively denote the
MTBF and
MTTR of the edge.
MTBF and
MTTR in Equations (2) and (3) are calculated by time between failures (
TBF) and
TTR in statistical period respectively.
can be expressed as follows:
Next, we will discuss the situations of . Because the state of and are always varying between normal state and failure state, the varying rule of can be analyzed by investigating the conversion process of and . This process can be divided into three phases for analysis:
(1) During the period from initial time
to the first failure occurred time
,
can be expressed as Equation (5):
(2) When the
kth
fault occurs, the items in Equation (4) are all constants except for
, so
varies only with the change of
, expressed by Equation (6).
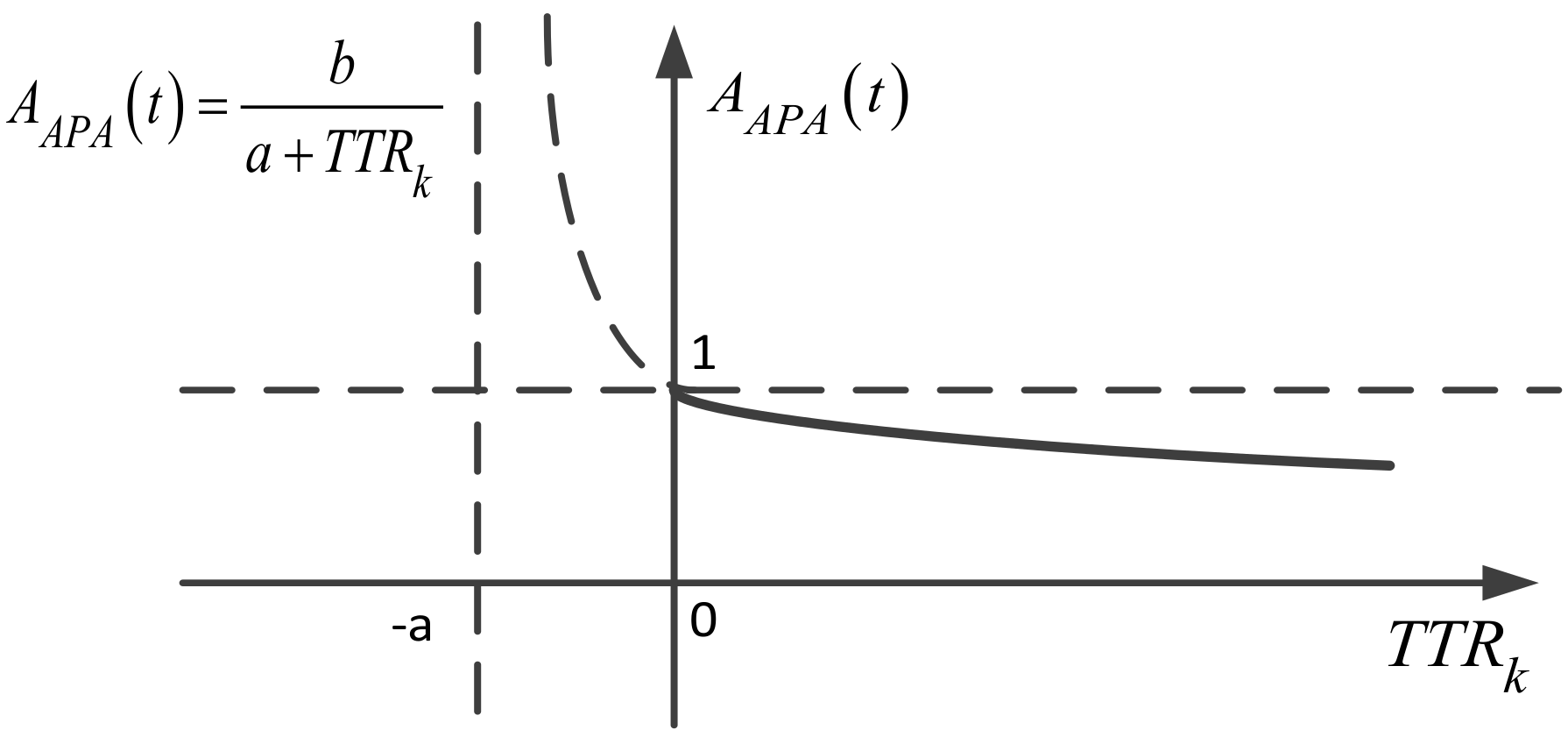
a,
b respectively, denote the cumulative availability time and the cumulative time when the
kth fault occurs and both of them are constants in this phase.
The varying curve of
in this phase is shown with the solid line in
Figure 1.
(3) When the channel returns to normal state from the
kth failure, the items in Equation (4) are all constants except for
, so
varies only with the change of
, expressed by Equation (7).
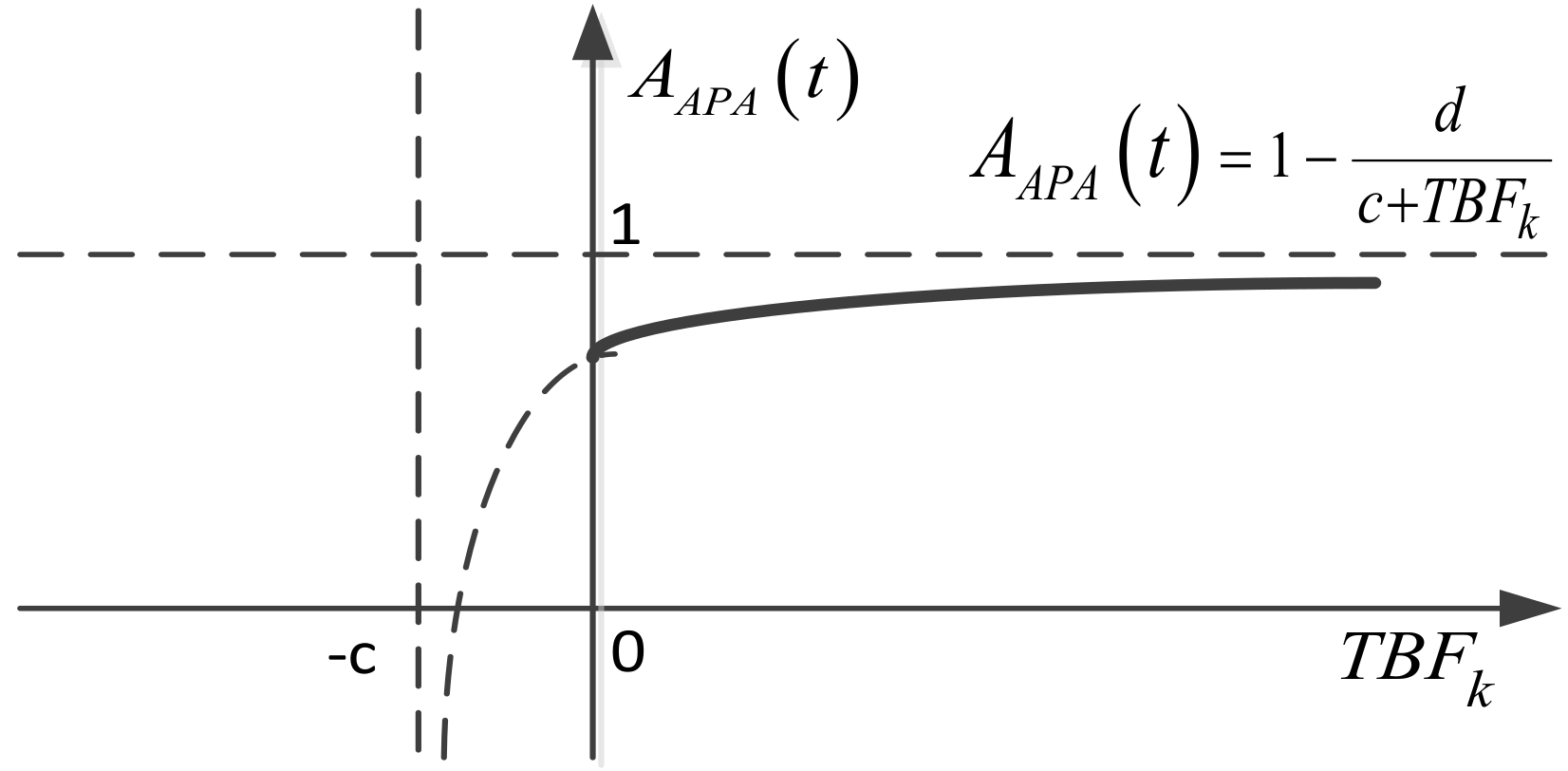
c,
d respectively denote the cumulative repair time and the cumulative time when the channel returns to normal state from the
kth failure and both of them are constants in this phase.
The varying curve of
in this phase is shown as the solid line in
Figure 2.
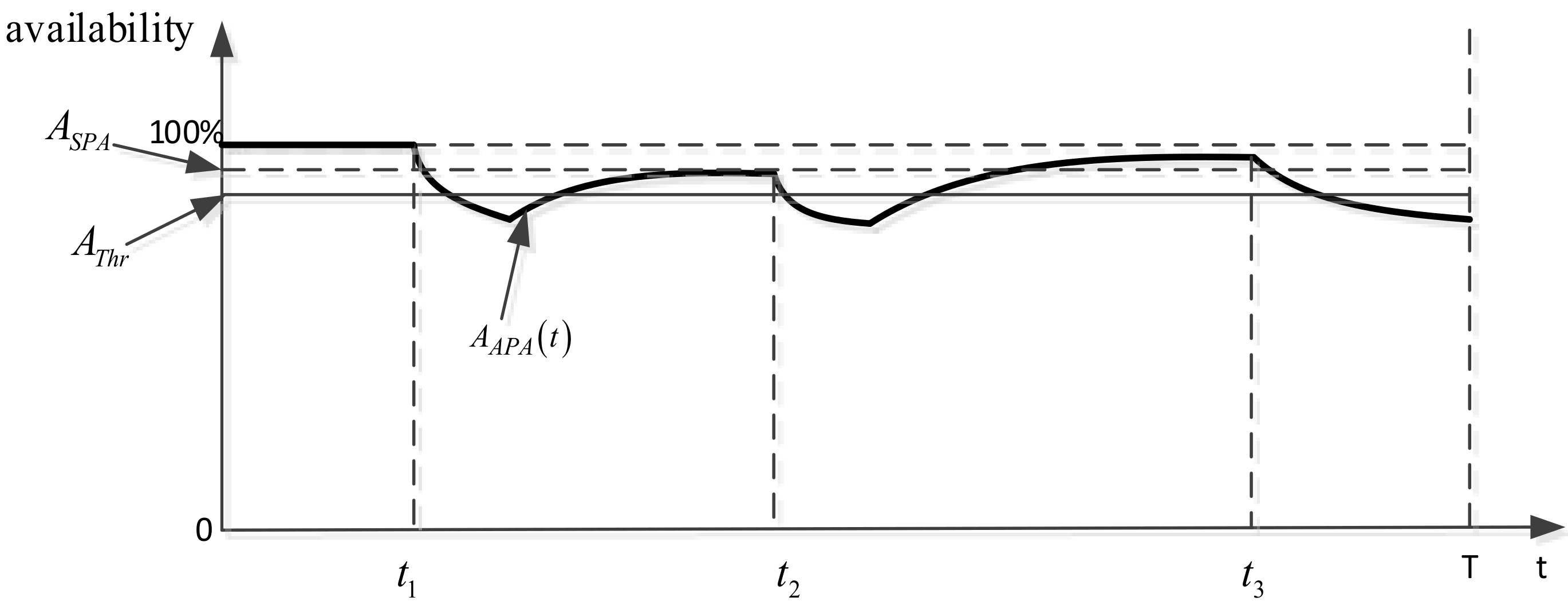
According to the analysis above, the varying curve of
changes with the channel’s conversion process between normal states and failure states, as is shown in
Figure 3.
in
Figure 3 denotes the availability threshold.
As shown in
Figure 3, the differences between
,
and
are clearly illustrated.
is the statistical mean value of
, which must be always greater than
and is expressed as a horizontal dashed line in
Figure 3.
can be used to describe the overall availability of service channel from a global perspective but it cannot reflect the influence of each failure and repair time to the service.
is the actual availability of the service channel and its value can be calculated by (4) after each failure. However, since , , failure arrival rate and FN of each channel all have the nature of randomness, may be significantly higher than sometimes or may be lower than sometimes because of the sudden random failure. Therefore, the occurrence of SFE is inevitable.
If the degree of SCVR can be quantified, then the impact caused by SFE can be controlled, thereby the number and the duration of the impacted services can be reduced. To achieve the purpose, the SCVRD model is discussed and established in the following paragraphs.
3.2. SCVRD Model
As shown in
Figure 3,
SCVRD which represents the probability of service channel violation risk
can be expressed by Equation (8):
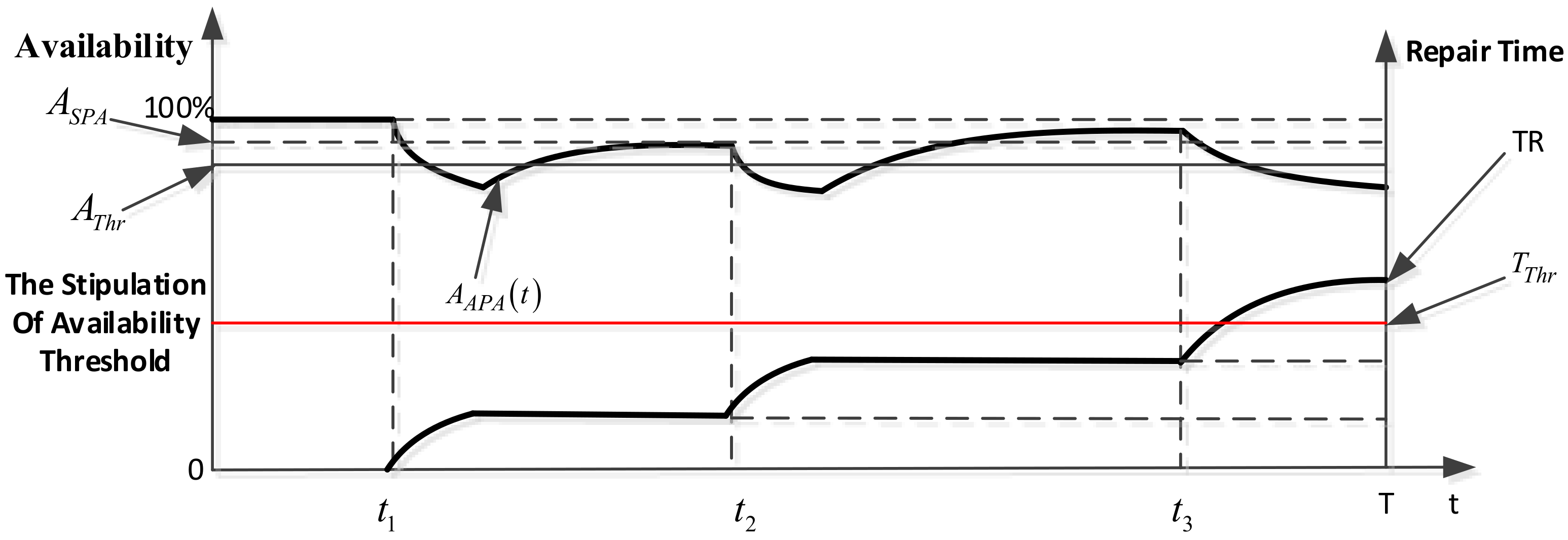
However,
SCVRD is hard to be accurately quantified and tracked due to the fluctuations of
. Thus, we introduce cumulative repair time TR and corresponding repair time threshold
in the statistical period to describe the service channel violation risk.
Then according to Equation (4),
SCVRD can be quantified by Equation (11).
Thus, the probability of service channel violation risk based on availability is converted to the probability of cumulative repair time exceeding the corresponding repair time threshold in the statistical period. The equivalence relationship is shown in
Figure 4.
Next, the characteristics of
SCVRD will be further analyzed. By further analyzing Equation (4), we can find that
is co-determined by
FN of the service channel and each failure
. According to [
23],
TTR of
and
is independent and they all obey the log-normal distribution as expressed by Equation (12). Therefore, TR subjects to the joint distribution of
, which means that SFE is a random process and
is a random probability model. Assume that
FN of service channel obeys the Poisson distribution with average arrival rate
λ, as expressed by Equation (13). Thus, the service channel violation risk caused by the
kth failure
during the statistical period can be expressed by Equation (14):
Because the failure occurrences of
and
are independent, according to the conditional probability Equation and the n-fold convolution Equation, Equation (14) can be expanded to Equation (15):
According to the total probability Equation, the Equation (15) can be expanded to (16).
Figure 5 is an example to illustrate the difference between
and
in the process of
SCVRD quantization.
In
Figure 5, an example for availability distribution diagram of the service channel violation risk is shown. There are two service channels named
and
with
= 99.8%. Assume
= 99.5%, the parameters of
are
and the parameters of
are
. Then, according to (16),
and
are found. During the calculation, we can find that
when
. As a result, when
, the precision requirement can be satisfied and this result is consistent with the fact that the repair time cannot be infinitely small.
Through this example, it can be found that although the of both and are all higher than , there is still a failure risk of about 0.389~0.426 for service channel. In addition, although the of and are the same, their failure risks are still different: and . Compared to , is more accurate to distinguish the differences of among the channels. Thus is more suitable in the quantization process of SFE.
6. Conclusions
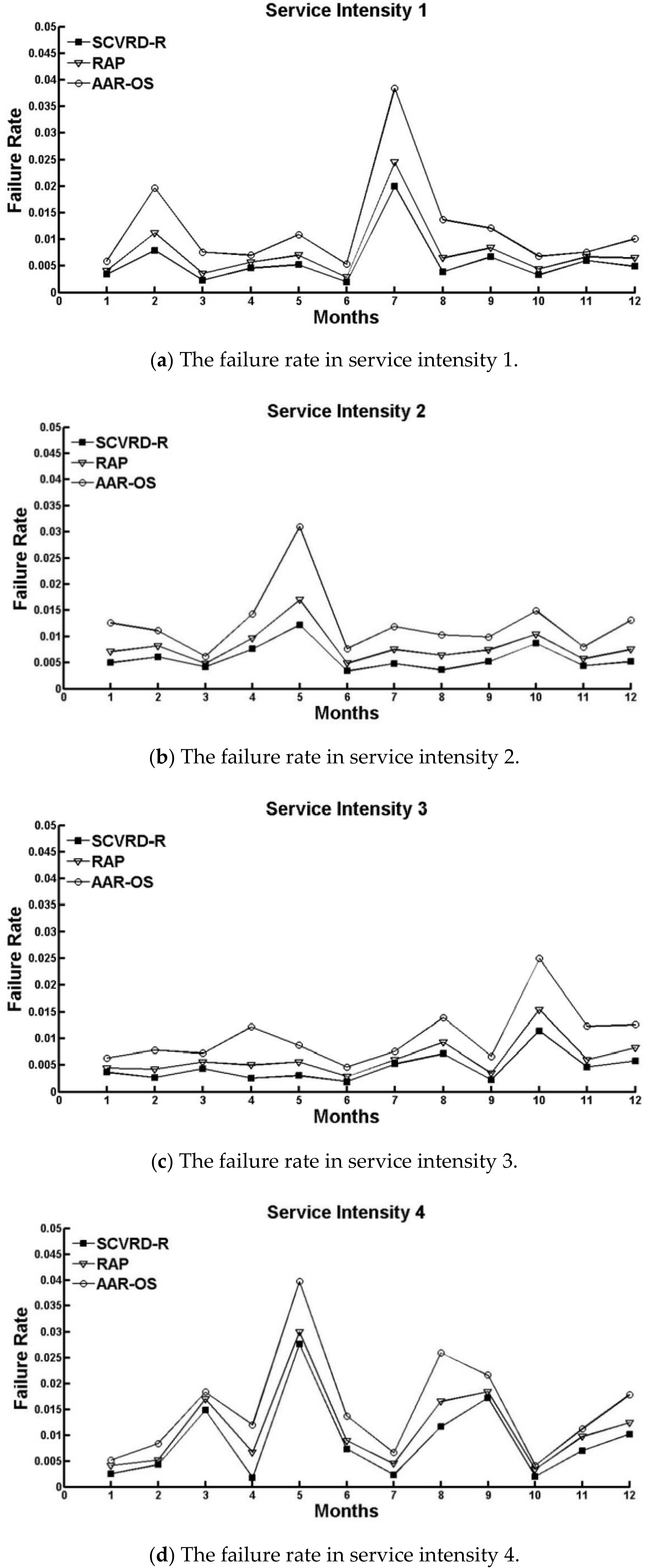
On account of the problems in electric power communication service route planning, a probability model of service channel violation risk, named SCVRD model, is proposed in this paper. Generally, the is calculated by mean value and is calculated based on some assumption, both of them cannot precisely track the violation risk change of service channel which is caused by the random failure under random TTR condition. To solve this problem, we deduce SCVRD model from the service channel violation risk model which is usually denoted by and denote SCVRD model by the probability of service channel cumulative failure duration exceeding the prescribed duration. The deduction is proved and then SCVRD model is simplified using mathematical method. Based on SCVRD, a service channel violation risk degree routing algorithm, named SCVRD-R algorithm, is proposed to reduce the risk caused by random failure of transmission equipment and optical cable and improve the availability of electric power communication service. Finally, the simulation results show that the average service channel failure rate of AAR-OS algorithm and RAP algorithm are respectively reduced by 15% and 6%.
In future work, we plan to further investigate how the failure rate convergence changes when optic cables reach the bandwidth limit. Furthermore, we intend to figure out the accurate numerical relationship among service intensity, service channel bandwidth and failure rate convergence to actually guide the service routing planning and optimization in electric power communication network. In many cases, the success of smart grid depends on their ability to support real-time decision-making. Therefore, we would make further efforts on the exploration of our proposed methodology in medium and short-term planning scenarios.