Efficient and Provably Secure Key Agreement for Modern Smart Metering Communications
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
1.3. Outline
2. Preliminaries
2.1. Bilinear Pairings
- Bilinear: Given , then , and for any .
- Nondegenerate: There exist , such that , with 1 the identity element of .
- Computable: For any , the value is efficiently computed.
- The Elliptic Curve Discrete Logarithm Problem (ECDLP). This problem states that given two points R and Q of an additive group G, generated by an elliptic curve (EC) of order q, it is computationally hard for any polynomial-time bounded algorithm to determine a parameter , such that .
- The Elliptic Curve Diffie Hellman Problem (ECDHP). Given two points of an additive group G, generated by an EC of order q with two unknown parameters , it is computationally hard for any polynomial-time bounded algorithm to determine the EC point .
2.2. Smart Metering Network Model
2.3. Thread Model
2.4. ECQV Certificates
3. Security Analysis of Authentication Schemes Recently Proposed in Literature
3.1. Review of Odelu et al.
- (A)
- Security in CK model: In the CK security model, a secure session reveal on the SM and SP, i.e., SSReveal(SM) and SSReveal(SP), is possible.We can assume the leakage of as it represents a local session state at the side of the SM. It is a local variable needed to be stored in order to be reused after reception of . Similarly, we can assume as a local session state at the side of the SP. Again, this variable needs to be stored as it is used two times in the calculations of the SP. Since, , thus only depends on these two local session states, the session key can be retrieved and the scheme turns out to be vulnerable under the CK security model.
- (B)
- Practical issues with registration phase: The generation of key material for both the SM and the SP from the TTP is not resistant against an honest but curious TTP, as the TTP derives the key material completely on its own and pushes it to the SM and SP. Consequently, the TTP can follow all the operations, and is able to track the SMs and SPs communications, and can collect the information.Moreover, in the registration phase, a secure channel is required between the SM, SP and TTP. Secure channels are often difficult to establish, especially in the case of SMs, where they are mostly in practice established through physical contact. Therefore, secure channels are not always practical.Finally, we also mention the weakness already noted by [11] regarding the key escrow problem. Once the private key of the TTP is revealed, all private keys of the SPs and SMs are easily derived. Once these private keys are revealed, impersonation attacks and many more attacks can start.
- (C)
- Late detection of MITM: Lead to DoS: The scheme behaves very weak with regard to MITM attacks that may lead to DoS attacks on the server side. Assume that an attacker (Tom) acts as MITM. Tom can capture and sends it () to the SP. Note that the SP can only decide about the validity of a request () after completing the whole process, i.e., after receiving the message . As a consequence, each request opens a buffer, where first several compute intensive pairings need to be computed, followed by the submission of a response. This buffer needs to be kept open until a response of the SM is received. Consequently, the memory can easily overflow by sending a huge number of invalid requests, where valid and invalid requests cannot be distinguished due to the late detection of forged messages.
3.2. Review of Chen et al.
- (A)
- Security in CK model: A similar type of attack as in [10] is possible. In the CK security model, a secure session reveal on the SM and SP, i.e., SSReveal(SM) and SSReveal(SP), is possible.As a result, the local states from SM and from SP are leaked. Since, , the security of the session key is broken.
- (B)
- Late detection of MITM: Lead to DoS: The same issue regarding the late detection of a MITM attack also holds in this scheme. After receiving , the SP is unable to check if this request is coming from a registered SM. Only after receiving the last message and verifying the hash value , the SP can decide if the key negotiation has been successfully executed. As a result, this weakness could lead to DoS threat.
3.3. Review of Abbasinezhad et al.
- (A)
- Security in CK model: The scheme is not resistant in the CK security model if the private keys and of the SM and SP respectively are leaked. This follows from the fact that and . As a result, the adversary is able to compute and the security of the session key is broken.
- (B)
- Late detection of MITM: Lead to DoS: The same issue regarding the late detection of a MITM attack also holds in this scheme. After receiving , the SP is unable to check if this request is coming from a registered SM. Only after receiving the last message and verifying the hash value , the SP can decide if the key negotiation has been successfully executed. As a result, this weakness could lead to a DoS threat.
3.4. Lessons Learned
- Resistance in CK model: Any possible definition of the SK should consist of a combination of both the local state variable and the private key of at least one entity. For instance, in [10,11], the SK can be written in a form only consisting of local state variables of the two entities and in [12], the SK is derivable to a form only consisting of the private keys of the two entities.
- Resistance to DoS attacks: In [10,11,12], the SP only retrieves the identity of the SMs after receiving a second message and is not able to detect malicious behaviour. Therefore, to avoid the SP keeping open a huge amount of (potential malicious) sessions, it is better to let the request initiated by the SP. The SM is less vulnerable since it can react when too many requests are sent as they are coming from only one entity, i.e., the SP.
4. Proposed Scheme
4.1. Setup Phase
4.2. Registration Phase
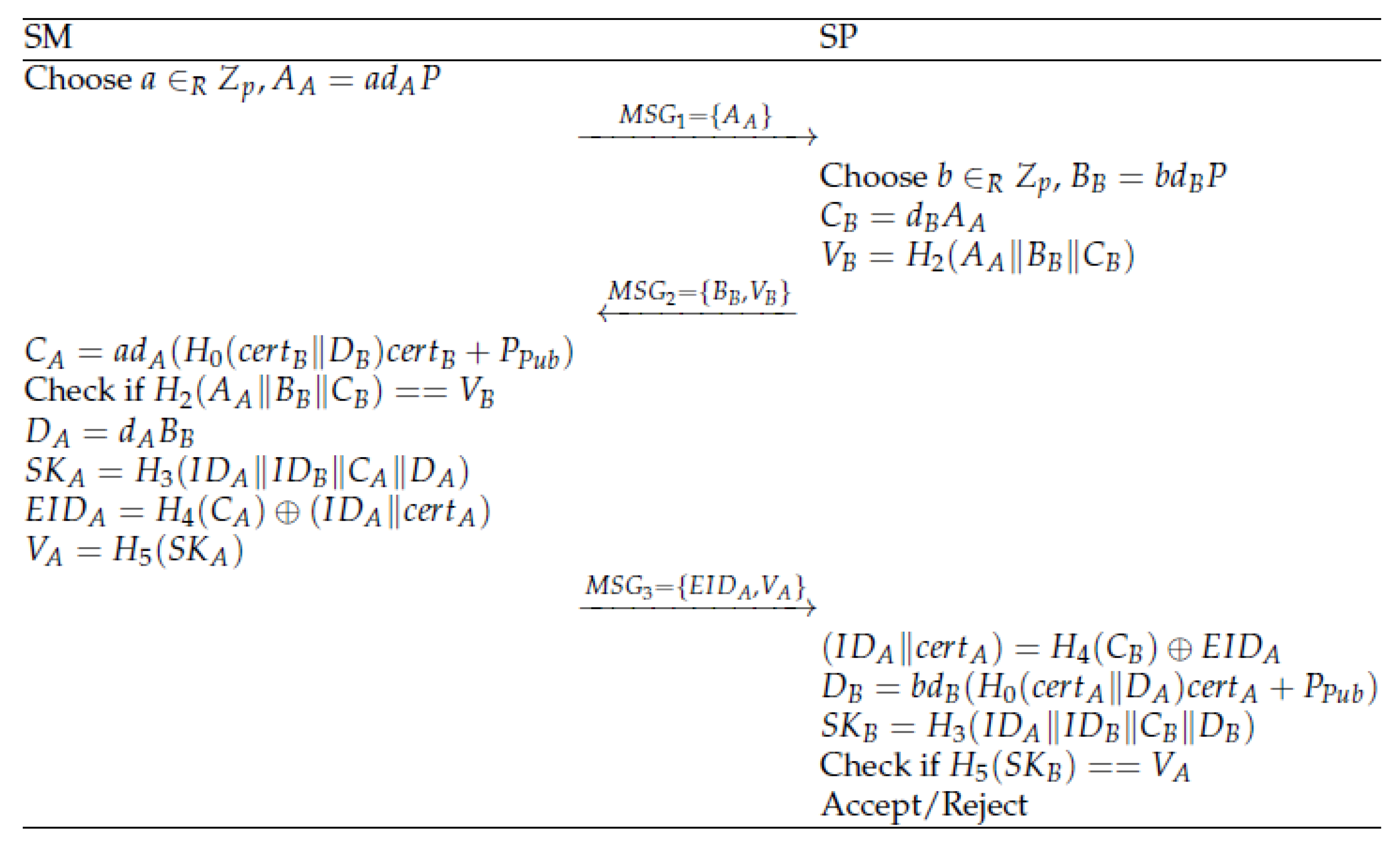
4.3. Key Agreement Phase
5. Security Analysis
5.1. Formal Security Analysis
- Hash queries with . If m already exists in the list , the value will be returned. Otherwise, a random value will be generated, added to the list , and returned.
- Send queries. These queries simulate active attacks, in which the adversary is able to modify the transmitted messages. As a result, a corresponding reply will be generated. Since there are three communication passes, four different Send queries need to be defined.
- –
- Send(0,SP). A random value is chosen to compute . The output of the query is .
- –
- Send(,SM). A random value is chosen to compute . Next, is determined, together with . Then, and are computed to derive . Finally, is computed. The message is returned.
- –
- Send(,SP). First, is determined, leading to . Then, is derived. Next, and are computed, to find and check against . If the verification is unsuccessful, the session can stop, otherwise is computed and is the output of the query.
- –
- Send(,SP). If is not valid, then the session is terminated. Otherwise, both SP and SM have successfully negotiated a common secret key SK.
- Execute queries. These queries simulate the passive attacks, in which the adversary can only eavesdrop onto the channel and is able to collect the transmitted messages. We can distinguish three different execute queries resulting from the first three Send queries, as defined above.
- Session specific state reveal queries (SSReveal). According to the CK adversary model, the attacker is able to retrieve session specific state information, derived by the SM and the SP, respectively. Note that no long-term private keys are revealed in this query.
- –
- SSReveal(SM). The output of this query results in .
- –
- SSReveal(SP). The output of this query results in .
- Corrupt queries. These queries give the private key of the entity as result. Note that only Corrupt(SM) and Corrupt(SP) exist and no corrupt queries with regards to the TTP, which is considered a completely trusted entity. They are included to prove the perfect forward security of the scheme.
- Session key reveal query (SKReveal). In this query, the established symmetric SK between SP and SM is returned in case it has been successfully generated.
- Test query. In this query, either the established SK or a random value is returned, dependent on the output or , respectively of a flipped coin c. Note that the test query cannot be issued when the SKReveal query, the SSReveal(SM) and Corrupt(SM), or SSReveal(SP) and Corrupt(SP), have been executed.
- The SP and SM are partners if they are exchanging messages directly and are the only entities able to successfully derive an authenticated common shared SK.
- The established shared secret key is said to be fresh if the SK has been established without SKReveal query by the adversary or Corrupt query of SM and SP.
- Game GM0. This is the real game, as defined in the semantic security framework. From the definition, we have that
- Game GM1. In this game, the oracles for the different queries are simulated and the resulting outputs of the queries are stored in the lists. In the random oracle model, it holds that
- Game GM2. In this game, also all oracles are simulated, but collisions are avoided in the output of the hash functions and the selection of the random values among the different sessions. Due to the birthday paradox, the probability that these two events appear is bounded by and respectively. Consequently, it holds
- Game GM3. In this game, the adversary is able to find the hash values without input of the random oracle Send queries. In this case, the scheme is simply terminated. Consequently, GM3 and GM2 are indistinguishable, if and only if the SM rejects or the SP rejects . Rejection only appears when the requested message belongs to the list of stored transcripts and when the hash value is also present in the list of stored record, kept by the adversary . As a consequence, due to the difference lemma, we have that
- Game GM4. In this game, we consider the CK adversary model and assume that either the session state variables or the long-term secret variables are revealed at each of the involved participants. The goal of the adversary is to find the SK by performing Execute and Hash queries, with four possible combinations of SSReveal and Corrupt queries. In each of the four scenarios, we show that for successfully deriving the SK, one should be able to both solve the ECDHP and to perform a successful hash query of .
- –
- SSReveal(SM) and SSReveal(SP). As a result of these queries, the adversary possesses and , respectively. In order to compute the session key,either or is required. An impersonation attack is also not possible due to the usage of the ECQV implicit certificates scheme [20] and the presence of both in the SK computation.
- –
- SSReveal(SM) and Corrupt(SP). Here, the adversary receives the information and , respectively. For the derivation of the SK, cf. Equation (6), also or is required.
- –
- Corrupt(SM) and SSReveal(SP). After performing these queries, the adversary learns the information and , respectively. However, for the derivation of the SK, cf. Equation (6), also or is required.
- –
- Corrupt(SM) and Corrupt(SP). In this case, as a result of these queries, the adversary possesses the information and , respectively. However, for the derivation of the SK, cf. Equation (6), also or is required.
5.2. Security Simulation Using AVISPA Tool [16]
5.3. Informal Security Analysis
- Resistance against replay attacks. There are two options, either is replayed in the same period of usage or it is replayed when a new is determined by the SP. In the first case, the same key as before is derived. However by capturing , which is a hash value containing the SK, no additional information can be derived by the attacker. If the server keeps track of the parameters sent during the period in which remains constant, further action of the SP can be avoided.In the second case, a new session key is generated by the SP. However, when checking the hash value a contraction is found by the SP as the SK is different. The session is then stopped immediately.
- Resistance against impersonation attacks. There are again two options, impersonation of messages and . First, it is impossible to impersonate the message as it is used to construct the SK by both the SM and the SP. Even if the SM is using , sent from a malicious entity, the corresponding SK computed by the SM will not correspond with the SK computed by the SP and at the point where is validated. At that moment, the session will be terminated.Also impersonation of the message sent by the SM is impossible. This follows from the fact that consists of the parameter . Only the SP is able to derive from the common shared key K with the SM in order to decrypt the ciphertext C for finding the identity and certificate of the SM. From these two parameters and the strength of the ECQV certificate mechanism, the SP can construct the corresponding public key of the SM. The construction of the SK by the SP exploits the usage of this public key and its own private key , which is also derivable by the SM who is in possession of the correct corresponding private key and the public key of the SP. Consequently, it is impossible for an attacker to impersonate without knowledge of a valid private-public key pair of a SM or to impersonate without knowledge of the private key of the SP.
- Resistance against MITM attacks. For the same reasons as explained in the replay and impersonation attacks, it is impossible to execute a MITM attack. Note that this resistance also strongly relies from the authentication feature established through the ECQV certificate mechanism.
- Anonymity. From the messages sent in the protocol, no information on the identity of the SM can be derived. The only identity related information is hidden in the message C, which is encrypted using a key only derivable by the SP.
- Resistance against DoS attacks. First of all, we here consider DoS attacks from the side of the server as resistance from the SM is easier to obtain by just blocking the amount of sent requests. Compared to the previous schemes in literature [10,11,12,14], our scheme is initiated by the SP with one single and common message to all interested SMs. Consequently, no separated buffers from received messages of different unknown SMs need to be saved by the SP. Upon arrival of a message from a particular SM, the SP can immediately check the validity and integrity of it in one single phase. If the check is not successful, it can drop the request and go to the next received message.
5.4. Comparison of Security Features
6. Performance Analysis
6.1. Computation Costs
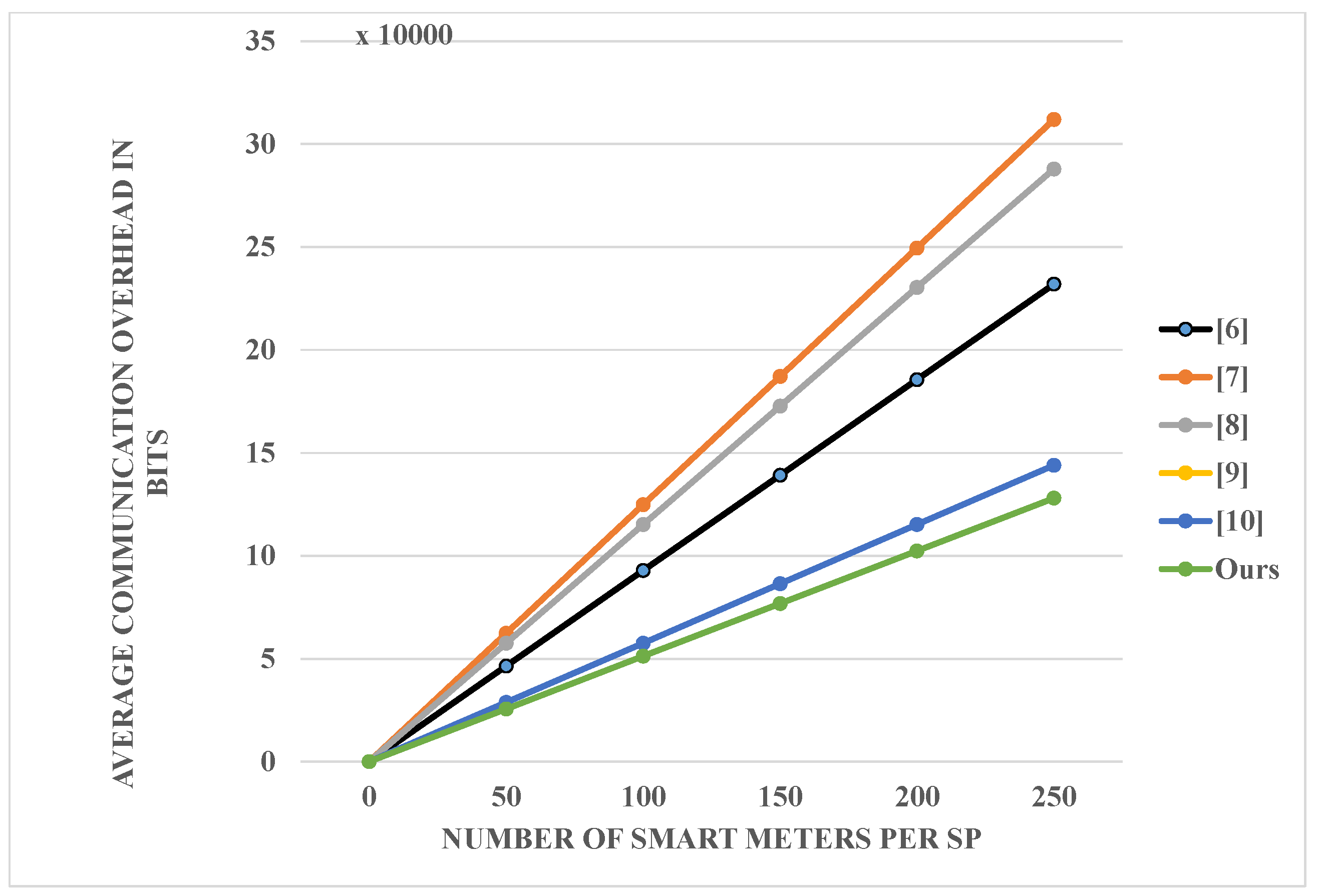
6.2. Communication Costs
6.3. Other Simulations
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ferrag, M.A.; Maglaras, L.A.; Janicke, H.; Jiang, J. A survey on privacy-preserving schemes for smart grid communications. arXiv, 2016; arXiv:1611.07722. [Google Scholar]
- Liang, G.; Weller, S.R.; Zhao, J.; Luo, F.; Dong, Z.Y. The 2015 ukraine blackout: Implications for false data injection attacks. IEEE Trans. Power Syst. 2017, 32, 3317–3318. [Google Scholar] [CrossRef]
- Canetti, R.; Krawczyk, H. Analysis of key-exchange protocols and their use for building secure channels. In Advances in Cryptology EUROCRYPT 2001; Springer: Berlin, Germany, 2001; pp. 453–474. [Google Scholar]
- Boyd, C.; Mao, W.; Paterson, K. Key agreement using statistically keyed authenticators. In Proceedings of the Second International Conference on Applied Cryptography and Network Security, St. Petersburg, Russia, 21–23 May 2011; Springer: Berlin, Germany, 2021; Volume 3089, pp. 248–474. [Google Scholar]
- Wu, D.; Zhou, C. Fault-tolerant and scalable key management for smart grid. IEEE Trans. Smart Grid 2011, 2, 375–381. [Google Scholar] [CrossRef]
- Xia, J.; Wang, Y. Secure key distribution for the smart grid. IEEE Trans. Smart Grid 2012, 3, 1437–1443. [Google Scholar] [CrossRef]
- Mahmood, K.; Chaudry, S.A.N.; Naqvi, H.; Shon, H.-T.; Ahmad, H.F. A lightweight message authentication scheme for Smart Grid Communications in power sector. Comput. Electr. Eng. 2016, 52, 114–124. [Google Scholar] [CrossRef]
- Mohammadali, A.; Haghighi, M.S.; Tadayon, M.H.; Nodooshan, A.M. A novel identity-based key establishment method for advanced metering infrastructure in smart grid. IEEE Trans. Smart Grid 2016, 9, 2834–2842. [Google Scholar] [CrossRef]
- Tsai, J.-L.; Lo, N.-W. Secure anonymous key distribution scheme for smart grid. IEEE Trans. Smart Grid 2016, 7, 906–914. [Google Scholar] [CrossRef]
- Odelu, V.; Kumar, A.; Wazid, M.; Conti, M. Provably Secure Authenticated Key Agreement Scheme for Smart Grid. IEEE Trans. Smart Grid. 2018, 9, 1900–1910. [Google Scholar] [CrossRef]
- Chen, Y.; Martinez, J.G.; Catellejo, P.; Lopez, L. An Anonymous Authentication and Key Establish Scheme for Smart Grid: FAuth. Energies 2018, 10, 1345. [Google Scholar] [CrossRef]
- Abbasinezhad-Mood, D.; Nikoohgadam, M. Anonymous ECC-Based Self-Certified Key Distribution Scheme for Smart Grid. IEEE Trans. Ind. Electron. 2018, 65, 8. [Google Scholar] [CrossRef]
- Li, X.; Ma, J.; Moon, S. On the Security of the Canetti-Krawczyk Model. In Proceedings of the Computational Intelligence and Security, Xi’an, China, 15–19 December 2005; Springer: Berlin, Germany, 2005; Volume 3802, pp. 356–363. [Google Scholar]
- Gope, P.; Sikdar, B. Privacy-Aware Authenticated Key Agreement Scheme for Secure Smart Grid Communication. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Yasunag, K.; Yuzawa, K. On the Limitations of Computational Fuzzy Extractors. ePrint Arch. 2014, 3, 7–9. [Google Scholar]
- Luca, V. Automated security protocol analysis with the AVISPA tool. Electron. Notes Theor. Comput. Sci. 2006, 155, 61–86. [Google Scholar]
- Braeken, A.; Kumar, P.; Martin, A. Efficient and Privacy-Preserving Data Aggregation and Dynamic Billing in Smart Grid Metering Networks. Energies 2018, 11, 2085. [Google Scholar] [CrossRef]
- Kumar, P.; Gurtov, A.; Sain, M.; Martin, A.; Ha, P. Lightweight Authentication and Key Agreement for Smart Metering in Smart Energy Networks. IEEE Trans. Smart Grid 2018. [Google Scholar] [CrossRef]
- Qu, M.; Vanstone, S.A. Implicit Certificate Scheme. US Patent 6,792,530, 14 September 2004. [Google Scholar]
- Brown, D.R.L.; Scott, R.-G.; Vanstone, A. Provably Secure Implicit Certificate Schemes. In Proceedings of the 5th International Conferenc on International Conference on Financial Cryptography, Grand Cayman, Cayman Islands, 19–22 February 2001; Volume 2339, pp. 156–165. [Google Scholar]
- Bellare, M.; Rogaway, P. The security of triple encryption and a framework for code-based game-playing proofs. In Proceedings of the 25th Eurocrypt Conference on Advances in Cryptology Eurocrypt 2006, St. Petersburg, Russia, 28 May–1 June 2006; Springer: Berlin, Germany, 2006; Volume 4004, pp. 409–426. [Google Scholar]
- Pointcheval, D.; Zimmer, S. Multi-factor authenticated key exchange. In Proceedings of the 6th International Conference Applied Cryptography and Network Security, New York, NY, USA, 3–6 June 2008; Springer: Berlin, Germany, 2008; pp. 77–95. [Google Scholar]
- Shoup, V. Sequences of Games: A Tool for Taming Complexity in Security Proofs. 2004. Available online: http://eprint.iacr.org/2004/332/ (accessed on 28 August 2018).
- Dolev, D.; Yao, A. On the security of public key protocols. IEEE Trans. Inf. Theory 1983, 29, 198–208. [Google Scholar] [CrossRef] [Green Version]
- He, D.; Zeadally, S.; Wang, H.; Liu, Q. Lightweight Data Aggregation Scheme against Internal Attackers in Smart Grid Using Elliptic Curve Cryptography. Wirel. Commun. Mob. Comput. 2017, 2017, 3194845. [Google Scholar] [CrossRef]
- Herder, C.; Yu, M.D.; Koushanfar, F.; Devadas, S. Physical Unclonable Functions and Applications: A Tutorial. Proc. IEEE 2014, 102, 1126–1141. [Google Scholar] [CrossRef]
- Dodis, Y.; Ostrovsky, R.; Reyzin, L.; Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noise data. SIAM J. Compt. 2008, 38, 97–139. [Google Scholar] [CrossRef]






| Security Services | Safe From |
|---|---|
| Confidentiality | MITM attack |
| Authentication | Replay attack |
| 2011 [5] | 2012 [6] | 2016 [7] | 2016 [8] | 2016 [9] | 2018 [10] | 2018 [11] | 2018 [12] | 2018 [14] | Ours | |
|---|---|---|---|---|---|---|---|---|---|---|
| R1 | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| R2 | Yes | No | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| R3 | No | No | Yes | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| R4 | No | No | No | No | Yes | Yes | Yes | Yes | Yes | Yes |
| R5 | No | No | Yes | No | No | No | No | No | Yes | Yes |
| R6 | No | No | No | No | No | No | Yes | Yes | No | Yes |
| R7 | No | No | No | No | No | No | No | No | No | Yes |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braeken, A.; Kumar, P.; Martin, A. Efficient and Provably Secure Key Agreement for Modern Smart Metering Communications. Energies 2018, 11, 2662. https://doi.org/10.3390/en11102662
Braeken A, Kumar P, Martin A. Efficient and Provably Secure Key Agreement for Modern Smart Metering Communications. Energies. 2018; 11(10):2662. https://doi.org/10.3390/en11102662
Chicago/Turabian StyleBraeken, An, Pardeep Kumar, and Andrew Martin. 2018. "Efficient and Provably Secure Key Agreement for Modern Smart Metering Communications" Energies 11, no. 10: 2662. https://doi.org/10.3390/en11102662
APA StyleBraeken, A., Kumar, P., & Martin, A. (2018). Efficient and Provably Secure Key Agreement for Modern Smart Metering Communications. Energies, 11(10), 2662. https://doi.org/10.3390/en11102662





