Assessing the Macro-Economic Benefit of Installing a Farm of Oscillating Water Columns in Scotland and Portugal
Abstract
1. Introduction
2. Methodology
2.1. WETFEET H2020 Project
- Survivability: Assessed by device submergence under bad weather conditions at sea.
- Operation and Maintenance: Assessed by continuous submergence and adjustment of elements and strategies.
- Power Take-Off (PTO): Assessed by the evaluation of new PTO options and their development via dielectric membrane, opposed to standard electromechanical approach.
- Array: Assessed by distributing the connections and seabed attachments between multiple devices.
- Performance: Assessed by the functionality of an experiment involving negative spring (NS) for OWC.
2.2. The Farm of Oscillating Water Column WECs
2.2.1. Farm Design
The Oscillating Water Column Device
Farm Size
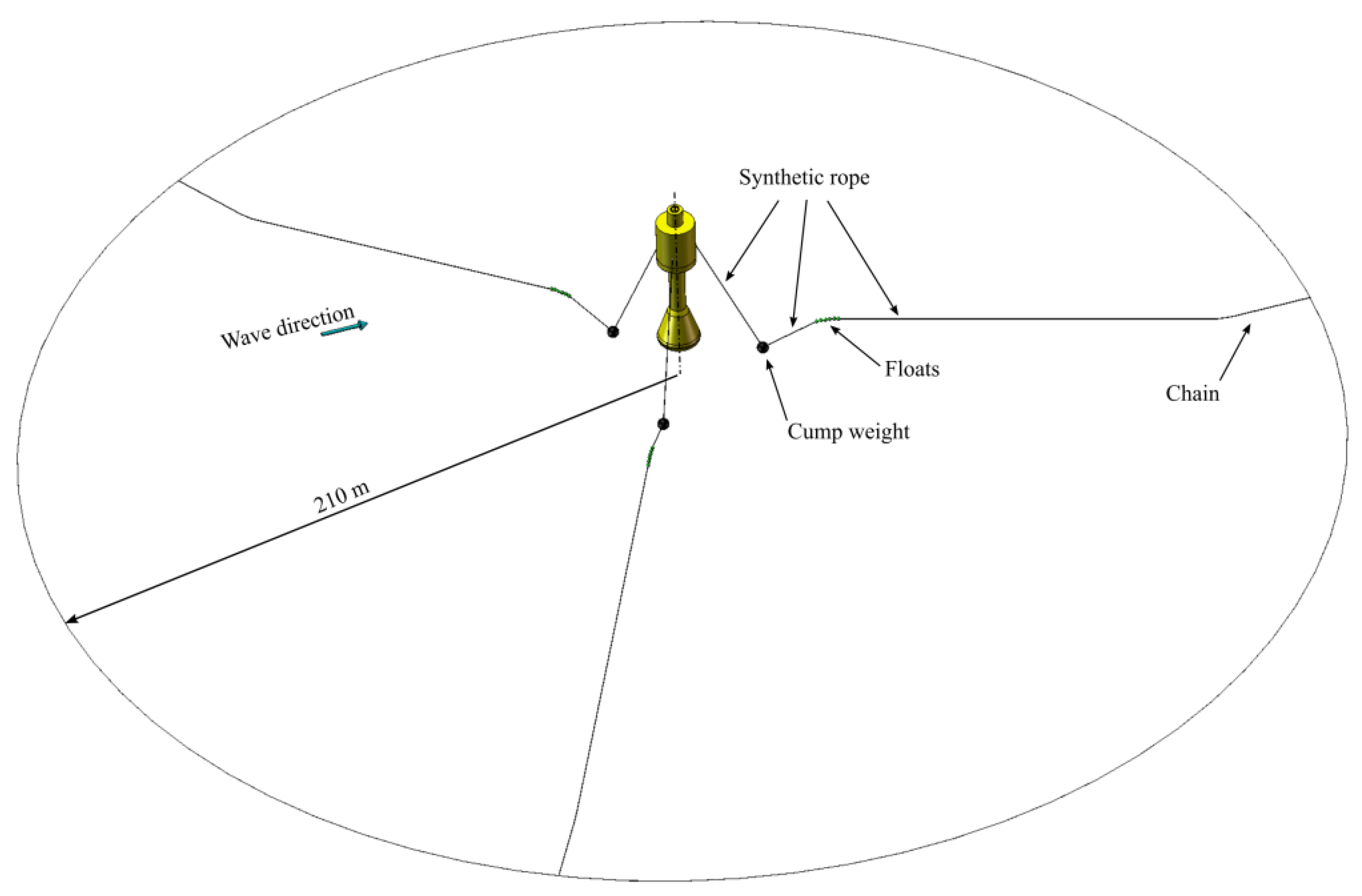
Moorings
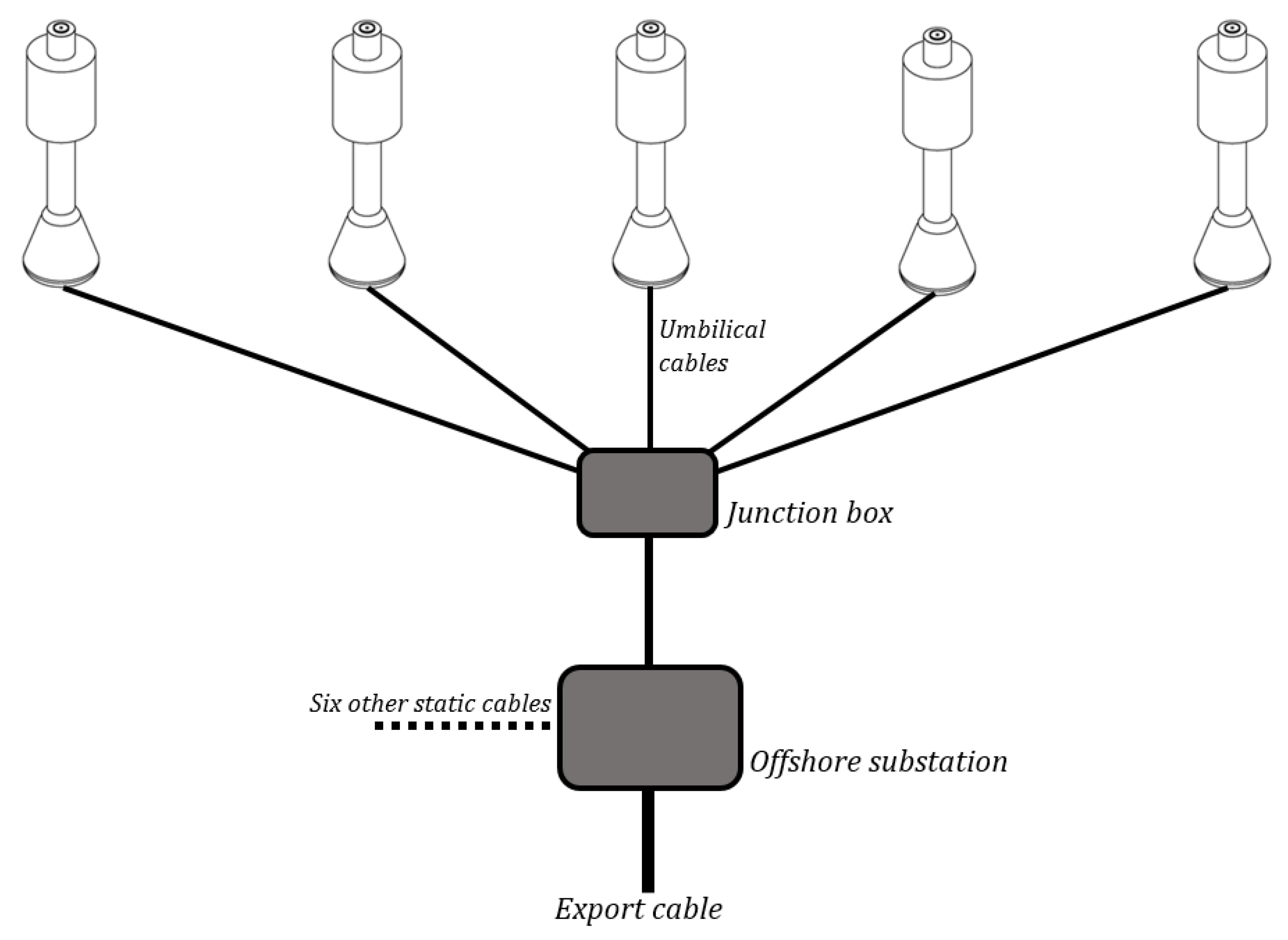
Array Layout and Configuration
2.2.2. Farm Lifetime
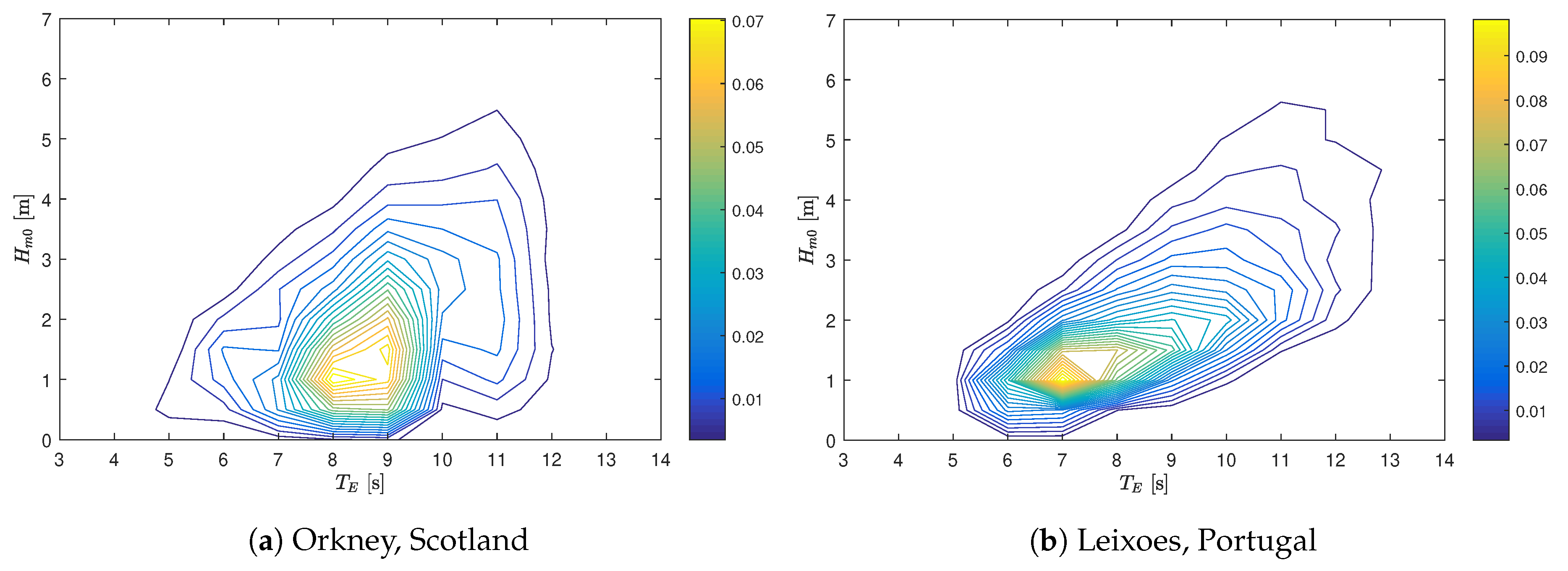
2.3. The Locations
- European Marine Energy Centre (EMEC) [25], Orkney, Scotland, UKGrid-connected test facility for wave and tidal energy devices
- Leixoes, PortugalMajor port in the north of Portugal, located in Matosinhos near the city of Porto.
2.4. Input-Output Modelling
- The supply side of the regional economy is passive, and does not itself influence demand
- The intervention with the model takes all supply regardless of external demand
- Fixed coefficients can be used to describe the interdependencies between sectors i.e., sectors inputs respond linearly to changes in output.
2.5. Model Implementation
2.5.1. Coupled Techno-economic–IO Model
Device
Location
Fixed Variables
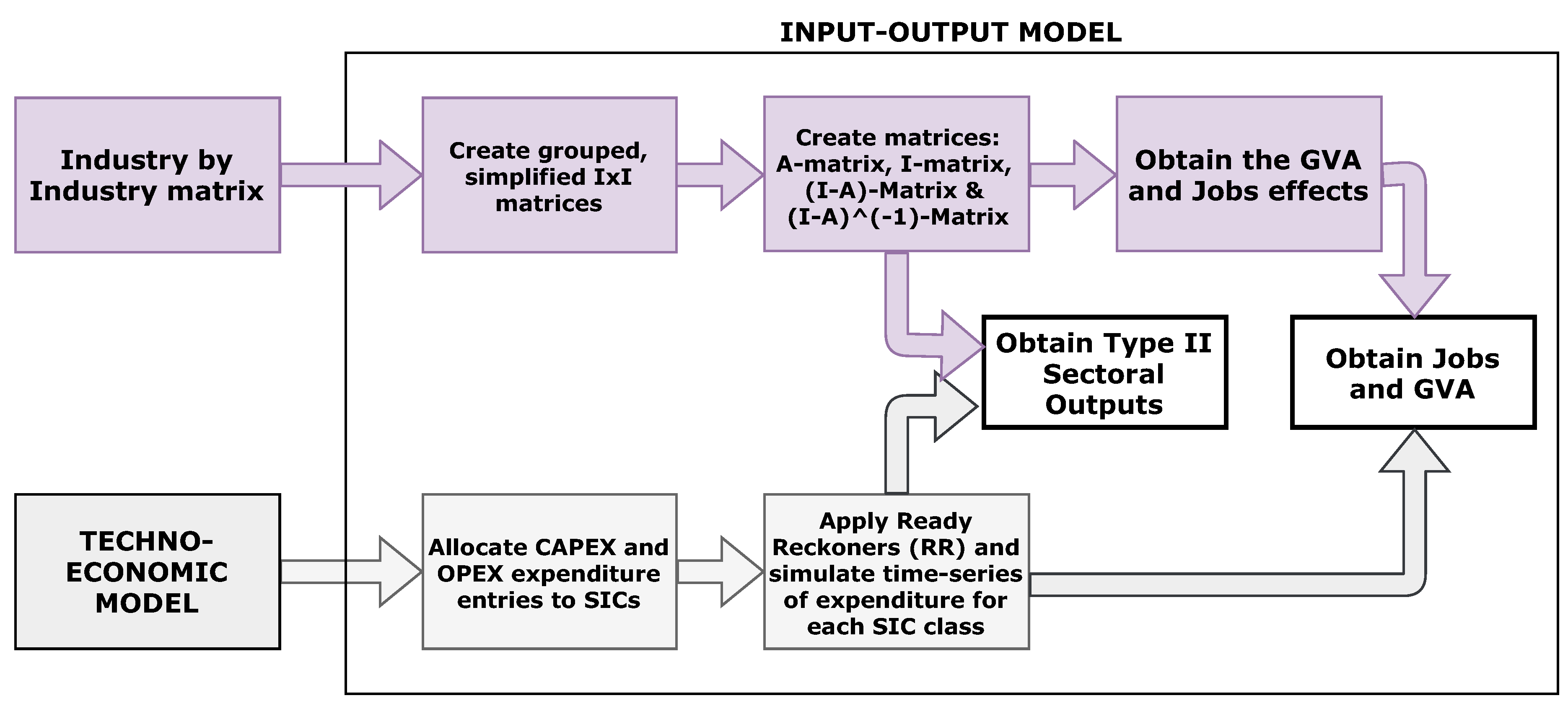
2.5.2. IO Modelling
- Allocate CAPEX and OPEX expenditure entries to SICs
- Create grouped, simplified IxI matrices
- Apply Ready Reckoners (RR) and simulate time-series of expenditure for each SIC class
- Compute IO model: obtain direct and type II output, jobs and GVA
Allocate CAPEX and OPEX Expenditure Entries to SICs
Create Grouped, Simplified IxI Matrices
Apply Ready Reckoners (RR) and Simulate Time-Series of Expenditure for Each SIC Class
Compute IO Model: Obtain Direct and Type II Output, Jobs and GVA
- Supply linked—due to companies’ supply chain. Sometimes referred as indirect multiplier.
- Income linked—due to expenditure from people whose income is supplied from the project. Sometimes called induced multiplier.
Type II Sector Output
Type II Employment and GVA
3. Results
3.1. Levelised Cost of Energy (LCOE)
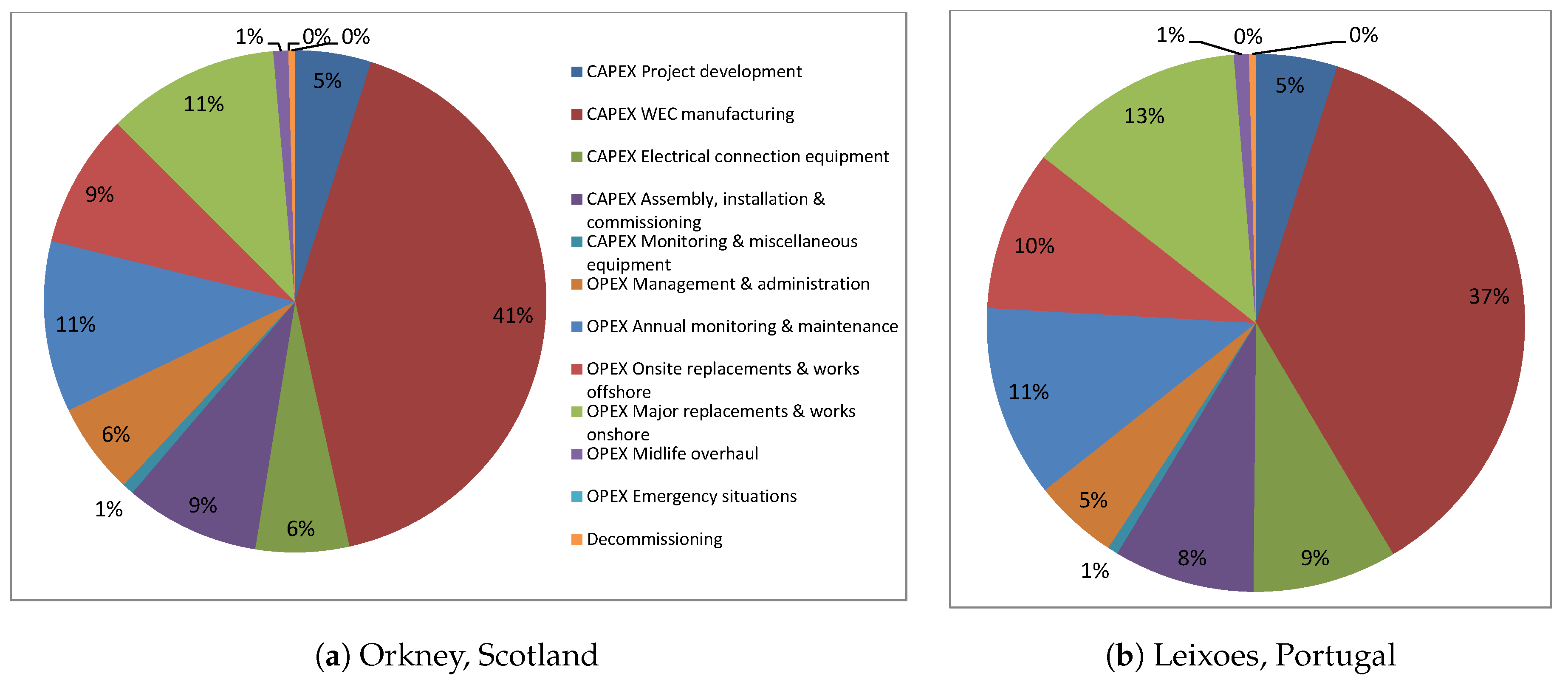
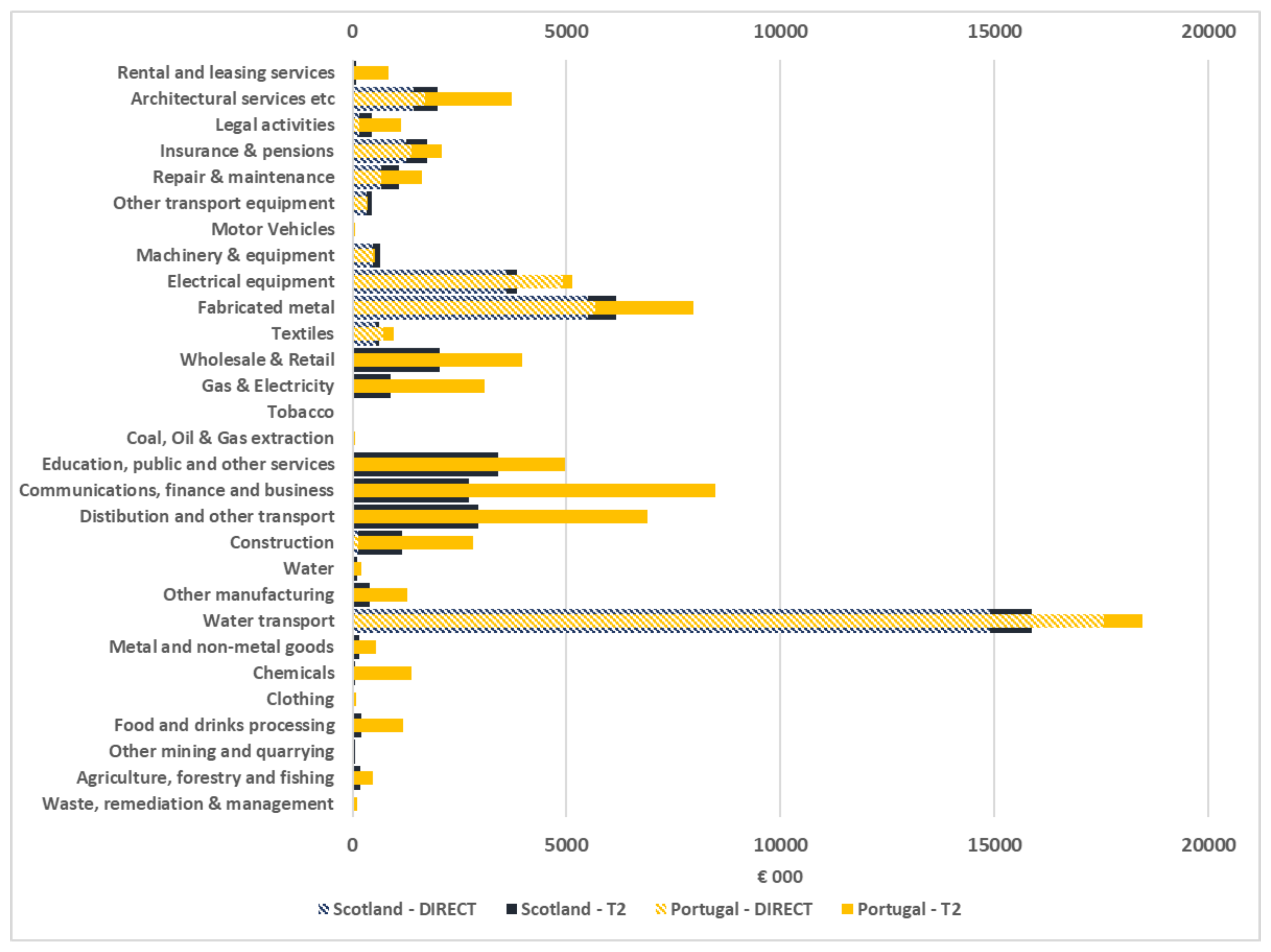
3.2. Direct and Type II Sectoral Outputs
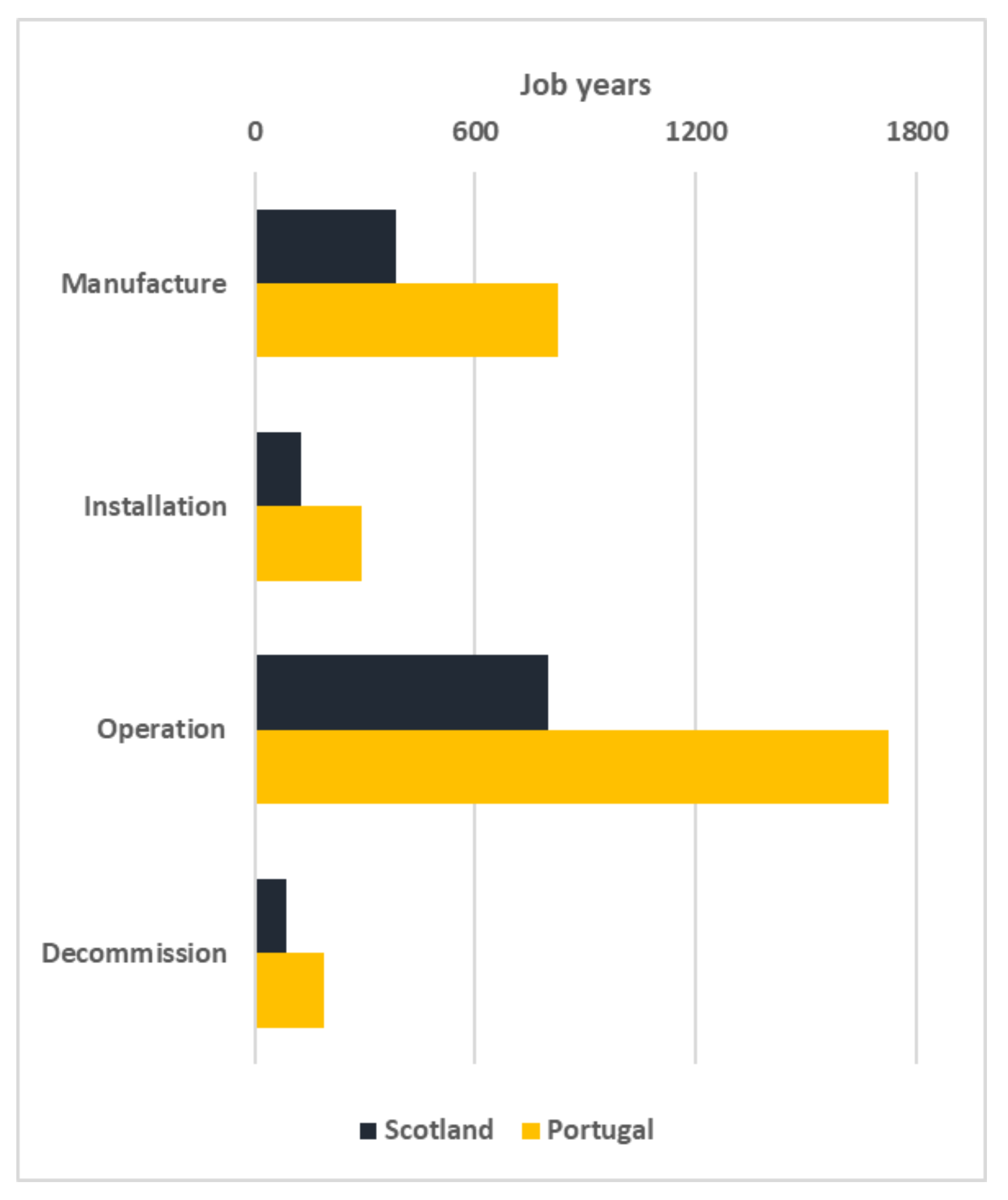
3.3. Jobs Creation
3.4. GVA
4. Discussion
4.1. Potential for Integrated Analysis Approach
4.2. Uncertainty and Model Sensitivity
4.2.1. Techno-Economic Component
4.2.2. Macro-Economic Component
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Evans, D.V. A theory for wave-power absorption by oscillating bodies. J. Fluid Mech. 1976, 77, 1–25. [Google Scholar] [CrossRef]
- Cheng, E. Area of Earth’s Oceans—The Physics Factbook. 1997. Available online: https://hypertextbook.com/facts/1997/EricCheng.shtml (accessed on 11 September 2018).
- Gunn, K.; Stock-Williams, C. Quantifying the global wave power resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- Mustapa, M.; Yaakob, O.; Ahmed, Y.M.; Rheem, C.K.; Koh, K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- ECONorthwest. Economic Impact Analysis of Wave Energy: Phase One; Technical report; ECONorthwest: Portland, OR, USA, 2009. [Google Scholar]
- Cucchiella, F. Future Trajectories of Renewable Energy Consumption in the European Union. Resources 2018, 7, 10. [Google Scholar] [CrossRef]
- De Andres, A.; Maillet, J.; Todalshaug, J.H.; Möller, P.; Bould, D.; Jeffrey, H. Techno-Economic Related Metrics for a Wave Energy Converters Feasibility Assessment. Sustainability 2016, 8, 1109. [Google Scholar] [CrossRef]
- Quitoras, M.R.D.; Abundo, M.L.S.; Danao, L.A.M. A techno-economic assessment of wave energy resources in the Philippines. Renew. Sustain. Energy Rev. 2018, 88, 68–81. [Google Scholar] [CrossRef]
- O’Connor, M.; Lewis, T.; Dalton, G. Techno-economic performance of the Pelamis P1 and Wavestar at different ratings and various locations in Europe. Renew. Energy 2013, 50, 889–900. [Google Scholar] [CrossRef]
- Costello, R.; Teillant, B.; Weber, J.; Ringwood, J.V. Techno-Economic Optimisation for Wave Energy Converters. In Proceedings of the 4h International Conference on Ocean Energy, Dublin, Ireland, 17–19 October 2012. [Google Scholar]
- Dalton, G.; Allan, G.; Beaumont, N.; Georgakaki, A.; Hacking, N.; Hooper, T.; Kerr, S.; O’Hagan, A.M.; Reilly, K.; Ricci, P.; et al. Economic and socio-economic assessment methods for ocean renewable energy: Public and private perspectives. Renew. Sustain. Energy Rev. 2015, 45, 850–878. [Google Scholar] [CrossRef]
- Bårdsen, G.; Nymoen, R. The Econometrics of Macroeconomic Modelling; Oxford Univeristy Press: Oxford, UK, 2004. [Google Scholar]
- Allan, G.J.; Lecca, P.; McGregor, P.G.; Swales, J.K. The economic impacts of marine energy developments: A case study from Scotland. Mar. Policy 2014, 43, 122–131. [Google Scholar] [CrossRef]
- Calculating the Economic Contribution of Beatrice Offshore Windfarm Limited; Beatrice Offshore Windfarm Ltd.: Moray Firth, UK, 2017; Available online: https://www.google.com.tw/url?sa=t&rct=j&q=&esrc= s&source=web&cd=1&ved=2ahUKEwi3toX9yZHeAhVOPHAKHad9D18QFjAAegQICRAC&url= http%3A%2F%2Fsse.com%2Fmedia%2F475205%2FBOWL-methodology-document-FINAL.pdf&usg= AOvVaw34RcX2spXhUXMh2RXwCjQG (accessed on 11 September 2018).
- Fraser of Allander Institute. Impact Study into the Development of the UK Offshore Renewable Energy Industry to 2020; Project Report; Fraser of Allander Institute: Glasgow, UK, 2014; pp. 1–24. [Google Scholar]
- Ernst & Young. Analysis of the Value Creation Potential of Wind Energy Policies; Ernst & Young: London, UK, 2012. [Google Scholar]
- Okkonen, L.; Lehtonen, O. Socio-economic impacts of community wind power projects in Northern Scotland. Renew. Energy 2016, 85, 826–833. [Google Scholar] [CrossRef]
- SQW Consulting. Socio-Economic Impact Assessment of Aquamarine Power’s Oyster Projects: Report to Aquamarine Power; Technical Report; SQW Consulting: Cambridge, UK, 2009. [Google Scholar]
- Crooks, D.; De Andres, A.; Medina-Lopez, E.; Jeffrey, H. Demonstration of a Socio-economic Cost of Energy Analysis of a Wave Energy Converter Array. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017; pp. 1–11. [Google Scholar]
- Allan, G.J.; Bryden, I.; McGregor, P.G.; Stallard, T.; Kim Swales, J.; Turner, K.; Wallace, R. Concurrent and legacy economic and environmental impacts from establishing a marine energy sector in Scotland. Energy Policy 2008, 36, 2734–2753. [Google Scholar] [CrossRef]
- WETFEET. WETFEET Project. 2018. Available online: http://www.wetfeet.eu/wetfeet-project/ (accessed on 11 September 2018).
- CORDIS. Wave Energy Transition to Future by Evolution of Engineering and Technology; H2020. CORDIS, 2015. Available online: https://cordis.europa.eu/project/rcn/193803_en.html (accessed on 11 September 2018).
- Teillant, B.; Debruyne, Y.; Sarmento, A.; Silva, M.; Simas, T.; Gomes, R.P.; Henriques, J.C.; Philippe, M.; Combourieu, A.; Fontana, M. D2.1—Designs and Specifications of an OWC Able to Integrate The Negative Spring; Technical Report 641334; WETFEET: Lisboa, Portugal, 2016. [Google Scholar]
- Evans, D.V. The oscillating water column wave energy device. IMA J. Appl. Math. 1978, 22, 423–433. [Google Scholar]
- EMEC. Facilities. 2015. Available online: http://www.emec.org.uk/facilities/ (accessed on 11 September 2018).
- Pontes, M.T.; Rebêlo, L.; Silva, P.; Pata, C. Database of wave energy potential in Portugal. In Proceedings of the ASME 2005 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 2–17 June 2005; pp. 803–809. [Google Scholar]
- Wave Energy Scotland. WES O&M Model: P2; Wave Energy Scotland: Inverness, UK, 2017. [Google Scholar]
- Teillant, B.; Raventos, A.; Chainho, P.; Victor, L.; Goormachtigh, J.; Nava, V.; Ruiz, P.; Minguela, R.J. Deliverable 5.1: Methodology Report and Logistic Model Flow Charts; DTOcean, 2014. Available online: https://www.google.com.tw/search?newwindow=1&ei=GlPJW4z7ApH1wAPoz6XADQ&q= Deliverable+5.1%3A+Methodology+Report+and+Logistic+Model+Flow+Charts&oq=Deliverable+5.1% 3A+Methodology+Report+and+Logistic+Model+Flow+Charts&gs_l=psy-ab.3...0.0.0.28320.0.0.0.0.0.0.0.0..0.0....0...1..64.psy-ab..0.0.0....0.zPkarVc4m_Q (accessed on 11 September 2018).
- Teillant, B.; Chainho, P.; Vrousos, C.; Vicente, P.; Charbonier, K.; Ybert, S.; Monbet, P.; Giebhardt, J. Report on Logistical Model for Ocean Energy Array and Considerations; Project Deliverable D5.6. DTOcean, 2016. Available online: http://www.dtocean.eu/Deliverables/Deliverables/Logistical-model (accessed on 11 September 2018).
- Silva, M.; Afferni, L.; Sebastian, R. D7.3 Techno-Economic Assessment of the Proposed Breakthroughs For Large Scale Deployment; Technical Report; WETFEET: Lisboa, Portugal, 2018. [Google Scholar]
- Draycott, S.; Szankowska, I.; Chaperon, C.; Yerzhanov, A. D7.5—LCA and Socio-Economic Implications of Large Scale Deployment of the Proposed Breakthroughs; Technical Report; WETFEET: Lisboa, Portugal, 2018. [Google Scholar]
- Scottish Enterprise. Additionality & Economic Impact Assessment Guidance Note; Scottish Enterprise: Glasgow, UK, 2008; pp. 1–28. [Google Scholar]
- Leontief, W. Input-Ouput Economics; Oxford University Press: Oxford, UK, 1986; p. 396. [Google Scholar]
- Crossdale, S.; Campbell, G.; O’Neill, K. Input-Output Methodology Guide; The Scottish Government: Edinburgh, UK, 2015. [Google Scholar]
- None, N. Annual Energy Outlook 2016 With Projections to 2040; Technical Report; USDOE Energy Information Administration (EI): Washington, DC, USA, 2016. [Google Scholar]
- Rutovitz, J.; Dominish, E.; Downes, J. Calculating Global Energy Sector Jobs: 2015 Methodology Update; Institute for Sustainable Futures: University of Technology, Sydney, Australia, 2015. [Google Scholar]
- Prieto-Sandoval, V.; Jaca, C.; Ormazabal, M. Towards a consensus on the circular economy. J. Clean. Prod. 2018, 179, 605–615. [Google Scholar] [CrossRef]
- Kirchherr, J.; Piscicelli, L.; Bour, R.; Kostense-Smit, E.; Muller, J.; Huibrechtse-Truijens, A.; Hekkert, M. Barriers to the Circular Economy: Evidence From the European Union (EU). Ecol. Econ. 2018, 150, 264–272. [Google Scholar] [CrossRef]
- McCarthy, A.; Dellink, R.; Bibas, R. The Macroeconomics of the Circular Economy Transition: A Critical Review of Modelling Approaches; Technical Report; OECD Publishing: Paris, France, 2018. [Google Scholar]
| 0.49 | 0.49 |
| (a) | (b) |

| 0.58 | 0.40 |
| (a) b | (b) b |

| Leixoes | EMEC | |
|---|---|---|
| Distance from nearest large port to site (km) | 25 | 13 |
| Distance from nearest small O&M port to site (km) | 25 | 13 |
| Distance from site to shore (km) | 26 | 3.7 |
| Distance from shore to substation/grid (km) | 2 | 0.25 |
| Water depth at central farm location (km) | 80 | 50 |
| SIC | Grouped Sector Names |
|---|---|
| 38.–39. | Waste, remediation & management |
| 01.–03. | Agriculture, forestry and fishing |
| 09. | Other mining and quarrying |
| 10.–11. | Food and drinks processing |
| 14. | Clothing |
| 19.–20. | Chemicals |
| 15.–18. | Metal and non-metal goods |
| 50. | Water transport |
| 21.–24., 31.–32. | Other manufacturing |
| 36.–37. | Water |
| 41.–43., 81 | Construction |
| 49., 51.–52. | Distribution and other transport |
| 61.–64., 66.–68., 82. | Communications, finance and business |
| 53.–60., 73.–75., 78.–80., 84.–97. | Education, public and other services |
| 05.–08. | Coal, Oil and Gas extraction |
| 12. | Tobacco |
| 35. | Gas and Electricity |
| 45.–47. | Wholesale and Retail |
| 13. | Textiles |
| 25. | Fabricated metal |
| 26.–27. | Electrical equipment |
| 28. | Machinery and equipment |
| 29. | Motor Vehicles |
| 30. | Other transport equipment |
| 33. | Repair and maintenance |
| 65. | Insurance and pensions |
| 69. | Legal activities |
| 70.–72. | Architectural services etc |
| 77. | Rental and leasing services |
| Textiles | Deadweight | Leakage | Displacement | Substitution |
|---|---|---|---|---|
| Cement lime and plaster | 0.00 | 0.50 | 0.00 | 0.00 |
| Fabricated metal | 0.00 | 0.50 | 0.00 | 0.00 |
| Electrical equipment | 0.00 | 0.50 | 0.00 | 0.00 |
| Machinery and equipment | 0.00 | 0.50 | 0.00 | 0.00 |
| Motor Vehicles | 0.00 | 0.50 | 0.00 | 0.00 |
| Other transport equipment | 0.00 | 0.80 | 0.25 | 0.25 |
| Repair and maintenance | 0.00 | 0.00 | 0.00 | 0.00 |
| Construction | 0.00 | 0.00 | 0.00 | 0.00 |
| Water transport | 0.00 | 0.00 | 0.25 | 0.50 |
| Insurance and pensions | 0.00 | 0.00 | 0.00 | 0.20 |
| Legal activities | 0.00 | 0.00 | 0.00 | 0.00 |
| Architectural services etc | 0.00 | 0.00 | 0.00 | 0.00 |
| Rental and leasing services | 0.00 | 0.00 | 0.00 | 0.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Draycott, S.; Szadkowska, I.; Silva, M.; Ingram, D.M. Assessing the Macro-Economic Benefit of Installing a Farm of Oscillating Water Columns in Scotland and Portugal. Energies 2018, 11, 2824. https://doi.org/10.3390/en11102824
Draycott S, Szadkowska I, Silva M, Ingram DM. Assessing the Macro-Economic Benefit of Installing a Farm of Oscillating Water Columns in Scotland and Portugal. Energies. 2018; 11(10):2824. https://doi.org/10.3390/en11102824
Chicago/Turabian StyleDraycott, Samuel, Iwona Szadkowska, Marta Silva, and David M Ingram. 2018. "Assessing the Macro-Economic Benefit of Installing a Farm of Oscillating Water Columns in Scotland and Portugal" Energies 11, no. 10: 2824. https://doi.org/10.3390/en11102824
APA StyleDraycott, S., Szadkowska, I., Silva, M., & Ingram, D. M. (2018). Assessing the Macro-Economic Benefit of Installing a Farm of Oscillating Water Columns in Scotland and Portugal. Energies, 11(10), 2824. https://doi.org/10.3390/en11102824






