Automatic Generation Control of Nuclear Heating Reactor Power Plants
Abstract
:1. Introduction
2. General Description of NHR-200II Power Plant
3. Plant Control Scheme with AGC Function
4. Automatic Genration Control Laws
4.1. State-Space Modeling for Control Design
4.2. Theorectical Control Problem Formulation
4.3. Active Disturbance Rejection Control Law
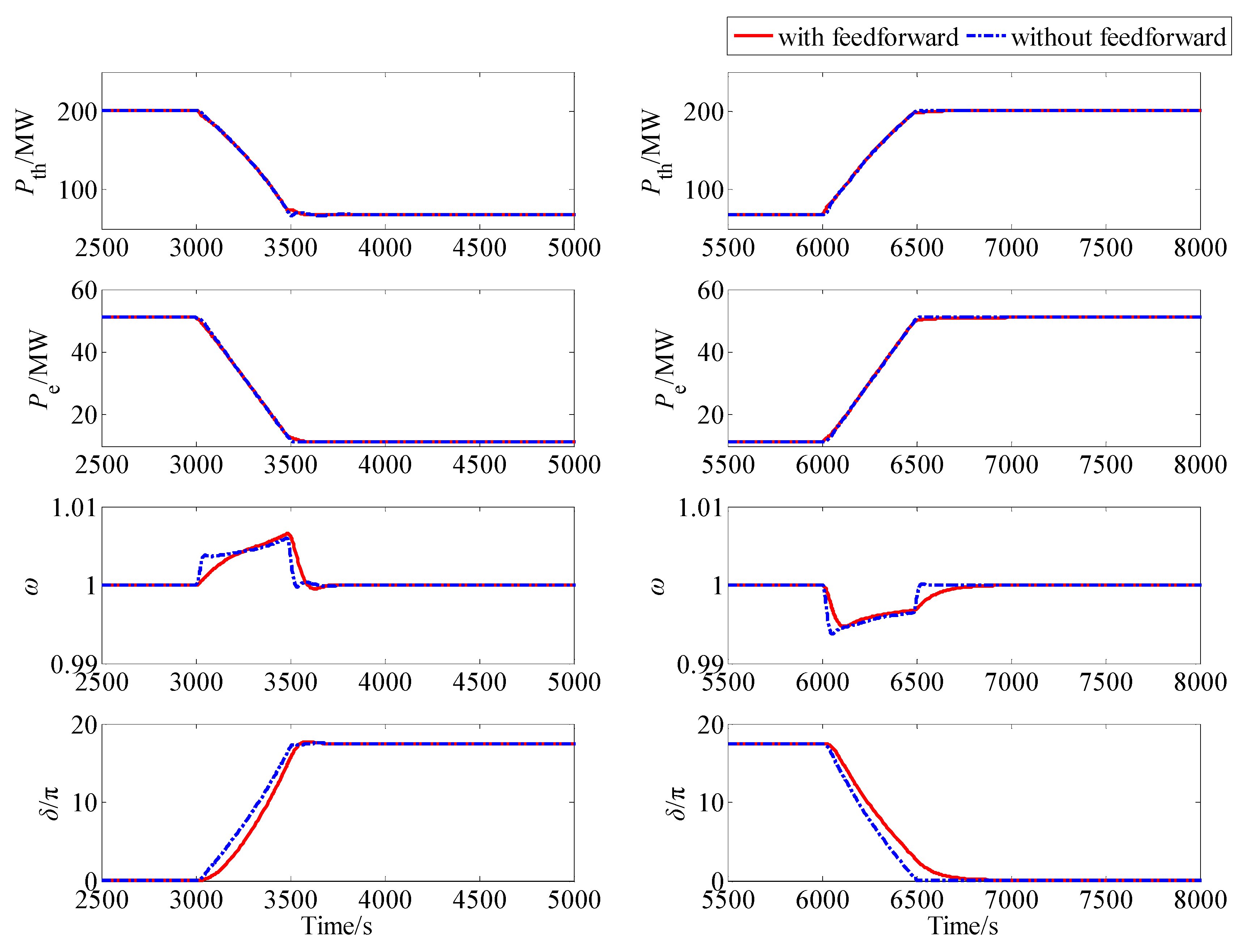
5. Simulation Results with Dissuction
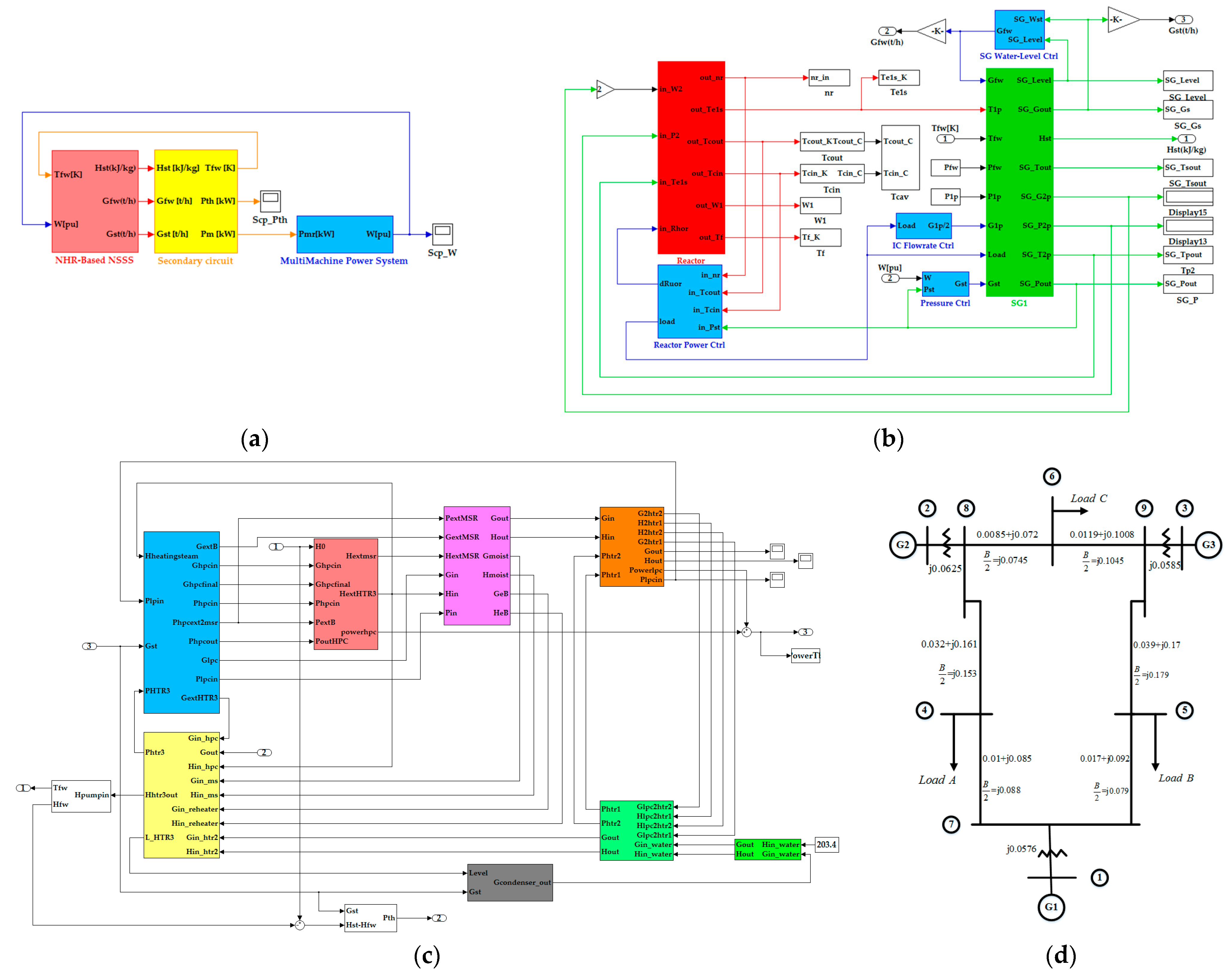
5.1. Simulation Program
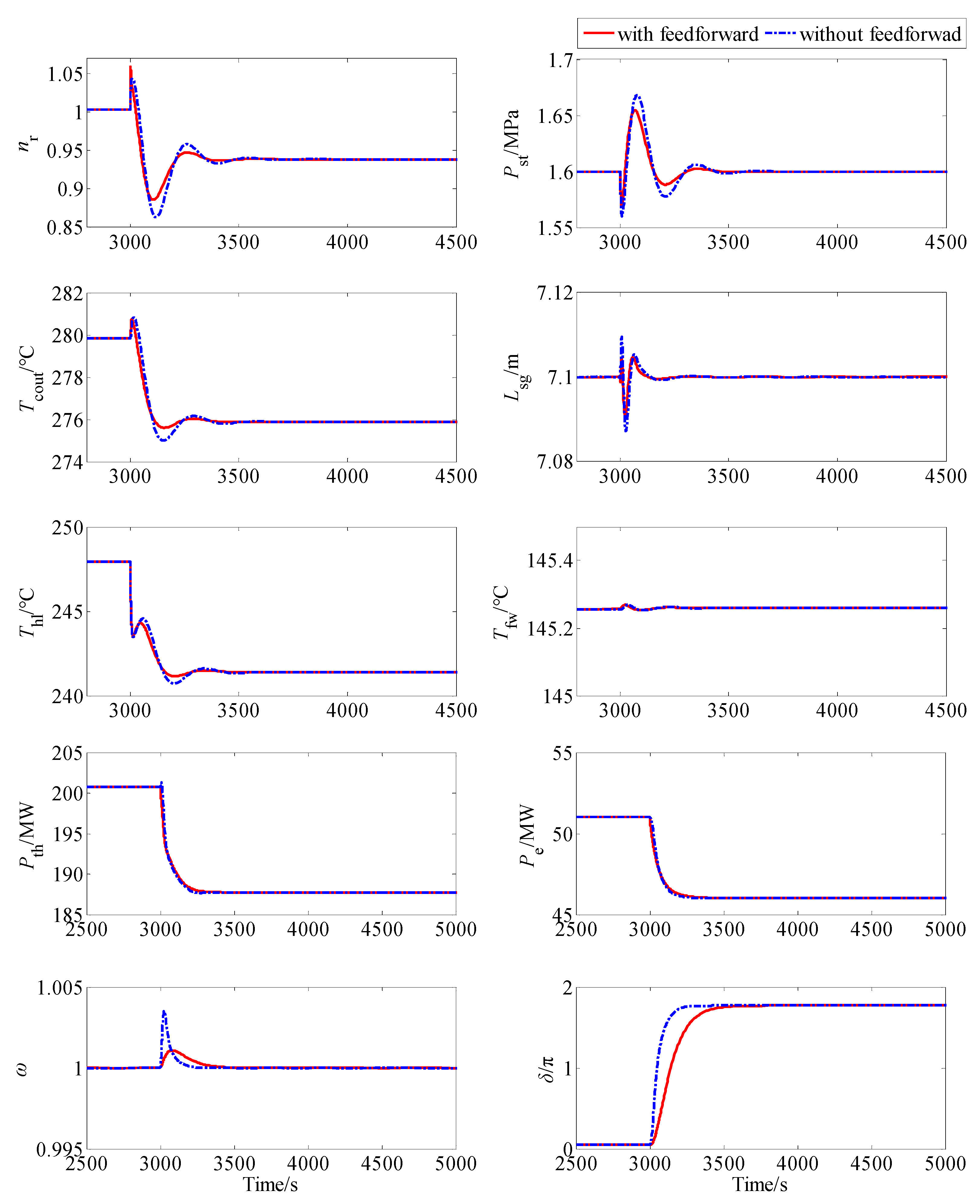
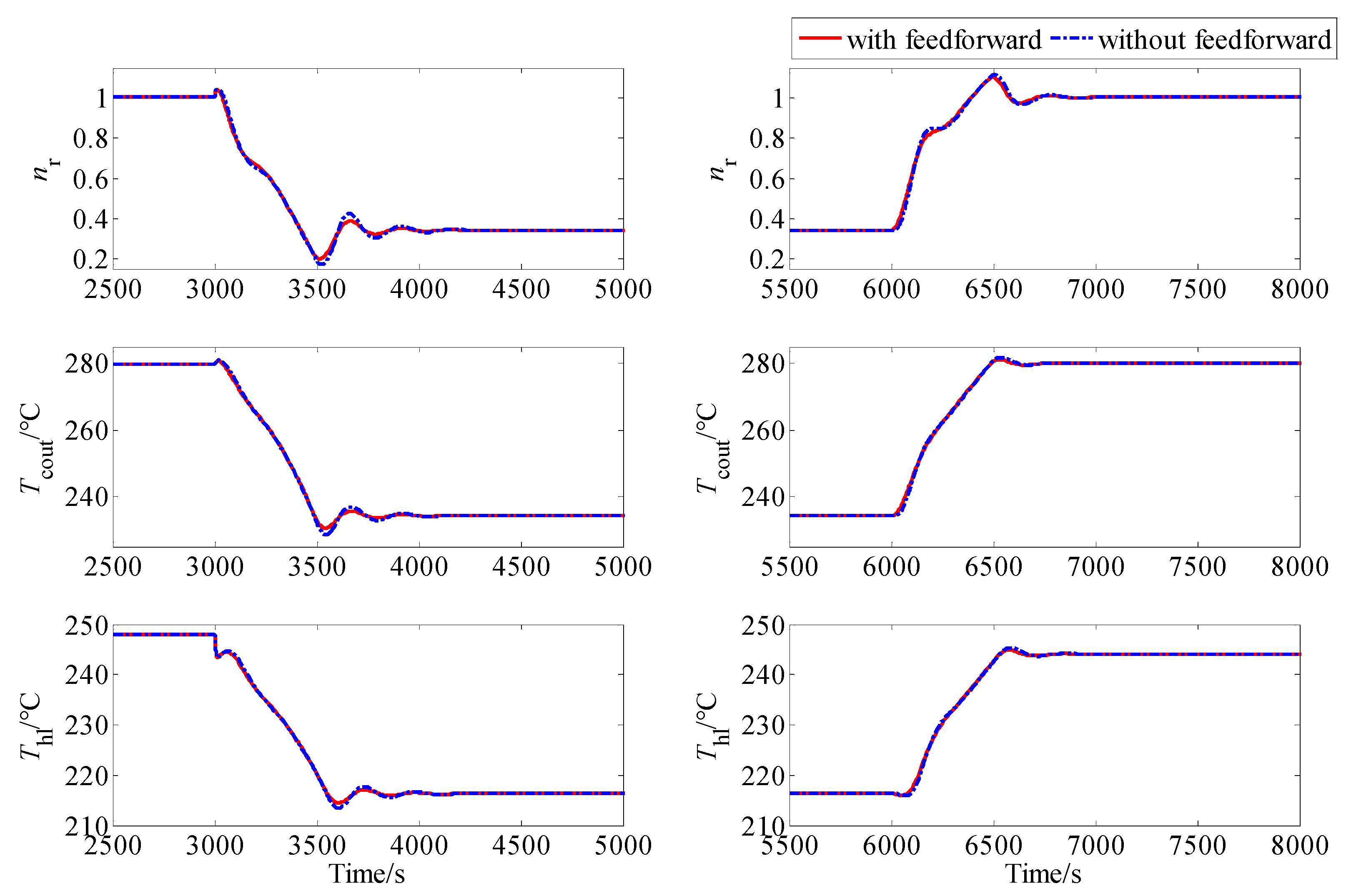
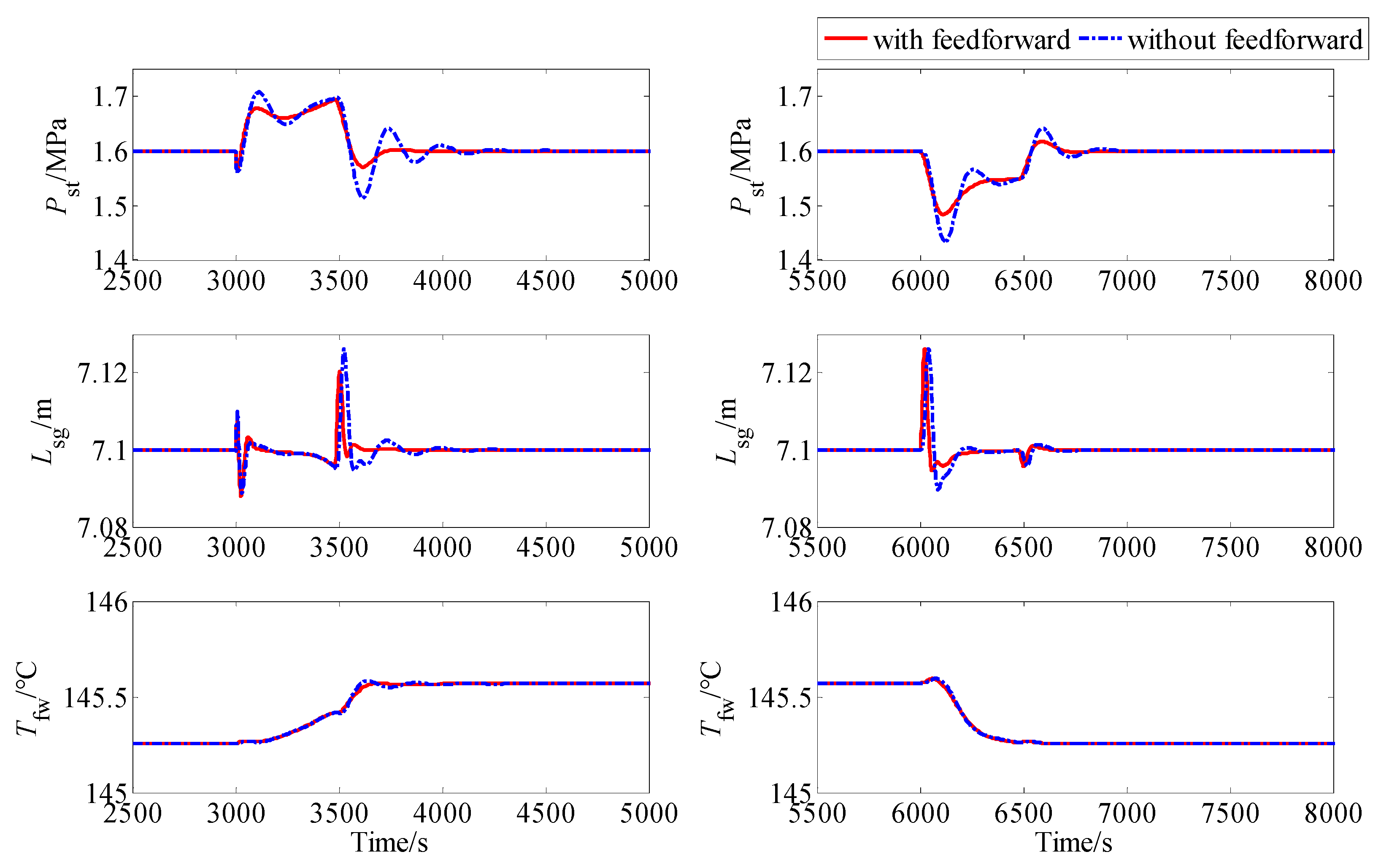
5.2. Simulation Results
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Suman, S. Hybrid nuclear-renewable energy systems: A review. J. Clean. Prod. 2018, 181, 166–177. [Google Scholar] [CrossRef]
- Ponciroli, R.; Wang, Y.; Zhou, Z.; Botterud, A.; Jenkins, J.; Vilim, R.B.; Canda, F. Profitability evaluation of load-following nuclear units with physics-induced operation constraints. Nucl. Technol. 2017, 200, 189–207. [Google Scholar] [CrossRef]
- Lykidi, M.; Gourdel, P. Optimal management of flexible nuclear power plants in a decarbonizing competitive electricity market: The French case. Energy 2017, 132, 171–185. [Google Scholar] [CrossRef]
- Cany, C.; Mansilla, C.; da Mathonnière, C.P. Nuclear power supply: Going against the misconceptions. Evidence of nuclear flexibility from the French experience. Energy 2018, 151, 289–296. [Google Scholar] [CrossRef]
- Jenkins, J.D.; Zhou, Z.; Ponciroli, R.; Vilim, R.B.; Ganda, F.; de Sisternes, F.; Botterud, A. The benefits of nuclear flexibility in power system operations with renewable energy. Appl. Energy 2018, 151, 872–884. [Google Scholar] [CrossRef]
- Baker, T.E.; Epiney, A.S.; Rabiti, C.; Shittu, E. Optimal sizing of flexible nuclear energy system components considering wind volatility. Appl. Energy 2018, 212, 498–508. [Google Scholar] [CrossRef]
- Ingersoll, D.T. Deliberately small reactors and the second nuclear era. Prog. Nucl. Energy 2009, 51, 589–603. [Google Scholar] [CrossRef]
- Vujić, J.; Bergmann, R.M.; Škoda, R.; Miletić, M. Small modular reactors: Simpler, safer, cheaper? Energy 2012, 45, 288–295. [Google Scholar] [CrossRef]
- Rowinski, M.K.; White, T.J.; Zhao, J. Small and medium sized reactors (SMR): A review of technology. Renew. Sustain. Energy. Rev. 2015, 44, 643–656. [Google Scholar] [CrossRef]
- Ingersoll, D.T.; Houghton, Z.J.; Bromm, R.; Desportes, C. NuScale small modular reactor for co-generation of electricity and water. Desalin 2014, 340, 84–93. [Google Scholar] [CrossRef]
- Wang, D.; Ma, C.; Dong, D.; Lin, J. Chinese nuclear heating test reactor and demonstration plant. Nucl. Eng. Des. 1992, 136, 91–98. [Google Scholar]
- Wang, D.; Zhang, D.; Dong, D.; Gao, Z.; Li, H.; Lin, J.; Su, Q. Experimental study and operation experiences of the 5 MW nuclear heating reactor. Nucl. Eng. Des. 1993, 143, 9–18. [Google Scholar]
- Wang, D. The design characteristics and construction experiences of the 5 MW nuclear heating reactor. Nucl. Eng. Des. 1993, 143, 19–24. [Google Scholar]
- Wang, D.; Zheng, W. Technical design features and safety analysis of the 200 MW nuclear heating reactor. Nucl. Eng. Des. 1993, 143, 1–7. [Google Scholar]
- Wang, D.; Dong, D.; Zheng, W. The 200 MW nuclear heating reactor and its possible application in seawater desalination. Desalin 1994, 99, 367–381. [Google Scholar] [CrossRef]
- Zheng, W.; Wang, D. NHR-200 nuclear energy system and its possible applications. Prog. Nucl. Energy 1995, 29, 193–200. [Google Scholar]
- Li, W.; Zhang, Y.; Zheng, W. Investigation on three seawater desalination processes coupled with NHR-200. Desalin 2012, 298, 93–98. [Google Scholar] [CrossRef]
- Dong, Z.; Pan, Y. A lumped-parameter dynamical model of a nuclear heating reactor cogeneration plant. Energy 2018, 145, 638–656. [Google Scholar] [CrossRef]
- Li, G.; Wang, X.; Liang, B.; Li, X.; Zhang, B.; Zou, Y. Modeling and control of nuclear reactor cores for electricity generation: A review of advanced technology. Renew. Sustain. Energy Rev. 2016, 60, 116–128. [Google Scholar] [CrossRef]
- Dong, Z. PD power-level control design for PWRs: A physically-based approach. IEEE Trans. Nucl. Sci. 2013, 60, 3889–3898. [Google Scholar] [CrossRef]
- Dong, Z.; Huang, X.; Feng, J. Water-level control for the U-tube steam generator of nuclear power plants based on output feedback dissipation. IEEE Trans. Nucl. Sci. 2009, 56, 1600–1612. [Google Scholar] [CrossRef]
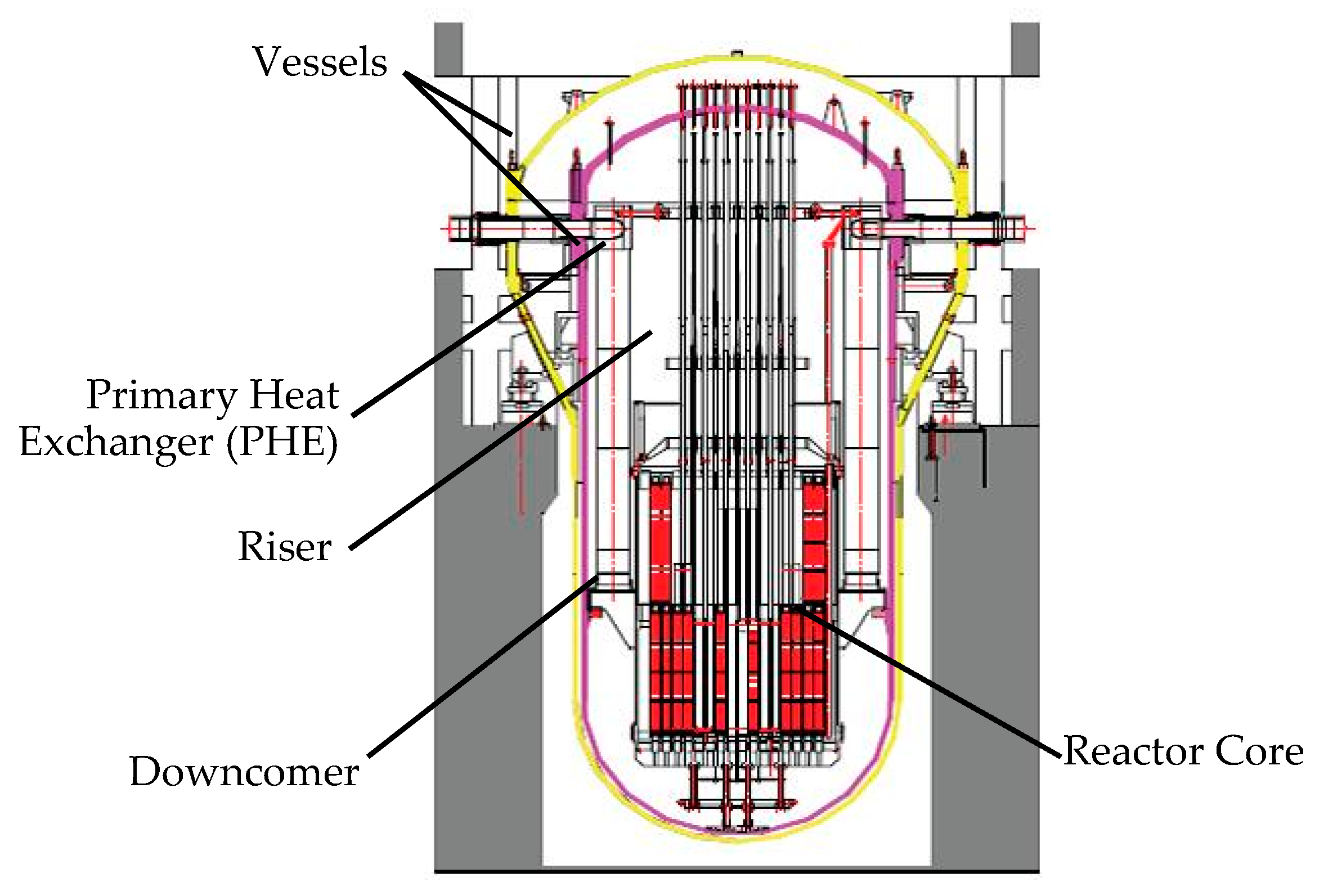
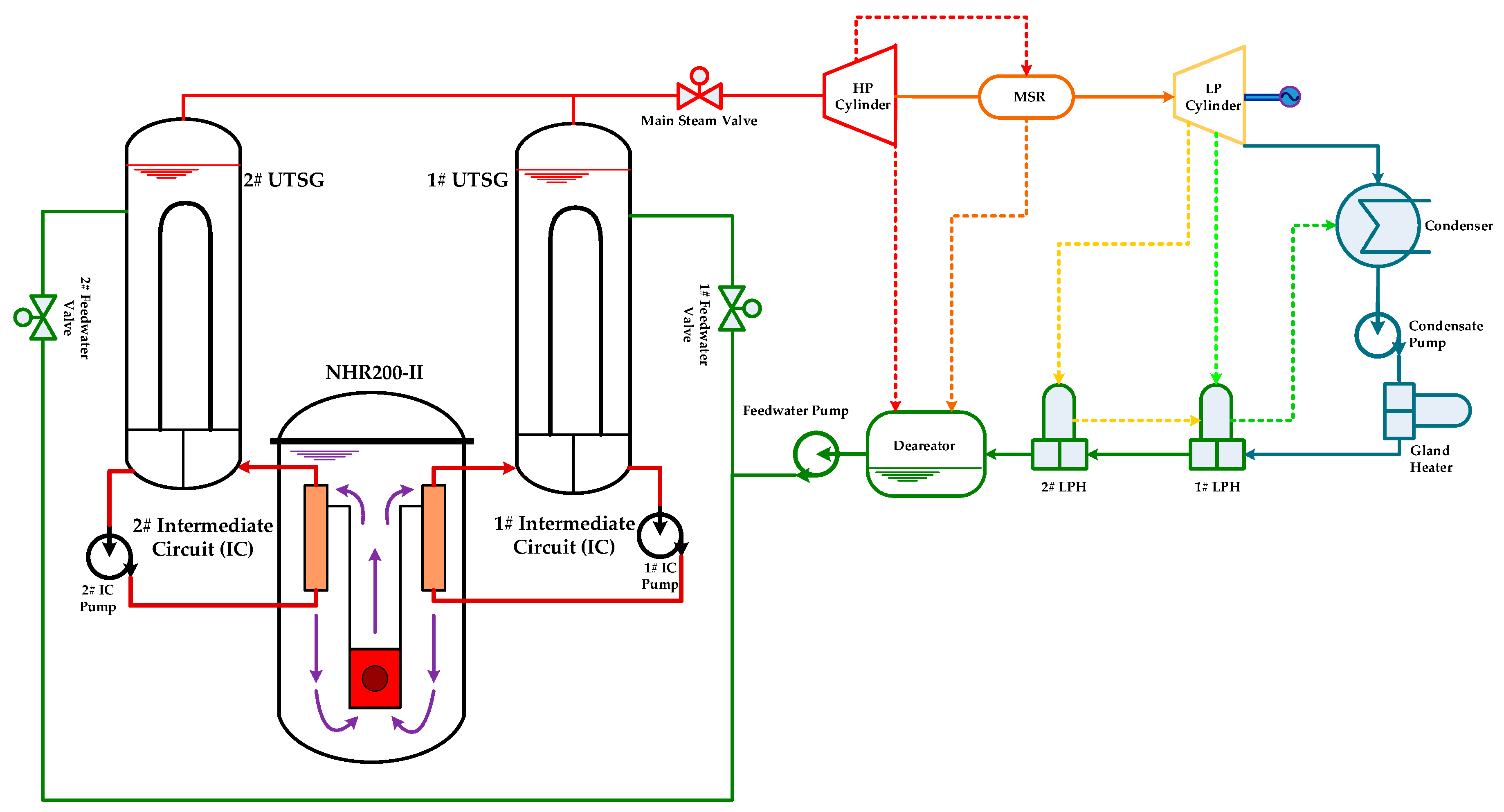
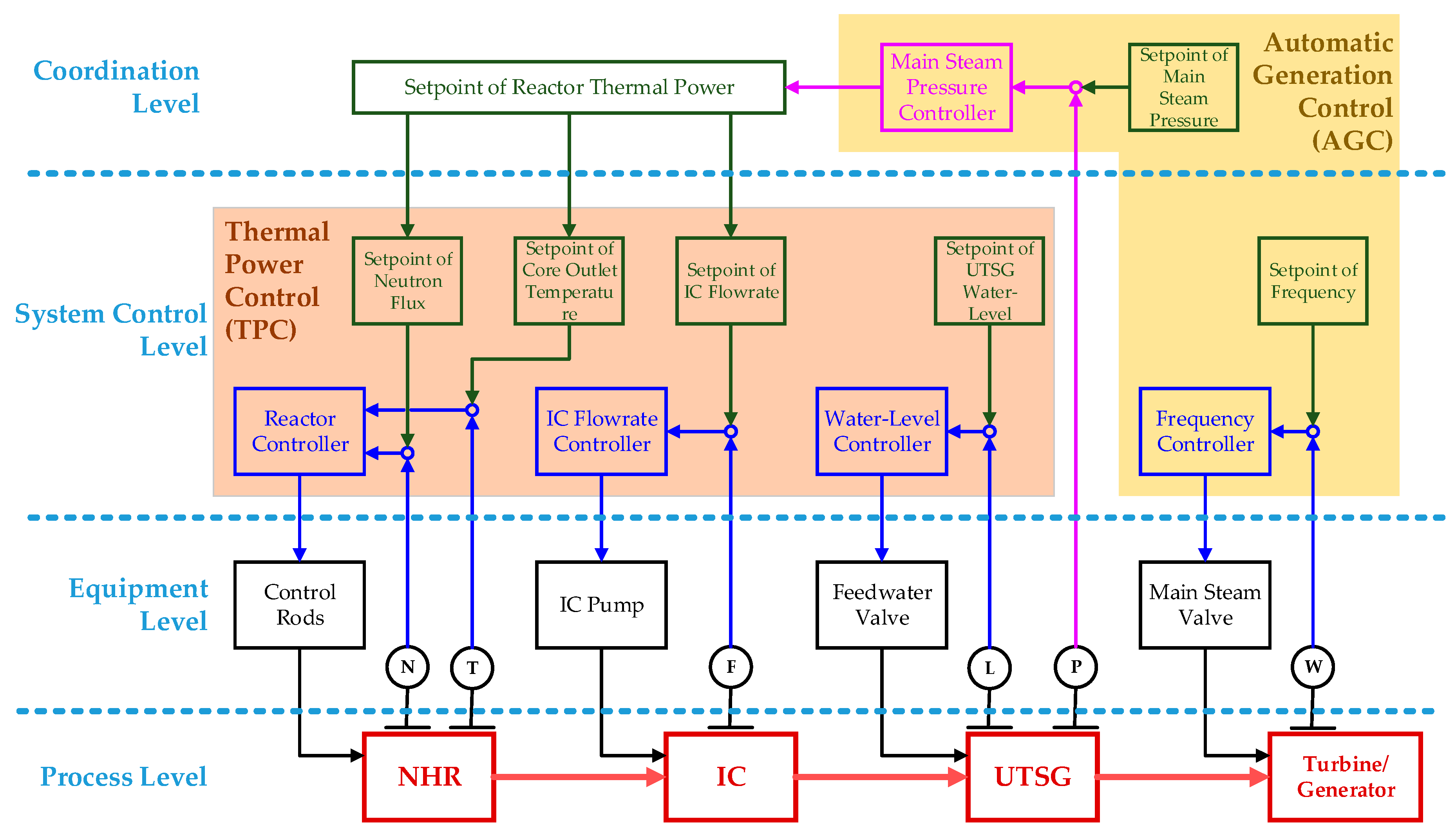
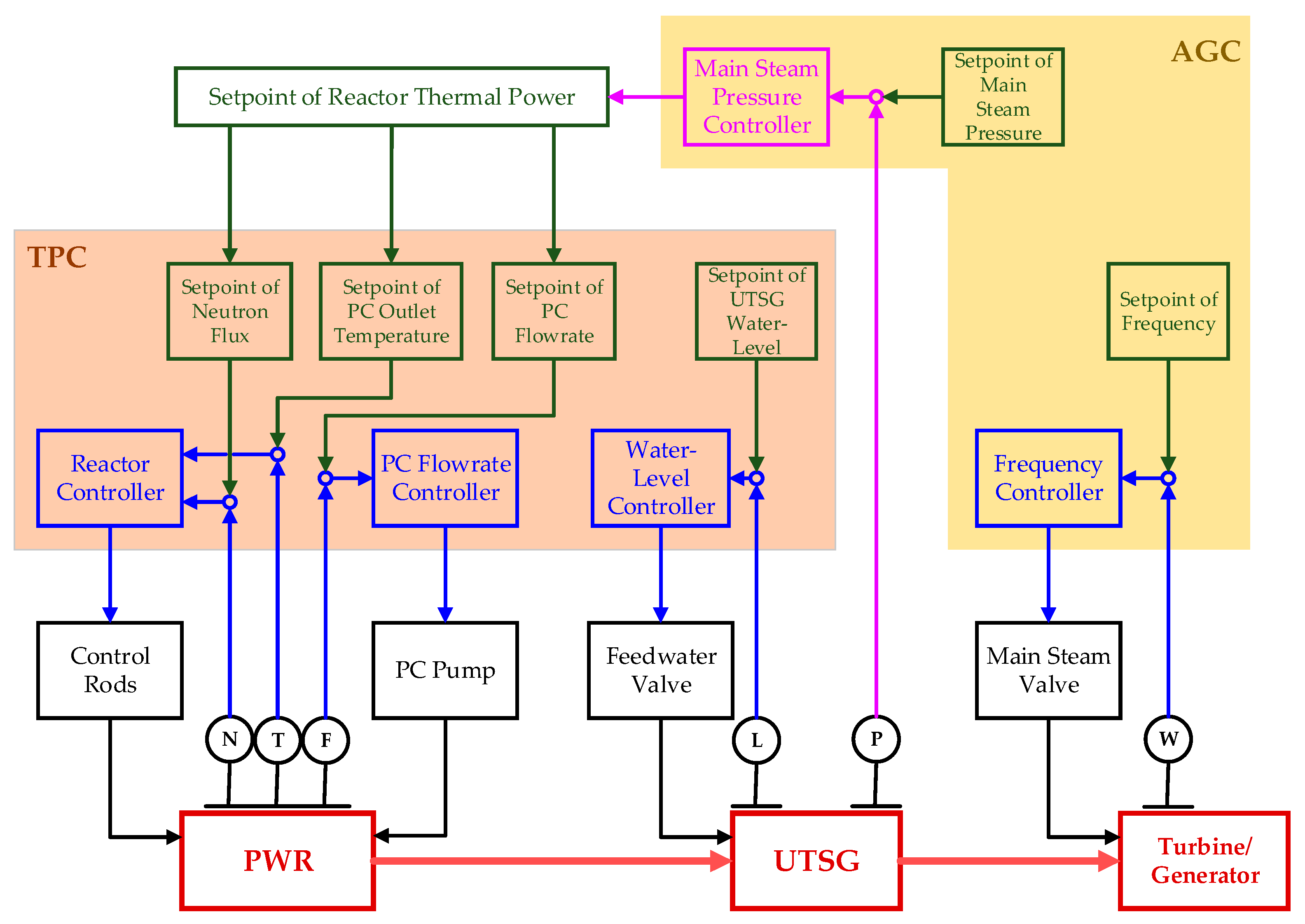
| Parameter | Unit | NHR-200 | NHR-200II |
|---|---|---|---|
| Thermal Power | MWth | 200 | 200 |
| Coolant/Moderator | Light Water | Light Water | |
| Circulation Type | Natural Circulation | Natual Circulation | |
| Primary Circuit Pressure | MPa | 2.5 | 8 |
| Core Inlet/Outlet Temperature | °C | 145/210 | 232/280 |
| Intermediate Circuit Pressure | MPa | 3.0 | 8.8 |
| IC Cold/Hot Leg Temperature | °C | 95/145 | 203/248 |
| Live Steam Pressure | Mpa | 0.25 | 1.6 |
| Live Steam Temperature | °C | 127.4 | 201.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Liu, M.; Jiang, D.; Huang, X.; Zhang, Y.; Zhang, Z. Automatic Generation Control of Nuclear Heating Reactor Power Plants. Energies 2018, 11, 2782. https://doi.org/10.3390/en11102782
Dong Z, Liu M, Jiang D, Huang X, Zhang Y, Zhang Z. Automatic Generation Control of Nuclear Heating Reactor Power Plants. Energies. 2018; 11(10):2782. https://doi.org/10.3390/en11102782
Chicago/Turabian StyleDong, Zhe, Miao Liu, Di Jiang, Xiaojin Huang, Yajun Zhang, and Zuoyi Zhang. 2018. "Automatic Generation Control of Nuclear Heating Reactor Power Plants" Energies 11, no. 10: 2782. https://doi.org/10.3390/en11102782
APA StyleDong, Z., Liu, M., Jiang, D., Huang, X., Zhang, Y., & Zhang, Z. (2018). Automatic Generation Control of Nuclear Heating Reactor Power Plants. Energies, 11(10), 2782. https://doi.org/10.3390/en11102782






