Abstract
With the growing of using photovoltaic (PV) units in power distribution systems, the role of high-performance power electronic converters is increasing. In this paper, modelling and control of Modular Multilevel Converter (MMC) are addressed for grid integration of PV units. Designing a proper controller for MMC is crucial during faulty conditions to make the converter stable and provide proper dynamic performance. To achieve this goal, a dynamic model of MMC is presented which it includes symmetrical components of voltage and current. Then, adaptive robust current controllers are developed based on sliding mode and fuzzy controllers for MMC and then the robustness and stability of the controllers are proved by the Lyapunov theory. To implement the proposed controllers under unbalanced grid voltage fault, positive and negative sequences current controllers are implemented to compensate the effect of grid voltage fault and load power variation. Finally, numerical results are shown to evaluate the performance of MMC. In the end, the experimental results are given to prove the controller performance. The outcome indicates that the proposed current controllers are more effective under voltage disturbance conditions and could satisfy the stability of MMC.
1. Introduction
Modular multilevel converters are coming solutions for providing high reliability, capability and good harmonic performance solution for power electronic converters [1,2]. MMCs are generally used in high-power applications such as grid-connected converters [3]. They consist of a high number of capacitors and power electronic switches. Accordingly, the MMC absorbs a small amount of active power to keep the capacitors’ DC voltage constant and compensate for power losses. However, a mismatch in conduction and the switching losses of power electronic switches, make the voltage of the capacitor unbalance. Balancing the voltages has been a major issue in the latest research [4,5,6,7]. Moreover, there have been investigations concerning the implementation of the advanced current controller for MMC. In Reference [8], a model predictive control strategy is proposed to regulate the AC side current, balance the capacitor voltages and control of circulating current concurrently using a single modified cost function. Another study in Reference [9] has proposed a design which controls the total energy and energy balancing between upper and lower arms. A method in Reference [10] for computing the circulating current reference by Lagrange-based multi-objective optimization has been introduced. This method is compared with the closed-loop methods and has proven better performance. In Reference [11], an algorithm for mitigation of circulating current is presented, in which shows that it is composed of negative sequence with double line frequency and DC component. Also, the hysteresis current control algorithms can be used to control MMC [12]. Recently in Reference [13], a novel control strategy has been proposed for MMC based on differential flatness theory, in which instantaneous active and reactive power values are considered as the flat outputs. To achieve this goal, a mathematical model of the MMC taking into account dynamics of the ac-side current and the dc-side voltage of the converter is derived in a d-q reference frame. Moreover, in Reference [14] presents a new function-based modulation control method for modular multilevel converters (MMCs). The main contribution of this study is the formulation of two new modulation functions for the required switching signals of the MMC’s upper and lower sub-modules, correspondingly. Furthermore, the stability analysis and control techniques for grid connected converter based on MMC is discussed in Reference [15]. In all above-mentioned literature, there is not a comprehensive model of MMC which could be considered for evaluation of MMC during unbalanced voltage conditions.
Moreover, dynamic operation and the control of Grid Connected-MMC (GC-MMC) under unbalanced grid voltage faults have not been referred in detail. Therefore, it seems essential to address the behaviour of this operation topology under different voltage disturbances in distribution power systems. Unsymmetrical condition on the grid voltages and its negative component sequence appears double supply frequency component in the DC-link voltage and consequently the third harmonic component on the AC side. Then it is a basis for flowing large negative-sequence current through the MMC; this may the grid connected-MMC lose its operation. Accordingly, the output voltages of the MMC are controlled to minimize the negative-sequence current flowing into the converter and it makes unbalance reduction on the grid voltages.
In this paper, a dynamic nonlinear model of a modular multilevel converter is developed. In the proposed model, symmetrical elements of voltage and current considering positive and negative sequences are involved. Then, because of the existing unbalance voltage conditions and uncertainties in the model, a robust adaptive current controller is developed for GC-MMC which includes a sliding mode and fuzzy controllers. In addition, the robustness and stability of the controllers have been proved by Lyapunov theory and completely guaranteed. Finally, to justify the potentiality of the recommended control strategy, a simulation study is fulfilled and the obtained results for normal and unbalanced fault conditions are presented.
2. Modelling of GC-MMC
To investigate the dynamic behaviour characteristics of GC-MMC, an accurate model is needed. The classic formation of an MMC is presented in Figure 1. Each sub module (SM) is a simple half-bridge formed by two power electronic switches, two anti-parallel diodes and a capacitor C. To develop an advanced control strategy for GC-MMC, nonlinear state space equations which are based on the average model of power electronic converters are extracted. According to Figure 1, the differential equations of an N-cells MMC using basic KCL and KVL laws are as follows [16]:
where iu, il, VCi_u, VCi_l are upper/lower values for arm currents and capacitor voltages receptively. Moreover, di Vdc and Va are gating signal of the upper gate of the i-th cell, DC-link voltage and phase a voltage separately.
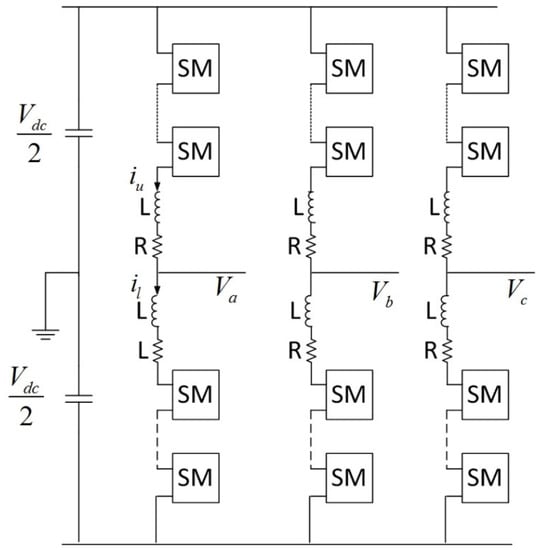
Figure 1.
The circuit topology of a typical MMC.
3. Fuzzy-Sliding Mode Control (FSMC) of GC-MMC
A block chart of the proposed control strategy for PV system is illustrated in Figure 2. The upper and lower arms of the MMC principally perform as controlled voltage sources and they are modulated using Pulse-Width Modulation (PWM) technique. The PWM method employed in this study is basically a carrier based Level-Shifted PWM strategy [14]. In Figure 1, the Maximum Power Point Tracker (MPPT) module which provides the voltage or current reference is utilized, where Vdc-ref is the reference dc-link voltage and Vdc is the actual dc-link voltage. The PV array’s voltage is remained close to a reference dc-link voltage. Then, the power control is implemented. To achieve this goal, current control strategy based on fuzzy sliding mode control is established. The details of suggested current controller are explained as follow.
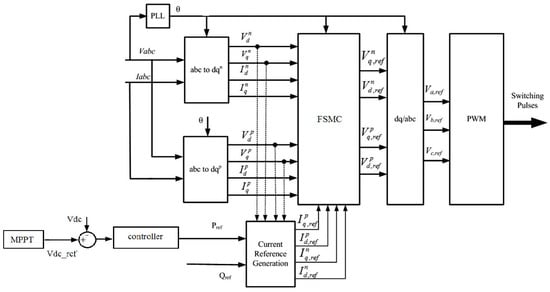
Figure 2.
Configuration of the proposed MMC-based PV conversion system.
Equation (1) is a nonlinear system with the presence of parameters uncertainties and external voltage disturbances. Generally, the state space equation of the nonlinear system including uncertainties is written as follows [16]:
where X(t) is the state vector; u(t) is the control input of system (1); ∆g expresses uncertainty part of the system (1) on R and L values; d(t) is the disturbance of the system (1) where it is considered as grid voltage variation here.
Moreover, the uncertain and disturbance parts of the nonlinear model are assumed to be bounded that is,
where δ and ε are two positive and known constraints, which mean the margins for the uncertain and disturbance parts.
The complexity of non-linear Equation (1) and demand for fast response during power tracking leads to an adaptive fuzzy sliding mode control structure which is proposed for designing current controllers of the GC-MMC. Sliding mode control (SMC) is one of the control methods used for current regulation in power electronic converters. However, the basic problem of employing SMC is chattering. Many different methods have been suggested to deal with this problem in SMC [17]. Recently a combination of fuzzy control and SMC has been employed for this purpose and the results are found to be effective [18,19].
When the fuzzy sliding control strategy is being designed to regulate converter’s output currents, the current tracking error is, firstly, defined for positive and negative sequence components as follows:
where idp_ref, iqp_ref, idn_ref and iqp_ref are reference currents of symmetrical dq components, respectively.
Secondly, a modified sorting method is used for stabilizing of SM capacitor voltage. Commonly, after modulation, the number of SMs should be activated or deactivated. Being so, the sorting algorithm is implemented to balance the capacitor voltages. On that account, the voltage error between SM capacitor voltages and their references takes a step forward, which results in minimum voltage error. It is considered as another error tracking signal. The voltage errors are calculated by:
where Vc,ref is the reference SM capacitor voltage.
The estimated capacitor voltage Vc,j for each SM is obtained by the formula below:
where ik,j is arm current and Ts is the control time period.
Regarding the above equations, the error vector could be formed as follow.
Then the time-varying sliding surface for first order system is proposed [14]:
where λ is a strict positive parameter and it is tuned based on the system bandwidth.
For grid-connected converters applications, the faults in grid voltage and uncertainties on output filter parameters are unknown and the control signal is designed by satisfying ds/dt = 0 as follow:
where the Xref is a vector which it is included the reference values for state variables.
In the traditional SMC, the control signal based on Lyapunov stability theory is defined as follows:
where kw is the switching gain.
u = ueq + kw·sgn(s)
The chattering phenomenon is the inherent challenge of SMC which is made by sign function on the overall control signal u. Hence, the fuzzy-sliding mode control is proposed to eliminate the chattering problem in current control loops of GC-MMC. By implementing this method, the robustness of the controller is satisfied. Also, the performance of the system is improved since the chattering has been eliminated. Consequently, the control signal of fuzzy-sliding mode controller could be written as follows:
In fact, in the proposed current controller, there is a fuzzy controller for each symmetrical component of dq sequences that has two inputs () including one output (u). There are also seven linguistic variables, NB (Negative Big), NM (Negative Medium), NS (Negative Small), ZE (Zero), PS (Positive Small), PM (Positive Medium), PB (Positive Big), which are used as inputs and outputs respectively. Furthermore, to procure appropriate dynamic response, achieve a high level of accuracy and guarantee the stability of the whole system, a set of decision rules for the fuzzy controller is designed that is presented in Table 1. These rules contain the input/output relationships which they are mapped by membership functions to describe the control strategy. Both input and output membership functions are scaled into the range of −1 and 1 with an equal span as shown in Figure 3. In order to guarantee the robustness and stability of the controller, an adaptive procedure based on Lyapunov theory is implemented which is completely given in Reference [19,20].

Table 1.
Rule base of the fuzzy controller.
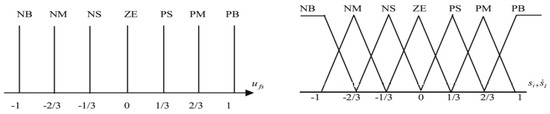
Figure 3.
Membership functions of the fuzzy control strategy.
4. Simulation Results and Analysis
The complete modelling of MMC is carried out in MATLAB/Simulink software to look into the performance of robust non-linear control strategy. The nominal parameters of the power converter and controller are presented in Table 2.

Table 2.
Parameters of Power converters and Controllers.
The reference values for the real power and reactive power are determined and implemented. The voltages of six capacitors of phase A are illustrated in Figure 4. As shown, they are around the nominal value of each SM capacitor initial voltage. The three-phase line to line voltages are given in Figure 5. Six levels of voltage are clearly seen as expected. It is obvious that the voltage levels vary within acceptable boundaries caused by charging and discharging of the capacitors.
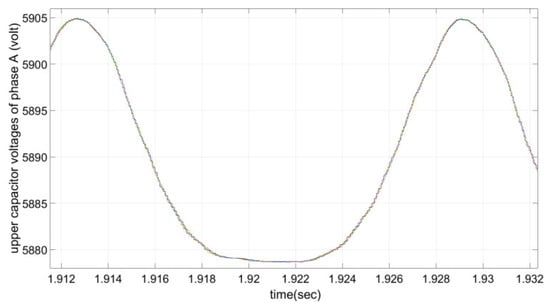
Figure 4.
The voltage of the capacitor.
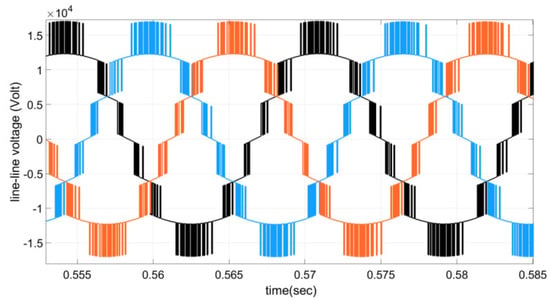
Figure 5.
Three-phase line-line voltages.
In Figure 6, the upper cell voltage of phase A is displayed. Because of 10 times switching of cell voltage in a cycle, the switching frequency of approximately 600 Hz is clearly observed for the power electronic switch. The dc current flowing which circulates through the arms and the dc side of the converter is illustrated in Figure 7. The DC current supports the power balance in the dc side’s capacitors.
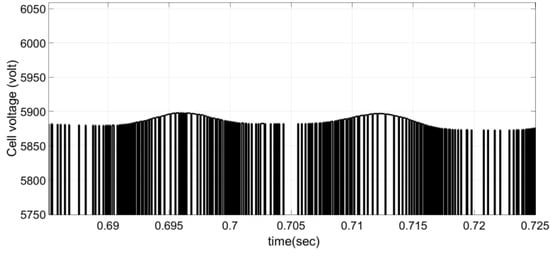
Figure 6.
Output Voltage of top cell in phase A.
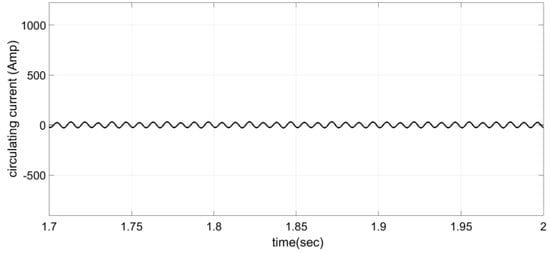
Figure 7.
The variations of circulating current.
Figure 8 illustrates how the GC-MMC replies to the requested active power at 2.5 s and 3.2 s of the reactive power. In this case, active power changes to 0.1 MW and reactive power goes up to 0.3 MVAr. It shows a corresponding variation in the exchanged active and reactive powers. There is also an enhancement in the response of steady-state and transient conditions when implementing the proposed controller.
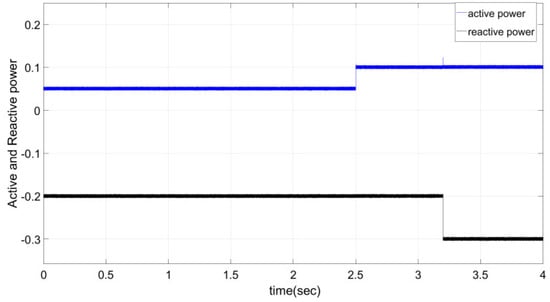
Figure 8.
Dynamic response of the GC-MMC to the step power command.
Moreover, to prove the robustness of the proposed controller, the inconsistency of output filter parameters is considered for R and L. Accordingly, the 1.1 R and 0.9 L are implemented in simulation models based on the nominal value in Table 1. In this case, the simulation is run alike the prior conditions. In Figure 9, the reactive power tracking of the proposed controller is presented due to the mismatches. It proves the robustness of the proposed controller during the changing of filter parameters. Also, it shows that fuzzy-sliding mode controller is not sensitive to plant uncertainties.
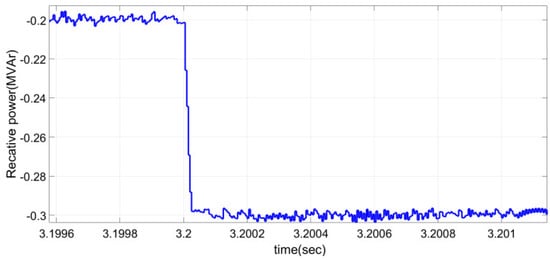
Figure 9.
Reactive power tracking of the proposed controller in presence of parameters mismatch.
Further evaluation of the proposed controller is carried out during grid voltage disturbance. In phase, A, voltage sag is considered to drop 20%. Regarding the unbalanced voltage fault, there are oscillations in active and reactive powers which are illustrated in Figure 10. These oscillations are related to the proposed current control strategy and it makes the oscillating on active and reactive powers. Finally, as it has been demonstrated, the capacitor voltages vary within acceptable limits and are not influenced by grid voltage faults.
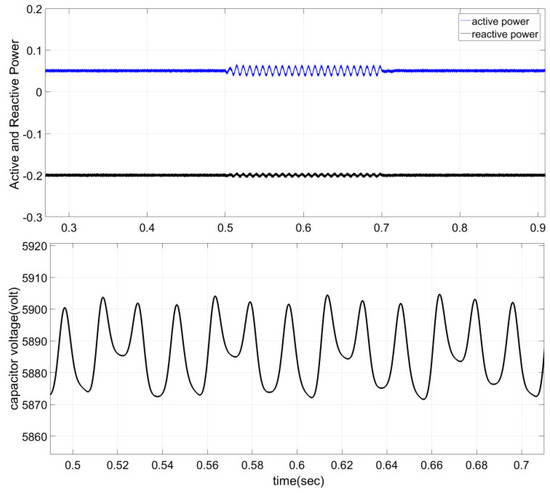
Figure 10.
Dynamic response (generated active and reactive powers and capacitor voltage) of the GC-MMC during unbalanced voltage sag.
In order to compare the fuzzy-sliding mode control with PI controller, some simulation tests were performed on MMC during unbalance voltage conditions. The design of PI is primarily based on a trial and error procedure. But during designing of fuzzy-sliding mode control, the triangular membership was considered because of its simplicity of implementation and because less computational intensity is required. The number of linguistic variables and the base width of linguistic variables have some effect on the response time and magnitude of ripple in the output voltage. However, they do not seriously affect the response as the change of gains in a PI controller does. In the design of the PI-controller, the gain selection is crucial. A set of gains can be ideal for one type of disturbance but not for another type of disturbance. The gains were selected to provide a performance compromise for supply voltage disturbance and load disturbance. Digital implementation at the sampling rate of 20 kHz was considered for all these controllers.
5. Experimental Results
To examine the performance of the proposed controller, an experimental setup has been developed. The test system is connected to 750 W rooftop solar system. Since the system required many input/outputs and sampling frequency up to 10 kHz, the dSPACE MicroLabBox was decided to be used as the real-time interface for control of the MMC. The structure of the test setup is shown in Figure 11. The experimental setup is of a low power, 3 levels, single phase MMC, as shown in Figure 11. In the laboratory, MPPT module is used to regulate the output voltage of PV panels. The parameters for the experimental setup are listed in Table 3.
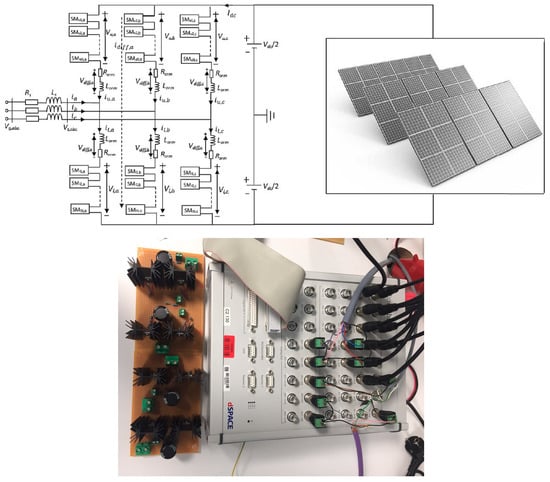
Figure 11.
The structure of the test setup and laboratory setup of a three-level, single phase MMC.

Table 3.
Parameters of Power converters and Controllers.
The experimental results only show the dynamic tracking properties of the proposed controller. The profile given to it was of 6 A current for the first 50 s and then it was increased to 9 A thereafter. In the test setup, the input voltage at MPP is around 29 V. The rms output voltage is illustrated in Figure 12. It is principally constant as the dc-link voltage should. The voltage across the capacitor of module 1 as obtained on the control desk can be seen in Figure 13. As the voltage was obtained at 𝑣dc ≈ 20 V, it is expected the average value across any submodule at any given time, when the sorting algorithm is active, should be approximately 10.
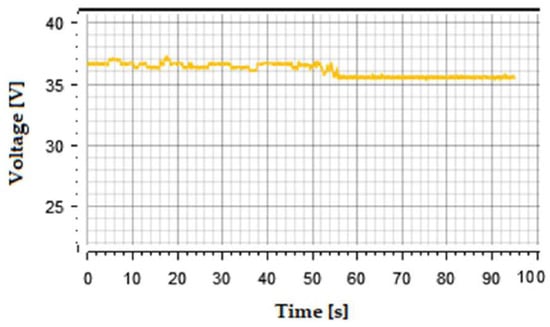
Figure 12.
The rms output Voltage waveform across the Load.
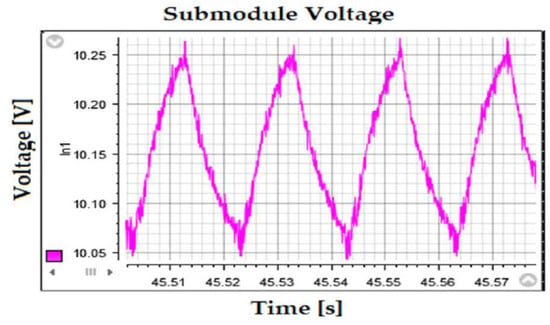
Figure 13.
Capacitor voltage for submodule 1 obtained from the experimental setup.
To survey the robustness of the proposed controller, the real value of arm inductance changes to 5.6 mH. The power supply was operated in a constant current mode, to emulate a PV module at a constant temperature but different insolation. Figure 14 shows the input current waveform.
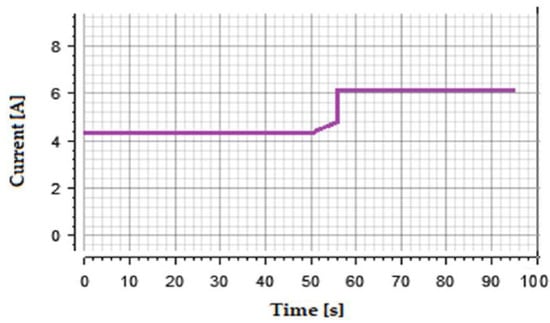
Figure 14.
Input current waveform.
The change in input current is only reflected as a change in output power which is illustrated in Figure 15. As depicted, the proposed controller properly follows the reference value and its dynamic performance is satisfied. By comparison between the simulation and experimental results, it is achieved the offered control strategy is able to overcome the parameter mismatches in the output filter. The dynamic performance is guaranteed during changing the demanded power. The dynamic performance is the trade-off between the kfc and the number of rule bases during designing of the fuzzy controller and it influences on both simulation and experimental results. From the simulation result, it is evident that the controller is capable to reduce the impact of the external events such as asymmetric grid voltage fault and it is very important during connection of photovoltaic systems to weak grid. From the simulation results, it can be observed that the proposed current controllers let retaining power as requested by the DC current source during and after the event. Despite the unbalance of AC voltages, the AC current controller can balance the resulting AC currents. As a result, the active as well as reactive powers start oscillating with double frequency of AC grid. Thanks to the developed current controller, the applied event is damped by the stored energy inside the MMC and consequently does not disturb the DC current and voltage.
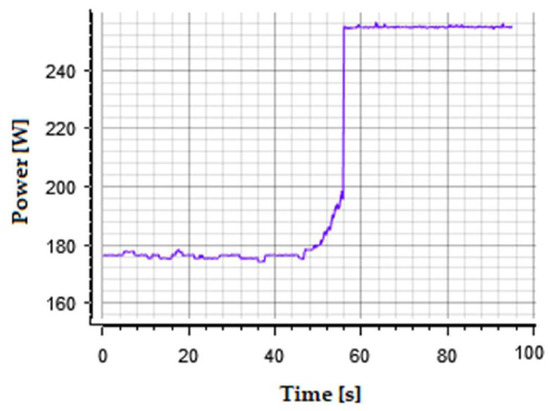
Figure 15.
Output power waveform.
6. Conclusions
This paper presents the fuzzy sliding mode current control strategy for GC-MMC configuration. Considering the unbalance voltage conditions and complexity of the model including a high number of state variables and parameters uncertainties, a robust adaptive current control structure using sliding mode control and fuzzy control, is developed for GC-MMC. The proposed control makes a proper performance for MMC and enables separate control of the symmetrical elements of grid currents. The simulation and experimental results suggest that the proposed controller is very robust during the changing of filter parameters. The dynamic response, also, proves that the fuzzy sliding mode controller is not sensitive to plant uncertainties and adequate dynamic response. Moreover, based on the proposed controller, the capacitor voltages fluctuate within acceptable limits and they are not influenced by grid voltage faults. In the simulation results, in phase, A, voltage sag is considered to drop 20%. From the simulation results, it can be observed that the proposed current controllers let retaining power as requested by the DC current source during and after the event. Moreover, it is obtained from the experimental results by changing 12% of real value of inductor in output filter; the current controller could overcome the parameter mismatch inside the MMC.
Author Contributions
S.M.H. designed the simulation of the proposed work and prepared the initial draft of paper. A.H. designed the formulation of the overall work and contributed significantly in writing the paper.
Funding
This research received no external funding.
Acknowledgments
Authors would like to thank the research council of Islamic Azad University, Damavand, Iran for financial support of this research project.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; the collection, analyses, or interpretation of data; the writing of the manuscript; and in the decision to publish the results.
References
- Martinez-Rodrigo, F.; Ramirez, D.; Rey-Boue, A.B.; de Pablo, S.; Herrero-de Lucas, L.C. Modular Multilevel Converters: Control and Applications. Energies 2017, 10, 1709. [Google Scholar] [CrossRef]
- Marquardt, R. Modular Multilevel Converter topologies with DC-Short circuit current limitation. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Korea, 30 May–3 June 2011; pp. 1425–1431. [Google Scholar]
- Song, Q.; Liu, W.; Li, X.; Rao, H.; Xu, S.; Li, L. A steady-state analysis method for a modular multilevel converter. IEEE Trans. Power Electron. 2013, 28, 3702–3713. [Google Scholar] [CrossRef]
- Moranchel, M.; Bueno, E.; Sanz, I.; Rodríguez, F.J. New approaches to circulating current controllers for modular multilevel converters. Energies 2017, 10, 86. [Google Scholar] [CrossRef]
- Moon, J.W.; Kim, C.S.; Park, J.W.; Kang, D.W.; Kim, J.M. Circulating current control in MMC under the unbalanced voltage. IEEE Trans. Power Deliv. 2013, 28, 1952–1959. [Google Scholar] [CrossRef]
- Saeedifard, M.; Iravani, R. Dynamic performance of a modular multilevel back-to-back HVDC system. IEEE Trans. Power Deliv. 2010, 25, 2903–2912. [Google Scholar] [CrossRef]
- Deng, F.; Chen, Z. A control method for voltage balancing in modular multilevel converters. IEEE Trans. Power Electron. 2014, 29, 66–76. [Google Scholar] [CrossRef]
- Qin, J.; Saeedifard, M. Predictive control of a modular multilevel converter for a back-to-back HVDC system. IEEE Trans. Power Deliv. 2012, 27, 1538–1547. [Google Scholar]
- Deng, Y.; Wang, Y.; Teo, K.H.; Harley, R.G. A Simplified Space Vector Modulation Scheme for Multilevel Converters. IEEE Trans. Power Electron. 2016, 31, 1873–1886. [Google Scholar] [CrossRef]
- Yao, W.; Hu, H.; Lu, Z. Comparisons of Space-Vector Modulation and Carrier-Based Modulation of Multilevel Inverter. IEEE Trans. Power Electron. 2008, 23, 45–51. [Google Scholar] [CrossRef]
- Li, X.; Song, Q.; Liu, W.; Rao, H.; Xu, S.; Li, L. Protection of Nonpermanent Faults on DC Overhead Lines in MMC-Based HVDC Systems. IEEE Trans. Power Deliv. 2013, 28, 483–490. [Google Scholar] [CrossRef]
- Nami, A.; Liang, J.; Dijkhuizen, F.; Demetriades, G.D. Modular Multilevel Converters for HVDC Applications: Review on Converter Cells and Functionalities. IEEE Trans. Power Electron. 2015, 30, 18–36. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Taheri, S.; Vechiu, I.; Catalão, J.P.S. Novel Control Strategy for Modular Multilevel Converters Based on Differential Flatness Theory. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 888–897. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Akorede, M.F.; Zabihi, S.; Catalão, J.P.S. Function-based modulation control for modular multilevel converters under varying loading and parameters conditions. IET Gener. Transm. Distrib. 2017, 11, 3222–3230. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Zabihi, S.; Vechiu, I.; Catalao, J.P.S. A multi-loop control technique for the stable operation of modular multilevel converters in HVDC transmission systems. Int. J. Electr. Power Energy Syst. 2018, 96, 194–207. [Google Scholar] [CrossRef]
- Deng, Y.; Harley, R.G. Space-Vector Versus Nearest-Level Pulse Width Modulation for Multilevel Converters. IEEE Trans. Power Electron. 2015, 30, 2962–2974. [Google Scholar] [CrossRef]
- Hajizadeh, A.; Norum, L.E.; Ahadpour shal, A. Nonlinear Control Structure of Grid Connected Modular Multilevel Converters. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’17), Málaga, Spain, 4–6 April 2017. [Google Scholar]
- Slotine, J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Rong-Jong, W. Fuzzy sliding-mode control using adaptive tuning technique. IEEE Trans. Ind. Electron. 2007, 54, 586–594. [Google Scholar]
- Ghiasi, M.I.; Golkar, M.A.; Hajizadeh, A. Lyapunov Based-Distributed Fuzzy-Sliding Mode Control for Building Integrated-DC Microgrid with Plug-In Electric Vehicle. IEEE Access 2017, 5, 7746–7752. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).