Power Decoupling of a Single Phase DC-AC Dual Active Bridge Converter Based on an Integrated Bidirectional Buck/Boost Stage
Abstract
1. Introduction
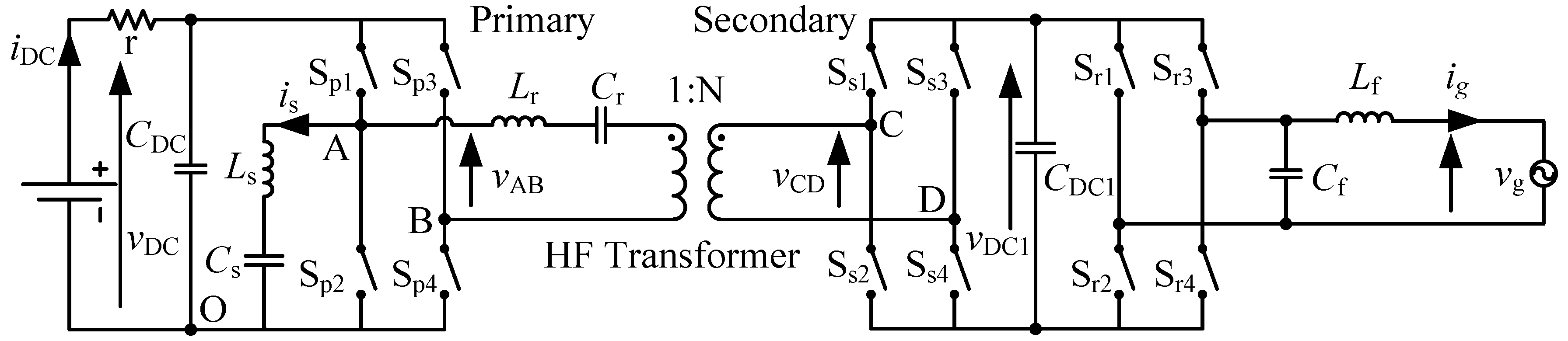
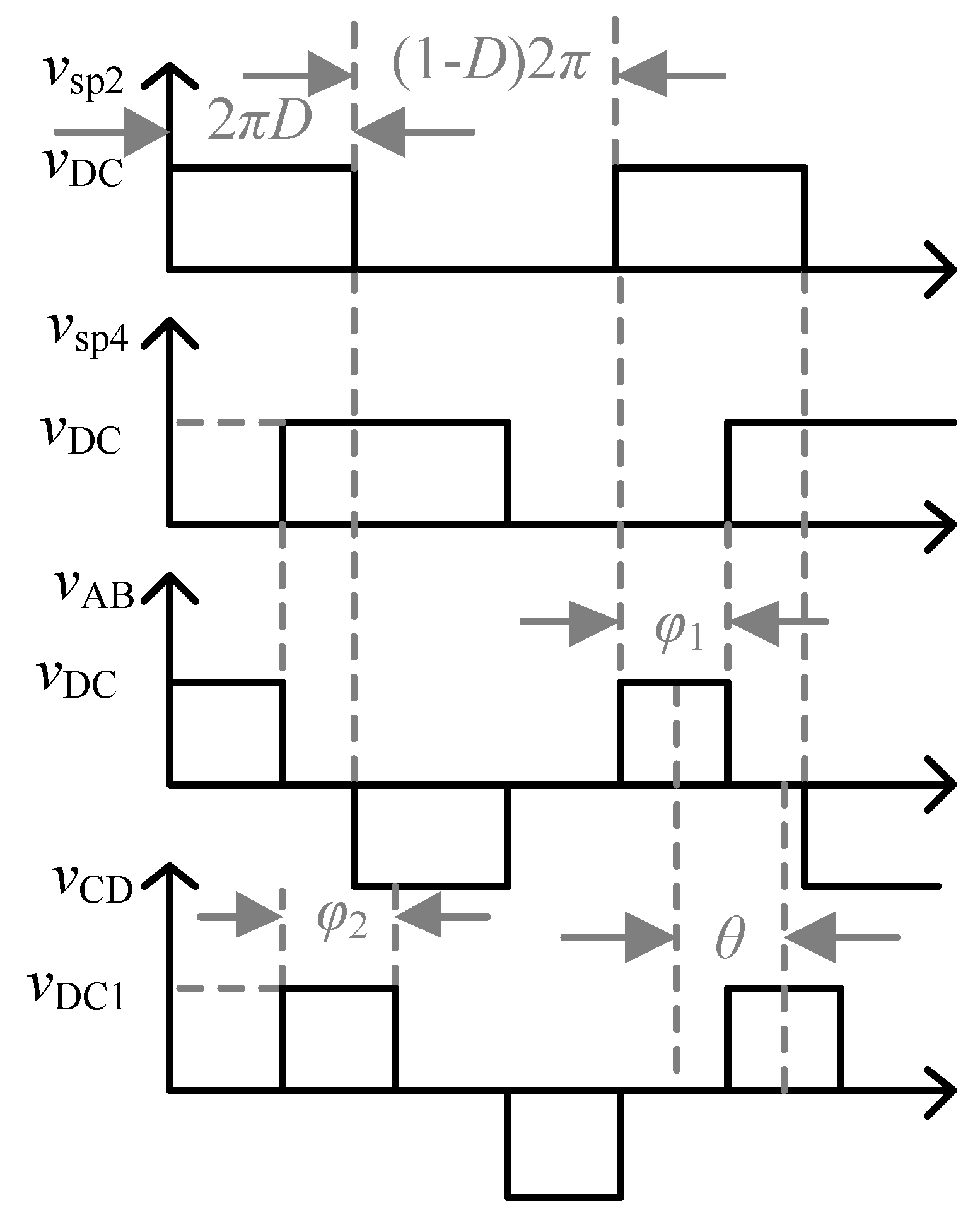
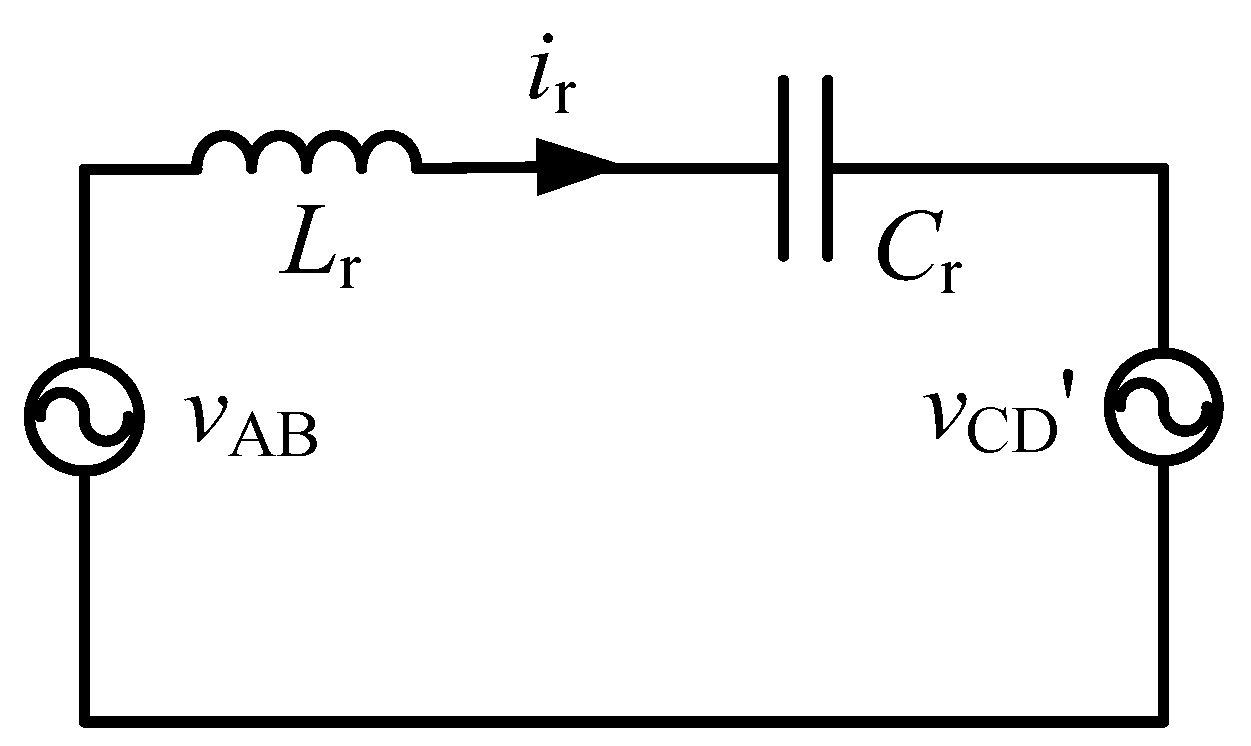
2. Mathematical Model of the Converter
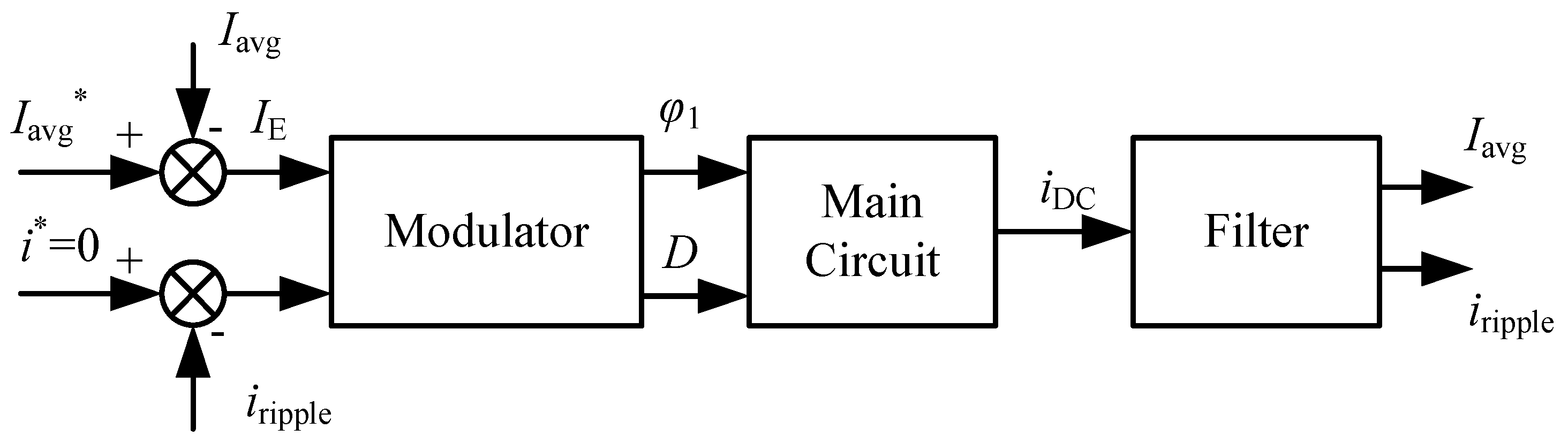
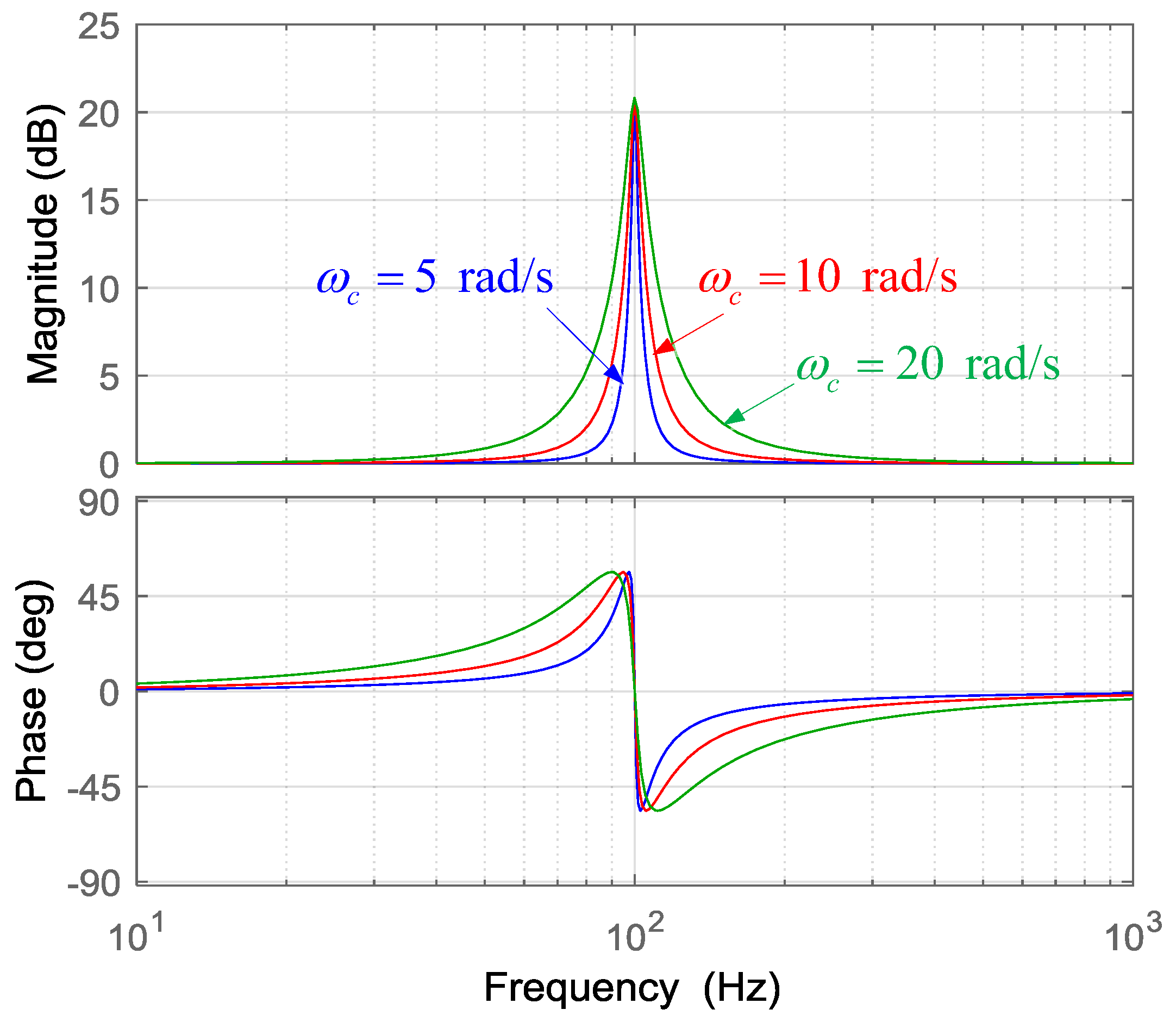
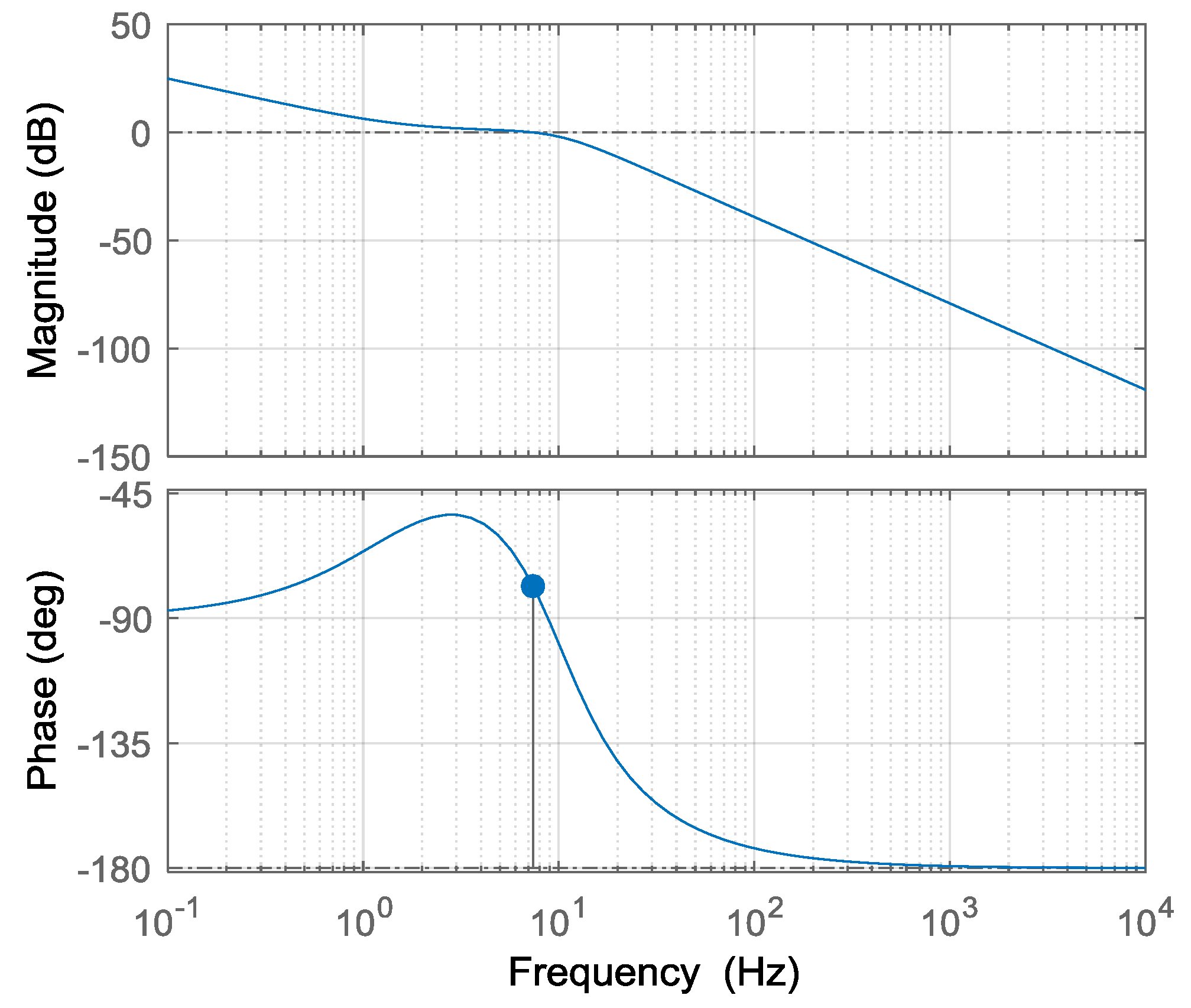
3. Control Strategy
4. Simulation and Experimental Results
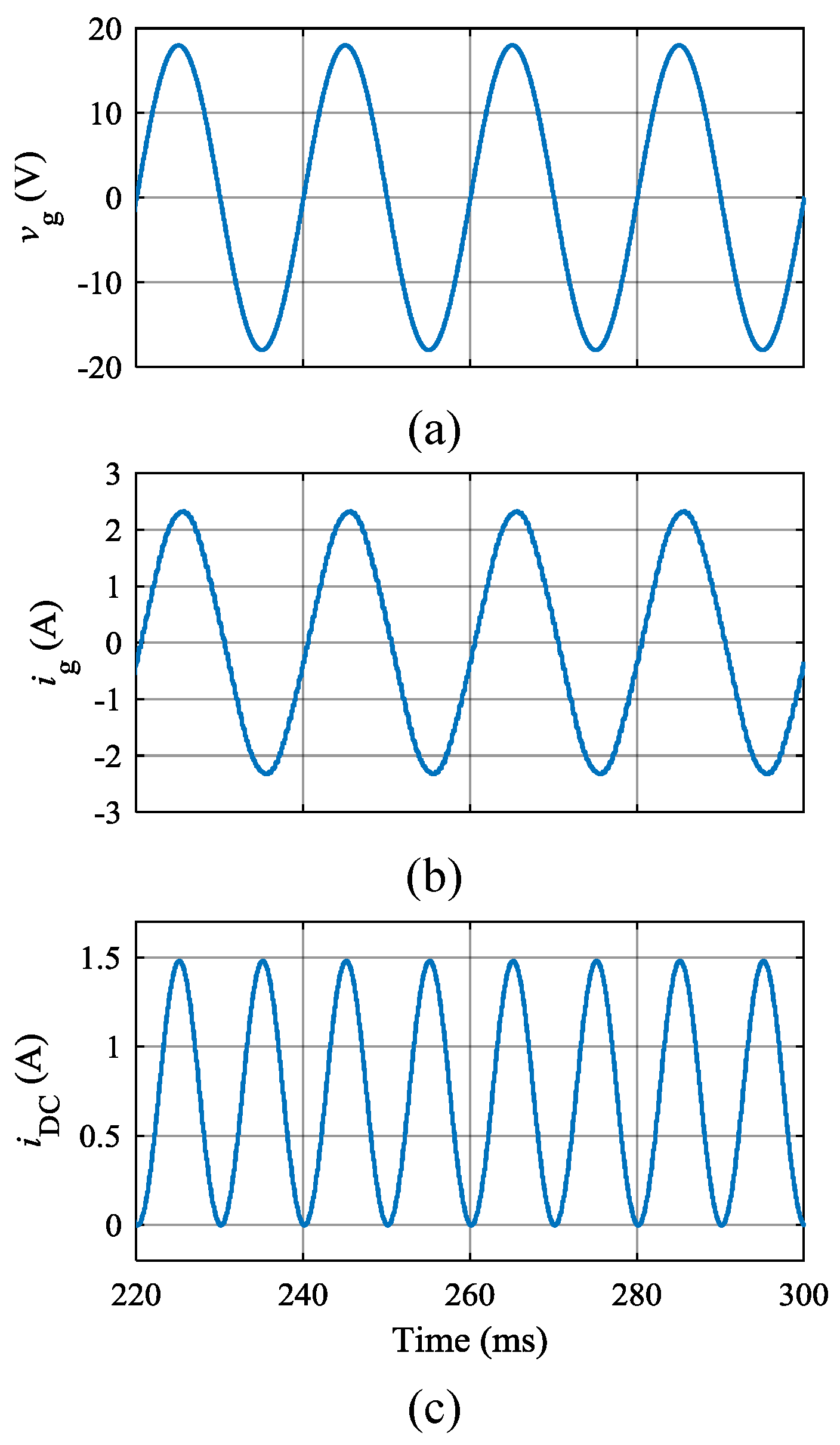
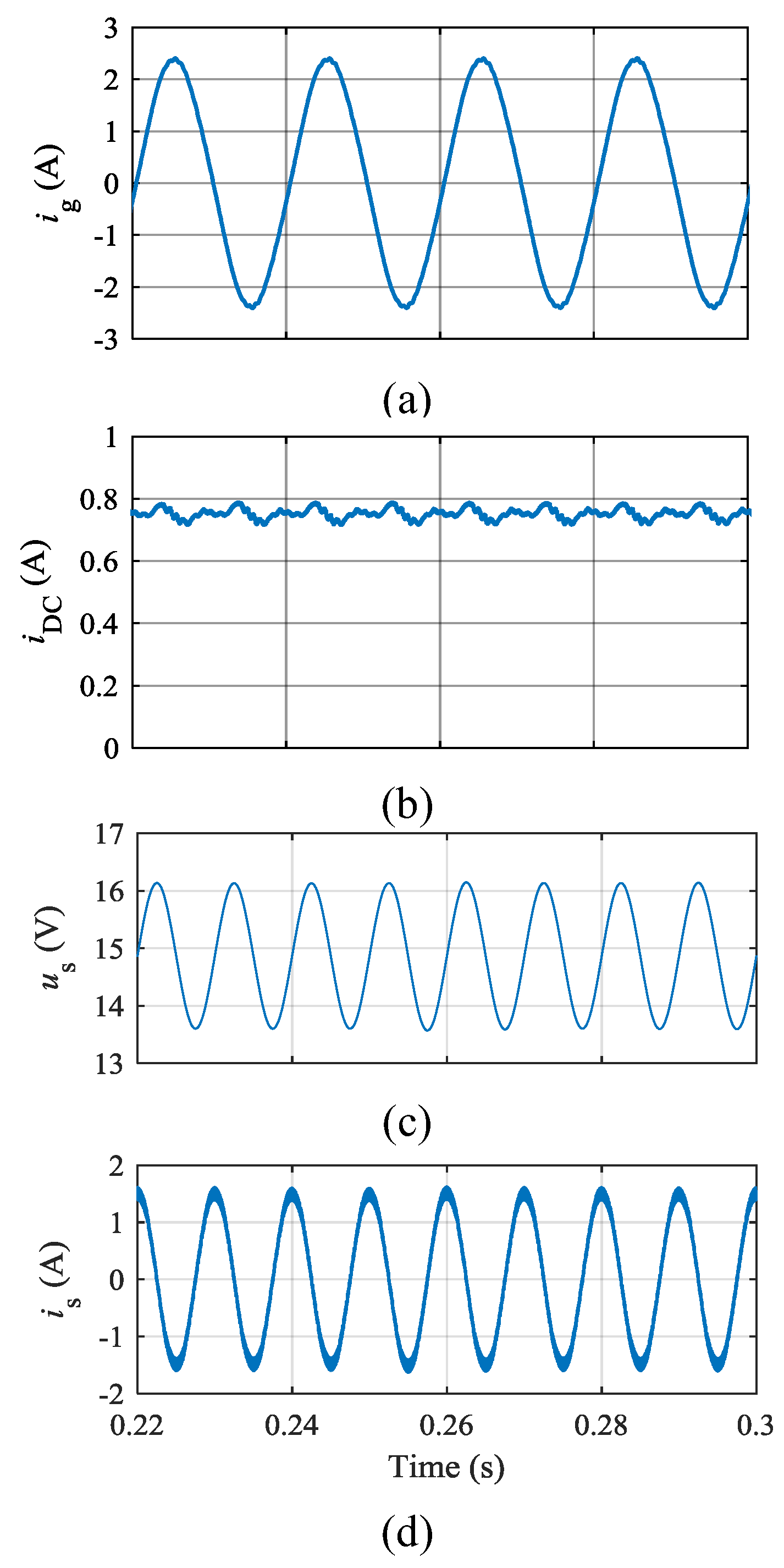
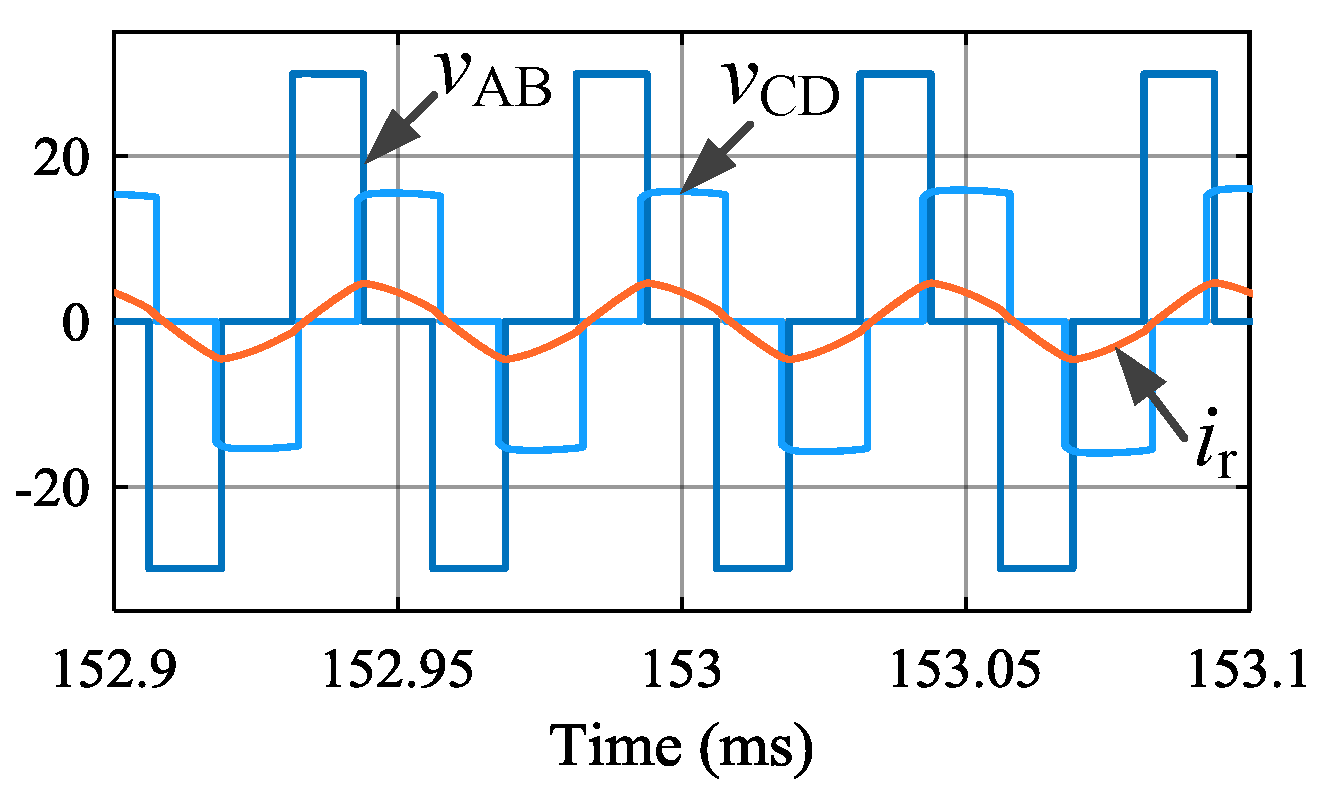
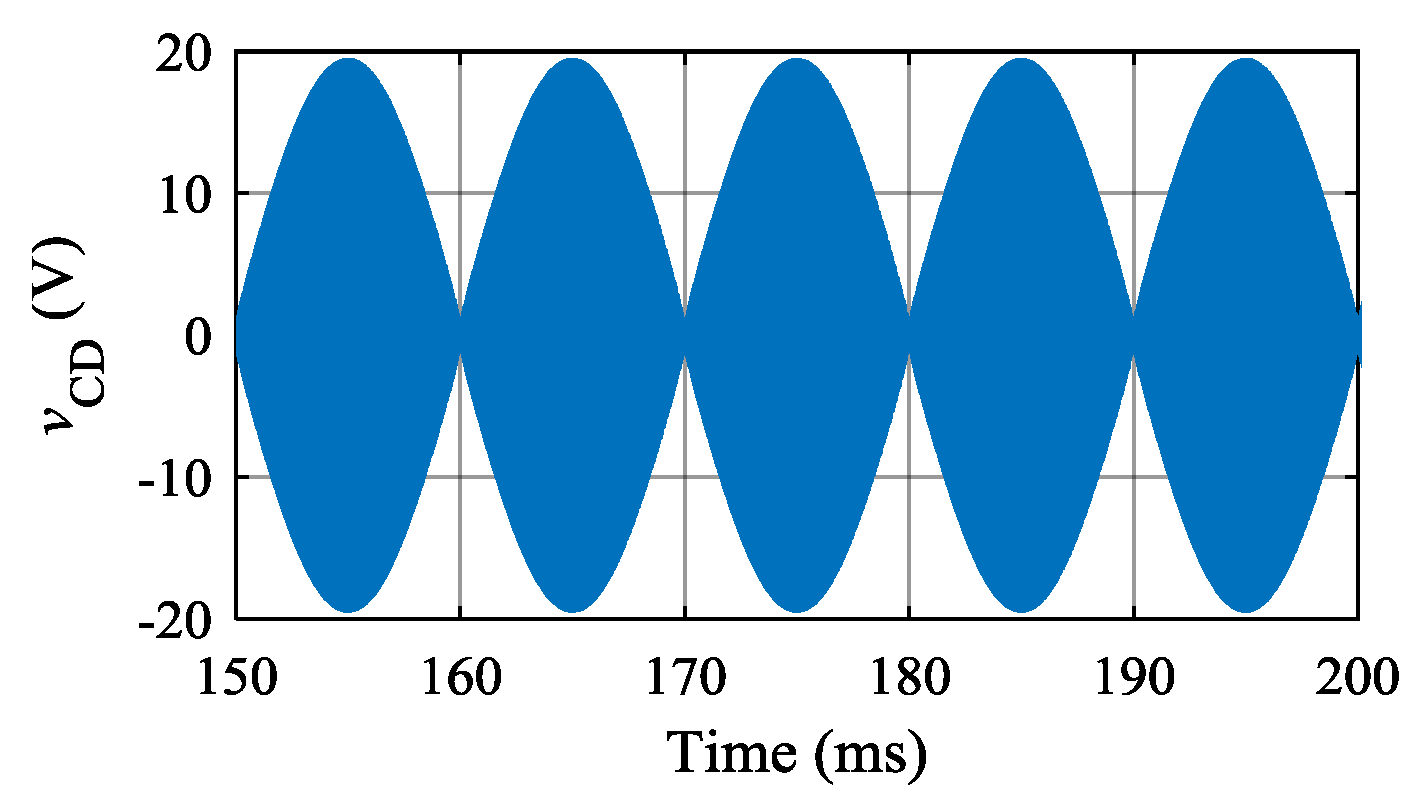
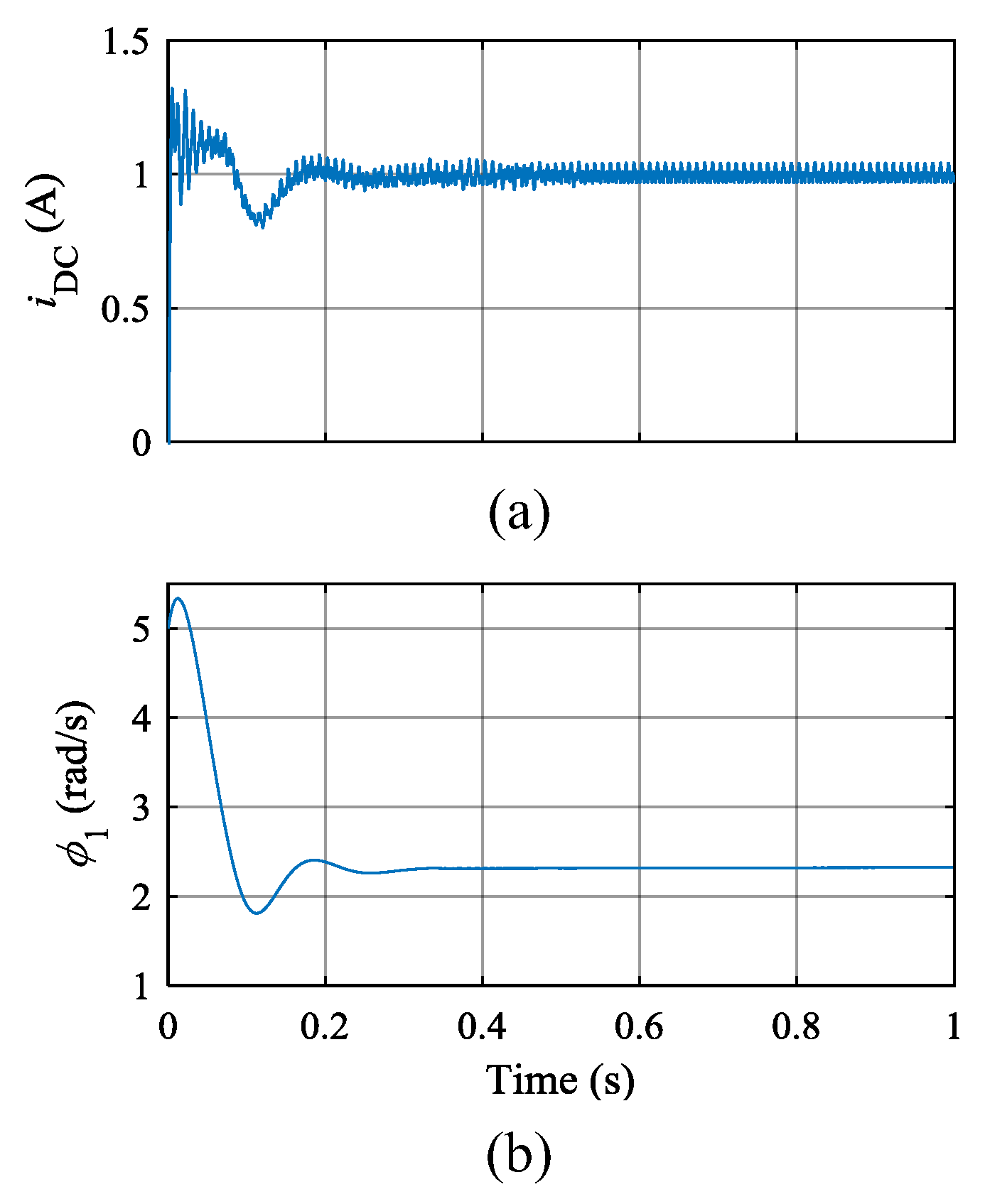
4.1. Simulation Results
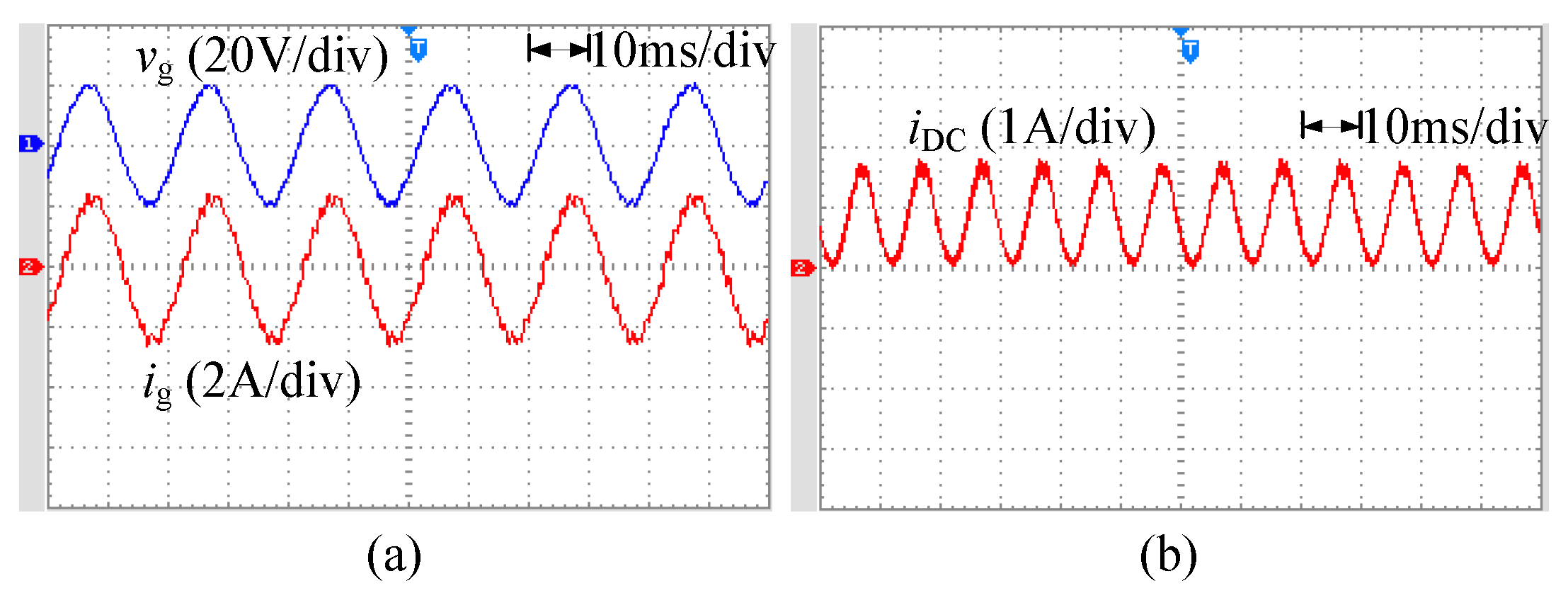
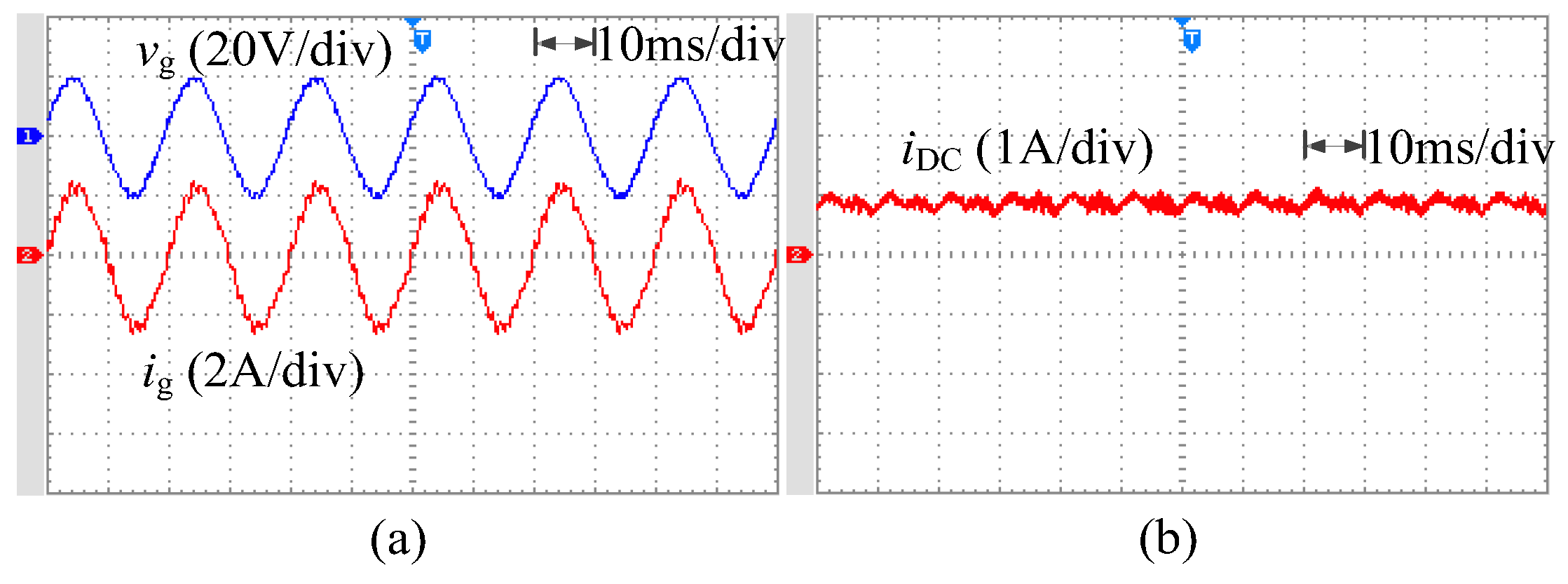
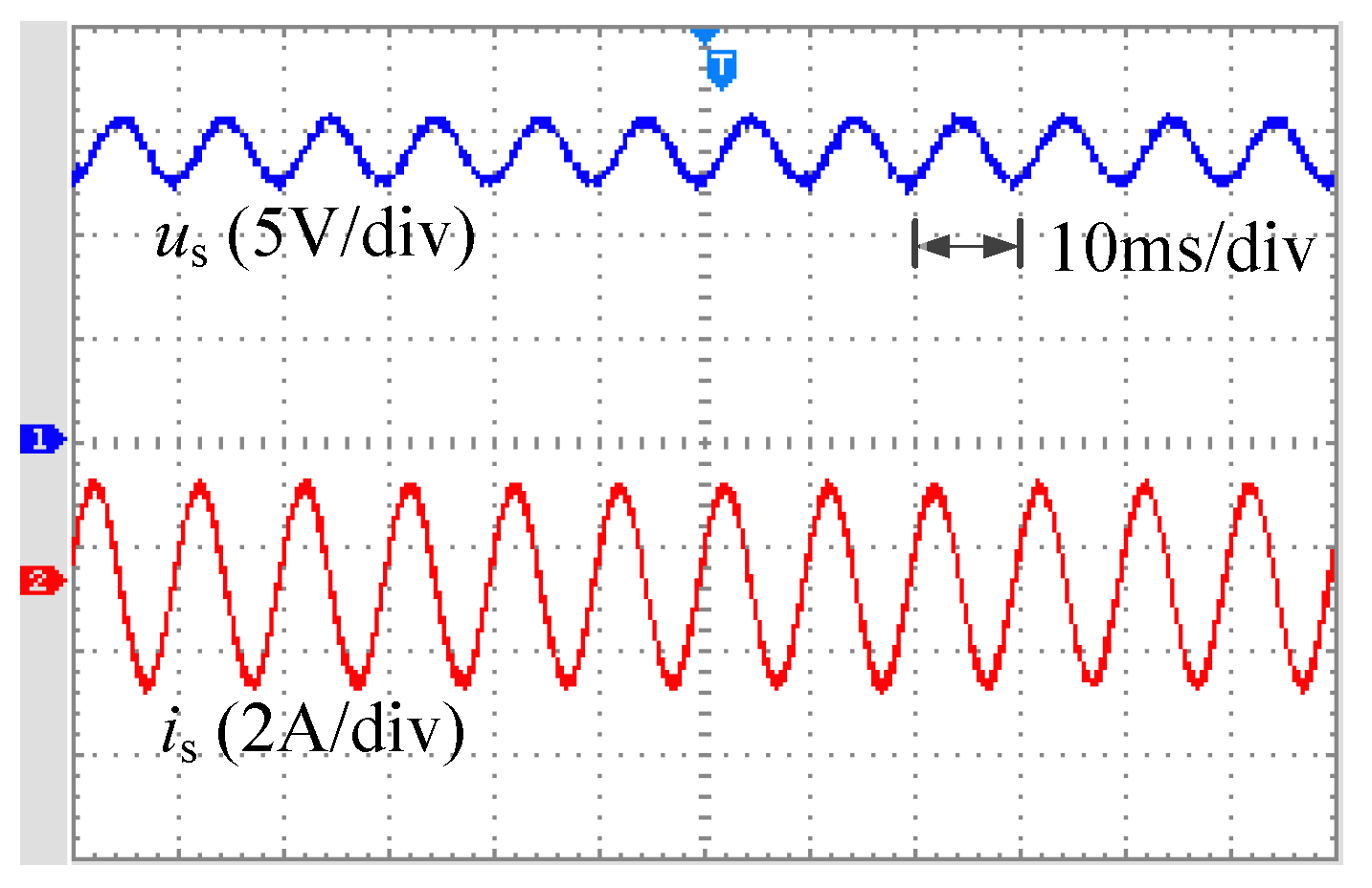
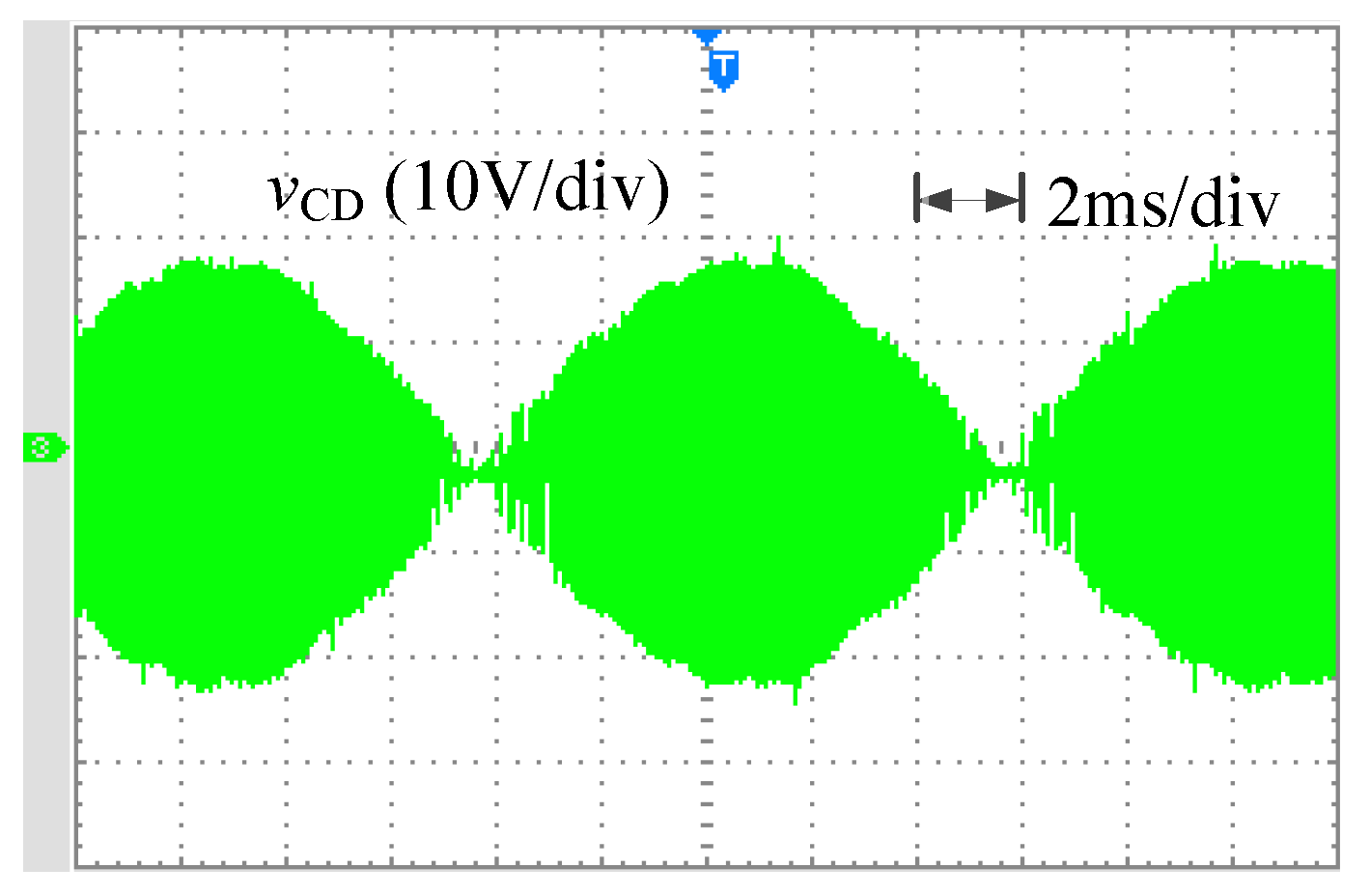
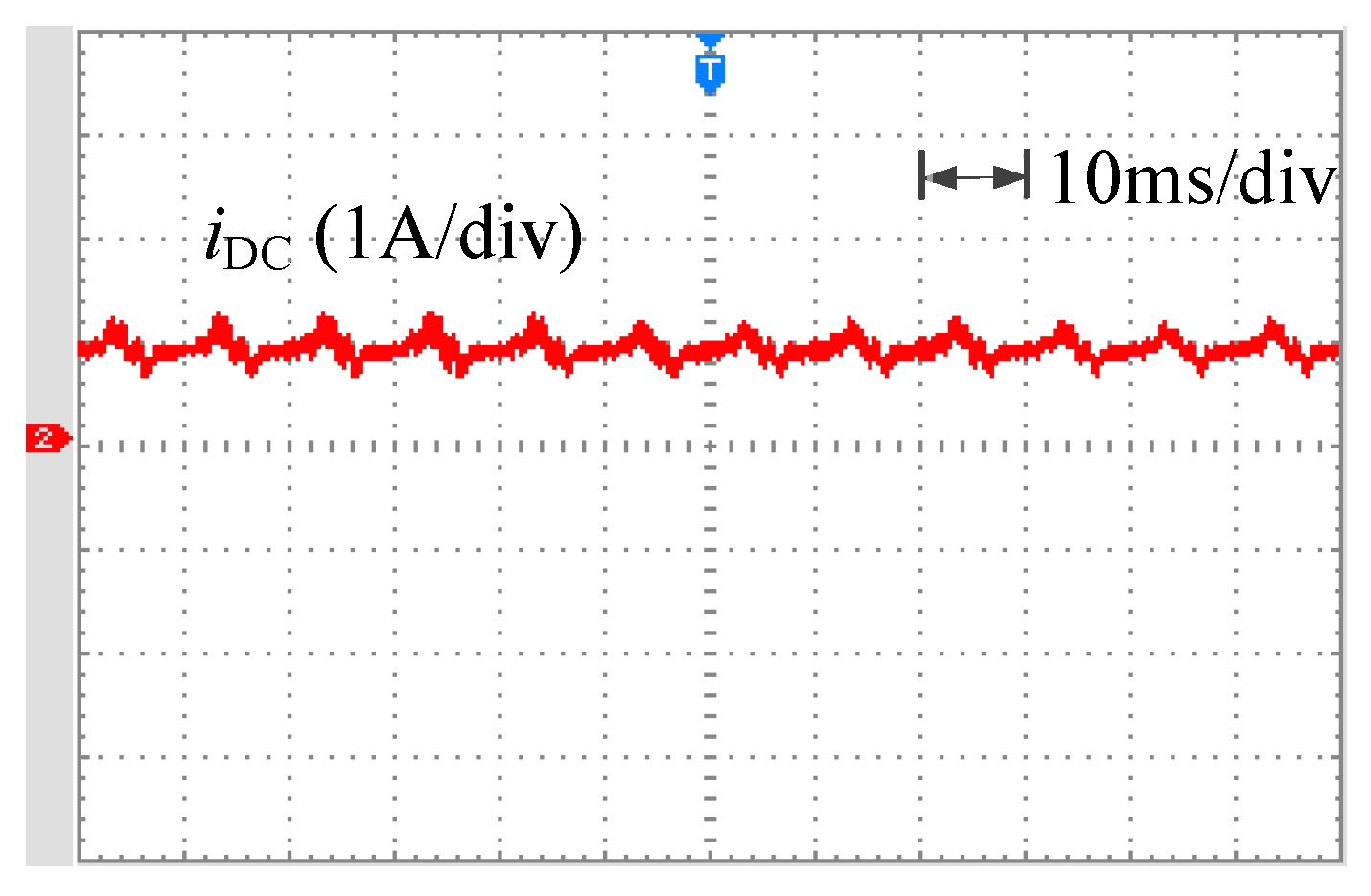
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- De Doncker, R.W.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high-power-density DC/DC converter for high-power applications. IEEE Trans. Ind. Appl. 1993, 27, 63–73. [Google Scholar] [CrossRef]
- Xue, L.; Shen, Z.; Boroyevich, D.; Mattavelli, P.; Diaz, D. Dual Active Bridge-Based Battery Charger for Plug-in Hybrid Electric Vehicle With Charging Current Containing Low Frequency Ripple. IEEE Trans. Power Electron. 2015, 30, 7299–7307. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Ni, F.-M.; Lee, T.-L. Hybrid Modulation of Bidirectional Three-Phase Dual-Active-Bridge DC Converters for Electric Vehicles. Energies 2016, 9, 492. [Google Scholar] [CrossRef]
- Wang, W.; Ruan, X.; Wang, X. A novel second harmonic current reduction method for dual active bridge used in photovoltaic power system. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013. [Google Scholar]
- Sathishkumar, P.; Himanshu; Piao, S.; Khan, M.A.; Kim, D.-H.; Kim, M.-S.; Jeong, D.-K.; Lee, C.; Kim, H.-J. A Blended SPS-ESPS Control DAB-IBDC Converter for a Standalone Solar Power System. Energies 2017, 10, 1431. [Google Scholar] [CrossRef]
- Vavilapalli, S.; Padmanaban, S.; Subramaniam, U.; Mihet-Popa, L. Power Balancing Control for Grid Energy Storage System in Photovoltaic Applications—Real Time Digital Simulation Implementation. Energies 2017, 10, 928. [Google Scholar] [CrossRef]
- Duman, T.; Marti, S.; Moonem, M.A.; Abdul Kader, A.A.R.; Krishnaswami, H. A Modular Multilevel Converter with Power Mismatch Control for Grid-Connected Photovoltaic Systems. Energies 2017, 10, 698. [Google Scholar] [CrossRef]
- Bekiarov, S.B.; Emadi, A. Uninterruptible power supplies: Classification, operation, dynamics, and control. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 10–14 March 2002. [Google Scholar]
- Jeong, D.K.; Ryu, M.H.; Kim, H.G.; Kim, H.J. Optimized Design of Bi-Directional Dual Active Bridge Converter for Low-Voltage Battery Charger. J. Power Electron. 2014, 14, 468–477. [Google Scholar] [CrossRef]
- Sha, D.; Xu, G.; Xu, Y. Utility Direct Interfaced Charger/Discharger Employing Unified Voltage Balance Control for Cascaded H-Bridge Units and Decentralized Control for CF-DAB Modules. IEEE Trans. Ind. Electron. 2017, 64, 7831–7841. [Google Scholar] [CrossRef]
- Lopes, J.A.P.; Soares, F.J.; Almeida, P.M.R. Integration of Electric Vehicles in the Electric Power System. Proc. IEEE 2011, 99, 168–183. [Google Scholar] [CrossRef]
- Fontes, G.; Turpin, C.; Astier, S.; Meynard, T.A. Interactions between Fuel Cells and Power Converters: Influence of Current Harmonics on a Fuel Cell Stack. IEEE Trans. Power Electron. 2007, 22, 670–678. [Google Scholar] [CrossRef]
- Shimizu, T.; Jin, Y.; Kimura, G. DC ripple current reduction on a single-phase PWM voltage-source rectifier. IEEE Trans. Ind. Appl. 2000, 36, 1419–1429. [Google Scholar] [CrossRef]
- Tang, Y.; Blaabjerg, F. Power decoupling techniques for single-phase power electronics systems—An overview. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Qin, Z.; Tang, Y.; Loh, P.C.; Blaabjerg, F. Benchmark of AC and DC Active Power Decoupling Circuits for Second-Order Harmonic Mitigation in Kilowatt-Scale Single-Phase Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 15–25. [Google Scholar] [CrossRef]
- Al-Atrash, H.; Batarseh, I. Boost-Integrated Phase-Shift Full-Bridge Converter for Three-Port Interface. In Proceedings of the IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007. [Google Scholar]
- Li, W.; Xiao, J.; Zhao, Y.; He, X. PWM Plus Phase Angle Shift (PPAS) Control Scheme for Combined Multiport DC/DC Converters. IEEE Trans. Power Electron. 2012, 27, 1479–1489. [Google Scholar] [CrossRef]
- Malan, W.L.; Vilthgamuwa, D.M.; Walker, G.R.; Broadmeadow, M.A.H.; Thrimawithana, D.; Madawala, U. A single phase AC–DC bidirectional converter with integrated ripple steering. In Proceedings of the IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016. [Google Scholar]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC–DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Weerasinghe, D.S.B.; Madawala, U.K.; Thrimawithana, D.J.; Vilathgamuwa, D.M. A technique for improving grid side harmonic distortion of matrix converter based bi-directional IPT systems. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society (IECON), Vienna, Austria, 10–13 November 2013. [Google Scholar]
- Weerasinghe, S.; Madawala, U.K.; Thrimawithana, D.J. A Matrix Converter-Based Bidirectional Contactless Grid Interface. IEEE Trans. Power Electron. 2017, 32, 1755–1766. [Google Scholar] [CrossRef]
- Weerasinghe, S.; Thrimawithana, D.J.; Madawala, U.K. Modeling Bidirectional Contactless Grid Interfaces with a Soft DC-Link. IEEE Trans. Power Electron. 2015, 30, 3528–3541. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEEE Proc. Electric Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Fukuda, S.; Yoda, T. A novel current-tracking method for active filters based on a sinusoidal internal model [for PWM invertors]. IEEE Trans. Ind. Appl. 2001, 37, 888–895. [Google Scholar] [CrossRef]
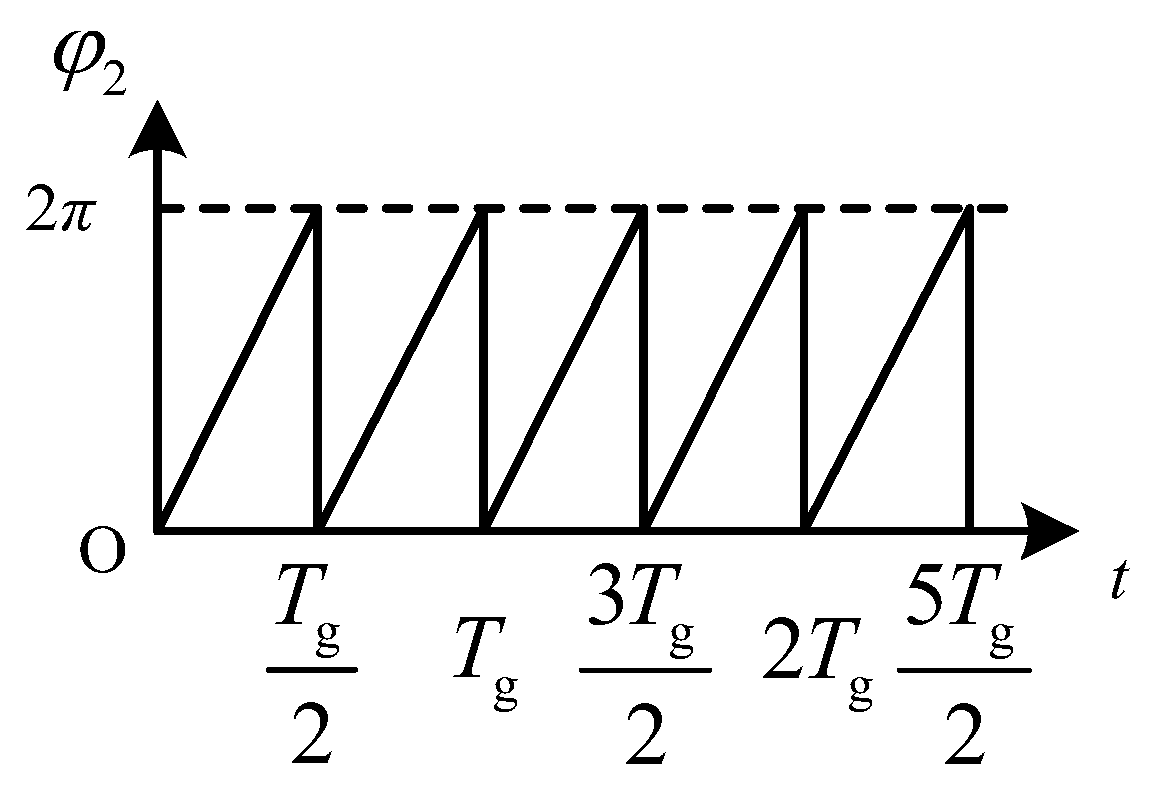
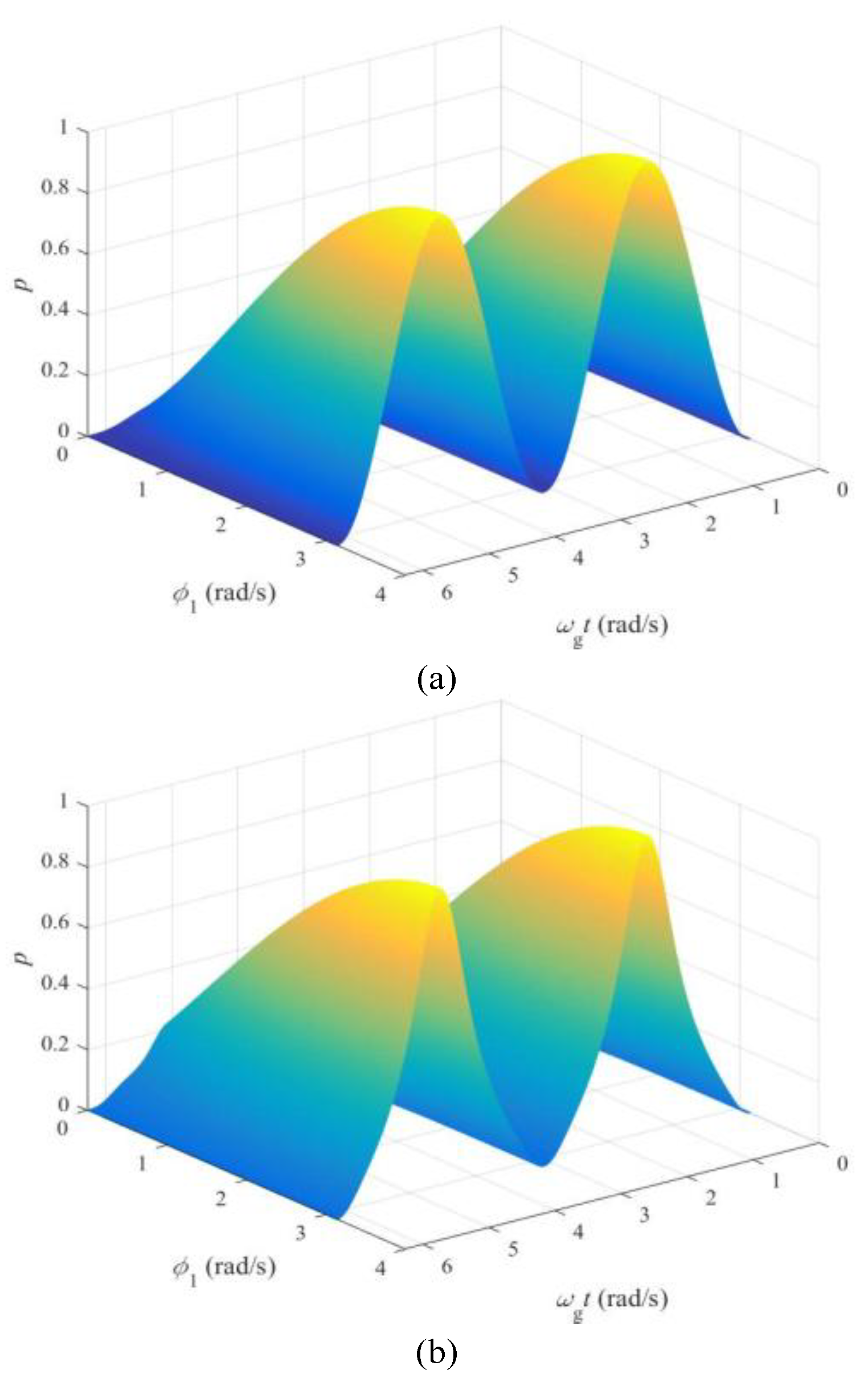
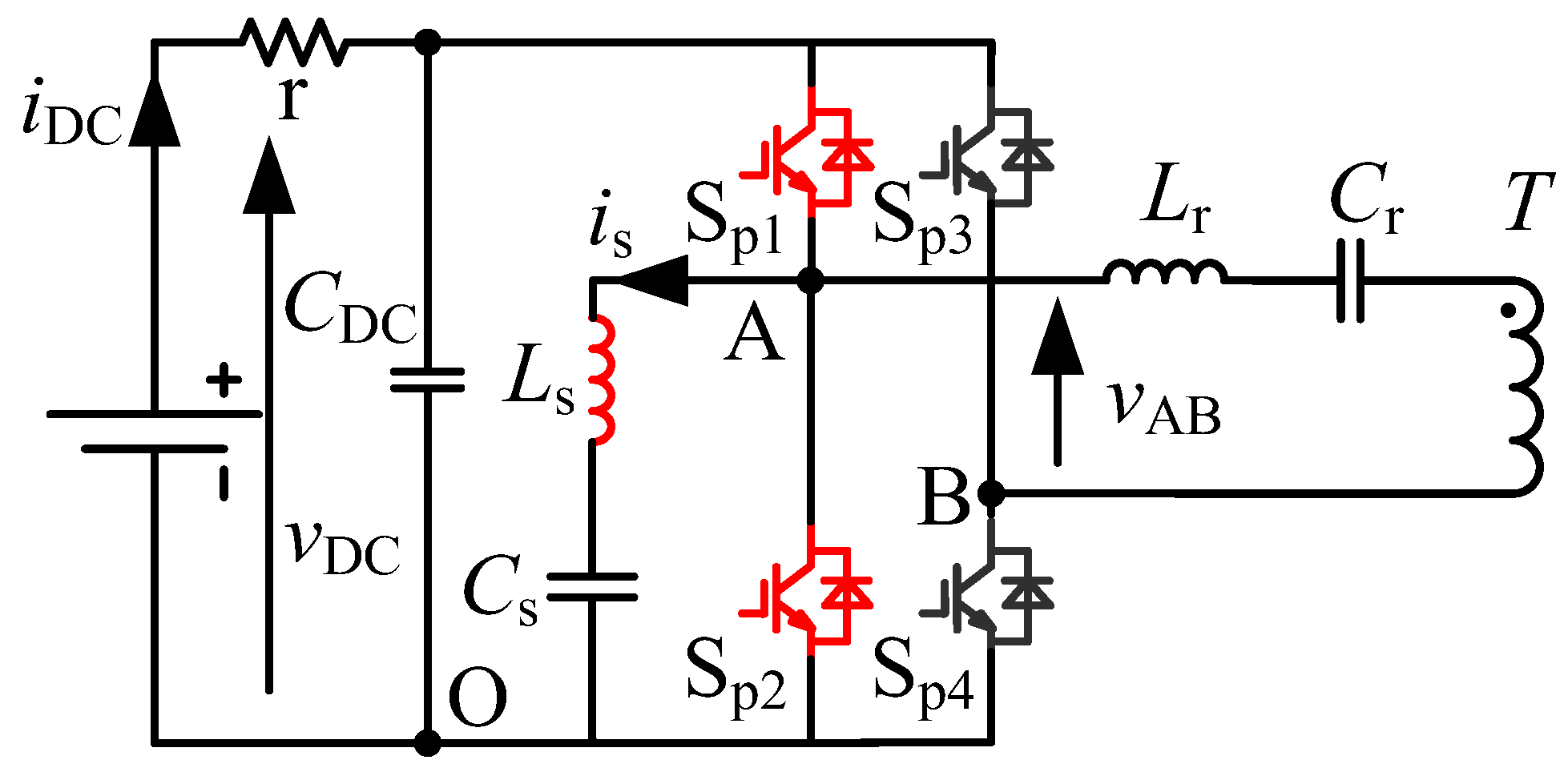
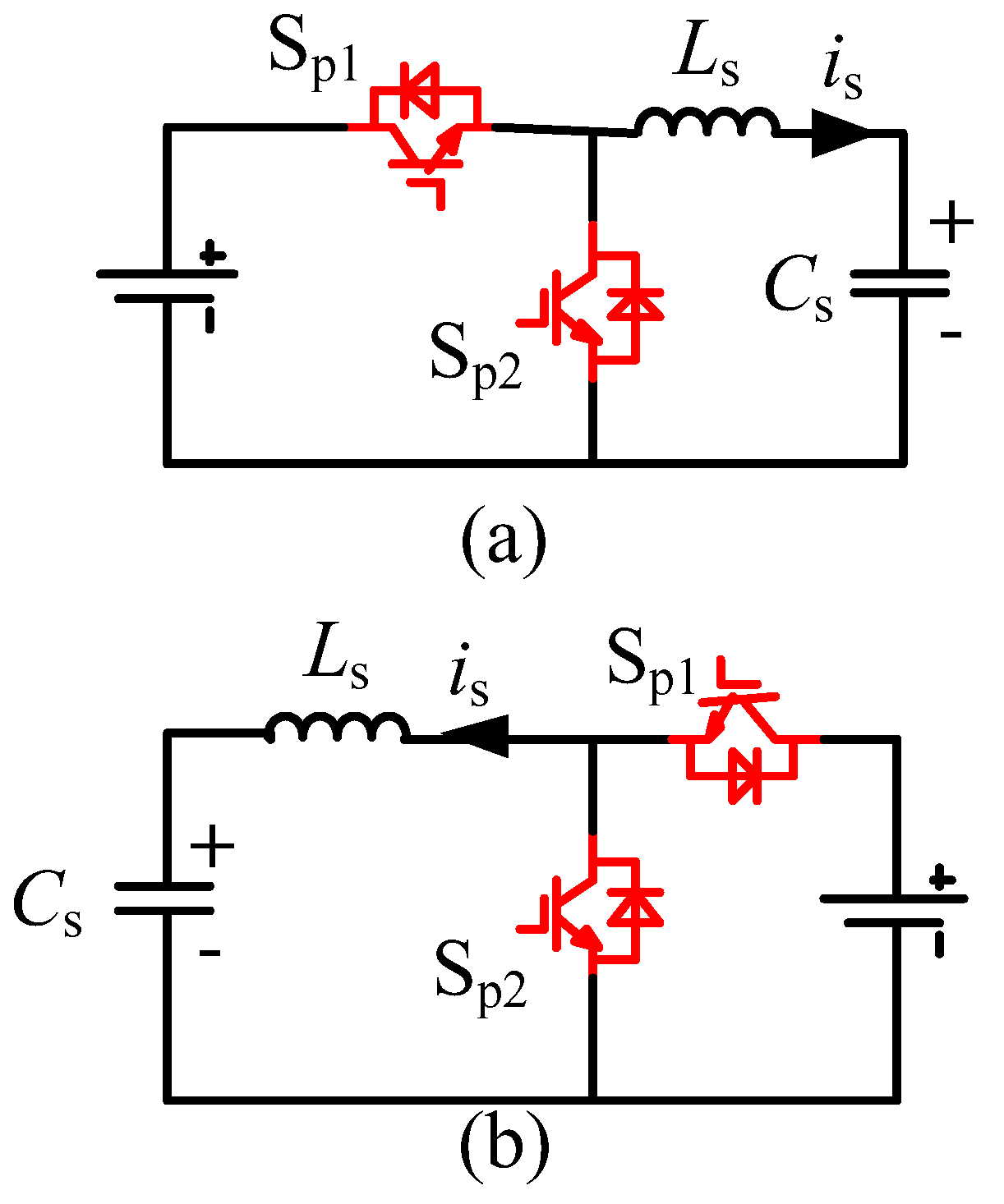
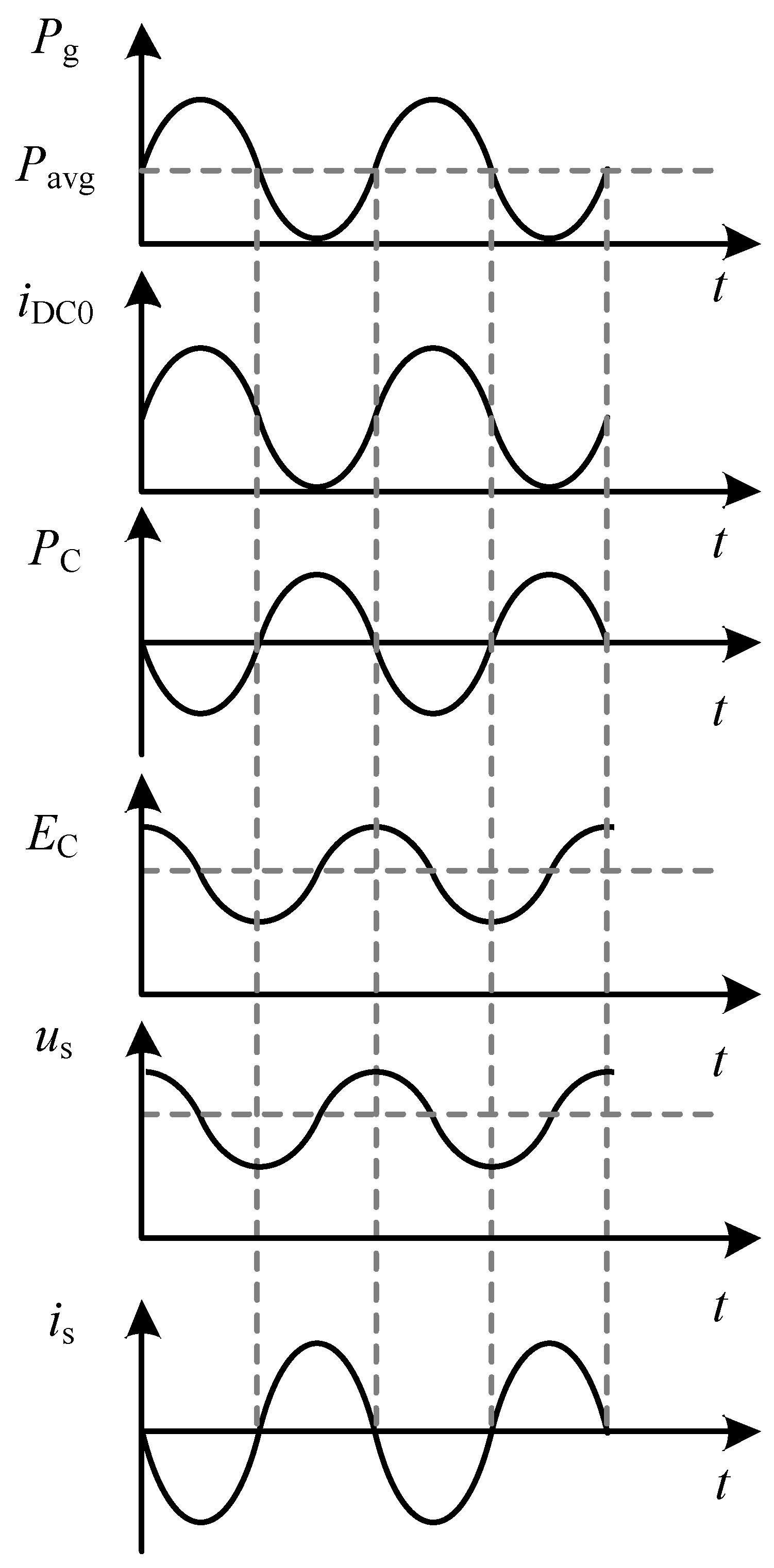


| Parameter | Value |
|---|---|
| vg | 18 V (Vg) |
| fg | 50 Hz |
| VDC | 30 V |
| fs | 20 kHz |
| Cs | 1900 µF |
| Cr | 1.4 µF |
| Lr | 102.5 µH |
| N | 1:1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, J.; Vilathgamuwa, M.; Yin, J.; Liu, Y.; Peng, J.; Jiang, H. Power Decoupling of a Single Phase DC-AC Dual Active Bridge Converter Based on an Integrated Bidirectional Buck/Boost Stage. Energies 2018, 11, 2746. https://doi.org/10.3390/en11102746
Hong J, Vilathgamuwa M, Yin J, Liu Y, Peng J, Jiang H. Power Decoupling of a Single Phase DC-AC Dual Active Bridge Converter Based on an Integrated Bidirectional Buck/Boost Stage. Energies. 2018; 11(10):2746. https://doi.org/10.3390/en11102746
Chicago/Turabian StyleHong, Jiatu, Mahinda Vilathgamuwa, Jian Yin, Yitao Liu, Jianchun Peng, and Hui Jiang. 2018. "Power Decoupling of a Single Phase DC-AC Dual Active Bridge Converter Based on an Integrated Bidirectional Buck/Boost Stage" Energies 11, no. 10: 2746. https://doi.org/10.3390/en11102746
APA StyleHong, J., Vilathgamuwa, M., Yin, J., Liu, Y., Peng, J., & Jiang, H. (2018). Power Decoupling of a Single Phase DC-AC Dual Active Bridge Converter Based on an Integrated Bidirectional Buck/Boost Stage. Energies, 11(10), 2746. https://doi.org/10.3390/en11102746






