Conceptual Design of Operation Strategies for Hybrid Electric Aircraft
Abstract
:1. Introduction
2. Propulsion Technology
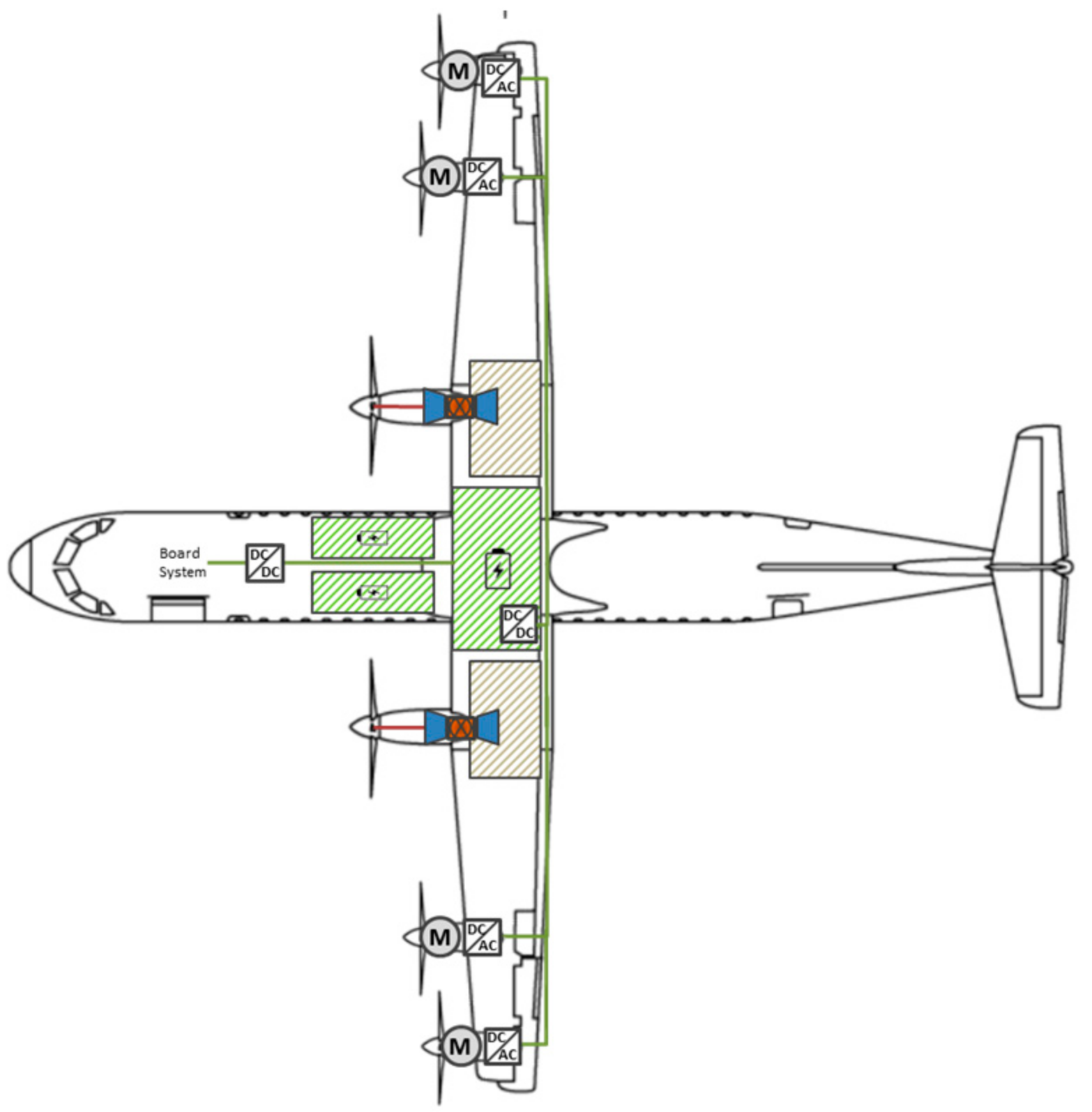
2.1. Propulsion Architecture
2.2. Scope of Propulsion Components
2.2.1. Conventional Propulsion Components
2.2.2. Electric Propulsion Components
2.3. Sizing and Operation Strategy
2.3.1. Degree of Hybridization (DoH)
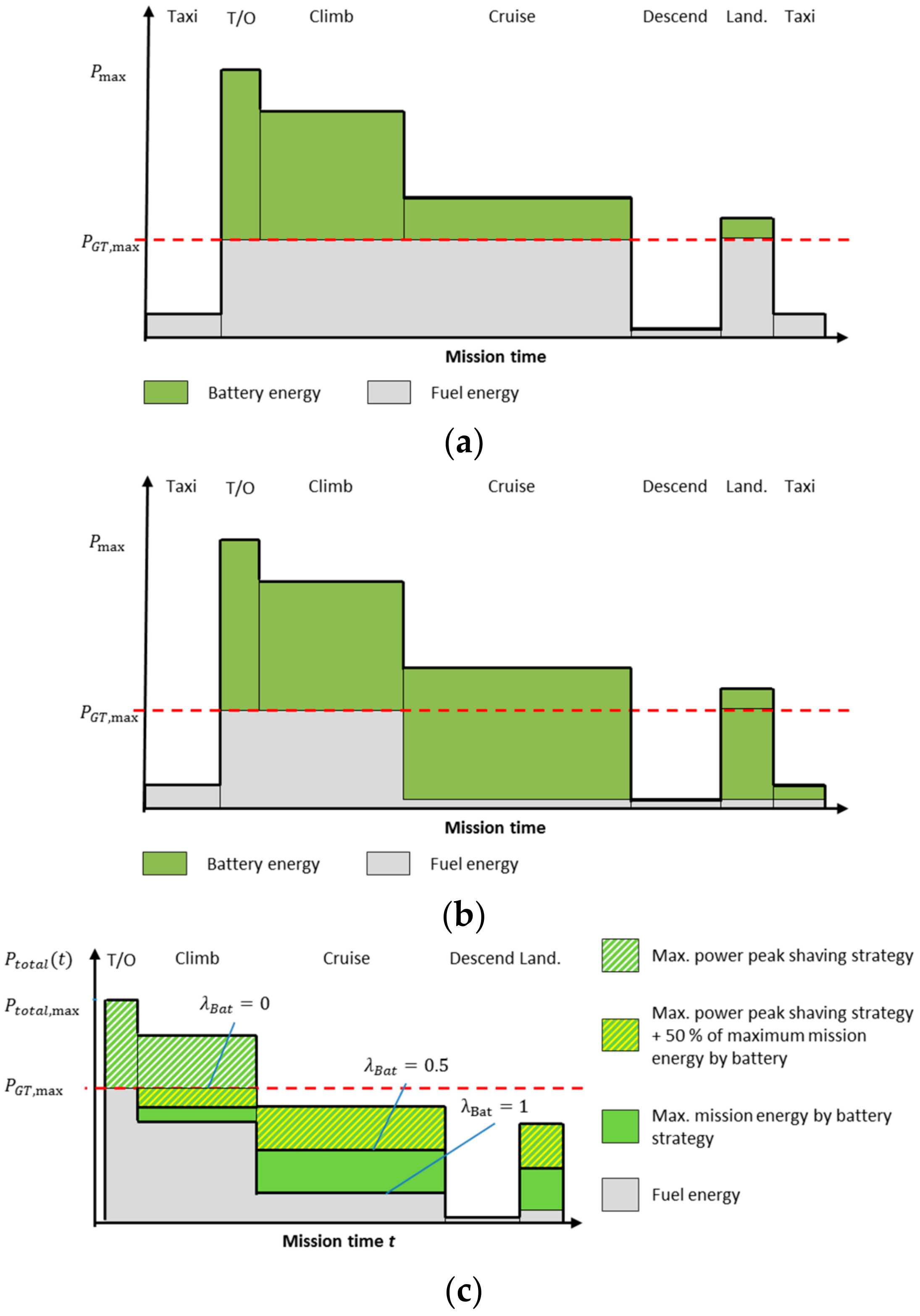
2.3.2. Battery Energy Strategy
2.3.3. Reserve Mission
2.4. Figures of Merit
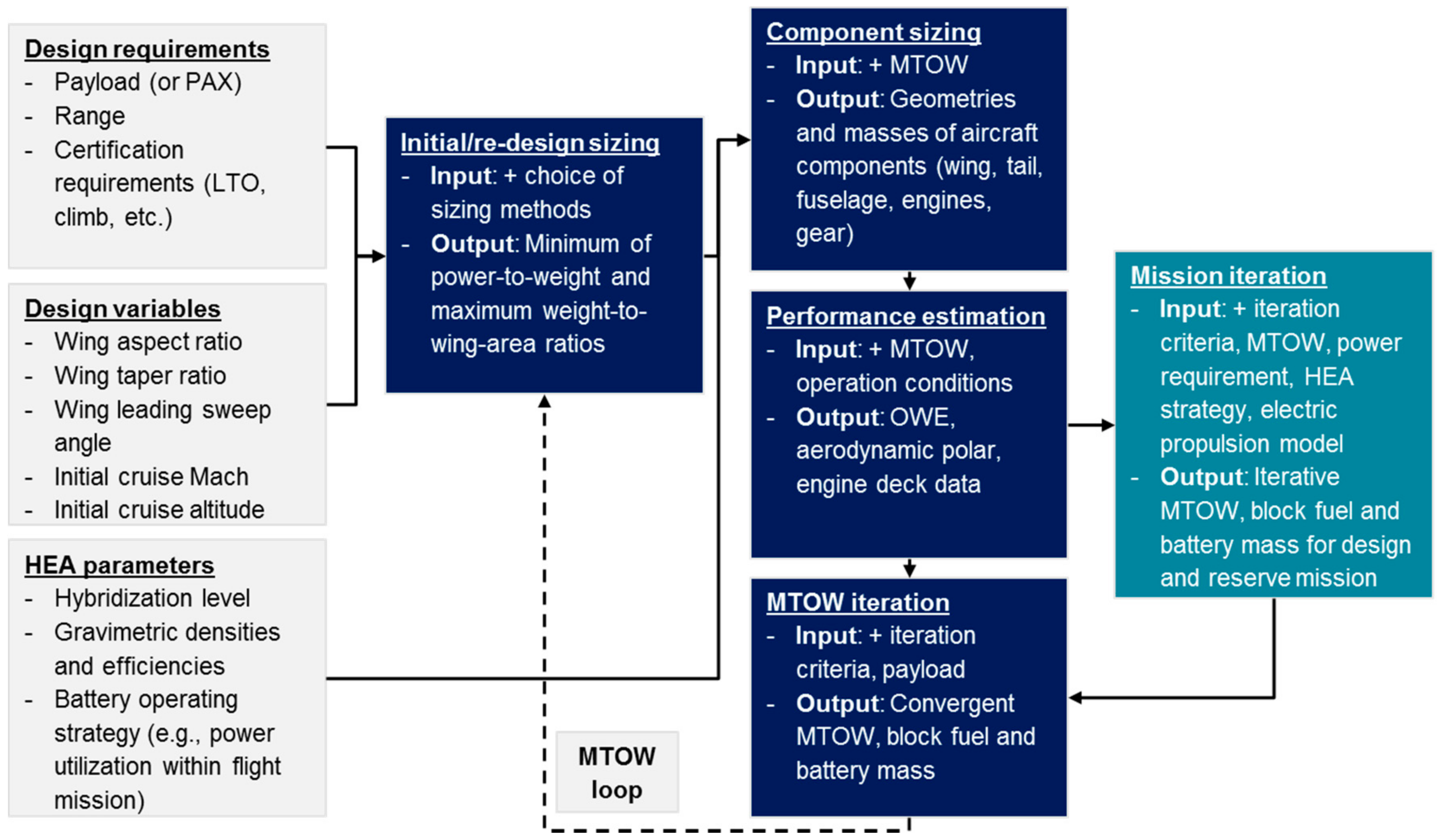
3. Simulation Methods
3.1. Aircraft Top-Level Requirements
3.2. Propulsion Parameters
3.3. Simulation Structure
3.4. Validation and Verification
4. Results
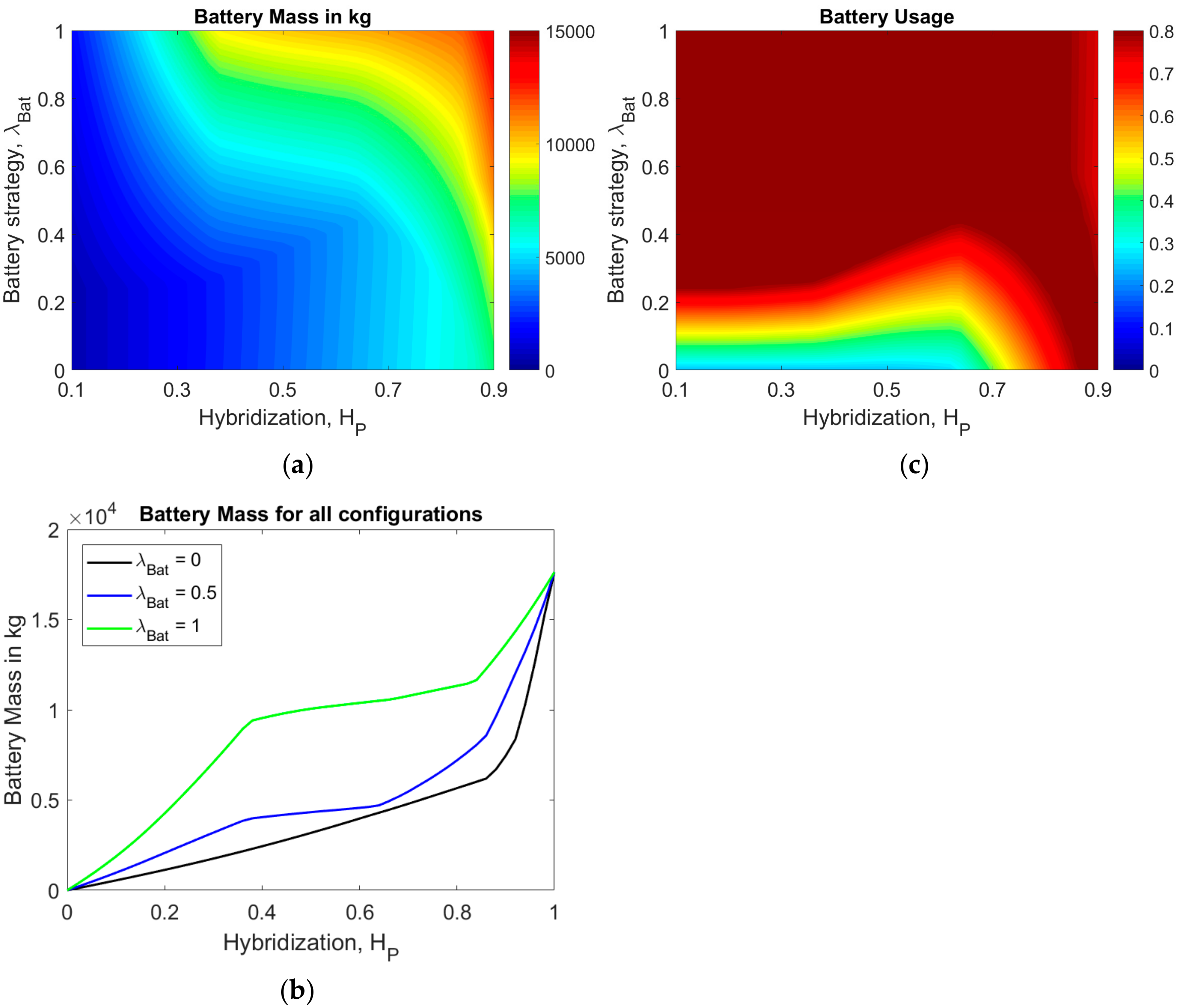
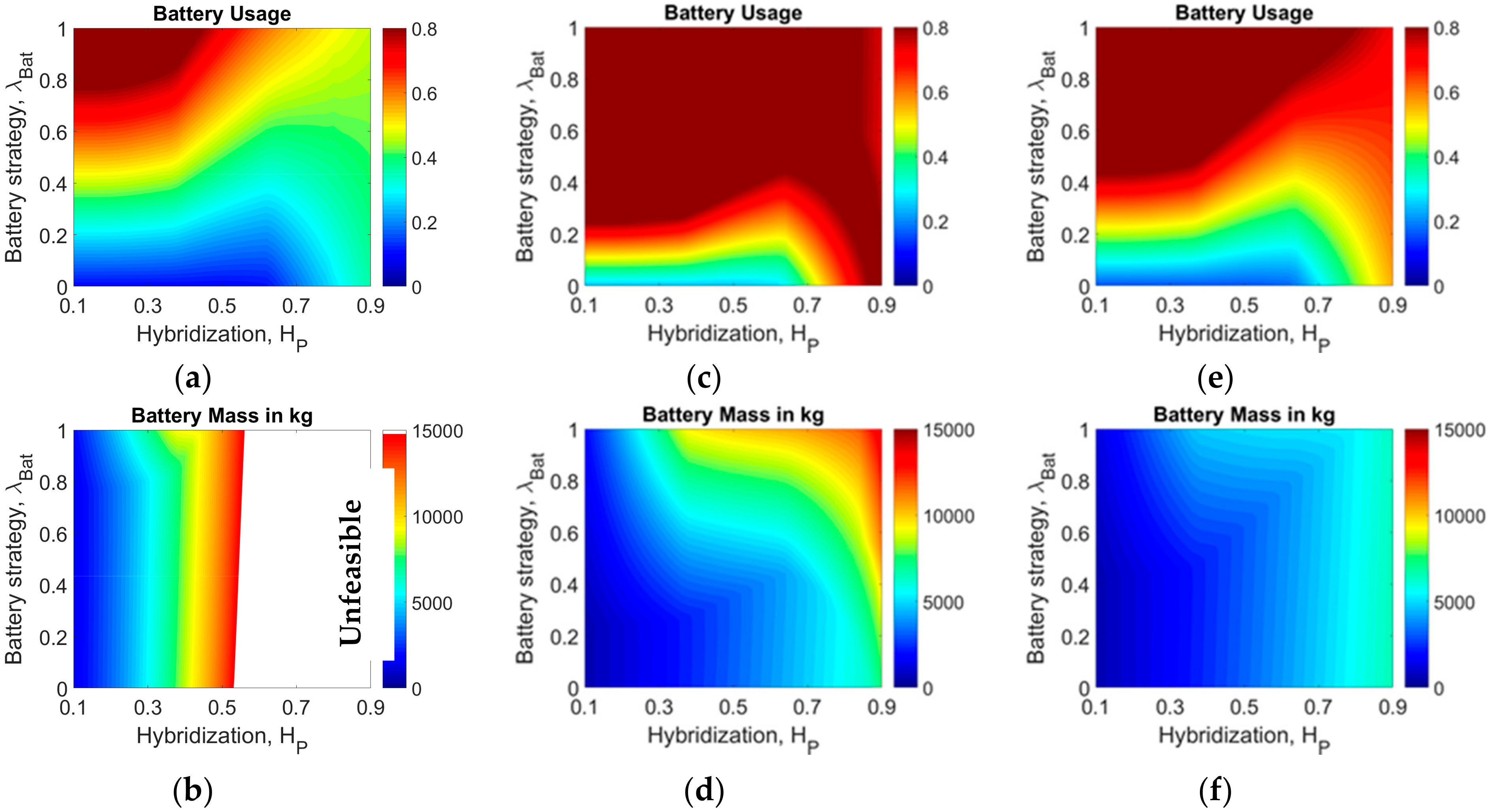
4.1. Fixed Battery Simulation
4.1.1. Battery Parameters
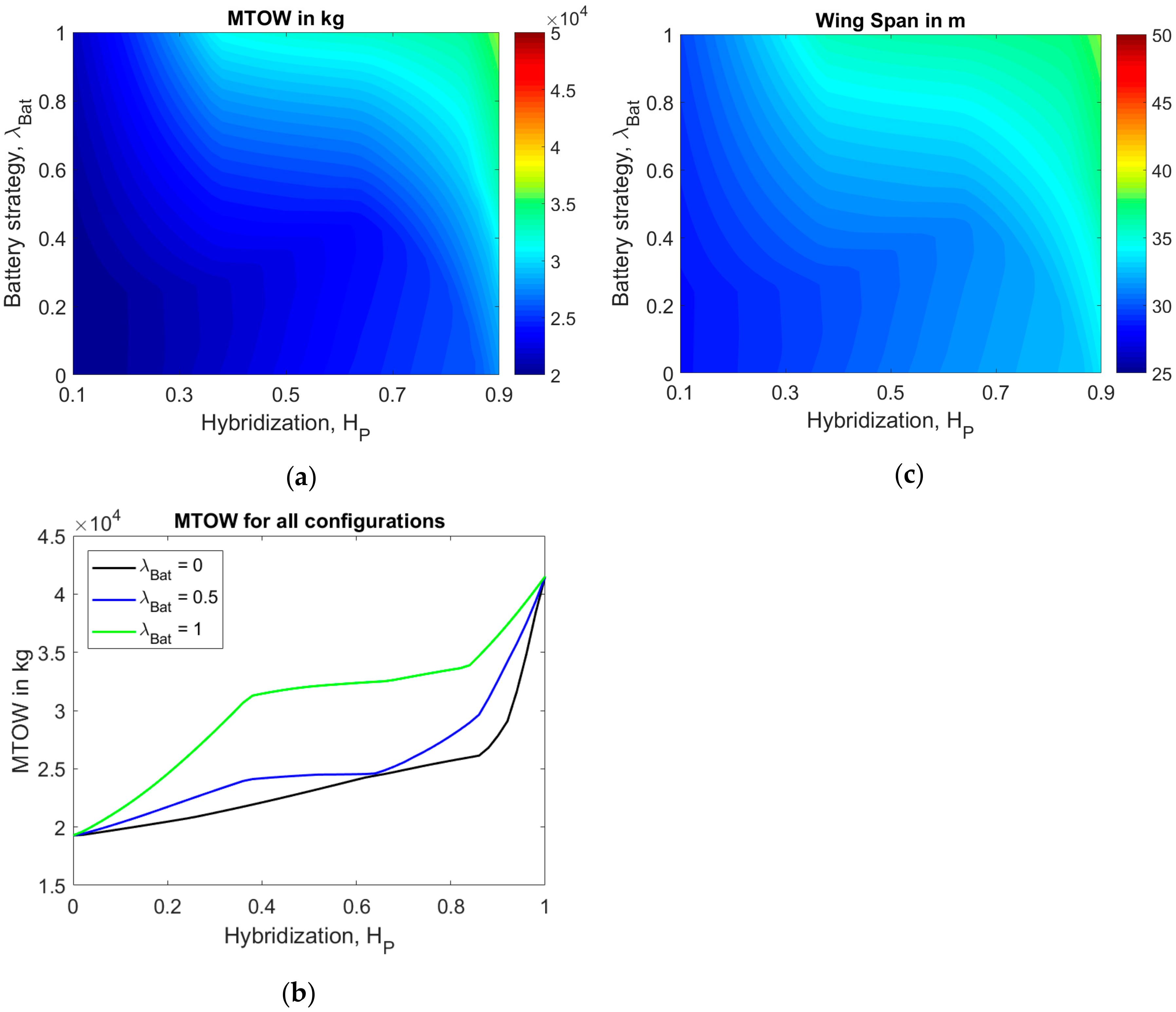
4.1.2. Impact on OAD
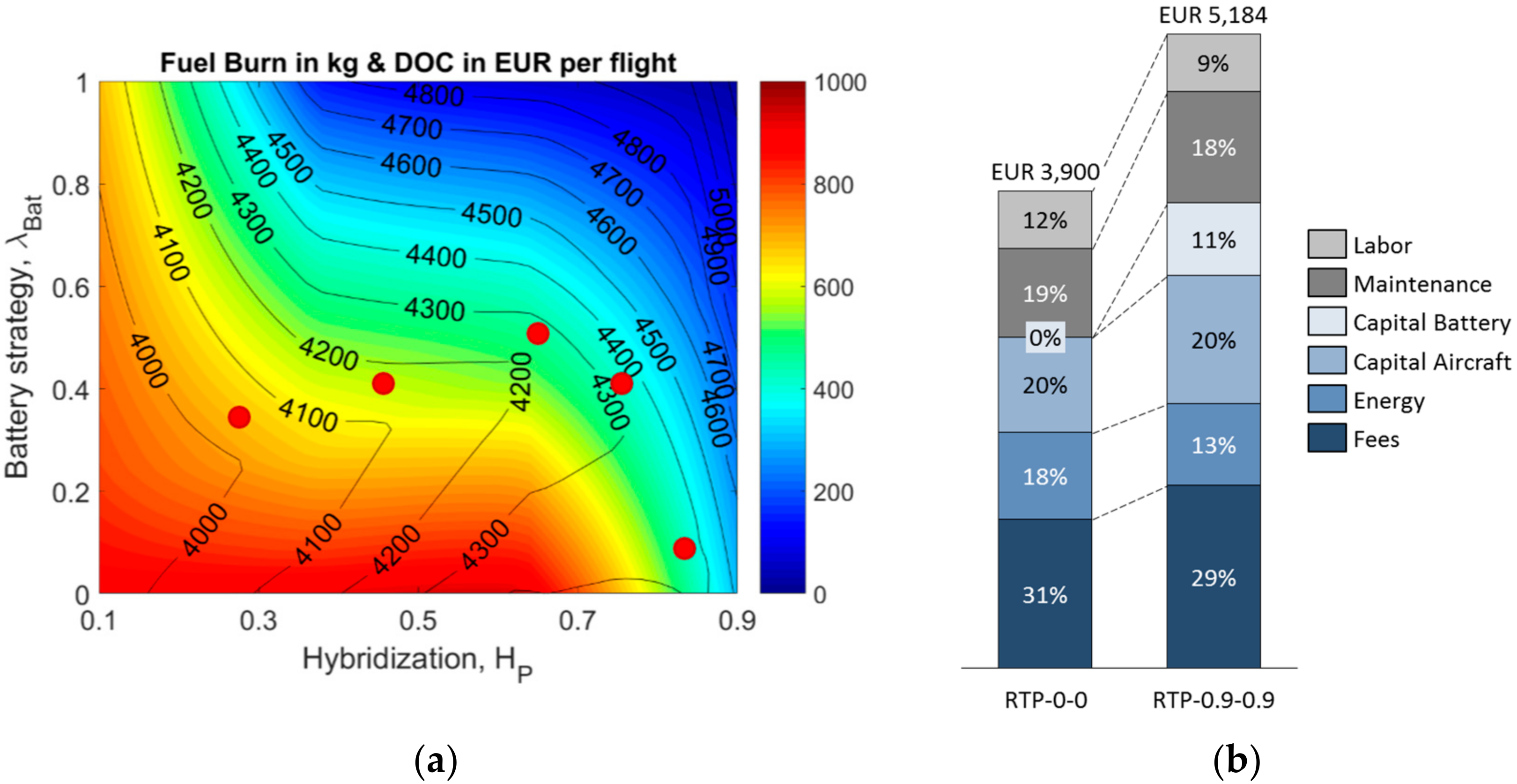
4.1.3. Impact on Figures of Merit
4.2. Different Batteries
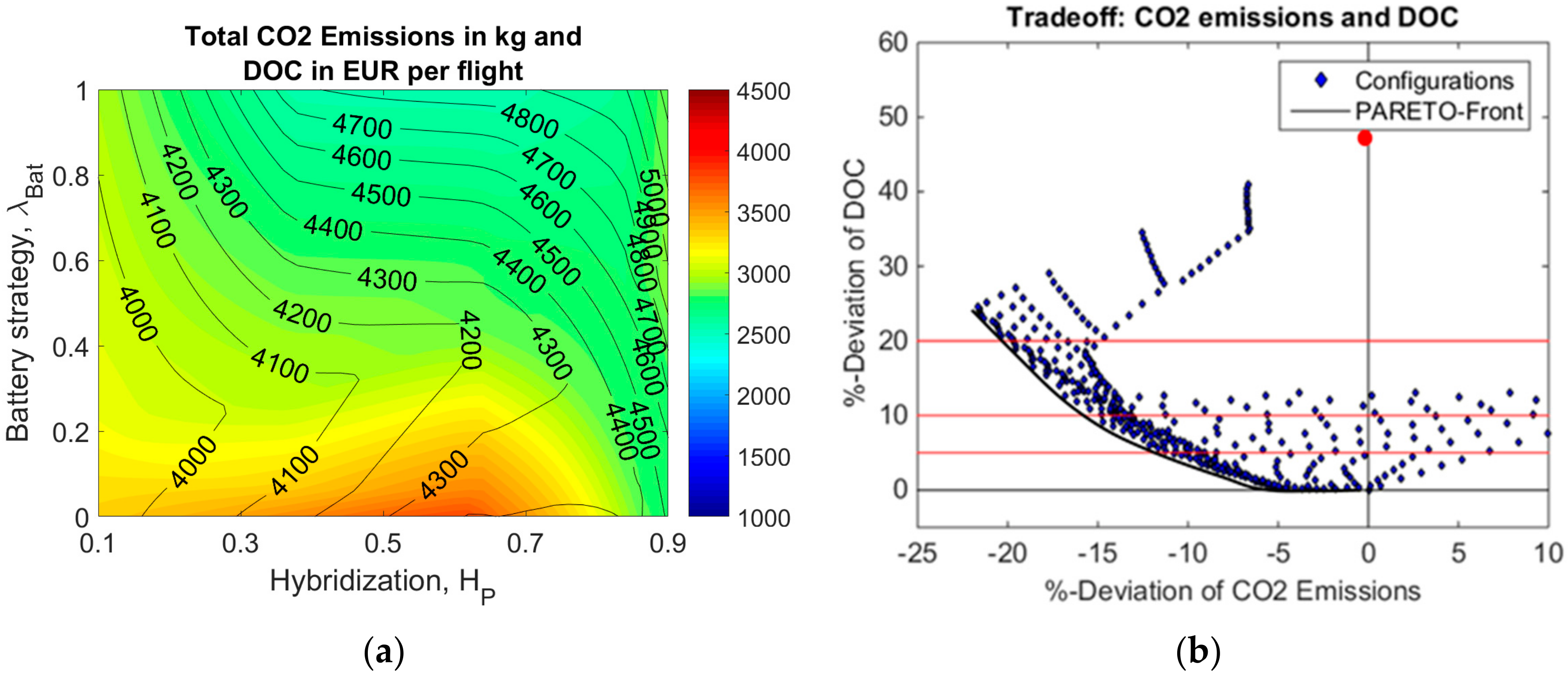
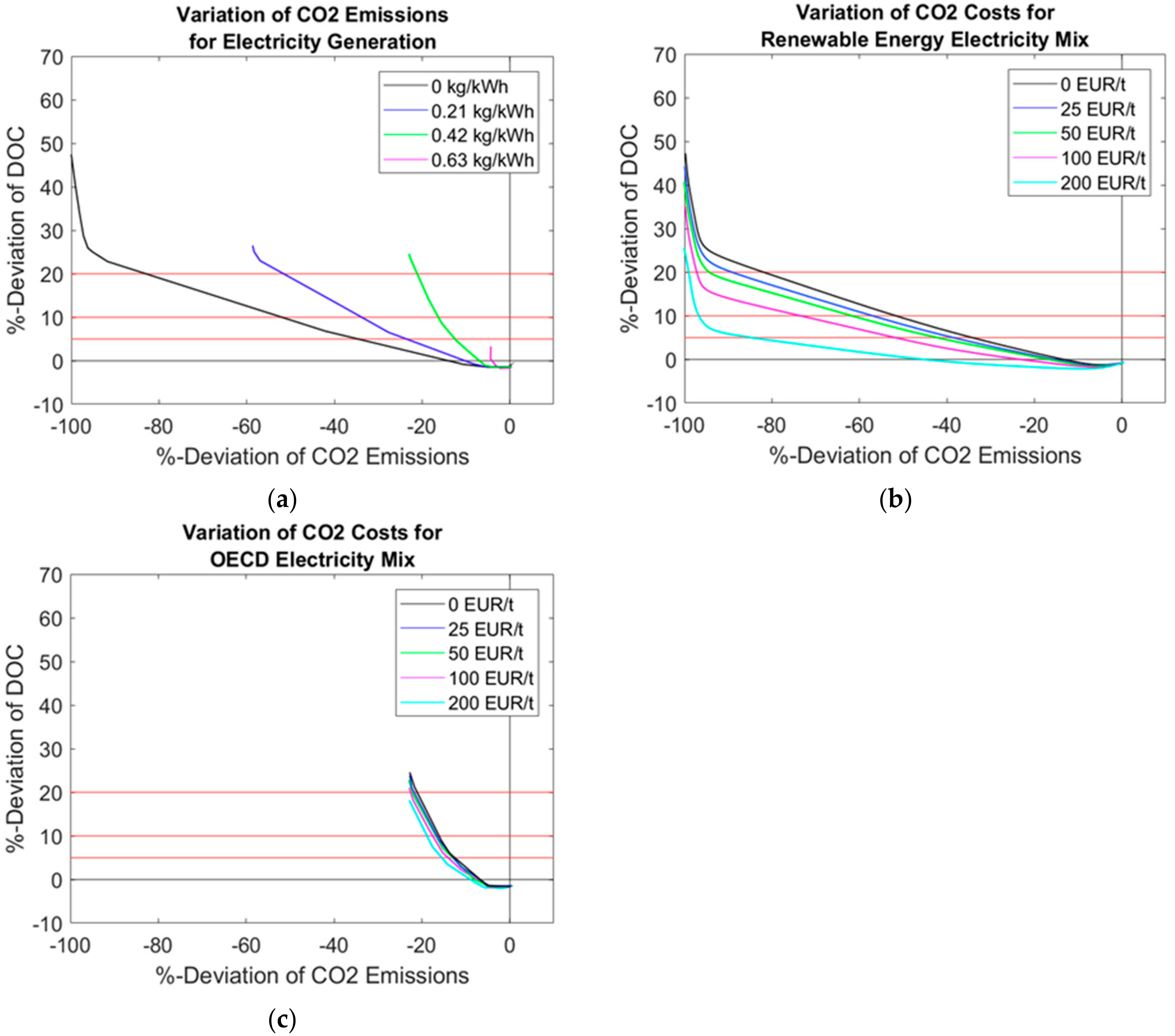
5. Environmental Impact and Sensitivity Studies
6. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ATM | Air traffic management |
| DOC | Direct operating costs |
| DoH | Degree of hybridization |
| FEA | Full electric aircraft |
| HEA | Hybrid electric aircraft |
| HTS | High-temperature superconducting |
| LTO | Landing and takeoff |
| MDO | Multidisciplinary design optimization |
| MTOW | Maximum takeoff weight |
| OAD | Overall aircraft design |
| OEI | One engine inoperative |
| OWE | Operating weight empty |
| P/E-ratio | Power-to-energy-ratio |
| PMAD | Power management and distribution |
| PSFC | Power specific fuel consumption |
| RTP | Regional turboprop |
| SOC | State of charge |
| Symbols | |
| Degree of hybridization | |
| Sea level maximum power | |
| Battery power | |
| Electric motor power | |
| Gas turbine power | |
| Battery strategy parameter | |
| Efficiency of total electric propulsion system | |
| Air density ratio |
Appendix A
Appendix A.1. Total DOC
Appendix A.2. Energy
Appendix A.3. Labor
Appendix A.4. Maintenance
Appendix A.5. Capital
| Components | Price p | Spare Parts Factor k | Source |
|---|---|---|---|
| Electric motor | EUR 150/kW | 0.2 | [70,71] |
| Inverter/converter | EUR 75/kW | 0.2 | [72,73] |
| Electric cable | Not considered 1 | - | - |
| Battery 2 (high power Li-S) | EUR 150/kW | - | [74] |
| Airframe | 1595.30 EUR/kg | 0.1 | [46,69] |
| Gas turbine | 551.50 EUR/kW | 0.3 | [68] |
Appendix A.6. Fees
References
- European Commission. Flightpath 2050—Europe’s Vision for Aviation; European Commission: Luxembourg City, Luxembourg, 2011. [Google Scholar]
- Boeing. Current Market Outlook 2016–2035; Boeing: Chicago, IL, USA, 2016. [Google Scholar]
- Airbus. Global Market Forecast—Mapping Demand 2016/2035; Airbus: Toulouse, France, 2016. [Google Scholar]
- Heinemann, P.; Schmidt, M.; Jeßberger, C.; Will, F.; Kaiser, S.; Hornung, M. Sizing implications of a regional aircraft for inner-city operations. Aircr. Eng. Aerosp. Technol. 2017, 89, 520–534. [Google Scholar] [CrossRef]
- Kuhn, H.; Seitz, A.; Lorenz, L.; Isikveren, A.T.; Sizmann, A. Progress and perspectives of electric air transport. In Proceedings of the 28th Congress of the International Council of the Aeronautical Sciences ICAS, Brisbane, Australia, 23–28 September 2012; Volume 6, pp. 4886–4899. [Google Scholar]
- Bijewitz, J.; Seitz, A.; Isikveren, A.T.; Hornung, M. Multi-Disciplinary Design Investigation of Propulsive Fuselage Aircraft Concepts. Aircr. Eng. Aerosp. Technol. 2016, 88, 257–267. [Google Scholar] [CrossRef]
- Isikveren, A.T.; Seitz, A.; Bijewitz, J.; Mirzoyan, A.; Isyanov, A.; Grenon, R.; Atinault, O.; Godard, J.-L.; Stueckl, S. Distributed Propulsion and Ultra-high By-Pass Rotor Study at Aircraft Level. Aeronaut. J. 2015, 119, 1327–1376. [Google Scholar] [CrossRef]
- Pornet, C.; Gologan, C.; Vratny, P.C.; Seitz, A.; Schmitz, O.; Isikveren, A.T.; Hornung, M. Methodology for Sizing and Performance Assessment of Hybrid Energy Aircraft. J. Aircr. 2014, 52, 1–12. [Google Scholar]
- Isikveren, A.T.; Kaiser, S.; Pornet, C.; Vratny, P.C. Pre-design strategies and sizing techniques for dual-energy aircraft. Aircr. Eng. Aerosp. Technol. 2014, 86, 525–542. [Google Scholar] [CrossRef]
- Isikveren, A.T.; Seitz, A.; Vratny, P.C.; Pornet, C.; Plötner, K.O.; Hornung, M. Conceptual studies of universally-electric systems architectures suitable for transport aircraft. In Proceedings of the Dtscher Luft-und Raumfahrt Kongress, Berlin, Germany, 10–12 September 2012. [Google Scholar]
- Stoll, A.M.; Bevirt, J.; Moore, M.D.; Fredericks, W.J.; Borer, N.K. Drag Reduction Through Distributed Electric Propulsion. In Proceedings of the 14th AIAA Aviation Technology, Integration, and Operations Conference, Atlanta, GA, USA, 16–20 June 2014; pp. 1–10. [Google Scholar]
- Welstead, J.; Felder, J.L. Conceptual Design of a Single-Aisle Turboelectric Commercial Transport with Fuselage Boundary Layer Ingestion. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; pp. 1–17. [Google Scholar]
- Antcliff, K.R.; Capristan, F.M. Conceptual Design of the Parallel Electric-Gas Architecture with Synergistic Utilization Scheme (PEGASUS) Concept. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017; pp. 1–15. [Google Scholar]
- Antcliff, K.R.; Guynn, M.D.; Marien, T.V.; Wells, D.P.; Schneider, S.J.; Tong, M.J. Mission Analysis and Aircraft Sizing of a Hybrid-Electric Regional Aircraft. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; pp. 1–18. [Google Scholar]
- Strack, M.; Chiozzotto, G.P.; Iwanizki, M.; Plohr, M.; Kuhn, M. Conceptual Design Assessment of Advanced Hybrid Electric Turboprop Aircraft Configurations. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017; pp. 1–20. [Google Scholar]
- Van Bogaert, J. Assessment of Potential Fuel Saving Benefits of Hybrid-Electric Regional Aircraft. Master’s Thesis, TU Delft, Delft, The Netherlands, 2015. [Google Scholar]
- Stückl, S.; van Toor, J.; Lobentanzer, H. VOLTAIR-The All Electric Propulsion Concept Platform—A Vision for Atmospheric Friendly Flight. In Proceedings of the 28th International Congress of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012; pp. 1–11. [Google Scholar]
- Bombardier. Market Forecast 2014–2033; Bombardier: Valcourt, QC, Canada, 2014. [Google Scholar]
- Madavan, N.; Heidmann, J.; Bowman, C.; Kascak, P.; Jankovsky, A.; Jansen, R. A NASA Perspective on Electric Propulsion Technologies for Commercial Aviation. In Proceedings of the Workshop on Technology Roadmap for Large Electric Machines, Urbana-Champaign, IL, USA, 5–6 April 2016. [Google Scholar]
- Moore, M.D.; Fredericks, B. Misconceptions of Electric Propulsion Aircraft and their Emergent Aviation Markets. In Proceedings of the 52nd Aerospace Sciences Meeting, AIAA SciTech Forum, National Harbor, MD, USA, 13–17 January 2014; pp. 1–17. [Google Scholar]
- ATR Aircraft. The ATR-600 Series: The Most Economical & Ecological Way to Fly Short-Haul Connections; ATR DC/E Mark: Blagnac Cedex, France, 2008. [Google Scholar]
- Hepperle, M. Aspects of Distributed Propulsion—A View on Regional Aircraft. In Proceedings of the Symposium Elektrisches Fliegen, Stuttgart, Germany, 18–19 February 2016. [Google Scholar]
- Propfe, B.; Redelbach, M.; Santini, D.J.; Friedrich, H. Cost Analysis of Plug-in Hybrid Electric Vehicles including Maintenance & Repair Costs and Resale Values. In Proceedings of the EVS26 International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium, Los Angeles, CA, USA, 6–9 May 2012. [Google Scholar]
- Hepperle, M. Electric Flight-Potential and Limitations. In Proceedings of the Energy Efficient Technologies and Concepts of Operation, Lisbon, Portugal, 22–24 October 2012. [Google Scholar]
- Kuhn, H.; Sizmann, A. Fundamental Prerequisites for Electric Flying. In Proceedings of the Dtscher Luft-Und Raumfahrt Kongress, Berlin, Germany, 10–12 September 2012; pp. 1–8. [Google Scholar]
- Hosking, E.; Kenny, D.P.; Mccormick, R.I.; Moustapha, S.H.; Sampath, P.; Smailys, A.A. The PW lOO Engine: 20 Years of Gas Turbine Technology Evolution. In Proceedings of the RTO AVT Symposium on Design Principles and Methods for Aircraft Gas Turbine Engines, Toulouse, France, 11–15 May 1998. [Google Scholar]
- Seitz, A.; Isikveren, A.T.; Hornung, M. Electrically Powered Aero-Propulsion Systems. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 15–17 July 2013; pp. 1–16. [Google Scholar]
- Vratny, P.C.; Kuhn, H.; Hornung, M. Influences of voltage variations on electric power architectures for hybrid electric aircraft. CEAS Aeronaut. J. 2017, 8, 31–43. [Google Scholar] [CrossRef]
- Berg, F.; Palmer, J.; Miller, P.; Husband, M.; Dodds, G. HTS electrical system for a distributed propulsion aircraft. IEEE Trans. Appl. Supercond. 2015, 25, 1–5. [Google Scholar] [CrossRef]
- Sivasubramaniam, K.; Zhang, T.; Lokhandwalla, M.; Laskaris, E.T.; Bray, J.W.; Gerstler, B.; Shah, M.R.; Alexander, J.P. Development of a high speed HTS generator for airborne applications. IEEE Trans. Appl. Supercond. 2009, 19, 1656–1661. [Google Scholar] [CrossRef]
- Brown, G.V. Weights and Efficiencies of Electric Components of a Turboelectric Aircraft Propulsion System. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar]
- Kim, H.D.; Felder, J.L.; Tong, M.T.; Armstrong, M. Revolutionary Aeropropulsion Concept for Sustainable Aviation: Turboelectric Distributed Propulsion. In Proceedings of the 2013 International Society for Air Breathing Engines, Busan, Korea, 9–13 September 2013. [Google Scholar]
- Madavan, N. Hybrid-Electric and Distributed Propulsion Technologies for Large Commercial Air Transports: A NASA Perspective. Advanced Air Transport Technology Project. In Proceedings of the ISABE 2015, Phoenix, AZ, USA, 25–30 October 2015. [Google Scholar]
- Pornet, C.; Isikveren, A.T. Conceptual design of hybrid-electric transport aircraft. Prog. Aerosp. Sci. 2015, 79, 114–135. [Google Scholar] [CrossRef]
- Masson, P.J.; Breschi, M.; Tixador, P.; Luongo, C.A. Design of HTS axial flux motor for aircraft propulsion. IEEE Trans. Appl. Supercond. 2007, 17, 1533–1536. [Google Scholar] [CrossRef]
- Jones, C.E.; Norman, P.J.; Galloway, S.J.; Armstrong, M.J.; Bollman, A.M. Comparison of Candidate Architectures for Future Distributed Propulsion Aircraft. IEEE Trans. Appl. Supercond. 2016, 26, 1–9. [Google Scholar] [CrossRef]
- Masson, P.J.; Luongo, C.A. HTS machines for applications in all-electric aircraft. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–6. [Google Scholar]
- Teichel, S.H.; Dörbaum, M.; Misir, O.; Merkert, A.; Mertens, A.; Seume, J.R.; Ponick, B. Design considerations for the components of electrically powered active high-lift systems in civil aircraft. CEAS Aeronaut. J. 2014, 6, 49–67. [Google Scholar] [CrossRef]
- Gerssen-Gondelach, S.J.; Faaij, A.P.C. Performance of batteries for electric vehicles on short and longer term. J. Power Sources 2012, 212, 111–129. [Google Scholar] [CrossRef]
- Wild, M.; O’Neill, L.; Zhang, T.; Purkayastha, R.; Minton, G.; Marinescu, M.; Offer, G.J. Lithium sulfur batteries, a mechanistic review. Energy Environ. Sci. 2015, 8, 3477–3494. [Google Scholar] [CrossRef]
- Nagata, H.; Chikusa, Y. All-Solid-State Lithium-Sulfur Battery with High Energy and Power Densities at the Cell Level. Energy Technol. 2016, 4, 484–489. [Google Scholar] [CrossRef]
- Song, M.; Zhang, Y.; Chairns, E. A long-life, high-rate lithium/sulfur cell: A multifaceted approach to enhancing cell performance. Nano Lett. 2013, 13, 5891–5899. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Tao, L.; Markham, J.; Zhang, Y.; Tan, E.; Batan, L.; Biddy, M.; Wang, W.; Tao, L.; Zhang, Y.; et al. Review of Biojet Fuel Conversion Technologies; NREL: Golden, CO, USA, 2016; p. 98. [Google Scholar]
- International Energy Agency (IEA). Recent Trends in the OECD: Energy and CO2 Emissions; International Energy Agency (IEA): Paris, France, 2016. [Google Scholar]
- Bardenhagen, A.; Gobbin, A. Flugzeugentwurf II; Universität Stuttgart: Stuttgart, Germany, 2017. [Google Scholar]
- ATR Aircraft. ATR 72-600; ATR Aircraft: Blagnac Cedex, France, 2014. [Google Scholar]
- Federal Aviation Administration (FAA). Part 25—Airworthiness Standards: Transport Category Airplanes Subpart B. 2017. Available online: https://www.ecfr.gov/cgi-bin/text-idx?SID=caefbbc53bccf4e355983e23e3c168a6&mc=true&node=se14.1.25_1121&rgn=div8 (accessed on 28 August 2017).
- Gammeter, C.; Krismer, F.; Kolar, J.W. Weight and efficiency analysis of switched circuit topologies for modular power electronics in MEA. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 3640–3647. [Google Scholar]
- Kraytsberg, A.; Ein-Eli, Y. Review on Li-air batteries—Opportunities, limitations and perspective. J. Power Sources 2011, 196, 886–893. [Google Scholar] [CrossRef]
- Bradley, M.K.; Droney, C.K. Subsonic Ultra Green Subsonic Ultra Green Aircraft Research: Phase I Final Report; Technical Report; Boeing Research and Technology: Huntington Beach, CA, USA, 2011. [Google Scholar]
- Liu, Y.; Elham, A.; Horst, P.; Hepperle, M. Exploring vehicle level benefits of revolutionary technology progress via aircraft design and optimization. Energies 2018, 11, 166. [Google Scholar] [CrossRef]
- Westphal, C.W.; Heinze, W.; Horst, P. Multidisciplinary Integrated Preliminary Design Applied to Unconventional Aircraft Configuration. J. Aircr. 2008, 45, 581–592. [Google Scholar] [CrossRef]
- Risse, K.; Anton, E.; Lammering, T.; Franz, K.; Hoernschemeyer, R. An integrated environment for preliminary aircraft design and optimization. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar]
- Botero, E.; Wendorff, A.D.; MacDonald, T.; Variyar, A.; Vegh, J.M.; Lukaczyk, T.W.; Alonso, J.J.; Orra, T.H.; Ilario da Silva, C.R. SUAVE: An Open-Source Environment for Multi-Fidelity Conceptual Vehicle Design. In Proceedings of the 54th AIAA Aerospace Sciences Meeting: American Institute of Aeronautics and Astronautics (AIAA SciTech Forum), San Diego, CA, USA, 4–8 January 2016; pp. 1–16. [Google Scholar]
- Greitzer, E.M.; Bonnefoy, P.A.; delaRosaBlanco, E.; Dorbian, C.S.; Drela, M.; Hall, D.K.; Hansman, R.J.; Hileman, J.I.; Liebeck, R.H.; Lovegren, J. N + 3 Aircraft Concept Designs and Trade Studies, Final Report Structures, Weight, and Thermodynamic Cycles; Rep. CR—2010-216794; NASA: Hampton, VA, USA, 2010.
- Howe, D. Aircraft Conceptual Design Synthesis; John Wiley & Sons: Chichester, UK, 2000. [Google Scholar]
- Kurzke, J. GasTurb 12-Design and Off-Design Performance of Gas Turbines. 2012. Manual. Available online: http://www.gasturb.de/manual.html (accessed on 2 December 2017).
- ATR Aircraft. ATR Family; ATR Aircraft: Blagnac Cedex, France, 2014. [Google Scholar]
- Obert, E.; Slingerland, R.; Leusink, D.J.W.; van den Berg, T.; Koning, J.H.; van Tooren, M.J.L. Aerodynamic Design of Transport Aircraft; IOS Press: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Young, K.; Wang, C.; Wang, L.Y.; Strunz, K. Electric Vehicle Integration into Modern Power Networks; Springer: New York, NY, USA, 2013. [Google Scholar]
- Kato, Y.; Hori, S.; Saito, T.; Suzuki, K.; Hirayama, M.; Mitsui, A.; Yonemura, M.; Iba, H.; Kanno, R. High-power all-solid-state batteries using sulfide superionic conductors. Nat. Energy 2016, 1, 16030. [Google Scholar] [CrossRef]
- McConnachie, D.; Wollersheim, C.; Hansman, R.J. The Impact of Fuel Price on Airline Fuel Efficiency and Operations. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013; pp. 1–14. [Google Scholar]
- Franz, K. CeRAS Direct Operating Cost (DOC) Model. 2014. Available online: http://ceras.ilr.rwth-aachen.de/trac/wiki/CeRAS/ToolsAndMethodologies/DOC. (accessed on 2 December 2017).
- EIA. Annual Energy Outlook 2017. U.S. Energy Information Administration, 2017. Available online: https://www.eia.gov/outlooks/aeo/data/browser/#/?id=12-aeo2017&cases=ref2017~ref_no_cpp&sourcekey=0 (accessed on 30 August 2017).
- Nita, M.F. Aircraft Design Studies Based on the ATR 72; Hamburg University of Applied Sciences: Hamburg, Germany, 2008. [Google Scholar]
- Ali, S.; Hampson, N. Aviation Finance-Fasten Your Seatbelts. Available online: https://www.pwc.com/im/en/publications/assets/shipping-aircraft-space/pwc-aviation-finance-fastern-your-seat-belts-pdf.pdf (accessed on 30 August 2017).
- Lufthansa Group. Geschäftsbericht 2016; Lufthansa Group: Cologne, Germany, 2016. [Google Scholar]
- Forecast International. The Market for Aviation Turboprop Engines; Forecast International: Newtown, CT, USA, 2010. [Google Scholar]
- The Flying Engineer. Proud to Fly a Turboprop: Q400 vs. ATR72. Available online: http://theflyingengineer.com/aircraft/proud-to-fly-a-turboprop-q400-vs-atr72/ (accessed on 30 August 2017).
- Schiff, N.; Schiferl, R. Latest Developments in Superconducting Motors. 2000. Available online: http://www.machinedesign.com/motorsdrives/latest-developments-superconducting-motors (accessed on 30 August 2017).
- Sung, H.-J.; Park, M.; Go, B.-S.; Yu, I.-K. A study on the required performance of a 2G HTS wire for HTS wind power generators. Supercond. Sci. Technol. 2016, 29, 54001. [Google Scholar] [CrossRef]
- Kochhan, R.; Fuchs, S.; Reuter, B.; Burda, P.; Matz, S.; Lienkamp, M. An Overview of Costs for Vehicle Components, Fuels and Greenhouse Gas Emissions; Technische Universität München, Fakultät für Maschinenwesen, Lehrstuhl für Fahrzeugtechnik: Garching, Germany, 2014; pp. 1–19. [Google Scholar]
- Blanco, M.I. The economics of wind energy. Renew. Sustain. Energy Rev. 2009, 13, 1372–1382. [Google Scholar] [CrossRef]
- Hagen, M.; Hanselmann, D.; Ahlbrecht, K.; Maça, R.; Gerber, D.; Tübke, J. Lithium-Sulfur Cells: The Gap between the State-of-the-Art and the Requirements for High Energy Battery Cells. Adv. Energy Mater. 2015, 5. [Google Scholar] [CrossRef]
| Components | Gravimetric Densities | Efficiencies | Sources |
|---|---|---|---|
| Electric motor | 15 kW/kg | 95% | [30,33,34,35] |
| Inverter/converter | 20 kW/kg | 98% | [37,48] |
| Electric cable | 0.00324 kg/A/m 1 | 98.5% | [38] |
| Battery 1 (low power Li-S) | 0.65 kWh/kg | 90% | [16,39,40] |
| 0.4 kW/kg | |||
| Battery 2 (high power Li-S) | 0.65 kWh/kg | 90% | [39,40,41] |
| 1 kW/kg | |||
| Battery 3 (similar to Li-Air) | 1 kWh/kg | 90% | [17,49] |
| 1 kW/kg |
| Parameters | Original Data ATR-42 | Calculated Data | Deviation (%) |
|---|---|---|---|
| Passenger number | 48 | 48 | 0 |
| Design range (NM) | 800 | 800 | 0 |
| MTOW (kg) | 16,150 | 16,132 | −0.11 |
| OWE (kg) | 10,253 | 9266 | −9.63 |
| Wing mass (kg) | 1565 | 1558 | −0.45 |
| Fuselage mass (kg) | 2587 | 2394 | −7.46 |
| Vertical tail plane mass (kg) | 322 | 319 | −0.93 |
| Operation Strategy | Maximum Electric Power Requirement | Total Energy Requirement 1 | P/E-Ratio |
|---|---|---|---|
| Full mission energy | 4 MW | 2.6 MWh | 1.54 kW/kWh |
| Takeoff power peak shaving | 0.3 × 4 MW = 1.2 MW | 0.1 MWh | 12 kW/kWh |
| Takeoff and climb power peak shaving | 0.6 × 4 MW = 2.4 MW | 0.5 MWh | 4.8 kW/kWh |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoelzen, J.; Liu, Y.; Bensmann, B.; Winnefeld, C.; Elham, A.; Friedrichs, J.; Hanke-Rauschenbach, R. Conceptual Design of Operation Strategies for Hybrid Electric Aircraft. Energies 2018, 11, 217. https://doi.org/10.3390/en11010217
Hoelzen J, Liu Y, Bensmann B, Winnefeld C, Elham A, Friedrichs J, Hanke-Rauschenbach R. Conceptual Design of Operation Strategies for Hybrid Electric Aircraft. Energies. 2018; 11(1):217. https://doi.org/10.3390/en11010217
Chicago/Turabian StyleHoelzen, Julian, Yaolong Liu, Boris Bensmann, Christopher Winnefeld, Ali Elham, Jens Friedrichs, and Richard Hanke-Rauschenbach. 2018. "Conceptual Design of Operation Strategies for Hybrid Electric Aircraft" Energies 11, no. 1: 217. https://doi.org/10.3390/en11010217
APA StyleHoelzen, J., Liu, Y., Bensmann, B., Winnefeld, C., Elham, A., Friedrichs, J., & Hanke-Rauschenbach, R. (2018). Conceptual Design of Operation Strategies for Hybrid Electric Aircraft. Energies, 11(1), 217. https://doi.org/10.3390/en11010217







