Viscosity Models for Polymer Free CO2 Foam Fracturing Fluid with the Effect of Surfactant Concentration, Salinity and Shear Rate
Abstract
:1. Introduction
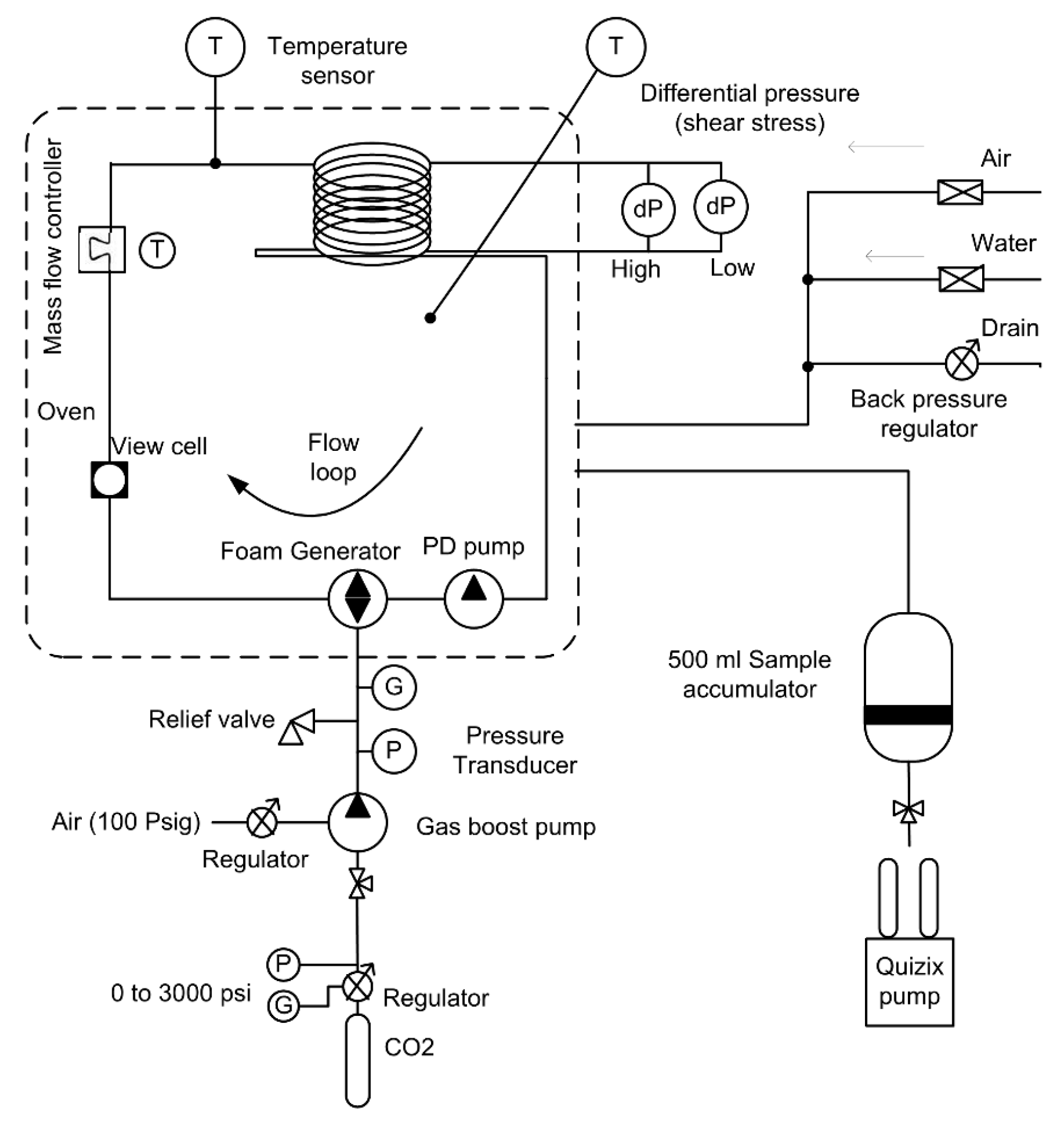
2. Experimental Methodology
3. Results and Discussion
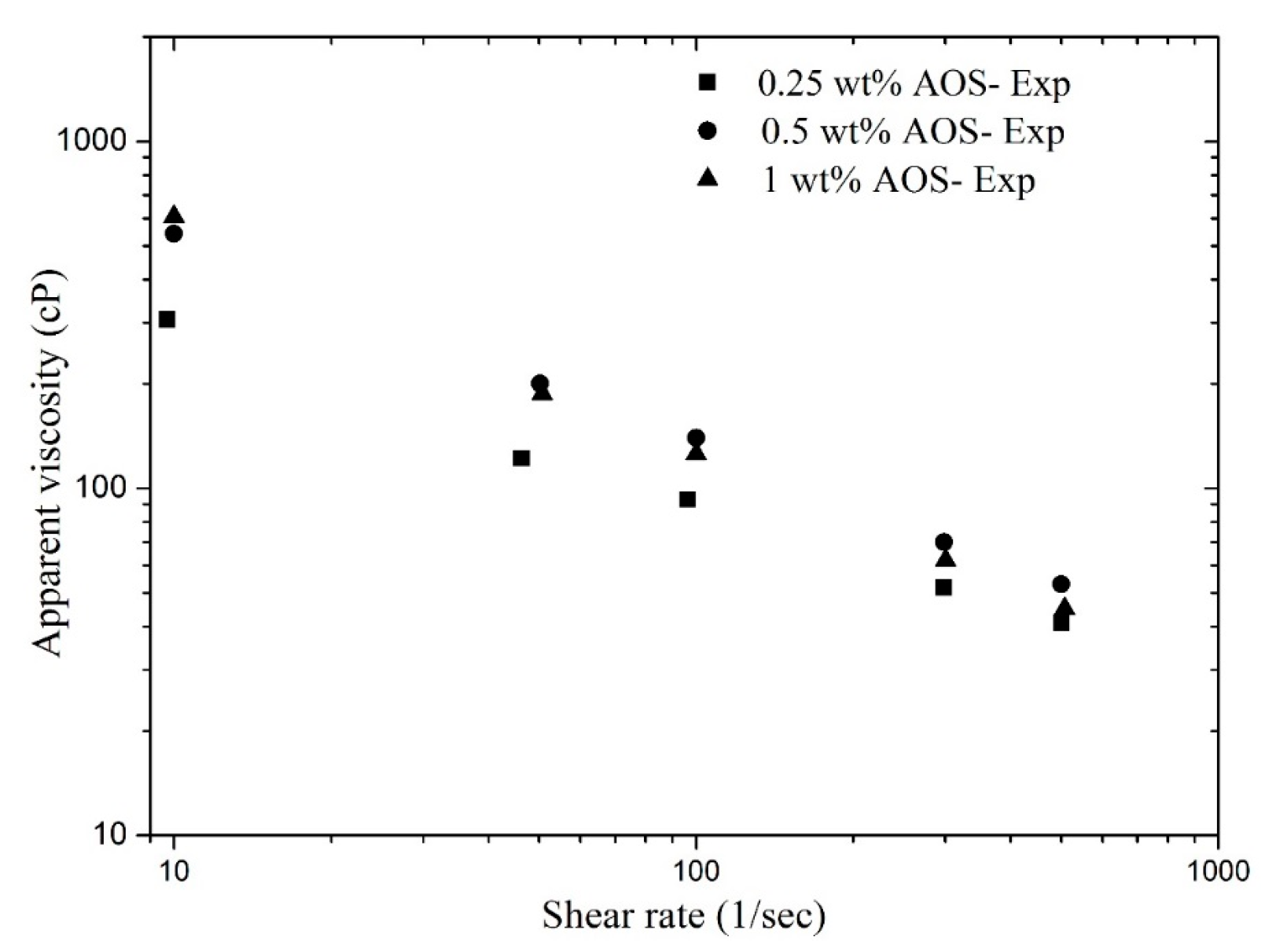
3.1. Effect of Shear Rate
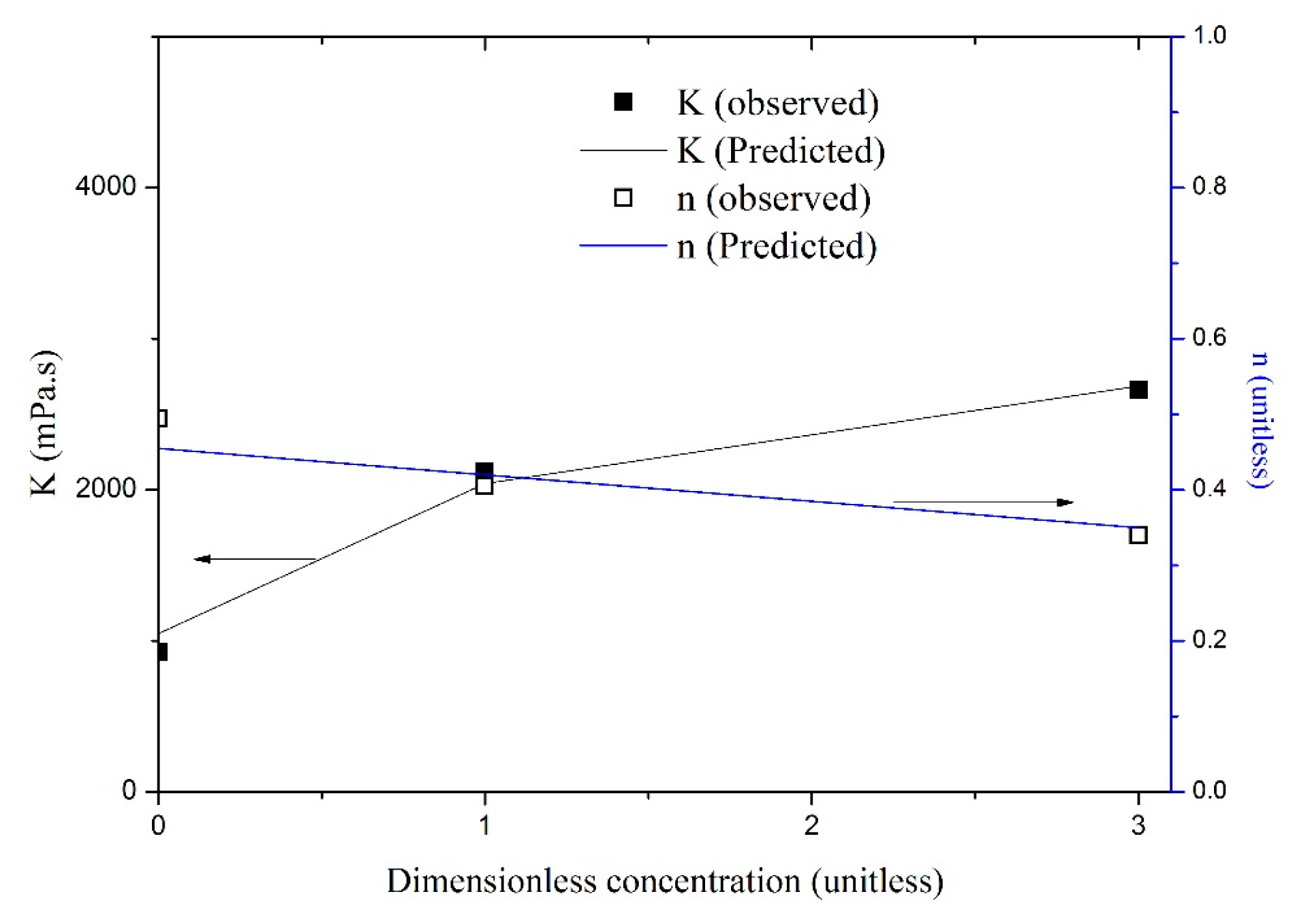
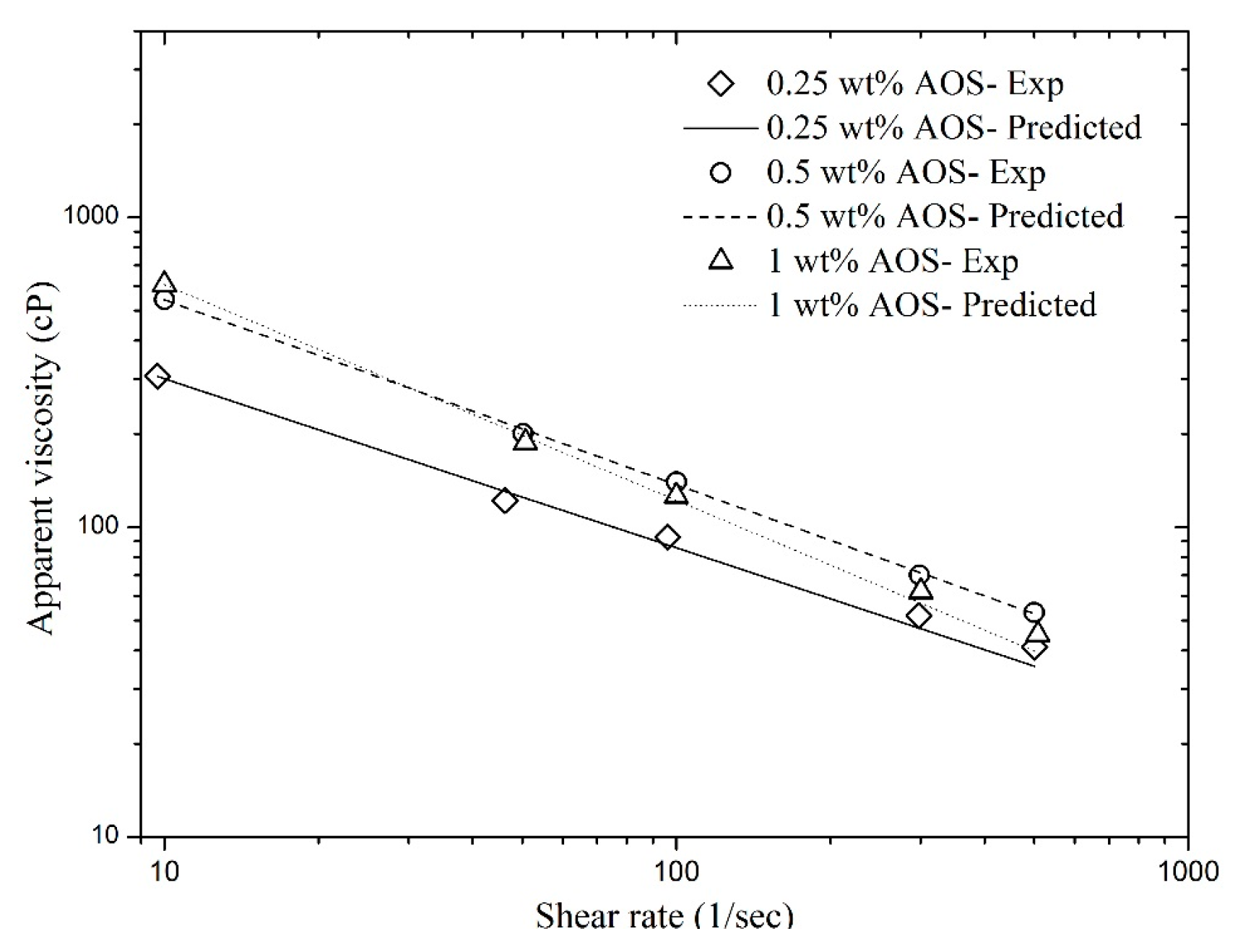
3.2. Effect of Surfactant Concentration
3.3. Effect of Salinity
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Harvey, T.; Gray, J. The Unconventional Hydrocarbon Resources of Britain’s Onshore Basins–Shale Gas; The Department of Energy & Climate Change: London, UK, 2013.
- Aguilera, R. Flow units: From conventional to tight-gas to shale-gas to tight-oil to shale-oil reservoirs. SPE Reserv. Eval. Eng. 2014, 17, 190–208. [Google Scholar] [CrossRef]
- Cipolla, C.L.; Lolon, E.P.; Erdle, J.C.; Rubin, B. Reservoir modeling in shale-gas reservoirs. SPE Reserv. Eval. Eng. 2010, 13, 638–653. [Google Scholar] [CrossRef]
- Mengal, S.A.; Wattenbarger, R.A. Accounting for Adsorbed Gas in Shale Gas Reservoirs. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 25–28 September 2011. [Google Scholar]
- Lee, K.S.; Kim, T.H. Integrative Understanding of Shale Gas Reservoirs; Springer: Heidelberg, Germany, 2016. [Google Scholar]
- Peles, J.; Wardlow, R.; Cox, G.; Haley, W.; Dusterhoft, R.; Walters, H.; Weaver, J. Maximizing well production with unique low molecular weight frac fluid. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar]
- Gu, M.; Mohanty, K. Rheology of polymer-free foam fracturing fluids. J. Pet. Sci. Eng. 2015, 134, 87–96. [Google Scholar] [CrossRef]
- Ribeiro, L.; Sharma, M. Fluid selection for energized fracture treatments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2013. [Google Scholar]
- Middleton, R.S.; Carey, J.W.; Currier, R.P.; Hyman, J.D.; Kang, Q.; Karra, S.; Jiménez-Martínez, J.; Porter, M.L.; Viswanathan, H.S. Shale gas and non-aqueous fracturing fluids: Opportunities and challenges for supercritical CO2. Appl. Energy 2015, 147, 500–509. [Google Scholar] [CrossRef]
- Barati, R.; Liang, J.T. A review of fracturing fluid systems used for hydraulic fracturing of oil and gas wells. J. Appl. Polym. Sci. 2014, 131, 40735. [Google Scholar] [CrossRef]
- Makhanov, K.; Habibi, A.; Dehghanpour, H.; Kuru, E. Liquid uptake of gas shales: A workflow to estimate water loss during shut-in periods after fracturing operations. J. Unconv. Oil Gas Resour. 2014, 7, 22–32. [Google Scholar] [CrossRef]
- Liu, F.; Ellett, K.; Xiao, Y.; Rupp, J.A. Assessing the feasibility of CO2 storage in the new albany shale (devonian–mississippian) with potential enhanced gas recovery using reservoir simulation. Int. J. Greenh. Gas Control 2013, 17, 111–126. [Google Scholar] [CrossRef]
- Busch, A.; Alles, S.; Gensterblum, Y.; Prinz, D.; Dewhurst, D.N.; Raven, M.D.; Stanjek, H.; Krooss, B.M. Carbon dioxide storage potential of shales. Int. J. Greenh. Gas Control 2008, 2, 297–308. [Google Scholar] [CrossRef]
- Shi, J.-Q.; Durucan, S. Modelling of mixed-gas adsorption and diffusion in coalbed reservoirs. In Proceedings of the SPE Unconventional Reservoirs Conference, Keystone, CO, USA, 10–12 February 2008. [Google Scholar]
- Edrisi, A.R.; Kam, S.I. A new foam rheology model for shale-gas foam fracturing applications. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. [Google Scholar]
- Heller, R. Laboratory measurements of matrix permeability and slippage enhanced permeability in gas shales. In Proceedings of the Unconventional Resources Technology Conference (URTEC), Denver, CO, USA, 12–14 August 2013. [Google Scholar]
- Kang, S.M.; Fathi, E.; Ambrose, R.J.; Akkutlu, I.Y.; Sigal, R.F. Carbon dioxide storage capacity of organic-rich shales. SPE J. 2011, 16, 842–855. [Google Scholar] [CrossRef]
- Luo, X.; Wang, S.; Wang, Z.; Jing, Z.; Lv, M. Experimental research on rheological properties and proppant transport performance of grf–CO2 fracturing fluid. J. Pet. Sci. Eng. 2014, 120, 154–162. [Google Scholar] [CrossRef]
- Gandossi, L. An Overview of Hydraulic Fracturing and Other Formation Stimulation Technologies for Shale Gas Production; Eur. Commisison Jt. Res. Cent. Tech. Reports; Publications Office of the European Union: Luxembourg, 2013. [Google Scholar]
- Sun, X.; Liang, X.; Wang, S.; Lu, Y. Experimental study on the rheology of CO2 viscoelastic surfactant foam fracturing fluid. J. Pet. Sci. Eng. 2014, 119, 104–111. [Google Scholar] [CrossRef]
- Edrisi, A.; Kam, S.I. A new foam model in pipes for drilling and fracturing application. SPE J. 2014, 19, 576–585. [Google Scholar] [CrossRef]
- Green, D.W.; Willhite, G.P. Enhanced Oil Recovery; Henry L. Doherty Memorial Fund of AIME, Society of Petroleum Engineers: Richardson, TX, USA, 1998. [Google Scholar]
- Pramudita, R.A.; Ryoo, W.S. Viscosity measurements of CO2-in-water foam with dodecyl polypropoxy sulfate surfactants for enhanced oil recovery application. Korea-Aust. Rheol. J. 2016, 28, 237–241. [Google Scholar] [CrossRef]
- Batôt, G.; Fleury, M.; Nabzar, L. Study of CO2 foam performance in a ccs context. In Proceedings of the 30th International Symposium of the Society of Core Analysts, Snowmass, CO, USA, 21–26 August 2016. [Google Scholar]
- Sherif, T.; Ahmed, R.; Shah, S.; Amani, M. Rheological correlations for oil-based drilling foams. J. Nat. Gas Sci. Eng. 2016, 35, 1249–1260. [Google Scholar] [CrossRef]
- Ostwald, W. Ueber die geschwindigkeitsfunktion der viskosität disperser systeme. I. Kolloid-Zeitschrift 1925, 36, 99–117. [Google Scholar] [CrossRef]
- Martins, A.; Lourenco, A.; Sa, C.; Silva, V., Jr. Foam rheology characterization as a tool for predicting pressures while drilling offshore wells in ubd conditions. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 27 February–1 March 2001. [Google Scholar]
- Ahmed, S.; Elraies, K.A.; Forooozesh, J.; Bt Mohd Shafian, S.R.; Hashmet, M.R.; Hsia, I.C.C.; Almansour, A. Experimental investigation of immiscible supercritical carbon dioxide foam rheology for improved oil recovery. J. Earth Sci. 2017, 28, 835–841. [Google Scholar] [CrossRef]
- Aronson, A.; Bergeron, V.; Fagan, M.E.; Radke, C. The influence of disjoining pressure on foam stability and flow in porous media. Colloids Surf. A Physicochem. Eng. Asp. 1994, 83, 109–120. [Google Scholar] [CrossRef]
- Apaydin, O.G.; Kovscek, A.R. Surfactant concentration and end effects on foam flow in porous media. Transp. Porous Media 2001, 43, 511–536. [Google Scholar] [CrossRef]
- Schramm, L.L. Emulsions, Foams, and Suspensions: Fundamentals and Applications; John Wiley & Sons: Weinheim, Germany, 2006. [Google Scholar]
- Georgieva, D.; Cagna, A.; Langevin, D. Link between surface elasticity and foam stability. Soft Matter 2009, 5, 2063–2071. [Google Scholar] [CrossRef]
- Wei, P.; Pu, W.; Sun, L.; Wang, B. Research on nitrogen foam for enhancing oil recovery in harsh reservoirs. J. Pet. Sci. Eng. 2017, 157, 27–38. [Google Scholar] [CrossRef]
- Tadros, T.F. Applied Surfactants: Principles and Applications; John Wiley & Sons: Weinheim, Germany, 2006. [Google Scholar]
- Bergeron, V. Disjoining pressures and film stability of alkyltrimethylammonium bromide foam films. Langmuir 1997, 13, 3474–3482. [Google Scholar] [CrossRef]
- Stubenrauch, C.; Miller, R. Stability of foam films and surface rheology: An oscillating bubble study at low frequencies. J. Phys. Chem. B 2004, 108, 6412–6421. [Google Scholar] [CrossRef] [PubMed]
- Espert, A.; Klitzing, R.v.; Poulin, P.; Colin, A.; Zana, R.; Langevin, D. Behavior of soap films stabilized by a cationic dimeric surfactant. Langmuir 1998, 14, 4251–4260. [Google Scholar] [CrossRef]
- Xue, Z.; Worthen, A.J.; Da, C.; Qajar, A.; Ketchum, I.R.; Alzobaidi, S.; Huh, C.; Prodanović, M.A.; Johnston, K.P. Ultradry carbon dioxide-in-water foams with viscoelastic aqueous phases. Langmuir 2015, 32, 28–37. [Google Scholar] [CrossRef] [PubMed]
- Walker, L.M. Rheology and structure of worm-like micelles. Curr. Opin. Colloid Interface Sci. 2001, 6, 451–456. [Google Scholar] [CrossRef]
- Feng, Y.; Chu, Z.; Dreiss, C. Smart wormlike micelles. Chem. Soc. Rev. 2013, 42, 7174–7203. [Google Scholar]
- Parker, A.; Fieber, W. Viscoelasticity of anionic wormlike micelles: Effects of ionic strength and small hydrophobic molecules. Soft Matter 2013, 9, 1203–1213. [Google Scholar] [CrossRef]
- Nguyen, Q.; Hirasaki, G.; Johnston, K. Novel CO2 Foam Concepts and Injection Schemes for Improving CO2 Sweep Efficiency in Sandstone and Carbonate Hydrocarbon Formations; University of Texas at Austin: Austin, TX, USA, 2015. [Google Scholar]
- Li, C.; Huang, Y.; Sun, X.; Gao, R.; Zeng, F.B.; Tontiwachwuthikul, P.; Liang, Z. Rheological properties study of foam fracturing fluid using CO2 and surfactant. Chem. Eng. Sci. 2017, 170, 720–730. [Google Scholar] [CrossRef]
- Ahmed, S.; Elraies, K.A.; Hashmet, M.R.; Shaifan, B.M.; Rohaida, S.; Hsia, I.C.C.; Bahrim, R.Z.K. Experimental investigation and optimization of polymer enhanced CO2 foam stability and apparent viscosity. In Proceedings of the SPE Annual Technical Symposium and Exhibition, Dhahran, Kingdom of Saudi Arabia, 24–27 April 2017; Society of Petroleum Engineers: Dhahran, Kingdom of Saudi Arabia, 2017. [Google Scholar]
- Ahmed, S.; Elraies, K.A.; Tan, I.M.; Hashmet, M.R. Experimental investigation of associative polymer performance for CO2 foam enhanced oil recovery. J. Pet. Sci. Eng. 2017, 157, 971–979. [Google Scholar] [CrossRef]
- Bonilla, L.F.; Shah, S.N. Experimental investigation on the rheology of foams. In Proceedings of the SPE/CERI Gas Technology Symposium, Calgary, AB, Canada, 3–5 April 2000. [Google Scholar]
- Xu, Q.; Nakajima, M.; Ichikawa, S.; Nakamura, N.; Roy, P.; Okadome, H.; Shiina, T. Effects of surfactant and electrolyte concentrations on bubble formation and stabilization. J. Colloid Interface Sci. 2009, 332, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Pandey, S.; Bagwe, R.P.; Shah, D.O. Effect of counterions on surface and foaming properties of dodecyl sulfate. J. Colloid Interface Sci. 2003, 267, 160–166. [Google Scholar] [CrossRef] [PubMed]



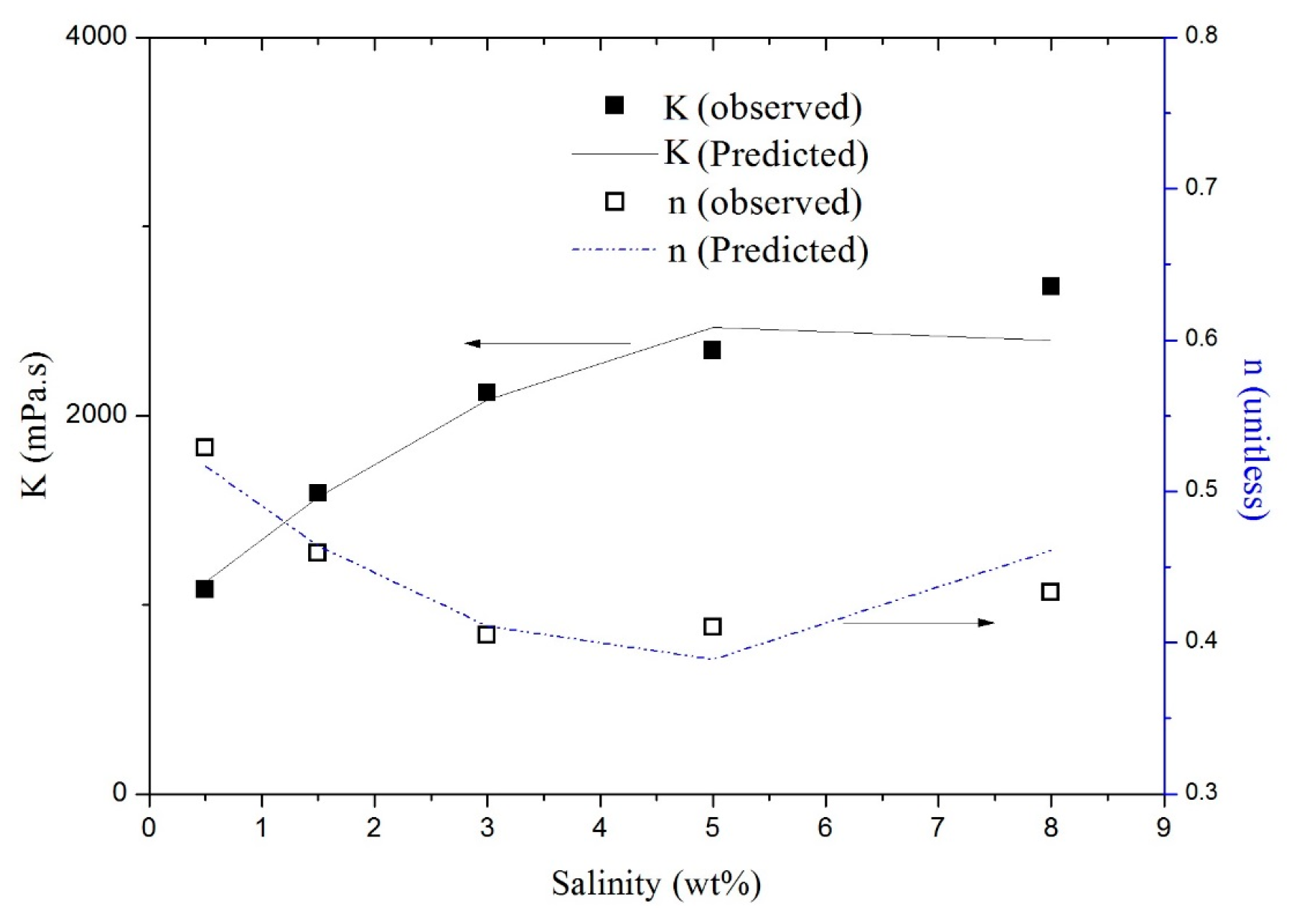
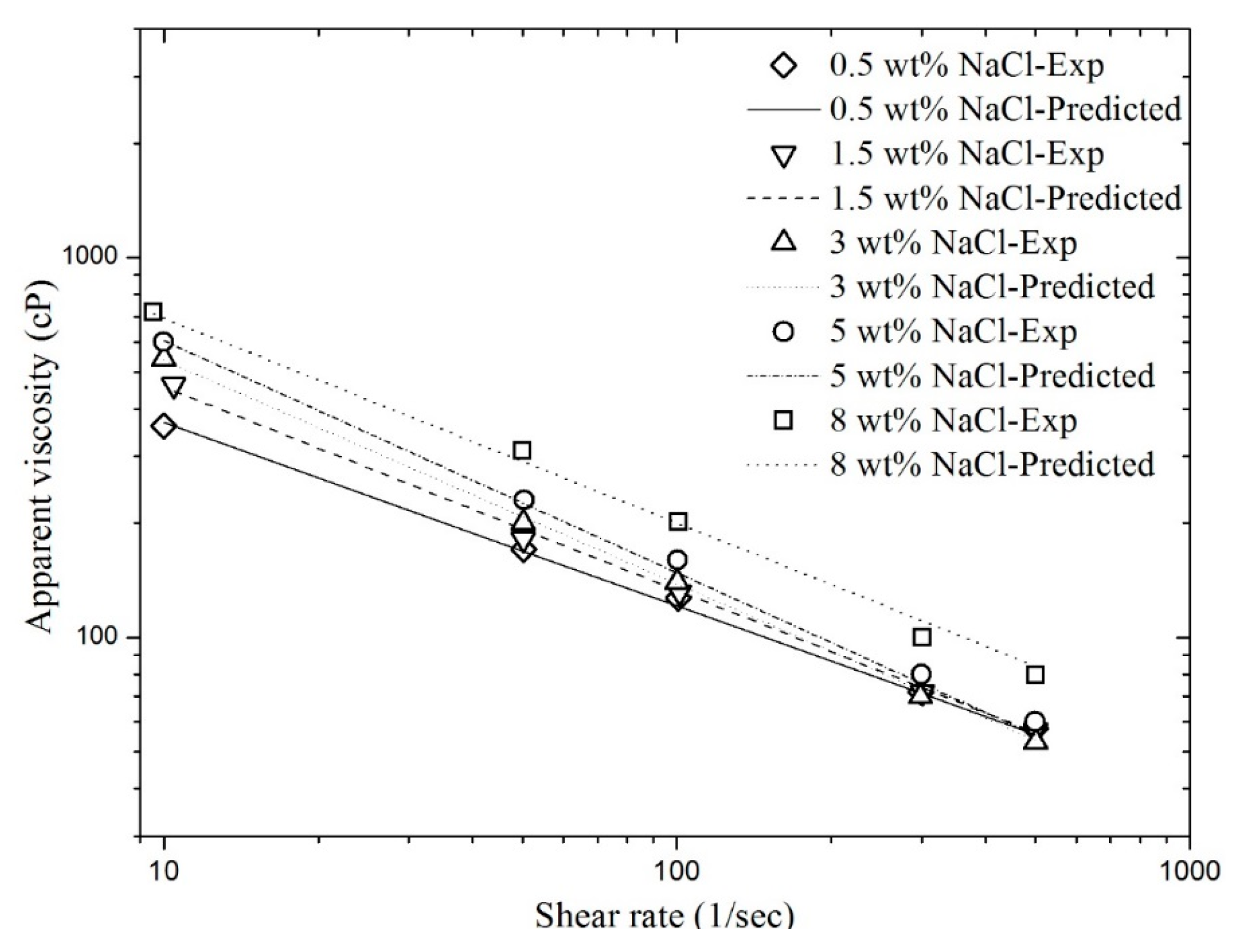
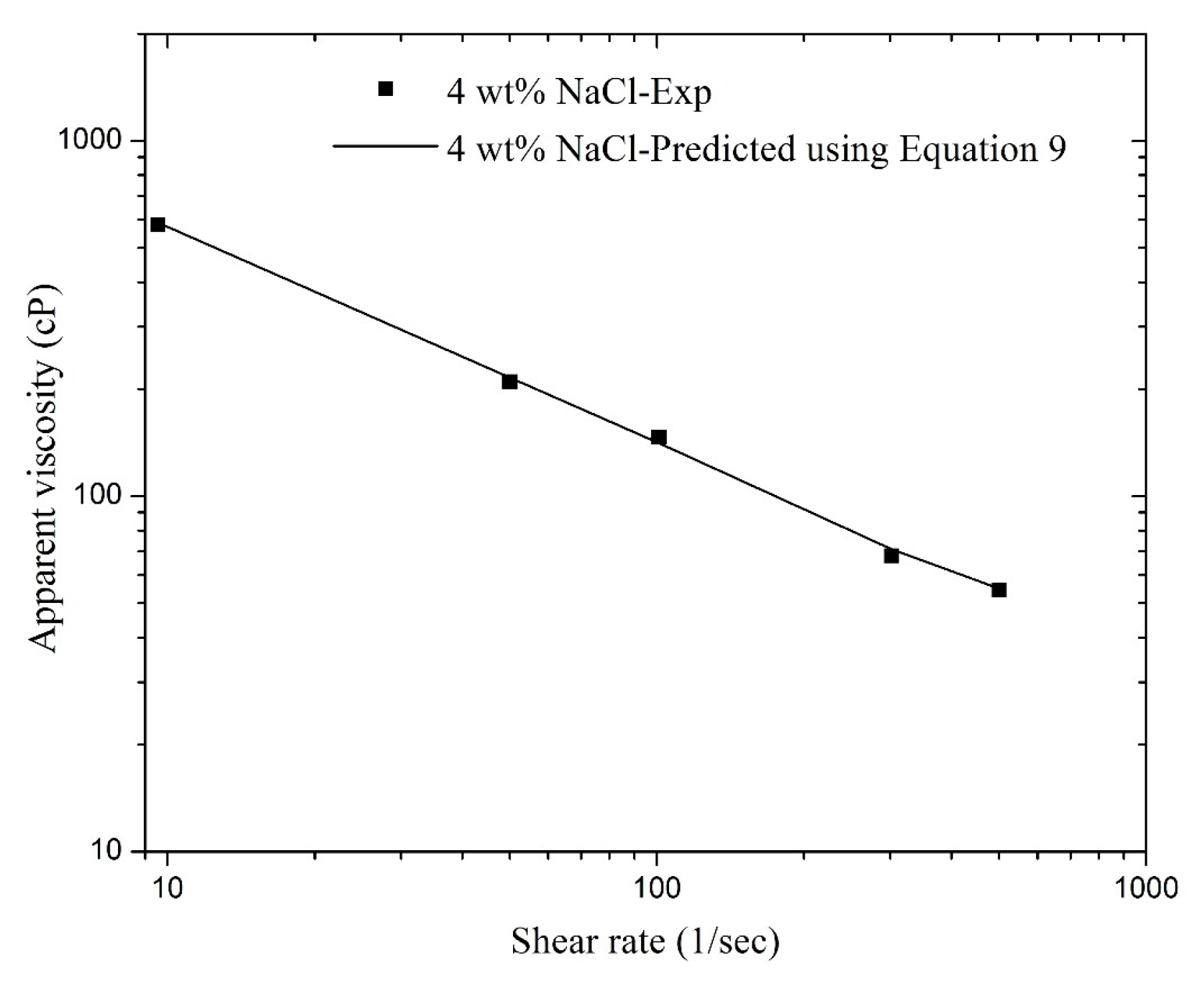
| Surfactant Concentration (wt %) | Betaine Concentration (wt %) | Salinity (wt %) | Parameter Estimates | R2 | ||
|---|---|---|---|---|---|---|
| K (mPa·s) | n (unitless) | |||||
| Set A | 0.25 | 0.5 | 3 | 924.23 | 0.494 | 0.999 |
| 0.5 | 0.5 | 3 | 2121 | 0.405 | 0.997 | |
| 1 | 0.5 | 3 | 2659.5 | 0.34 | 0.999 | |
| Set B | 0.5 | 0.5 | 0.5 | 1080.2 | 0.529 | 0.996 |
| 0.5 | 0.5 | 1.5 | 1591.2 | 0.459 | 0.999 | |
| 0.5 | 0.5 | 3 | 2121 | 0.405 | 0.999 | |
| 0.5 | 0.5 | 5 | 2344.4 | 0.41 | 0.999 | |
| 0.5 | 0.5 | 8 | 2683.2 | 0.433 | 0.98 | |
| Concentration (ppm) | Dimensionless Concentration, CD (Unitless) |
|---|---|
| 0.25 | 0 |
| 0.5 | 1 |
| 1 | 3 |
| Parameter Estimates | |||
|---|---|---|---|
| Parameter | Estimate | Standard Error (%) | R2 |
| g1 | −212.31 | 5.7 | 0.999 |
| g2 | 1287.583 | 3.74 | |
| g3 | 1059.9 | 4.0 | |
| h1 | –0.05 | 7.0 | |
| h2 | 0.454 | 2.86 | |
| Parameter Estimates | |||
|---|---|---|---|
| Parameter | Estimate | Standard Error (%) | R2 |
| l1 | −43.273 | 6.8 | 0.998 |
| l2 | 538.338 | 5.57 | |
| l3 | 859.755 | 3.57 | |
| m1 | 0.007 | 7.28 | |
| m2 | −0.067 | 5.62 | |
| m3 | 0.549 | 3.09 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.; Elraies, K.A.; Hashmet, M.R.; Hanamertani, A.S. Viscosity Models for Polymer Free CO2 Foam Fracturing Fluid with the Effect of Surfactant Concentration, Salinity and Shear Rate. Energies 2017, 10, 1970. https://doi.org/10.3390/en10121970
Ahmed S, Elraies KA, Hashmet MR, Hanamertani AS. Viscosity Models for Polymer Free CO2 Foam Fracturing Fluid with the Effect of Surfactant Concentration, Salinity and Shear Rate. Energies. 2017; 10(12):1970. https://doi.org/10.3390/en10121970
Chicago/Turabian StyleAhmed, Shehzad, Khaled Abdalla Elraies, Muhammad Rehan Hashmet, and Alvinda Sri Hanamertani. 2017. "Viscosity Models for Polymer Free CO2 Foam Fracturing Fluid with the Effect of Surfactant Concentration, Salinity and Shear Rate" Energies 10, no. 12: 1970. https://doi.org/10.3390/en10121970
APA StyleAhmed, S., Elraies, K. A., Hashmet, M. R., & Hanamertani, A. S. (2017). Viscosity Models for Polymer Free CO2 Foam Fracturing Fluid with the Effect of Surfactant Concentration, Salinity and Shear Rate. Energies, 10(12), 1970. https://doi.org/10.3390/en10121970





