Anaerobic Digestion of Feedstock Grown on Marginal Land: Break-Even Electricity Prices
Abstract
1. Introduction
2. Methods
2.1. Description of the Representative Farm in the UK Farm Context
2.2. Model
3. Data
3.1. Base Project Scenarios
3.2. Capital and Operating Expenditure Costs
3.3. Stochasticity in Parameters
4. Results
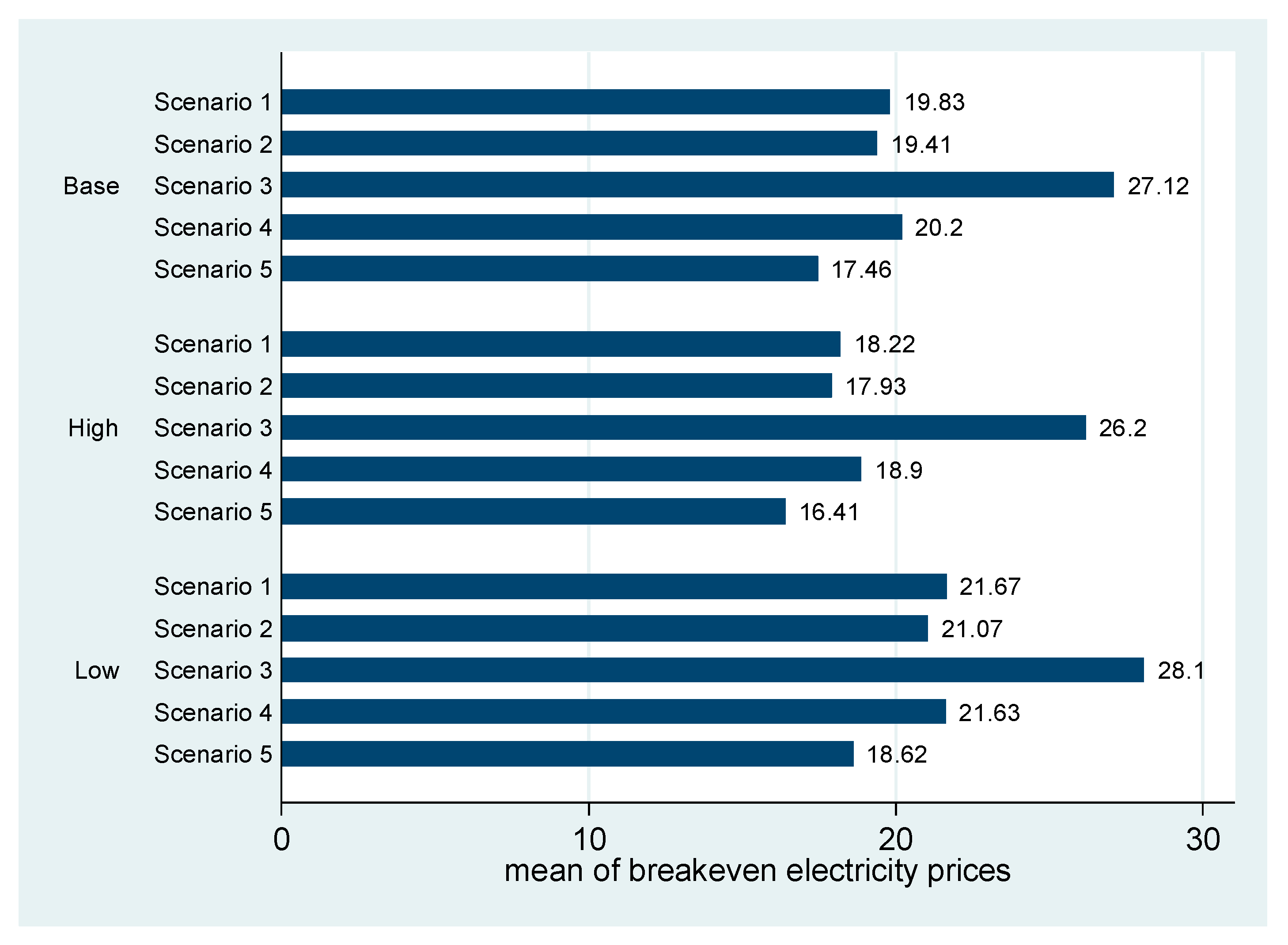
4.1. Base Results
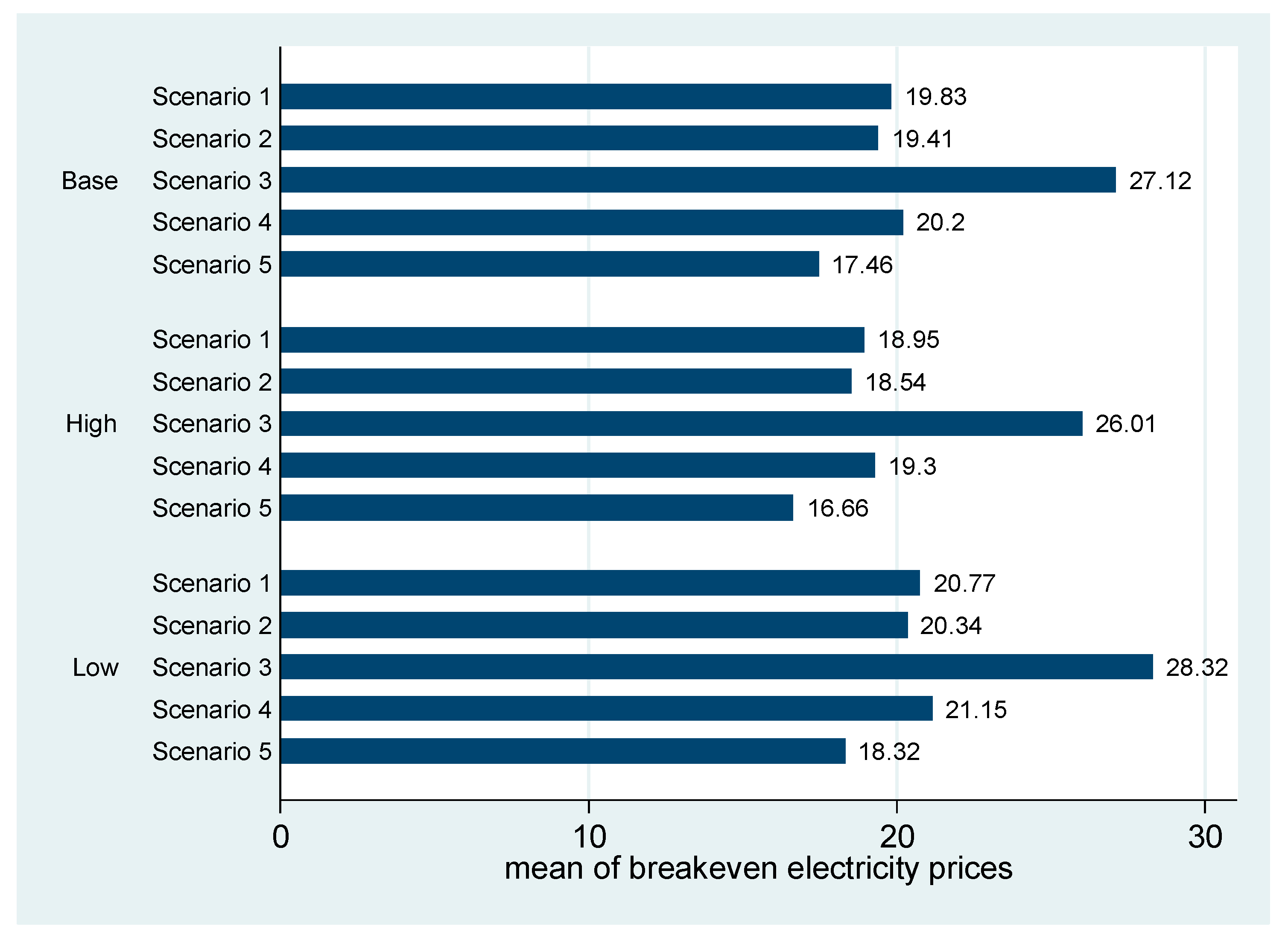
4.2. Sensitivity Analysis
4.2.1. Biogas Yield
4.2.2. Runtime
4.2.3. Debt and Equity Financing
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Feedstock | Base Setting | Low Setting | High Setting |
|---|---|---|---|
| Solid manure | [min 60, mode 90, max 120] | [min 60, mode 72, max 120] | [min 60, mode 108, max 120] |
| Liquid cattle manure | [min 20, mode 25; max 30] | [min 20, mode 22; max 30] | [min 20, mode 28; max 30] |
| Whole crop rye | [min 170, mode 195, max 220] | [min 170, mode 180, max 220] | [min 170, mode 2010, max 220] |
| Grass silage | [min 170, mode 185, max 200] | [min 170, mode 176, max 200] | [min 170, mode 194, max 200] |
| Fodder beet | [min 75, mode 107.5, max 140] | [min 75, mode 88, max 140] | [min 75, mode 127, max 140] |
| Range | Base Setting | Low Setting | High Setting |
|---|---|---|---|
| Min | 7000 | 7000 | 7500 |
| Mode | 7500 | 7250 | 7750 |
| Maximum | 8000 | 7500 | 8000 |
Appendix B
| Scenarios | Indicators | Heat (p/kWh) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5.00 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | 6.75 | 7.00 | ||
| Scenario 1 | Mean | 22.53 | 22.29 | 22.09 | 21.88 | 21.67 | 21.45 | 21.24 | 21.05 | 20.83 |
| S.D. | 1.45 | 1.45 | 1.45 | 1.45 | 1.43 | 1.43 | 1.41 | 1.44 | 1.43 | |
| Scenario 2 | Mean | 21.91 | 21.70 | 21.48 | 21.29 | 21.07 | 20.85 | 20.64 | 20.45 | 20.21 |
| S.D. | 1.30 | 1.30 | 1.29 | 1.28 | 1.30 | 1.30 | 1.30 | 1.29 | 1.30 | |
| Scenario 3 | Mean | 28.94 | 28.71 | 28.50 | 28.32 | 28.10 | 27.87 | 27.66 | 27.44 | 27.24 |
| S.D. | 1.54 | 1.54 | 1.57 | 1.56 | 1.55 | 1.55 | 1.55 | 1.56 | 1.56 | |
| Scenario 4 | Mean | 22.50 | 22.25 | 22.05 | 21.82 | 21.63 | 21.42 | 21.20 | 20.99 | 20.80 |
| S.D. | 1.29 | 1.30 | 1.28 | 1.28 | 1.30 | 1.30 | 1.30 | 1.30 | 1.29 | |
| Scenario 5 | Mean | 19.47 | 19.30 | 19.06 | 18.86 | 18.62 | 18.44 | 18.22 | 18.03 | 17.81 |
| S.D. | 1.16 | 1.15 | 1.14 | 1.15 | 1.15 | 1.15 | 1.15 | 1.15 | 1.14 | |
| P(GT+ET) is 0.00 for all project scenarios, regardless of the heat price | ||||||||||
| Scenarios | Indicators | Heat (p/kWh) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5.00 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | 6.75 | 7.00 | ||
| Scenario 1 | Mean | 19.07 | 18.84 | 18.64 | 18.43 | 18.22 | 18.00 | 17.79 | 17.59 | 17.38 |
| S.D. | 1.22 | 1.22 | 1.23 | 1.22 | 1.21 | 1.20 | 1.19 | 1.21 | 1.21 | |
| Scenario 2 | Mean | 18.78 | 18.56 | 18.35 | 18.15 | 17.93 | 17.71 | 17.50 | 17.31 | 17.07 |
| S.D. | 1.12 | 1.12 | 1.12 | 1.11 | 1.12 | 1.12 | 1.12 | 1.11 | 1.12 | |
| Scenario 3 | Mean | 27.04 | 26.81 | 26.60 | 26.42 | 26.20 | 25.98 | 25.76 | 25.54 | 25.34 |
| S.D. | 1.45 | 1.46 | 1.48 | 1.47 | 1.47 | 1.47 | 1.47 | 1.47 | 1.47 | |
| Scenario 4 | Mean | 19.77 | 19.53 | 19.32 | 19.10 | 18.90 | 18.69 | 18.47 | 18.27 | 18.07 |
| S.D. | 1.15 | 1.16 | 1.15 | 1.15 | 1.16 | 1.16 | 1.16 | 1.16 | 1.15 | |
| Scenario 5 | Mean | 17.26 | 17.09 | 16.85 | 16.65 | 16.41 | 16.23 | 16.01 | 15.82 | 15.60 |
| S.D. | 1.05 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.04 | 1.03 | |
| P(GT+ET) is 0.00 for all project scenarios, regardless of the heat price | ||||||||||
| Scenarios | Indicators | Heat (p/kWh) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5.00 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | 6.75 | 7.00 | ||
| Scenario 1 | Mean | 21.63 | 21.39 | 21.20 | 20.98 | 20.77 | 20.56 | 20.34 | 20.15 | 19.94 |
| S.D. | 1.34 | 1.34 | 1.34 | 1.33 | 1.33 | 1.32 | 1.30 | 1.33 | 1.32 | |
| Scenario 2 | Mean | 21.18 | 20.96 | 20.75 | 20.55 | 20.34 | 20.11 | 19.90 | 19.71 | 19.47 |
| S.D. | 1.22 | 1.22 | 1.21 | 1.20 | 1.22 | 1.22 | 1.22 | 1.21 | 1.21 | |
| Scenario 3 | Mean | 29.16 | 28.93 | 28.71 | 28.53 | 28.32 | 28.09 | 27.88 | 27.66 | 27.46 |
| S.D. | 1.54 | 1.54 | 1.56 | 1.55 | 1.55 | 1.55 | 1.55 | 1.56 | 1.55 | |
| Scenario 4 | Mean | 22.02 | 21.77 | 21.57 | 21.35 | 21.15 | 20.94 | 20.72 | 20.52 | 20.32 |
| S.D. | 1.25 | 1.25 | 1.24 | 1.24 | 1.25 | 1.25 | 1.25 | 1.25 | 1.24 | |
| Scenario 5 | Mean | 19.18 | 19.01 | 18.77 | 18.57 | 18.32 | 18.15 | 17.92 | 17.73 | 17.52 |
| S.D. | 1.12 | 1.12 | 1.11 | 1.12 | 1.11 | 1.11 | 1.12 | 1.12 | 1.11 | |
| P(GT+ET) is 0.00 for all project scenarios, regardless of the heat price | ||||||||||
| Scenarios | Indicators | Heat (p/kWh) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5.00 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | 6.75 | 7.00 | ||
| Scenario 1 | Mean | 19.81 | 19.57 | 19.38 | 19.16 | 18.95 | 18.74 | 18.52 | 18.33 | 18.11 |
| S.D. | 1.25 | 1.25 | 1.25 | 1.25 | 1.24 | 1.23 | 1.22 | 1.24 | 1.24 | |
| Scenario 2 | Mean | 19.39 | 19.17 | 18.96 | 18.76 | 18.54 | 18.32 | 18.11 | 17.92 | 17.68 |
| S.D. | 1.14 | 1.14 | 1.13 | 1.12 | 1.14 | 1.14 | 1.14 | 1.13 | 1.13 | |
| Scenario 3 | Mean | 26.85 | 26.62 | 26.41 | 26.23 | 26.01 | 25.78 | 25.57 | 25.35 | 25.15 |
| S.D. | 1.43 | 1.44 | 1.46 | 1.45 | 1.44 | 1.44 | 1.45 | 1.45 | 1.45 | |
| Scenario 4 | Mean | 20.17 | 19.93 | 19.72 | 19.50 | 19.30 | 19.09 | 18.88 | 18.67 | 18.47 |
| S.D. | 1.16 | 1.17 | 1.15 | 1.15 | 1.17 | 1.17 | 1.17 | 1.17 | 1.15 | |
| Scenario 5 | Mean | 17.51 | 17.34 | 17.10 | 16.90 | 16.66 | 16.48 | 16.26 | 16.07 | 15.85 |
| S.D. | 1.05 | 1.04 | 1.04 | 1.05 | 1.04 | 1.04 | 1.04 | 1.05 | 1.03 | |
| P(GT+ET) is 0.00 for all project scenarios, regardless of the heat price | ||||||||||
| Scenarios | Indicators | Heat (p/kWh) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5.00 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | 6.75 | 7.00 | ||
| Scenario 1 | Mean | 24.12 | 23.88 | 23.69 | 23.48 | 23.27 | 23.05 | 22.84 | 22.64 | 22.43 |
| S.D. | 1.40 | 1.40 | 1.40 | 1.40 | 1.39 | 1.38 | 1.36 | 1.39 | 1.38 | |
| Scenario 2 | Mean | 23.71 | 23.49 | 23.27 | 23.08 | 22.86 | 22.64 | 22.43 | 22.24 | 22.00 |
| S.D. | 1.27 | 1.27 | 1.26 | 1.26 | 1.27 | 1.27 | 1.27 | 1.26 | 1.27 | |
| Scenario 3 | Mean | 31.54 | 31.31 | 31.10 | 30.92 | 30.70 | 30.48 | 30.26 | 30.04 | 29.84 |
| S.D. | 1.55 | 1.55 | 1.58 | 1.57 | 1.56 | 1.56 | 1.56 | 1.57 | 1.57 | |
| Scenario 4 | Mean | 24.12 | 23.88 | 23.68 | 23.45 | 23.26 | 23.05 | 22.83 | 22.62 | 22.43 |
| S.D. | 1.27 | 1.27 | 1.26 | 1.26 | 1.27 | 1.28 | 1.27 | 1.27 | 1.26 | |
| Scenario 5 | Mean | 21.06 | 20.89 | 20.65 | 20.45 | 20.20 | 20.03 | 19.80 | 19.61 | 19.40 |
| S.D. | 1.14 | 1.14 | 1.13 | 1.14 | 1.13 | 1.13 | 1.14 | 1.14 | 1.12 | |
| P(GT+ET) is 0.00 for all project scenarios, regardless of the heat price | ||||||||||
| Scenarios | Indicators | Heat (p/kWh) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5.00 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | 6.75 | 7.00 | ||
| Scenario 1 | Mean | 30.99 | 30.75 | 30.56 | 30.34 | 30.13 | 29.92 | 29.70 | 29.51 | 29.29 |
| S.D. | 1.61 | 1.61 | 1.61 | 1.61 | 1.60 | 1.59 | 1.57 | 1.59 | 1.59 | |
| Scenario 2 | Mean | 30.61 | 30.39 | 30.18 | 29.99 | 29.77 | 29.55 | 29.34 | 29.14 | 28.90 |
| S.D. | 1.46 | 1.45 | 1.45 | 1.44 | 1.46 | 1.46 | 1.45 | 1.45 | 1.45 | |
| Scenario 3 | Mean | 38.69 | 38.46 | 38.25 | 38.07 | 37.85 | 37.63 | 37.41 | 37.19 | 36.99 |
| S.D. | 1.68 | 1.68 | 1.71 | 1.69 | 1.69 | 1.69 | 1.69 | 1.70 | 1.69 | |
| Scenario 4 | Mean | 30.24 | 30.00 | 29.80 | 29.57 | 29.38 | 29.17 | 28.95 | 28.74 | 28.55 |
| S.D. | 1.39 | 1.40 | 1.38 | 1.39 | 1.40 | 1.40 | 1.39 | 1.40 | 1.38 | |
| Scenario 5 | Mean | 26.54 | 26.37 | 26.13 | 25.93 | 25.68 | 25.51 | 25.28 | 25.09 | 24.88 |
| S.D. | 1.25 | 1.25 | 1.24 | 1.25 | 1.24 | 1.24 | 1.24 | 1.25 | 1.23 | |
| P(GT+ET) is 0.00 for all project scenarios, regardless of the heat price | ||||||||||
| Debt Level | ∆ Modal Biogas Yield | Modal Runtime (h) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7000 | 7100 | 7200 | 7300 | 7400 | 7500 | 7600 | 7700 | 7800 | 7900 | 8000 | ||
| 0% | −20.00% | 19.25 | 19.10 | 19.00 | 18.87 | 18.76 | 18.63 | 18.52 | 18.42 | 18.30 | 18.19 | 18.07 |
| −17.50% | 18.82 | 18.72 | 18.60 | 18.46 | 18.35 | 18.25 | 18.11 | 18.03 | 17.90 | 17.79 | 17.70 | |
| −15.00% | 18.45 | 18.32 | 18.20 | 18.08 | 17.97 | 17.89 | 17.74 | 17.64 | 17.51 | 17.42 | 17.31 | |
| 0.00% | 18.05 | 17.94 | 17.83 | 17.70 | 17.63 | 17.49 | 17.39 | 17.24 | 17.17 | 17.05 | 16.96 | |
| +15.00% | 17.70 | 17.58 | 17.45 | 17.35 | 17.23 | 17.12 | 17.00 | 16.90 | 16.80 | 16.70 | 16.60 | |
| +17.50% | 17.32 | 17.23 | 17.11 | 17.00 | 16.88 | 16.77 | 16.68 | 16.56 | 16.48 | 16.35 | 16.25 | |
| +20.00% | 16.97 | 16.87 | 16.77 | 16.65 | 16.55 | 16.45 | 16.33 | 16.23 | 16.13 | 16.01 | 15.91 | |
| 25% | −20.00% | 22.18 | 22.03 | 21.91 | 21.78 | 21.65 | 21.53 | 21.38 | 21.24 | 21.12 | 21.00 | 20.88 |
| −17.50% | 21.72 | 21.58 | 21.44 | 21.31 | 21.20 | 21.09 | 20.95 | 20.82 | 20.70 | 20.56 | 20.43 | |
| −15.00% | 21.30 | 21.15 | 21.01 | 20.90 | 20.77 | 20.63 | 20.51 | 20.39 | 20.27 | 20.15 | 20.04 | |
| 0.00% | 20.85 | 20.74 | 20.61 | 20.49 | 20.35 | 20.22 | 20.11 | 19.99 | 19.87 | 19.75 | 19.64 | |
| +15.00% | 20.43 | 20.31 | 20.21 | 20.06 | 19.95 | 19.82 | 19.72 | 19.59 | 19.46 | 19.34 | 19.25 | |
| +17.50% | 20.06 | 19.94 | 19.83 | 19.67 | 19.56 | 19.43 | 19.31 | 19.18 | 19.09 | 18.97 | 18.85 | |
| +20.00% | 19.67 | 19.55 | 19.42 | 19.31 | 19.18 | 19.07 | 18.94 | 18.84 | 18.72 | 18.59 | 18.48 | |
| 50% | −20.00% | 25.11 | 24.95 | 24.82 | 24.68 | 24.53 | 24.37 | 24.26 | 24.09 | 23.96 | 23.83 | 23.67 |
| −17.50% | 24.60 | 24.44 | 24.31 | 24.16 | 24.03 | 23.91 | 23.77 | 23.61 | 23.49 | 23.34 | 23.22 | |
| −15.00% | 24.13 | 23.96 | 23.84 | 23.70 | 23.56 | 23.42 | 23.28 | 23.15 | 23.03 | 22.88 | 22.76 | |
| 0.00% | 23.66 | 23.53 | 23.38 | 23.21 | 23.12 | 22.95 | 22.83 | 22.69 | 22.55 | 22.43 | 22.31 | |
| +15.00% | 23.22 | 23.07 | 22.93 | 22.79 | 22.66 | 22.53 | 22.41 | 22.26 | 22.13 | 22.01 | 21.87 | |
| +17.50% | 22.75 | 22.61 | 22.49 | 22.36 | 22.23 | 22.08 | 21.95 | 21.83 | 21.71 | 21.58 | 21.45 | |
| +20.00% | 22.34 | 22.22 | 22.08 | 21.91 | 21.79 | 21.67 | 21.55 | 21.44 | 21.31 | 21.17 | 21.05 | |
| 75% | −20.00% | 28.04 | 27.89 | 27.71 | 27.58 | 27.42 | 27.24 | 27.08 | 26.94 | 26.78 | 26.65 | 26.48 |
| −17.50% | 27.49 | 27.33 | 27.17 | 27.02 | 26.87 | 26.72 | 26.56 | 26.44 | 26.25 | 26.12 | 25.96 | |
| −15.00% | 26.96 | 26.82 | 26.66 | 26.52 | 26.36 | 26.20 | 26.05 | 25.89 | 25.77 | 25.63 | 25.49 | |
| 0.00% | 26.47 | 26.32 | 26.15 | 26.01 | 25.85 | 25.71 | 25.56 | 25.41 | 25.27 | 25.12 | 24.98 | |
| +15.00% | 25.97 | 25.81 | 25.66 | 25.52 | 25.40 | 25.21 | 25.10 | 24.94 | 24.82 | 24.65 | 24.52 | |
| +17.50% | 25.50 | 25.35 | 25.19 | 25.06 | 24.89 | 24.76 | 24.62 | 24.49 | 24.32 | 24.18 | 24.05 | |
| +20.00% | 25.03 | 24.87 | 24.73 | 24.61 | 24.45 | 24.29 | 24.17 | 24.02 | 23.89 | 23.74 | 23.62 | |
| 100% | −20.00% | 30.97 | 30.79 | 30.61 | 30.44 | 30.27 | 30.12 | 29.92 | 29.80 | 29.63 | 29.46 | 29.29 |
| −17.50% | 30.38 | 30.20 | 30.04 | 29.86 | 29.70 | 29.54 | 29.36 | 29.21 | 29.05 | 28.90 | 28.74 | |
| −15.00% | 29.82 | 29.64 | 29.48 | 29.32 | 29.14 | 28.98 | 28.84 | 28.68 | 28.51 | 28.34 | 28.21 | |
| 0.00% | 29.26 | 29.08 | 28.94 | 28.80 | 28.61 | 28.47 | 28.32 | 28.13 | 27.99 | 27.82 | 27.66 | |
| +15.00% | 28.74 | 28.58 | 28.41 | 28.26 | 28.08 | 27.93 | 27.78 | 27.61 | 27.48 | 27.31 | 27.19 | |
| +17.50% | 28.22 | 28.08 | 27.90 | 27.72 | 27.59 | 27.42 | 27.28 | 27.12 | 26.94 | 26.82 | 26.65 | |
| +20.00% | 27.73 | 27.55 | 27.41 | 27.24 | 27.07 | 26.93 | 26.78 | 26.62 | 26.49 | 26.35 | 26.19 | |
Appendix C
Appendix C.1. A Conceptual AD Plant Model
Appendix C.2. Feedstock and Biogas
Appendix C.3. Revenues
Appendix C.4. Capital Investment Costs
References
- Harvey, M.; Pilgrim, S. The new competition for land: Food, energy, and climate change. Food Policy 2011, 36, S40–S51. [Google Scholar] [CrossRef]
- McMichael, P. Agrofuels in the food regime. J. Peasant Stud. 2010, 37, 609–629. [Google Scholar] [CrossRef]
- Popp, J.; Lakner, Z.; Harangi-Rákos, M.; Fári, M. The effect of bioenergy expansion: Food, energy, and environment. Renew. Sustain. Energy Rev. 2014, 32, 559–578. [Google Scholar] [CrossRef]
- Rathmann, R.; Szklo, A.; Schaeffer, R. Land use competition for production of food and liquid biofuels: An analysis of the arguments in the current debate. Renew. Energy 2010, 35, 14–22. [Google Scholar] [CrossRef]
- Searchinger, T.; Heimlich, R.; Houghton, R.A.; Dong, F.; Elobeid, A.; Fabiosa, J.; Tokgoz, S.; Hayes, D.; Yu, T.-H. Use of US croplands for biofuels increases greenhouse gases through emissions from land-use change. Science 2008, 319, 1238–1240. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Zhang, X.; Wang, D. Land availability for biofuel production. Environ. Sci. Technol. 2010, 45, 334–339. [Google Scholar] [CrossRef] [PubMed]
- Gelfand, I.; Sahajpal, R.; Zhang, X.; Izaurralde, R.C.; Gross, K.L.; Robertson, G.P. Sustainable bioenergy production from marginal lands in the US Midwest. Nature 2013, 493, 514–517. [Google Scholar] [CrossRef] [PubMed]
- Shortall, O. “Marginal land” for energy crops: Exploring definitions and embedded assumptions. Energy Policy 2013, 62, 19–27. [Google Scholar] [CrossRef]
- Don, A.; Osborne, B.; Hastings, A.; Skiba, U.; Carter, M.S.; Drewer, J.; Flessa, H.; Freibauer, A.; Hyvönen, N.; Jones, M.B. Land-use change to bioenergy production in Europe: Implications for the greenhouse gas balance and soil carbon. GCB Bioenergy 2012, 4, 372–391. [Google Scholar] [CrossRef]
- Creutzig, F.; Ravindranath, N.; Berndes, G.; Bolwig, S.; Bright, R.; Cherubini, F.; Chum, H.; Corbera, E.; Delucchi, M.; Faaij, A. Bioenergy and climate change mitigation: An assessment. GCB Bioenergy 2015, 7, 916–944. [Google Scholar] [CrossRef]
- Pulighe, G.; Bonati, G.; Fabiani, S.; Barsali, T.; Lupia, F.; Vanino, S.; Nino, P.; Arca, P.; Roggero, P.P. Assessment of the agronomic feasibility of bioenergy crop cultivation on marginal and polluted land: A GIS-based suitability study from the Sulcis area, Italy. Energies 2016, 9, 895. [Google Scholar] [CrossRef]
- Liu, T.; McConkey, B.; Ma, Z.; Liu, Z.; Li, X.; Cheng, L. Strengths, weaknessness, opportunities and threats analysis of bioenergy production on marginal land. Energy Proced. 2011, 5, 2378–2386. [Google Scholar] [CrossRef]
- Bryngelsson, D.K.; Lindgren, K. Why large-scale bioenergy production on marginal land is unfeasible: A conceptual partial equilibrium analysis. Energy Policy 2013, 55, 454–466. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, J.; Lin, G.; Jiang, D.; Yan, X. Switchgrass-based bioethanol productivity and potential environmental impact from marginal lands in China. Energies 2017, 10, 260. [Google Scholar] [CrossRef]
- Milbrandt, A.R.; Heimiller, D.M.; Perry, A.D.; Field, C.B. Renewable energy potential on marginal lands in the United States. Renew. Sustain. Energy Rev. 2014, 29, 473–481. [Google Scholar] [CrossRef]
- Nilsson, D.; Rosenqvist, H.; Bernesson, S. Profitability of the production of energy grasses on marginal agricultural land in Sweden. Biomass Bioenergy 2015, 83, 159–168. [Google Scholar] [CrossRef]
- Schmidt, T.; Fernando, A.L.; Monti, A.; Rettenmaier, N. Life cycle assessment of bioenergy and bio-based products from perennial grasses cultivated on marginal land in the Mediterranean region. Bioenergy Res. 2015, 8, 1548–1561. [Google Scholar] [CrossRef]
- National Grid. The Potential for Renewable Gas in the UK; National Grid: London, UK, 2009. [Google Scholar]
- Ghafoori, E.; Flynn, P.C.; Checkel, M.D. Carbon credits required to make manure biogas plants economic. Int. J. Green Energy 2007, 4, 339–349. [Google Scholar] [CrossRef]
- Leuer, E.R.; Hyde, J.; Richard, T.L. Investing in methane digesters on Pennsylvania dairy farms: Implications of scale economies and environmental programs. Agric. Resour. Econ. Rev. 2008, 37, 188–203. [Google Scholar] [CrossRef]
- Balussou, D.; Kleyböcker, A.; McKenna, R.; Möst, D.; Fichtner, W. An economic analysis of three operational co-digestion biogas plants in Germany. Waste Biomass Valoriz. 2012, 3, 23–41. [Google Scholar] [CrossRef]
- Heffels, T.; McKenna, R.; Fichtner, W. Direct marketing of electricity from biogas and biomethane: An economic analysis of several business models in Germany. J. Manag. Control 2012, 23, 53–70. [Google Scholar] [CrossRef]
- Slee, B.; Harnmeijer, J. Scottish community energy. In A Critical Review of Scottish Renewable and Low Carbon Energy Policy: Implications for the Independence Debate; Palgrave Macmillan: London, UK, 2017. [Google Scholar]
- Stokes, J.R.; Rajagopalan, R.M.; Stefanou, S.E. Investment in a methane digester: An application of capital budgeting and real options. Rev. Agric. Econ. 2008, 30, 664–676. [Google Scholar] [CrossRef]
- Department of Energy and Climate Change (DECC). Updated Energy and Emissions Projections; Department of Energy and Climate Change (DECC): London, UK, 2016.
- Brown, I.; Castellazzi, M. Changes in climate variability with reference to land quality and agriculture in Scotland. Int. J. Biometeorol. 2015, 59, 717–732. [Google Scholar] [CrossRef] [PubMed]
- Rivington, M.; Matthews, K.; Buchan, K.; Miller, D.; Bellocchi, G.; Russell, G. Climate change impacts and adaptation scope for agriculture indicated by agro-meteorological metrics. Agric. Syst. 2013, 114, 15–31. [Google Scholar] [CrossRef]
- Miller, D.; Mathes, K.; Buchan, K. Future CAP Payment; The James Hutton Institute: Dundee, UK, 2012. [Google Scholar]
- Wright, I.A.; Birnie, R.V.; Malcolm, A.; Towers, W.; Mckeen, M. The Potential Use of Land Capability for Agriculture Classification for Determining Support to Disadvantaged Areas of Scotland; The Macaulay Institute: Aberdeen, UK, 2006. [Google Scholar]
- Anderson, R.C.; Hilborn, D.; Weersink, A. An economic and functional tool for assessing the financial feasibility of farm-based anaerobic digesters. Renew. Energy 2013, 51, 85–92. [Google Scholar] [CrossRef]
- Binkley, D.; Harsh, S.; Wolf, C.A.; Safferman, S.; Kirk, D. Electricity purchase agreements and distributed energy policies for anaerobic digesters. Energy Policy 2013, 53, 341–352. [Google Scholar] [CrossRef]
- The Waste and Resources Action Programme (WRAP). Digestate and Compost Use in Agriculture; The Waste and Resources Action Programme (WRAP): Banbury, UK, 2016. [Google Scholar]
- Brealey, R.; Myers, S.C.; Marcus, A.J. Fundamentals of Corporate Finance; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
- SAC Consulting. Farm Management Handbook; SAC Consulting: Monastir, Tunisie, 2017. [Google Scholar]
- Fachagentur für Nachwachsende Rohstoffe e.V. (FNR). Leitfaden Biogas-Von der Gewinnung zur Nutzung; Fachagentur für Nachwachsende Rohstoffe e.V. (FNR): Gülzow, Germany, 2010. [Google Scholar]
- Gemmeke, B.; Rieger, C.; Weiland, P.; Schröder, J. Biogas-Messprogramm II, 61 Biogasanlagen im Vergleich; Fachagentur für Nachwachsende Rohstoffe e.V. (FNR): Gülzow, Germany, 2009. [Google Scholar]
- Lusk, P. Methane Recovery from Animal Manures the Current Opportunities Casebook; National Renewable Energy Lab.: Golden, CO, USA, 1998.
- Wilkie, A.C. Anaerobic digestion of dairy manure: Design and process considerations. In Dairy Manure Management: Treatment, Handling, and Community Relations; Natural Resource, Agriculture, and Engineering Service (NRAES) Cooperative Extension: Ithaca, NY, USA, 2005; pp. 301–312. [Google Scholar]
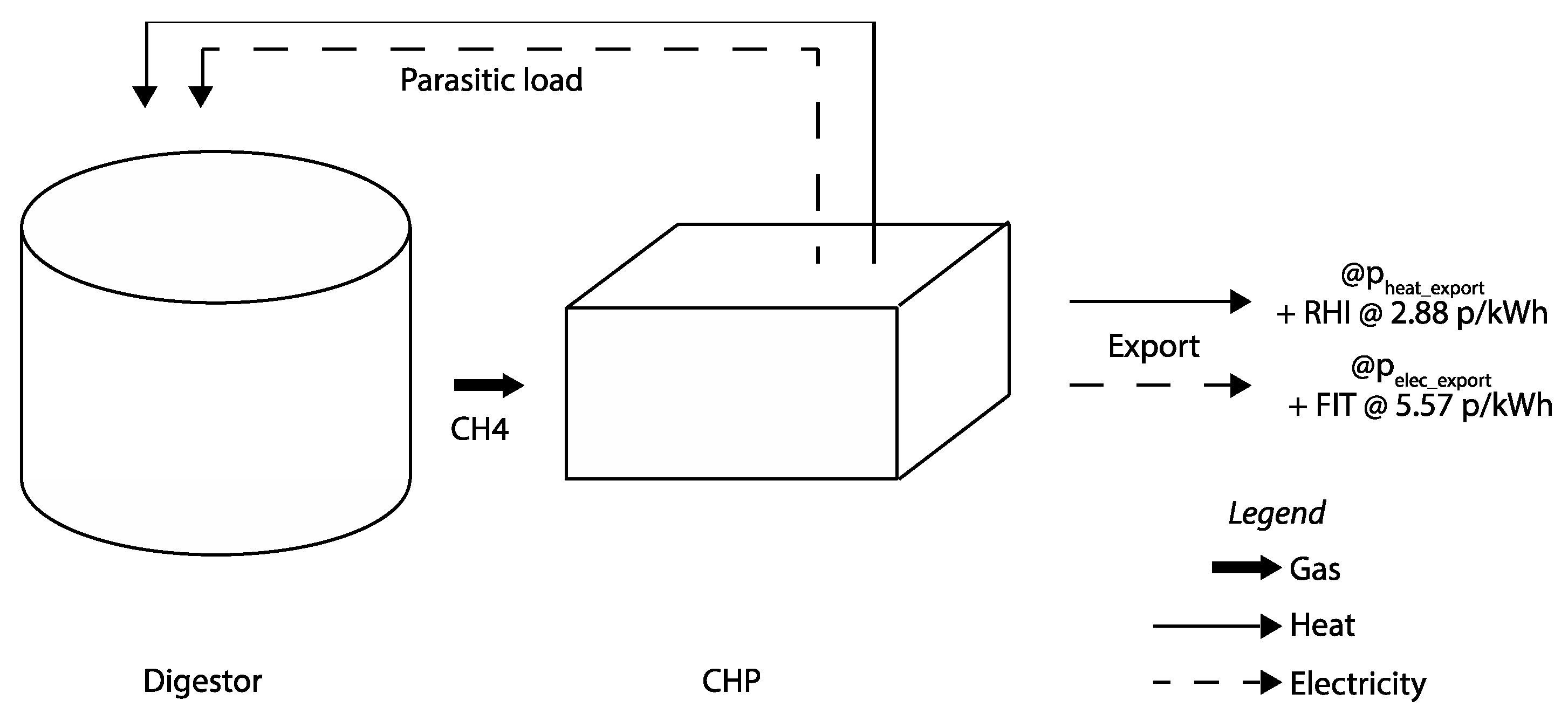
| Support Mechanism | Capacity Band | Before * | Current Rates ** | |
|---|---|---|---|---|
| (kW) | (p/kWh) | (p/kWh) | Δ (%) | |
| FIT | <250 | 8.21 | 5.57 | −32.16 |
| 250–500 | 7.58 | 5.27 | −30.47 | |
| 500–5000 | 7.81 | 1.99 | −74.52 | |
| RHI | <200 | 6.94 | 2.88 | −58.50 |
| 200–600 | 5.45 | 2.26 | −58.53 | |
| >600 | 2.04 | 0.86 | −57.84 | |
| Feedstock | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 |
|---|---|---|---|---|---|
| Solid manure | |||||
| Amount (tonnes/year) | 3040 | 3040 | - | 3040 | 3040 |
| Dry matter (%) | 25 | 25 | - | 25 | 25 |
| Biogas yield (m3/tonne) | 90 | 90 | - | 90 | 90 |
| Liquid cattle manure | |||||
| Amount (tonnes/year) | 1786 | 5118 | 5118 | 1786 | 5118 |
| Dry matter (%) | 10 | 10 | 10 | 10 | 10 |
| Biogas yield (m3/tonne) | 25 | 25 | 25 | 25 | 25 |
| Whole crop rye | |||||
| Amount (tonnes/year) | - | - | 750 | 375 | 625 |
| Dry matter (%) | - | - | 33 | 33 | 33 |
| Biogas yield (m3/tonne) | - | - | 200 | 200 | 200 |
| Production area (ha) | - | - | 25 | 12.5 | 25 |
| Grass silage | |||||
| Amount (tonnes/year) | - | - | 650 | 650 | 650 |
| Dry matter (%) | - | - | 30 | 30 | 30 |
| Biogas yield (m3/tonne) | - | - | 185 | 185 | 185 |
| Production area (ha) | - | - | 20 | 20 | 20 |
| Fodder beet | |||||
| Amount (tonnes/year) | - | - | - | 1063 | - |
| Dry matter (%) | - | - | - | 18 | - |
| Biogas yield (m3/tonne) | - | - | - | 85 | - |
| Production area (ha) | - | - | - | 12.5 | - |
| Total tonnage | 4826 | 8158 | 6628 | 7024 | 9543 |
| Capital Expenditure | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 |
|---|---|---|---|---|---|
| Machinery, £ | |||||
| CHP unit | 144,000 | 210,000 | 210,000 | 256,000 | 260,000 |
| Feedstock insertion | 64,000 | 64,000 | 55,000 | 80,000 | 70,000 |
| Total | 208,000 | 274,000 | 265,000 | 336,000 | 330,000 |
| Building and constr., £ | |||||
| Digestate store | 66,000 | 82,500 | 110,000 | 135,000 | 120,000 |
| Digester | 112,000 | 165,000 | 135,000 | 155,000 | 150,000 |
| Manure storage | 100,000 | 100,000 | 0.00 | 100,000 | 100,000 |
| Silage storage | 0.00 | 0.00 | 145,000 | 120,000 | 145,000 |
| Additional storage | 0.00 | 0.00 | 0.00 | 110,000 | 0.00 |
| Access infrastructure | 50,000 | 60,000 | 60,000 | 70,000 | 65,000 |
| Planning expenses | 12,000 | 14,000 | 14,000 | 18,000 | 16,000 |
| Project management | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 |
| Grid connection | 12,000 | 12,000 | 12,000 | 12,000 | 12,000 |
| Electrics | 12,000 | 12,000 | 12,000 | 13,000 | 13,000 |
| Health & Safety, etc | 12,000 | 12,000 | 12,000 | 13,000 | 13,000 |
| Total | 396,000 | 477,500 | 520,000 | 766,000 | 654,000 |
| £ | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 |
|---|---|---|---|---|---|
| Loader | 8000 | 8000 | 8000 | 8000 | 8000 |
| Labour for feedstock insertion | 2230 | 2230 | 1108 | 3322 | 3230 |
| Labour for plant operation | 9680 | 12,360 | 11,880 | 15,400 | 16,170 |
| Slurry haulage | 0.00 | 1530 | 1530 | 0.00 | 1530 |
| Operating supplies | 24,000 | 30,000 | 30,000 | 28,000 | 28,000 |
| Maintenance and repairs | 24,200 | 29,000 | 28,000 | 44,000 | 45,000 |
| Digestate testing | 300 | 300 | 300 | 300 | 300 |
| Grass silage | 0.00 | 0.00 | 13,200 | 13,200 | 13,200 |
| Whole crop cereal silage | 0.00 | 0.00 | 30,000 | 15,000 | 0.00 |
| Whole crop cereal legume silage | 0.00 | 0.00 | 0.00 | 0.00 | 25,000 |
| Fodder beet | 0.00 | 0.00 | 0.00 | 23,375 | 0.00 |
| Total | 68,410 | 83,420 | 124,018 | 150,597 | 140,430 |
| Parameter | Stochastic? | Distribution | Values |
|---|---|---|---|
| Feedstock quantity | Yes | Uniform | [Min = 90% of base quantity; Max = base quantity]; See Table 2 for base quantities of all feedstock |
| Biogas yield (m3/tonne) | Yes | Triangular | |
| Solid manure | [min 60, mode 90, max 120] | ||
| Liquid cattle manure | [min 20, mode 25; max 30] | ||
| Whole crop rye | [min 170, mode 195, max 220] | ||
| Grass silage | [min 170, mode 185, max 200] | ||
| Fodder beet | [min 75, mode 107.5, max 140] | ||
| Number of AD scenarios | No | - | 5 |
| Number of case studies | No | - | 10,000 |
| Planning horizon (years) | No | - | 20 |
| Lifetime machinery (years) | No | - | 7 |
| Runtime (hours) | Yes | Triangular | [min 7000, mode 7500, max 8000] |
| Energy in methane (kWh/m3) | No | - | 11.2 |
| Percent methane in biogas (%) | Yes | Uniform | [min 45, max 55] |
| Plant electricity efficiency (%) | Yes | Uniform | [min 33, max 45] |
| Plant heat efficiency (%) | Yes | Uniform | [min 38, max 48] |
| Overall plant inefficiency (%) | Yes | Uniform | [min 5, max 15] |
| Parasitic load, electricity (%) | Yes | Uniform | [min 6, max 10] |
| Parasitic load, heat (%) | Yes | Uniform | [min 20, max 40] |
| Annual operation cost, £ | Yes | Uniform | [Min = 90% of base cost; Max = 110% × base cost]; see Table 4 for base costs |
| Inflation rate for electricity and heat price, (%) | No | - | 5 |
| Inflation rate for FIT and RHI level 1 and 2 tariffs, (%) | No | - | 3 |
| Money and finance | |||
| Debt in capital expenditure (%) | No | - | 0.0 |
| Debt interest rate (%) | No | - | 6.5 |
| General inflation rate (%) | No | - | 3 |
| Repayment term (years) | No | - | 10 |
| Tax rate (%) | No | - | 0.0 |
| Scenarios | Indicators | Heat Price (p/kWh) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5.00 | 5.25 | 5.5 | 5.75 | 6 | 6.25 | 6.5 | 6.75 | 7.00 | ||
| Scenario 1 | Mean | 20.69 | 20.45 | 20.26 | 20.04 | 19.83 | 19.62 | 19.4 | 19.21 | 18.99 |
| S.D. | 1.30 | 1.30 | 1.30 | 1.30 | 1.29 | 1.28 | 1.27 | 1.29 | 1.29 | |
| Scenario 2 | Mean | 20.25 | 20.04 | 19.82 | 19.63 | 19.41 | 19.19 | 18.98 | 18.78 | 18.55 |
| S.D. | 1.18 | 1.18 | 1.18 | 1.17 | 1.19 | 1.19 | 1.19 | 1.18 | 1.18 | |
| Scenario 3 | Mean | 27.97 | 27.74 | 27.52 | 27.34 | 27.12 | 26.90 | 26.69 | 26.47 | 26.27 |
| S.D. | 1.49 | 1.50 | 1.52 | 1.51 | 1.50 | 1.51 | 1.51 | 1.52 | 1.51 | |
| Scenario 4 | Mean | 21.06 | 20.82 | 20.62 | 20.39 | 20.20 | 19.99 | 19.77 | 19.56 | 19.36 |
| S.D. | 1.21 | 1.22 | 1.20 | 1.20 | 1.21 | 1.22 | 1.22 | 1.22 | 1.20 | |
| Scenario 5 | Mean | 18.32 | 18.15 | 17.91 | 17.71 | 17.46 | 17.29 | 17.06 | 16.87 | 16.66 |
| S.D. | 1.09 | 1.09 | 1.08 | 1.09 | 1.08 | 1.09 | 1.09 | 1.09 | 1.08 | |
| P(GT+ET) is 0.00 for all project scenarios, regardless of the heat price | ||||||||||
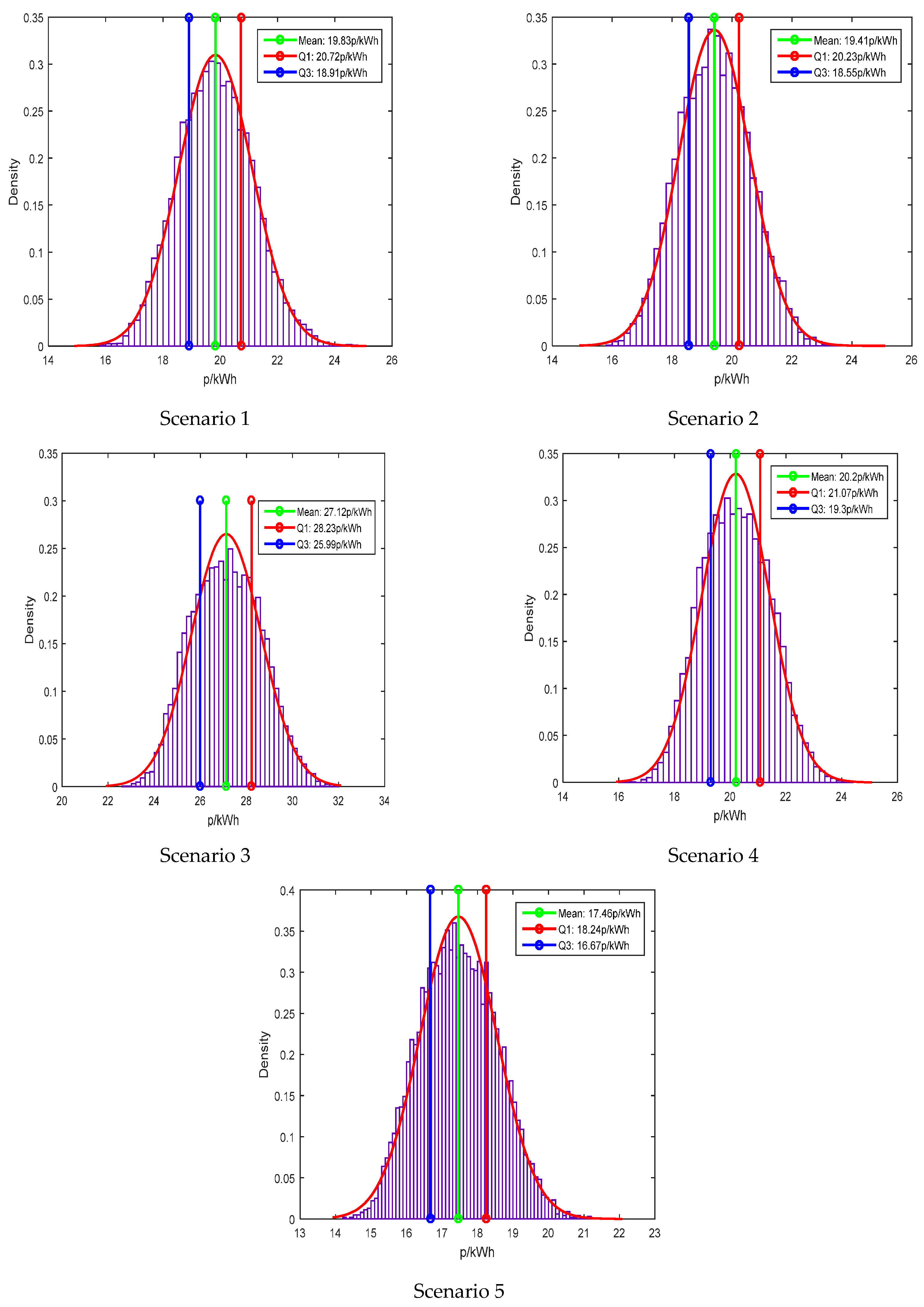
| Scenarios | Mean | Median | S.D. | 95% Confidence Interval | |
|---|---|---|---|---|---|
| Lower | Upper | ||||
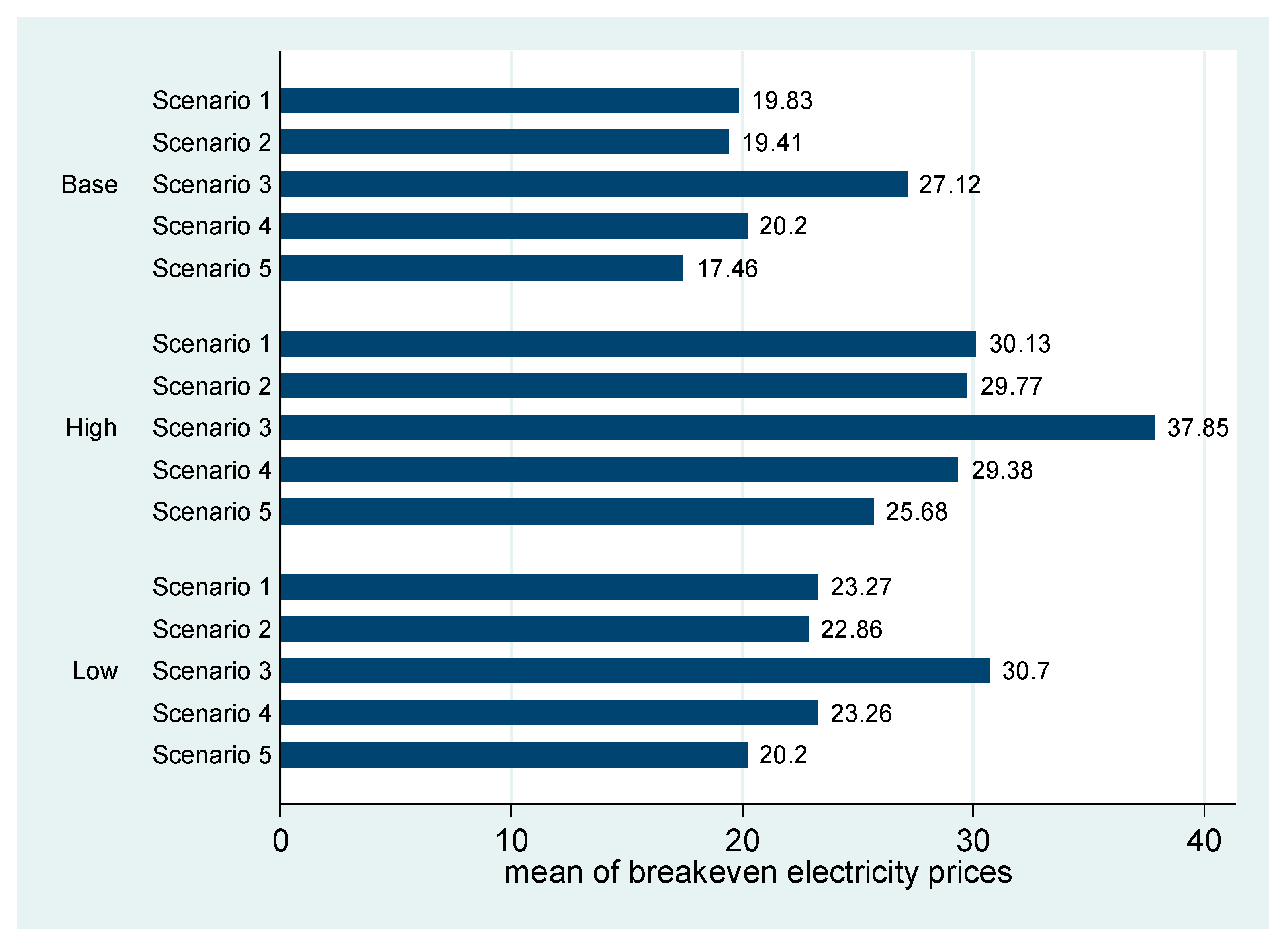
| Scenario 1 | 19.83 | 19.81 | 1.29 | 19.81 | 19.86 |
| Scenario 2 | 19.41 | 19.40 | 1.19 | 19.39 | 19.43 |
| Scenario 3 | 27.12 | 27.12 | 1.51 | 27.09 | 27.15 |
| Scenario 4 | 20.20 | 20.17 | 1.21 | 20.17 | 20.22 |
| Scenario 5 | 17.46 | 17.44 | 1.08 | 17.44 | 17.48 |
| P(GT+ET) is 0.00 for all project scenarios | |||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdul-Salam, Y.; Ehlers, M.-H.; Harnmeijer, J. Anaerobic Digestion of Feedstock Grown on Marginal Land: Break-Even Electricity Prices. Energies 2017, 10, 1416. https://doi.org/10.3390/en10091416
Abdul-Salam Y, Ehlers M-H, Harnmeijer J. Anaerobic Digestion of Feedstock Grown on Marginal Land: Break-Even Electricity Prices. Energies. 2017; 10(9):1416. https://doi.org/10.3390/en10091416
Chicago/Turabian StyleAbdul-Salam, Yakubu, Melf-Hinrich Ehlers, and Jelte Harnmeijer. 2017. "Anaerobic Digestion of Feedstock Grown on Marginal Land: Break-Even Electricity Prices" Energies 10, no. 9: 1416. https://doi.org/10.3390/en10091416
APA StyleAbdul-Salam, Y., Ehlers, M.-H., & Harnmeijer, J. (2017). Anaerobic Digestion of Feedstock Grown on Marginal Land: Break-Even Electricity Prices. Energies, 10(9), 1416. https://doi.org/10.3390/en10091416






