Elimination of Chattering by Control Strategy Based on the Multiphase Sliding Model Control for Efficient Power Conversion in a DC-DC Circuit ^†

Abstract

In this paper, a multiphase sliding mode (MPSM) control method with a master–slave structure is proposed and analyzed in order to suppress ripples at input terminals or output terminals in DC/DC converter applications. With the proposed MPSM, the switching frequency of a multiphase DC/DC converter does not need to be operating such a high switching frequency as adopted in a conventional sliding mode control-based DC/DC converter. As a result, switching power losses could be reduced in this converter. Another advantage of this proposed method is that the master–slave multiphase slide control loop could figure out a proper phase shift between each switching phase of a DC/DC converter instead of precalculated phase shift. The proposed concepts are proven by the PSIM computer simulations and the feasibility of the proposed concepts is validated through the test experiments.

1. Introduction

As the popularity of renewable energy is increased drastically, the improvement and development of advanced power interface circuits such as DC/AC or DC/AC converters are always needed in terms of the efficiency of the system. In renewable/alternative energy applications such as photovoltaic or fuel cell energy system, due to a low voltage output with a high current density, normally a boost mode DC/DC power converter is required. Recently, the ripple current generated from the fuel cells has been issued even in residential and vehicle power applications because this ripple current can propagate through the system, and such a ripple current effect may shorten the fuel cell life and cause a frequent trip due to overcurrent and even harmonics problems. The ripple current suppression is mentioned in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. The slide mode control theory was initially carried out for variable structure systems (VSS) [3]. Since then, due to the fact that switching frequencies of power converters has to be controlled and limited, sliding mode controller (SMC) has been difficult to apply for practical applications directly [4,5]. Seyed et al. [6] proposed a sliding mode algorithm and designed a second order sliding mode model for a DC/DC buck converter for achieving the robust control and fast response especially under load and input voltage variations. The frequency is limited by a complicated algorithm. In order to expand the SMC theory on power converters, a time-optimal-based SMC method for stabilizing output voltage of buck converter under perturbations was introduced [7]. Komurcugil [8] proposed an adaptive terminal sliding-mode control strategy for assuring a finite time convergence of converters. To improve the dynamic response of DC-DC converter, the SMC was explicitly investigated by Tan [9]. Compared to the SMC study on a single phase converter, this paper aims at a multiphase converter. As the switching frequency is bounded in a range, to achieve a certain performance in terms of convergences or stability, the switching frequency will be varied in various ways. Due to the nature of a single-phase converter, the ripple component will vary with the switching frequency, meaning the ripple component generated by SMC cannot be directly controlled. In a typical single-phase power converter, larger inductance or a higher switching frequency could be a solution for mitigating this ripple component, resulting in bulky volumes of the inductor or larger switching power losses. On the contrary to the single-phase power converter, a multiphase power converter with SMC can drive to generate lower harmonics contents and less switching losses [3,10,11,14,16]. For instance, with the same input and output operation conditions, a two-phase power converter will have only one-fourth of the switching losses compared to a single-phase converter. The yielded harmonics from the multiphase power converter will have a smaller amplitude and higher frequency such that the harmonics could be easily filtered away. To generate a proper phase shift between each switching cell, a master–slave structure [17,18,19] is adopted because of the simplicity in terms of self-adjusting and easy implementation instead of the ring configuration proposed in [14,20]. In the following sections, the description of the single-phase SMC and geometric ripple cancellation with multiple switching phase is provided in Section 2. In Section 3, the PSIM simulation and experimental results are provided for demonstrating the operation and validation of multiple-phase slide control mode. The conclusion is provided in Section 4.

2. Sliding Mode Control

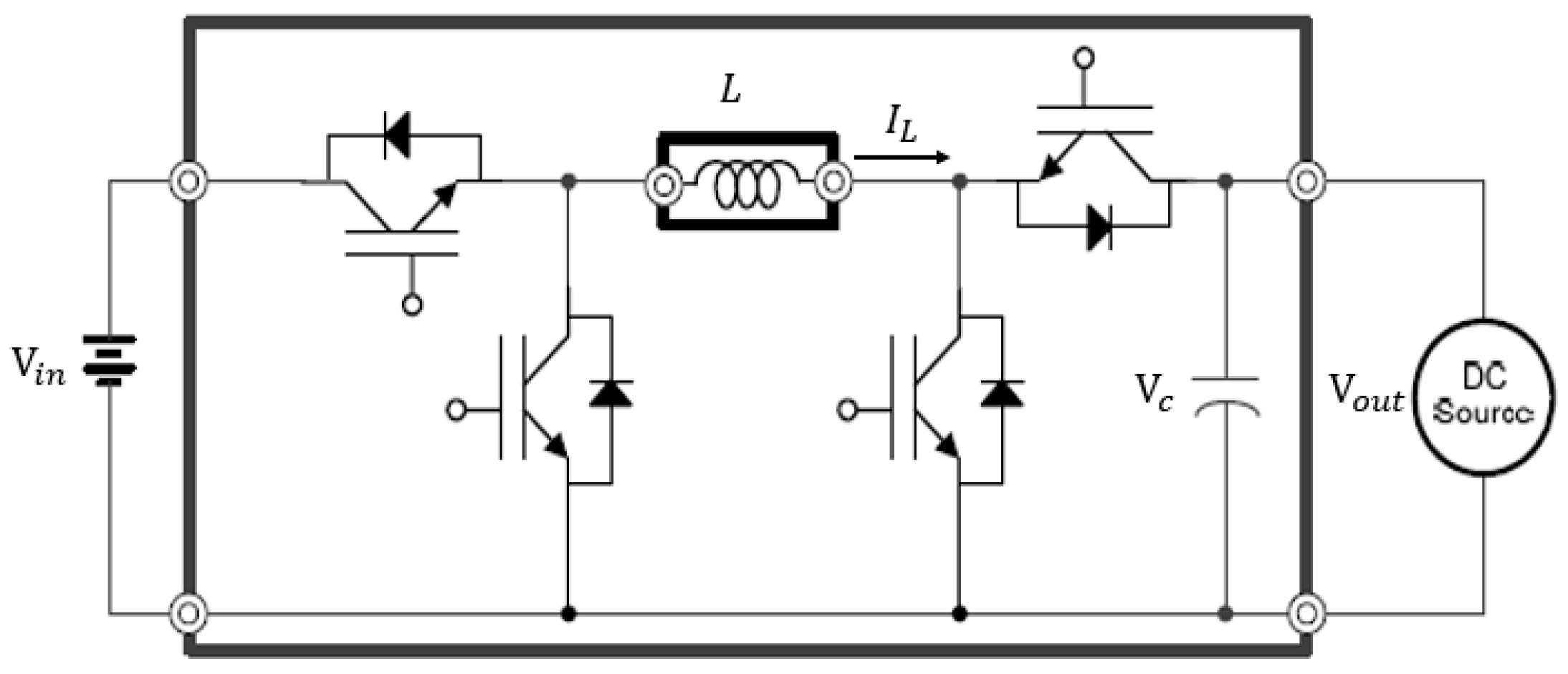
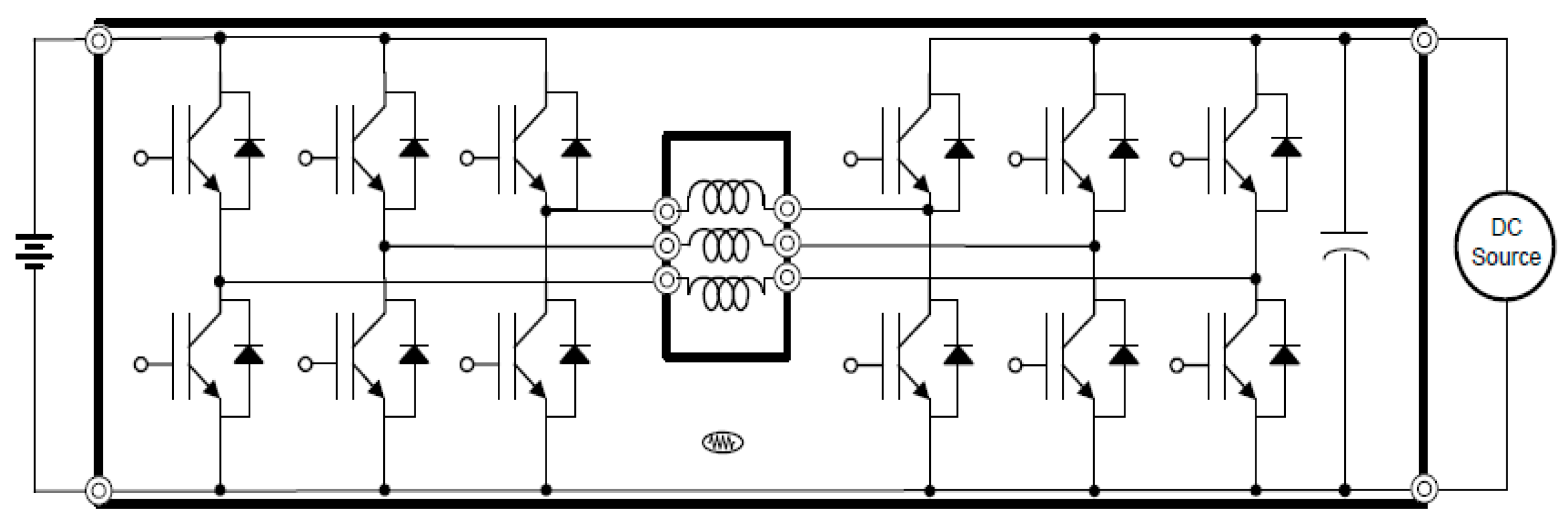
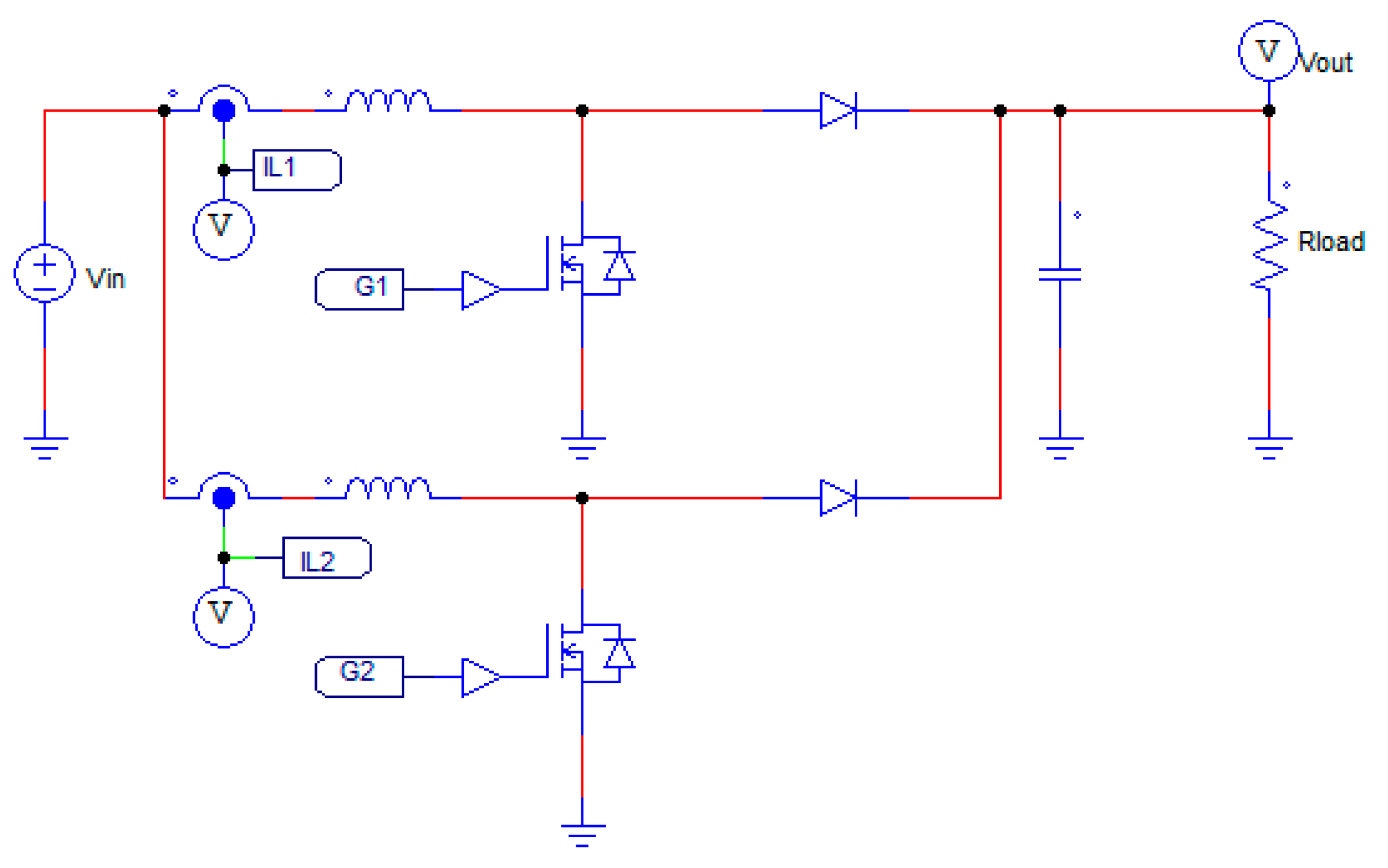
To control a DC/DC converter shown in Figure 1 and Figure 2, one can directly use predesigned pulse width modulation (PWM) signals with known few factors such as a load current, switching cell, acceptable ripple amplitudes, etc. It is quite simple to run a DC/DC converter under a fixed condition. In fact, the operating conditions of a practical DC-DC converter are changing under various circumstances. As a result, the ripple amplitude will be varying based on the traditional PWM control method whereas e Slide Mode Control (SMC) method can have a better advantage for this issue. By informing the control loop with the desired tolerances in advance, SMC loop can identify the switching frequency. To run a DC/DC converter using traditional PWM control method, we have to properly design a controller to avoid instability issues whenever the operating point changes with heavy control design. On the contrary, as long as the input parameters of the slide mode control loop are selected correctly, which means that those parameters can achieve Lyapunov stability in the overall operating ranges, the controller could be built easily with a minimal calculation. For example, when the circuit shown in Figure 1 works as a traditional boost converter, we can design a SMC controller based on Equations (1)–(3). In this case, the input inductor current will be selected as the control input. As long as Equation (1) is always greater than zero, and Equation (2) is always less than zero, the SMC DC/DC boost converter will be always stable. To assist comprehensive understanding of the SMC, a single-phase hysteresis loop is shown in Figure 3.

$$V=s^2={\left(I_{ref}-I_L\right)}^2$$

(1)

where V is Lyapunov candidate, s is the switching surface, I_ref is the reference current and I_L is the Inductor current.

$$\dot{V}=\dot{s}s=-s\times \left(\frac{V_{in}}{L}-\frac{V_c}{L}\times (1-u)\right),\begin{array}{cc}& u=\frac{1+\mathrm{sign}(s)}{2}\end{array}$$

(2)

where V_in is the input voltage, V_c is the capacitor voltage, and u is the control input.

(i) Single-Phase SMC

In general, a system could be written as the following form:

$$\dot{x}=f\left(x\right)+b\left(x\right)u$$

(3)

where

• u is the system input and has a definition of –M sign($\mathsf{\sigma }$).
• $\sigma$ is the selected slide manifold of the system.
• M is the positive constant.

If the sliding surface $\sigma$ is linearly related to the system state, x, then the derivative of the system could be drawn as:

$$\dot{\sigma }=A\left(x\right)+B\left(x\right)u$$

(4)

where

$$\frac{\partial \mathsf{\sigma }}{\partial \mathrm{t}}=\frac{\partial \mathsf{\sigma }}{\partial x}\times \frac{\partial x}{\partial t}=\frac{\partial \mathsf{\sigma }}{\partial x}\dot{x}=\frac{\partial \mathsf{\sigma }}{\partial x}f\left(x\right)+\frac{\partial \mathsf{\sigma }}{\partial x}b\left(x\right)u$$

Let’s use A(x) for denoting $\frac{\partial \mathsf{\sigma }}{\partial x}f\left(x\right)$, and use B(x) for denoting $\frac{\partial \mathsf{\sigma }}{\partial x}b\left(x\right)$.

Assume that there are no additional unmodeled dynamics, the width of the chattering of this one-dimensional system could be presented by:

$$\Delta =\left|{\dot{\sigma }}_{+}\right|\times T_{\sigma +}=\left|{\dot{\sigma }}_{-}\right|\times T_{\sigma -}$$

(5)

where

$$\begin{gathered} \left|{\dot{\sigma }}_{+}\right|=A\left(x\right)-B\left(x\right)\times M \\ \left|{\dot{\sigma }}_{-}\right|=A\left(x\right)+B\left(x\right)\times M \end{gathered}$$

To understand the correlation between the widths of the chattering, dynamic the system trajectories, there should be additional information:

$$T_{sw}=T_{\sigma +}+T_{\sigma -}$$

(6)

Also, if the system is assumed to be stable, B(x)M should be greater than A(x) because if the system is unstable during both turn-on and turn-off periods, then the system trajectory will be definitely deviated from the slide surface, which is totally undesirable. Therefore, the $T_{sw}$ could be further written as:

$$T_{sw}=\frac{2\Delta B\left(x\right)M}{B{\left(x\right)}^2{M}^2-A{\left(x\right)}^2}$$

(7)

As a result:

$$\Delta =\frac{B{\left(x\right)}^2{M}^2-A{\left(x\right)}^2}{2\Delta B\left(x\right)M}\times T_{sw}$$

(8)

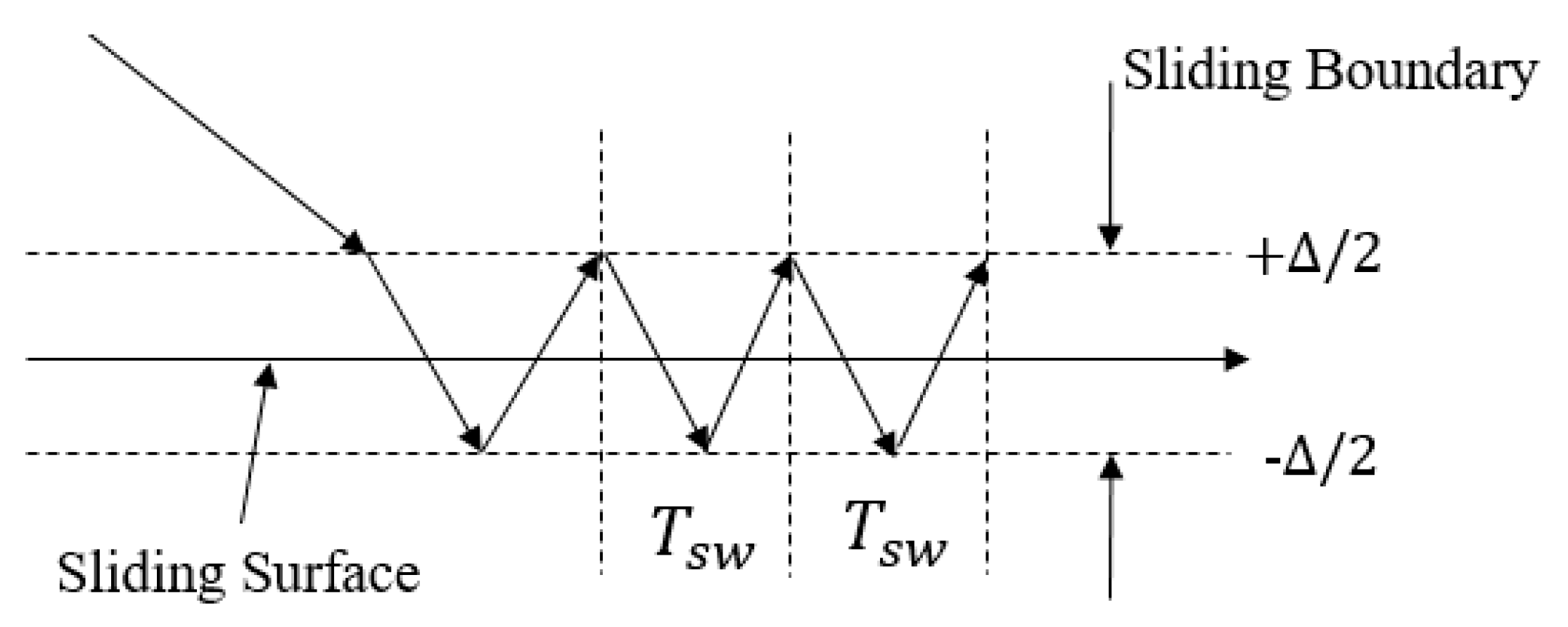
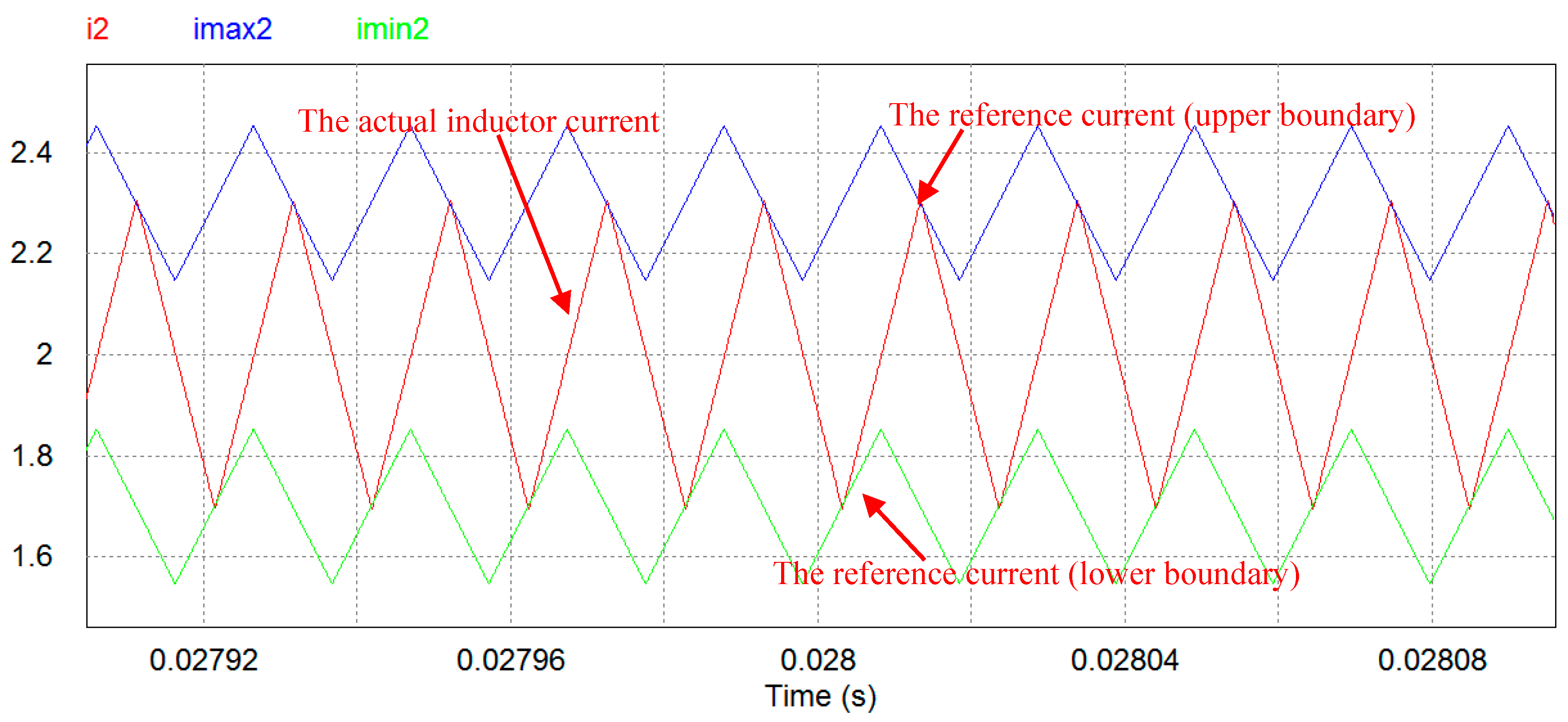
In a power converter system, the parameters of passive components such as inductor and capacitor will be definitely invariant during the operation. It means that as long as the input and output parameters (currents and voltages) of the power converter and the switching period are kept constant while operating, the sliding boundary would be inherently limited, which is shown in Figure 4. Changes in input parameters or output parameters potentially introduce an increase in the sliding boundary. If so, in order to diminish the chattering amplitude in a single-phase power converter, the switching frequency of the power converter has to be increased. As mentioned above, increasing switching frequency may not be beneficial for the system efficiency. Also, the width of the hysteresis loop determines the amplitude of the current chattering so that the single-phase SMC control still shares the same issue being faced with traditional PWM control. However, the multiphase converter shown in Figure 5 can be a reasonable solution if the phase error between each phase could be maintained.

(ii) Multiple-Phase SMC

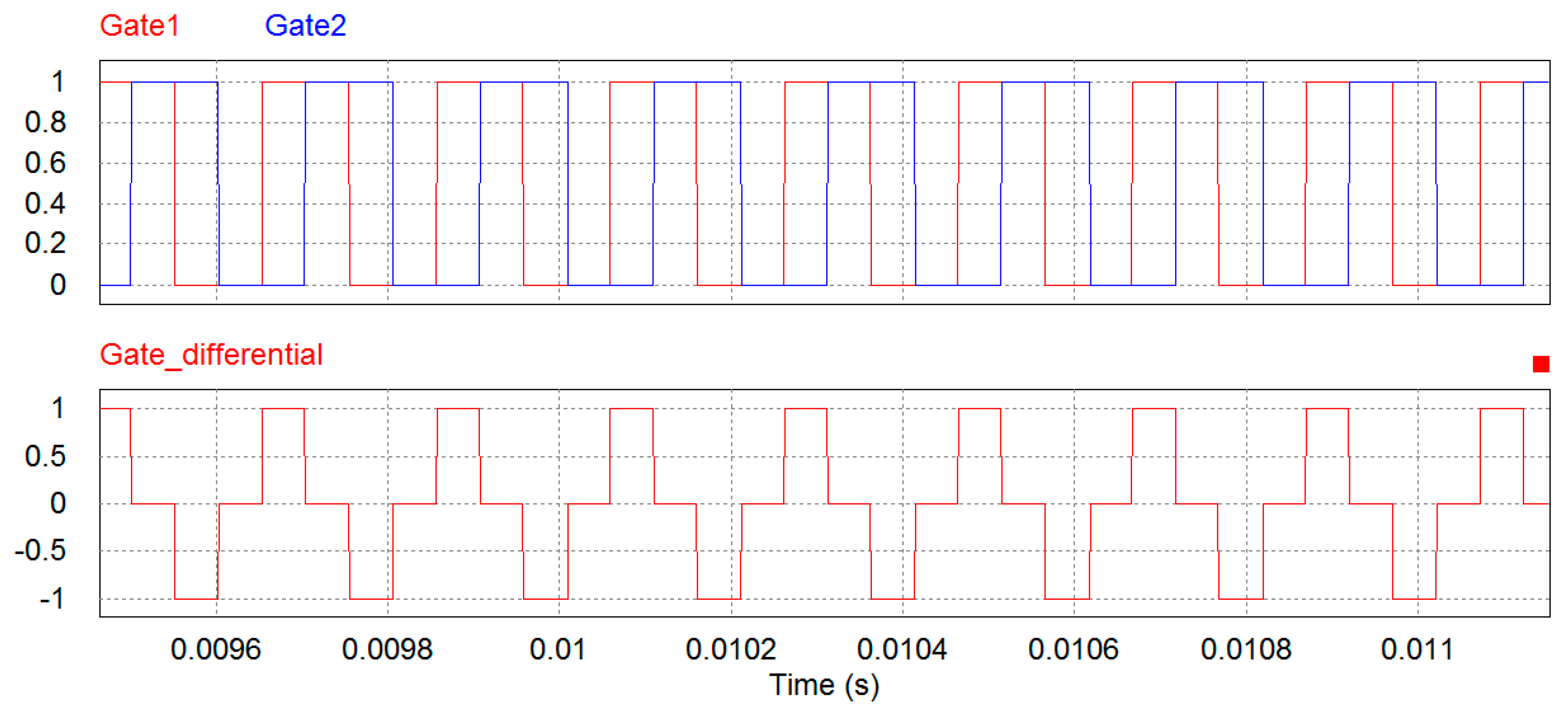
On the contrary, by using a multiple-phase power converter, the chattering issue could be dramatically mitigated, while the difficulty of the SMC design of a multiplephase power converter will get higher. It may be easy to choose an appropriate switching frequency and phase error for meeting the chattering tolerance, as long as the system parameters such as voltage, current, inductance, and capacitance are known in advance. Therefore, the multiphase SMC scheme is supposed to be handling the various system dynamics while suppressing the chattering.

There are two questions to be answered: (1) How to build the intercorrelated phase error; (2) how we could dynamically manipulate the switching frequency if the system status changes.

(1) Build intercorrelated phase error:

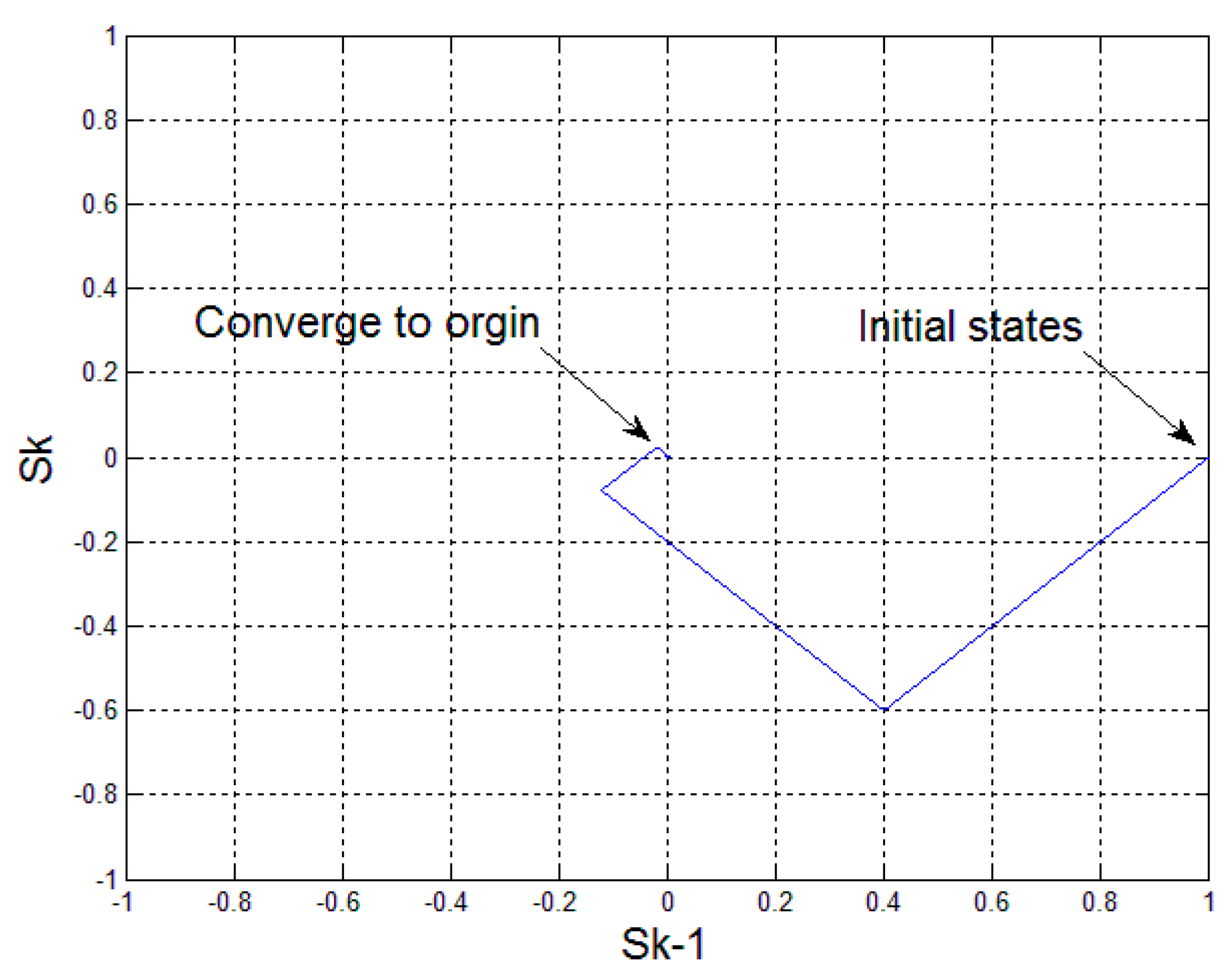
Based on the slide mode control scheme, the objectives in this section are to guarantee the desired phase error while making sure each slide surface will eventually converge to zero.

Given the Lyapunov theories, as long as the sliding mode condition $s_k·\dot{s_k}<0$ is guaranteed, each switching phase of the system could be definitely stable. Also, two consecutive slide surfaces can have an intercorrelation as follows:

$$\begin{gathered} {\dot{s}}_{k-1}=-2\mathrm{sign}\left(s_{k-1}\right)+3\mathrm{sign}\left(s_k\right) \\ {\dot{s}}_k=-3\mathrm{sign}\left(s_{k-1}\right)-2\mathrm{sign}\left(s_k\right) \end{gathered}$$

(9)

where k = 1, 2, 3, …

According to the Figure 6, the Lyapunov stability on each slide surface is assured, and also every phase converges to zero eventually, which is desirable on a multiphase SMC system.

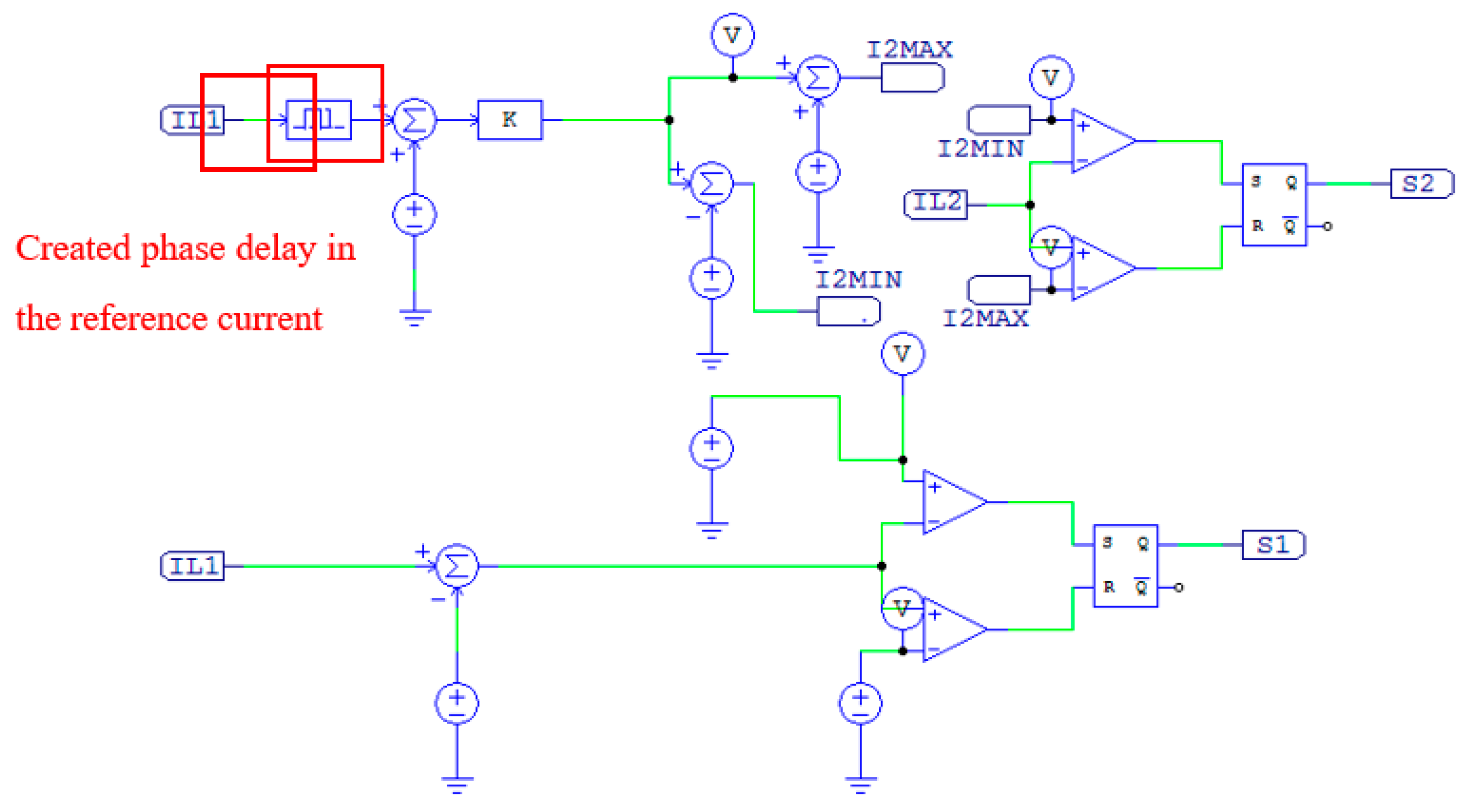
(2) Propose a master-slave slide mode control scheme:

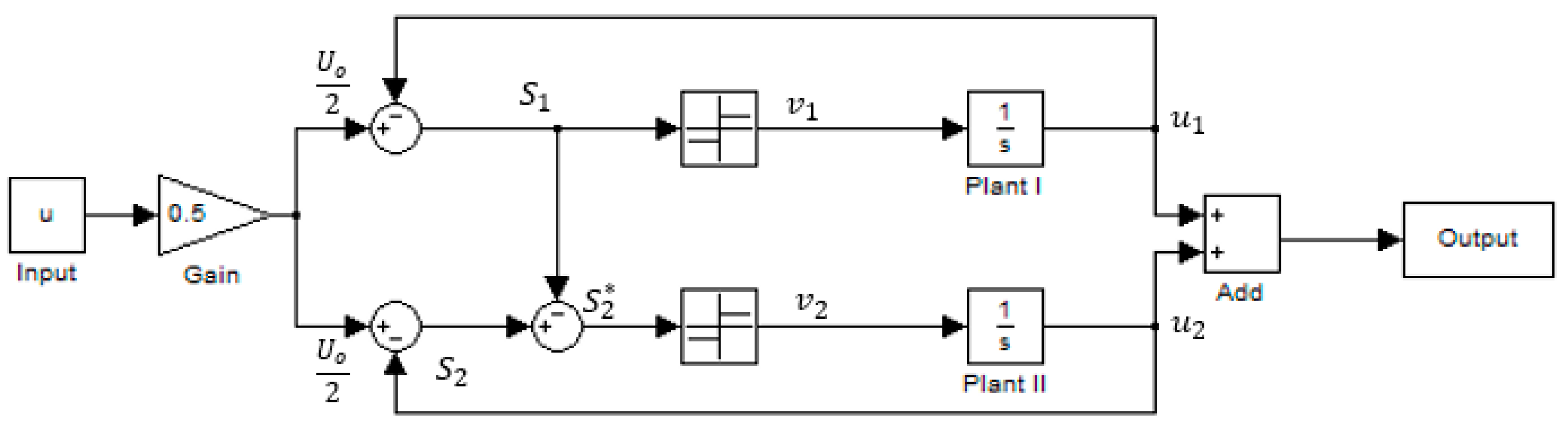
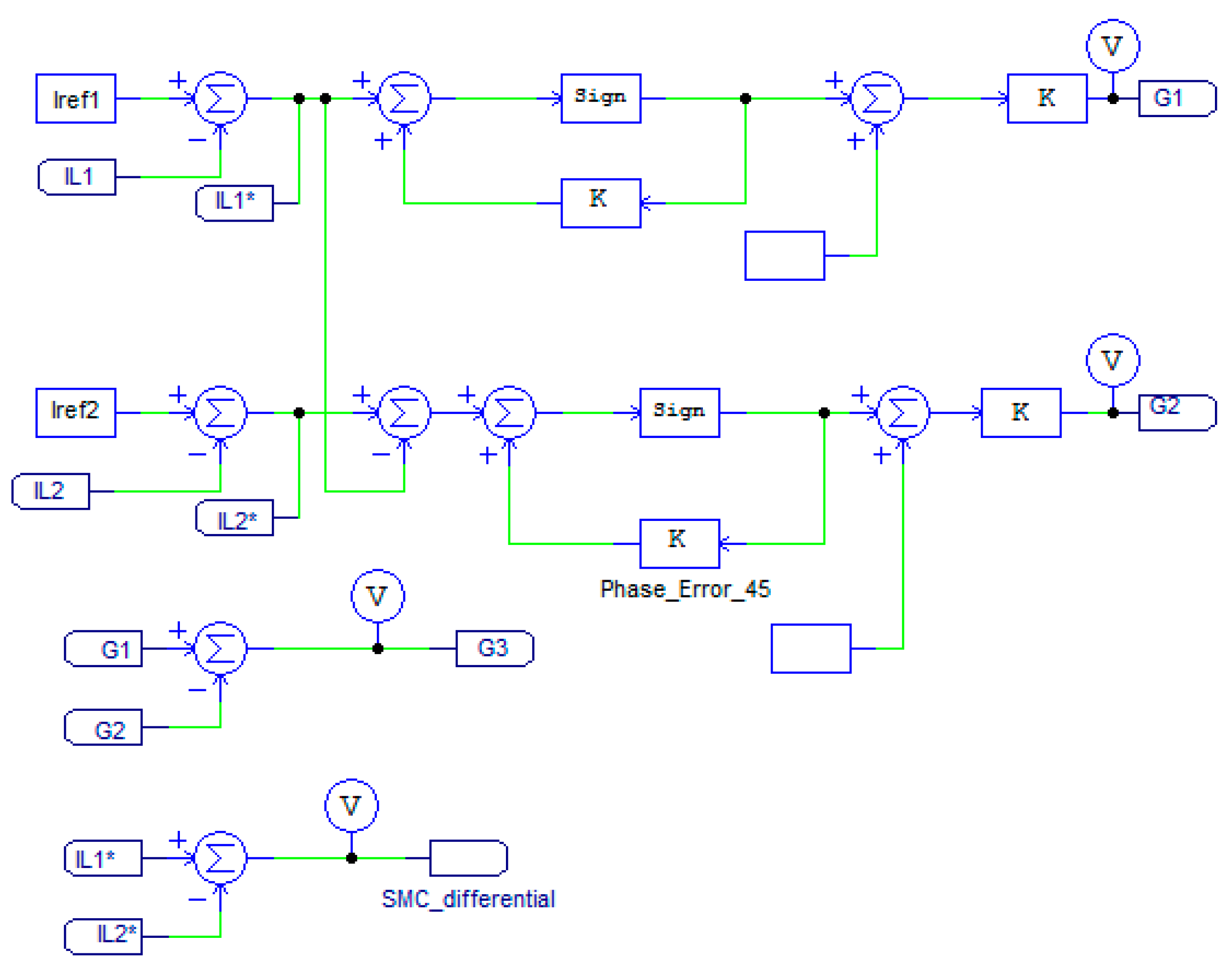
To achieve the desired phase error, a master–slave slide mode control scheme is proposed. The methodology is to have the first switching phase chattering around its desired slide surface, and then refer this trajectory to the second switching phase. And then refer the trajectory of the second sliding surface to the third switching phase. A two-phase master slide mode system can be seen in Figure 7.

Given Figure 7, the following equations can be considered:

$$\begin{gathered} {\dot{s}}_1=a-M\mathrm{sign}\left(s_1\right) \\ {\dot{s}}_2{}^{*}=M\mathrm{sign}\left(s_1\right)-M\mathrm{sign}\left(s_2\right) \end{gathered}$$

(10)

where s₁ and s₂ are switching surfaces for each phase.

$$\begin{array}{c}{s}_2{}^{*}=s_2-s_1\hfill \\ s_1=\frac{U_0}{2}-u_1;s_2=\frac{U_0}{2}-u_1;\hfill \\ v_1=M\mathrm{sign}\left(s_1\right);v_2=M\mathrm{sign}\left(s_2{}^{*}\right)\hfill \end{array}$$

M is the switching gain. (In the case shown in Figure 7, M equals 1), $a$ is the circuit nature. (In the case shown in Figure 7, $a$ equals 0).

Because both ${\dot{s}}_1$ and ${\dot{s}}_2{}^{*}$ have different dynamics, $s_1$ and $s_2{}^{*}$ will definitely have different hysteresis. However, $s_1$ and $s_2$ are supposed to have the same hysteresis. Before further the discussing of the multiphase control, the following information could be derived.

$$T_{sw}=\frac{\Delta }{M+a}+\frac{\Delta }{M-a}=\frac{2M\Delta }{M^2-a^2}$$

(11)

In general, the passive components in a power electronic system will be fixed in terms of parameters like inductance, capacitance, and resistance. Therefore, M is to be constant. Assume that the multiphase SMC system works properly and the first slide surface can provide a calculated switching frequency as long as the hysteresis width of the chattering could be given. Then the hysteresis of $s_2{}^{*}$ could be further derived with the calculated switching frequency, and a desired phase error. Based on the nature of the ON/OFF switching signal and above Equation (10), the slope of the $s_2{}^{*}$ is supposed to be 2M during the phase delay (assume that $\mathrm{sign}\left(s_1\right)$ can be 1, and $\mathrm{sign}\left(s_2{}^{*}\right)$ can be 0, and vice versa). So the width of the hysteresis $s_2{}^{*}$ is:

$${\Delta }^{*}=2M{T}_{\theta }$$

(12)

where $T_{\theta }$ is the desired phase delay.

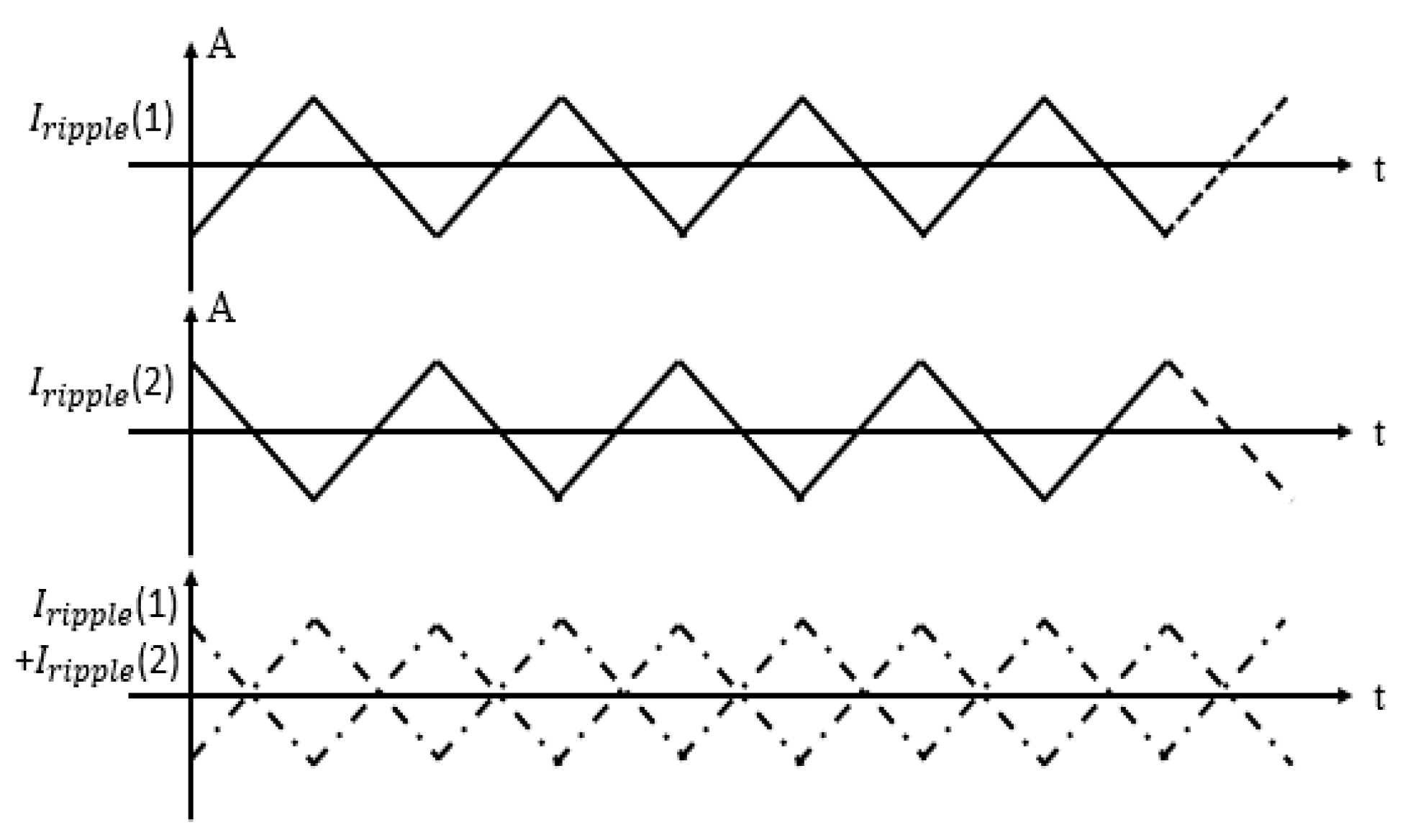
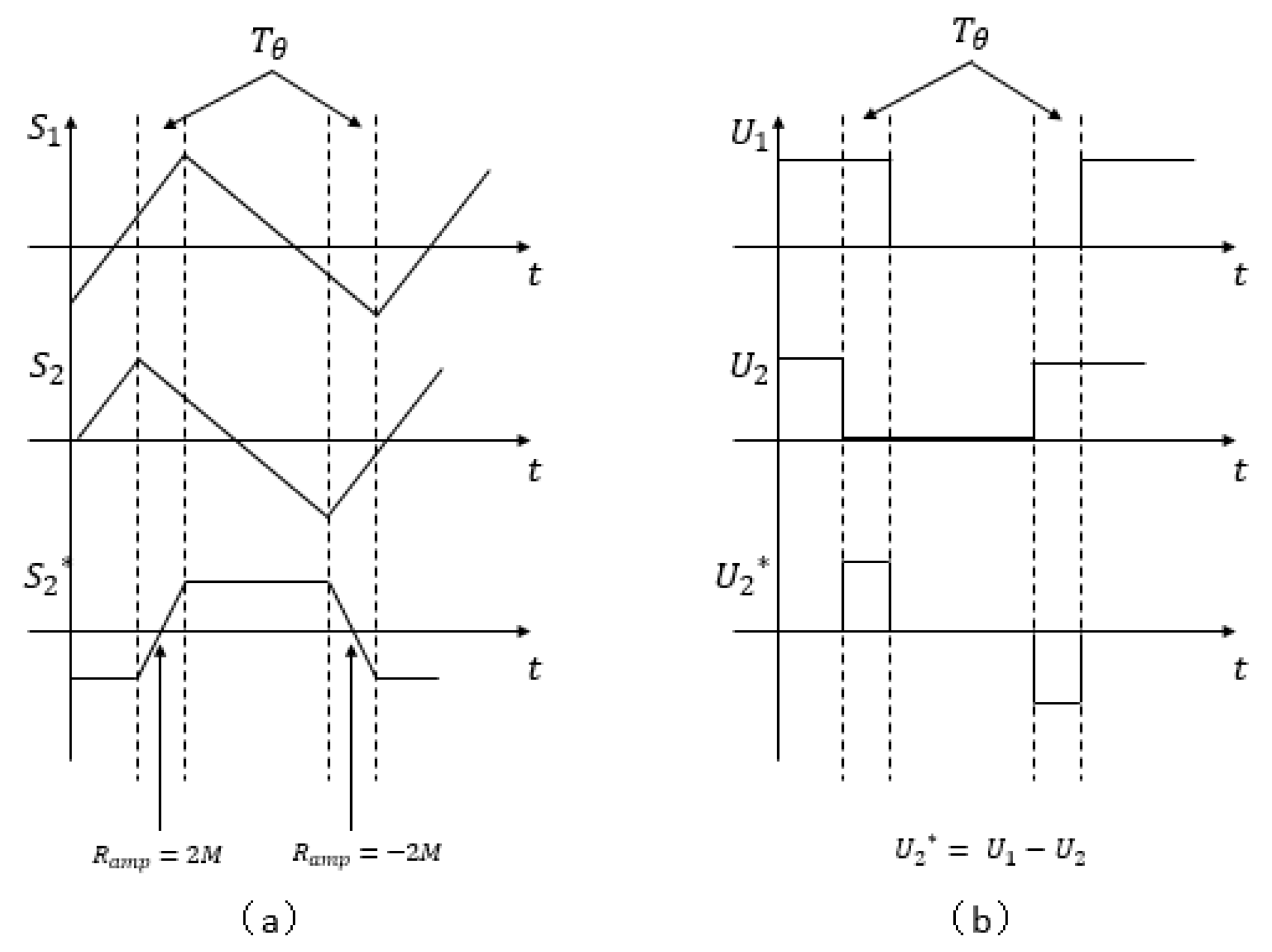
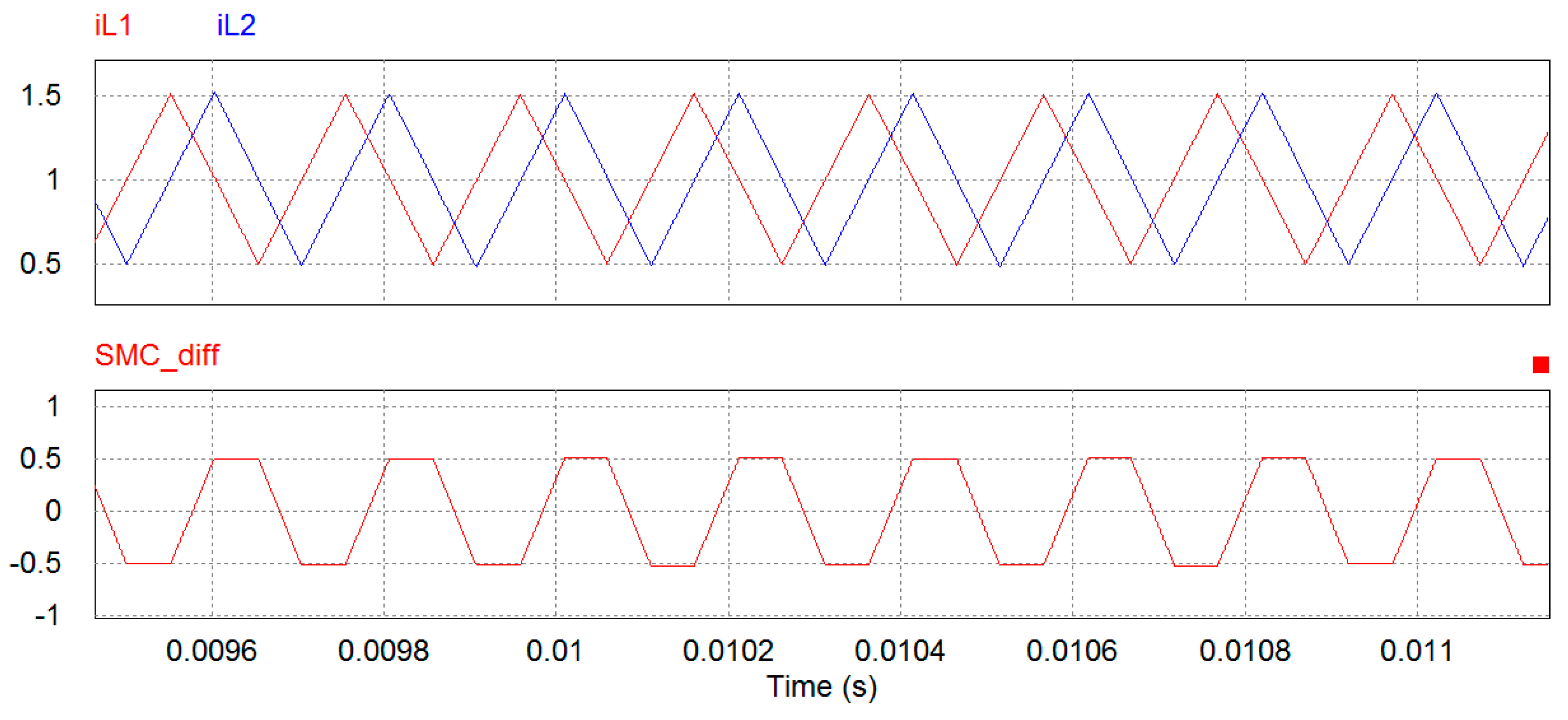
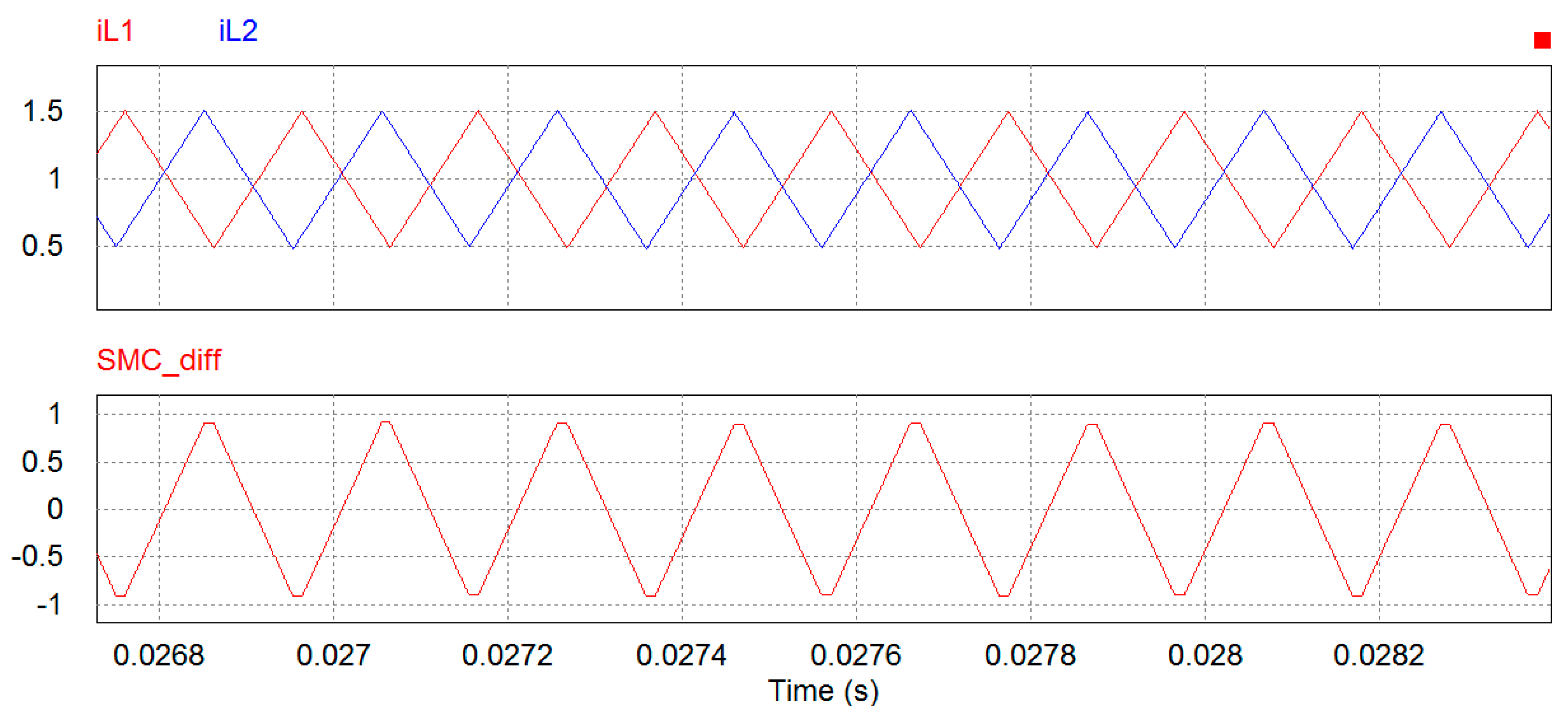
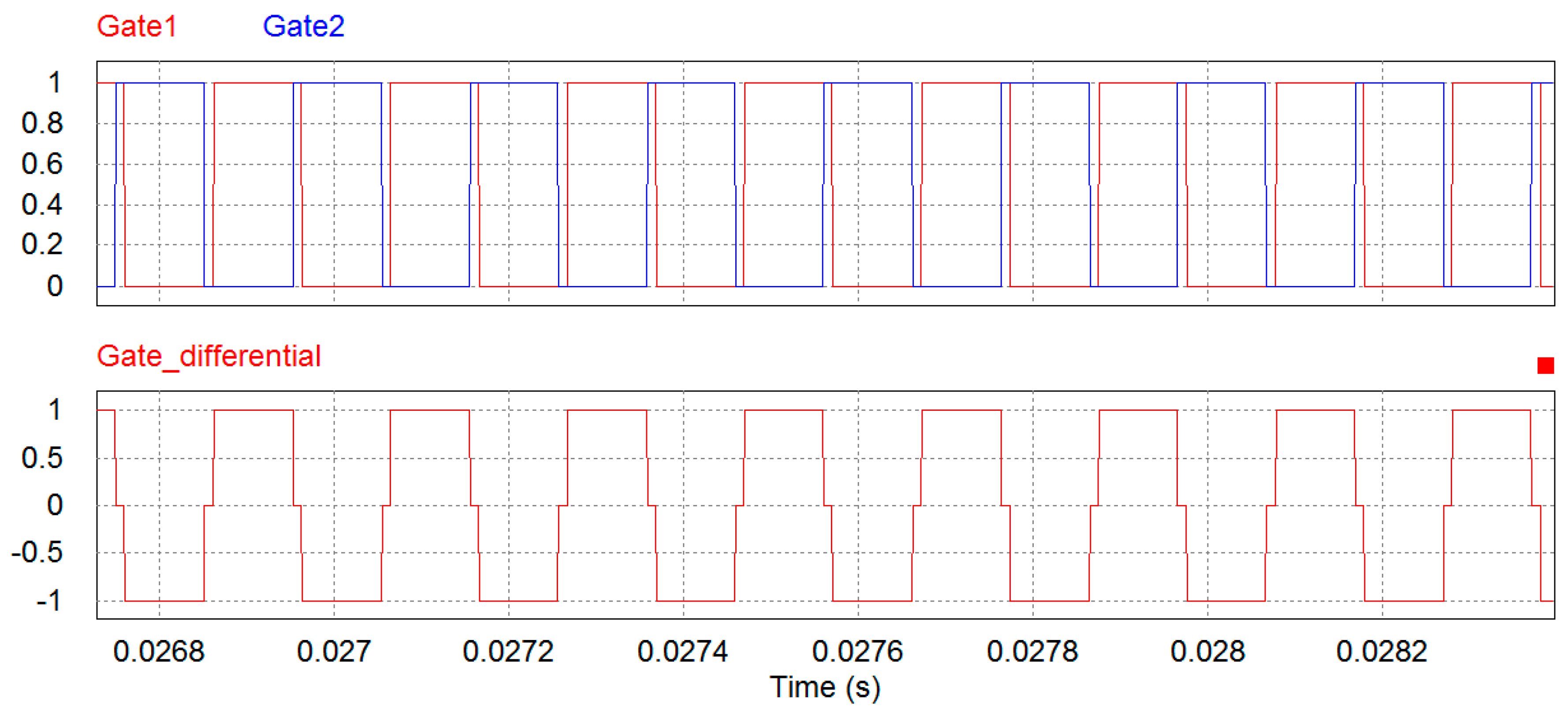
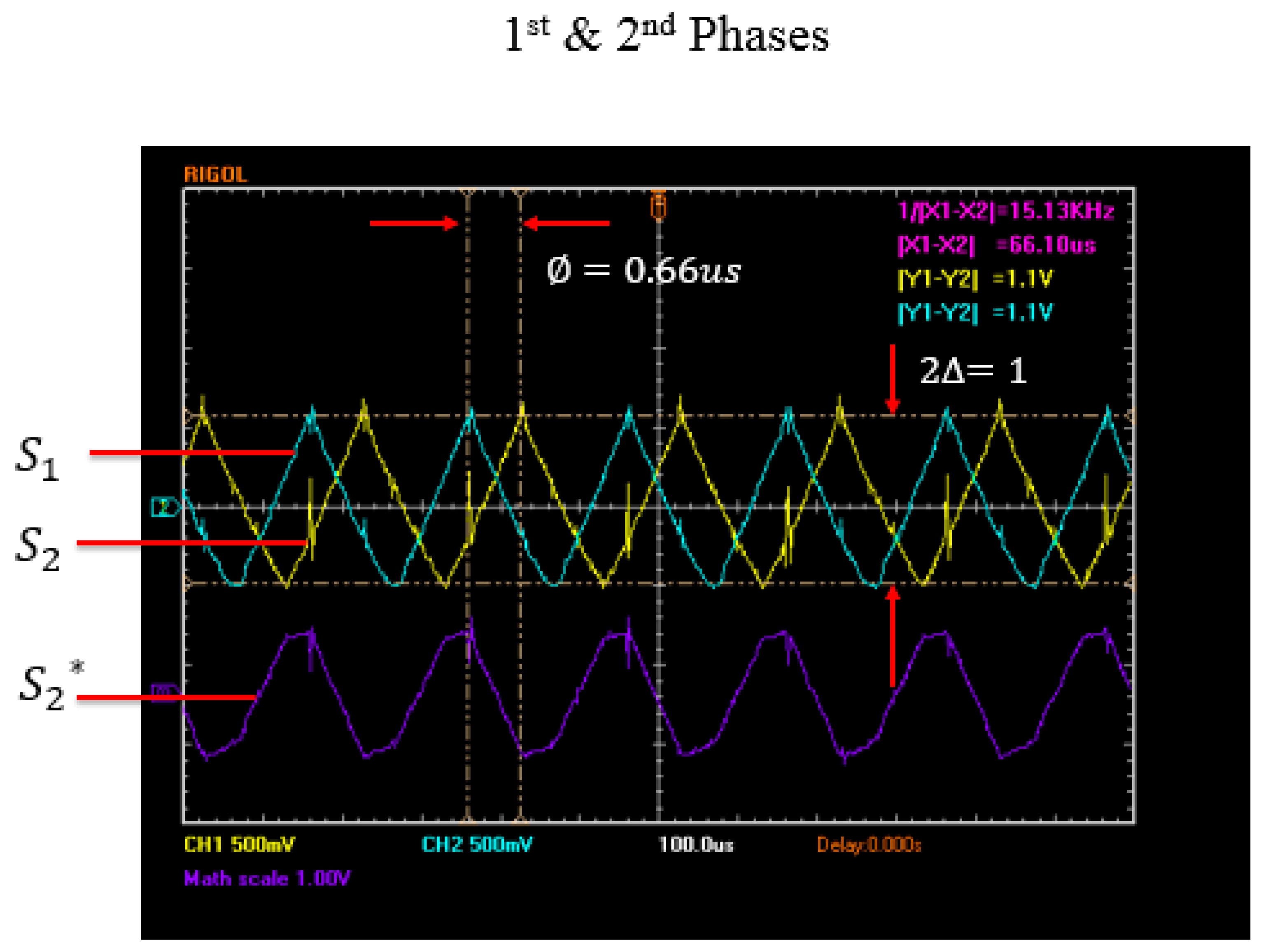
Figure 8a illustrates the consequence of having a phase delay between two switching phases. $s_2{}^{*}$ directly presents a hysteresis loop between two switching phases. Ideally, if parameters of two switching phases, $s_1$ and $s_2$ are identical, then the ramps of the rising edge and falling edge of $s_2{}^{*}$ are supposed to be also identical in terms of absolute values. In Figure 8b, $U_2{}^{*}$ represents the difference between inputs of two slide surfaces $s_1$ and $s_2$. The polarity of $U_2{}^{*}$ accordingly indicates the rising edge and falling edge of $s_2{}^{*}$.

3. Simulation and Experimental Results

3.1. Simulation

This concept could be validated by the following PSIM simulations.

Figure 9 and Figure 10 show a two-phase boost converter and its two-phase master–slave SMC loop. In the case that the boost converter is operated at 5 kHz of the switching frequency, the hysteresis width of the first switching phase could be as 1 A based on the load current. If 1/4 $T_{sw}$ delay between two phases is desirable, according to the SMC principle above, the hysteresis width of the $s_2{}^{*}$ will be 0.5 A. Figure 11 and Figure 12 can validate these hysteresis setups.

The state–space equations of a two-phase boost converter are:

$$\begin{gathered} L\frac{diL1}{dt}=V_{in}-V_{out}(\frac{1+\mathrm{sign}\left(s_1\right)}{2}) \\ L\frac{diL2}{dt}=V_{in}-V_{out}(\frac{1+\mathrm{sign}\left(s_2\right)}{2}) \\ C\frac{dVc}{dt}=I_{L1}+I_{L2}-\frac{V_{out}}{R} \end{gathered}$$

(13)

where L and C are inductor and capacitor values.

Assume that the physical parameters of the two switching phases are identical. Whenever sign(s₁) and sign(s₂) are different, the rising edge and falling edge of the hysteresis of s₂ will be formed. The velocity of the ramp signal based on the given the state–space equations of a two-phase boost converter above would be $\frac{V_{out}}{L}$, where s_n is the n-th inductor current slide surface.

For example:

s₁ = i_L1 − i_Lref/2
 s₂ = i_L2 − i_Lref/2

(14)

If sign(s₁) and sign(s₂) are identical, then the velocity of s₂* would be zero.

$$\dot{s_2{}^{*}}=s_1-s_2=V_{in}-V_{out}(\frac{1+\mathrm{sign}\left(s_1\right)}{2})-[V_{in}-V_{out}(\frac{1+\mathrm{sign}\left(s_2\right)}{2})]=0$$

(15)

where the sign of s₁ equals the sign of s₂.

If sign(s₁) and sign(s₂) are different, for example, sign(s₁) equals +1, and sign(s₂) equals −1, then;

$$\begin{gathered} L\times \dot{s_2{}^{*}}=s_1-s_2=V_{in}-V_{out}(\frac{1+\mathrm{sign}\left(s_1\right)}{2})-[V_{in}-V_{out}(\frac{1+\mathrm{sign}\left(s_2\right)}{2})] \\ =-V_{out}-0=-V_{out} \\ \dot{s_2{}^{*}}=-\frac{V_{out}}{L} \end{gathered}$$

(16)

If sign(s₁) equals +1 and sign(s₂) equals −1, then;

$$\begin{gathered} L\times \dot{s_2{}^{*}}=s_1-s_2=V_{in}-V_{out}(\frac{1+\mathrm{sign}\left(s_1\right)}{2})-[V_{in}-V_{out}(\frac{1+\mathrm{sign}\left(s_2\right)}{2})] \\ =0-(-V_{out})=V_{out} \\ \dot{s_2{}^{*}}=\frac{V_{out}}{L} \end{gathered}$$

(17)

According to the above equations, the ramps of rising edge and falling edge of the hysteresis of $s_2{}^{*}$ are only determined by the output voltage and input inductance, where $s_2{}^{*}$ are the joint slide surface of the slide surface $s_1$ and the slide surface $s_2$. This feature could be also seen in a multiphase boost converter system.

In this case, $V_{out}$, L, and desired phase delay will jointly determine the shape of the hysteresis which could be seen in Figure 11 in the time domain.

Figure 13 and Figure 14 illustrate the cases where the phase delay of the two-phase boost is set to 45% of the switching frequency, T_s. The changes in the hysteresis of s₂* could be easily seen.

To realize the hysteresis loop control, there will be multiple solutions. In this paper, the switch-gain solution seen in Figure 10 is used because the switch-gain solution is easy to implement in a DSP-controlled system. The control loop could be seen in Figure 15. As seen in Figure 16, the actual inductor current is limited and formed by the two-phase delayed current reference signals within the boundaries. And such actual inductor current will inherently possess the phase delay carried by the reference signals. The disadvantage of this reference-signal solution is the complexity in terms of implementations. It is obvious that more switch phases are needed, more phase-delayed reference signals and flip-flop devices are required. For example, a two-phase system needs four reference signals with different time delay and DC offset. A three-phase system needs six reference signals with different time delay and DC offset and vice versa. The I_L1 means the inductor current of the first switching phase.

3.2. Experiment

For the experimental validation of the proposed strategy, a three-phase boost converter is built. The parameters of the system inputs, outputs, and each phase are summarized in

Table 1. System parameters.

Three-Phase Boost Mode
Components	Parameters
$V_{in}$	10 V
$V_{out}$	20 V
L	1 mH
$R_{load}$	20 Ω
$f_s$	5 kHz
M	1
$\alpha$(3 phases)	0.6667

.

The control diagram (boost mode) is shown in Figure 17, where the control diagram is embedded into TI 28335. The 1st and 2nd phase inductor currents of the three-phase boost converter are shown in Figure 9. The snapshot of 2nd and 3rd phase inductor current is the same as Figure 9 although it is not seen in the digest.

Figure 17 shows the DSP implementation based on TI DSP 28335. The 1st and 2nd phase currents are shown in Figure 18. As in Figure 11 and Figure 13, a similar s₂* is observed.

4. Conclusions

In this paper, the concept of multiphase slide mode control method is analyzed. The PSIM simulations and experimental results have proven the validity of the proposed control method. For an experimental validation, a three-phase DC/DC buck converter has been constructed. The switching frequency generated by the multiphase sliding mode (MPSM) control loop is limited around 10 kHz for achieving a better visible illustration. For building a practical MPSM converter, the switching frequency range could be in few hundreds of KHz depending the PCB layout and DSP capacity. Consequently, the ripples could be further suppressed and the power density of the circuitry could be increased if equipped with MPSM.