Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods
Abstract
:1. Introduction
2. MPPT Algorithms
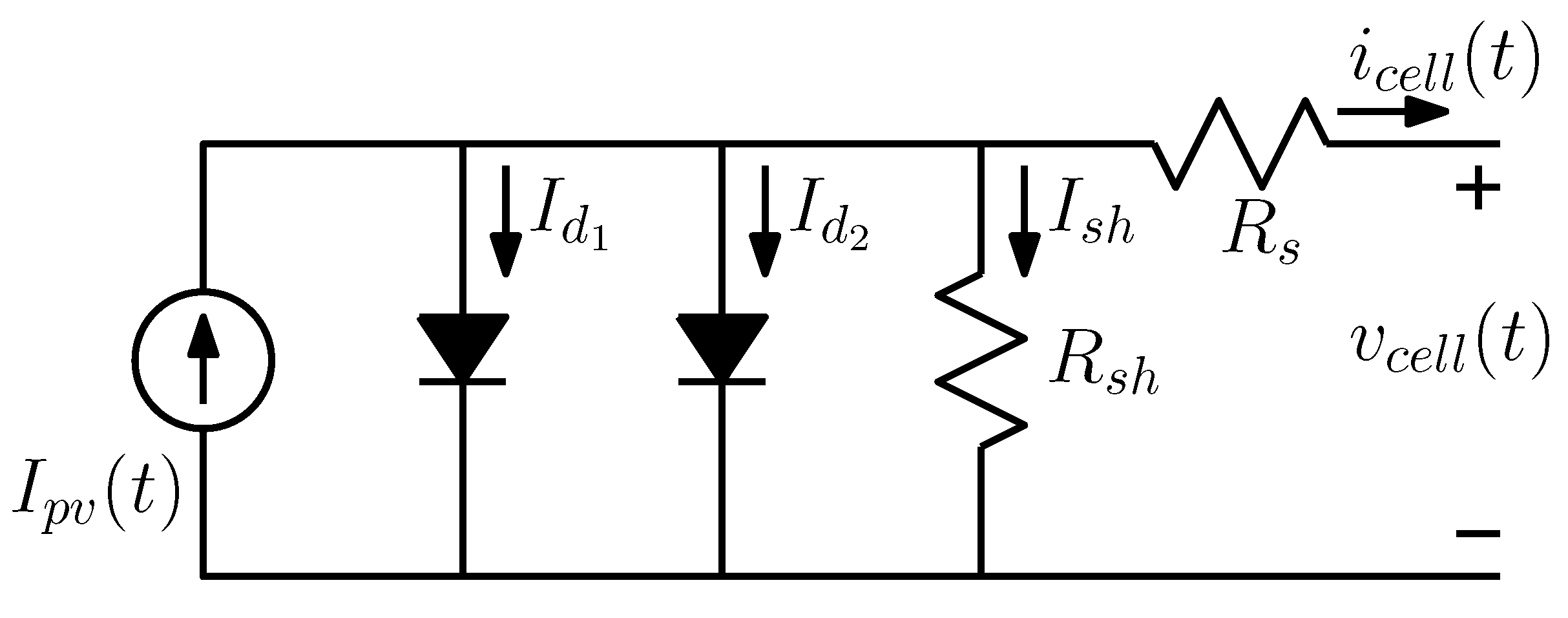
2.1. Power Electronics
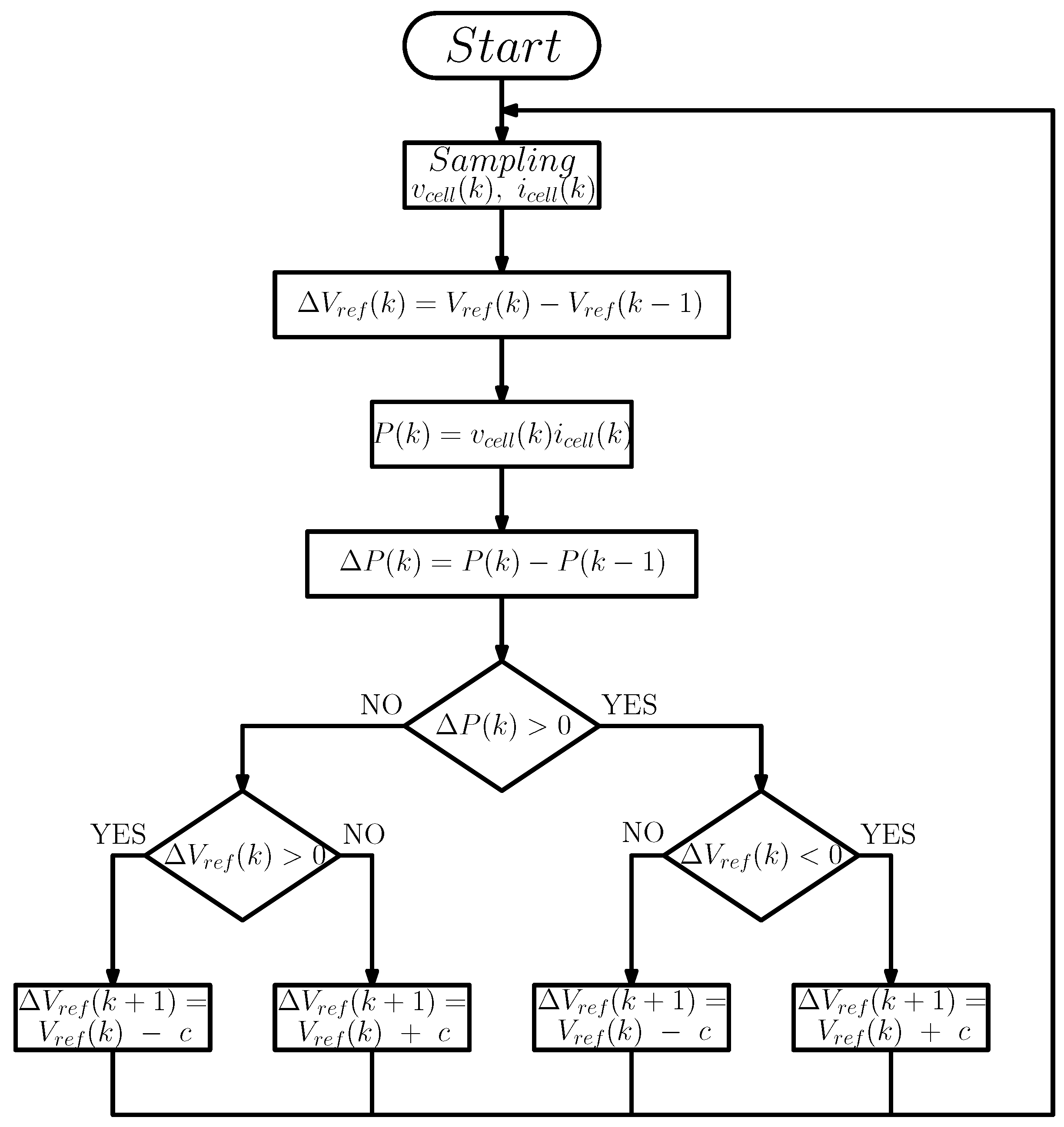
2.2. MPPT Algorithms Based on P&O
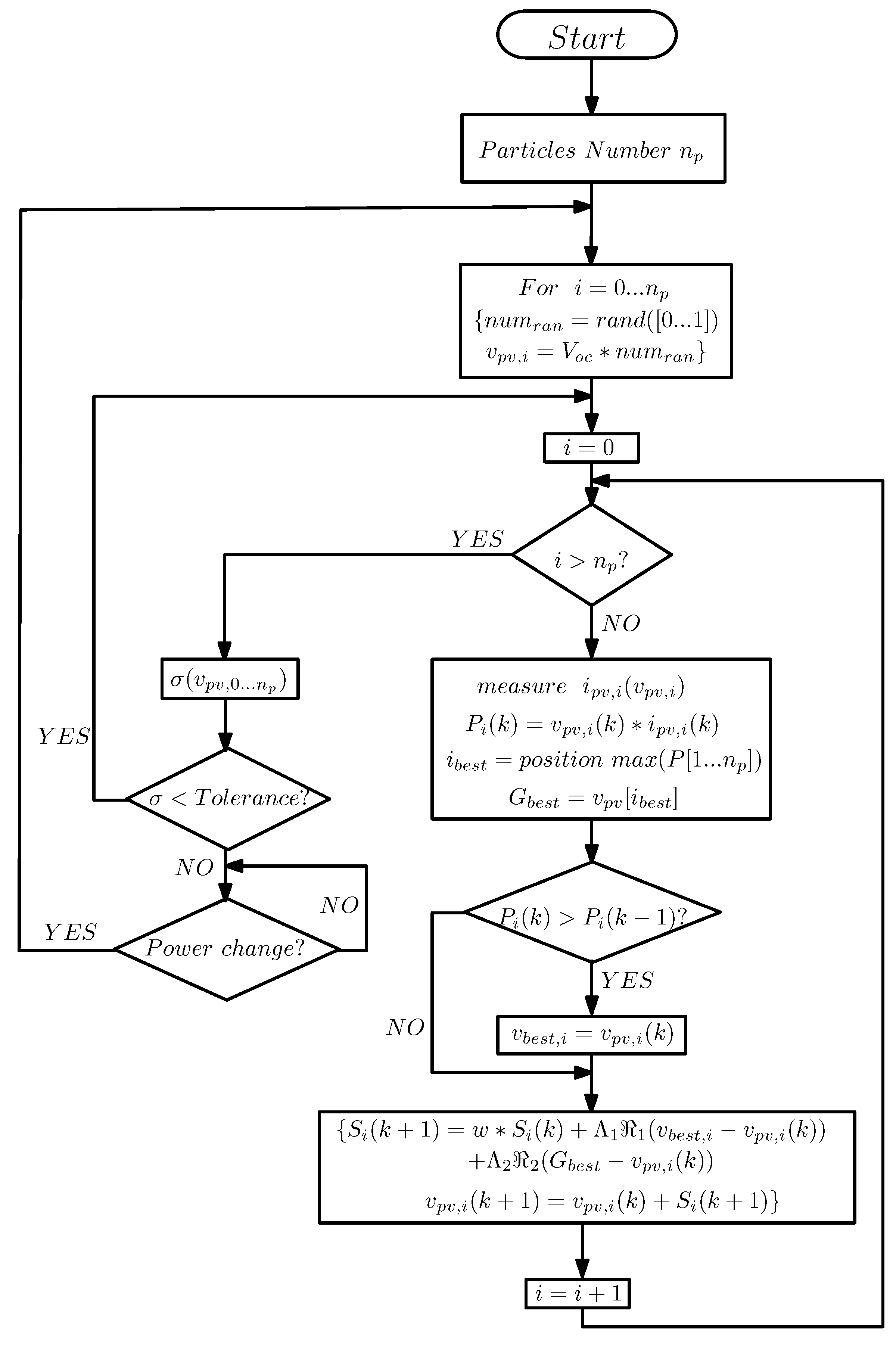
2.3. MPPT Algorithm Based on PSO
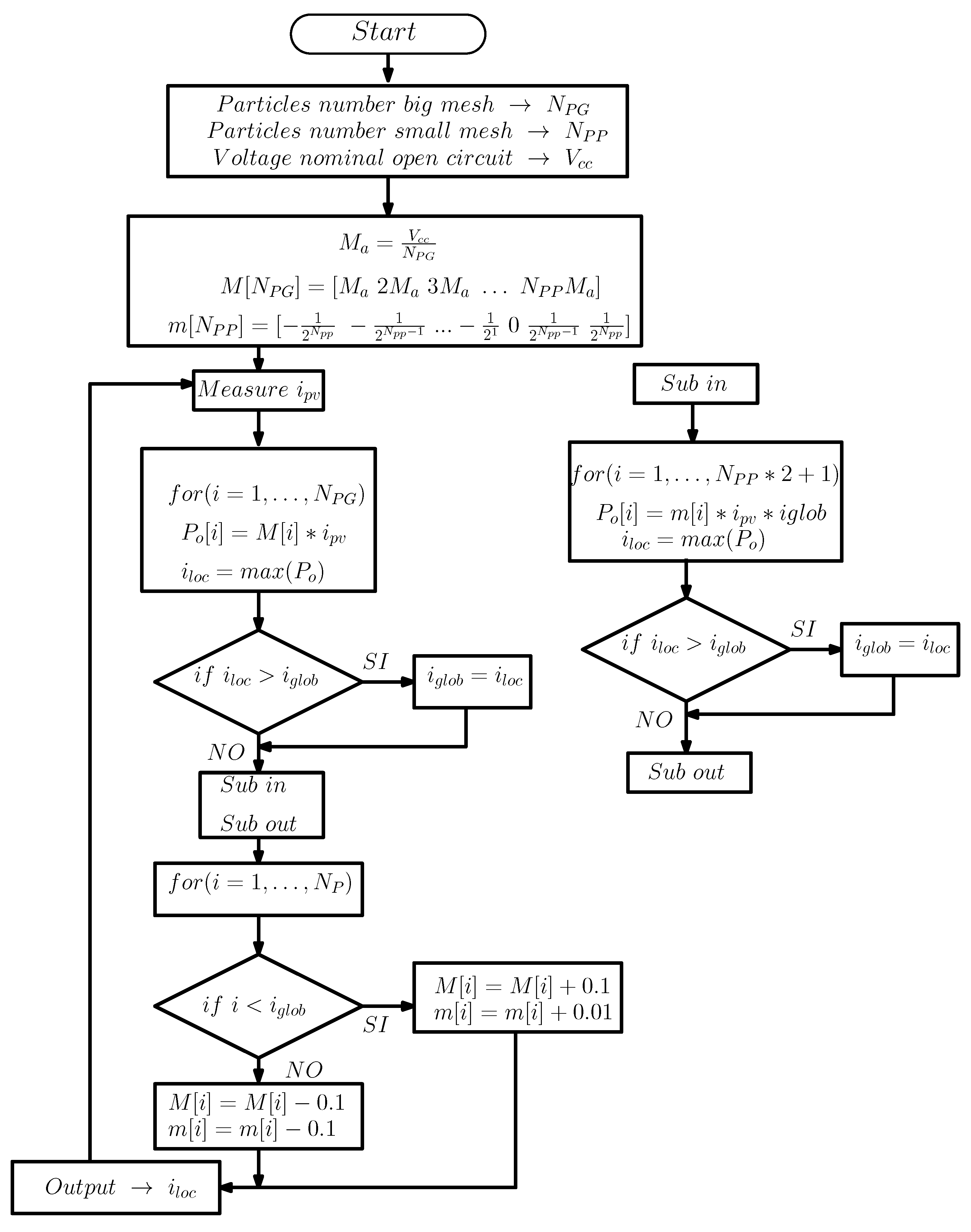
3. MPPT Algorithm Based on IPSM
3.1. Convergence Results of the IPSM
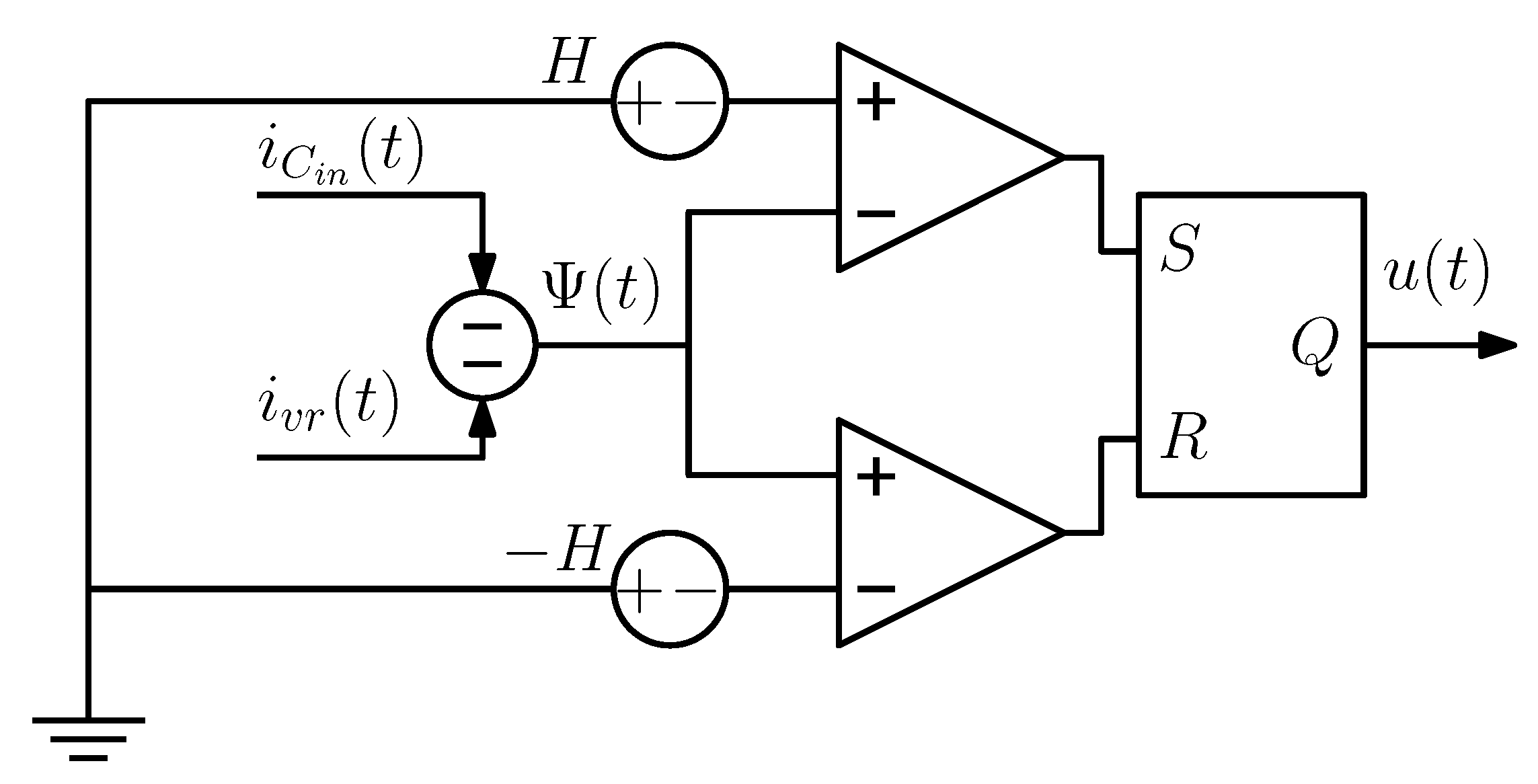
3.2. Sliding Mode Control
4. Results
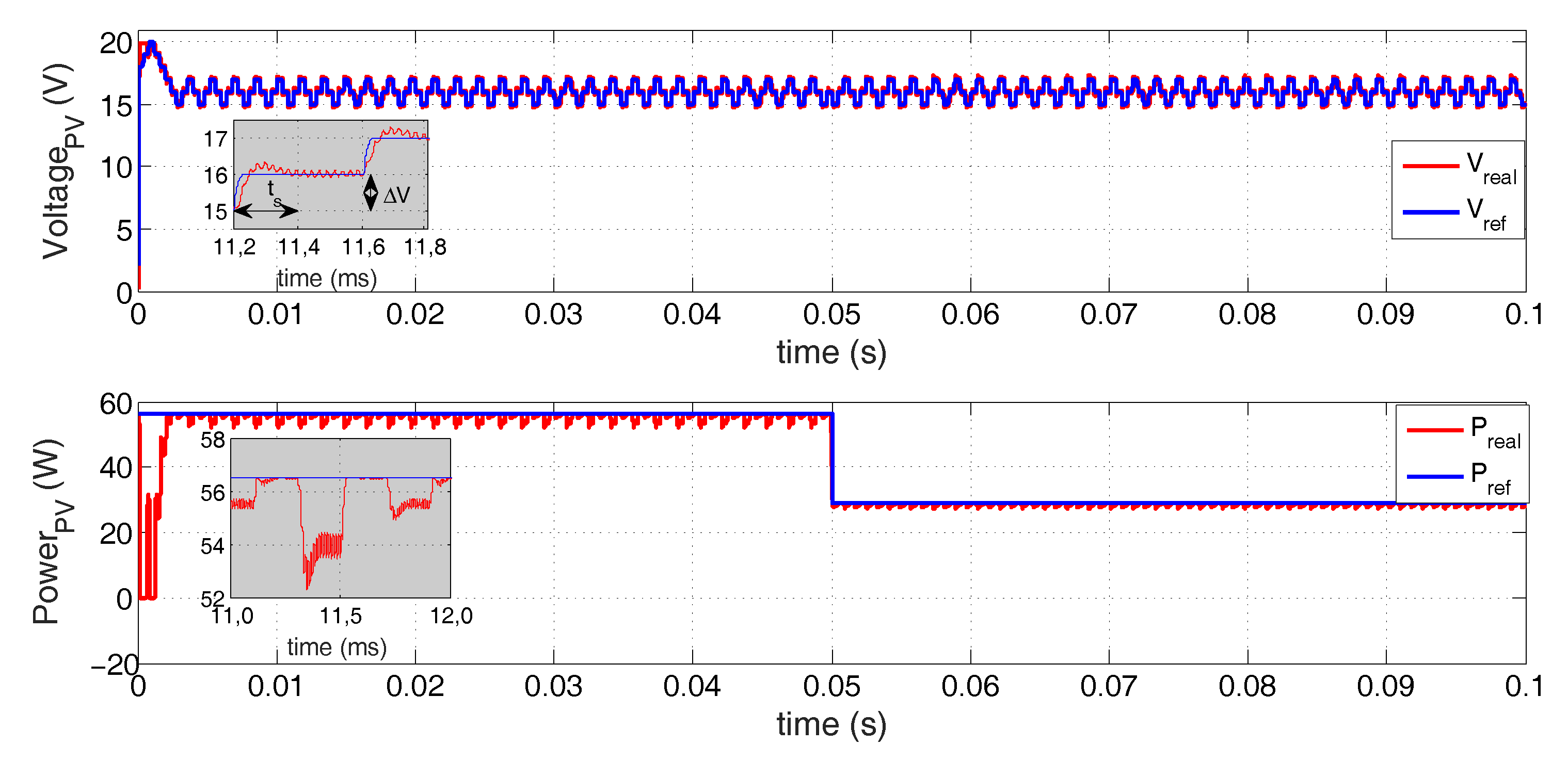
4.1. Response Using P&O
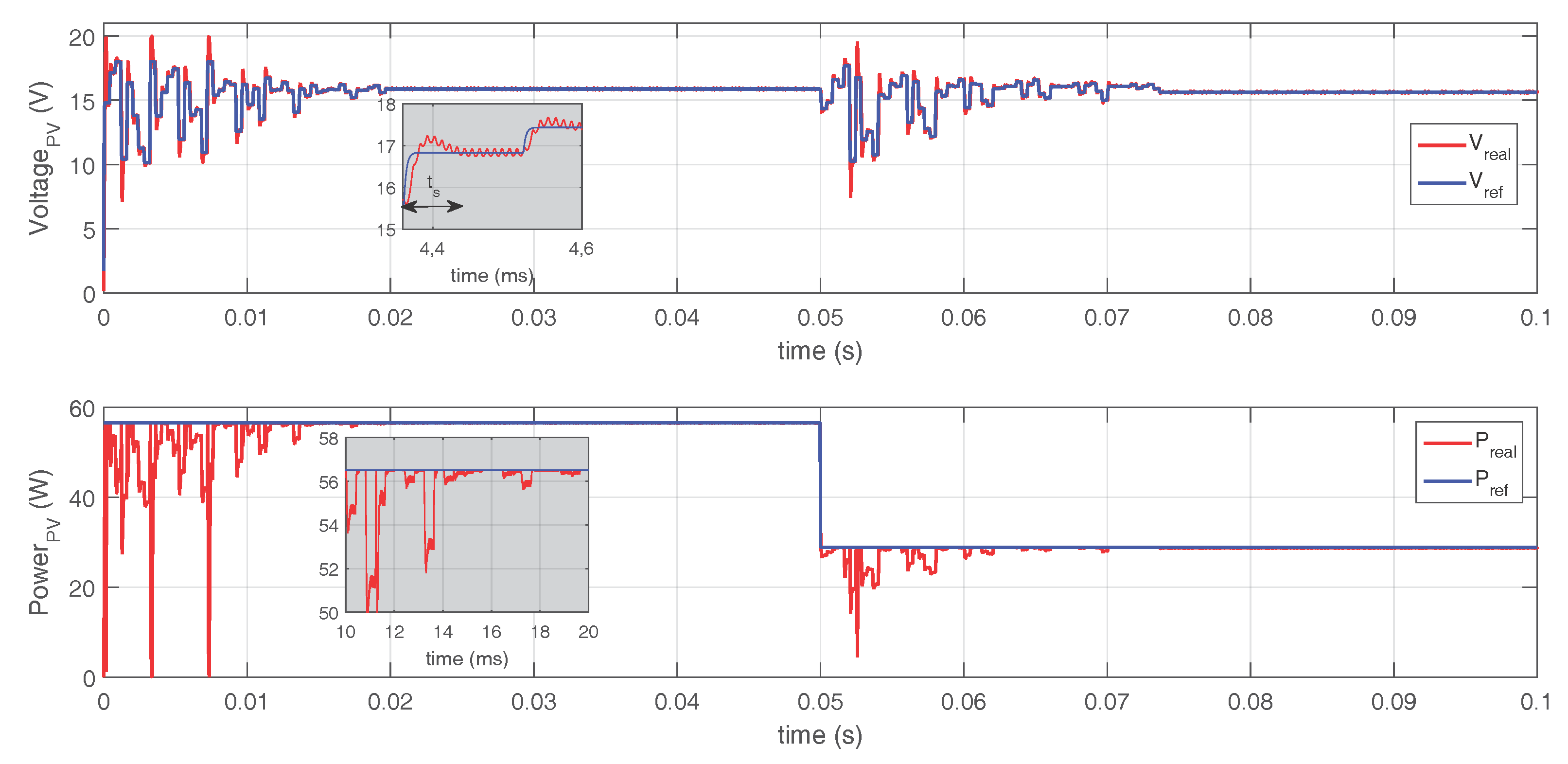
4.2. Response Using PSO
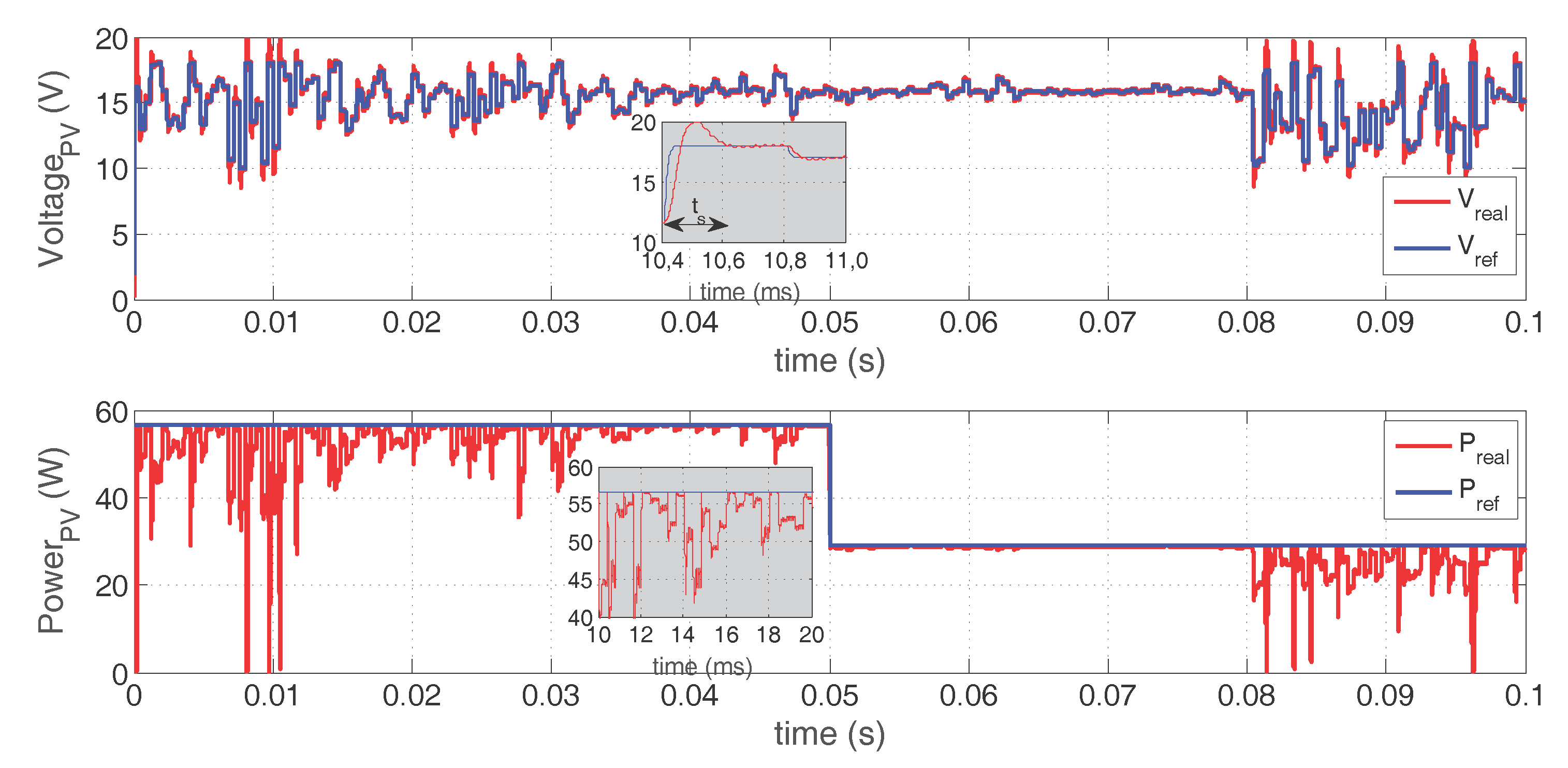
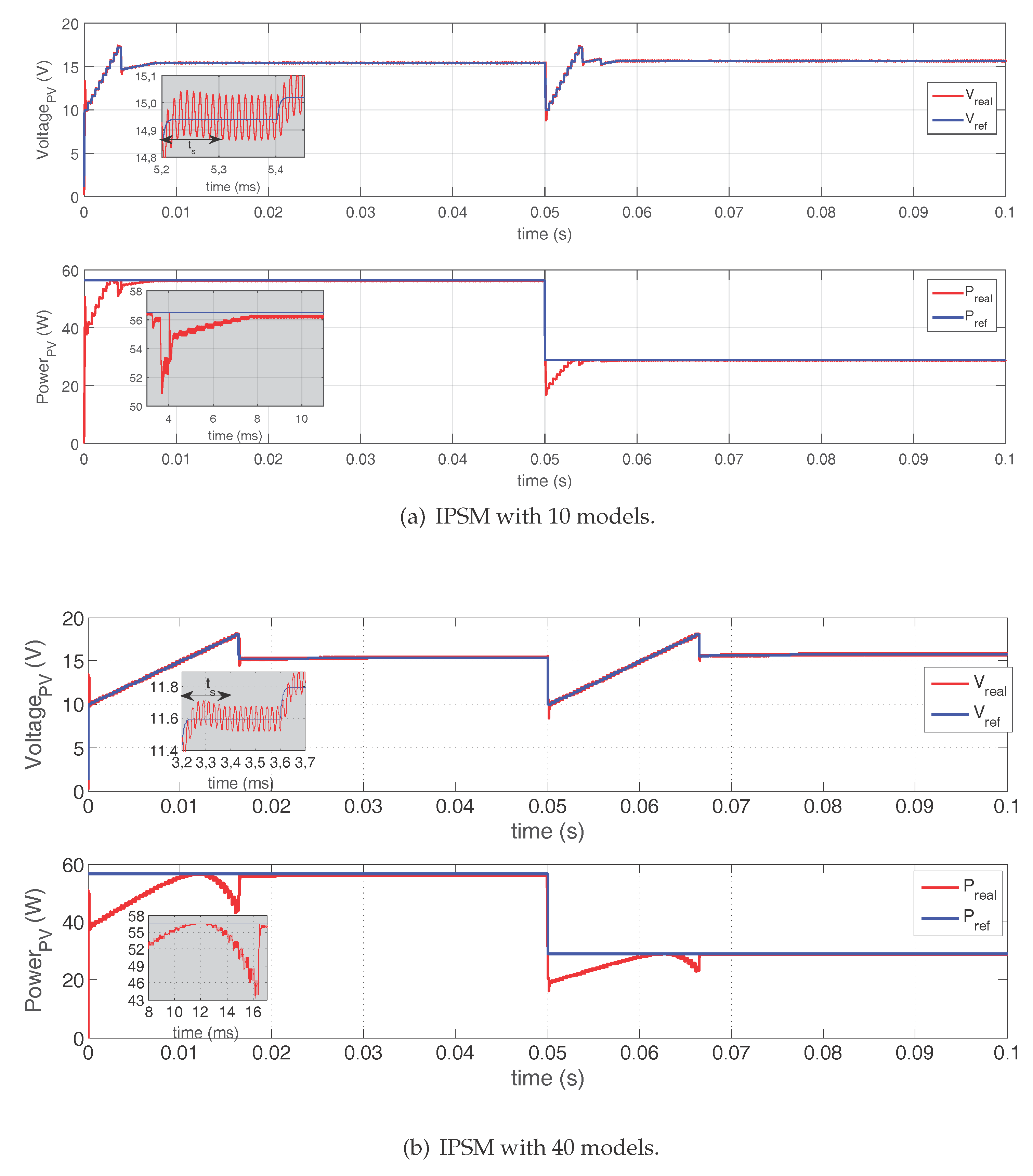
4.3. Response Using IPSM
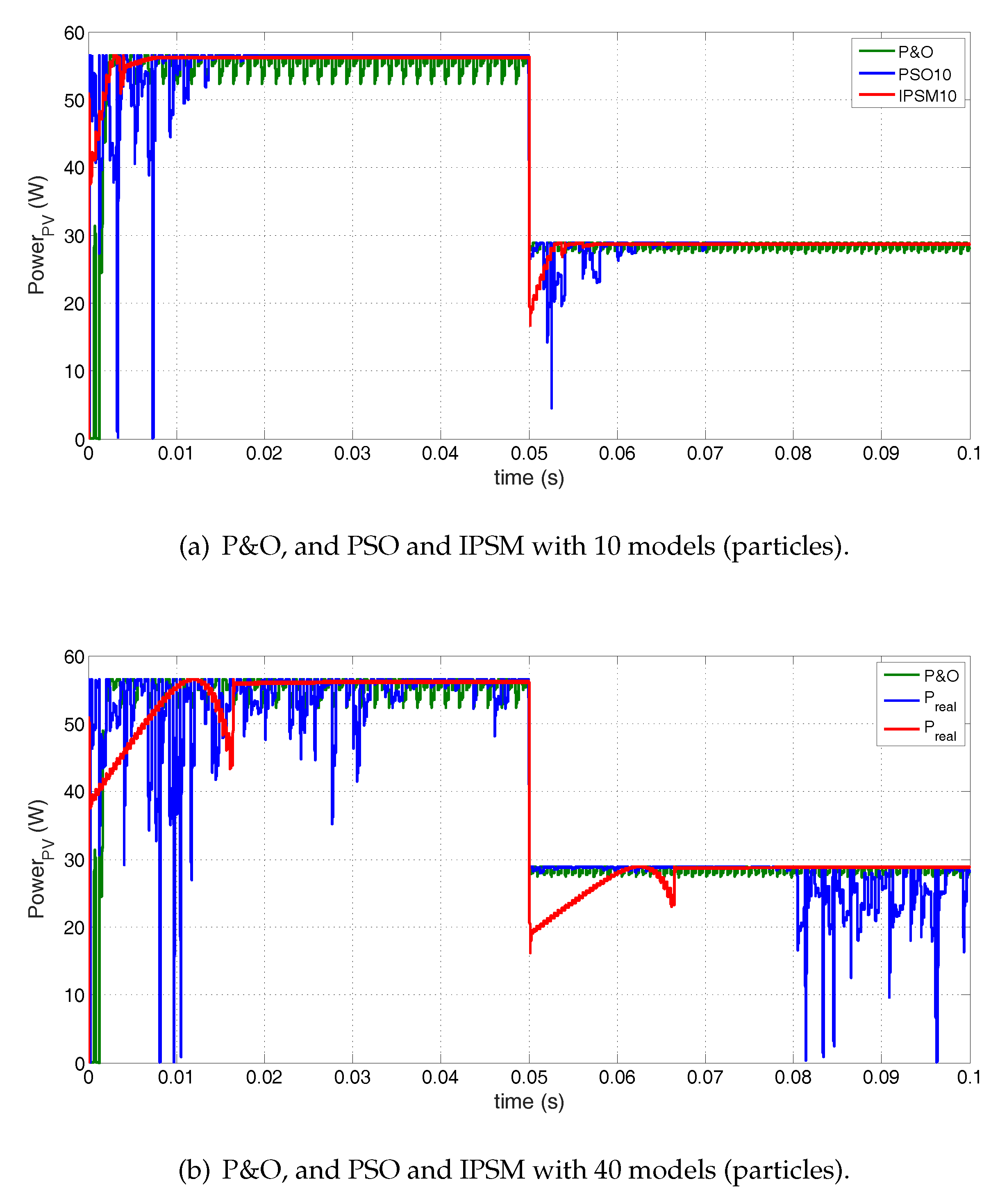
4.4. Comparative Analysis of MPPT Algorithms
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Karami, N.; Moubayed, N.; Outbib, R. General review and classification of different {MPPT} Techniques. Renew. Sustain. Energy Rev. 2017, 68, 1–18. [Google Scholar] [CrossRef]
- Masoum, M.A.S.; Dehbonei, H.; Fuchs, E.F. Theoretical and experimental analyses of photovoltaic systems with voltage- and current-based maximum power-point tracking. IEEE Trans. Energy Convers. 2002, 17, 514–522. [Google Scholar] [CrossRef]
- Schoeman, J.J.; Wyk, J.D. A simplified maximal power controller for terrestrial photovoltaic panel arrays. In Proceedings of the Power Electronics Specialists Conference, Cambridge, MA, USA, 14–17 June 1982; pp. 361–367. [Google Scholar]
- Yamashita, H.; Tamahashi, K.; Michihira, M.; Tsuyoshi, A.; Amako, K.; Park, M. A novel simulation technique of the PV generation system using real weather conditions. In Proceedings of the Power Conversion Conference, Osaka, Japan, 2–5 April 2002; Volume 2, pp. 839–844. [Google Scholar]
- Pan, C.T.; Chen, J.Y.; Chu, C.P.; Huang, Y.S. A fast maximum power point tracker for photovoltaic power systems. In Proceedings of the 25th Annual Conference of the IEEE Industrial Electronics Society, San Jose, CA, USA, 29 November–3 December 1999; pp. 390–393. [Google Scholar]
- Mulmule, A.; Vatti, R.; Porwal, P. MPPT Technique to improve efficiency in wind-solar hybrid system. Int. J. Electr. Eng. Technol. 2013, 4, 74–82. [Google Scholar]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Piegari, L.; Rizzo, R. Adaptive perturb and observe algorithm for photovoltaic maximum power point tracking. IET Renew. Power Gener. 2010, 4, 317–328. [Google Scholar] [CrossRef]
- Kazan, F.; Karaki, S.; Jabr, R.; Mansour, M. Maximum power point tracking using ripple correlation and incremental conductance. In Proceedings of the 47th International Universities Power Engineering Conference (UPEC), London, UK, 4–7 September 2012; pp. 1–6. [Google Scholar]
- Kish, G.; Lee, J.; Lehn, P. Modelling and control of photovoltaic panels utilising the incremental conductance method for maximum power point tracking. IET Renew. Power Gener. 2012, 6, 259. [Google Scholar] [CrossRef]
- Messalti, S.; Harrag, A.; Loukriz, A. A new variable step size neural networks {MPPT} controller: Review, simulation and hardware implementation. Renew. Sustain. Energy Rev. 2017, 68, 221–233. [Google Scholar] [CrossRef]
- Bahgat, A.; Helwa, N.; Ahmad, G.; Shenawy, E.E. Maximum power point traking controller for {PV} systems using neural networks. Renew. Energy 2005, 30, 1257–1268. [Google Scholar] [CrossRef]
- Kang, S.; Ko, J.; Choi, J.; Jang, M.; Mun, J.; Lee, J.; Chung, D. A Novel MPPT Control of photovoltaic system using FLC algorithm. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems (ICCAS), Gyeonggi-do, Korea, 26–29 October 2011; pp. 434–439. [Google Scholar]
- Liu, Y.H.; Liu, C.L.; Huang, J.W.; Chen, J.H. Neural-network-based maximum power point tracking methods for photovoltaic systems operating under fast changing environments. Solar Energy 2013, 89, 42–53. [Google Scholar] [CrossRef]
- Mellit, A.; Kalogirou, S.A. MPPT-based artificial intelligence techniques for photovoltaic systems and its implementation into field programmable gate array chips: Review of current status and future perspectives. Energy 2014, 70, 1–21. [Google Scholar] [CrossRef]
- Veerachary, M.; Yadaiah, N. ANN based peak power tracking for PV supplied DC motors. Solar Energy 2000, 69, 343–350. [Google Scholar] [CrossRef]
- Adly, M.; Besheer, A. A meta-heuristics search algorithm as a solution for energy transfer maximization in stand-alone photovoltaic systems. Int. J. Electr. Power Energy Syst. 2013, 51, 243–254. [Google Scholar] [CrossRef]
- Chiu, C. T-S Fuzzy Maximum Power Point Tracking Control of Solar Power Generation Systems. IEEE Trans. Energy Convers. 2010, 25, 1123–1132. [Google Scholar] [CrossRef]
- Larbes, C.; Cheikh, S.A.; Obeidi, T.; Zerguerras, A. Genetic algorithms optimized fuzzy logic control for the maximum power point tracking in photovoltaic system. Renew. Energy 2009, 34, 2093–2100. [Google Scholar] [CrossRef]
- Liu, C.L.; Chen, J.H.; Liu, Y.H.; Yang, Z.Z. An Asymmetrical Fuzzy-Logic-Control-Based MPPT Algorithm for Photovoltaic Systems. Energies 2014, 7, 2177–2193. [Google Scholar] [CrossRef]
- Salah, C.B.; Ouali, M. Comparison of fuzzy logic and neural network in maximum power point tracker for {PV} systems. Electr. Power Syst. Res. 2011, 81, 43–50. [Google Scholar] [CrossRef]
- Chowdhury, S.R.; Saha, H. Maximum power point tracking of partially shaded solar photovoltaic arrays. Solar Energy Mater. Solar Cells 2010, 94, 1441–1447. [Google Scholar] [CrossRef]
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
- Amine, H.M.; Abdelaziz, H.; Najib, E. Maximum Power Point Tracking Using IT2FL Tuned with GA. Energy Procedia 2015, 83, 399–407. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, X.; Gao, Z.; Ma, Y.; Qin, Z. A novel global maximum power point tracking strategy (GMPPT) based on optimal current control for photovoltaic systems adaptive to variable environmental and partial shading conditions. Solar Energy 2017, 144, 767–779. [Google Scholar] [CrossRef]
- Das, N.; Wongsodihardjo, H.; Islam, S. Modeling of multi-junction photovoltaic cell using MATLAB/ Simulink to improve the conversion efficiency. Renew. Energy 2015, 74, 917–924. [Google Scholar] [CrossRef]
- Jouda, A.; Elyes, F.; Rabhi, A.; Abdelkader, M. Optimization of Scaling Factors of Fuzzy—MPPT Controller for Stand-alone Photovoltaic System by Particle Swarm Optimization. Energy Procedia 2017, 111, 954–963. [Google Scholar] [CrossRef]
- Soufi, Y.; Bechouat, M.; Kahla, S. Fuzzy-PSO controller design for maximum power point tracking in photovoltaic system. Int. J. Hydrog. Energy 2017, 42, 8680–8688. [Google Scholar] [CrossRef]
- Yaqoob-Javed, M.; Faisal-Murtaza, A.; Ling, Q.; Qamar, S.; Majid-Gulzar, A. A novel MPPT design using generalized pattern search for partial shading. Energy Build. 2016, 133, 59–69. [Google Scholar] [CrossRef]
- Audet, C. Convergence results for generalized pattern search algorithms are tight. Optim. Eng. 2004, 5, 101–122. [Google Scholar] [CrossRef]
- Herrera, J.; Ibeas, A.; Alcántara, S.; de la Sen, M.; Serna, S. Identification and control of delayed SISO systems through pattern search methods. J. Frankl. Inst. 2013, 350, 3128–3148. [Google Scholar] [CrossRef]
- Herrera, J.; Ibeas, A.; de la Sen, M. Identification and control of integrative MIMO systems using pattern search algorithms: An application to irrigation channels. Eng. Appl. Artif. Intell. 2013, 26, 334–346. [Google Scholar] [CrossRef]
- Booker, A.J.; Dennis, J.J.E.; Frank, P.D.; Serafini, D.B.; Torczon, V.; Trosset, M.W. A rigorous framework for optimization of expensive functions by surrogates. Struct. Optim. 1999, 17, 1–13. [Google Scholar] [CrossRef]
- Bianconi, E.; Calvente, J.; Giral, R.; Mamarelis, E.; Petrone, G.; Ramos-Paja, C.A.; Spagnuolo, G.; Vitelli, M. A Fast Current-Based MPPT Technique Employing Sliding Mode Control. IEEE Trans. Ind. Electron. 2013, 60, 1168–1178. [Google Scholar] [CrossRef]
- Petrone, G.; Ramos-Paja, C.; Spagnuolo, G. Photovoltaic Sources Modeling; Wiley-IEEE: Hoboken, NJ, USA, 2017. [Google Scholar]
- Attivissimo, F.; Nisio, A.D.; Savino, M.; Spadavecchia, M. Uncertainty Analysis in Photovoltaic Cell Parameter Estimation. IEEE Trans. Instrum. Meas. 2012, 61, 1334–1342. [Google Scholar] [CrossRef]
- Ahmad, T.; Sobhan, S.; Nayan, M.F. Comparative Analysis between Single Diode and Double Diode Model of PV Cell: Concentrate Different Parameters Effect on Its Efficiency. J. Power Energy Eng. 2016, 4, 31–46. [Google Scholar] [CrossRef]
- Cuk, S.; Middlebrook, R. Advances in Switched-Mode Power Conversion Part I. IEEE Trans. Ind. Electron. 1983, 1, 10–19. [Google Scholar] [CrossRef]
- Middlebrook, R. Modeling current-programmed buck and boost regulators. IEEE Trans. Power Electron. 1989, 4, 36–52. [Google Scholar] [CrossRef]
- Wester, G.; Middlebrook, R.; Member, S. Low-Frequency Characterization of Switched dc-dc Converters. IEEE Trans. Aerosp. Electron. Syst. 1973, 3, 376–385. [Google Scholar] [CrossRef]
- Hussein, K.; Muta, I.; Hshino, T.; Osakada, M. Maximum photovoltaic power tracking: An algorithm for rapidly changing atmospheric conditions. Proc. Inst. Elect. Eng. 1995, 142, 59–64. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Ji, X.; Luo, X.; Wang, M.; Zhang, Y. A comparative study of the maximum power point tracking methods for PV systems. Energy Convers. Manag. 2014, 85, 809–816. [Google Scholar] [CrossRef]
- Nedumgatt, J.; Jayakrishnan, K.; Umashankar, S.; Vijayakumar, D. Perturb and Observe MPPT Algorithm for Solar PV Systems-Modeling and Simulation. In Proceedings of the 2011 Annual IEEE India Conference (INDICON), Hyderabad, India, 16–18 December 2011. [Google Scholar]
- Sridhar, R.; Selvan, N.T.; Jeevananthan, S.; Chowdary, P.S. Performance Improvement of a Photo Voltaic Array Using MPPT (P&O) Technique. In Proceedings of the 2010 IEEE International Conference on Communication Control and Computing Technologies (ICCCCT), Ramanathapuram, India, 7–9 October 2010; pp. 191–195. [Google Scholar]
- Salam, Z.; Ahmed, J.; Merugu, B. The application of soft computing methods for MPPT of PV system: A technological and status review. Appl. Energy 2013, 107, 135–148. [Google Scholar] [CrossRef]
- Soon, J.; Low, K.; Member, S. Photovoltaic Model Identification Using Particle Swarm Optimization with Inverse Barrier Constraint. IEEE Trans. Power Electron. 2012, 27, 3975–3983. [Google Scholar] [CrossRef]
- Herrera, J.; Ibeas, A.; De La Sen, M.; Rivera, E.; Peláez, J. Generalized Pattern Search Methods for control of stable, unstable and integrating systems with unknown delay under step input. Math. Comput. Simul. 2015, 115, 37–48. [Google Scholar] [CrossRef]
- Herrera, J.; Ibeas, A.; Alcántara, S. Identification and adaptive control of delayed unstable systems. In Proceedings of the 2010 IEEE International Symposium on Intelligent Control (ISIC), Yokohama, Japan, 8–10 September 2010; pp. 767–772. [Google Scholar]
- Audet, C.; Dennis, J.J.E. Mesh adaptive direct search algorithms for constrained optimization. SIAM J. Optim. 2006, 17, 188–217. [Google Scholar] [CrossRef]
- Trentelman, H.; Stoorvogel, A.A.; Hautus, M. Control Theory for Linear Systems; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Serna-Garcés, S.; Gonzalez Montoya, D.; Ramos-Paja, C. Sliding-Mode Control of a Charger/Discharger DC/DC Converter for DC-Bus Regulation in Renewable Power Systems. Energies 2016, 9, 245. [Google Scholar] [CrossRef]
- PSIM Tutorial: How to Use Solar Module Physical Model. Powersim Inc. Available online: https://powersimtech.com/drive/uploads/2016/04/Tutorial-Solar-Module-physical-model.pdf (accessed on 24 August 2017).
- MSX-60 and MSX-64 Photovoltaic Modules; Solarex: Frederick, MD, USA, 1997.

| Panel MSX-60 | Boost Converter | Controllers | MPPT |
|---|---|---|---|
| A V A V A Ω ω. | μF μH V kHz | μs A | μs V (P& O) V (40 p.) V (10 p.) LPF@20 kHz |
| 0.25 | 8.8 | 0.14% | 63.1 |
| 0.50 | 5.2 | 0.44% | 77.4 |
| 0.75 | 4.9 | 1.18% | 111.0 |
| 1.00 | 4.4 | 1.59% | 143.1 |
| 1.50 | 3.2 | 6.02% | 301.8 |
| PSO 10 P. | PSO 40 P. | |||
|---|---|---|---|---|
| Simulation | ts (ms) | Error MPP | Energy Losses (mJ) | Energy Losses (mJ) |
| 1 | 26.4 | 0.05% | 108.3 | 233.7 |
| 2 | 20.4 | 0.03% | 80.7 | 216.4 |
| 3 | 30.4 | 0.25% | 119.1 | 249.8 |
| 4 | 24.4 | 0.03% | 132.1 | 239.5 |
| 5 | 18.4 | 0.05% | 76.2 | 263.2 |
| 6 | 18.4 | 0.03% | 70.1 | 250.0 |
| 7 | 18.4 | 0.20% | 89.8 | 229.0 |
| 8 | 24.4 | 0.03% | 87.6 | 340.5 |
| 9 | 23.4 | 0.06% | 90.7 | 211.9 |
| 10 | 22.4 | 0.39% | 115.2 | 234.0 |
| Average | 22.70 | 0.11% | 96.98 | 246.80 |
| Models | |||
|---|---|---|---|
| 10 | 7.6 | 0.64% | 70.8 |
| 40 | 32.0 | 0.50% | 189.9 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tobón, A.; Peláez-Restrepo, J.; Villegas-Ceballos, J.P.; Serna-Garcés, S.I.; Herrera, J.; Ibeas, A. Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods. Energies 2017, 10, 1316. https://doi.org/10.3390/en10091316
Tobón A, Peláez-Restrepo J, Villegas-Ceballos JP, Serna-Garcés SI, Herrera J, Ibeas A. Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods. Energies. 2017; 10(9):1316. https://doi.org/10.3390/en10091316
Chicago/Turabian StyleTobón, Andrés, Julián Peláez-Restrepo, Juan P. Villegas-Ceballos, Sergio Ignacio Serna-Garcés, Jorge Herrera, and Asier Ibeas. 2017. "Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods" Energies 10, no. 9: 1316. https://doi.org/10.3390/en10091316
APA StyleTobón, A., Peláez-Restrepo, J., Villegas-Ceballos, J. P., Serna-Garcés, S. I., Herrera, J., & Ibeas, A. (2017). Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods. Energies, 10(9), 1316. https://doi.org/10.3390/en10091316







